当前位置：文档之家 › 大学物理实验有效数字

大学物理实验有效数字

  • 格式：ppt
  • 大小：647.50 KB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

大学物理实验绪论实验报告有效数字和数据处理

大学物理实验绪论实验报告有效数字和数据处理
读法：先读仪器能分辨的可靠数字，
再估计最小分度的下一位。
(a)分度值1mm
01 2 34
L=3.23cm
三位
(b)分度值1cm
0 1 2 34
L=3.2cm
二位
2、定步长仪器 如游标卡、数字显示仪表等
读法：最小步长量
3、等级仪器 如电压表、电流表等
读法：仪量程 等级 %
有效数字中的基本问题
1、有效数字位数越多，测量精度越高 米 尺： L=5.2 mm 游标卡尺： L=5.22 mm 千 分 尺： L=5.221 mm
(3)乘方、立方、开方运算 有效数字位数与底数的相同
7.88296.224 10.34510.171
(5)常数
不参与有效数字运算
数据处理的基本方法
一、列表法
表1 不同温度下的金属电阻值
n
1
2
3
4
5
6
7
t(C) 10.5 26.0 38.3 51.0 62.8 75.5 85.7
R() 10.423 10.892 11.201 11.586 12.025 12.344 12.670
作图步骤
1.选择坐标分度值，确定坐标纸大小
坐标分度值的应能基本反映测量值的准确度或精密度。 U 轴可选1mm对应于0.20V，I 轴可选1mm对应于0.40mA； 定坐标纸略大于数据范围（如130mm×130mm）。
1.选择坐标分度值，确定坐标纸大小
坐标分度值的应能基本反映测量值的准确度或精密度。 U 轴选1mm对应于0.20V，I 轴选1mm对应于0.40mA； 定坐标纸略大于数据范围（如130mm×130mm）。
弹 簧x(伸cm长)位71置(x2x1 x1)x2 (线理均xx3性量值3等连，。x间续求x24隔)变其地化间 x测的隔5 量物平(xx68xx7 7)x8

大学物理实验教学中有效数字运算的几点讨论

大学物理实验教学中有效数字运算的几点讨论

大学物理实验课是－ －／ ＇ ３ 基 础课程 ． 是学生进入大学的第一 门基础 实验课 ， 是后续实验课的基础 。这 门课程首先介绍测量误差及数据处 理 的基础知识 ， 其 中涉及到有效数字 的运算 。 在许多实验教材 中， 对有 效数 字运 算仅仅给出运算规则 、 结论性 的规则 ， 没有告诉初 学者规则 之 所以然 ： 而且 ． 有的文献谈及有效数字 运算过程 中对参 与运算的各 分量修约到第几位数尽不相同 、 甚 至不修约【 ｌ 】 。 运算结果保 留几位有效 位数说法不统一 。 使得初学者难 以理解 。 容易混淆 ， 不便记忆。 本文通
越小 。
一
大， 则在运算 过程中其余各分量及结果取三位， 有：
（ ３ ） 测量结果 的有 效数字位数 由不确定度 来确定 ． 测量值 的最后 位一般要与不确定度的最后 一位取齐 （ ４ ） 当不确 定度 的首位数字 ≤３ ， 不 确定度的有效数 字可取两位 ； 当首 位数字大于 ３ 时。 可只取一位有效数字日 。 （ ５ ） 间接测量量合成不确定度 的两个计算公式： 间接 测量量 Ｎ ＝ ｆ （ ｘ ， ， …， ％） ， 其中 。 ， ， …， 为若 干直接测
科技・ 瓣 ・ 争｜ Ｉ ｌ
Ｓ ｃ 科 ｉ ｅ ｎ ｃ ｅ ＆ 技 Ｔ ｅ ｃ ｈ 视 ｎ ｏ ｌ ｏ ｇ ｙ 界 Ｖ ｉ ｓ ｉ ｏ ｎ
大学物理实验教学中有效数字运算的几点讨论
唐文 强 （ 桂 林理 工大 学理 学院 ， 广 西 桂林 ５ ４ １ ０ ０ ４ ）
【 摘 要】 本文结合 笔者多年 的教 学体会 ， 通过列举实例探讨有 效数 字运算规则 ， 为初 学者加深对有效数字运算规 算术平 均值 ； 累积测量
＾ ｄ
例２ Ⅳ － ，其 中， ｌ ＝ ３ ９ ． ５ ， ２ ＝ ４ ． ０ ８ ４ ３ ７ ， ： ０ ． ０ ０ １ ３ ， ４ ＝ ８ ６ ７ ． ８ ， （ １ ） 对于一组测量 数据 ． 其结果可疑数 字所在位数越高不确 定度 求 Ｎ。 越大 。 （ ２ ） 对 于一组测 量数据 ． 其结果有效数 字位数越 多相对 不确定度 中 的有效数 字位数最少 ， 有两 位 ， 相对不确定度 最 。、 、 、

有效数字与不确定度

有效数字与不确定度

有效数字与不确定度1、大学物理角度解读“有效数字与不确定度”2、计量专业角度解读“有效数字与不确定度”大学物理角度解读“有效数字与不确定度”1.有效数字概念测量结果中从第一位非零数位算起，所有可靠数字和一位欠准数字统称为有效数字。

有效数字的个数则称为有效位数。

数字有效位数1.32545 624.675 56589Q 50.579 30.000982 30.21067 5注意点：①数值前面的"0”不是有效数字②有效位数不是“小数位数"③单位换算应保持有效位数不变把不同单位用10的不同次幕表示，从而保持有效数字不变。

如：3.7 m=3.7 x10 mm2.有效数字的相关规定直接测量的读数规则：可以估读的仪器一定要估读！5.737mm①可以估读的仪器一定要估读。

②按最小分度值的1/2、1/5或1/10估读。

游标类器具（游标卡尺，分光计度盘，大气压计等）读至游标最小分度的整数倍，即无需估读。

数显仪表及有十进步式标度盘的仪表（电阻箱、电桥，电位差计、数字电压表等）一般应直接读取仪表的示值。

（2）关于误差的规定①误差的有效位数一般取T立，最多取两位。

②测量结果的最后T航Z该和误差位对齐。

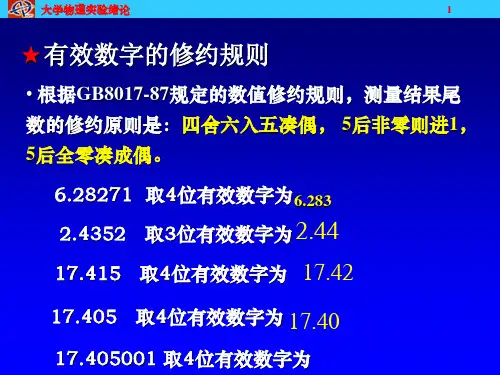
去尾方法：四舍六入五凑偶。

✓要舍弃的数字最左一位小于5时，舍去。

✓要舍弃的数字的最左一位大于5时（包括等于5且其后尚有非零的数）时，进1。

✓要舍弃数字最左一位是5，同时5后面没有数字或者数字全是0，若所保留的末位为奇数则进1，为偶数或者0则舍弃。

✓负数修约时先把绝对值按上述规定修约，然后在修约值前加负号。

有效数字（1）有效数字加减运算:最后结果的欠准数与参与运算的诸数中最先出现欠准数的位置对齐。

（2）有效数字乘除运算：最后结果的有效位数和乘（除）数中有效位数最少的相同。

（3）有效数字乘方及开方运算：最后结果的有效位数和底数的有效位数相同。

（4）有效数字对数运算：对数的有效位数和真数相同。

（5）有效数字常数运算：运算中它们的有效位数是任意的.（6）有效数字三角函数运算：三角函数的可疑数和角度的最小单位对应的那一位对齐。

大学物理实验教学中有效数字问题浅析

大学物理实验教学中有效数字问题浅析

第33卷第6期2020年12月大学物理实验PHYSICAL EXPERIMENT OF COLLEGEVol.33No.6Dec.2020文章编号：1007-2934(2020)06-0105-03大学物理实验教学中有效数字问题浅析李志刚1,张利巍1,陈凌云$,刘倩B(1.东北石油大学物理与电子工程学院，黑龙江大庆163318；2,石油工程学院，黑龙江大庆163318；3.大庆油田采油二厂第六作业区南三西工区，黑龙江大庆163000)摘要：有效数字的讲解是大学物理实验教学中必不可少的内容，不同的讲解方法会有不同的教学效果。

结合学生最常见的“长度测量”问题举例分析,既可以提高学生的学习兴趣，又可以加深学生的理解和印象，起到事半功倍的效果。

关键词：大学物理实验教学;有效数字;长度测量中图分类号:04-33文献标志码：A DOI:10.14139/22-122&2020.06.027张丽等从理论和实际两个角度对测量结果不确定度的有效数字位数取位问题进行了讨论⑴，唐文强讨论了有效数字运算规则⑵，段坤杰讨论了单次测量中有效数字的应用⑶，于金华等讨论了大学物理实验中电表及几项实验有效数字读取的方法⑷。

目前，尚无人对大学物理实验教学中有效数字的讲解问题进行讨论，根据20多年的教学经验,对这一问题提出浅显的分析，望广大读者批评指正。

1有效数字教学在大学物理实验中的重要性有效数字的应用领域非常广泛,李富恩、项念念、戴可、孙燕平等人在近几年的不同领域研究了有效数字问题［剧，因此，很多工科院校的学生在毕业后都有可能遇到有效数字问题。

有效数字的讲解是大学物理实验教学中必不可少的内容，而 在工科院校中，大学物理实验课程是很多学生系统学习有效数字问题的第一门课程。

因此，在大学物理实验课程教学中设计好有效数字问题的讲解方法，对于学生正确认识、理解有效数字问题,端正对待有效数字问题的态度至关重要。

2有效数字教学一般现状有效数字,测量定义:分析工作中实际能够测量到的数字；数学定义:在数学中,有效数字是指在一个数字中，从该数的第一个非零数字起，直到末尾数字止的数字称为有效数字。

3有效数字及其运算

3有效数字及其运算

37643÷217＝？ ÷ ＝？
结论： 结论： 乘除法运算： ⑵乘除法运算：最后结果有效数字的位数一般与诸因子 8 中有效数字位数最少者相同。 位数最少者相同 中有效数字位数最少者相同。
1 7 3.4 2 1 7⌡3 7 6 4 3 217 1594 1519 753 651 1020 868 152 运算结果： 运算结果：取173
第三节 有效数字及其运算
《大学物理实验》 大学物理实验》
三、确定测量结果有效数字的方法
1. 在大学物理实验中，测量结果有效数字一般只取一 在大学物理实验中， 位可疑数字即可， 位可疑数字即可， 测量结果的（不确定度）表示： 测量结果的（不确定度）表示：
u X = (x ± u) 单位 和 E = ⋅100% x
若不确定度 u＝0.1m，则 ，
x = 3.548m x = 3.5m
X = (3.5 ± 0.1) m = (3.5 ± 0.1) ×103 mm
11
第三节 有效数字及其运算
《大学物理实验》 大学物理实验》
例：以下表示正确与否？ 以下表示正确与否？ ＝（1.00±0.02）cm （正确） （1）L＝（ ） ＝（ ± ） 正确） ＝（360±0.5）µA （2）I＝（ ） ＝（ ± ） （错误） 错误）
4
第三节 有效数字及其运算
《大学物理实验》 大学物理实验》
一、有效数字：可靠数字＋存疑（可疑）数字 有效数字：可靠数字＋存疑（可疑）
6.遇到大数目或小数目时 ， 均可按科学记数法处理 ， 但 遇到大数目或小数目时， 均可按科学记数法处理， 遇到大数目或小数目时 要保持有效数字的位数不变，且含一位整数。 要保持有效数字的位数不变，且含一位整数。 例如： 例如：18.20 km＝?mm ＝ 不能写成18200000mm， ， 不能写成 而应写成1.820×107 mm。 × 而应写成 。

大物实验 有效数字

大物实验 有效数字
2.乘除法
3.乘方与开方 4.函数运算
对数函数 lgx结果的尾数与x的有效位数相同
例7
lg 100 = 2.000 lg 1.983 = 0.297322714 0.2973 lg 1983 = 3.29732714 3.2973
四、间接测量量有效数字的确定 ——有效数字的运算法则
1.加减法
（3）用误不确定度决定结果的有效数字
N 58 . 3 0 . 1 cm
2
N AB /C
其中：
A 3 . 21 0 . 01 cm , B 6 . 5 0 . 2 cm , C 21 . 843 0 . 00 c
试确定N的有效数字。
解：
（1）先计算N
2 A 2 B 2 C
测量值本身的大小、仪器的准确度
米尺 L=2.52cm （三位有效数字） 20分度游标卡尺 L=2.525cm （四位有效数字）
螺旋测微计 L=2.5153cm （五位有效数字）
4.误差和不确定度的有效数字
1. 系统误差、相对误差、修正值具有若干位可靠数字 和1位可疑数字；
如，某指针式电流表的仪器误差为1mA，零差为12mA，为2位有效数字；修正 值-12mA也是2位有效数字； 再如，重力加速度测量值 g=(9.685±0.004)m/s2, 公认值为 9.792m/s2 ，则绝 对误差-0.107m/s2为3位有效数字；相对误差Eg=-1.10%也是3位有效数字；
2.乘除法
3.乘方与开方 4.函数运算
5.自然数与常量
①自然数不是测量值，不存在误差， 故有效数字是无穷位。
如在D=2R中，2不是一位有效数字，而是无穷位
②常数、e等的位数可与参加运算的 量中有效数字位数最少的位数相同 或多取一位。

大物理论课实验6新4-5有效数字及数据处理

乘除运算后结果的有效数字一般以参与运算 各数中有效数字位数最少的为准。
– – – 例 5 3.21 6.5 = – 21 3.21 – 6.5 ————— –– ––
– ————— 结果为 21 –– ––
1605 – 1926
20.865
3.乘方与开方 结果的有效数字与其底或被开 运算规则：
②.小数点前面的“0” 和紧接 小数点后面的“0”不算作有效 数字
如：0.0123dm、0.123cm、0.00123m 均是3位有效数字。
注意：在十进制单位中，进行 单位换算时，有效数字的位数 不变。
（二）数值的科学记数法
数据过大或过小时，可以 用科学表达式。
某电阻值为20000（欧姆），保留三位有 效数字时写成 2.00104 又如数据为0.0000325 m，使用科学记数 法写成3.2510-5 m
f (H Z ) f S (H Z )
25.0 26.1 1.1
f ( H Z )
（二）作图规则
① 决定作图参量、选取坐标纸。
测量数据中的可靠数字在图上也应是可靠的，即图 纸上一小格对应数据中可靠数字的最后一位，而误 差位在小格之间估计。
坐标原点不一定与变量的零点一致。如果曲线上某一 段相对于x或y基本不变化，也可以省略这一部分（用 图线省略标记“∫∫”表示，如省略了一段的横线表示为 “—∫∫—”），以把有限的图幅用于其它部分。
U (V)
至此一张图才算完成
电阻伏安特性曲线
3. 校正曲线
举例：用电势差计校准量程为1mV的毫伏表， 测量数据如下（表中单位均为mV）。在如 图所示的坐标中画出毫伏表的校准曲线，并 对毫伏表定级别。
毫伏表读数 电势差计读数 修正值△U 毫伏表读数 电势差计读数 修正值△U 0.100 0.1050 0.005 0.600 0.6030 0.003 0.200 0.2150 0.015 0.700 0.6970 -0.003 0.300 0.3130 0.013 0.800 0.7850 -0.015 0.400 0.4070 0.007 0.900 0.8920 -0.008 0.500 0.5100 0.010 1.000 1.0070 0.007

大学物理实验课件有效数字和不确定度


•
→ L=（1.54±0.01） cm
相对不确定度
Euc x 10% 0（取两位有效数字）
x • 常用于比较不同测量结果的好坏，E越小，测量结果质量越好。例：
•
比较L1=(85.07±0.05)cm与L2=(3.246±0.005)mm测量结果的优劣。
•
EL1=0.05/85.07=0.059%，L2=0.005/3.246=0.15%
3. 本中心物理实验课程的设置 物理实验分两学期完成： 第一学期为基础实验，由 “测量不确定度及数据处理”和七个实验组成； 第二学期几十个实验分一般实验、独立完成实验和综合设计实验，可根据兴趣和所在学院的学分要求
选择。
实验选课及成绩查询网址: 校园网→教务处→学生园地→实验教学管理系统
4. 物理实验课的教学环节及要求 物理实验课由课前预习、课堂实际操作、课后完成实验报告三个基本教学环节组成。
•
待测量=（平均值±A类不确定度）单位
•
如：已测得同一电阻两端施加不同电压U 时产生的电流 I ，求电阻的阻值R （R = U / I）。
四、有效数字及其运算
1.
有效数字的概念
2.
有效数字的运算与修约
1. 有效数字的概念
• 测量结果中的所有可靠数字加上一位或两位有误差的数字（也称可疑数字）合称有效数字。 • 有效数字也是测量数据中有意义的数字，它在一定程度上反映了测量误差的存在。图中方块的长为
•
此单次测量的结果应写为：
•
L=（3.750±0.005）cm
多次直接测量
• 多次直接测量的结果可以表示为：
•
待测量 =（平均值±标准不确定度）单位
•
例2：用最小分度为0.01mm千分尺多次测量某圆柱体的直径 D，得到数据4.552mm、

大学物理实验1.10 有效数字

有效数字1. 有效数字的定义、读取方法实验中我们会遇到两类数字：一类是准确数字如确切的人数、个数、次数及公式中的常数等；另一类是测量结果。

测量得到的数字与被测量的实际大小相比，一般会存在误差。

为了使测量结果能反映被测量实际大小的全部信息，实验中的测量结果由可靠数字和欠准数位构成，需要用有效数字表示。

有效数字的定义是：从左起第一个非零数字起，到第一位欠准数位止的全部数字。

如：0. 00786是三位有效数字; 9.1乘以10的19次方，是两位有效数字; 1000mm是四位有效数字；1.0乘以10的3次方mm，是两位有效数字。

后面这两个例子告诉我们，从有效数字角度讲1000mm和1.0乘以10的3次方mm这两种写法所表示的长度信息是不同的。

前者的精确程度更好。

有效数字是测量结果的客观描述。

有效数字的位数是由具体的测量手段、测量方法、测量理论、测量环境等因素决定的。

人为地改变有效数字的位数，将失去客观描述的意义。

如何读取有效数字呢？用量具或仪器测得的数由两部分构成，一部分按仪器的刻度读出，可以读到它的最小刻度，这部分以刻度为依据，应视为准确的，称为可靠数字。

而最小刻度值以下的那一位，没有刻度为依据，是估读的，不够准确，称为欠准数位，两部分之和构成了测量得到的有效数字。

即有效数字= 可靠数字+ 1位欠准数字例如，用毫米刻度尺测某一物体长度，结果如图所示。

从尺上可准确读到15mm，并可看出真实长度在15mm到16mm之间，为使测量值更接近于真实值，在mm以下再估读一位，比如为0.2mm，则对物体长度测量得到的有效数字为15.2mm，它是三位有效数字，由两位可靠数字和一位欠准数字构成。

一般来说，在测量读数时，对于刻度为十分位的测量仪器，应读到最小分度的下一位。

如精度为mm的米尺可读到0.1mm位。

不过也有一些情况无需进行估读，仅需读到最小刻度所在位。

例如数字式仪表、电阻箱、最小分度值为0.2或0.5的仪器，还有一类等差细分仪器如游标卡尺，都不能估读到下一位。

有效数字大学物理

测量与有效数字1、有效数字的基本概念有效数字：实验时处理的数值，应是能反映出被测量的实际大小的数值，即记录与运算后保留的应为能传递出被测量实际大小信息的全部数字，这样的数字称为有效数字。

可靠数可疑数1.35 cm0.5 1.0 1.5[1] 位置介于35.7 — 35.8之间, 可以估计为35.75， 35.76，35.77，不妨取35.76cm 。

cm 35 36[3] [2] [1] [3] 位置为35.00cm ,不能写成 35cm 。

[2] 位置为35.40cm ,不能写成 35.4cm 。

对于直接测量，在仪器、仪表上读取数据时要读到Δ仪所在的那一位为止。

∆⨯==100mA0.1%0.1mA仪单位变换不应影响有效数字位数 有效数字的单位换算规则在记录时，由于选择单位不同，会出现一些“0”。

243.6010 3.6010m mμ-⨯=⨯m μ36000cm60.3m 0360.040.0006350.000002m (6.350.02)10m -±=±⨯215.74cm 5.37cm 84.5238cmS =⨯=cm74.15cm37.53、运算后的有效数字215.73cm 5.36cm 84.3128cm S =⨯=（1）根据不确定度确定有效数字的位数不确定度只取一位或二位有效数字，测量值有效数字的末位和不确定度末位对齐。

用单摆测得某地重力加速度：-2±=(⋅gcms)8.12.981①加减运算后的有效数字213.2516.7+ 0.124230.074 结果: 230.1 加减运算后有效数字的末位，应当和参加运算各数中最先出现的可疑位一致。

（2）有效数字的运算规则（2）有效数字的运算规则②乘除运算后的有效数字和参与运算各数中有效数字位数最少的相同。

3=.0⨯(三位)014÷25.78.052.00599897③乘方和开方运算结果的有效数字位数与其底数的有效数字位数相同。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
14
北方民族大学物理实验中心 Fundamental physics experiment
10
（1）加减运算 时，“尾数取齐”。 + 例如： 278.2+12.451=290.7。
1 2 3. 4 5 6
1. 1
1 2 4. 5 5 6
= 1 2 4. 6
（2）乘除运算时， “位数取齐”。 × 例如：5.438×20.5=111
1 2 3. 4 5 6 1. 1 12 3456
+ 123 456
5
3、游标类量具，读到卡尺分度值。
多不估读，特殊情况估读到游标分度值的一半。例
4、数字式仪表及步进读数仪器不需估读。例 5、特殊情况，直读数据的有效数字由仪器的灵敏 阈决定。 例如在“灵敏电流计研究”中，测临界电阻时，调 10 ”，仪器才刚有反应，尽管最小步 节电阻箱“ 进为0.1 ，电阻值只记录到“ 10 ”。 6、若测值恰为整数，必须补零，直补到可疑位。
12
（4）对数运算，小数点后的后面的位数取成与 真数的位数相同；例如：ln56.7=4.038 指数函数运算结果的有效数字中，小数点后的 位数取成与指数中小数点后的位数相同； 例如：
e9.14=1.03×104
(5)三角函数运算-试探法
sin 924 0.163325962 (计算器)
sin 925 0.163612937 (计算器)
例如：1.5kg可写成1.5×103g，不能写成1500g。 （5234±1）km应写成（5.234±0.001）×106m。
（0.000456±0.000003）s应写成（4.56±0.03）
×10-4s。
北方民族大学物理实验中心 Fundamental physics experiment
4
二、有效数字的读取
0在数字中间和末位有效,在小数点前面或紧接 小数点后的是无效的.
北方民族大学物理实验中心 Fundamental physics experiment
3
（3）测量结果的科学表示方法
测量结果的表示，一般应采用科学表示法，即用有
效数字乘以10的幂指数的形式来表示。一般小数点前
只取一位数字，幂指数不是有效数字。
8
北方民族大学物理实验中心 Fundamental physics experiment
返回 9
三.有效数字的运算规则
准确数字 准确数字
与
准确数字 可疑数字
准确数字 可疑数字 可疑数字
与
可疑数字
最终结果
与
可疑数字
只保留一位可疑数字
北方民族大学物理实验中心 Fundamental physics experiment
1 3 5. 8 0 1 6
= 1 .4×102
北方民族大学物理实验中心 Fundamental physics experiment
11
(3)乘方、立方、开方
有效数字位数与底数的相同
7.889 62.24
2
103.45 10.171
北方民族大学物理实验中心 Fundamental physics experiment
sin 924 0undamental physics experiment
13
四、舍入法则
有效数字的修约规则
四舍六入五凑偶
对算术平均 值
规 则
两位： 1.2
5下舍去5上入，整5前位凑偶数
1.2499 1.25001 1.3 1.250 1.2 1.350 1.4 1.050 1.0
北方民族大学物理实验中心 Fundamental physics experiment
6
53.0mv
53.5mv
读数 5.454mm
返回
北方民族大学物理实验中心 Fundamental physics experiment
7
13+0.34=13.34mm 13mm
17×0.02=0.34mm
北方民族大学物理实验中心 返回 Fundamental physics experiment
§3.有效数字的记录与计算
一．有效数字的概念
1．有效数字定义及其意义
先看一个例子：用米尺（最小刻度是1mm） 测量钢棒的长度:4.26cm，4.27cm，或 4.28cm？
“4.2” -确切数字 6、7、8（第三位数） ——可疑数字 L=4.2 ？ cm 北方民族大学物理实验中心
Fundamental physics experiment
进行直接测量时，由于仪器多种多样，正确读 取有效数字的方法大致归纳如下：
1、指针式仪表及其它器具，读数时估读到仪器 最小分度的1/2, 1/5,1/10 。例
2、有时读数的估计位，就取在最小分度位。
例如，仪器的最小分度值为0.5，则0.1-0.4,0.6-0.9都 是估计的，不必估到下一位。
北方民族大学物理实验中心 Fundamental physics experiment
1
有效数字:
所有准确数字和一位可疑数字
有效数字的意义：
其位数反映所使用仪器的测量精度 和测量结果的准确度。
北方民族大学物理实验中心 Fundamental physics experiment
2
有效数字的特点
（1）位数与小数点的位置无关。 35.76cm = 0.3576m = 0.0003576km （2）0 的地位 0.0003576 3.005 3.000 都是四位