晶体密度的计算
- 格式:ppt
- 大小:960.00 KB
- 文档页数:15

5、已知Mg2+半径为0.072nm,O2-半径为0.140nm,计算MgO晶体结构的堆积系数(球状离子占据晶胞的体积分数)与密度。
解一和解二对晶胞参数棱长有不同解法,那种正确?解一:MgO为NaCl型,O2-做密堆积,Mg2+填充空隙。
r O2- =0.140nm,r Mg2+=0.072nm,z=4,a=2(r++r-) =0.424nm晶胞中质点体积:(4/3×πr O2-3+4/3×πr Mg2+ 3)×4,,晶胞体积=a3,堆积系数=晶胞中MgO体积/晶胞体积=68.5%,密度=晶胞中MgO质量/晶胞体积=3.49g/cm3。
(认为阴阳离子紧密接触)解二:在MgO晶体中,O2-采用面心立方密堆积,Mg2+填入空隙中。
在面心立方中,八个顶点的原子分别被八个晶胞共享,所以每个晶胞只占有八分之一,六个面心的原子分别被两个晶胞共享,每个晶胞占有二分之一,这样八个八分之一和六个二分之一加起来就是四,也就是每个晶胞中有4个O2-,相应地也就有4个Mg2+,这样就可以计算出每个晶胞的质量。
然后根据O2-的半径可以计算晶胞的体积和离子的体积,注意六面体两个相邻顶点的原子不是直接接触的,只有对角线方向的原子(O原子)是直接接触的,因此计算棱长的时候先计算对角线长度(即4倍的离子半径),然后再计算棱长。
晶胞质量m=(24.3+16.0)g/mol*4÷6.02*10^23/mol=2.68*10^-22g 注意相对原子质量在数之上等于摩尔质量,直接计算得到的是1mol晶胞的质量,需要除以阿伏加德罗常数。
面对角线长度L=4r=0.140nm*4=0.560nm晶胞参数(即棱长)a=L*sin45=0.396nm晶胞体积V=a^3=0.0621nm3=6.21*10^-23cm3密度ρ=m/V=4.31g/cm3根据球形体积公式计算O2-、Mg2+体积分别为0.0115nm3、0.00156nm3,故晶胞中离子总体积为(0.0115nm3+0.00156nm3)*4=0.0522nm3堆积系数=0.0522/0.0621=84.2%(认为阴离子紧密接触。

晶胞密度计算公式是MZ/NAV,利用晶胞参数可计算晶胞体积(V),根据相对分子质量(M)、晶胞中粒子数(Z)和阿伏伽德罗常数NA,可计算晶体的密度。
晶胞是能完整反映晶体内部原子或离子在三维空间分布之化学-结构特征的平行六面体最小单元。
其中既能够保持晶体结构的对称性而体积又最基本特称“单位晶胞”,但亦常简称晶胞。
例题
.干冰晶胞是一个面心立方体,在该晶体中每个顶角各有1个二氧化碳分子,每个面心各有一个二氧化碳分子,实验测得-25℃时干冰晶体的晶胞边长为acm,其摩尔质量为Mg/mol,则该干冰晶体的密度为(单位:g/cm3)()
干冰晶胞是面心立方晶胞,所以每个晶胞中含有二氧化碳分子个数=8×1818+6×1212=4,晶胞边长为acm,则体积为a3cm3,晶胞密度=MNA×4V MNA×4V.解答解:干冰晶胞是面心立方晶胞,所以每个晶胞中含有二氧化碳分子个数=8×1818+6×1212=4,晶胞边长为acm,则体积为a3cm3,晶胞密度=MNA×4V MNA ×4V=MNA×4a3MNA×4a3g/cm3=4Ma3N A4Ma3NA g/cm3,故选D.
点评本题考查晶胞计算,侧重考查分析计算及空间想象能力,利用均摊法计算晶胞中二氧化碳分子个数,知道密度公式中各个字母含义,题目难度不大.。


面心立方致密度计算过程
面心立方结构是一种晶体结构,它由六个面上有原子的正方形构成。
每个原子周围都有12个最近邻原子,其中6个在同一平面上,另外6个在相邻平面上。
计算面心立方晶体的密度需要从晶体结构的参数开始。
首先,需要知道晶格常数,表示晶体中单元格的大小。
对于面心立方结构,晶体中一个原子与其最近邻原子之间的距离为a/√2,其中a是晶格常数。
然后需要计算晶体中每个原子的质量,通常可以从元素周期表中获得。
假设晶体中有一种元素,则每个原子的质量为m。
接下来,需要知道每个原子的数量,通常由晶体的化学式提供。
最后,可以使用以下公式计算面心立方结构的密度ρ:
ρ= (Z ×m) / (a^3 ×N_A)
其中,Z是晶胞中原子的数量,a是晶格常数,N_A是阿伏伽德罗常数。
需要注意的是,这个公式仅适用于理想情况下的面心立方结构,而实际晶体中可能会存在缺陷或空位,这可能会影响密度的计算结果。

晶体的密度知识点总结一、密度的定义密度是一个物质单位体积中的质量,通常用g/cm³或kg/m³来表示。
密度是一个物质的固有属性,它与物质的种类和状态都有关系。
二、晶体的结构晶体是由原子、离子或分子在晶格结构中有序排列而成的固体,晶体的结构由晶格和晶格中的原子、离子或分子构成。
1. 立方晶系在立方晶系中,晶格是由等长、相互垂直的三条边界定的,晶格中的原子、离子或分子分别负责构成了简单立方晶系、面心立方晶系和体心立方晶系。
2. 其他晶系除了立方晶系以外,晶体还包括六方晶系、四方晶系、三方晶系和斜方晶系。
每一种晶系都由特殊的晶格结构和原子、离子或分子构成。
三、密度与晶体结构之间的关系晶格的尺寸和晶体结构对晶体的密度有着重要的影响。
晶体的密度是其晶格参数和元素质量决定的。
1. 晶格参数和密度晶格参数是指晶格的几何参数,包括晶格常数和晶胞体积。
晶格常数是指晶格中原子(离子或分子)之间的距离,它与晶体的密度有直接关系。
晶胞体积是晶格中一个晶胞的体积,它是晶体密度的重要参量。
2. 元素质量和密度元素的质量是影响晶体密度的另一个重要因素。
在晶体中,元素的原子质量越大,对应的晶体密度也会越大。
晶体中所含元素的种类和质量配比也会直接影响晶体的密度。
四、密度的测定方法晶体密度的测定是由晶体结构分析和物理化学性质测定两种方法来进行的。
1. 晶体结构分析X射线晶体衍射是晶体结构分析的重要方法。
它是利用X射线在晶体中的衍射现象来测定晶体的晶格参数和原子位置,从而间接得到晶体密度。
2. 物理化学性质测定物理化学性质测定是直接测定晶体的密度。
这种方法包括比重瓶法、气体置换法、卧式浮力法和压力法等。
五、密度的应用晶体的密度对材料科学和化学领域有着重要的应用价值。
1. 材料科学晶体的密度是其关键的材料物性之一,它反映了材料的紧密程度。
晶体密度的测定可以为材料的制备、性能评价和应用提供重要的参考依据。
2. 化学领域在化学领域,物质的密度不仅影响着物质的物性,还用于物质的定性和定量分析。



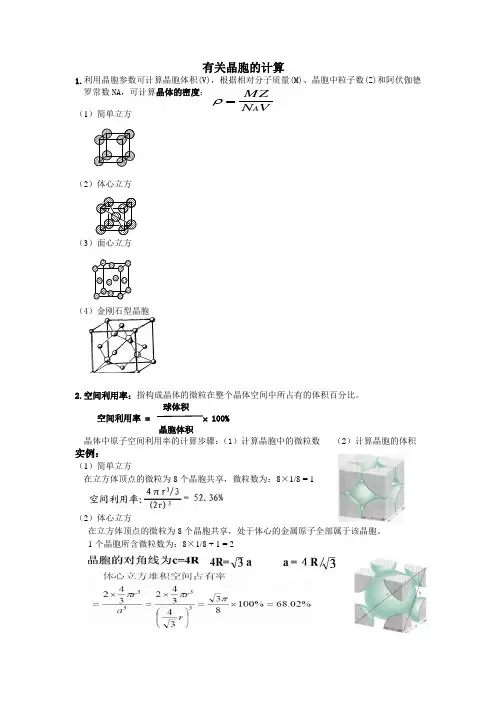
有关晶胞的计算
1.利用晶胞参数可计算晶胞体积(V),根据相对分子质量(M)、晶胞中粒子数(Z)和阿伏伽德罗常数NA,可计算晶体的密度:
(1)简单立方
(2)体心立方
(3)面心立方
(4)金刚石型晶胞
球体积
空间利用率 = 100%
晶胞体积
晶体中原子空间利用率的计算步骤:
(1)计算晶胞中的微粒数(2)计算晶胞的体积
实例:
(1)简单立方
在立方体顶点的微粒为8个晶胞共享,微粒数为:8×1/8 = 1
(2)体心立方
在立方体顶点的微粒为8个晶胞共享,处于体心的金属原子全部属于该晶胞。
1个晶胞所含微粒数为:8×1/8 + 1 = 2
晶胞的对角线为C=4R
V
N
MZ
A
=
ρ
(3)面心立方
在立方体顶点的微粒为8个晶胞共有,在面心的为2个晶胞共有。
1个晶胞所含微粒数为:8×1/8 + 6×1/2 = 4
空间占有率为
(4)金刚石型晶胞
金刚石晶胞是面心立方堆完之后还在四个四面体里有原子
原子半径和晶胞边长的契合点在于体对角线上连着排了四个原子,所以是8个半径等于根号3个边长
所以a:r=8:根号3。

几种碳晶体理论密度的计算
碳晶体理论密度的计算是一个重要的物理问题,用于研究晶体的性质和结构。
根据碳晶体结构,可以分别采用不同的理论密度计算方法来计算碳晶体的理论密度。
主要有以下几种:
1. Weber-Fechner定律
Weber-Fechner定律通过研究碳晶体中晶体尺寸与碳晶体表面能的关系来计算理论密度。
该方法计算结果较为准确,等于自由空气中气体分子理论密度的2/3。
2. 分子理论
分子理论可以用来计算碳晶体的密度,通过研究晶体尺寸、气体分子体积和碳晶体的分子张力来计算理论密度。
该方法计算结果比Weber-Fechner定律更加准确,通常等于空气中气体分子理论密度。
3. 贝尔定律
贝尔定律也可以用来计算碳晶体的理论密度。
该方法通过研究晶体内成分分子数量、分子大小和分子尺寸之间的关系来计算理论密度。
该方法计算出来的密度要比Weber-Fechner定律要精确得多,一般等于自由空气中空气分子理论密度的3/4。
4. 計量定律
計量定律是根据碳晶体的性质,以及晶体中的元素的性质,计算碳晶体理论密度的一种方法。
该方法可以从分子团簇的数量、碳晶体表面特性及相对论效应中推断出晶体密度,而不用考虑晶体尺寸和自由空气中气体分子的理论密度。
总之,Weber-Fechner定律、分子理论、贝尔定律和计量定律都是用于计算碳晶体的理论密度的不同方法。
它们的结果有所不同,但都对研究碳晶体结构和性质具有重要意义。
因此,精确的理论密度计算方法对碳晶体的研究起着至关重要的作用。
有关晶胞的计算1.利用晶胞参数可计算晶胞体积(V),根据相对分子质量(M)、晶胞中粒子数(Z)和阿伏伽德罗常数NA,可计算晶体的密度:(1)简单立方(2)体心立方(3)面心立方(4)金刚石型晶胞2.球体积空间利用率 = ⨯ 100%晶胞体积晶体中原子空间利用率的计算步骤:(1)计算晶胞中的微粒数(2)计算晶胞的体积实例:(1)简单立方在立方体顶点的微粒为8个晶胞共享,微粒数为:8×1/8 = 1(2)体心立方在立方体顶点的微粒为8个晶胞共享,处于体心的金属原子全部属于该晶胞。
1个晶胞所含微粒数为:8×1/8 + 1 = 2VNMZA=ρ(3)面心立方在立方体顶点的微粒为8个晶胞共有,在面心的为2个晶胞共有。
1个晶胞所含微粒数为:8×1/8 + 6×1/2 = 4【练习】1.CaO与NaCl的晶胞同为面心立方结构,已知CaO晶体密度为ag·cm-3,N A表示阿伏加德罗常数,则CaO晶胞体积为__________cm32.金属钨晶体为体心立方晶格,实验测得钨的密度为19.30 g・cm-3,原子的相对质量为183假定金属钨原子为等径的刚性球。
(1)试计算晶胞的边长;(2)试计算钨原子的半径。
3. ZnS晶体结构如下图所示,其晶胞边长为540.0pm,其密度为g·cm-3,a位置S2-离子与b位置Zn2+离子之间的距离为 pm。
4.已知铜晶胞是面心立方晶胞,铜原子的半径为 3.62⨯10-7cm,每一个铜原子的质量为1.055⨯10-23g(1)利用以上结果计算金属铜的密度(g·cm-3)。
(2)计算空间利用率。

晶体密度的计算公式
晶体密度计算公式是p=NM/(V×NA),晶体(crystal)是由大量微观物质单位(原子,离子,分子等)按一定规则有序排列的结构,因此可以从结构单位的大小来研究判断排列规则和晶体形态。
密度是对特定体积内的质量的度量,密度等于物体的质量除以体积,可以用符号ρ表示,国际单位制和中国法定计量单位中,密度的单位为千克/米。
晶体(crystal)是原子、离子或分子按照一定的周期性,在结晶
过程中,在空间排列形成具有一定规则的几何外形的固体。
其分布非常广泛,自然界的固体物质中,绝大多数是晶体。
气体、液体和非晶物质在一定的合适条件下也可以转变成晶体。
晶体特征
(1)自然凝结的、不受外界干扰而形成的晶体拥有整齐规则的几
何外形,即晶体的自范性。
(2)晶体拥有固定的熔点,在熔化过程中,温度始终保持不变。
(3)单晶体有各向异性的特点。
(4)晶体可以使X光发生有规律的衍射。
宏观上能否产生X光衍射现象,是实验上判定某物质是不是晶体的主要方法。
(5)晶体相对应的晶面角相等,称为晶面角守恒。
1。
化学晶胞密度单位换算
化学结构是物质研究中的重要组成部分,其中晶胞密度是一项基
础性质。
晶胞密度是指晶体中每个晶胞所占的体积大小,通常用单位
体积的质量来表示。
密度的计算常用单位有克/立方厘米、克/立方米、克/毫升等。
化学中的晶胞密度单位换算是非常重要的,在化学研究中必须掌握。
以下就为大家介绍几种常用的晶胞密度单位换算方法。
克/立方厘米与克/立方米的转换:克/立方厘米表示晶体中每个
立方厘米所占的质量,而克/立方米表示晶体中每个立方米所占的质量。
两者的转换只需将克/立方厘米的数值除以1000000即可得到克/立方
米的数值。
克/立方米与克/毫升的转换:克/立方厘米表示晶体中每个立方
厘米所占的质量,而克/毫升表示每个毫升所占的质量。
两者的转换需
要先知道晶体的密度,然后将密度除以1000得到单位为克/立方毫米
的数值,再将其乘以1000即可得到单位为克/毫升的数值。
以上是常用的晶胞密度单位换算方法,大家可以根据需要进行转换。
需要注意的是,在实际的计算中,应根据实际情况选择合适的单位,以保证计算的准确性。
除了常用的晶胞密度单位换算方法,还需要注意一些常见的错误。
例如,在进行计算时,应正确使用单位符号、小数点、计算器等。
同
时,在实际测量中,也需要注意实验仪器的精度,以确保实验数据的可靠性。
综上所述,晶胞密度单位换算是化学中的基础知识之一,掌握它将有助于化学研究的深入和准确性。
我们要注意合理选择单位、正确使用单位符号及小数点、注意仪器精度等,这样才能保证计算结果的准确性。
晶体密度计算公式
晶体密度是指晶体中单位体积的质量,通常用克/立方厘米(g/cm³)表示。
晶体密度的计算公式为:晶体密度=晶体分子量/晶体摩尔体积。
晶体分子量是指晶体中一个分子的质量,通常用克/摩尔(g/mol)表示。
晶体摩尔体积是指晶体中一个摩尔物质所占据的体积,通常用立方厘米/摩尔(cm³/mol)表示。
晶体分子量可以通过化学分析或者质谱分析等实验手段进行测定。
晶体摩尔体积则可以通过X射线衍射或者中子衍射等技术进行测定。
在实际应用中,晶体密度是晶体结构分析、晶体生长、材料科学等领域重要的物理性质之一。
例如,在晶体生长领域,晶体的密度与生长条件密切相关,密度的变化直接影响晶体生长的速率和质量。
在材料科学领域,晶体密度可以用来评估材料的物理性质和化学性质等。
除了晶体密度,还有一种相关的物理量叫做晶格常数。
晶格常数是指晶体中相邻两个原子或者分子间距离的大小,通常用埃(Å)表示。
晶格常数与晶体密度有着密切的关系,可以通过晶格常数和晶体结构参数来计算晶体密度。
晶体密度是晶体物理性质中的重要参数之一,其计算公式为晶体密
度=晶体分子量/晶体摩尔体积。
在实际应用中,晶体密度可以用来评估晶体的生长速率和质量、材料的物理性质和化学性质等。