几何辅助线之中点专题

初中数学几何辅助线添加技巧：中点模型的构造
初中数学视频课程（配电子版讲义）
全套初中数学视频课程，如需资料，请私信回复“初中数学”
中点常见的联想路径：
1.已知任意三角形一边上的中点，可以考虑：
①倍长中线或类中线（与中点有关的线段）构造全等三角形②三角形中位线定理
2.已知直角三角形斜边上中点，可以考虑构造斜边中线。

3.已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一”
4.有些题目的中点不直接给出，此时需要我们挖掘题目中的隐含中点，例如直角三角形中斜边中点，等腰三角形底边上的中点，当没有这些条件的时候，可以用辅助线添加。

中点常见的辅助线中点经常所在的三角形：全等三角形等腰三角形：三线合一直角三角形：斜边上的中线、三角形的中位线：一、一个中点常见的辅助线(1）利用中点构建全等形：倍长中线至二倍，构建全等三角形(2）有中点联想直角三角形的斜边上的中线(3）由中点联想到等腰三角形的“三线合一”1、在△ABC中,AD是BC边上的中线，若AB=2，AC=4，则AD的取值范围是________．2、已知：如图，△ABC（AB≠AC）中,D、E在BC上，且DE=EC, 过D作DF∥BA 交AE于点F，DF=AC．求证：AE平分∠BAC．3、正方形ABCD中,E为CD的中点,B F⊥AE于F ,连接CF,求证;CF=CB4．如图，四边形ABCD中，∠DAB=∠BCD=90°，M为BD中点，N为AC中点，求证：MN ⊥AC．5．如图所示，在△ABC中,∠C=2∠B，点D是BC上一点，AD=5，且AD⊥AB，点E是BD的中点,AC=6.5,则AB的长度为_________．6、已知梯形ABCD 中，A D ∥BC,且AD+BC=AB ，E 为CD 的中点，连接AE 、BE求证；(1)AE 平分∠BAD(2) BE 平分∠ABC（3)A E ⊥BE练习：1、已知正方形ABCD 中，E 为CD 的中点，AE 平分∠BAF ．求证：AF=BC+CF6、在△ABC （AB ≠AC)中，在∠A 的内部任做一条射线，过B 、C 两点做此射线的垂线BE 和CF ，交此射线于E 、F ，M 为BC 的中点，求证：MD=ME ．等腰直角△ABC 和等腰直角△DCE 如图所示放置，M 为AE 的中点，连接DM 、BM,（1）求证:BM ∥CE（2)若AB=a,DE=2a,求DM 、BM 的长.A MED CBA二、两个或多个中点常见的辅助线：当图中有多个中点时，我们要细致分析图形特点,是否有直角三角形，等腰三角形，等边三角形，有时，要利用中点的性质分析，同时还要考虑中位线，(一)直接连接中点构建中位线：1．已知：在四边形ABCD中，E、F、G、H分别是BC、AD、BD、AC的中点．①求证:EF与GH互相平分；②当四边形ABCD的边满足_________条件时,EF⊥GH．（二)取三角形一边的中点,构建中位线：2、如图，在四边形ABCD中，对角线AC、BD交于点O，E、F分别是AB、CD的中点，且AC=BD．求证：OM=ON．（三)添加三角形的第三边，构建中位线:如图，已知E、F分别为△ABC的边AB、BC的中点，G、H为AC边上的两个三等分点，连EG、FH，且延长后交于点D,求证:四边形ABCD是平行四边形四、添加三角形的另一边并取中点，构建中位线：在四边形ABCD中，E、F、M分别是AB、CD、BD的中点，AD=BC．求证:∠EFM=∠FEM．如图，在四边形ABCD中，一组对边AB=CD，另一组对边AD≠BC,分别取AD、BC的中点M、N,连接MN．则AB与MN的关系是( ）A．AB=MN B．AB＞MN C．AB＜MN D．上述三种情况均可能出现已知：如图，在四边形ABCD中,AD=BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F．求证：∠DEN=∠F．五、条件中无中点时，完善图形得中位线:如图，△ABC 边长分别为AB=14,BC=16，AC=26,P 为∠A 的平分线AD 上一点，且BP ⊥AD,M 为BC 的中点,则PM 的值是_______．11．如图，自△ABC 顶点A 向∠C 与∠B 的角平分线CE 、BD 作垂线AM 、AN,垂足分别是M 、N ，已知△ABC 三边长为a 、b 、c,则MN=_______．在△ABC 中，∠B=2∠A ，C D ⊥AB 于D,E 为AB 的中点，求证：DE=21BC多个中点中点经常所在的三角形:等腰三角形：三线合一直角三角形：斜边上的中线、三角形的中位线:已知如图：在△ABC 中，AB 、BC 、CA 的中点分别是E 、F 、G ，AD 是高．求证：∠EDG=∠EFG ．（2015•广东模拟）某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：（1）如图1所示在等腰△ABC 中，AB=AC ，分别以AB 、AC 为斜边，向△ABC 的外侧作等腰直角三角形，如图1所示，其中DF ⊥AB 于点F ，EG ⊥AC 于点G ，M 是BC 的中点，连结MD 和ME ，求证:①AF=AG =21AB; ②MD=ME ．（2）在任意△ABC 中，仍分别以AB 、AC 为斜边，向△ABC 的内侧作等腰直角三角形，如图2所示，M 是BC 的中点,连结MD 和ME ，试判断△MDE 的形状．（直接写答案，不需要写证明过程）．（3）在任意△ABC 中，分别以AB 、AC 为斜边,向△ABC 的外侧作等腰直角三角形，如图3所示，M 是BC 的中点，连结MD 和ME ，则MD 与ME 有怎样的数量关系？6、△ABC 中, ∠CAB=120°，分别以AB 、AC 为边分别向外做正△ABD 和△ACE ，M 为AD 的中点，N 为AE 的中点，P 为BC 的中点，（1）求证：PM=PN（2）试求∠MPN 的度数变式一：△ABC 中， ∠CAB=120°,分别以AB 、AC 为边分别向外做等腰直角△ABD 和等腰直角△ACE,M 为AD 的中点，N 为AE 的中点,P 为BC 的中点, 求证：PM=PN变式二:△ABC 中， ∠CAB=120°,分别以AB 、AC 为边分别向外做等腰△ABD 和等腰△ACE ，M 为AD 的中点，N 为AE 的中点，P 为BC 的中点， 求证:PM=PN变式三：△ABC 中, ∠CAB=120°，分别以AB 、AC 为边分别向外做等腰△ABD 和等腰△ACE ，M 为BD 的中点,N 为CE 的中点,P 为BC 的中点， 求证：PM=PN2．如图，点P 为△ABC 的边BC 的中点，分别以AB ，AC 为斜边作Rt △ABD 和Rt △ACE ，且∠BAD=∠CAE ，求证:PD=PE ．2．如图，点O 为△ABC 内的一点,OD ⊥AB,OE ⊥AC ，∠1=∠2,F 为BC 的中点，链接FD 、FE,求证：FD=FE ．A D EMN P A B C DEM NP A F DE OCB 1 2。

一、中点的应用1、已知任意三角形一边上的中点：01、倍长中线和类中线构造全等三角形。

作用：a全等b平行线c把分散的线段转移到一个三角形中02、三角形中位线定理。

2、已知直角三角形斜边中点，考虑构造斜边中线。

3、已知等腰三角形底边中点，考虑与顶点连接，用“三线合一”。

4、挖掘题目隐含中点。

1如图，在△ABC中，AD为BC边上的中线，求证：AB+AC＞2AD.2如图，已知在△ABC中，AD是BC边上的中线，E是AD上的一点，延长BE交AC于F，AF=EF，求证：AC=BE.3如图,在中,,点D为BC中点,点E、F分别为AB、AC上的点,且.以线段BE、EF、FC为边能否构成一个三角形?若能,请判断此三角形的形状.4、如图,在中,BE、CF分别为边AC、AB上的高,D为BC的中点,于M.求证:.5、已知:和都是直角三角形,且.如图甲,连接DE,设M为DE的中点.(1)说明:;(2)设,固定,让绕顶点A在平面内旋转到图乙的位置,试问:是否还能成立?并证明其结论.6、(1)如图1,在四边形ABCD中,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则,求证:(2)如图2,在中,点O是BC边的中点,D是AC边上一点,E是AD的中点,直线OE交BA的延长线于点G,若,,求OE的长度.(3)如图，四边形ACBD中，AB与CD交于点O，AB＝CD，E，F分别是BC，AD的中点，连接EF，分别交DC，AB于点M，N，试判断△OMN 的形状.(4)如图，在△ABC中，AC>AB，D点在AC上，AB＝CD，E、F分别是BC、AD的中点，连接EF并延长，与BA的延长线交于G，若∠EFC ＝60°，连结GD，判断△AGD的形状并证明．7、如图在△ABC中, AB＝AC, CE是AB边上的中线, 延长AB到D, 使BD＝AB, 连结CD,证明CD＝2CE.1、证明：延长AD至点E，使ED=AD，连接CE，如图所示：∵AD为BC边上的中线，∴BD=CD.在△ABD和△ECD中，AD=ED，∠ADB=∠EDC，BD=CD，∴△ABD≌△ECD.∴AB=EC.在△ACE中，∵AC+EC＞AE=2AD，∴AB+AC＞2AD.2、证明：如图，延长AD到点G，使得AD=DG，连接BG∵AD是BC边上的中线(已知)，∴DC=DB，在△ADC和△GDB中，AD＝DG∠ADC＝∠GDB(对顶角相等)DC＝D ∴△ADC≌△GDB(SAS)，∴∠CAD=∠G，BG=ACB∵AF=EF，∴∠FAE=∠AEF，∵∠BED=∠AEF，∴∠BED=∠FAE，即：∠BEG=∠CAD，∴∠BEG=∠G∴BE=BG ∴AC=BE3、:作,与FD延长线交于G,连接EG,,,,在和中,,,,,,,,,,为直角三角形,、EF、FC为边能构成一个三角形,且为直角三角形. 4、证明:连接DE,DF,、CF分别为边AC、AB上的高,D为BC的中点,,,,即是等腰三角形.,点M时EF的中点,即.5证明：延长CM、DB交于G，∵△ABD和△ACE都是直角三角形，∴CE∥BD，即CE∥DG，∴∠CEM=∠GDM，∠MCE=∠MGD又∵M是DE中点，即DM=EM，∴△ECM≌△DMG，∴CM=MG，∵G在DB的延长线上，∴△CBG是Rt△CBG，∴在Rt△CBG中，BM= CG=CM.证明:(1)作点M作于点P,..为DE的中点,,是BC的中垂线,;(2)成立.取AD、AE的中点F、G,连接BF、MF、MG、CG显然线段MG、MF都是的中位线,四边形MFAG是平行四边形,,,,又,斜边中线,,,,,,,.6(1)证明:连结BD,取DB的中点H,连结EH、FH.、F分别是BC、AD的中点,,,,,,,;(2)解:连结BD,取DB的中点H,连结EH、OH,,,,,,是等边三角形,,.(3)首先取BD的中点G，连接EG，FG，则由E，F分别是BC，AD的中点，所以EG，FG分别是△CDB，△ADB的中位线，则由三角形的中位线定理得EG∥CD，EG＝12CD；FG∥AB，FG＝12AB；又由AB＝CD，所以EG＝FG，所以∠GFE＝∠GEF，又由EG∥CD，FG∥AB，所以∠G FE＝∠ONM，∠OMN＝∠GEF，所以∠OMN＝∠ONM，所以OM＝ON，即△OMN是等腰三角形.【答案】解：△OMN是等腰三角形；理由：如图，先取BD的中点G，连接EG，FG，∵E，F分别是BC，AD的中点，∴EG，FG分别是△CDB，△ADB的中位线，∴EG∥CD，EG＝12CD；FG∥AB，FG＝12AB；又∵AB＝CD，∴EG＝FG，∴∠GFE＝∠GEF，又∵EG∥CD，FG∥AB，∴∠GFE＝∠ONM，∠OMN＝∠GEF，∴∠OMN＝∠ONM，∴OM＝ON，即△OMN是等腰三角形.故答案为：△OMN是等腰三角形.(4)连接bd，k为bd的中点，连接fk、ek7、证法一: 取DC的中点为F, 联结BF, 则BF AC,又BE＝AB AB＝AC ∴BF＝BE∠FBC＝∠BCA＝∠ABC又∵ BC＝BC∴△FBC≌△EBC∴ FC＝CE即 CD＝2CE证法二: 延长CE到F, 使EF＝CE, 连结FB∵ CE为△ABC中线∴ BE＝AE又∠1＝∠2∴△FBE≌△CAE∴ FB＝AC ∠3＝∠A∵ AB＝AC＝BD∴ FB＝BD ∠ABC＝∠ACB ∠3+∠ABC＝∠A+∠ACB 即∠FBC＝∠DBC又∵ BC公用∴△FBC≌△DBC∴ FC＝DC又∵ FC＝2CE∴ CD＝2CE。

第一节等腰底中垂分解题方法技巧1.等腰三角形中有底边中点或证是底边中点时，常连底边中线，利用等腰三角形“三线合一”性质证题2.有中点时，也可过中点作垂线，构造垂直平分线，利用垂直平分线上的点和线段两个端点距离相等证题如图，在ABC中，AB=AC,取BC中点D，连接AD,则AD是BAC∠的平分线，又是BC边上的高和BC边上的中线，这样为证明题目增添了很多条件。

例1 已知：如图，在矩形ABCD中，E为CB延长线上一点且AC=CE,F为AE的中点。

求证：BF FD⊥.例2 如图，AB=AE,ABC AED∠=∠,BC=ED,点F是CD的中点（1）求证：AF CD⊥（2）在你连接BE后，还能得出什么新结论？请写出三个（不要求证明）。

练习 1.如图，在ABC中，AB=AC=5，BC=6，点M为BC的中点，MN AC⊥于点N，则MN等于（）A 65B95C125D1652.已知：如图，在等腰ABC中，AB=AC,D是BC的中点，过A的直线MN//BC,在直线MN 上点A的两侧分别取点E,F且AE=AF.求证：DE=DF.3. 已知:如图，在等腰ABC 中，AB=AC,D 是BC 的中点，过A 作,,AE DE AF DF ⊥⊥且AE=AF.求证：EDB FDC ∠=第二节 斜边中 是一半解题方法技巧直角三角形中，有斜边中点时常作斜边中线；有斜边的倍分关系线段时，也常常作斜边中线如图，在Rt ABC 中，D 为斜边AB 的中点，连接CD ，则得CD=AD=BD,从而构造出等腰三角形。

如图，在Rt ABC 中，AB=2BC,作斜边AB 的中线CD ，则得相等的线段AD=BD=CD=BC,从而得到BCD 为等边三角形，为研究等边三角形，求角的大小提供了条件。

例 如图，在Rt ABC 中，AB=AC,90BAC ∠=︒,O 为BC 的中点。

（1） 写出点O 到ABC 的三个顶点A,B,C 的距离的关系：（不需证明）（2） 如果点M,N 分别在线段AB,AC 上移动，在移动中保证AN=BM,请判断OMN 的形状，并证明你的结论。

一点，G，H分别为EF，BF的中点，连接GH，则GH的长是( D )
A．6
B．5.5
C．6.5
D．5
【解析】连接BE.∵四边形ABCD是矩形，∴∠A＝90°.∵AD＝12，E为
1
AD 的 中 点 ， ∴ AE ＝ AD ＝ 6. ∵ AB ＝ 8 ， ∴ 在 Rt△ABE 中 ， BE ＝
2
2 ＋ 2 ＝10.∵G，H分别为EF，BF的中点，∴GH是△BEF的中位
1
1
BD.∵BD⊥AC，AE＝BD，∴EF⊥AC，EF＝ AE，∴∠CFE＝∠AFE
2
2
＝90°，∠EAF＝30°，∴∠AEF＝60°.又∵∠C＝55°，∴∠CEF＝
35°，∴∠AEB＝180°－∠AEF－∠CEF＝85°.故选D.
2.如图，菱形ABCD的对角线BD的长为8，E，F分别是AD，CD边的中
点，连接EF.若EF＝3，则菱形ABCD的面积是( A )
A．24
B．20
C．12
D．6
【解析】连接AC.∵E，F分别是AD，CD边上的中点，即EF是△ACD的中
1
1
位线，∴AC＝2EF＝6，∴S菱形ABCD＝ AC·BD＝ ×6×8＝24.故选A.
2
2
3.如图，在矩形ABCD中，AB＝8，AD＝12，E为AD的中点，F为CD边上

AD，∠B＝∠DCB，∠A＝∠ACD
模型
总结
当遇等腰三角形底边上的中点
当遇直角三角形斜边上的
时，考虑作底边上的中线，利用 中点时，考虑作斜边上的
“三线合一”解题
中线
例2
如图，在等腰直角三角形ABC中，∠ABC＝90°，D为边AC的中
点，过点D作DE⊥DF，交AB于点E，交BC于点F，连接EF.若AE＝4，

专题29 几何问题辅助线添加技巧专题知识点概述全国各地每年的中考试卷里都会出现考查几何的证明和计算问题，在解答试题过程中，我们发现当题设条件不够，必须添加辅助线，把分散条件集中，建立已知和未知的桥梁，结合学过的知识，采用一定的数学方法，把问题转化为自己能解决的问题。

学会添加辅助线技巧，是培养学生科学思维、科学探究的重要途径。

所以希望大家学深学透添加辅助线的技巧和方法。

一、以基本图形为切入点研究添加辅助线的技巧策略1.三角形问题方法1：有关三角形中线的题目，常将中线加倍。

含有中点的题目，常常利用三角形的中位线，通过这种方法，把要证的结论恰当的转移，很容易地解决了问题。

方法2：含有平分线的题目，常以角平分线为对称轴，利用角平分线的性质和题中的条件，构造出全等三角形，从而利用全等三角形的知识解决问题。

方法3：结论是两线段相等的题目常画辅助线构成全等三角形，或利用关于平分线段的一些定理。

方法4：结论是一条线段与另一条线段之和等于第三条线段这类题目，常采用截长法或补短法，所谓截长法就是把第三条线段分成两部分，证其中的一部分等于第一条线段，而另一部分等于第二条线段。

2.平行四边形问题平行四边形（包括矩形、正方形、菱形）的两组对边、对角和对角线都具有某些相同性质，所以在添辅助线方法上也有共同之处，目的都是造就线段的平行、垂直，构成三角形的全等、相似，把平行四边形问题转化成常见的三角形、正方形等问题处理，其常用方法有下列几种，举例简解如下：（1）连对角线或平移对角线：（2）过顶点作对边的垂线构造直角三角形；（3）连接对角线交点与一边中点，或过对角线交点作一边的平行线，构造线段平行或中位线；（4）连接顶点与对边上一点的线段或延长这条线段，构造三角形相似或等积三角形；（5）过顶点作对角线的垂线，构成线段平行或三角形全等。

3.梯形问题梯形是一种特殊的四边形。

它是平行四边形、三角形知识的综合，通过添加适当的辅助线将梯形问题化归为平行四边形问题或三角形问题来解决。

2015年中考解决方案构造中位线学生姓名：X X X上课时间:2014 x xxx构造中位线自检自查必考点知识点一中点一、与中点有关的概念三角形中线的定义：三角形顶点和对边中点的连线三角形中线的相关定理：直角三角形斜边的中线等于斜边的一半等腰三角形底边的中线三线合一（底边的中线、顶角的角平分线、底边的高重合）三角形中位线定义：连结三角形两边中点的线段叫做三角形的中位线.三角形中位线定理：三角形的中位线平行于第三边并且等于它的一半.中位线判定定理：经过三角形一边中点且平行于另一边的直线必平分第三边.直角三角形斜边中线：直角三角形斜边中线等于斜边一半斜边中线判定：若三角性一边上的中线等于该边的一半，则这个三角形是直角三角形二、与中点有关的辅助线秘籍一：倍长中线解读：凡是出现中线或类似中线的线段，都可以考虑倍长中线，倍长中线的目的可以旋转等长度的线段, 从而达到将条件进行转化的目的。

秘籍二：构造中位线解读：凡是岀现中点，或多个中点，都可以考虑取另一边中点，或延长三角形一边，从而达到构造三角形中位线的目的。

秘籍三：构造三线合一解读：只要出现等腰三角形，或共顶点等线段，就需要考虑构造三线合一，从而找到突破口秘籍四：构造斜边中线解读：只要出现直角三角形，或直角，则考虑连接斜边中线段，第一可以出现三条等线段，第二可以出现 两个等腰三角形，从而转化线段关系。

/中考满分必做题—、构造三角形中位线抄考点说明：①凡是出现中点，或多个中点，都可以考虑取四边形对角线中点、等腰三角形底边中点、直 角三角形斜边中点或其他线段中点，②延长三角形一边，从而达到构造三角形中位线的目的。

“题中有中点，莫忘中位线"・与此很相近的几何思想是“题中有中线，英忘加倍延"，这两个是常用几何思 想，但注意倍长中线的主要目的是通过构造三角形全等将分散的条件集中起来.平移也有类似功效.【练1】如右下图，在AA3C 中，若= AD 丄BC , E 为边的中点.求证：AB = 2DE .【答案】如右下图，则取AC 边中点F,连结EF 、DF .由中位线可得，EF=」AB JL ZB = ZCEF . DF 为RtAADC 斜边上的中线，・\ DF = CF .A ZCDF = ZC ,又ZDFE + ZFDE = ZCEF ,即ZC + ZDFE = 2ZC ,其他位置的也要能看出他位置的也要能看出【例1】 已知：AD 是△ABC 的中线，AE 是的中线，且求证：AC = 2AE.72 7 2 2 故 DF = DE .再证△ ADE^/\ADF ,得 AE=AF./. ZDFE = ZEDF ,・*. DE = EF =^AB ,・\ AB = 2DE .【练2】在厶ABC屮，CD、AE分別为AB、BC边上的高，ZB = 60°,求证：DE = -AC.【考点】三角形的中位线，30。

方法专题:中点的妙用联想是一种非常重要的数学品质。

善于联想，才能更好的寻求解决问题的方法。

同学们当你遇到中点时，你会产生哪些联想呢学习完这个专题后，能给你带来一定的启示。

看到中点该想到什么1、等腰三角形中遇到底边上的中点，常联想“三线合一”的性质；2、直角三角形中遇到斜边上的中点，常联想“斜边上的中线，等于斜边的一半”；3、三角形中遇到两边的中点，常联想“三角形的中位线定理”；4、两条线段相等，为全等提供条件（遇到两平行线所截得的线段的中点时，常联想“八字型”全等三角形）；5、有中点时常构造垂直平分线；6、有中点时，常会出现面积的一半（中线平分三角形的面积）；7、倍长中线8、圆中遇到弦的中点，常联想“垂径定理”中点辅助线模型一、等腰三角形中遇到底边上的中点，常联想“三线合一”的性质1、如图1所示，在△ABC 中，AB=AC=5，BC=6，点M 为BC 中点，MN ⊥AC 于点N ，则MN 等于（ ）A ．65B ．95C ．125 D ．165二、直角三角形中遇到斜边上的中点，常联想“斜边上的中线，等于斜边的一半”2、如图，在Ｒｔ⊿ABC 中，∠A=90°,AC=AB,M 、N 分别在AC 、AB 上。

且AN=为斜边BC 的中点.试判断△OMN 的形状，并说明理由.3、如图，正方形ABCD 的边长为2, 将长为2的线段QF 的两端放在正方形相邻的两边上同时滑动．如果点Q 从点A 出发，沿图中所示方向按A D CB A →→→→滑动到点A 为止，同时点F 从点B 出发，沿图中所示方向按B A D C B →→→→滑动到点B 为止，那么在这个过程中，线段QF 的中点M所经过的路线围成的图形的面积为（ ）A. 2B. 4－πBC 第8题图QFMC.πD.1π-三、三角形中遇到两边的中点，常联想“三角形的中位线定理”4、（直接找线段的中点，应用中位线定理）如图，已知四边形ABCD 的对角线AC 与BD 相交于点O ，且AC=BD ，M 、N 分别是AB 、CD 的中点，MN 分别交BD 、AC 于点E 、F.你能说出OE 与OF 的大小关系并加以证明吗5、（利用等腰三角形的三线合一找中点，应用中位线定理）如图所示，在三角形ABC 中，AD 是三角形ABC ∠BAC 的角平分线，BD ⊥AD ，点D 是垂足，点E 是边BC 的中点，如果AB=6,AC=14，求DE 的长6、（利用平行四边形对角线的交点找中点，应用中图2-1FEDMNCB A位线定理）如图所示，AB ∥CD ，BC ∥AD ，DE ⊥BE ，DF=EF ，甲从B 出发，沿着BA 、AD 、DF 的方向运动，乙B 出发，沿着BC 、CE 、EF 的方向运动，如果两人的速度是相同的，且同时从B 出发，则谁先到达F 点7、（综合使用斜边中线及中位线性质，证明相等关系问题）如图，等腰梯形ABCD 中，CD ∥AB ，对角线AC 、BD 相交于点O ，60ACD ∠=︒，点S 、P 、Q 分别是DO 、AO 、BC 的中点.求证：△SPQ 是等边三角形。

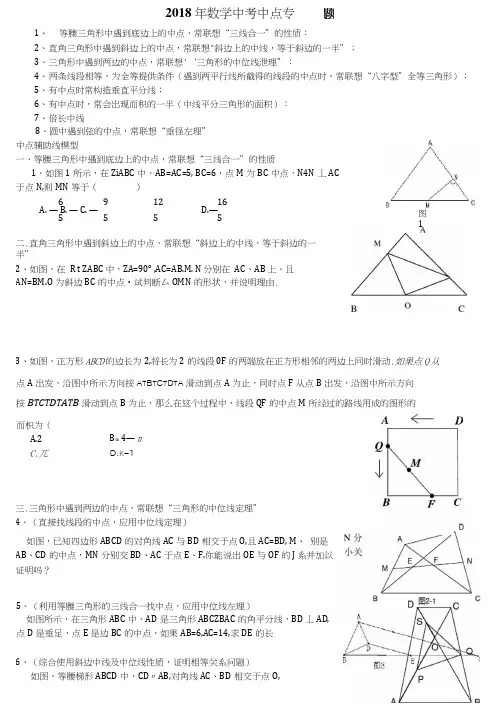
2018年数学中考中点专1、等腰三角形中遇到底边上的中点，常联想“三线合一”的性质：2、直角三角形中遇到斜边上的中点，常联想"斜边上的中线，等于斜边的一半”；3、三角形中遇到两边的中点，常联想'‘三角形的中位线泄理”：4、两条线段相等，为全等提供条件（遇到两平行线所截得的线段的中点时，常联想“八字型”全等三角形）：5、有中点时常构造垂直平分线；6、有中点时，常会出现而积的一半（中线平分三角形的面积）：7、倍长中线8、圆中遇到弦的中点，常联想“垂径左理”中点辅助线模型一、等腰三角形中遇到底边上的中点，常联想“三线合一”的性质1、如图1所示，在ZiABC中，AB=AC=5, BC=6，点M为BC中点，N4N丄AC于点N,则MN等于（）6 9 12 16A. —B. —C. —D.—5 5 5 5图1二.直角三角形中遇到斜边上的中点，常联想“斜边上的中线，等于斜边的一半”2、如图，在R t ZABC 中，ZA=90° ,AC=AB.M. N 分别在AC、AB 上。

且AN=BM.O为斜边BC的中点•试判断厶OMN的形状，并说明理由.3、如图，正方形ABCD的边长为2,将长为2的线段0F的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发，沿图中所示方向按A T B T C T D T A滑动到点A为止，同时点F从点B出发，沿图中所示方向按B T C T D T A T B滑动到点B为止，那么在这个过程中，线段QF的中点M所经过的路线用成的图形的而枳为（A.2 C.兀B r. 4—n D.K-1三.三角形中遇到两边的中点，常联想“三角形的中位线定理”4、（直接找线段的中点，应用中位线定理）如图，已知四边形ABCD的对角线AC与BD相交于点O,且AC=BD, M、别是AB、CD的中点，MN分别交BD、AC于点E、F.你能说出OE与OF的J 系并加以证明吗？5、（利用等腰三角形的三线合一找中点，应用中位线左理）如图所示，在三角形ABC中，AD是三角形ABCZBAC的角平分线，BD 丄AD,点D是垂足，点E是边BC的中点，如果AB=6,AC=14,求DE的长6、（综合使用斜边中线及中位线性质，证明相等关系问题）ZACD = 60°t点s、p、Q 分别是DO、AO. BC 的中点.求证：ZkSPQ是等边三角形。

则MN的长为 5 .
连结AM
第6题图
微专题 五种方法解决中点问题
方法四 遇到三角形一边垂线过这边中点时，可以考虑用垂直平分线的性质
模型分析 如图，当三角形一边垂线过这边中点时，可以考虑用垂直平分线的性质得到： BE＝CE，证明线段间的数量关系.
微专题 五种方法解决中点问题
针对训练
7.如图，在Rt△ABC中，∠ACB＝90°，BC＝6，AB的垂直平分线交AB于点D， 25
方法五 遇到三角形一边上的中点，考虑倍长中线法构造全等三角形
模型分析 如图，当遇见中线或者中点时，可以尝试用倍长中线法构造全等三角形，证 明线段间的数量关系.
微专题 五种方法解决中点问题
针对训练 9.如图，已知AB＝24，AB⊥BC于点B，AB⊥AD于点A，AD＝10，BC＝20，连 接CD.若点E是CD的中点，则AE的长为 13 .
延长AE交BC于点F
F
第9题图
微专题 五种方法解决中点问题
10.如图，在△ABC中，AD是BC边上的中线，E是AD上一点，延长BE交AC于点 F，AF＝EF，求证：AC＝BE.
第10题图
微专题 五种方法解决中点问题
解：如解图，延长AD到点G，使DG＝AD，连接BG.
∵BD＝CD，∠BDG＝∠CDA，AD＝GD，
连结DE，CD
第2题图
微专题 五种方法解决中点问题
方法二 已知直角三角形斜边中点，可以考虑（构造）斜边中线 模型分析 如图，在直角三角形中，当遇见斜边中点时，经常会作斜边上的中线，利用直 角三角形斜边上的中线等于斜边的一半，即CD＝ 1 AB，来证明线段间的数量
2 关系，而且可以得到两个等腰三角形：△ACD和△BCD.
5 是BD的中点，则CM的长为____2_____.

初中数学辅助线添加技巧：中点方法总结很多几何题会给出“点×是线段××的中点”这样的条件，那么看到“中点”我们应该想到什么呢？“中点”有哪些作用呢？1．已知任意三角形一边上的中点，可以考虑：（1）倍长中线或类中线（与中点有关的线段）构造全等三角形，如下图．DEOC BADOCBA（2）三角形中位线定理．2．已知直角三角形斜边中点，可以考虑构造斜边中线．3．已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一”．4．有些题目的中点不直接给出，此时需要我们挖掘题目中的隐含中点，例如直角三角形中斜边中点，等腰三角形底边上的中点．当没有这些条件的时候，可以用辅助线添加．典例精析例1．在△ABC 中，11,15AB AC ==，则BC 边上的中线AD 的长的取值范围是什么？DCBA解：延长AD 到点E ，使得DE =AD ，连接CE ．EDCBA,,AD ED ADB EDC BD CD =∠=∠=，∴△ABD ≌△ECD ∴CE =BA ．在△ACE 中，AC CE AE AC CE -<<+，即15111511AE -<<+ ∴426AE << ∵12AD AE =∴213AD <<例2． 如图，已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，延长BE 交AC 于F ，AF EF =，求证：AC BE =．F EDCBA证明：证法一：如图，延长AD 到点G ，使DG =AD ，连接BG ．GF EDCBA∵,,.DB DC BDG CDA AD GD =∠=∠= ∴△ADC ≌△GDB 又∵AF EF =， ∴EAF AEF ∠=∠， ∵AEF BED ∠=∠ ∴G BED ∠=∠， ∴BE BG =， ∴BE AC =，证法二：如图，延长ED 到点G ，使得DG =DE ，连接CG ．GF EDCBA∵点D 是BC 中点， ∴BD CD = ∵BDE CDG ∠=∠∴△BDE ≌△CDG ∴,G BED BE CG ∠=∠= ∵AF EF =∴FAE AEF BEG ∠=∠=∠ ∴G DAC ∠=∠，即G EAF ∠=∠ ∴AC GC = ∴.AC BE = 举一反三1．如图，已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE AC =，延长BE 交AC 于F ，AF 与EF 相等吗？为什么？F EDCBA2． 如图，在△ABC 中，AD 交BC 于点D ，点E 是BC 中点，EF AD ∥交CA 的延长线于点F ，交EF 于点G ，若BG CF =，求证：AD 为ABC ∆的角平分线．GF EDCBA例3． 在Rt △ABC 中，90A ∠=︒，点D 为BC 的中点，点E 、F 分别为AB 、AC 上的点，且ED FD ⊥．以线段BE 、EF 、FC 为边能否构成一个三角形？若能，该三角形是锐角三角形、直角三角形或钝角三角形？FEDCBA答：以线段BE 、EF 、FC 为边能构成一个直角三角形． 证明：如图，延长FD 到点G ，使得GD =FD ，连接EG 、BG ．GFEDCBA∵,,CD BD CDF BDC FD GD =∠=∠= ∴△CDF ≌△BDG∴,CF BG FCD GBD =∠=∠ ∴ACBG ．∵90BAC ∠=︒ ∴90EBG ∠=︒ ∵,GD FD ED DF =⊥ ∴EF EG =∵在Rt △EBG 中，222BE BG EG +=，∴故以线段BE 、EF 、FC 为边能构成一个直角三角形． 举一反三1．已知AM 为△ABC 的中线，AMB ∠，AMC ∠的平分线分别交AB 于E 、交AC 于F ．求证：BE CF EF +>．F EDCBA2．如图所示，在△ABC 中，D 是BC 的中点，DM 垂直于DN ，如果2222BM CN DM DN +=+，求证()22214AD AB AC =+． EFDCBA点拨：例1——例3是利用倍长中线或倍长类中线的方法，将想要求证的线段或角，用全等化到另一个图形中，从而得到所求．例4． 如右下图，在△ABC 中，BE 、CF 分别为边AC 、AB 的高，D 为BC 的中点，DM ⊥EF 于M ．求证：FM =EM ．M E FDCBA证明：如图，连接DF 、DE ．M E FDCBA∵BE 、CF 分别为边AC 、AB 上的高， ∴90BEC BFC ∠=∠=︒． 在Rt △BFC 和Rt △BEC 中， ∵D 是BC 边中点， ∴11,22DE BC DF BC ==，∴DE DF =． 又∵DM ⊥EF ，∴DM 是EF 的垂直平分线． ∴.EM FM =例5． 如图所示，已知△ABD 和△ACE 都是直角三角形，且90ABD ACE ︒∠=∠=，连接DE ，设M 为DE 的中点．求证：MB MC =．E证明：延长BM 交CE 于点N ，E∵90ABD ACE ∠=∠=︒， ∴DBCE ，∴.MDB MEN ∠=∠∵,MD ME BMD NME =∠=∠， ∴△MBD ≌△MNE ．∴MB MN =，即M 是BN 的中点． ∵90BCN ∠=︒， ∴MC MB =．点拨：例4、例5是利用直角三角形斜边中线的性质来证明线段相等，特别是例5隐藏中点的发现．例6．（1）已知，如图四边形ABCD 中，AD BC =，E 、F 分别是BC 和AD 的中点，连接EF 并延长，分别与BA 、CD 的延长线分别交于M 、N 两点． 求证：BME CNE ∠=∠．（2）已知，如图四边形ADBC 中，AB 与CD 相交于点O ，AB CD =，E 、F 分别是BC 、AD 的中点，连接EF ，分别交DC 、AB 于点M 、N ，判断△OMN 的形状，请直接写出结论．（3）已知，△ABC 中，AC AB >，D 点在AC 上，AB CD =，EF 分别是BC 、AD 的中点，连接EF 并延长，与BA 的延长线交于点G ，若60EFC ∠=︒，连接GD ，判断△AGD 的形状并证明．(3)(2)(1)ABCDGO F E ABC DNM FE NM EF DCBA证明：（1）连接BD ，取BD 的中点H ，连接HE 、HF ，H NM E F DCBA∵AB CD =，E 、F 分别是BC ，AD 的中点， ∴1,2HE DC HE NC =．∴HE HF =，∴HFE HEF ∠=∠．∵,HF MB HE NC ，∴,BME HFE CNE FEH ∠=∠∠=∠． ∴BME CNE ∠=∠．（2）等腰三角形（提示：取AC 中点H ，连接FH 、EH ）． （3）△AGD 是直角三角形证明：连接BD ，取BD 的中点H ，连接FH 、EH ．321H ABCDGFE∵F 是AD 的中点， ∴1,2HFAB HF AB =． ∴13∠=∠． 同理，1,2HECD HE CD =．∴2EFC ∠=∠． ∵AB CD =， ∴HF HE =． ∴12∠=∠． ∵60EFC ∠=︒，∴360EFC AFG ∠=∠=∠=︒． △AGF 是等边三角形． ∴AF FG =， ∴GF FD =，∴30FGD FDG ∠=∠=︒．∴90AGD ∠=︒，即△AGD 是直角三角形．点拨：例6是利用三角形中位线的性质，将相等的线段缩小一半放在了新的图形中，减半的线段仍相等．例7． 如图，已知△ABC 中，AB =AC ，CE 是AB 边上的中线，延长AB 到点D ，使BD =AB ．求证：CE =2CE ．ABCDE解法一：如图所示，延长CE 到F ，使EF CE =．解法一ABCDFE容易证明EBF EAC ∆∆≌，从而BF AC =，而AC AB BD ==，故BF BD =． 注意到CBD BAC ACB BAC ABC ∠=∠+∠=∠+∠， CBF ABC FBA ABC CAB ∠=∠+∠=∠+∠，故CBF CBD ∠=∠，而BC 公用，故CBF CBD △≌△， 因此2CD CF CE ==．解法二：延长CE 到点F ，使得EF =CE ，连接AF ．解法二ABCDFE容易证明△EAF ≌△EBC ，从而AF =BC ，而AC AB BD ==． 注意到，FAB ABC ACB ∠=∠=∠CBD BAC ACB BAC FAB FAC ∠=∠+∠=∠+∠=∠，故△FAC ≌△CBD ，因此2CD CF CE ==．解法三：延长BC 到点F ，使CF =CB ，如解法三图．解法三AB CDFE由题意可知AC AB BD ==．注意到FAB ABC ACB ∠=∠=∠，CBD BAC ACB BAC CBA FCA ∠=∠+∠=∠+∠=∠， 故△FAC ≌△DCB ，因此CD =AF ,又C 、E 分别为AB 、BF 的中点，故CE 为△ABF 的中位线， 因此CD =AF =2CE ．解法四：如图所示，取CD 的中点F ，连接BF ．C解法四AB DFE因为F 是CD 的中点，B 是AD 的中点， 故BF 是DAC △的中位线，从而1122BF AC AB BE ===， 由BF ∥AC 可得FBC ACB ABC EBC ∠=∠=∠=∠，CB CB =，故BCE BCF △≌△， 从而EC =FC ，2CD CE =．解法五：延长AC 到F ，使得CF =AC ．连接BF 、DF ．C解法五AB DFE∵AF =2AC =2AB =AD ． 易得△ABF ≌△ACD ． ∴BF =CD ． ∵E 是AB 中点，∴CE 是△ABF 的中位线． ∴CD =BF =2CE ．解法六：证明：取AC 的中点F ，连接BF ，C解法六AB DFE∵AB =AC ，点E ，F 分别是AB ，AC 的中点， ∴AE =AF ，∵∠A =∠A ，AB =AC ， ∴△ABF ≌△ACE （SAS ）， ∴BF =CE ，∵BD =AB ，AF =CF ， ∴DC =2BF ， ∴DC =2CE ．点拨：这是一道多解题，思路很宽，利用中点作中线、倍长中线、中位线等辅助线是常用的解题方法．例8．（1）△ABC 中，点D 是AB 边的中点，AE ⊥BC ，BF ⊥AC ，垂足分别为点E 、F ，AE 、BF 交于点M ，连接 DE 、DF ．若DE =kDF ，则k 的值为 ．（2）△ABC 中，CB CA =，点D 是AB 边的中点，点M 在△ABC 内部，且MAC MBC ∠=∠．过点M 分别作ME ⊥BC ，MF ⊥AC ，垂足分别为点E 、F ，连接DE 、DF ，求证：DE DF =．（3）若将（2）中的条件“CB CA =”变为“CB CA ≠”，其它条件不变，试探究DE 、DF 之间的数量关系，并证明你的结论．(3)(2)(1)ABCDE F M A BCDE FMMFEDCBA解：（1）1；（2）证明：∵CB CA =， ∴CBA CBA ∠=∠ ∵MAC MBC ∠=∠∴CBA MAC CBA MBC ∠-∠=∠-∠ 即MAB MBA ∠=∠ ∴MA MB =∵,,ME BC MF AC ⊥⊥垂足分别为E 、F ， ∴90AFM BFM ∠=∠=︒．∵,,AFM BEM MAF MBE MA MB ∠=∠∠=∠=， ∴△AFM ≌△BEM ． ∴AF BE =∵点D 是AB 边的中点， ∴BD AD =∵,,BD AD DBE DAF BE AF =∠=∠=， ∴△BDE ≌△ADF ． ∴DE DF =．（3）证明：分别取AM 、BM 的中点G 、H ，连接DG 、FG 、DH 、EH ，HGA BCD EF M∵点D 、G 、H 分别是AB 、AM 、BM 的中点， ∴,DGBM DHAM ，且11,22DG BM DH AM ==．∴四边形DHMG 是平行四边形． ∴DHM DGM ∠=∠，∵,,ME BC MF AC ⊥⊥垂足分别为E 、F ， ∴90AFM BEM ∠=∠=︒． ∴11,22FG AM AG EH BM BH ====． ∴,,,FG DH DG EH GAF GFA HBE HEB ==∠=∠∠=∠． ∴2,2FGM FAM EHM EBM ∠=∠∠=∠． ∵FAM EBM ∠=∠ ∴FGM EHM ∠=∠．∴DGM FGM DHM EHM ∠+∠=∠+∠即DGF DHE ∠=∠． ∵,,EH DG EHD DGF HD GF =∠=∠=， ∴△EHD ≌△DGF ． ∴DE DF =． 跟踪训练1．在等腰直角三角形ABC 中，90ABC ∠=︒，D 为AC 边上中点，过点D 作DE DF ⊥，交BC 于点F ．若AE =4，FC =3，求EF 长．ABCDEF2．在正方形ABCD 中，F 是AB 中点，连接CF ，作DE CF ⊥交BC 于点E ，交CF 于点M ，求证：AM AD =．ABCDEFM3． 如图所示，90BAC DAE ∠=∠=︒，M 是BE 的中点，AB AC =，AD AE =，求证AM CD ⊥．ABCDEM4． 等腰梯形ABCD 中，AB CD ∥，AC BD =，AC 与BD 交于点O ，60AOB ∠=︒，P 、Q 、R 分别是OA 、BC 、OD 的中点，求证：PQR ∆是正三角形．QP R OABCD5．在△ABC 中，若2B C ∠=∠，AD BC ⊥，E 为BC 边的中点，求证：2AB DE =．BC6．如图，分别以△ABC 的边AB 、AC 为边，向三角形的外侧作正方形ABDE 和正方形ACFG ，点M 为BC 中点．（1）求证：AM EG ⊥,（2）求证：2EG AM =．GAFMEDCB7．在△ABC 的两边AB 、AC 向形外作正方形ABDE 和ACFG ，取BE 、BC 、CG 的中点M 、Q 、N ．判断△MNQ 的形状．QGNAFMEDCB8．如图，在五边形ABCDE 中，90,,ABC AED BAC EAD ∠=∠=︒∠=∠点F 为CD 的中点，求证：BF EF =．AB CDE F中考前瞻如图，在平行四边形ABCD 中，点M 为边AD 的中点，过点C 作AB 的垂线交AB 于点E ，若3EMD MEA ∠=∠．求证：2BC AB =．A BCDE M。

中点相关辅助线一、中点相关辅助线通常可以分为三类：1.构造中心对称的全等三角形2.构造中位线3.三角形中线二、典例精析：知识点1：中点相关辅助线1能力目标：1.熟练掌握中点相关辅助线模型。

2.讲解通过中点构造中心对称的全等三角形及构造中位线【例1】在中，点P为BC的中点。

（1）如图①，求证：;(2)如图②，延长AB到D，使得BD=AC，延长AC到E，使得CE=AB，连接CE=AB,连接DE。

连接BE，若,请你探究线段BE与线段AP之间的数量关系，写出你的结论，并加以证明。

(1)倍长中线法方法一：延长AP至点K,使PK=AP，连接BK,方法二：延长AP至点K，使PK=AP,连接CK，之后同方法一。

方法三：延长AP至点K,使PK=AP,连接BK、CK，则四边形ABKC是平行四边形，之后同一。

内构中位线法：方法一：取AB得中点H,连接PH，应用三角形中位线定理。

方法二：取AC中点G，连接PG，之后同方法一。

外构中位线：方法一：延长BA至点M,使AM=AB，连接MC,则AP线。

方法二：延长CA至点N，使AN=AC，连接NB，之后同方法一。

（2是等边三角形，通过测量可知.方法一：倍长中线直接构造2AP不好确定倍长中线后辅助线的位置，因此采用迂回的方法。

作证明三角形全等。

证明三点共线，得到2AP。

通过全等三角形证明AK=BE.方法二：外构中位线延长CA至点M,使AM=AC,连接MB,则MB=2AP.BM与BE所在三角形不全等，故需要构造全等三角形，作BK//AE,证方法三：内构中位线取AB中点H，连接PH，作BK//AE,通过ASA即可。

方法总结：与中点相关的题目方法很多，可尽量尝试可能的方法，通常情况下倍长中线和构造中位线可以互通，即两个方法都可以解题。

知识点2：中线相关辅助线21.熟练掌握和差倍分模型。

2.讲解垂直平分线构造辅助线和构造直角三角形斜边中线的方法。

【例2】如图所示，AD平分求证：.思路分析：题目求证的是线段和差倍分问题，可以通过结论构造辅助线，角平分线和垂直也是构造辅助线的重要方向，但本题通过角平分线构造轴对称的全等三角形时行不通的，因为得到的结论和所求没有关系。

与中点有关的辅助线作法例析安徽省利辛县教育局督导室夏飞线段的中点是几何图形中的一个特殊点. 在解决与中点有关的问题时，如果能适当地添加辅助线、巧妙地利用中点，贝y是处理中点问题的关键. 但由于含有中点条件问题的辅助线的作法灵活，不少同学难以掌握。

下面就针对中点问题举例谈谈几种添加辅助线的方法.一、遇到中点找中点这种方法常用于解决三角形和梯形的有关问题，主要是连接两个中点作中位线，并利用其性质•因此，在三角形中，已知三角形两边中点，连结两个中点，即可构造三角形的中位线；在梯形中，已知梯形两腰中点，连结两个中点，即可构造梯形的中位线.例1 :如图1，「-, E、F分别为BC、AD的中点，射线BA、EF交于点G,射线CD、EF交于点H .求证：- 一［壬•@1分析：连接AC,并取其中点P,构造△ PEF,证明戸三二，再利用中位线的性质即可得证.证明：连接AC,取AC的中点P,连接PE、PF.•/ E 为BC 的中点，••• PE// AB , 1同理PF / CD , -•—上'一・二，•二PE , 二二占F三，由PE // AB ，得二三三E 二―"S5 ,由PF // CD，得—CFiS =r 二込=-二上三•说明：已知三角形一边的中点或梯形一腰的中点，常过中点作中位线.二、遇到中点作中线这种方法常用于解决直角三角形或等腰三角形的有关问题，主要是运用直角三角形斜边上的中线或等腰三角形底边上的中线性质. 因此，遇到直角三角形斜边上的中点或等腰三角形底边上的中点，应联想到作中线.DR=-AB 例2 :如图2, △ ABC中，一三一——",AD为高，E为BC的中点，求证：】A分析：在厶ABC中，出现了Rt△ ADC和Rt△ ADB这两个直角三角形；又因为E为BC 的中点，即题目中有中点与直角三角形的条件•按照“遇到中点找中点”的方法，可取Rt △ ADC斜边AC的中点F （或AB的中点），连接EF,即得△ ABC的中位线；再依据“遇到中点作中线”的方法，连接DF，即得到Rt△ ADC斜边AC上的中线，然后只要证明EF =2 即可.证明：取AC的中点F,连接EF、DF.•/ E、F 分别为BC、AC 的中点，••• EF // AB , ；•/ AD是高，•△ ADC是直角三角形.DF = -AC=FC又••• F为斜边AC的中点，•••］，二［二二1 .由EF II AB，得一匚二二上二匚=2—】.又T 一］一一.丨—说明：若一点是直角三角形斜边的中点或等腰三角形底边的中点，则应常想到作中线.三、遇到中点倍长线段这种方法是指：若图中出现由中点引出的线段，则应常想到成倍延长这一线段，可为解题提供更为广阔的思路.例3:如图3，在△ ABC中，已知D为BC边中点，FD丄ED于点D，交AB、AC于点F、E.求证：FF 「三三F .分析：待证的线段BF、CE、EF之间没有明显关系。