信号与系统第三章习题

第三章习题3.1、试求序列k01(k)=2f ⎧⎪⎛⎫⎨ ⎪⎪⎝⎭⎩， 的差分(k)f ∆、(k)f ∇和i=-(i)kf ∞∑。

3.6、求下列差分方程所描述的LTI 离散系统的零输入相应、零状态响应和全响应。

1）()-2(-1)(),()2(),(-1)-1y k y k f k f k k y ε===3）()2(-1)(),()(34)(),(-1)-1y k y k f k f k k k y ε+==+= 5）1()2(-1)(-2)(),()3()(),(-1)3,(-2)-52k y k y k y k f k f k k y y ε++====3.8、求下列差分方程所描述的离散系统的单位序列响应。

2）()-(-2)()=y k y k f k5）()-4(-1)8(-2)()+=y k y k y k f k3.9、求图所示各系统的单位序列响应。

（a）（c）3.10、求图所示系统的单位序列响应。

3.11、各序列的图形如图所示，求下列卷积和。

（1）12()()f k f k *（2）23()()f k f k *（3）34()()f k f k *（4）[]213()-()()f k f k f k *3.13、求题3.9图所示各系统的阶跃响应。

3.14、求图所示系统的单位序列响应和阶跃响应。

3.15、若LTI 离散系统的阶跃响应()()()0.5k g k k ε=，求其单位序列响应。

3.16、如图所示系统，试求当激励分别为（1）()()f k k ε= （2）()()0.5()kf k k ε=时的零状态响应。

3.18、如图所示的离散系统由两个子系统级联组成，已知()1=2cos4k h k π，()()2=k h k k a ε，激励()()()=--1f k k a k δδ，求该系统的零状态响应()zs k y 。

（提示：利用卷积和的结合律和交换律，可以简化运算。

）3.22、如图所示的复合系统有三个子系统组成，它们的单位序列响应分别为()()1=h k k ε，()()2=-5h k k ε，求复合系统的单位序列响应。

信号与系统练习题——第1-3章信号与系统练习题（第1-3章）一、选择题1、下列信号的分类方法不正确的是（A ）A 、数字信号和离散信号B 、确定信号和随机信号C 、周期信号和非周期信号D 、连续信号和离散信号2、下列离散序列中，哪个不是周期序列? （D ）A 、165()3cos()512f k k ππ=+ B 、2211()5cos()712f k k ππ=+ C 、33()9sin()5f k k π= D 、433()7sin()45f k k π=+ 3、下列哪一个信号是周期性的？（C ）。

A 、()3cos 2sin f t t t π=+；B 、()cos()()f t t t πε=；C 、()sin()76f k k ππ=+； D 、1()cos()53f k k π=+。

4、周期信号()sin6cos9f t t t =+的周期为（D ）A 、πB 、2πC 、12π D 、23π5、周期信号()sin3cos f t t t π=+的周期为（C ）。

A 、πB 、2πC 、无周期D 、13π 6、以下序列中，周期为5的是（D ） A. 3()cos()58f k k π=+ B. 3()sin()58f k k π=+ C. 2()58()j k f k eπ+= D. 2()58()j k f k e ππ+=7、下列说法正确的是（D ）A 、两个周期信号()x t ，()y t 的和信号()()x t y t +一定是周期信号B 、两个周期信号()x t ，()y t 的周期分别为2()()x t y t +是周期信号C 、两个周期信号()x t ，()y t 的周期分别为2和π，则信号()()x t y t +是周期信号D 、两个周期信号()x t ，()y t 的周期分别为2和3，则信号()()x t y t +是周期信号8、下列说法不正确的是（A ）A 、两个连续周期信号的和一定是连续周期信号B 、两个离散周期信号的和一定是离散周期信号C 、连续信号()sin(),(,)f t t t ω=∈-∞+∞一定是周期信号D 、两个连续周期信号()x t ，()y t 的周期分别为2和3，则信号()()x t y t +是周期信号9、(52)f t -是如下运算的结果（C ）A 、(2)f t -右移5B 、(2)f t -左移5C 、(2)f t -右移25 D 、(2)f t -左移25 10、将信号()f t 变换为（A ）称为对信号()f t 的平移。

3-1判断下列信号是周期信号还是非周期信号，若是周期信号，试求出其周期。

(1)．t t 6cos 4sin +(2)．2)(sin t π(3)．)1(sin -πt3-2．周期信号)38cos(2)65sin(cos 3)(π--π-+=t t t t f ，试分别画出此信号的单边、双边幅度频谱和相位频谱图。

3-3．已知)()(ω↔F t f ，求↔-)26(t f3-4．求下列信号的傅氏反变换。

(1)ωπ-ωε-+ωε5cos )]5()5([ (2)1)1sin(1)1sin(-ω-ω++ω+ω (3)2sin ωω-j3-5.已知)()(ωF t f ↔，求下列信号的傅氏变换：(1))2(t tf (2))()2(t f t -(3))2()2(t f t -- (4)dt t df t )( (5))1(t f - (6))1()1(t f t -- (7))52(-t f3-6．已知ττωd f t f F t f t )]1(2[)(),()(1211-=↔⎰∞-，求↔)(2t f3-6求下列函数的的傅氏变换。

)(a 、t t f 1)(1=，)(b 、t t f =)(2，)(c 、)()(3t t t f ε=，)(d 、t t f =)(4 3-7利用傅氏变换的性质,求下列谱函数的傅氏变换。

)(a 、)(0ωωδ-，)(b 、)(2ωε3-8已知某系统函数65)(2++-=ωωωωj j H ，输入)()(t e t x tε-=，试求系统的零状态响应，并指出响应中的强制分量和自然分量。

3-9．若系统函数11)(+=ωωj H ，激励为周期信号t t t e 3sin sin )(+=。

试求零状态响应)(t y ，并讨论经传输是否引起失真。

3-10．理想高通滤波器的系统函数为⎪⎩⎪⎨⎧<>=-cc t jde H ωωωωωω0)(，其中c ω为截止角频率，d t 为延迟时间。

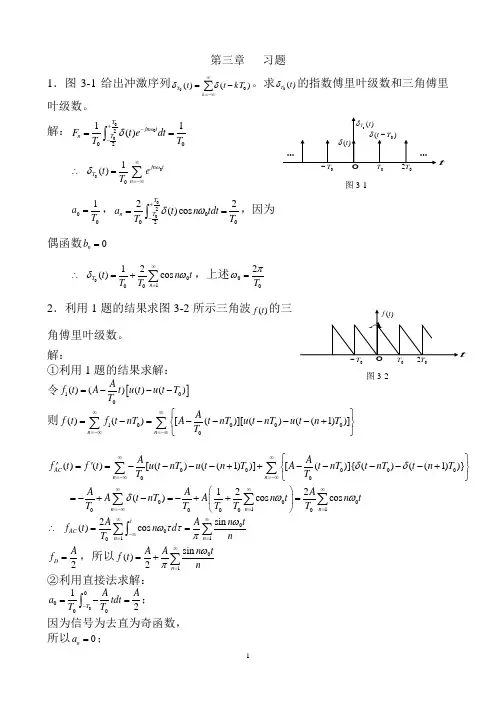
第三章习题基础题3.1 证明cos t , cos(2)t , …, cos()nt (n 为正整数)，在区间(0,2)π的正交集。

它是否是完备集? 解：(积分???)此含数集在(0,2)π为正交集。

又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰，对于所有的m和n 。

由完备正交函数定义所以此函数集不完备。

3.2 上题的含数集在(0,)π是否为正交集？解：由此可知此含数集在区间(0,)π内是正交的。

3.3实周期信号()f t 在区间(,)22T T-内的能量定义为222()TT E f t dt -=⎰。

如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-内相互正交，证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的，求和信号的总能量。

解：(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰（少乘以2）由1()f t 与2()f t 在区间内正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。

和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰（少乘以2吧？）由1()f t 与2()f t 在区间(,)22T T-内不正交可得 2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。

3-1 求图3-1所示对称周期矩形信号的傅利叶级数〔三角形式和指数形式〕。

图3-1解 由图3-1可知，)(t f 为奇函数，因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以，三角形式的傅利叶级数〔FS 〕为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数〔FS 〕的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以，指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。

假设：图3-22T-2-重复频率kHz f 5= 脉宽s μτ20=幅度V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。

解 对于图3-2所示的周期矩形信号，其指数形式的傅利叶级数〔FS 〕的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n那么的指数形式的傅利叶级数〔FS 〕为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入，可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 假设周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示，)(1t f 的参数为s μτ5.0=，s T μ1= ，V E 1=； )(2t f 的参数为s μτ5.1=，s T μ3= ，V E 3=，分别求：〔1〕)(1t f 的谱线间隔和带宽〔第一零点位置〕，频率单位以kHz 表示； 〔2〕)(2t f 的谱线间隔和带宽； 〔3〕)(1t f 与)(2t f 的基波幅度之比； 〔4〕)(1t f 基波与)(2t f 三次谐波幅度之比。

《信号与系统》（第3版）习题解析高等教育目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解 (a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。

1-2 给定题1-2图示信号f ( t )，试画出下列信号的波形。

[提示：f ( 2t )表示将f ( t )波形压缩，f (2t)表示将f ( t )波形展宽。

](a) 2 f ( t - 2 ) (b) f ( 2t )(c) f ( 2t)(d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。

图p1-21-3 如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。

题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i Lt u L L d )(d )(= ⎰∞-=tC C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。

S RS LS C题1-4图解 系统为反馈联接形式。

设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有)()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解 设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) + f 2( t )，则)()()]([111t y t f t f T == )()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。

《信号与系统》课程习题与解答第三章习题(教材上册第三章p160-p172)3-1～3-3,3-5,3-9,3-12,3-13,3-15～3-17,3-19,3-22,3-24,3-25,3-29,3-32第三章习题解答3-2 周期矩形信号如题图3-2所示。

若：求直流分量大小以及基波、二次和三次谐波的有效值。

解：直流分量⎰⎰--=⨯==2222301105)(1ττv Edt dt t f T a TTf(t)为偶函数，∴0=n b)(2cos )(222T n Sa T E tdt n t f T a n πττωττ⎰-==)(21T n Sa T E a F n n πςτ== 基波 =1a )1.0s i n (20)(2πππττ=T Sa T E有效值 39.11.0sin 22021≈=ππa二次谐波有效值 32.122≈a三次谐波有效值 21.123≈a3-3 若周期矩形信号)(1t f 和 )(2t f 波形如题图3-2所示，)(1t f 的参数为s μτ5.0=，s T μ1=，E=1V ；)(2t f 的参数为s μτ5.1=，s T μ3=，E=3V ，分别求：（1）)(1t f 的谱线间隔和带宽（第一零点位置），频率单位以kHz 表示； （2）)(2t f 的谱线间隔和带宽； （3） )(1t f 和 )(2t f 的基波幅度之比； （4） )(1t f 基波与)(2t f 三次谐波幅度之比。

解：（1）)(1t f s μτ5.0= s T μ1= E=1V 谱线间隔：khZ T 10001==∆带宽：KHzB f 20001==τ(2) )(2t f s μτ5.1= s T μ3= E=3V间隔：khZ T 310001==∆谱线带宽：KHzB f 320001==τ(3) )(1t f 基波幅度：ππτ2)2cos(4201==⎰dt t T E T a )(2t f 基波幅度：ππτ6)2cos(4201==⎰dt t T E T a幅度比：1：3（4） )(2t f 三次谐波幅度：ππτ2)23cos(4203-=⨯=⎰dt t T E T a 幅度比：1：13-5 求题图3-5所示半波余弦信号的傅立叶级数。

信号与系统徐天成第3版第3章习题答案3-1 已知周期矩形脉冲信号的重复频率，脉宽，幅度，如图题5 kHz f=20 s τ=μ10V E =3-1所示。

用可变中心频率的选频回路能否从该周期矩形脉冲信号中选取出5，12，20，50，80及频率分量来？要求画出图题3-1所示信号的频谱图。

100 kHz 图 题3-1解：，，，，5kHz f =20μs τ=10V E =11200T s fμ==41210f ππΩ==频谱图为从频谱图看出，可选出5、20、80kHz 的频率分量。

3-3 求图题3-3所示周期锯齿信号指数形式的傅里叶级数，并大致画出频谱图。

图 题3-3解： 在一个周期（0，T 1）内的表达式为： ()f t 11()()Ef t t T T =--111110011111()()(1,2,3)2T T jn tjn t n E jE F f t e dt t T e dt n T T T n π-Ω-Ω==--=-=±±±⎰⎰ 11010011111()()2T T E E F f t dt t T dt T T T ==--=⎰⎰傅氏级数为：111122()22244j t j t j t j tE jE jE jE jE f t e e e e ππππΩ-ΩΩ-Ω=-+-+-(1,2,3)2n E F n n π==±±± (0)2(0)2n n n πϕπ⎧->⎪⎪=⎨⎪<⎪⎩3-4 求图题3-4 所示半波余弦信号的傅里叶级数，若, ，大致画出幅10 V E =10 kHz f =度谱。

图 题3-4解：由于是偶函数，所以展开式中只有余弦分量，故傅氏级数中，另由图()f t 0n b =可知有直流分量， 在一个周期（，）内的表达式为：()f t ()f t 2T -2T其中：111cos 4()04T E t t f t T t ⎧Ω<⎪⎪=⎨⎪>⎪⎩112T πΩ=11112401112411()cos T T T T E a f t dt E tdt T T π--==Ω=⎰⎰111111241112422()cos T T jn t jn t T T n n a c f t e dt E t e dt T T -Ω-Ω--===Ω⋅⎰⎰211sin sin 2122cos 3,5,71112n n E E n n n n n πππππ+-⎡⎤⎢⎥=+=-=⎢⎥+--⎢⎥⎣⎦111211122()2T j t T E a c f t e dt T -Ω-===⎰所以，的三角形式的傅里叶级数为：()f t 11122()cos cos 2cos 42315E E E Ef t t t t πππ=+Ω+Ω-Ω+ 3-6 利用信号的对称性，定性判断图题3-6中各周期信号的傅里叶级数中所含有()f t的频率分量。