下载文档原格式
MATLAB练习四1. 绘制两个一元函数的曲线图（例如y=sin(x)、y=cos(x)），加上标注说明，包括坐标、抬头、曲线说明等。
%lianxi41.mx=0:pi/30:2*pi;y=sin(x);plot(x,y,'-ob','markersize',10);hold ony1=cos(x);plot(x,y1,'-.dm','markersize',10);legend('sinx','cosx');title('sin和cos函数的曲线图')xlabel('x');ylabel('y');2. 寻找一组数据拟合多项式，写出M文件，包括拟合的次数，数值的计算，数学表达式的呈现，图形的呈现等。
%lianxi42x=0:pi/20:pi;y=sin(x);n=input('n=');p=polyfit(x,y,n);x1=0:pi/20:pi*2;y1=sin(x1);y2=polyval(p,x1)plot(x1,y1,'-ob',x1,y2,':dm');legend('原曲线','拟合曲线');xlabel('x');ylabel('y');title('sin的拟合曲线和原曲线');axis([-0.2,6.5,-1.2,1.2])3. 求解一个代数方程，写出M文件，应该包括函数式M文件和命令式M文件。
%fc3.mfunction f=fc3(x)f='3*x-1=0';%lianxi43clc;clear;close;sprintf('原方程和其解析解的结果为：')s=solve(fc3)sprintf('保留10位有效数字的结果为：')digits(10)sprintf('数值解的结果为：')x=vpa(s)4. 求解一个代数方程组，写出M文件，应该包括函数式M文件和命令式M文件。
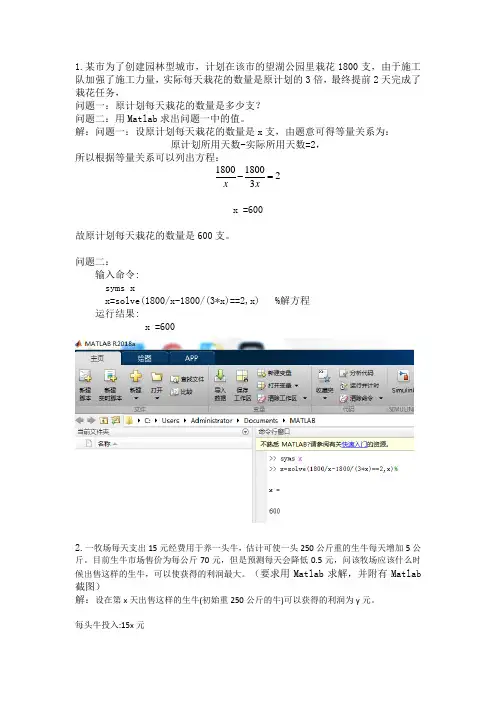
1.某市为了创建园林型城市，计划在该市的望湖公园里栽花1800支，由于施工队加强了施工力量，实际每天栽花的数量是原计划的3倍，最终提前2天完成了栽花任务，
问题一：原计划每天栽花的数量是多少支？
问题二：用Matlab求出问题一中的值。
解：问题一：设原计划每天栽花的数量是x支，由题意可得等量关系为：
原计划所用天数-实际所用天数=2，
所以根据等量关系可以列出方程：
18001800
-=
2
3
x x
x =600
故原计划每天栽花的数量是600支。
问题二：
输入命令:
syms x
x=solve(1800/x-1800/(3*x)==2,x) %解方程
运行结果:
x =600
2.一牧场每天支出15元经费用于养一头牛，估计可使一头250公斤重的生牛每天增加5公斤。
目前生牛市场售价为每公斤70元，但是预测每天会降低0.5元，问该牧场应该什么时候出售这样的生牛，可以使获得的利润最大。
（要求用Matlab求解，并附有Matlab 截图）
解：设在第x天出售这样的生牛(初始重250公斤的牛)可以获得的利润为y元。
每头牛投入:15x元
产出:(70-0.5x)(250+5x)元
利润:y=(70-0.5x)(250+5x)-15x=-2.5x^2+210x+17500
使用Matlab软件计算，得
当天数x=42时,利润y取得最大值21910(元)。
故该牧场应该在第42天时候出售这样的生牛，可以使获得的利润最大。
附Matlab计算截图：
①利润y取得最大值的Matlab计算截图
②天数x=42天的Matlab计算截图。
习题：1， 计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。
2， 对于B AX =，如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ，求解X 。
3， 已知：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ，分别计算a 的数组平方和矩阵平方，并观察其结果。
4， 角度[]604530=x ，求x 的正弦、余弦、正切和余切。
(应用sin,cos,tan.cot)5， 将矩阵⎥⎦⎤⎢⎣⎡=7524a 、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵： （1）组合成一个4⨯3的矩阵，第一列为按列顺序排列的a 矩阵元素，第二列为按列顺序排列的b 矩阵元素，第三列为按列顺序排列的c 矩阵元素，即 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡237912685574（2）按照a 、b 、c 的列顺序组合成一个行矢量，即 []2965318772546， 将(x -6)(x -3)(x -8)展开为系数多项式的形式。
(应用poly,polyvalm)7， 求解多项式x 3-7x 2+2x +40的根。
(应用roots)8， 求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。
(应用poly,polyvalm)9， 计算多项式9514124234++--x x x x 的微分和积分。
(应用polyder,polyint ，poly2sym)10， 解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡66136221143092x 。
(应用x=a\b)11， 求欠定方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡5865394742x 的最小范数解。
(应用pinv) 12， 矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=943457624a ，计算a 的行列式和逆矩阵。
(应用det,inv)13， y =sin(x )，x 从0到2π，∆x =0.02π，求y 的最大值、最小值、均值和标准差。
1.用dsolve求常微分方程的初值问题dy/dx+3y=8,y|x=0=2的解>>r=dsolve('Dy+3*y=8','y(0)=2','x')r=8/3-2/3*exp(-3*x)2.用dsolve求常微分方程的初值问题（1+x^2）y’’=2xy’,y|x=0=1,y’|x=0=3的解>>r=dsolve('D2y*(1+x^2)=2*x*Dy','y(0)=1,Dy(0)=3','x')r=1+x^3+3*x3.用dsolve求微分方程y’’’’-2y'''+y’’=0的解>>r=dsolve('D4y-2*D3y+D2y=0','x')r=C1*exp(x)+C2*exp(x)*x+C3+C4*x4.用dsolve求微分方程组的特解{2*dx/dt+4*x+dy/dt-y=e^t,x|t=0=3/2;{dx/dt+3x+y=0,y|t=0=0;>>[X,Y]=dsolve('2*Dx+4*x+Dy-y=exp(t),Dx+3*x+y=0','x(0)=3/2','y(0)=0')X=-3/2*exp(7^(1/2)*t)*(1/3*7^(1/2)+1/3)-3/2*exp(-7^(1/2)*t)*(-1/3*7^(1/2)+1/3)+1/6*exp(t)+1/2 *7^(1/2)*exp(7^(1/2)*t)*(1/3*7^(1/2)+1/3)-1/2*7^(1/2)*exp(-7^(1/2)*t)*(-1/3*7^(1/2)+1/3)Y=exp(7^(1/2)*t)*(1/3*7^(1/2)+1/3)+exp(-7^(1/2)*t)*(-1/3*7^(1/2)+1/3)-2/3*exp(t)1.选择适当的ode函数，求常微分方程的初值问题dy/dx+3y=8,y|x=0=2的解dy/dx+3y=8即是y’=8-3*y;y|x=0=2即是y(0)=2;故建立m-file文件function test1ode45(@fun,[0,1],2)%---%function f=fun(x,y)f=8-3*y;run之后结果2.选择适当的ode函数，求常微分方程的初值问题（1+x^2）y’’=2xy’,y|x=0=1,y’|x=0=3的解。
matlab考试题目及答案1. 题目：编写一个MATLAB函数，实现计算并返回一个向量中所有元素的平方和。
答案：以下是一个简单的MATLAB函数，用于计算并返回一个向量中所有元素的平方和。
```matlabfunction sumOfSquares = calculateSumOfSquares(vector)sumOfSquares = sum(vector.^2);end```2. 题目：给定一个3x3的矩阵A，使用MATLAB编写代码，求出矩阵A 的转置。
答案：可以通过简单的转置操作来求得矩阵A的转置。
```matlabA = [1 2 3; 4 5 6; 7 8 9];A_transpose = A';```3. 题目：编写一个MATLAB脚本，实现对一个二维数组进行排序，并返回排序后的数组。
答案：以下是一个MATLAB脚本，用于对一个二维数组进行排序，并返回排序后的数组。
```matlabfunction sortedArray = sort2DArray(array)sortedArray = sort(array(:));end```4. 题目：给定一个向量x，使用MATLAB编写代码，计算并返回向量x的元素个数。
答案：可以通过内置函数`numel`来计算向量x的元素个数。
```matlabx = [1, 2, 3, 4, 5];numElements = numel(x);```5. 题目：编写一个MATLAB函数，实现计算并返回两个向量元素的点积。
答案：以下是一个简单的MATLAB函数，用于计算两个向量的点积。
```matlabfunction dotProduct = calculateDotProduct(vector1, vector2)dotProduct = dot(vector1, vector2);end```6. 题目：给定一个矩阵B，使用MATLAB编写代码，求出矩阵B的行列式。
matlab试题及答案# MATLAB试题及答案一、选择题1. MATLAB的基本数据单位是：A. 矩阵B. 向量C. 标量D. 数组答案：A2. 下列哪个命令可以用来绘制函数图形？A. `plot`B. `graph`C. `draw`D. `chart`答案：A3. MATLAB中，以下哪个是正确的矩阵转置操作？A. `transpose(A)`B. `A'`C. `A^T`D. `flip(A)`答案：B二、简答题1. 简述MATLAB中矩阵的基本操作。
答案：在MATLAB中，矩阵是最基本的数据结构，可以进行加、减、乘、除等基本运算。
矩阵的创建可以使用方括号`[]`，例如`A = [1 2;3 4]`。
矩阵的转置使用单引号`'`，例如`A'`。
矩阵的求逆使用`inv`函数，例如`inv(A)`。
2. MATLAB中如何实现循环结构？答案：MATLAB中实现循环结构主要有两种方式：`for`循环和`while`循环。
`for`循环用于已知迭代次数的情况，例如：```matlabfor i = 1:5disp(i);end````while`循环用于迭代次数未知的情况，例如：```matlabi = 1;while i <= 5disp(i);i = i + 1;end```三、计算题1. 给定矩阵A和B，请计算它们的乘积C，并求C的行列式。
A = [1 2; 3 4]B = [5 6; 7 8]答案：首先计算矩阵乘积C：```matlabC = A * B;```然后计算C的行列式：```matlabdetC = det(C);```结果为：```matlabC = [19 22; 43 50]detC = -16```2. 编写一个MATLAB函数，计算并返回一个向量的范数。
答案：```matlabfunction norm_value = vector_norm(v)norm_value = norm(v);end```四、编程题1. 编写一个MATLAB脚本，实现以下功能：- 随机生成一个3x3的矩阵。
练习1matlab练习一、矩阵及数组操作：1．利用基本矩阵产生3×3和15×8的单位矩阵、全1矩阵、全0矩阵、均匀分布随机矩阵（[-1，1]之间）、正态分布矩阵（均值为1，方差为4）,然后将正态分布矩阵中大于1的元素变为1，将小于1的元素变为0。
2．利用fix及rand函数生成[0，10]上的均匀分布的10×10的整数随机矩阵a，然后统计a中大于等于5的元素个数。
3．在给定的矩阵中删除含有整行内容全为0的行，删除整列内容全为0的列。
4．随机生成10阶的矩阵，要求元素值介于0~1000之间，并统计元素中奇数的个数、素数的个数。
二、绘图：5．在同一图形窗口画出下列两条曲线图像，要求改变线型和标记：y1=2x+5；y2=x^2-3x+1，并且用legend标注。
6．画出下列函数的曲面及等高线：z=sinxcosyexp(-sqrt(x^2+y^2))．7．在同一个图形中绘制一行三列的子图，分别画出向量x=[158101253]的三维饼图、柱状图、条形图。
三、程序设计：8．编写程序计算（x 在[-8，8]，间隔0.5）先新建的，在那上输好，保存，在命令窗口代数；9．用两种方法求数列：前15项的和。
10．编写程序产生20个两位随机整数，输出其中小于平均数的偶数。
11．试找出100以内的所有素数。
12．当)1(433221)(+⨯++⨯+⨯+⨯=n n n f 时，?)20()30()40(=+f f f 四、数据处理与拟合初步：13.随机产生由10个两位随机数的行向量A,将A 中元素按降序排列为B,再将B 重排为A 。
14．通过测量得到一组数据：t 12345678910y 4.8424.3623.7543.3683.1693.0383.0343.0163.0123.005分别采用y=c1+c2e^(-t)和y=d1+d2te^(-t)进行拟合，并画出散点及两条拟合曲线对比拟合效果。
matlab模拟试题及答案MATLAB模拟试题及答案1. 编写一个MATLAB函数，计算并返回一个向量中所有元素的和。
```matlabfunction sumVector = sumVectorElements(vector)sumVector = sum(vector);end```2. 给定一个矩阵A，编写一个MATLAB脚本，找出矩阵中的最大元素及其位置。
```matlabA = [1, 2, 3; 4, 5, 6; 7, 8, 9];[maxValue, maxIndex] = max(A(:));[maxRow, maxCol] = ind2sub(size(A), maxIndex);disp(['最大元素为: ', num2str(maxValue), '，位于第',num2str(maxRow), '行，第', num2str(maxCol), '列。
']);```3. 编写一个MATLAB函数，实现一个向量元素的排序。
```matlabfunction sortedVector = sortVector(vector)sortedVector = sort(vector);end4. 给定两个向量X和Y，编写一个MATLAB脚本，计算这两个向量的点积。
```matlabX = [1, 2, 3];Y = [4, 5, 6];dotProduct = dot(X, Y);disp(['X和Y的点积为: ', num2str(dotProduct)]);```5. 编写一个MATLAB函数，计算一个矩阵的行列式。
```matlabfunction determinant = calculateDeterminant(matrix)determinant = det(matrix);end```6. 给定一个向量，编写一个MATLAB脚本，找出向量中的最大值和最小值。
数学建模matlab例题参考及练习数学实验与数学建模实验报告学院：专业班级：姓名：学号：完成时间：年⽉⽇承诺书本⼈承诺所呈交的数学实验与数学建模作业都是本⼈通过学习⾃⾏进⾏编程独⽴完成，所有结果都通过上机验证，⽆转载或抄袭他⼈，也未经他⼈转载或抄袭。
若承诺不实，本⼈愿意承担⼀切责任。
承诺⼈：年⽉⽇数学实验学习体会（每个⼈必须要写字数1200字以上，占总成绩的20%）练习1 ⼀元函数的图形 1．画出x y arcsin =的图象.2．画出x y sec =在],0[π之间的图象. 3．在同⼀坐标系中画出x y =，2x y =，3x y =，3x y =，x y =的图象.4．画出3232)1()1()(x x x f ++-=的图象，并根据图象特点指出函数)(x f 的奇偶性.5．画出)2ln(1++=x y 及其反函数的图象.6．画出321+=x y 及其反函数的图象.练习2 函数极限1．计算下列函数的极限.(1)xxx1lim4-+π→.程序：sym x;f=(1+sin(2*x))/(1-cos(4*x)); limit(f,x,pi/4)运⾏结果：lx21ans =1(2).程序：sym x;f=(1+cos(x))^(3*sec(x)); limit(f,x,pi/2)运⾏结果：lx22ans =exp(3)(3)22)2xx-ππ→.程序：sym x;f=log(sin(x))/(pi-2*x)^2; limit(f,x,pi/2)运⾏结果：lx23ans =-1/8(4)212lim xxex→.程序：x xx sec32)sym x ;f=x^2*exp(1/x); limit(f,x,0) limit(f,x,0,'right') limit(f,x,0,'left')运⾏结果：lx24ans = NaNans = Infans = 0%左极限为零，存在，右极限为⽆穷⼤，在x 趋近于零时函数没有极限(5))215(lim 122x x x x +-∞→.程序：sym x ;f=5*x^2/(1-x^2)+2^(1/x); limit(f,x,inf)运⾏结果：>> lx25ans = -4(6)x x x x x -+-→32112lim .程序：sym x ;f=(x^2-2*x+1)/(x^3-x); limit(f,x,1)运⾏结果：>> lx26ans = 0(7)x x x 11lim 20-+→.程序：sym x ;f=(sqrt(1+x^2)-1)/x; limit(f,x,0))3sin(cos 21lim 3π--π→x x x . 程序：sym x ;f=(1-2*cos(x))/sin(x-pi/3); limit(f,x,pi/3)运⾏结果：>> lx28ans = 3^(1/2)(9)tgxx x )1(lim 0+→.程序：sym x ;f=(1/x)^tan(x); limit(f,x,0,'right')运⾏结果：>> lx29ans =(10)xx arctgx )2(lim π+∞→.程序：sym x ;f=(2/pi*atan(x))^x; limit(f,x,inf,'left')运⾏结果：>> lx210ans =Inf2．解⽅程012=-?x x . 程序：sym x ;X=solve(x*2^x-1)运⾏结果：>> lx202 X =lambertw(0, log(2))/log(2)%⽅程有两个解X=solve(3*sin(x)+1-x)运⾏结果：>> lx203 X =-0.53847936154．解⽅程03=++q px x .(p 、q 为实数) 程序：X=solve('x^3+p*x+q=0','x')运⾏结果： X =((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3) - p/(3*((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)) p/(6*((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)) -((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)/2 - (3^(1/2)*i*(p/(3*((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)) + ((p^3/27 + q^2/4)^(1/2) -q/2)^(1/3)))/2 p/(6*((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)) - ((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)/2 + (3^(1/2)*i*(p/(3*((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)) + ((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)))/2练习 3 导数及偏导数计算1.求下列函数的导数.(1))11)(1(-+=x x y程序：sym x ;f=(sqrt(x)+1)*(1/sqrt(x)-1); diff(f)运⾏结果：>> lx31ans =(1/x^(1/2) - 1)/(2*x^(1/2)) - (x^(1/2) + 1)/(2*x^(3/2))(2)x x x y ln sin =程序：sym x ;f=x*sin(x)*log(x); diff(f)运⾏结果：>> lx32ans =sin(x) + log(x)*sin(x) + x*cos(x)*log(x)2.求下列参数⽅程所确定的函数的导数.(1)??==t y t x 44程序：ans =1/t^3(2)??-=+=arctgt t y t x )1ln(2程序：sym t ;f1=log(1+t^2);f2=t-atan(t); diff(f2)/diff(f1)运⾏结果：>> lx322ans =-((t^2 + 1)*(1/(t^2 + 1) - 1))/(2*t) 3.求下列隐函数的导数.(1)22ln y x xyarctg+=程序：syms x y ;f=atan(y/x)-log(sqrt(x^2+y^2));yx=-diff(f,x)/diff(f,y)运⾏结果；>> lx331 yx =(x/(x^2 + y^2) + y/(x^2*(y^2/x^2 + 1)))/(1/(x*(y^2/x^2 + 1)) - y/(x^2 + y^2)) (2)x y y x=程序：syms x y ; f=x^y-y^xyx=-diff(f,x)/diff(f,y)运⾏结果：>> lx332 f =x^y - y^x yx =f=exp(x)*sin(x); diff(f,x,4)运⾏结果：>> lx34 ans =(-4)*exp(x)*sin(x)5.验证x e y xsin =满⾜关系式:022=+'-''y y y程序：sym x ;f=exp(x)*sin(x); y2=diff(f,x,2); y1=diff(f,x,1); y=f;y2-y1*2+2*y=='0' 运⾏结果：>> lx35ans =1%运⾏结果为1表⽰y2-y1*2+2*y=='0'成⽴6.设)ln(y x x u +=，求22x u ??，22y u，y x u 2. 程序：syms x y ; f=x*log(x+y); uxx=diff(f,x,2) uyy=diff(f,y,2) f1=diff(f,x); uxy=diff(f1,y)运⾏结果： >> lx36uxx =2/(x + y) - x/(x + y)^2uyy =-x/(x + y)^2uxy =1/(x + y) - x/(x + y)^27.求下列多元隐函数的偏导数y zx z ,.(1)1cos cos cos 222=++z y x程序：syms x y z ;-(cos(x)*sin(x))/(cos(z)*sin(z)) zy =-(cos(y)*sin(y))/(cos(z)*sin(z))(2)xyz e z= 程序：syms x y z ; f=exp(z)-x*y*zzx=-diff(f,x)/diff(f,z) zy=-diff(f,y)/diff(f,z)运⾏结果：>> lx372 f =exp(z) - x*y*z zx =(y*z)/(exp(z) - x*y) zy =(x*z)/(exp(z) - x*y) 8.证明函数22)()(lnb y a x u -+-=(b a ,为常数)满⾜拉普拉斯⽅程:02222=??+??y u x u （提⽰：对结果⽤simplify 化简）练习4 积分计算1.计算下列不定积分.(1)?+dxx x 12 (2)+x xdx 2sin 12sin2.计算下列定积分.(1)?exdxx 1ln (2)ππ342sin dxxx3.求?+tdx x x x4.求摆线)cos 1(),sin (t a y t t a x -=-=的⼀拱(π≤≤20t )与x 轴所围成的图形的⾯积.5.计算⼆重积分 (1)??≤++122)(y x dxdyy x (2)??≤++xy x dxdyy x 22)(226.计算?+Ldsy x 22 L 为圆周)0(22>=+a ax y x7.计算?++-L dy y x dx y x )()(2222，其中L 为抛物线2x y =上从点(0，0)到点(2，4)的⼀段弧.练习5 matlab ⾃定义函数与导数应⽤1.建⽴函数x x a a x f 3sin 31sin ),(+=，当a 为何值时，该函数在3π=x 处取得极值，它是极⼤值还是极⼩值，并求此极值.2.确定下列函数的单调区间.（1）7186223---=x x x y （2）)0(82>+=x xx y3.求下列函数的最⼤值、最⼩值.（1）2332x x y -=41≤≤-x（2）312824≤≤-+-=x x x y练习6 matab 矩阵运算与数组运算1．计算（1）???--521111204321+???21（2）??-01301213?03010*******????? ??-205101(3)52422??- 2．设????? ??-=243121013A ,??-=112111201B ,求满⾜关系B X A =-23的X ．练习7 矩阵与线性⽅程组１．求下列矩阵的秩．(1)???-321110021 (2)4820322513454947513253947543173125 ２．求下列矩阵的⾏列式，如可逆，试⽤不同的⽅法求其逆矩阵．（1）??--285421122 （2）??---6201111121324321 ３．设X ????? ?-111012111==--+=+-+=+-+=+-+6223312433862344224221432143214321x x x x x x x x x x x x x x x x (2)-=+--=+--=-+-212201432143214321x x x x x x x x x x x x练习8 常微分⽅程与级数求1-6题微分⽅程的通解1．1222+='y y y x 2．x y x y dx dy -+= 3．x xx y y +='cos 4．1)2sin cos (='+y y y x 5．x e y y y x2cos 3=-'+'' 6．x x y y sin 14++=+'' 求7、8题初值问题的解7．==-++-+=10)2(212222x y dx dy x xy y y xy x8．===++==0000222,02V dt dx x x x a dt dxn dtx d t t9．给出函数x x e x f xx cos 2sin )(+=在点0=x 的7阶taylor 展开式以及在x=1处的 5阶taylor 展开式．10．判别下列级数的敛散性，若收敛求其和．(1)+++311(2)∑∞=+112n nntgπ11．求幂级数∑∞=--22)1(nnnnnx的和函数．12．求函数项级数∑∞=-1nnnn xπ的和函数．。
数学实验与数学建模实验报告学院：专业班级：姓名：学号：完成时间：年月日承 诺 书本人承诺所呈交的数学实验与数学建模作业都是本人通过学习自行进行编程独立完成，所有结果都通过上机验证，无转载或抄袭他人，也未经他人转载或抄袭。
若承诺不实，本人愿意承担一切责任。
承诺人：年 月 日数学实验学习体会（每个人必须要写字数1200字以上，占总成绩的20%）练习1 一元函数的图形1． 画出x y arcsin =的图象.2． 画出x y sec =在],0[π之间的图象.3． 在同一坐标系中画出x y =，2x y =，3x y =，3x y =，x y =的图象. 4． 画出3232)1()1()(x x x f ++-=的图象，并根据图象特点指出函数)(x f 的奇偶性. 5． 画出)2ln(1++=x y 及其反函数的图象. 6． 画出321+=x y 及其反函数的图象.练习2 函数极限1．计算下列函数的极限.(1)xxx4cos12sin1lim4-+π→.程序：sym x;f=(1+sin(2*x))/(1-cos(4*x));limit(f,x,pi/4)运行结果：lx21ans =1(2).程序：sym x;f=(1+cos(x))^(3*sec(x));limit(f,x,pi/2)运行结果：lx22ans =exp(3)(3)22)2(sinlnlimxxx-ππ→.程序：sym x;f=log(sin(x))/(pi-2*x)^2;limit(f,x,pi/2)运行结果：lx23ans =-1/8(4)212lim xxex→.程序：x xx sec32)cos1(lim+π→sym x ;f=x^2*exp(1/x);limit(f,x,0)limit(f,x,0,'right')limit(f,x,0,'left')运行结果：lx24ans =NaNans =Infans =%左极限为零，存在，右极限为无穷大，在x 趋近于零时函数没有极限(5))215(lim 122x x x x +-∞→.程序：sym x ;f=5*x^2/(1-x^2)+2^(1/x);limit(f,x,inf)运行结果：>> lx25ans =-4(6)x x x x x -+-→32112lim .程序：sym x ;f=(x^2-2*x+1)/(x^3-x);limit(f,x,1)运行结果：>> lx26ans =0 (7)x x x 11lim 20-+→.程序：sym x ;f=(sqrt(1+x^2)-1)/x;limit(f,x,0)运行结果：>> lx27ans =0 (8))3sin(cos 21lim 3π--π→x xx .程序：sym x ;f=(1-2*cos(x))/sin(x-pi/3);limit(f,x,pi/3)运行结果：>> lx28ans =3^(1/2) (9)tgxx x )1(lim 0+→.程序：sym x ;f=(1/x)^tan(x);limit(f,x,0,'right')运行结果：>> lx29ans =(10)xx arctgx )2(lim π+∞→.程序：sym x ;f=(2/pi*atan(x))^x;limit(f,x,inf,'left')运行结果：>> lx210ans =Inf2． 解方程012=-⋅x x .程序：sym x ;X=solve(x*2^x-1)运行结果：>> lx202X =lambertw(0, log(2))/log(2)%方程有两个解3． 解方程1sin 3+=x x .程序：sym x ;X=solve(3*sin(x)+1-x)运行结果：>> lx203X =-0.53847936154． 解方程03=++q px x .(p 、q 为实数)程序：X=solve('x^3+p*x+q=0','x')运行结果：X =((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3) - p/(3*((p^3/27 + q^2/4)^(1/2)- q/2)^(1/3))p/(6*((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)) - ((p^3/27 + q^2/4)^(1/2)- q/2)^(1/3)/2 - (3^(1/2)*i*(p/(3*((p^3/27 + q^2/4)^(1/2) -q/2)^(1/3)) + ((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)))/2p/(6*((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)) - ((p^3/27 + q^2/4)^(1/2)- q/2)^(1/3)/2 + (3^(1/2)*i*(p/(3*((p^3/27 + q^2/4)^(1/2) -q/2)^(1/3)) + ((p^3/27 + q^2/4)^(1/2) - q/2)^(1/3)))/2练习 3 导数及偏导数计算1.求下列函数的导数. (1))11)(1(-+=x x y程序：sym x ;f=(sqrt(x)+1)*(1/sqrt(x)-1);diff(f)运行结果：>> lx31ans =(1/x^(1/2) - 1)/(2*x^(1/2)) - (x^(1/2) + 1)/(2*x^(3/2))(2)x x x y ln sin =程序：sym x ;f=x*sin(x)*log(x);diff(f)运行结果：>> lx32ans =sin(x) + log(x)*sin(x) + x*cos(x)*log(x)2.求下列参数方程所确定的函数的导数.(1)⎩⎨⎧==t y t x 44程序：sym t ;f1=t^4;f2=4*t;diff(f2)/diff(f1)运行结果：>> lx321ans =1/t^3(2)⎩⎨⎧-=+=arctgt t y t x )1ln(2程序：sym t ;f1=log(1+t^2);f2=t-atan(t);diff(f2)/diff(f1)运行结果：>> lx322ans =-((t^2 + 1)*(1/(t^2 + 1) - 1))/(2*t)3.求下列隐函数的导数. (1)22ln y x x y arctg +=程序：syms x y ;f=atan(y/x)-log(sqrt(x^2+y^2));yx=-diff(f,x)/diff(f,y)运行结果；>> lx331yx =(x/(x^2 + y^2) + y/(x^2*(y^2/x^2 + 1)))/(1/(x*(y^2/x^2 + 1)) - y/(x^2 + y^2))(2)xy y x =程序：syms x y ;f=x^y-y^xyx=-diff(f,x)/diff(f,y)运行结果：>> lx332f =x^y - y^xyx =(x^(y - 1)*y - y^x*log(y))/(x*y^(x - 1) - x^y*log(x))4.设x e y x cos =，求)4(y .程序：sym x ;f=exp(x)*sin(x);diff(f,x,4)运行结果：>> lx34ans =(-4)*exp(x)*sin(x)5.验证x e y x sin =满足关系式:22=+'-''y y y程序： sym x ;f=exp(x)*sin(x);y2=diff(f,x,2);y1=diff(f,x,1);y=f;y2-y1*2+2*y=='0'运行结果：>> lx35ans =1%运行结果为1表示y2-y1*2+2*y=='0'成立6.设)ln(y x x u +=，求22x u ∂∂，22y u∂∂，y x u ∂∂∂2. 程序：syms x y ;f=x*log(x+y);uxx=diff(f,x,2)uyy=diff(f,y,2)f1=diff(f,x);uxy=diff(f1,y)运行结果：>> lx36uxx =2/(x + y) - x/(x + y)^2uyy =-x/(x + y)^2uxy =1/(x + y) - x/(x + y)^27.求下列多元隐函数的偏导数y zx z ∂∂∂∂,.(1)1cos cos cos 222=++z y x程序：syms x y z ;f=(cos(x))^2+(cos(y))^2+(cos(z))^2-1;zx=-diff(f,x)/diff(f,z)zy=-diff(f,y)/diff(f,z)运行结果：>> lx371zx =-(cos(x)*sin(x))/(cos(z)*sin(z))zy =-(cos(y)*sin(y))/(cos(z)*sin(z))(2)xyz e z =程序：syms x y z ;f=exp(z)-x*y*zzx=-diff(f,x)/diff(f,z)zy=-diff(f,y)/diff(f,z)运行结果：>> lx372f =exp(z) - x*y*zzx =(y*z)/(exp(z) - x*y)zy =(x*z)/(exp(z) - x*y)8.证明函数22)()(ln b y a x u -+-=(b a ,为常数)满足拉普拉斯方程: 02222=∂∂+∂∂y u x u（提示：对结果用simplify 化简）练习4 积分计算1.计算下列不定积分. (1)⎰+dx x x 12 (2)⎰+x xdx 2sin 12sin2.计算下列定积分.(1)⎰e xdx x 1ln (2)⎰ππ342sin dx x x 3.求⎰+t dx x x x 12)ln (ln 1并用diff 对结果求导.4.求摆线)cos 1(),sin (t a y t t a x -=-=的一拱(π≤≤20t )与x 轴所围成的图形的面积.5.计算二重积分(1)⎰⎰≤++122)(y x dxdy y x (2)⎰⎰≤++x y x dxdy y x 22)(22 6.计算⎰+L ds y x 22 L 为圆周)0(22>=+a ax y x7.计算⎰++-L dy y x dx y x )()(2222，其中L 为抛物线2x y =上从点(0，0)到点(2，4)的一段弧.练习5 matlab 自定义函数与导数应用1.建立函数x x a a x f 3sin 31sin ),(+=，当a 为何值时，该函数在3π=x 处取得极值，它是极大值还是极小值，并求此极值.2.确定下列函数的单调区间.（1）7186223---=x x x y （2）)0(82>+=x x x y3.求下列函数的最大值、最小值.（1）2332xx y -=41≤≤-x （2）312824≤≤-+-=x x x y练习6 matab 矩阵运算与数组运算1． 计算（1）⎪⎪⎪⎭⎫ ⎝⎛--521111204321+⎪⎪⎪⎭⎫ ⎝⎛--232002101041221 （2）⎪⎪⎭⎫ ⎝⎛-01301213⎪⎪⎪⎪⎪⎭⎫ ⎝⎛030101020501⎪⎪⎪⎭⎫ ⎝⎛-205101 (3)52422⎪⎪⎭⎫ ⎝⎛- 2．设⎪⎪⎪⎭⎫ ⎝⎛-=243121013A ,⎪⎪⎪⎭⎫ ⎝⎛-=112111201B ,求满足关系B X A =-23的X ．练习7 矩阵与线性方程组１．求下列矩阵的秩．(1)⎪⎪⎪⎭⎫ ⎝⎛-321110021 (2)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛4820322513454947513253947543173125 ２．求下列矩阵的行列式，如可逆，试用不同的方法求其逆矩阵．（1）⎪⎪⎪⎭⎫ ⎝⎛--285421122 （2）⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---6201111121324321 ３．设X ⎪⎪⎪⎭⎫ ⎝⎛-111012111=⎪⎪⎪⎭⎫ ⎝⎛521234311求X ． ４．解下列线性方程组．(1)⎪⎪⎩⎪⎪⎨⎧=--+=+-+=+-+=+-+6223312433862344224221432143214321x x x x x x x x x x x x x x x x (2)⎪⎪⎩⎪⎪⎨⎧-=+--=+--=-+-212201432143214321x x x x x x x x x x x x练习8 常微分方程与级数 求1-6题微分方程的通解1．1222+='y y y x 2．x y x y dx dy -+= 3．x x x y y +='cos 4．1)2sin cos (='+y y y x 5．x e y y y x 2cos 3=-'+'' 6．x x y y sin 14++=+'' 求7、8题初值问题的解7．⎪⎩⎪⎨⎧==-++-+=10)2(212222x y dx dy x xy y y xy x8．⎪⎪⎩⎪⎪⎨⎧===++==0000222,02V dt dxx x x a dt dx n dt x d t t9．给出函数x x e x f x x cos 2sin )(+=在点0=x 的7阶taylor 展开式以及在x=1处的 5阶taylor 展开式．10．判别下列级数的敛散性，若收敛求其和．(1)++++7151311(2)∑∞=+112n nntgπ11．求幂级数∑∞=--22)1(nnnnnx的和函数．12．求函数项级数∑∞=-1)2sin)1(nnnn xπ的和函数．。
