CP CPK PP PPK详细定义与计算方法

CPCPKPPPPKCMK的计算公式过程能力指数公式过程能力指数是用来评估一个过程的稳定性和一致性的指标，常见的过程能力指数有CP、CPK、PP、PPK和CMK。

下面将介绍这些指标的计算公式和过程。

1.CP指数：CP指数是最简单的过程能力指标，它只考虑了过程的标准离差和规格范围。

CP指数的计算公式如下：CP = (USL - LSL) / (6 * sigma)其中，USL表示规格上限，LSL表示规格下限，sigma表示过程的标准离差（标准偏差）。

CP指数的取值范围是0到无穷大，当CP>1时，表示过程能够满足规格要求；当CP=1时，表示过程的规格分布和规格范围相同；当CP<1时，表示过程不能完全满足规格要求。

2.CPK指数：CPK指数是对CP指数的改进，它考虑了过程的中心性偏移。

CPK指数的计算公式如下：CPK = Min[(USL - xbar) / (3 * sigma), (xbar - LSL) / (3 * sigma)]其中，xbar表示过程的平均值。

CPK指数的取值范围是-1到1，当CPK>1时，表示过程能够满足规格要求；当CPK=1时，表示过程的规格分布和规格范围相同；当CPK<1时，表示过程不能完全满足规格要求。

3.PP指数：PP指数是由过程的高度分布范围和规格范围来衡量的。

PP指数的计算公式如下：PP = (USL - LSL) / (6 * sigma)PP指数的取值范围也是0到无穷大，与CP指数相同。

4.PPK指数：PPK指数是对PP指数的改进，它考虑了过程的中心性偏移。

PPK指数的计算公式如下：PPK = Min[(USL - xbar) / (3 * sigma), (xbar - LSL) / (3 * sigma)]PP和PPK指数与CP和CPK指数的计算公式完全相同。

5.CMK指数：CMK指数是以过程的中心值和规格范围来评估过程的能力。

CMK指数的计算公式如下：CMK = Min[(USL - xbar) / (3 * sigma), (xbar - LSL) / (3 * sigma)]CMK指数的取值范围是-1到1，与CPK指数相同。

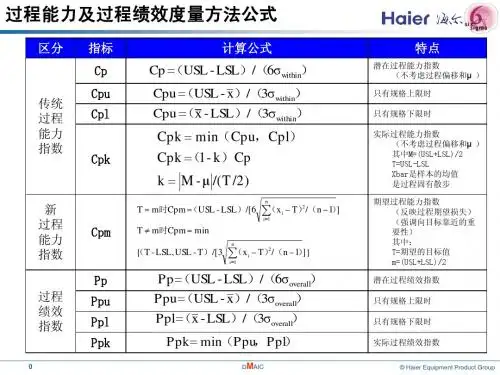
ppk,cpk,mk三者的区别及计算、首先我们先说明Pp、Cp两者的定义及公式Cp（Capability Indies of Process）：稳定过程的能力指数，定义为容差宽度除以过程能力，不考虑过程有无偏移，一般表达式为：Pp（Performance Indies of Process）：过程性能指数，定义为不考虑过程有无偏移时，容差范围除以过程性能，一般表达式为：（该指数仅用来与Cp及Cpk对比，或/和Cp、Cpk一起去度量和确认一段时间内改进的优先次序）CPU：稳定过程的上限能力指数，定义为容差范围上限除以实际过程分布宽度上限，一般表达式为：CPL：稳定过程的下限能力指数，定义为容差范围下限除以实际过程分布宽度下限，一般表达式为：2、现在我们来阐述Cpk、Ppk的含义Cpk：这是考虑到过程中心的能力（修正）指数，定义为CPU与CPL的最小值。

它等于过程均值与最近的规范界限之间的差除以过程总分布宽度的一半。

即：Ppk：这是考虑到过程中心的性能（修正）指数，定义为：或的最小值。

即：其实，公式中的K是定义分布中心μ与公差中心M的偏离度，μ与M的偏离为ε=| M-μ|3、公式中标准差的不同含义①在Cp、Cpk中，计算的是稳定过程的能力，稳定过程中过程变差仅由普通原因引起，公式中的标准差可以通过控制图中的样本平均极差估计得出。

因此，Cp、Cpk一般与控制图一起使用，首先利用控制图判断过程是否受控，如果过程不受控，要采取措施改善过程，使过程处于受控状态。

确保过程受控后，再计算Cp、Cpk。

②由于普通和特殊两种原因所造成的变差，可以用样本标准差S来估计，过程性能指数的计算使用该标准差。

4、几个指数的比较与说明① 无偏离的Cp表示过程加工的均匀性（稳定性），即“质量能力”，Cp越大，这质量特性的分布越“苗条”，质量能力越强；而有偏离的Cpk表示过程中心μ与公差中心M的偏离情况，Cpk越大，二者的偏离越小，也即过程中心对公差中心越“瞄准”。

关于Cp、Cpk、Cpm、Cpmk、Pp、Ppk什么是过程能力？过程能力是指加工方面满足加工质量的能力。

此种能力表现在过程稳定的程度，σ越小，过程能力越稳定，|M-μ|的值越小，表示过程能力的偏差越小，99.73％的质量特性散布区间在[μ-3σ,μ+3σ]。

过程能力指数Cp、CpkCp是表征过程固有的波动状态，即技术水平。

它是在过程的平均值μ与目标值M重合的情形，过程处于统计控制状态时（非分析状态），过程能力指数Cp可用下式表示：Cp=(USL-LSL)/6σ=T/6σCp与不良品率的关系Cp P1.0 0.27%1.33 0.007%1.5 6.8PPm2.0 2.0PPb实际过程中，平均值与目标志重合的情形非常少，因此引入了偏移度的概念，即过程平均值与目标值的偏离过程K=2|M-μ|/TCp-Cpk=|M-μ|/3σCpk与不良品率的关系Cpk P(%)1.0 0.13~0.271.1 0.05~0.101.2 0.02~0.031.3 48.1~96.2PPM1.4 13.4~26.7PPM过程能力指数Cpm、Cpmk过程能力指数是根据田口玄一关于质量损失函数而设计出来的。

将目标值与均值的偏差也考虑进来，因为有实际的改进意义Cpm=(USL-LSL)/6SQRT((σp)2+(|M-μ|)2)Cpm<Cp，这是因为考虑了过程平均值与目标值发生偏差的结果过程能力指数Cpmk是考虑过程能力与平均值偏离目标值的综合结果，因此又叫综合过程能力指数Cpmk=Cpk/SQRT(1+((|M-μ|)/σ)2)过程绩效指数Pp、Ppk过程Pp=(USL-LSL)/6σ总Ppk=min((USL-u)/3σ总,(u-LSL)/3σ总)Cpk——过程能力指数CPK= Min[ (USL- Mu)/3s, (Mu - LSL)/3s]Cpk应用讲义1. Cpk的中文定义为：制程能力指数，是某个工程或制程水准的量化反应，也是工程评估的一类指标。

CP、CPK、PP、PPK的定义与关系CP、CPK、PP、PPK的定义与关系CP、CPK、PP、PPK的定义与关系最近常看见论坛里面有些关于CP、CPK、PP、PPK定义的帖子，其实论坛里面都解释的很清楚了，只需要大家认真找找。

我整理了一部分，传上来，希望以后不要没认真找就随便发没多少价值帖子。

1、基本定义：σST ：短期差异，σST = Rbar/d2σLT ：长期差异，σLT =(这里本来是一个图片，可惜粘不上来)ε ：分布中心u与规范中心M的偏移，ε=∣u - M∣K ：分布中心u与规范中心M的偏移度，K=ε/2T = 2ε/T2、定义：CP ：无偏移短期过程能力指数（或无偏移固有过程能力指数）CP = T/6σ≈T/6σSTCPK：有偏移短期过程能力指数（或有偏移固有过程能力指数）CPK=（1-K）CP≈（T-2ε）/6σSTPP ：无偏移长期过程能力指数（或无偏移实绩过程能力指数）PP = T/6σ≈（TU-TL）/6σLTPPU：无偏移上单侧长期过程能力指数（或无偏移上单侧实绩过程能力指数）PPU=（TU-u）/3σ≈（TU-Xbar）/3σSTPPL：无偏移上单侧长期过程能力指数（或无偏移上单侧实绩过程能力指数）PPL=（u-TL）/3σ≈（Xbar- TL）/3σSTPPK：有偏移长期过程能力指数（或有偏移实绩过程能力指数）PPK=Min（PPU，PPL）3、比较与关系无偏移情况的CP表示过程加工的一致性，即“质量能力”，CP越大，则质量特性值的分布越“苗条”，质量能力越强；而有偏移情况的CPK表示过程中心u与规范中心M的偏移情况下的过程能力指数，CPK越大，则二者偏移越小，也即过程分布中心对规范中心越“瞄准”，是过程的“质量能力”与“管理能力”二者综合的结果。

故CP与CPK二者的着重点不同，需要同时加以考虑。

类似的，PP与PPK也需要联合应用。

对于同一个过程而言，通常，长期标准差的估计值σLT大于短期标准差的估计值σST。

CPCPKPPPPK详细定义与计算方法CP、CPK、PP、PPK是统计质量指标，用于衡量一个过程的性能，特别是其稳定性和一致性。

下面详细介绍它们的定义和计算方法。

1. CP（Process Capability，过程能力）：CP是指过程分布的极限范围与规范限制范围之间的比值。

它反映了过程的能力，即过程在可控范围内的变异性。

CP值越大，代表过程性能越好。

CP=(USL-LSL)/(6*标准差)其中，USL是规格上限（Upper Specification Limit），LSL是规格下限（lower Specification Limit）。

标准差是过程数据的平均离差平方根。

2. CPK（Process Capability Index，过程能力指数）：CPK是针对过程两侧规格限制范围的过程能力指标，考虑了偏斜度和过程中心值。

与CP相比，CPK更全面地衡量了过程性能。

CPK = min(USL - 平均值, 平均值 - LSL) / (3 * 标准差)CPK值越大，代表过程能满足规格要求的能力越强。

当CPK值大于1时，说明过程能基本满足规格要求。

3. PP（Process Performance，过程性能）：PP是指过程性能在规格限制范围内的比例，即过程的能力指数。

PP 值越大，说明过程在规格范围内变异性越小，能力越强。

PP=(USL-LSL)/(6*历史标准差)其中，历史标准差是过去的过程数据的平均离差平方根。

4. PPK（Process Performance Index，过程性能指数）：PPK是过程指标，类似于PP，但它也考虑了过程中心值。

PPK比PP更全面地评估了过程的性能。

PPK = min(USL - 平均值, 平均值 - LSL) / (3 * 历史标准差)PPK值越大，代表过程能满足规格要求的概率越高。

当PPK值大于1时，表明过程性能能够基本满足规格要求。

计算方法中常涉及的术语解释：-规格上限（USL）：产品或过程的上限要求。

CPCPKPPPPKCMK的计算公式过程能力指数公式在质量管理中，过程能力指数是用于衡量一个过程的稳定性和性能的指标。

它们可以帮助我们评估一个生产过程是否能够达到预期的质量水平。

以下是CP、CPK、PP、PPK和CMK的计算公式及其过程能力指数的定义：1.CP(过程能力指数)CP是最常用的过程能力指数，它用于评估一个过程的稳定性和可控性。

CP表示过程能力与产品的规格要求之间的比例关系。

CP的计算公式为：CP=(USL-LSL)/(6*标准差)其中，USL是上限规格限制，LSL是下限规格限制。

CP的值越接近1，表示该过程越能够满足规格要求。

如果CP小于1，则表示过程能力不足以满足规格要求。

2.CPK(过程能力指数)CPK是一种综合性的过程能力指数，它不仅考虑了过程的稳定性，还考虑了过程的中心位置。

CPK可以帮助我们评估过程是否能够在正常分布曲线的两侧均能满足规格要求。

CPK的计算公式为：CPK = min((USL - 平均值) / (3 * 标准差), (平均值 - LSL) / (3 * 标准差))CPK的值越接近1，表示该过程越能够满足规格要求。

如果CPK小于1，则表示过程能力不足以满足规格要求。

3.PP(过程性能指数)PP用于评估长期过程的能力，即过程在不同时间段内的表现。

PP基于过程能力指数CP的基础上，考虑了过程的长期变化。

PP的计算公式为：PP=(USL-LSL)/(6*标准差)PP的值越接近1，表示过程在不同时间段内的表现越能够满足规格要求。

如果PP小于1，则表示长期过程能力不足以满足规格要求。

4.PPK(过程性能指数)PPK是一种综合性的过程性能指数，它不仅考虑了过程的稳定性，还考虑了过程的中心位置。

PPK可以帮助我们评估长期过程是否能够在正常分布曲线的两侧均能满足规格要求。

PPK的计算公式同CPK的计算公式：PPK = min((USL - 平均值) / (3 * 标准差), (平均值 - LSL) / (3 * 标准差))PPK的值越接近1，表示长期过程在不同时间段内的表现越能够满足规格要求。

CP_CPK_PP_PPK详细定义与计算方法解析CP, CPK, PP, and PPK are statistical process capability indices used to evaluate the ability of a process toconsistently produce products or services within specified tolerances. These indices provide a numerical measure of process performance and are widely used in Six Sigma and other quality management approaches to assess process capability.1. CP (Process Capability Index):CP measures the capability of a process to produce products or services within the specified tolerance limits. It is calculated using the following formula:CP = (USL - LSL) / (6 * Standard deviation)Where:- USL refers to the upper specification limit, which is the maximum allowable value for a characteristic of the product or service.- LSL refers to the lower specification limit, which is the minimum allowable value for the characteristic.- Standard deviation is a measure of the dispersion or spread of the process data.A CP value greater than 1 indicates that the process is capable of meeting the specifications, while a CP value less than 1 indicates that the process is not capable.2. CPK (Process Capability Index with Centering):CPK is an improvement over CP as it takes into account the centering of the process along with its spread. It is calculated using the following formula:CPK = Min [(USL - Mean) / (3 * Standard deviation), (Mean - LSL) / (3 * Standard deviation)]Where:- USL is the upper specification limit.- LSL is the lower specification limit.- Mean is the mean or average value of the process data.3. PP (Process Performance Index):PP measures the overall performance of a process in meeting the specifications. Unlike CP and CPK, PP does not consider the centering of the process. It is calculated using the following formula:PP = (USL - LSL) / (6 * Sample standard deviation)Where:- USL is the upper specification limit.- LSL is the lower specification limit.- Sample standard deviation is the estimate of the population standard deviation based on a sample.A PP value greater than 1 indicates that the process is capable of meeting the specifications, while a value less than 1 indicates that the process is not capable.4. PPK (Process Performance Index with Centering):PPK is similar to CPK but uses sample estimates of the mean and standard deviation instead of the process mean and standard deviation. It is calculated using the following formula: PPK = Min [(USL - Sample mean) / (3 * Sample standard deviation), (Sample mean - LSL) / (3 * Sample standard deviation)]Where:- USL is the upper specification limit.- LSL is the lower specification limit.- Sample mean is the average value of the process data.- Sample standard deviation is the estimate of the population standard deviation based on a sample.PPK provides a measure of process performance considering both centering and spread, using sample estimates. A PPK valuegreater than 1 indicates that the process is capable of meeting the specifications; otherwise, it is not capable.In conclusion, CP, CPK, PP, and PPK are statistical process capability indices used to assess the ability of a process to meet specifications. CPK and PPK are improvements over CP and PP, respectively, as they consider both the spread and centering of the process. The formulas for these indices involve specifications, mean, standard deviation, and sample estimates.。

【秒懂】PPK与CPK定义，差异分析及计算定义：PP （Performance Index of Process）不考虑过程有⽆偏移，容差范围除以过程性能。

Cpk （Preliminary process Capability）考虑过程有偏差时，样本数据的过程性能。

*ppk 通常⽤来与cp及Cpk对⽐，度量和确认内改进的优先次序。

适⽤环境ppk：过程性能指数，表⽰的是过程在⼀段时间内的表现1:输出满⾜规格要求+预测图形+长期不稳定过程（不要求过程稳定）2:⼩批⽣产（试产）的过程性能评价，要求Ppk>1.67；3·⽤于实时过程性能研究和初始过程能⼒评估.Cpk：过程能⼒指数，表⽰过程本⾝的能⼒，⼀种理想的状态下的指数。

1:过程稳定+⾜够历史数据/初始数据（More than 100个体数据&25⼦组2:⼤批量⽣产后的⽣产能⼒的评价，要求Cpk>1.333:主要⽤于周期性的过程评价.注解：1、有时CPK需要借助PPK的控制界限来作控制2、PPK表⽰所有数据之间的变差；CPK剔除组内变差（组内均值），仅考虑⼦组变差。

3、PPK和CPK的区别就好像是⼀个⼈的⼯作表现和⼯作能⼒之间的差别⼀样。

4、Cpk计算之前，⼀定要检查过程是否稳定。

⼀般要求有100个数据，25个均值。

取样⽅式：⼦样定间隔时间选取（如：每隔1⼩时连续取4个样本，计算均值。

通过xbar-R图来检查过程是否稳定。

如果稳定，计算得到的是Cpk。

5、PPK不要求检查过程是否稳定。

取样⽅式：⽆需1⼩时间隔，连续取100个数据。

因PPK未检查过程是否稳定（风险），要求⽬标PPK>1.67.因PPK中可能有特殊原因变差不能称之为过程能⼒指数，⽽是过程性能指数。

6、过程不稳定，则需查明特殊原因并消除后重新进⾏评估（过程繁琐）。

对于初期数据匮乏案例，在客户同意后可采⽤PPK。

7、当过程稳定+CPK满⾜要求时，利⽤控制图来监视过程。

CPKPPKCPCA计算公式
CPK和PPK是统计过程控制（SPC）中，用来衡量过程是否满足规定
的质量要求以及过程能否稳定的指标。

CPK是针对单个过程性能的指标，
而PPK是针对整个过程能力的指标。

CPK是能力指数，用来评估过程的稳定性和一致性，可以度量过程的
直观能力，用来判断过程能否满足规定的质量要求。

计算CPK的公式如下：CPK = min((USL-Xbar)/3σ,(Xbar-LSL)/3σ)
其中，USL 是上限规格限，即过程中的上限，LSL 是下限规格限，即
过程中的下限，Xbar 是过程的平均值，σ 是过程的标准差。

PPK是潜在过程能力指数，用来评估过程的整体能力和稳定性，是计
算过程性能指数（CP）的一种方法。

计算PPK的公式如下：
PPK = min((USL-Xbar)/3σ,(Xbar-LSL)/3σ1.5)
其中，σ1.5是过程标准差的1.5倍，通常被用于计算PPK，以提供
更具挑战性和更保守的评估。

计算CP和CA的公式如下：
CP=(USL-LSL)/(6σ)
其中，CP是过程能力指数，表示过程的能力。

CP值越大，表示过程
的能力越好，也就是过程稳定性越高。

CA=(USL-LSL)/(2σ)
其中，CA是过程调整指数，表示规格带宽与过程离散度的比值。

CA
值越小，说明过程的调整能力越好。

需要注意的是，以上公式中的 Xbar 和σ 需要通过对一系列数据进行统计分析来获得，而 USL 和 LSL 则是根据产品规格要求确定的。

Cp、Cpk、Pp、Ppk过程能力计算及评价方法：1．稳定过程能力指数Cp、Cpk计算及评价方法：（1）计算公式：K=2︱M-μ︱/T注：T=规格上限USL-规格下限LSL，规范中心M= （USL+LSL）/2，μ为过程输出中心。

（A. Cp = T / 6σ（当产品和/或过程特征为双边规格时）或Cpu（上稳定过程能力指数）=（USL-μ）/3σ（当产品和/或过程特征为单边规时）Cpl（上稳定过程能力指数）=（μ-LSL）/3σ（当产品和/或过程特征为单边规时）注：σ =R / d2 （R 为全距之平均值，d2为系数，和抽样样本大小n相关，当n = 4时，d2 = 2.059；当n = 5时，d2 = 2.3267）B. Cpk=min{ USL-μ, μ-LSL}/3σ=(1-K)*Cp当产品特征为单边规格时，Cpk值即以Cpu值或Cpl值计算，但需取绝对值；Cpk值取Cpu 值和Cpl值中最小值。

(2) 等级评价及处理方法：等级Cp值判定处理方法等级说明特级CP≥1.67 过程能力过剩为提升质量，对关键项目再次缩小公差范围：为提升效率降低成本放宽波动幅度，减低设备等级。

Cp值当T和3σ比越大，Cp值也越大，也就是说过程越稳定。

1级1.67＞CP≥1.33 过程能力充足不是关键项目时可：1.放宽波动幅度。

2.降低对材料要求。

3.降低检验频次。

2级1.33＞CP≥1 过程能力尚可必需用控制图或其它方法进行控制和监督：对产品按常规进行检验。

3级1＞CP≥0.67 过程能力不足分析散步大原因，全数检验或增加检验频次。

4级0.67＞CP 过程能力严重不足停止继续加工，找出原因。

不然全数检验挑选出不合格品。

Cpk等级评价等级Cpk值改善方法处理方法等级说明A Cpk≥1.67 继续保持制程很稳定，继续保持，当Cpk大于2倍时，能够考虑缩小规格。

Cpk 值越大，则制造过程能力越稳定。

B 1.67＞Cpk≥1.33 需要改善情况理想。

Cp、Cpk、Pp、Ppk 详解1. 背景Cp, Cpk, Pp 和 Ppk这几个概念在工业制造领域的应用已经很普遍了，但是这些概念往往被混淆。

网上的解释各执其词，而且错误百出（如下图）。

就连国外网站上的讨论也是众说不一⑥。

当这些概念用中文解释时，那就更复杂了。

比如这些概念里共有的"P" 是一个简单的英语词"process"，可被翻译成什么的都有，比如"过程，工艺，工序，制程…"等等。

可想而知加了其他词以后就更复杂了。

为了方便起见，以下process均采用"过程"。

笔者2003年在学校里就学习了这些概念，而且在之后的十几年的工作中也不断地在应用这些概念。

但始终觉得没有完全理解其本质区别。

多年下来一直都是在照猫画虎，套公式，得出结果，做出判断，完事。

更有甚者，现在有现成的计算机软件，点一点鼠标就可以得到结果。

更不用知道其后台是如何计算的了。

一般来说，能做到此，也就可以了。

所以下面的解析是为有意愿深入了解这些概念的差别的读者准备的。

Cp, Cpk, Pp 和 Ppk都是用来体现过程能力的指标①②，它们是用来测量过程能力的指数（process capability index），不是过程能力本身。

很多人只知道计算这些指数，却并不知道过程的固有能力到底是什么。

那什么是过程能力（process capability）？2. 过程能力的定义过程能力是指过程本身在没有外因干预、没有漂移（drift）（即统计学意义上可控under statistical control）的情况下其产出品的均一程度 (uniformity of product)②③。

不难理解，我们不可能直接测量过程本身，而只能通过测量其产出品的某个特性来体现其能力③。

通常用被测量的特性的离散程度，即标准方差，（西格玛），来表示过程能力。

而且过程能力被量化为，即其总宽度为6个西格玛。

Cp,Cpk,Pp和Ppk之间的关系详解所有的质量经理都想知道事情是否“在控制之中”。

“受控”通常意味着过程（Process）正在生产100%合格的产品（Product）。

为此，要有一个好的过程能力或性能指数来做评价过程（Process）。

能力与性能指数有四个能力与性能指数最为常用。

虽然不断有人提出了许多其他的指数，但这四个指数有效地总结了过程和产品规格之间的关系。

Cp能力指数使用上下规格之间的差异来定义可用范围，并将其与以最小方差运行的过程所需的通用范围进行比较。

所需的通用范围为六倍的组内标准差，即6 sigma（x）。

因此，Cp是指数据的规格范围是波动范围的多少倍，这个值越高，说明数据波动幅度相对越小，过程能力强。

然而，Cp却没有考虑数据的居中性，有可能数据波动范围很小，但是却是在规格范围外波动。

Cpk则在Cp的基础上还考虑了数据波动的中心位置，从而可以用来衡量过程的中心能力。

下面这张图说明了Cp与Cpk之间的差异，数据的波动幅度一致，当数据中心偏移时，Cp不变，但Cpk就变小了。

Pp性能指数使用上下规格之间的差异作为可用范围，并将其与过去过程实际表现的标准差做比较。

在计算能力指数时，我们用的是组内标准差Sigma(X),而在计算性能指数时，用的将是样本标准差s。

因此，性能指数Pp将可用于评价过去的过程表现。

但是，它不考虑过去过程表现的中心位置中心性能指数Ppk则是通过来定义过程的有效可用范围将过程中心位置考虑了进来。

这些指数是如何相互关联的？这四个指数之间的关系如下图所示。

图上半部分的Cp与Cpk描述的是过程的潜在能力，下半部分的Pp与Ppk描述的是过程过去所表现出来的性能。

随着一个过程的运行越来越接近发挥其全部潜力，那么Pp与Ppk将向上移动，接近上层的Cp与Cpk。

上图的解读：左侧两个指数假定了过程中心与规范中心重叠，而右侧考虑了二者之间偏离的程度。

当过程中心接近规格的中心时，右边的值会向左边的值靠近。

一、 双侧公差情况的过程能力指数1﹑对于侧公差能情况，过程能力指数CP 的定义如下； σσ66L U T T T CP −== ① T 为技术公差的幅度，u t ﹑L t 分别为上﹑下公差限，σ为质量特性值分布的总体标准差。

当σ未知时，可用σ=R （bar ）/d2或σ=S （bar ）/C4估计，其中R 为样本的极差，R （bar ）为平均数，S 为样本的标准差，S （bar ）为平均数；D2、C4为修正系数，可根据样本组的个数查表获得；注意；估计值必须在稳定的状态下进行，在GB/T4091-2001《常规控制图》中有明确的规定；当CP=2、σ=0·5时，P=2ppm=2×910=。

事实上，从CP=1，σ=1时，可以得出CP=1=T/6σ，即T=6，于是σ-1/CP 。

故对于CP=2，σ=1/2=0·5，也就是说能力指数与不合格率是一一对应的。

二、单侧公差情况的能力指数1、 若只有上限要求时，而对下限没有要求时，则过程能力指数计算如下；σµ3−=U PU T C （μ< T U ） C PU 为上单侧过程能力指数，当μ≥TU 时，记作C PU =0上限要求2、 若只有下限要求时，而对上限没有要求时，则过程能力指数计算如下；σµ3lpl t c −= （μ>T L ）C PL 为下单侧过程能力指数，当μ≤TL 时，记作C PL =0下限要求上面二例中的μ与σ未知时，可用样本估计，例如用X （bar ）估计μ，用S 估计σ，三、有偏移情况的过程能力指数当产品质量特性分布的均值μ与公差中心Μ不重合，即有偏移时，不合格率必然回增大，CP 值降低，当过程能力指数不能反映有偏移的实际情况，需要加以修正，记修正后的过程能力指数为CPK ，则计算公式为；),min(PL PU C C CPK =记作分布中心μ对于公差中心M 的偏移为ε=|M-μ|，定义μ与M 的相对偏移（偏移度）K 为； TT k εε22/== （0≤K <1） 则过程能力指数修正为； ∧−≈−=−=σσ6)1(6)1()1(T K T K C K C P PK 这样，当μ=M （即分布中心与公差中心重合无偏移）时，K=0，CPK=CP ，注意CPK 也必须是在稳定状态下求得；美国的三大汽车公司（福特Ford 、通用GE 、克莱斯特Crysler ）联合制定了QS —9000标准，对于统计方法的应用提出更高的要求，QS —9000标准的认证是以ISO9000标准的认证为前提的，在QS 中提出PP 、PPK 的新概念，称之为过程性能指数（Process Perfomance Index ），又称为长期过程能力指数。

Ppk、Cpk，还有Cmk三‎者的定义是什‎么？有什么区别？如何计算？1、首先我们先说‎明Pp、Cp两者的定‎义及公式Cp（Capabi‎l ity Indies‎of Proces‎s）：稳定过程的能‎力指数，定义为容差宽‎度除以过程能‎力，不考虑过程有‎无偏移，一般表达式为‎：Pp（Perfor‎m ance Indies‎of Proces‎s）：过程性能指数‎，定义为不考虑‎过程有无偏移‎时，容差范围除以‎过程性能，一般表达式为‎：（该指数仅用来‎与Cp及Cp‎k对比，或/和Cp、Cpk一起去‎度量和确认一‎段时间内改进‎的优先次序）CPU：稳定过程的上‎限能力指数，定义为容差范‎围上限除以实‎际过程分布宽‎度上限，一般表达式为‎：CPL：稳定过程的下‎限能力指数，定义为容差范‎围下限除以实‎际过程分布宽‎度下限，一般表达式为‎：2、现在我们来阐‎述Cpk、Ppk的含义‎Cpk：这是考虑到过‎程中心的能力‎（修正）指数，定义为CPU‎与CPL的最‎小值。

它等于过程均‎值与最近的规‎范界限之间的‎差除以过程总‎分布宽度的一‎半。

即：Ppk：这是考虑到过‎程中心的性能‎（修正）指数，定义为：或的最小值。

即：Cmk是德国‎汽车行业常采‎用的参数，称为临界机器‎能力指数，它仅考虑设备‎本身的影响，同时考虑分布‎的平均值与规‎范中心值的偏‎移；由于仅考虑设‎备本身的影响‎，因此在采样时‎对其他因素要‎严加控制，尽量避免其他‎因素的干扰，计算公式与P‎p k相同，只是取样不同‎。

目录编辑本段概念CP(或Cpk)工序能力指数‎，是指工序在一‎定时间里，处于控制状态‎(稳定状态)下的实际加工‎能力。

它是工序固有‎的能力，或者说它是工‎序保证质量的‎能力。

这里所指的工‎序，是指操作者、机器、原材料、工艺方法和生‎产环境等五个‎基本质量因素‎综合作用的过‎程，也就是产品质‎量的生产过程‎。

产品质量就是‎工序中的各个‎质量因素所起‎作用的综合表‎现CPK：强调的是过程‎固有变差和实‎际固有的能力‎；CMK：考虑短期离散‎，强调设备本身‎因素对质量的‎影响；CPK：分析前提是数‎据服从正态分‎布，且过程受控；(基于该前提，CPK 一定>0)CMK：用于新机验收‎时、新产品试制时‎、设备大修后等‎情况；CPK：至少1.33CMK：至少1.67CMK一般在‎机器生产稳定‎后约一小时内‎抽样10组5‎0样本CPK在过程‎稳定受控情况‎下适当频率抽‎25组至少1‎00个样本CMK相关知‎识对Cmk，我们关心的是‎机器设备本身‎的能力，在取样过程中‎要尽量消除其‎他因素的影响‎，因此，在尽量短的时‎间内（减少环境影响‎），相同的操作者‎（减少人的因素‎影响），采用标准的作‎业方法（法），针对相同的加‎工材料（同一批原材料‎），只考核机器设‎备本身的变差‎。

什么是过程能力？过程能力是指加工方面满足加工质量的能力。

此种能力表现在过程稳定的程度，σ越小，过程能力越稳定，|M-μ|的值越小，表示过程能力的偏差越小，99.73％的质量特性散布区间在[μ-3σ,μ+3σ]。

过程能力指数Cp、CpkCp是表征过程固有的波动状态，即技术水平。

它是在过程的平均值μ与目标值M重合的情形，过程处于统计控制状态时（非分析状态），过程能力指数Cp可用下式表示：Cp=(USL-LSL)/6σ=T/6σCp与不良品率的关系Cp P1.0 0.27%1.33 0.007%1.5 6.8PPm2.0 2.0PPb实际过程中，平均值与目标志重合的情形非常少，因此引入了偏移度的概念，即过程平均值与目标值的偏离过程K=2|M-μ|/TCp-Cpk=|M-μ|/3σCpk与不良品率的关系Cpk P(%)1.0 0.13~0.271.1 0.05~0.101.2 0.02~0.031.3 48.1~96.2PPM1.4 13.4~26.7PPM过程能力指数Cpm、Cpmk过程能力指数是根据田口玄一关于质量损失函数而设计出来的。

将目标值与均值的偏差也考虑进来，因为有实际的改进意义Cpm=(USL-LSL)/6SQRT((σp)2+(|M-μ|)2)Cpm<Cp，这是因为考虑了过程平均值与目标值发生偏差的结果过程能力指数Cpmk是考虑过程能力与平均值偏离目标值的综合结果，因此又叫综合过程能力指数Cpmk=Cpk/SQRT(1+((|M-μ|)/σ)2)过程绩效指数Pp、Ppk过程Pp=(USL-LSL)/6σ总Ppk=min((USL-u)/3σ总,(u-LSL)/3σ总)。