能带论计算方法简介

第三章 能带的计算方式周期场中的单电子波动方程除少数几种简单的理想模型外，都只能用近似方式求解。

目前，主要的近似方式有：准自由电子近似，紧束缚近似，原胞法，正交化平面波法，赝势法和P K•法等。

每一种近似方式都有其长处，也有其局限性，只能用于必然的情况。

在这一章中简单介绍两种。

§3-1准自由电子近似法在这种近似方式中假设原子的外层电子在晶体的周期性势场中运动，且势能的周期性转变部份很小，可作为微扰来处置。

这种处置，电子的运动一方面和自由电子相近，另一方面又能反映出周期场中运动的电子所具有的周期性特征。

这种方式较粗糙，适用于金属中的电子。

一．一维情况设周期为a 、长度为L 的线状晶体沿x 方向。

电子波动方程为)()()](2[222x E x x V dxd m ψψ=+- （3-1） 式中，∑∑≠≠+=+=02000)(m ax mi m m xiK m eV V eV V x V m π （m aK m π2=为任意倒格矢）具有晶格的周期性，V 0是电子在晶体中的平均势能。

由于V(x)为实数，故有*m m V V =-令：W(x)为势函数中周期性转变部份，则 ∑≠=02)(m ax mi meVx W π （3-2）于是波函数可改写为)()()](2[0222x E x x W V dxd m ψψ=++- （3-3） 按照准自由电子近似的大体假设，W(x)很小，可看成微扰。

从而可先求解无微扰的电子波动方程)()(]2[0000222x E x V dxd m k k ψψ=+- （3-4）其解为平面波ikx k e Lx 1)(0=ψ （3-5）相应的能量谱值02202)(V mk k E += （3-6） 这里，k 是平面波的波矢量。

在周期性边界条件下，k 只能取断续值：l Lk π2=， ,3,2,1,0±±±=l 这些知足周期性边界条件的平面波彼此正交并归一化'''',,0)(20)(11l l k k L Lxl l i L x k k i dx e L dx eL δδπ===⎰⎰-- （3-7） 当存在周期性转变的微扰W(x)时，波动方程的零级能量谱值为E 0(k)。

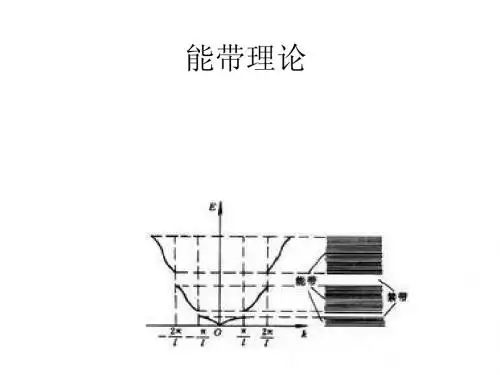
能带理论能带理论是目前研究固体中电子运动的一个主要理论基础，它预言固体中电子能量会落在某些限定范围或“带"中，因此，这方面的理论称为能带理论。

对于晶体中的电子，由于电子和周围势场的相互作用，晶体电子并不是自由的,因而其能量与波失间的关系E （k ）较为复杂，而这个关系的描述这是能带理论的主要内容.本章采用一些近似讨论能带的形成,并通过典型的模型介绍能带理论的一些基本结论和概念。

一、三个近似绝热近似：电子质量远小于离子质量，电子运动速度远高于离子运动速度，故相对于电子的运动，可以认为离子不动，考察电子运动时,可以不考虑离子运动的影响，取系统中的离子实部分的哈密顿量为零。

平均场近似:让其余电子对一个电子的相互作用等价为一个不随时间变化的平均场。

周期场近似: 无论电子之间相互作用的形式如何，都可以假定电子所感受到的势场具有平移对称性。

原本哈密顿量是一个非常复杂的多体问题，若不简化求解是相当困难的，但 经过三个近似处理后使复杂的多体问题成为周期场下的单电子问题，从而本章的中心任务就是求解晶体周期势场中单电子的薛定谔方程，即其中二、两个模型(1）近自由电子模型1、模型概述 在周期场中，若电子的势能随位置的变化（起伏）比较小，而电子的平均动能要比其势能的绝对值大得多时，电子的运动就几乎是自由的.因此,我们可以把自由电子看成是它的零级近似，(222U m ∇+)()(r U R r U n=+而将周期场的影响看成小的微扰来求解。

（也称为弱周期场近似）2、怎样得到近自由电子模型近自由电子近似是晶体电子仅受晶体势场很弱的作用，E （K ）是连续的能级。

由于周期性势场的微扰 E （K ）在布里渊区边界产生分裂、突变形成禁带,连续的能级形成能带，这时晶体电子行为与自由电子相差不大，因而可以用自由电子波函数来描写今天电子行为。

3、近自由电子近似的主要结果1) 存在能带和禁带：在零级近似下，电子被看成自由粒子，能量本征值 E K0 作为 k 的函数具有抛物线形式.由于周期势场的微扰，E （k ）函数将在 处断开，本征能量发生突变,出现能量间隔2︱V n ︱,间隔内不存在允许的电子能级，称禁带；其余区域仍基本保持自由电子时的数值。

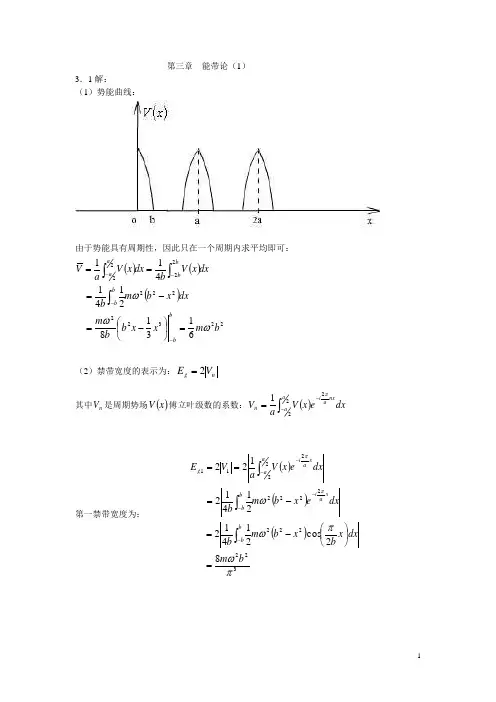
第三章 能带论（1） 3．1解：（1）势能曲线：由于势能具有周期性，因此只在一个周期内求平均即可： ()()()223222222222613182141411bm x x b b m dxxbm bdxx V bdx x V aV bbbb bbaaωωω=⎪⎭⎫ ⎝⎛-=-===----⎰⎰⎰（2）禁带宽度的表示为：n g V E 2=其中n V 是周期势场()x V 傅立叶级数的系数：()dx ex V aV aanxain ⎰--=2221π第一禁带宽度为：()()()32222222222221182c o s 2141221412122πωπωωππbm dx x b xbm bdxexb m b dxex V aV E bbxa i bbaaxaig =⎪⎭⎫⎝⎛-=-===⎰⎰⎰-----第二禁带宽度为：()()()222222222222422c o s 2141221412122πωπωωππbm dx x b xbm bdxexb m bdxex V aV E bb xb ibbaaxaig =⎪⎭⎫⎝⎛-=-===⎰⎰⎰-----3．2解：周期性势能可改写成：()()()()()[]rk i rk i rk i rk i y a x a i y a x a i y a x a i y ax a i yaiya i x ai xa i eeeeU eeee U ee ee U y a x a U y x V 1,11,11,11,12222222222222cos 2cos 4,+++-=⎥⎥⎦⎤⎢⎢⎣⎡+++-=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+-=⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛+--ππππππππππππππ由上式给出的周期性势能只有下面四个傅氏分量不为零： ()()()()()()()()U k V k V k V k V -====----1,11,11,11,1而⎪⎭⎫⎝⎛a a ππ,点正好处于()211,1b b k +=的垂直平分线上，即处在第一布里渊区边界上，故电子能量在那里发生分裂，其能隙大小为()()U k V E g 221,1==3．4（1）证：由教材p61(3.2.30)和（3.2.31）两式，对于基元中原子数p>1的复式晶格，且由同种原子组成的基元，有：()∑⋅-=jj h Gd G i f S he x p ① ()()fS G V G V hGh h1=②其中：()h G V 是复式晶格周期势()r V对其某一倒格矢h G 的傅立叶分量。

晶体的能带理论一、能带理论（Energy band theory ）概述能带理论是讨论晶体（包括金属、绝缘体和半导体的晶体）中电子的状态及其运动的一种重要的近似理论。

它首先由 F.布洛赫和L.-N.布里渊在解决金属的导电性问题时提出，它把晶体中每个电子的运动看成是独立的在一个等效势场中的运动，即是单电子近似的理论；对于晶体中的价电子而言，等效势场包括原子实的势场、其他价电子的平均势场和考虑电子波函数反对称而带来交换作用，是一种晶体周期性的势场。

即认为晶体中的电子是在整个晶体内运动的共有化电子，并且共有化电子是在晶体周期性的势场中运动的；由此得出，共有化电子的本征态波函数是Bloch函数形式，能量是由准连续能级构成的许多能带。

二、能带的形成图11.电子共有化对于只有一个价电子的简单情况：电子在离子实电场中运动，单个原子的势能曲线表示如图1。

图2 当两个原子靠得很近时：每个价电子将同时受到两个离子实电场的作用，这时的势能曲线表示为图2。

当大量原子形成晶体时，晶体内形成了周期性势场，周期性势场的势能曲线具有和晶格相同的周期性!（如图3所示）即:在N 个离子实的范围内，U 是以晶格间距d 为周期的函数。

实际的晶体是三维点阵，势场也具有三维周期性。

图3分析：1.能量为E1的电子，由于E1小，势能曲线是一种势阱。

因势垒较宽，电子穿透势垒的概率很微小，基本上仍可看成是束缚态的电子，在各自的原子核周围运动；2.具有较大能量E3 的电子，能量超过了势垒高度，电子可以在晶体中自由运动；3.能量E2 接近势垒高度的电子，将会因隧道效应而穿越势垒进入另一个原子中。

这样在晶体场内部就出现了一批属于整个晶体原子所共有的电子，称为电子共有化。

价电子受母原子束缚最弱，共有化最为显着！可借助图4理解电子共有化：图4晶体中大量的原子集合在一起，而且原子之间距离很近.致使离原子核较远的壳层发生交叠，壳层交叠使电子不再局限于某个原子上，有可能转移到相邻原子的相似壳层上去，也可能从相邻原子运动到更远的原子壳层上去，这种现象称为电子的共有化。

文章标题：能带结构计算质量的方法及应用序在固体物理学和材料科学领域，能带结构是一种重要的理论工具，用于描述固体材料中电子的动力学行为。

根据能带的结构计算质量的方式在材料设计和性能预测中发挥着重要作用。

本文将就能带结构计算质量的方式进行深入探讨，探索其在材料科学中的应用。

一、了解能带结构的基本概念在讨论能带结构计算质量的方式之前，首先需要了解能带结构的基本概念。

在固体物理学中，能带结构描述了材料中电子的能级分布情况，可以用来预测材料的导电性、光学性质等。

能带结构的计算是通过量子力学的理论方法来实现的，其中包括密度泛函理论(DFT)、紧束缚模型等。

二、常用的能带结构计算方法1. 密度泛函理论(DFT)：DFT是计算固体材料能带结构的常用方法之一。

它基于电子的密度分布来描述材料的物理性质，通过求解Kohn-Sham方程得到能带结构。

DFT方法在预测材料性质方面具有广泛的应用，但也存在一些近似和误差。

2. 紧束缚模型：紧束缚模型是另一种常用的计算能带结构的方法。

它将材料中原子之间的相互作用考虑在内，通过调整模型参数得到能带结构。

紧束缚模型在研究局域材料的能带结构和杂质效应方面具有优势。

3. 第一性原理计算：第一性原理计算是以量子力学为基础，通过解薛定谔方程来计算材料性质的方法。

它不依赖于经验参数，可以较准确地描述材料的能带结构，但计算成本较高。

三、能带结构计算在材料科学中的应用1. 材料设计：通过计算材料的能带结构，可以预测材料的导电性、光学性质等，有助于材料设计和合成。

2. 材料性能预测：能带结构计算可以帮助预测材料的电子传输性质、光学吸收谱等重要性能指标，为材料性能预测提供依据。

3. 材料优化：根据能带结构计算的结果，可以对材料进行结构优化，提高材料的性能和稳定性。

四、个人观点和理解能带结构计算是材料科学中一项重要的研究工作，对于材料设计和性能预测具有重要意义。

在未来的研究中，我认为可以结合机器学习等新技术，进一步改进能带结构计算的精度和效率，推动材料科学领域的发展。