现代控制理论刘豹第三版
- 格式:pptx
- 大小:5.27 MB
- 文档页数:70


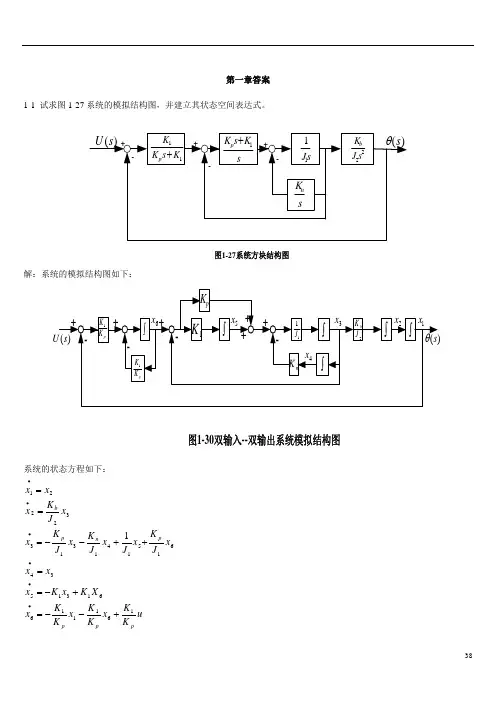
第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
图1-27系统方块结构图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。

bpppp K x x x x J xx K xJx K K K x x u K K K xJ J K x x p x K xK xxx Ax+Buy=CxA=BCM Mf f M MM y f K c c B y yM y f K c B y K c c B y yffx Ax+Buy=CxA=By y y y u usG ss s sa a ab b bAB n n n b nba a ab a b aC bba b a a b a aabb a b a T TBCa ab a aa aa aaby y y y u u us sG ss s sb b b bCBTW s C SI A B d SI ASSS S S S SSSSSAA P P P A P P P T P P TPPP P T ATJ T ATT BCTW s W s I W s W s2 4.At e10140 A5 15!4!Atett 11A P P112T jP222A P P212T jP1122Tj j412cos 2sin 214sin 22cos 22At t tt e Te T t t 112111()444S S SI A S SS22t t 22))jt jt e21141A223323232233112!3!13715,2!66281344,1562!At e I AtA t A t t t t t t t t t t t t t 6e At e 3031()31()4t tt t t e e t e e 0Ate I 1T2.010001(1,0)xx u y x 1(0),()1x u t 22.1...2!A I Att ()00201()122111222tAt A t t t td t td t x x = =01te e Bu d)(10t t 110110110t27.231.00()()(0)(),()At At t t x x x t e x e t u K BK Ku ()00()t At A t e e B d x x K ()00()t At A t e e d x B ()00|At A t e e0At At e e B x 2t t u K 0(0)x x ()01()t d ()00t At A t e e d B x K 1()00|At A t t e A e B x K 10()At At e A e I B x K 1x x K Kx K B K ()1()A e e B t 0At t3()1()t t u k 0(0)x x ()00(t)1()tAt A t e eB t d x x K 00tAt A At e e d e B x K ()'A A e e A e A 0t 000|t t A tA A e e d A e A 0|t110|A A t Ate A e 11()A At A te A e I 210()()At At At At t e A e I A tee B x x 210()At At e A e I A t B x KK d 00t 1t A A e d Ae e d2-9.2-21s,0.1T s 11u 2u 111212x x Ku x x u 12u u y210120;1.11110010I A P P 1101T P 22200011I A P P 112P 0111T 1T 11101100()0AT T T G T eT T e e 000()0101001(1)T TAt t T T K H T e dtBdt e e K e K T e T T 111Te t e 11K T e TT 0(1)011221212(1)()()()()(1)()()()0()11()(1)0()(1)T TT T12x k x k G T H T u k x k x k x k ex k eu k K e u k K T e T12()()21()u k x k y k x k 0.1Ts0.110.1210.12(1)0(1)()()x k ex k e K e u k K e12()()21()x k y k x k 1Ts10.1)(1x k ()x k ()u k 12109).9)0.9)0.1(1111221112(1)()0(1)()11()(1)0()1x k x k e x k x k eu k K e u k Ke12()()21()x k y k x k 112222(1)()()()(1)()()()()100()()10x k x k u k TA I TBx k x k u k x k u k T KT x k u k TT20.1T ss12112212(1)()0.90(1)()0.11()0.10()0.1x k x k x k x k u k K u k 1T 1122(1)()()000(1)()()111x k x k u k K x k x k u k 1111At e t2AB BA3-11x u2x4 ya, b, c, d1122334412340001000110000100010x x a x x b u x x c x x dx x yx x 02M b AbA bA b 22100001001a a a a c a ac c a c d,a, b, c, d4rankM 323223222230011100C CA c NCA a c b c cCA a ac c b bc c c 4rankN 00,a, b, c, d 222121110x x a b u x x c dx yx 11b a M b Abc d11b a Ma b c c dda b c d1110C NCA a bb3abcdabcd331121[]1M b Ab 210M211211C NCA 21N212121234A 11b10c 123411M bAbrank 2M 3412det 0M12341TC N C CACA2det 0N20432233231341322232831441333232223232332232323det 1410142510486624M M 012123b Ab A b1220010141413C NCA CA det 0N 32226825()14343s s s W s s s s s I 0134A 01b52Tc1II01TA2b 01T 1d 311200011012MbA bdet 0M 3rankM 3425d c Ab010001100cR det 0c3R 1cR 0011000101014ˆ1202c cA R AR 1ˆ100Tc b R b cc cR 3()W s 231()1s s W s s s2111231001001001001sss12101,,10010000r r rrrI A I II200100100r crrI0010000000000011010000000000000000002r00000000,001001r cr rB I 012cC 00:20000000000c cc cC NC A C A 100011001000001000()36Rank N c 1010100100000110011o R 1000110011000000001000010100000010000o R 00000100110010000010001000oR 100000010121212121ˆˆˆˆ0000000000000000ˆ00110000100011001000o oA AR AR AAA 1ˆˆ1000ˆ00o BBB R B10000112ˆ0ˆˆoCCR C C 100100000001211111111ˆˆˆ00110ˆˆ100,00,00001100ˆ010m mA B C W AA B B C C W s 23()11001001001001ss W s s s s s s120012000110,,011000312()01200000000000000100000001000000010000100mm m om m mmmmIA I I I I 000,0100B 00001000000001o m m mC I :1000101122000000010000010000100100100100001001o o o ooMB A B A B 36rankM 1cR 010010100000100100001000cR 0010000100001000100010000000001000110011000100000cR 10110ˆc o cAR A R 000010100000010100ˆ00000c oBR B 00000000000000000001100100ˆ001000o cCC R 11111111ˆˆˆ010ˆˆ000,100100ˆ001m mA B C W AA B B C C 1n 1001,00M b Ab A b1nA 233-33234-11()TQ P x x 121322233233P P P P P P P P P x 110112131P =0220317.750i221101003()Q x 2TQ x x 131P11233160()Q x ()117.75ix P 11434-22112211221221A a a a a a a1211221211221221a aa a a aQ IPTA12221222122221221001 a a P P P P a a11112112()1a P a P211211221112122()a a P a P a P121221222()1a P a PP=11P1221222P PAP PA QP Pa a P P a a1121111211121112112r P t A A222r P t A A11222111122r a a a a P t A A r t AA1122r t A a a 11221221A a a a a P11P 112212244r r P P P t A At A A22111212212()()04r a a a a t A A 112212210A a a a a 11P 0A0r t A 1122a a 112212210a a a a 1122a a 4-3121()v x22x x 0ex ()0v x22121()266v x x x x x 2336PP 2i0iiiP ()0v x x()v x TA P PAQQI302x xP T111P120P22212()v xx x11x 22x5-21120010,,01011010100990Mb Ab A b 3rankM)100k 2010,,01011010100990M b Ab A b 3rankM2I321111A1112112212100100010010110100111019901001011111 cIT A b Ab b10cIA20120100011111A bKb T0.13221()(11)(11)f *32()122440f 40131K314 1.20.c KKT 15-512Mb Ab A b 24001015det 0M 5-8(1);1100200c A B20121010det detdet10c A B c A B Ec A B;RankM 13kMc A B 05-10(1)cNcA(2)II:01y cTx x(3)12,gGg :12221()det()1g f I A Gc g g g (4):*2()()(2)322f r r rr(*222113ˆ;2002rrx u y rr2ˆˆˆ()0113ˆˆ()002Ax bu G y y r;x u y yr(1)(2)22101- =10000g g A Gc g g 2121=detf I A Gcg g g :*2()()(2)322f r r r r232r Gr12g 11)(det[(-)]。

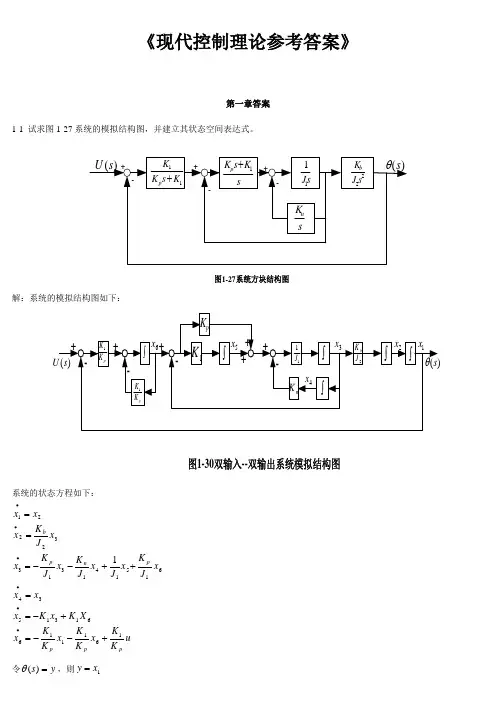
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。