复变函数极限
- 格式:doc
- 大小:1.59 MB
- 文档页数:17

关于复变函数求极限的方法浅谈复变函数是数学中的一个重要分支,它在物理、工程、经济等领域都有着广泛的应用。
在复变函数中,求极限是一个基本且重要的问题,它可以帮助我们理解函数的性质和行为。
本文将就复变函数求极限的一些方法进行浅谈,希望能够帮助读者更好地理解这个问题。
1. 利用极限的定义在求解复变函数的极限时,我们可以直接运用极限的定义。
设f(z)是一个复变函数,z0是一个复数,则当z趋向z0时,如果对于任意的ε>0,都存在一个δ>0,使得当0<|z-z0|<δ时,有|f(z)-A|<ε成立,那么我们就称A是f(z)当z趋向z0时的极限,记作lim(z→z0)f(z)=A。
这种方法直接运用极限的定义来求解复变函数的极限,可以帮助我们理解极限的概念和性质。
2. 利用复变函数的性质复变函数在求解极限时,通常会利用其性质进行变换和简化。
比如利用复变函数的加法和乘法的性质,可以将复变函数进行分解和合并;利用复变函数的倒数性质,可以将复变函数进行倒数运算,从而简化计算。
这些性质可以帮助我们更好地理解和处理复变函数的极限问题。
4. 利用洛必达法则洛必达法则是求解极限问题的一个重要工具,它也适用于复变函数的极限问题。
当复变函数的极限存在,并且是无穷大或者无穷小的形式时,可以利用洛必达法则对极限进行运算。
具体来说,当被求极限的函数以及其极限为0或无穷时,可以对其进行求导,然后再求极限,从而简化极限的计算。
这种方法在处理复杂的复变函数极限问题时非常有用。
5. 利用泰勒展开对于复变函数,我们还可以利用泰勒展开来求解其极限。
泰勒展开是将一个函数在某一点附近展开成一个无穷级数的形式,可以将一个复变函数表示为一系列幂函数的和。
利用泰勒展开,可以帮助我们更好地理解复变函数的性质和行为,从而求解其极限。
复变函数求极限是一个重要且基础的问题,对于复变函数的理解和应用都有着重要的意义。
在求解复变函数的极限时,可以运用极限的定义、复变函数的性质、极限的性质、洛必达法则和泰勒展开等方法,从而更好地理解和处理复变函数的极限问题。

关于复变函数求极限的方法浅谈复变函数是指在复平面上定义的函数。
复变函数具有许多特殊的性质和求极限的方法,下面就复变函数求极限的方法进行浅谈。
对于复变函数f(z)而言,极限的概念与实变函数有所不同。
在复平面上,点z趋于复数a时,函数f(z)的极限L存在的充要条件是,对于给定的ε>0,存在某个δ>0,使得当0<|z-a|<δ时,有|f(z)-L|<ε。
也就是说,当z趋于a时,函数值f(z)逼近于极限L。
对于复变函数f(z)而言,求极限时可以利用以下几种方法:1. 直接代入法:对于一些简单的复变函数,可以直接代入极限点计算得到极限值。
当z→0时,f(z)=sin(z)/z,可以直接代入得到f(0)=1。
2. 利用实部和虚部的性质:复变函数可以表示为实部和虚部的和或积,因此可以利用实部和虚部的性质来求解极限。
当z→0时,f(z)=Re(z)+Im(z),可以分别计算出Re(z)和Im(z)的极限再求和得到f(0)的极限。
3. 利用极坐标表示法:复数可以用极坐标表示:z=ρ eiθ,其中ρ为模,θ为幅角。
当z→a时,可以将z和a都表示为极坐标形式,即z=ρ eiθ和a=ρ' e iθ',然后进行化简。
当z→0时,f(z)=|z|·e iarg(z),可以将z表示为z=ρ eiθ,然后进行化简计算。
4. 利用洛必达法则:洛必达法则可以用来处理一些特殊的复变函数极限。
如果f(z)和g(z)在某个点a的邻域内除了可能在a处,都有定义且连续,且g(z)≠0,当z→a时均趋于0,且f(a)=g(a)=0,那么可以利用洛必达法则求解f(z)/g(z)的极限。
5. 利用级数展开:复变函数可以用级数展开的形式来表示。
当z→a时,可以利用级数展开来计算函数的极限值。
当z→1时,f(z)=1/(1-z),可以利用泰勒展开将f(z)展开成无穷级数形式,然后进行计算。
复变函数求极限的方法有很多种。


复变函数极限 -回复复变函数极限是数学中的重要概念之一,它涉及到复数域中函数的趋近性和趋势变化。
复变函数是指以复数为自变量和函数值的函数,其极限是指当自变量趋近于某一点时,函数的取值趋近于某一特定值的性质。
复数是由实部和虚部组成的数字,可以写成a+bi的形式,其中a 和b分别代表实部和虚部,i为虚数单位。
复变函数既可以是常数函数,也可以是多项式函数、三角函数、指数函数等形式。
对于复变函数而言,它的极限可以被定义为在某一点或者在无穷远处的趋于稳定的取值。
在复分析中,我们可以使用类似于实数函数的极限定义来定义复变函数的极限。
具体而言,对于一个给定的复值函数f(x)而言,如果存在一个复数c,对于任意给定的正实数ε,存在一个正实数δ,当|x-z|<δ时,|f(z)-c|<ε成立,则我们说函数f在x处的极限为c,记作lim(f(z), z→x) = c。
这意味着当自变量z趋近于x时,函数的取值趋近于c。
值得注意的是,复变函数的极限与实变函数的极限有些微妙的差异。
在实数域中,我们可以使用左极限和右极限的概念来定义函数在某一点的极限,但是在复数域中,这种思想并不适用。
复数域中的函数极限更依赖于函数性质的整体趋势,而非局部的趋势。
复变函数极限的性质与实变函数极限的性质相似。
例如,对于两个复变函数f(x)和g(x)而言,如果它们在x处分别存在极限c和d,则有lim(f(z)±g(z), z→x) = c±d,lim(f(z)g(z), z→x) = cd,lim(f(z)/g(z), z→x) = c/d(其中d≠0)成立。
这些性质与实数域中函数极限的性质类似,但需要额外考虑复数的实部和虚部。
在复变函数极限中,我们还可以遇到一些特殊情况和特殊函数。
例如,当复变函数在某一点出现间断时,它的极限是否存在就成为一个关键的问题。
另外,柯西-黎曼方程是判定复变函数在某一点处可导性的重要条件,它要求函数满足一定的实部和虚部的偏导数关系。

关于复变函数求极限的方法浅谈1. 引言1.1 什么是复变函数求极限复变函数求极限是复变函数分析中的一个重要概念。
在实数域中,我们可以通过极限来描述函数在某一点的趋势和性质,而在复数域中,复变函数的极限同样可以帮助我们理解函数的行为。
复变函数求极限是指当自变量趋向某一复数时,函数值的极限值,即函数在该复数处的极限。
复变函数求极限不仅在复变函数分析中具有重要意义,而且在实际问题中也有着广泛的应用。
例如在电磁场理论、量子力学等领域,复变函数求极限都扮演着重要的角色。
深入理解复变函数求极限的方法和技巧对于提升数学建模能力和解决实际问题具有重要意义。
1.2 为什么重要复变函数求极限在数学领域中具有重要意义,其重要性主要体现在以下几个方面:1. 深化对复变函数性质的理解复变函数求极限是研究复变函数性质的基础和关键。
通过求解极限可以揭示函数在某一点的变化趋势和收敛性质,进而帮助我们更深入地理解函数在复平面上的特性,包括奇点、极点、函数的连续性等,从而促进对复变函数整体性质的认识和掌握。
2. 解决实际问题中的数学模型在物理学、工程学、经济学等领域,常常会遇到复杂的数学模型,其中不可避免地涉及到复变函数的极限求解。
通过对复变函数求极限,可以得到模型中一些关键参数的数值解,为实际问题的分析和解决提供数学基础和支持。
3. 拓展数学研究领域复变函数求极限是数学分析领域中的重要课题之一,其研究涉及到实分析、复分析、函数论等多个数学分支领域,对数学理论的发展和进步具有重要促进作用。
深入研究复变函数求极限的方法和技巧,可以拓展数学研究的范围,促进学科的交叉融合和知识的交流传播。
2. 正文2.1 极限存在的条件复变函数求极限在数学中起着重要的作用,但要确保复变函数的极限存在,需要满足一定的条件。
主要条件包括函数在取极限点附近有定义、极限点是函数的解析点、极限值与路径无关、以及函数在极限点附近单值和连续等。
函数在取极限点附近必须有定义,否则无法讨论极限的存在与否。


关于复变函数求极限的方法浅谈复变函数求极限是复变函数分析中的一个重要内容,它涉及到复变函数的收敛性、极限性质以及复变函数在无穷远处的行为等问题。
针对复变函数求极限的问题,我们可以采用一些特定的方法来进行求解和分析。
在本文中,我们将就复变函数求极限的一些常用方法进行浅谈,希望能够帮助读者更好地理解和应用复变函数极限的相关知识。
一、复变函数的极限概念在复变函数中,我们通常也会关注函数的收敛性和极限性质。
对于复变函数f(z)=u(x,y)+iv(x,y),当z趋于复数z_0=x_0+iy_0时,如果存在一个复数w_0=u_0+iv_0,使得对于任意给定的\varepsilon>0,都存在一个\delta>0,使得当|z-z_0|<\delta时,都有|f(z)-w_0|<\varepsilon成立,那么我们就称w_0为复变函数f(z)在z=z_0处的极限,记作\lim_{z\to z_0}f(z)=w_0。
在求复变函数的极限时,我们需要特别关注复平面上的收敛路径和极限点的位置,因为复数的极限性质可能会受到路径的选择和极限点的不同而产生变化。
在实际求解中,我们通常需要结合具体的例子来进行分析和讨论。
1、直接法在实际应用中,我们也可以通过直接法来求解其他复变函数的极限,具体的操作步骤和思路与实数函数的极限求解类似,读者在学习和掌握了复变函数的极限定义后,可以通过这种方法来进行练习和巩固。
2、间接法对于复变函数的极限求解,有时候直接采用定义来求解可能会比较困难。
这时,我们可以采用一些间接的方法来进行求解。
我们可以通过等价变形、夹逼定理、洛必达法则等方法来简化问题,从而使得求解变得更加方便和简洁。
对于函数f(z)=\frac{z^2-1}{z-1},当z\to 1时,我们可以将分子进行因式分解得到f(z)=z+1,从而将原函数转化为更加简单的形式。
这样一来,我们就可以直接求出极限\lim_{z\to 1}f(z)=2。


关于复变函数求极限的方法浅谈复变函数是指定义在复数域上的函数。
在复数域上,函数的极限存在的判定方法与实数域上的函数有所不同。
本文将从极限的定义、极限存在的条件以及极限计算方法等方面进行讨论。
1. 极限的定义对于复数列{zn},当复数z无论多么接近于z0时,对应的函数值f(z)都无论多么接近于某个复数A时,称A为函数f(z)在复数点z0处的极限,记作lim_(z→z0)(f(z))=A。
2. 极限存在的条件与实数域上的函数类似,极限存在的充要条件是满足柯西收敛准则。
即对于任意正数ε,存在正数δ,使得当|z - z0| < δ时,有|f(z) - A| < ε。
3. 极限计算方法3.1 用直接代入法计算极限当函数在z0附近连续时,可以直接将z0代入函数中计算极限。
计算极限lim_(z→1)((z+1)/(z-1))时,直接代入z=1可得lim_(z→1)((z+1)/(z-1))=2。
3.2 用极坐标法计算极限对于复数z=r(cosθ+isinθ),可以将其表示为极坐标形式,即z=|z|e^(iθ)。
利用极坐标形式计算复变函数的极限可以简化计算过程。
计算极限lim_(z→0)(z^2/(z^4+1)),可以将z=r(cosθ+isinθ)代入,得到lim_(z→0)(z^2/(z^4+1))=lim_(z→0)((r^2(cosθ+isinθ)^2)/((r^4(cosθ+isinθ)^4+1)))。
再利用欧拉公式化简即可。
3.3 用洛必达法则计算极限当计算存在一个不定型的复变函数极限时,可以使用洛必达法则。
洛必达法则适用于计算函数之间的极限,不论是实数函数还是复变函数。
计算极限lim_(z→0)((cosz-1)/z),可以利用洛必达法则转化为计算lim_(z→0)(-sinz),最终得到极限为0。
3.4 用级数展开法计算极限级数展开法是一种常用的计算复变函数极限的方法,特别适用于计算指数函数和三角函数类型的复变函数。

关于复变函数求极限的方法浅谈【摘要】复变函数是复数域上的函数,求解其极限是分析复变函数性质的重要方法之一。
本文从Cauchy定理、洛必达法则、泰勒展开、复平面几何法和绝对值不等式五个方面介绍了求解复变函数极限的方法。
通过深入浅出地讲解各种方法的原理和应用,为读者提供了多种角度理解复变函数极限的途径。
在总结了不同方法的优缺点,并给出了方法选择的建议,帮助读者更好地掌握和运用复变函数求极限的技巧。
本文全面而系统地探讨了复变函数求极限的方法,为复变函数研究者提供了重要的参考和指导。
【关键词】复变函数、求极限、Cauchy定理、洛必达法则、泰勒展开、复平面几何法、绝对值不等式、方法选择、优缺点比较。
1. 引言1.1 复变函数的概念复变函数,顾名思义,就是有两个变量的函数,通常表示为f(z),其中z是一个复数,即z=x+iy,其中x和y分别是实部和虚部。
复变函数在数学上扮演着非常重要的角色,它们可以用来描述许多自然现象,比如电磁场、流体力学等。
在实际应用中,复变函数也经常被用来解决一些复杂的问题,比如求解积分、微分方程等。
复变函数的概念最早是由欧拉引入的,他定义了复数域C,并且定义了一些复变函数的基本运算规则,比如加法、减法、乘法、除法等。
随后,高斯、柯西等数学家对复变函数进行了更深入的研究,提出了许多重要的理论和定理,比如柯西-黎曼方程、柯西定理等。
复变函数与实变函数有很多共同之处,但也有很多不同之处。
实变函数只有一个独立变量,而复变函数有两个独立变量;实变函数可以用曲线来表示,而复变函数则需要用复平面来表示。
复变函数是一种更加复杂和丰富的数学对象,它具有许多独特的性质和特点,为我们解决一些复杂的问题提供了更多的可能性。
1.2 极限的定义极限是复变函数求解过程中非常重要的概念。
在复变函数中,极限的定义与实数函数中的定义略有不同。
复变函数的极限定义如下:设f(z) 在点z_0 的某个去心邻域内有定义,则对于任意给定的正数\varepsilon,存在正数\delta,使得当0 < |z - z_0| < \delta 时,对应的|f(z) - A| < \varepsilon 成立。
复变函数极限 -回复复变函数极限是指在复平面上,当自变量趋于某一点时,函数值趋于某个确定的数值。
这个数值可以是实数或复数。
对于实函数,我们学过单个变量的极限如何计算。
而对于复变函数,它是由一个自变量所构成的复平面上的向量,因此极限的计算方式也有所不同。
考虑一个复变数函数f(z),当z趋近于某个常数z0时,f(z)的极限可以等于实数,也可以等于复数。
这种情况下,我们可以用复平面上的序列来定义极限。
若存在一个复数L,使得该函数对任意一个接近z0的复数序列z1,z2,...,zn...,其映射后的序列f(z1),f(z2),...,f(zn),...都无限趋近于L,则称函数f(z)在z0处具有极限L,记作:lim f(z)=L,其中z趋近于z0。
需要注意的是,与实变数中极限的定义不同,复变函数的极限通常不等于函数在该点的值。
即使在该点的函数值已经定义,其极限也可以不等于函数值。
因此,极限的存在和唯一性是复变函数理论中研究的重点。
对于复变函数,如果把极限的存在性和唯一性分开讨论,计算它们的方法也不同。
首先,我们来看含有单一自变量的复变函数。
如果函数只依赖于一个自变量,那么从该点出发的任意曲线上的极限都应该是相同的。
这意味着,从z0出发,极限只需要沿着坐标轴以及平行于坐标轴的直线路径来计算即可。
当自变量沿任何路径趋近于z0时,只要其极限都存在,则称函数在z0处全纯。
而对于含有多个自变量的复变函数,确定它们的极限则需要使用更丰富的工具和结论。
在这种情况下,需要先确定自变量沿着那一条路径趋近于z0。
当然,这个路径是任意选取的。
然后才能计算函数的极限。
在计算复变函数的极限时,还需要考虑函数的复杂性。
如果函数在z0处不光滑,那么极限一般是不存在的。
例如,如果函数在z0处有一个极点,那么当自变量趋近于该点时,函数值会无限趋近于无穷大或无穷小。
此时,我们通常将其认为是没有极限的。
如果函数在z0处具有其他的复杂性质,如奇点、震荡等,也可能会导致函数在该处无极限。
复变函数的极限于秀芝(渤海大学数学系辽宁锦州121000 中国)摘要:这是一篇讨论复变函数极限的论文,把我们所熟悉的数学分析中实变函数极限的定义、定理、性质,推广到复变函数中,并加以证明。
但是实变函数极限的定义、定理、性质,并不完全适用于复变函数。
例如:复变函数的极限没有保序性、正性,复变函数没有左、右极限等等。
同时,复变函数极限的定义与数学分析中的二元函数极限的定义相似,故它又具有二元函数的某些性质。
本篇论文由四个方面组成。
首先,我们讨论的是复变函数在某个定点时极限的定义,即描述性极限的定义和表达式极限的定义。
其次,我们讨论的是复变函数极限的定理,如Heine定理、Cauchy 准则、复合函数极限的定理等等,并给出了详细的证明。
再次,我们讨论的是复变函数极限的性质,即唯一性、绝对值的极限、局部有界性、四则运算法则等等,同时,我们也给了详细的证明。
最后,我们讨论的是复变函数在无穷远点的极限。
在这方面,我们将极限从有限的定点逐渐引入到无穷远点,进而给出了函数在无穷远点处极限的定义、运算法则、定理,并给予了相应的应用。
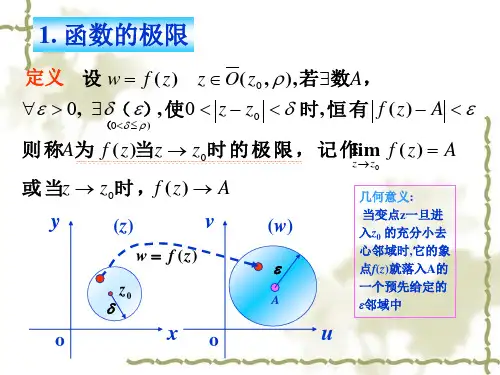
关键词:Heine 定理Cauchy 准则极限复数列Complex variable function limitYu Xiuzhi(Department of Mathematics Bohai University Liaoning Jinzhou 121000 China) Abstract:This is a discussion about complex variable function limit paper. It promotes the definition, theorem, nature of the real variable function limit to the complex variable function limit and performs to prove it .But the definition, the theorem, the nature of the real variable function limit aren’t completely suitable for the complex variablefunction.For example, complex variable f unction limit doesn’t have order nature,positive nature , and complex variable function doesn’t have left limit and right limit , and so on . Simultaneously,the definition of the complex variable function limit and the definition of the dual function limit of mathematica lanalysis is similar.So it also has some natures of dual function limit.This paper has four aspects.First,We discuss the defination of the complex variable function in some apex time , namely the definition of description limit and the definition of expression limit.Next,we discuss the theorem of the complex variable function limit.For example ,Heine theorem, Cauchy criterion,the theorem of composite function limit,and so on. And it has produced the detailed proof. Once more,we discuss the nature of the complex variable function limit. Namely unique nature , absolute value limit nature ,partially having nature, mathematical operations principle nature ,and so on . At the same time, we have also gave the detailed proof. Finally ,we discuss the complex variable function limit in the infinite point. In this aspect, we gradually introduce the limit from the limited fixed point to the infinite point, and then we have produced the definition and the theorem of limit in the infinite point . And we have gave the corresponding application.Key words: Heine theorem Cauchy criterion Limit Duplicate sequence一、复变函数极限的定义1.定义定义I :设f 在点0z 的去心邻域内有定义,当z 趋于0z 时 ,()f z 的极限为0w , 或是00lim ()z zf z w →=,指的是()w f z =可以任意接近0w ,只要我们选的点z足够地接近0z ,而不等于它。
定义Ⅱ:00lim ()z zf z w →=,表明对每一个正实数ε,都存在一个正实数δ,使得当:0<0z z |-| <δ时,有|()f z -0()f z |<ε.2.几何意义从几何意义上来说,这个定义指的是:0w 的每一个ε邻域|0|w w -<ε,有0z 的一个去心邻域0<0| z-z |<δ,使得其中的每一个z 的像w 位于0w 的ε邻域中。
注意:即使我们要考虑去心邻域0<0z z |-|<δ的所有的点,也并不要求它们的像要添满整个邻域0w w |-|<ε中。
例如:如果()f z 为常数0w ,那么z 的像,总是整个邻域的中心点,一旦δ被找到,那么它还可以由更小的正实数代替,比如说δ/2。
定义Ⅱ要求f 定义在0z 的去心邻域内,当0z 是()f z 的定义域内的一个内点时,这样的去心邻域当然总是存在的,我们可以通过如下的方式来把极限的定义拓宽到当0z 是边界点的时候,只要让不等式中的z 同时在区域内,而且在去心邻域内。
例1 我们将要证明:如果()f z =2iz 在开圆z ||<1内,那么 1lim ()2z i f z →=。
证明:点1位于f 的定义域的边界上,观察到当在区域1z ||<时,有= 22iz i|-| = 12z |-|因此,对于这样的z 和任意的正实数ε,我们可以得到,当012z <|-|<ε时 ,有因此,当δ是等于或者小于2ε的正实数时,在01z <||<中的任意点都满足定义Ⅱ中的条件,如下图所示:如果0z 是f 的定义域的内点,定义I 中的极限存在,定义Ⅱ中的第二个不等式应该对去心邻域00z z <|-|<δ内的所有的点z 都成立。
所以,符号0z z →表示z 允许以任意的方式趋近于0z ,而不是以某一特定的方向趋近于0z 。
下面的例子要强调这一点 。
例2 如果()Zf Z =⎺Z,则极限0lim ()Z f Z →不存在。
证明:<反证法> 如果极限0lim ()Z f Z →存在,则可以使点(,)Z x y =以任意的方式趋于原点,而极限值是唯一的,但是(,0)Z x =是实数轴上的非零点,则此时且当(0,)Z y =是虚轴上的非零点,则此时0()10iyf Z iy+==--。
于是,让Z 沿实数轴趋于原点时,我们发现极限值为1; 另一方向,让Z 沿虚轴趋于原点时,我们发现极限值为-1。
但是,由复变函数极限值的唯一性知,函数()f z 的极限是不存在的。
(该函数沿实数轴和虚轴趋于原点的图象,为下图所示) 二、复变函数的定理定理1 设()f z (,)(,)u x y iv x y =+,000z x iy =+,000w u iv =+,那么00lim ()z zf z w →=,当且仅当000(,)(,)lim(,)x y x y u x y u →=且000(,)(,)lim(,)x y x y v x y v →=。
证明:(充分性)假如000(,)(,)lim(,)x y x y u x y u →=且000(,)(,)lim(,)x y x y v x y v →=成立,那么()f z 的极限存在。
设极限值为000w u iv =+,即 0000lim ()z z f z w u iv →==+。
由000(,)(,)lim(,)x y x y u x y u →=知道,对任意的正实数ε,都存在正实数1δ,使得当10<<δ时,有:02u u ε|-|<(1) 对上述的ε,由000(,)(,)lim(,)x y x y v x y v →=知,存在2δ>0,使得当20<<δ时,有:02v v ε|-|<(2) 令δ取1δ和2δ中较小的数,由= 00)(u u i v v ∣(-+-)∣≤ 0u u |-|+0v v |-|和= 00()()x x i y y ∣-+-∣= ∣00()()x iy x iy +-+∣由(1)(2)所述, 有成立,只要0< 00()()x iy x iy |+-+|<δ即可.这就是说,函数()f z 的极限存在。
(必要性)假使函数()f z 的极限存在 ,即 0lim()z zf z →=0w . 由此,对于每一个正实数ε,都存在一个正实数δ,使得00()()u iv u iv |+-+|< ε (3)成立,只需 0 <00()()x iy x iy |+-+|<δ (4) 但是 0u u |-|≤00)()u u i v v |(-+-|=00()()u iv u iv |+-+| 并且因此,由不等式(3)(4)可知0u u |-|<ε,0v v |-|<ε 成立,只需0<< δ .这样就得到了00(,)(,)lim(,)x y x y u x y → = 0u ,00(,)(,)lim(,)x y x y v x y →=0v .例3 求数列 { n Z }= {1[]2ni +}的极限。