1-2复变函数的极限解析

关于复变函数求极限的方法浅谈复变函数是数学中的一个重要分支，它在物理、工程、经济等领域都有着广泛的应用。

在复变函数中，求极限是一个基本且重要的问题，它可以帮助我们理解函数的性质和行为。

本文将就复变函数求极限的一些方法进行浅谈，希望能够帮助读者更好地理解这个问题。

1. 利用极限的定义在求解复变函数的极限时，我们可以直接运用极限的定义。

设f(z)是一个复变函数，z0是一个复数，则当z趋向z0时，如果对于任意的ε>0，都存在一个δ>0，使得当0<|z-z0|<δ时，有|f(z)-A|<ε成立，那么我们就称A是f(z)当z趋向z0时的极限，记作lim(z→z0)f(z)=A。

这种方法直接运用极限的定义来求解复变函数的极限，可以帮助我们理解极限的概念和性质。

2. 利用复变函数的性质复变函数在求解极限时，通常会利用其性质进行变换和简化。

比如利用复变函数的加法和乘法的性质，可以将复变函数进行分解和合并；利用复变函数的倒数性质，可以将复变函数进行倒数运算，从而简化计算。

这些性质可以帮助我们更好地理解和处理复变函数的极限问题。

4. 利用洛必达法则洛必达法则是求解极限问题的一个重要工具，它也适用于复变函数的极限问题。

当复变函数的极限存在，并且是无穷大或者无穷小的形式时，可以利用洛必达法则对极限进行运算。

具体来说，当被求极限的函数以及其极限为0或无穷时，可以对其进行求导，然后再求极限，从而简化极限的计算。

这种方法在处理复杂的复变函数极限问题时非常有用。

5. 利用泰勒展开对于复变函数，我们还可以利用泰勒展开来求解其极限。

泰勒展开是将一个函数在某一点附近展开成一个无穷级数的形式，可以将一个复变函数表示为一系列幂函数的和。

利用泰勒展开，可以帮助我们更好地理解复变函数的性质和行为，从而求解其极限。

复变函数求极限是一个重要且基础的问题，对于复变函数的理解和应用都有着重要的意义。

在求解复变函数的极限时，可以运用极限的定义、复变函数的性质、极限的性质、洛必达法则和泰勒展开等方法，从而更好地理解和处理复变函数的极限问题。

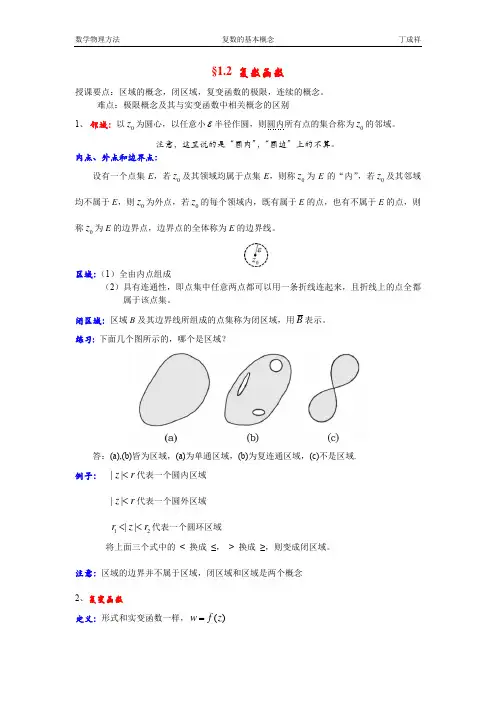
§1.2 复数函数授课要点：区域的概念，闭区域，复变函数的极限，连续的概念。

难点：极限概念及其与实变函数中相关概念的区别1、 邻域：以0z 为圆心，以任意小ε半径作圆，则圆内所有点的集合称为0z 的邻域。

注意，这里说的是“圆内”，“圆边”上的不算。

内点、外点和边界点：设有一个点集E ，若0z 及其领域均属于点集E ，则称0z 为E 的“内”，若0z 及其邻域均不属于E ，则0z 为外点，若0z 的每个领域内，既有属于E 的点，也有不属于E 的点，则称0z 为E 的边界点，边界点的全体称为E 的边界线。

区域：（1）全由内点组成 （2）具有连通性，即点集中任意两点都可以用一条折线连起来，且折线上的点全都属于该点集。

闭区域：区域B 及其边界线所组成的点集称为闭区域，用B 表示。

练习: 下面几个图所示的，哪个是区域？答：(a),(b)皆为区域，(a)为单通区域，(b)为复连通区域，(c)不是区域.例子： ||z r <代表一个圆内区域||z r <代表一个圆外区域12||r z r <<代表一个圆环区域将上面三个式中的 < 换成 ≤， > 换成 ≥，则变成闭区域。

注意：区域的边界并不属于区域，闭区域和区域是两个概念2、复变函数定义：形式和实变函数一样，()w f z =复变函数的定义域不再限于实轴上某个区间，而是复平面上的某个区域. 函数的值域也可以对应复平面上的某个区域（也可能不是）：变量：z x iy =+函数：()(,)(,,)w f z u x y iv x y ==+复变函数的实部和虚部都是一个二元函数（实函数），关于二元实变函数的很多理论都可用于复变函数中（形式可能有所变化）极限：设函数f (z )在0z 点的领域内有定义，如果存在复数A ，对于任意的0ε>，总能找到一个()0δε>，使得：当0||z z δ-<时，恒有|()|f z A ε-<，则称0z z →时f (z )的极限为A ，即0lim ()z z f z A →=对于非数学专业的学生而言，这段话略显晦涩，一个不太严格但直观的表述是：当z 以任意方式逼近0z ，()f z 都逼近A不会因为z 逼近方式之不同，而导致()f z 逼近不同的值，或者发散举例：（1）222()()xy f z i x y x y=+++ 222(,)xy u x y x y =+ 2222lim 22(,)010kx k u x y x x ky k y ==→++→ 结果将因k 之不同而不同，故极限不存在.（2）实变函数例子1()f x x= 0lim ()x f x +→=+∞， lim ()x xf x -→=-∞ 连续：00lim ()()z z f z A f z →== 因为()(,)(,)f z u x y iv x y =+，所以，复变函数的连续问题，可以归结为两个二元实变函数的连续问题。

关于复变函数求极限的方法浅谈复变函数是指定义在复数域上的函数。

在复数域上，函数的极限存在的判定方法与实数域上的函数有所不同。

本文将从极限的定义、极限存在的条件以及极限计算方法等方面进行讨论。

1. 极限的定义对于复数列{zn}，当复数z无论多么接近于z0时，对应的函数值f(z)都无论多么接近于某个复数A时，称A为函数f(z)在复数点z0处的极限，记作lim_(z→z0)(f(z))=A。

2. 极限存在的条件与实数域上的函数类似，极限存在的充要条件是满足柯西收敛准则。

即对于任意正数ε，存在正数δ，使得当|z - z0| < δ时，有|f(z) - A| < ε。

3. 极限计算方法3.1 用直接代入法计算极限当函数在z0附近连续时，可以直接将z0代入函数中计算极限。

计算极限lim_(z→1)((z+1)/(z-1))时，直接代入z=1可得lim_(z→1)((z+1)/(z-1))=2。

3.2 用极坐标法计算极限对于复数z=r(cosθ+isinθ)，可以将其表示为极坐标形式，即z=|z|e^(iθ)。

利用极坐标形式计算复变函数的极限可以简化计算过程。

计算极限lim_(z→0)(z^2/(z^4+1))，可以将z=r(cosθ+isinθ)代入，得到lim_(z→0)(z^2/(z^4+1))=lim_(z→0)((r^2(cosθ+isinθ)^2)/((r^4(cosθ+isinθ)^4+1)))。

再利用欧拉公式化简即可。

3.3 用洛必达法则计算极限当计算存在一个不定型的复变函数极限时，可以使用洛必达法则。

洛必达法则适用于计算函数之间的极限，不论是实数函数还是复变函数。

计算极限lim_(z→0)((cosz-1)/z)，可以利用洛必达法则转化为计算lim_(z→0)(-sinz)，最终得到极限为0。

3.4 用级数展开法计算极限级数展开法是一种常用的计算复变函数极限的方法，特别适用于计算指数函数和三角函数类型的复变函数。

关于复变函数求极限的方法浅谈【摘要】复变函数是数学中重要的研究对象，求解复变函数的极限是其中一个重要的问题。

本文首先介绍了复数和复变函数的基本概念，然后深入讨论了复变函数的收敛性和极限。

接着介绍了极限存在的判定方法，包括利用epsilon-delta定义和夹逼定理等方法。

对于复变函数极限的计算方法，本文主要涉及了无穷小和无穷大的概念，以及使用极坐标表示法求解的方法。

通过实际例子展示了复变函数极限在物理、工程等领域的应用，让读者更好地理解其重要性。

文章通过对复变函数求极限的方法进行深入探讨，旨在帮助读者掌握相关知识，提高数学分析能力。

【关键词】复数、复变函数、收敛性、极限、存在的判定方法、计算方法、应用、总结。

1. 引言1.1 引言在数学分析中，复变函数是指定义域和值域是复数集合的函数。

与实变函数不同的是，复变函数具有更为丰富的性质和特点。

复数可以写成实部和虚部的形式，这使得复变函数的运算更加灵活和复杂。

复数是由实数和虚数构成的，其中实数可以看作是复数的特殊情况。

复数在平面坐标系中对应于二维空间中的一个点，这样就可以用复数表示平面内的点。

复数的加法和乘法满足交换律和结合律，这使得复变函数的运算更加方便。

复数的共轭和模也为复变函数的计算提供了便利。

复变函数在分析学中的应用十分广泛，它可以描述许多物理、工程和经济现象。

在实际问题中，经常需要求解复变函数的极限。

复变函数的极限求解方法和实变函数有所不同，需要结合复数的性质和收敛性来进行推导和计算。

在接下来的内容中，我们将详细介绍复变函数的定义和性质，以及如何求解复变函数的极限。

通过深入理解复变函数的极限性质，我们可以更好地应用于实际问题的求解和分析中。

2. 正文2.1 复数和复变函数简介复数是由实数和虚数组成的数，可以用a+bi的形式表示，其中a 为实部，bi为虚部，i为虚数单位，满足i²=-1。

复数形式为a+bi的数称为复数，其中a为实部，bi为虚部。

复变函数的极限与连续性例题和知识点总结在复变函数的学习中，极限与连续性是非常重要的概念。

理解和掌握它们对于解决各种复变函数的问题至关重要。

下面我们将通过一些具体的例题来深入探讨复变函数的极限与连续性，并对相关知识点进行总结。

一、复变函数极限的定义设函数＼（w ＝ f(z)＼）定义在＼（z_0\）的某个去心邻域内，如果对于任意给定的正数＼（＼epsilon\），总存在正数＼（＼delta\），使得当＼（ 0 ＜｜z z_0| ＜＼delta\）时，都有＼（｜f(z) A| ＜＼epsilon\），则称＼（ A\）为＼（ f(z)＼）当＼（ z\）趋于＼（ z_0\）时的极限，记作＼（＼lim_{z ＼to z_0} f(z) ＝ A\）。

二、复变函数连续性的定义如果函数＼（ f(z)＼）在＼（ z_0\）处满足＼（＼lim_{z ＼toz_0} f(z) ＝ f(z_0)＼），则称＼（ f(z)＼）在＼（ z_0\）处连续。

如果＼（ f(z)＼）在区域＼（ D\）内处处连续，则称＼（ f(z)＼）在＼（ D\）内连续。

三、例题解析例 1：求＼（＼lim_{z ＼to 1 ＋ i} （z^2 2z ＋ 2)＼）解：将＼（ z ＝ 1 ＋ i\）代入＼（ z^2 2z ＋ 2\）得：＼begin{align}＆（1 ＋ i)＾2 2(1 ＋ i) ＋ 2\＼＝＆1 ＋ 2i ＋ i^2 2 2i ＋ 2\＼＝＆1 ＋ 2i 1 2 2i ＋ 2\＼＝＆0＼end{align}＼所以＼（＼lim_{z ＼to 1 ＋ i} （z^2 2z ＋ 2) ＝ 0\）例 2：判断函数＼（ f(z) ＝＼frac{z^2 1}｛z 1}＼）在＼（ z ＝1\）处的连续性。

解：先对函数进行化简：＼＼begin{align}f(z)＆＝＼frac{z^2 1}｛z 1}＼＼＆＝＼frac{（z 1)（z ＋ 1)｝｛z 1}＼＼＆＝ z ＋ 1＼end{align}当＼（ z ＼to 1\）时，＼（＼lim_{z ＼to 1} f(z) ＝ 2\），而＼（ f(1)＼）不存在，所以函数＼（ f(z)＼）在＼（ z ＝ 1\）处不连续。

复变函数的级数展开和解析延拓复变函数是数学中的一个重要概念，它在实数域上的连续性和可微性不能直接应用于复数域。

复数函数的级数展开和解析延拓是研究复变函数性质的重要方法。

本文将介绍复变函数级数展开和解析延拓的基本概念、方法和应用。

一、级数展开的基本概念复变函数的级数展开是指通过无限项的级数来表示一个复变函数。

常用的级数展开方法有泰勒级数和洛朗级数。

1. 泰勒级数展开泰勒级数展开是将一个复变函数在某点z₀处展开成幂级数的形式，表示为：f(z) = ∑[n=0,∞] [f^(n)(z₀)/n!] × (z-z₀)^n其中，f(z)是复变函数，f^(n)(z₀)表示函数f(z)在点z₀处的n阶导数。

2. 洛朗级数展开洛朗级数展开是将一个复变函数在其奇点z₀的一个环域内展开成幂级数和幂函数的形式，表示为：f(z) = ∑[n=0,∞] a_n × (z-z₀)^n + ∑[n=1,∞] b_n × (z-z₀)^(-n)其中，a_n和b_n为展开系数，可通过计算获得。

二、解析延拓的基本概念解析延拓是指将一个复变函数在定义域外继续解析成一个更大的域内的函数。

解析延拓的基本方法是通过级数展开和幂函数来延拓函数定义。

1. 极限解析延拓对于某个定义在开集D上的函数f(z)，若存在开集G，使得开集D 包含在G中，且在开集G上存在一个函数F(z)，满足：F(z) = f(z)，z∈D则称F(z)是f(z)的解析延拓。

在实际操作中，可以通过级数展开或利用幂函数的性质来进行解析延拓。

2. 常用的解析延拓方法（1）洛朗展开法：根据洛朗级数展开的形式，将函数在解析延拓域内进行展开，得到解析延拓函数。

（2）泛函方程法：通过泛函方程求解得到解析延拓函数。

（3）全纯延拓法：将局部解析延拓到整个域内。

（4）反复延拓法：在已知的定义域上反复延拓，直到无法再延拓为止。

三、级数展开和解析延拓的应用级数展开和解析延拓在数学和物理学等领域具有广泛应用。