当前位置：文档之家 › 财务管理第二章

财务管理第二章

  • 格式：ppt
  • 大小：347.00 KB
  • 文档页数：58

下载文档原格式

  / 58

合集下载

财务管理第二章

财务管理第二章

第一节
• • • • • •
资金的时间价值
一、资金时间价值的概念 二、资金时间价值的计算 （一）单利的计算 （二）复利的计算 （三）年金的计算 三、时间价值计算中的特殊问题
第二节 风险报酬率
• • • • • • • 一、风险及风险报酬率的概念 二、风险的衡量 三、风险收益率 四、风险报酬的计算 五、风险对策 六、风险的规避 七、资本资产定价模型（了解）
• 案例所涉及到的问题
案例所涉及到的问题
• • • • 现值的概念 终值的概念 现值与终值如何计算 引申出时间价值的概念
一、资金的时间价值的概念
1.西方传统观点：它是在没有风险和没有通货膨胀条件下，
股东投资就牺牲了当时使用或消费的权利，按牺牲时间计算的代 价或报酬，称为资金时间价值。
2.凯恩斯观点：是投资者放弃灵活偏好所得到的报酬。 3.马克思观点：是工人创造剩余价值的一部分。
融资租赁费现值P=9.5×5.7466=54.5927万元 低于现在购买成本60万元，因此，应选择融资租赁方式。
思考：某人贷款购买轿车一辆，在六年内每年年 末付款26500元，当利率为5%时，相当于现在 一次付款多少？(答案取整)
解：
P=A•PVIFAi,n=26500×PVIFA5%,6=26500X5.0757 =134506 (元) 轿车的价格=134506元
方法二： 先算年金现值，再算复利现值
P = A × PVIFAi,n×PVIFi,m
eg.从第三年起每年收入1000元，其现值多少？
年金现值 (n-m) 复利现值 m 0 1 2 3
i=10%
n
4 5
方法1
P=AXPVIFAi,n-mXPVIFi,m =1000XPVIFA10%,3XPVIF10%,2 =1000X2.4869X0.8264=2055.17(元)

财务管理-第二章

财务管理-第二章
6-19
流动比率
资产负债表比率
流动比率
流动比率
衡量公司用流动资产 偿还短期债务的能力.
流动资产
流动负债
用 B W公司 19X3.12.31
的数据
$1,195 = 2.39 $500
6-20
流动比率比较
流动比率
年
BW
行业平均
19X3
2.39
2.15
19X2
2.26
2.09
19X1
1.91
2.01
流动比率比行业平均水平要高
6-27
应收账款周转率
损益表 / 资产负债表
比率
应收帐款周转率
(假定所有销售都是信用销售.)
年销售净额 应收帐款
效率比率 衡量公司利用其资产的有
效程度.
6-28
For Basket Wonders December 31, 19X3
$2,211 = 5.61 $394
存货周转率
损益表 / 资产负债表
的权益. c. 购买商品和接受劳务产生
的欠款. d. 已发生但尚未支付的义务 e. 一年内需偿还的债务. f. 偿还期超过一年的债务（
长期债券）. g. 股东投入公司的最初投资
额. h. 保留在公司内部的盈利.
资产负债表的局限
计价基础是历史成本。
6-8
B W公司的 损益表
B W公司 损益表 (千元)
6-30
盈利能力比率
1、销售毛利率 2、销售净利率 3、资产收益率（ROA） 4、净资产收益率（ROE）
6-31
销售毛利率
损益表 / 资产负债表
比率
盈利能力比率
反映公司经营效率和公司 的定价政策.

第二章财务管理之时间价值和风险价值

第二章财务管理之时间价值和风险价值
先把递延年金视为普通年金，求出递延 期期末的现值，再将此现值调整到第一 期期初。
递延年金现值的计算
例15 某企业向银行借入一笔款项，银行贷款
的年利息率为8%，银行规定前10年不用还本 付息，但从第11年至第20年每年年末偿还本息 1000元，问这笔款项的现值应为多少？
思路一
P=A*[（P/A，i，n+m）- （P/A，i，m）]
A ＝ 150× （ A/F ， 8% ， 3 ） =150/3.2462=46.21万元
（三）普通年金现值的计算
P A(1 i)1 A(1 i)2 A(1 i)(n1) A(1 i)n 1 (1 i)n
P A i
P A(P / A,i, n)
举例：普通年金现值计算
例9：某企业未来5年每年年末等额从银 行取1万元，为职工发奖金，年利率3%， 现在应该存入多少金额以保证未来5年每 年末从银行等额提出1万元？
=1000*1.08*14.487
=15 645
例13 某企业租用一设备，在10年中每年年 初要支付租金5 000元，年利息率为8%， 问这些租金的现值是多少？
思路一
P=A*[（F/A，i，n-1）+1] =1000* [（F/A，8%,9）+1 ] =1000*（6.247+1） =36 235元
风险是“一定时期内”的风险。
与风险相联系的另一个概念是不确定性。严格说 来，风险和不确定性有区别。
风险可能给投资人带来超出预期的收益，也可能 带来超出预期的损失。
财务管理中的风险按形成的原因一般可分为经营 风险和财务风险两大类。
二、风险程度的衡量——概率分析法
确定概率分布 计算期望值 计算标准离差
25

财务管理-第2章ppt课件

财务管理-第2章ppt课件
第2章：财务管理的基础概念
2021/4/23
1
引例
如果你现在借给我100元钱，我承诺下课后 还你100元钱，你愿意吗？
如果你现在借给我100元钱，我承诺今后5年 每年还给你20元钱，你愿意吗？
如果你现在借给我100元钱，我承诺今后5年 每年付给你2000元钱，你愿意吗？
如果你现在借给我1万元钱，我承诺今后5年 每年付给你20万元钱，你愿意吗？
7
一、时间价值的概念
时间价值是扣除风险报酬和通货膨胀贴水后的真实报酬率。
货币时间价值是指货币经历一定时间的投资和再投资所增加的价值 ，也称为资金的时间价值。
时间价值有绝对数（时间价值额）和相对数（时间价值率） 两种表现形式。
在实务中，人们习惯使用相对数字表示货币的时间价值，即用增加价 值占投入货币的百分数来表示。
（2）普通年金现值的计算
计算普通年金现值的一般公式：
P= A(1+i)-1+A(1+i)-2+A(1+i)-3+…+ A(1+i)-n
等式两边同乘(1+i)：
(1+i) P=A+A(1+i)-1+A(1+i)-2+A(1+i)-3+…+ A(1+i)-(n-1)
后式减前式：
(1+i) P- P=A-A(1+i)-n
31
复利、年金的相关练习题
（1） F=10×（F/ P ，4%，5）=10*1.2167=12.167（万元） （1） F=10×（F/A，4%，5）= 10*5.4163=54.163 （万元） （1） P=10×（P/F，4%，5）=10*0.8219=8.219 （万元） （1） P=10×（P/A，4%，5）=10*4.4518=44.518 （万元）

《财务管理学》第二章财务管理的价值观念

《财务管理学》第二章财务管理的价值观念

价值观念的重要性
价值观念对于财务管理人员在进行财务决策时具有重要影响。正 确的价值观念能够帮助财务管理人员做出更加科学、合理和有效 的决策，提高企业的经济效益和社会效益。
财务管理中价值观念的应用
01
风险与收益的权衡
在财务管理中，风险和收益的权衡是重要的价值观念之一。财务管理人
员需要正确评估风险和收益的关系，以实现企业价值的最大化。
资源来促进社会和环境的可持续发展。
THANK YOU
感谢聆听
02
是指在不同时间点上，等额货币的价值不等，随着时间的推移， 货币的价值会增长。
计算
货币的时间价值通常通过现值和终值的计算来体现。现值是指未来某一时点的 现金流量折现到现在的价值，而终值则是指现在某一时点的现金流量在未来某 一时点的价值。
复利与年金
复利
债务与权益的权衡
在融资决策中，企业需权衡债 务和权益融资的优缺点，以确 定最优的融资方式。
企业分配决策中的价值观念
利润分配政策
01
企业需制定合理的利润分配政策，以满足股东的利益诉求和企
业的可持续发展。
股东财富最大化
02
企业应以股东财富最大化为目标，制定合理的股利分配方案。
社会责任
03
企业在追求经济效益的同时，应关注社会责任，通过合理分配
时间价值的特殊情况
通货膨胀
通货膨胀是指货币的购买力下降，物 价上涨。在通货膨胀的情况下，货币 的时间价值需要考虑通货膨胀率的影 响。
不确定性
不确定性是指未来的现金流量和时间 的不确定性。在不确定性较高的情况 下，货币的时间价值需要更加谨慎地 考虑风险和收益的平衡。
03
风险与报酬的权衡
风险的定义与分类

财务管理学第二章

财务管理学第二章

永续年金的计算
四.永续年金(特点：没有终值的年金,是 普通年金的特殊形式） 永续年金是指无限期支付的年金 V=A*1/i
几个特殊问题
五.时间价值计算中的几个特殊问题 1.不等额现金流量现值的计算 例：有一组现金流量分别为第一年年末为200，
第二年年末为300，第三年年末为150. 贴现率 为5%， 这组现金流量的现值之和是多少？ PV=200*PVIF5%,1+300*PVIF5%,2+150*PVIF5%,3=
货币时间价值

例 ：A企业购买一台设备，采用付现方式
，其价款40万元。如延期5年后付款，则价 款52万元，假设5年期存款利率为10%。试 问现付和5年后付款，哪个更有利？

货币时间价值
5年期存款：
40*10%*5+40＝60万元
显然延期付款有利。
财务管理的价值观念
一、资金的时间价值的概念
延期年金现值的计算


0 +n
1
2
1
m m+1 m+2 m+
+---+---+---+---+---+---+---+---+

两种计算方法： V=A*PVIFAi,n*PVIF 两种计算方法：i,m
⑴
V=A*(PVIFAi,m+n - PVIFAi,m)
V=A*PVIFAi,n * PVIFi,m
例：某人准备在第5年末获得1000元收入，年利息率为 10%，计算：
（1）每年计息一次，问现在存入多少钱？
（2）每半年计息一次，现在应存入多少钱？ （1）PV=1000*PVIF10%，5=621元

财务管理-第二章--财务管理的价值观念

财务管理-第二章--财务管理的价值观念
复利终值系数
复利终值公式：FV=PV(1+i)n
其中 FV ―复利终值； PV―复利现值； i―利息率； n―计息期数； (1+i)n为复利终值系数，记为FVIFi,n或(F/P,i,n)
FV=PV ·FVIFi,n
某企业为开发新产品，向银行借款100 万元，年利率为10%。借款期限为5年，问 5年后一次归还银行的本利和是多少？
FA=A·FVIFA8%,5 =A(F/A,8%,5) ＝100×5.8666＝586.66（元）
拟在5年后还清100000元债务，从现在起每年等额存入银 行一笔款项。假设银行存款利率为10%，每年需要存入多少元？
已知：5年后的终值10万元，求A？ F=A（F/A，i，n） A=F / （F/A，i，n）
2000 2000 2000 2000 2000
0
1
2
3
4
5 年末
这是期限为5年每年收入2000元的普通年金的现金流
0
1
2
3
4
5 年初
3000 3000 3000 3000 3000 这是期限为5年每年支付为3000元的预付年金的现金流
年金案例
• 学生贷款偿还 • 汽车贷款偿还 • 保险金 • 抵押贷款偿还 • 养老储蓄
•关系：利率一年内复利多次时，实际利率大于名义 利率, 假设r—名义利率；M—每年复利次数；i—实
际利率
•第一年末 F=P×(1+r/M)M
•
I=P ×(1+r/M)M－P=P[(1+r/M)M－1]
•
i= I/P=(1+r/M)M –1
•接上题：
• F=P×(1+r/M)M = 100（F/P，5%，4）

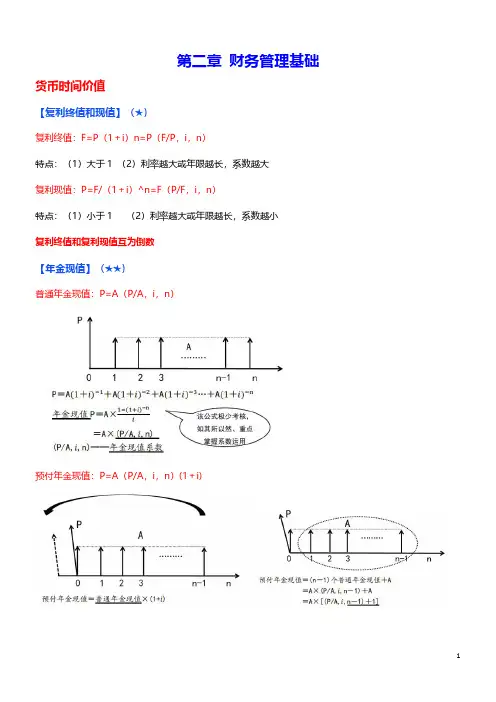
第二章 财务管理基础要点总结

第二章 财务管理基础要点总结

第二章财务管理基础货币时间价值【复利终值和现值】（★）复利终值：F=P（1＋i）n=P（F/P，i，n）特点：（1）大于1（2）利率越大或年限越长，系数越大复利现值：P=F/（1＋i）^n=F（P/F，i，n）特点：（1）小于1（2）利率越大或年限越长，系数越小复利终值和复利现值互为倒数【年金现值】（★★）普通年金现值：P=A（P/A，i，n）预付年金现值：P=A（P/A，i，n）(1＋i)递延年金现值：n代表免租期或建设期，m代表租期经营期永续年金现值：P=A/i永续增长年金现值（戈登模型）:P=A/(i-g)A代表第一年年末的金额。

【年金终值】（★★）普通年金终值：F=A（F/A，i，n）递延年金终值：F=A(F/A,i,n)预付年金终值：F=A（F/A，i，n）(1＋i)预付年金终值＝普通年金终值×(1+i)预付年金终值＝(n＋1)个普通年金终值－A＝A×(F/A,i,n＋1)－A＝A×[(F/A,i,n＋1)-1]【年偿债基金和年资本回收额】（★★）年偿债基金：A=F/（F/A，i，n）年资本回收额：A=P/（P/A，i，n）PS:普通年金终值和年偿债基金互为倒数普通年金现值和年资本回收额互为倒数插值法举例：当折现率为12%时，净现值为-50；当折现率为10%时，净现值为150，求内含报酬率。

(12%-10%）/（12%-IRR）=（-50-150）/（-50-0）。

解得：IRR=11.5%名义利率与实际利率的换算：i=（1+r/m）"-1式中：r为名义利率；m为年复利次数实际利率=（1＋名义利率）/（1＋通货膨胀率）-1实际收益率=利息（股息）率+资本利得收益率流动负债管理中的实际利率的计算（原理）实际利率=一年中付的利息等成本实际可用的资金补偿性余额下的实际利率=名义利率1一补偿性余额贴现法：实际利率=名义利率1−名义利率加息法：实际利率=2×名义利率放弃现金折扣的信用成本率=折扣率1−折扣率X360付款期−折扣期风险的衡量指标绝对数:方差σ²、标准差σ。

《财务管理》第二章：财务管理基础【货币时间价值】

《财务管理》第二章：财务管理基础【货币时间价值】

第二章财务管理基础本章主要内容本章教材主要变化删除了资金时间价值的重复例子；增加了企业风险的概念、风险矩阵以及风险管理原则的相关表述。

第一节货币时间价值1.货币时间价值的概念货币时间价值，是指在没有风险和没有通货膨胀的情况下，货币经历一定时间的投资和再投资所增加的价值，也称为资金的时间价值。

用相对数表示的货币的时间价值也称为纯粹利率（简称纯利率），纯利率是指在没有通货膨胀、无风险情况下资金市场的平均利率。

没有通货膨胀时，短期国债利率可以视为纯利率。

2.复利终值和现值利息有两种计算方法：单利计息和复利计息。

单利计息是指按照固定的本金计算利息的一种计息方式，即只对本金计算利息，各期利息相等。

复利计息是指不仅对本金计算利息，且本期的利息从下期开始也要计算利息的一种计息方式，俗称“利滚利”，各期利息不同。

【例题】A将1000元本金存入银行，利率3%，期限3年，求按单利计算的利息。

【答案】按单利计算的利息=1000×3%×3=90元【解析】按单利计算利息时，只对本金1000元计算利息，每年的利息是相等的，都是1000×3%=30元，故3年的利息是30×3=90元。

【例题】A将1000元本金存入银行，利率3%，期限3年，求按复利计算的利息。

【答案】按复利计算的利息=1000×3%+1000×（1+3%）×3%+1000×（1+3%）（1+3%）×3%=92.73元【解析】按复利计算利息时，第一年只对本金1000元计算利息，第二年对本金1000元和第一年的利息再计算利息，第三年对本金1000元和第一、第二年的利息再计算利息，每年的利息不相等。

(1)复利终值终值是指现在一定量的货币按给定的利息率折算到未来某一时点所对应的金额。

复利终值指现在的特定资金按复利计算方法，折算到将来某一时点的价值。

也可以理解为，现在的一定本金在将来一定时间，按复利计算的本金与利息之和，简称本利和。

财务管理学课件(第二章)

财务管理学课件(第二章)

（2）先付年金的终值和现值
A、终值
比普通年金终值计算加一期，减A
B、现值
比普通年金终值计算减一期，加A
（3）递延年金的终值和现值 A、终值 与普通年金计算一样 递延年金的现值与 普通年金一样吗？
B、现值
递延年金的现值
0 1 2
m A m＋1 m＋2 m＋n－1 m＋n
A
A
A
A
P=A· (P/A,i· n)
相比，将多得多少钱？
例题解答


30年后的终值FVA=500×FVIFA(5%，30)
=500×66.4388=33219.42

利息=33219.42－15000=18219.42
例题

某项目在营运后各年的现金流量如下（单 位：万元），贴现率为10%。
1 2 3 4 5 6 7 8
100 100 100 200 200 150 150 150 •根据你的理解，此项目的总回报是多少？
甲
500 乙 -1000
400
300
200
100
选择甲还是乙？
二、时间价值的计算





单利（Simple interest):在规定的时间内，对 本金计算利息 复利(Compound interest)在规定的时间内， 对本金和产生的利息计算利息 例:100元，按10%的单利存2年： 本利和=P+SI=P+P*i*n=100+100*10%*2=120 按10%的复利存2年： 本利和 =(P+P*i)(1+i)=100(1+10%)(1+10%)=121 时间价值的计算一般采用复利的概念

《财务管理学》第二章 货币的时间价值

《财务管理学》第二章 货币的时间价值

普通年金终值计算公式的推导如下：
0 1 2 n-2 n-1 n
理 财
A
A
A
A
A
A(1+i)0 A(1+i)1 A(1+i)2
FVAn = A(1+i)0+A(1+i)1+A(1+i)2+…+A(1+i)n-2+A(1+i)n-1
其中(1+i)0+(1+i)1+(1+i)2+…+(1+i)n-2+(1+i)n-1为一公比为 1+i的等比数列求和式，其值由i和n确定，称其为利率为i期 数为n的年金终值系数，简写为FVIFAi,n。
第二节 风险报酬
思考：你认为什么是风险？
理 财
一、风险的概念
•
在做某件事乊前我们就知道这件事必然会 出现什么样的结果，那么做这事有风险吗？ 答：没有风险。 • 如果我们判断：这事八九成是一个什么什 么结果，我们会得出什么结论？
答：做这事很有把握，风险不大。
如果我们说这事结果很难说，你会得 出什么结论？ 答：做这事风险很大。
理 财
课堂作业
1.某人准备为他刚读初中一年级的小 孩存一笔 款以支付其读大学的学费。预计６年以后的 学费是４万元，现银行存款利率为５％，那 么此人现在应存入多少钱？
当2中每年存款额相等时则有简便算 法，这就是年金的计算。
理 财
四、年金终值与年金现值的计算
年金是一定时期内发生的一系列金额相等的 收支款项，如折旧、租金、养老金、银行按 揭贷款的等额还款额、零存整取或整存零取 储蓄等等。年金按款项收付发生的时点不同 分为普通年金（后付年金）、先付年金、延 期年金、永续年金等。

财务管理第二章

财务管理第二章

财务管理第二章
3、风险的计量
（3）标准差－
（4）标准差系数——衡量风险
PPT文档演模板
财务管理第二章
标准差
标准差：以绝对数衡量投资项目的风 险，在期望值相同的情况下，标准 差越大，风险越大，反之亦然。
标准差系数：在期望值不同的情况下， 标准差系数越大，风险越大，反之 成立。
PPT文档演模板
财务管理第二章
PPT文档演模板
财务管理第二章
证券投资组合的策略与方法
策略
v 保守型策略 v 冒险型策略 v 适中型策略
PPT文档演模板
财务管理第二章
方法
v 选择足够数量的证券进行组合 v 把不同风险程度的证券组合在一起
v 把投资收益呈负相关的证券组合在一 起。
PPT文档演模板
财务管理第二章
财务决策按风险的程度分类
9%
6.418
PPT文档演模板
财务管理第二章
资金时间价值的几个特殊问题
贴现率的计算
8%
6.710
? x% 1%
6.667 0.043 0.292
9%
6.418
x/1% = 0.043/0.292
x = 0.147 求得利息率为：8% + 0.147% = 8.147%
PPT文档演模板
财务管理第二章
多个可加权平均，单个由证券服务机构给出。
证券组合的综合系数
PPT文档演模板
财务管理第二章
美国几家公司2011年3月16日的β系数
公司名称
β系数
雀巢
0.55
星巴克
1.26
谷歌
1.19
AT&T
0.66
耐克

《财务管理第二章》PPT课件

《财务管理第二章》PPT课件
期限为5年，年利率为10%，则到期时的本 利和为：
FV5=1000 ×(1+10% ×5)=15000（元）
• 2、单利现值
•
PV=FVn/(1+ni)
• 例2：某公司打算在3年后用60000元购置新
设备，目前的银行利率为5%，则公司现在
应存入：
PV=60000/(1+5% ×3)=52173.91（元）
– 某人存款2500元，年利率为8%，半年按复利计息一 次，试求8年后的本利和。
F2500(18% )164682.45 2
• 例：Harry以12%的名义年利率投资5000美元，按季复 利计息，那末他的资金五年后会变为多少？
[1 (0.12)]45 4
• 名义利率与实际利率：
– 名义利率只有在给出计息间隔期的情况下才有意义。 – 如若名义利率为10%，1美元每半年按复利计息情况下，
PVAn=A×[1-(1+i)-n]/i=A/i • 例：一项每年年底的收入为800元的永续年金投资，
利率为8%，则其现值为多少？
5、时间价值计算中的几个特殊问题
A、不等额现金流量现值的计算：
• 不等额现金流的终值计算公式： FVn=∑Ct(1+i)t
• 不等额现金流的现值计算公式： PVn=∑Ct/(1+i)t
• 2.若麦克每年拿出工资的5%，以利率8%存款，到 他60岁时，存款为多少？
• 3.若麦克打算在此后5年里等额消费这笔存款，每 年他可消费多少？
第二节风险衡量与风险报酬
• 问题引入： • 若买地要200万元，建造楼房要花费200
万元，但你的房地产顾问并不能肯定该 楼房未来的价值一定是420万元，而若 此时你可以花4 00万元购买政府债券从 而保证获得4 2万元收入时，你还会投资 建造楼房吗？

财务管理学第二章PPT课件

财务管理学第二章PPT课件

概率 50% 30% 20%
11
不确定型决策
决策者不清楚。
在财务管理中，通常为不确定性决策规定一些主观 概率，以便进行定量分析；不确定性规定了主观概 率后，与风险就十分相近了。因此，在企业财务管
理中，对风险和不确定性并不作严格区分。
例：A公司将100万美元投资于煤炭开发公司的股票，若 该开发公司能顺利找到煤矿，则A公司可获100%报酬； 若该开发公司不能顺利找到煤矿，A公司的报酬则为 100%，但能否找到煤矿并不知道。
14
风险-期望报酬
期
投机型普通股
望
保守型普通股
报
优先股
酬
中级公司债券
投资级公司债券
长期 Government Bonds 一级商业票据 U.S. Treasury Bills (无风险证券)
%
风险
15
二、单项资产的风险报酬
1.确定概率分布 一个事件的概率是指这一事件可能发生的机会。 设概率为Pi，则概率分布必须符合以下两个要求：
决策者对未来的情况是完全确定的或已知的决策
例：A公司将100万美元投资于利率为8%的国库 券
10
风险型决策
决策者对未来的情况不能完全确定，但它们出现的 可能性（概率）的具体分布是己知的或可估计的。
A公司将100万美元投资于某玻璃制造公司的股票，已知：
经济 繁荣 一般 衰退
报酬率 14% 12% 10%
资产定价理论：投资风险是资产对投资 组合风险的贡献。
2
1、含义:预期结果的不确定性
1、风险是事件本身的不确定性，具有客观性；
2、风险是指“一定条件下”的风险。如购买股
理
票 的所处行业、现有业绩、宏观环境等；

财务管理学第二章财务管理价值观念

财务管理学第二章财务管理价值观念

V 0 10 • (P 0V 0 8 % 2I 0 ,P FV A 8 % 1) I 0 , 1 F0 A (9 .0 8 0 1 6 .7 8 )1 31 (元 )08
财务管理学
21
2.1 货币时间价值
4、永续年金现值的计算 永续年金是指期限为无穷的年金。绝大多数优先股因为有固定的股利而又无到期日，因而其股利也 可以视为永续年金。另外，期限长、利率高的年金现值，可以按永续年金现值的计算公式计算其近 似值。 永续年金现值的计算公式为：
P V Fn• V (1 1 i)n20 (1 0 8 1 0 % 3 )15 (元 8 ) 8
P V F n V P8 V % 3 ,2 IF 0 0 .7 0 9 1 04 ( 5 元 )88
财务管理学
9
2.1 货币时间价值
➢ 2.1.4 年金终值和现值 年金是指一定时期内每期相等金额的收付款项。折旧、利息、租金、保险费等均表现为年金形式。 年金按付款方式，可分为后付年金（普通年金）、先付年金（即付年金）、延期年金和永续年金。
V0
A
•
1 i
财务管理学
22
2.1 货币时间价值
例2—8 一项每年年底的收入为800元的永续年金投资，利息率为8%，其现值为： ➢ 2.1.5 时间价值计算中的几个特殊问题
1其、现不值等计额算现公金式流为量：现值V 的0 计算80081 %100(元 0)0
P0V A 0(1 1i)0A 1(1 1i)1A 2(1 1i)2...A n1(11 i)n1A n(1 1i)n
At1(1i)t
n 1
t 1 (1 i ) t
PVIFAi,n
ADF i , n
财务管理学
13
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

•3、实际利率和名义利率的计算方法 •第一种方法：先调整为实际利率i ，再计算。实际利率 计算公式为： i=（1+r/m）m－1 终值计算公式为：
F=P ×（1＋ i）n
= P ×[1+ （1+r/m）m－1 ] n =P ×（1＋r/m）m×n
•第二种方法：直接调整相关指标，即利率换为r/m ，期 数换为m×n 。计算公式为：
教学重点与难点
• 资金时间价值的理解与计算 • 投资风险报酬的理解与计算
第一节
资金的时间价值
一、资金时间价值的概念 二、单利的计算 三、复利的计算 四、年金的计算 五、几个特殊问题
货币在使用中随时 间的推移而发生的 增值
一、资金时间价值的概念
资 金 时 间 价 值 要 素
时间(t) 利息(I) 终值(F) 折现率 (i) 现值(P)
3.单利现值的计算
p ＝F/(1+i×t)或p=F-I=F-F×i×t=F(1-i×t)
假设例1企业急需用款，该票于6月27日到银行办理贴现， 贴现率为6%，问银行付企业的金额是多少？ P＝1208× (1－6%×48/360)＝1198.34
将所生利息加入 本金再计利息
三、复利计算
1.复利终值 F=P(1+i)n 其中(1+i)n为复利终值系数，记为FVIFi,n
某人在6年内分期付款，每年年初付款500元，银行利率为10%，该项 分期付款购价相当于现在一次现金支付的购价为多少? P=A· (PVIFAi,n-1+1) =500 ×（3.7908＋1）=2395.40（元）
递延年金终值
F=A· FVIFAi,n
递延年金的终值 大小与递延期无 关
某人从第四年末起，每年年末支付100元，利率为10%， 问第七年末共支付利息多少？
•13、永续年金现值：P=A/i •14、折现率：
i=[（F/p）1/n]-1（一次收付款项）
i=A/P（永续年金）
本节时间价值的主要公式（4）
普通年金折现率先计算年金现值系数或年金终值系数再查 有关的系数表求i，不能直接求得的则通过内插法计算。
•15、名义利率与实际利率的换算： 第一种方法：r=（1+i/m）m –1； F=P ×（1＋ r）n 第二种方法： F=P ×（1＋i/m）m×n 式中：i为名义利率；m为年复利次数
•单利的现值系数与终值系数
•复利的现值系数与终值系数
•后付年金终值系数与年偿债基金系数
•后付年金现值系数与年资本回收系数
本节时间价值的主要公式（1）
•1、单利：I=P×i×n
•2、单利终值：F=P（1+i×n） •3、单利现值：P=F/（1+i×n） •4、复利终值：F=P（1+i）n 或：P（F/P，i，n） •5、复利现值：P=F×（1+i）-n 或：F（P/F，i，n） •6、普通年金终值：F=A[（1+i）n-1]/i 或：A（F/A，i，n）
二、单利的计算
1. 单利利息的计算
利息不计入本金重 复计算利息
I＝p×i×t
某企业有一张带息期票，面额为1200元，票面利率为4%， 出票日期为6月15日，8月14日到期（共60天），求到期时的利息。 I＝1200×4%×60/360 ＝8（元）
2.单利终值的计算 F＝p+p×i×t=p(1+i×t) 接上例：F＝1200(1+4%×60/360)＝1208（元）
其中
为年金终值系数记为FVIFAi,n
5年中每年年底存入银行100元，存款利率为8%，求 第5年末年金终值？
FVA5=A· FVIFA8%,5 =100×5.867=586.7（元） 思考：拟在5年后还清10000元债务，从现在起每年等额 存入银行一笔款项。假设银行存款利率为10%，每年需要 存入多少元？ 偿债基金
预付年金现值
P=A+A(1+i)-1+ A(1+i)-2+ A(1+i)-3+…+ A(1+i)-(n-1)
=A· PVIFAi,n· (1+i)或 A· (PVIFAi,n-1+1)
它是普通年金现值系数期数要减1，而系数要加1，可记作 [PVIFAi,n-1+1] 可利用“普通年金现值系数表”查得（n-1) 的值，然后加1，得出1元的预付年金现值。
=1000(4.355-1.736)=2619
或 P=A×PVIFA10%,4×PVIF10%,2 =1000×3.1699×0.8264=2619.61
永续年金没 有终值
永续年金
现值可通过普通年金现值公式导出:
当n
A ∞时， P i
五、几个特殊问题
•名义利率与实际利率
1、概念：当利息在1年内要复利几次时，给出的利 率就叫名义利率。 2、关系：i=(1+r/M)M-1或[(1+r/M)MN-1]/N r：名义利率 M：1年复利次数 I：实际利率
选择题练习
1.在复利条件下，已知现值、终值和贴现率，求计息期数，应先计 算（ ）。 A.年金现值系数 C.复利现值系数 B.年金终值系数 D.复利终值系数
2.为在第三年末获本利和1000元，求每年年末存款多少，应用 （ ）。 A.年金现值系数 C.复利终值系数 B.年金终值系数 D.复利现值系数 ）。
3.即付年金终值系数与普通年金终值系数相比，是（ A.期数减1，而系数加1 B. 期数减1，而系数减1 C.期数加1，而系数减1 D.期数加1，而系数加1
4.下列关于货币时间价值的表述正确的是（ A.货币时间价值是由于时间原因形成的价值
）。
B.货币时间价值是随着时间推移而增加的价值 C.货币时间价值是货币经过一段时间的投资和再投资所增加的价值 D.货币时间价值是没有风险条件下的货币价值 5.下列表述正确的是（ ）。
A.递延年金的终值与递延期有关，其计算方法与普通年金终值相同 B.递延年金的终值与递延期无关，其计算方法与普通年金终值相同 C.递延年金的终值与递延期无关，其计算方法与普通年金终值不同 D.递延年金的终值与递延期有关，其计算方法与普通年金终值不同
各位请注意：我们现在学 到四对互为倒数关系的系 数，你知道吗？
普通年金现值
0
A(1+i)-1 A(1+i)-2 A(1+i)-(n-1) A(1+i)-n
1
2
n-1 n
A A
A A
其中
为年金现值系数，记为PVIFAi,n
某人现在存入银行一笔现金，计划每年年末从银行提取 现金4000元，连续8年，在年利率为6%的情况下，现在应存 入银行多少元？ PVA8=A· PVIFA6%,8 =4000×6.210=24840（元） 思考：假设以10%的利率借款20000元，投资于某个寿命 为10年的项目，每年至少要收回多少现金才是有利的？ 投资回收
F=P ×（1＋r/m）m×n
4、例题： 〖例6〗本金1000元，投资5年，年利率8%，每季度复利 一次，问5年后终值是多少？ 方法一：每季度利率＝8%÷4＝2% 复利的次数＝5×4＝20 FVIF20=1000×FVIF2%,20
=1000×1.486=1486
求实际利率：
FVIF5=PV×FVIFi,5
某人将10000元投资于一项事业，年报酬率为6%，问第三 年的期终金额是多少？
F=P(1+i)3=10000×1.1910=11910（元）
2.复利现值 F=P(1+i)n
P
F (1 i ) n
其中
为现值系数，记为PVIFi,n
某人拟在5年后获得本利和10000元，假设投资报酬率 为10%，他现在应投入多少元？ P= F · PVIF10%,5 =10000× PVIF10%,5 =10000×0.621=6210（元）
1486=1000×FVIFi,5 FVIF8%,5=1.469 FVIFi,5=1.486 FVIF9%,5=1.538
i=8.25% ＞8%
方法二： i=(1+r/M)M-1
(元)
•不等额现金流量现值的计算
1、概念：指每年或每次的收入或付出的款项不相等。 2、公式：
At
第t年末的付款
•年金和不等额现金流量现值混合情况下的计算
第二章 • • • • •
财务管理的价值观念
教学目的 教学重点与难点 教学内容 复习思考 案例分析
教学目的
本章讲授影响企业财务管理工作中面临的 三个基本要素——时间价值，风险报酬，利息 率，它们均是财务决策的基本依据。学习本章， 必须要求学生准确掌握各因素的概念和计算方 法，使学生不仅树立起财务管理价值观念，而 且能熟练地运用，根据已知和预测的各种条件 进行财务决策，为以后各章学习奠定基础。
1、方法：能用年金公式计算现值便用年金公式计算，不能 用年金计算的部分便用复利公式计算。 2、例题：参见教材
•计算期短于1年时间价值的计算
例题： 〖例19〗某企业年末存入10万元，年利率为12%，每季复利 一次，问10年末企业本利和为多少？
答案： FV40=10· FVIF3%,40 =32.62(万元) 〖例20〗参见教材 •贴现率的计算 方法：计算出复利终值、复利现值、年金终值 、年金现值 等系数，然后查表求得。 例题：参见教材
可根据临界系数和临界利率计算出，其公式为：
1 i i1 (i2 i1 ) 2 1
一个内插法（插值法或插补法）的例子
某公司于第一年年初借款20000元，每年年末还本付息额均为4000元，连 续9年还清。问借款利率应为多少？
0
1
2
3
4
100
5
100
6
100