黑龙江省哈尔滨市第二十六中学2019届高三9月月考考试数学(文)试题

2019年黑龙江省哈尔滨市第二十六中学高三数学文联考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 给出以下三幅统计图及四个命题:①从折线统计图能看出世界人口的变化情况②2050年非洲人口大约将达到近15亿③2050年亚洲人口比其他各洲人口的总和还要多④从1957年到2050年各洲中北美洲人口增长速度最慢其中正确的个数是（）A．1 B．2 C．3D．4参考答案：B2. 已知动点在椭圆上,若点坐标为,,且,则的最小值是( ).（A）（B）（C）（D）参考答案：C3. 已知等差数列{a n}的前n项和为S n，，，则等于（）A. B. 1 C. 2 D. 3参考答案：B【分析】根据数列的通项公式可求得的值，再代入前项和公式，即可得答案；【详解】，故选：B.【点睛】本题考查等差数列的通项公式和前项和公式，考查运算求解能力，属于基础题.4. 已知双曲线的离心率为2，若抛物线的焦点到双曲线C1的涟近线的距离是2，则抛物线C2的方程是（）参考答案：【知识点】抛物线的简单性质；点到直线的距离公式；双曲线的简单性质．L4【答案解析】D 解析：双曲线的离心率为2．所以，即：=4，所以；双曲线的渐近线方程为：抛物线的焦点到双曲线C1的渐近线的距离为2，所以2=，因为，所以p=8．抛物线C2的方程为．故选D．【思路点拨】利用双曲线的离心率推出a，b的关系，求出抛物线的焦点坐标，通过点到直线的距离求出p，即可得到抛物线的方程．5. 在等比数列{a n}中，，，则（）A. 3B. ±3C.D.参考答案：A【分析】先设等比数列的公比为，根据题中条件判断公比为正，再由等比数列的性质，即可求出结果.【详解】设等比数列的公比为，因为，所以，又，所以.故选A【点睛】本题主要考查等比数列的性质，熟记等比数列性质即可，属于基础题型.6. （5分）已知函数f（x）=e x﹣mx+1的图象为曲线C，若曲线C存在与直线y=ex垂直的切线，则实数m的取值范围是（）A．（﹣∞，） B．（，+∞） C．（，e） D．（e，+∞）参考答案：B【考点】：利用导数研究曲线上某点切线方程．【专题】：导数的概念及应用．【分析】：求函数的导数，利用导数的几何意义以及直线垂直的等价条件，转化为（e x﹣m）e=﹣1，有解，即可得到结论．解：函数的f（x）的导数f′（x）=e x﹣m，若曲线C存在与直线y=ex垂直的切线，则切线斜率k=e x﹣m，满足（e x﹣m）e=﹣1，即e x﹣m=﹣有解，即m=e x+有解，∵e x+＞，∴m＞，故选：B【点评】：本题主要考查导数的几何意义的应用，以及直线垂直的关系，结合指数函数的性质是解决本题的关键．7. 若曲线与曲线有四个不同的交点,则实数的取值范围是A．B．C．D．参考答案：C8. 一竖立在地面上的圆锥形物体的母线长为4m，侧面展开图的圆心角为，则这个圆锥的体积等于（）A．πm3 B．πm3 C．πm3 D．πm3参考答案：D【考点】旋转体（圆柱、圆锥、圆台）．【专题】计算题；函数思想；综合法；空间位置关系与距离；立体几何．【分析】根据已知求出圆锥的底面半径和高，代入圆锥体积公式，可得答案．【解答】解：设圆锥的底面半径为r，圆锥形物体的母线长l=4m，侧面展开图的圆心角为，故2πr=l，解得：r=m，故圆锥的高h==m，故圆锥的体积V==πm3，故选：D【点评】本题考查的知识点是旋转体，熟练掌握圆锥的几何特征和体积公式是解答的关键．9. 已知中，, ,则的周长为()A．B．C．D．参考答案：C设三边分别为，则，的周长10. 一个几何体的三视图如图所示，则该几何体外接球的表面积为A. 28πB.32πC.πD. π参考答案：C二、填空题:本大题共7小题,每小题4分,共28分11. 若框图（右图）所给的程序运行结果为，那么判断框中应填入的关于的条件是___________.参考答案：12. 已知命题“?x∈R，x2+2ax+1＜0”是真命题，则实数a的取值范围是．参考答案：（﹣∞，﹣1）∪（1，+∞）【考点】命题的真假判断与应用．【分析】命题为真命题，得到判别式大于0，解不等式即可．【解答】解：∵“?x∈R，x2+2ax+1＜0”为真命题，∴△=4a2﹣4＞0，∴a＜﹣1或a＞1．则实数a的取值范围是：（﹣∞，﹣1）∪（1，+∞）故答案为：（﹣∞，﹣1）∪（1，+∞）13. 函数，则函数的所有零点所构成的集合为参考答案：【知识点】函数的零点问题 B9.解析：当时，，∴∴当时，，∴；当时，；当时，所以函数的所有零点所构成的集合为：，故答案为.【思路点拨】欲求函数函数的零点，即求方程的解，下面分：当时，当时分别求出函数的所有零点所构成的集合即可．14. 若椭圆的方程为+=1，且此椭圆的焦距为4，则实数a= ．参考答案：4或8【考点】椭圆的简单性质．【专题】圆锥曲线的定义、性质与方程．【分析】首先分两种情况：①焦点在x轴上．②焦点在y轴上，分别求出a的值即可．解：①焦点在x轴上时：10﹣a﹣（a﹣2）=4②焦点在y轴上时a﹣2﹣（10﹣a）=4解得：a=8故答案为：4或8．【点评】本题考查的知识要点：椭圆方程的两种情况：焦点在x轴或y轴上，考察a、b、c的关系式，及相关的运算问题．15. 如图，⊙O中，直径AB和弦DE互相垂直，C 是DE延长线上一点，连结BC与圆O交于F，若,,，则________．参考答案：16. 如图，在直角梯形ABCD中，AB⊥AD，AD=DC=1， AB=3，动点P在△BCD内运动（含边界），设，则的取值范围是 .参考答案：略17. 已知函数的图象关于轴对称，则实数的值是_______________.参考答案：【分析】本题考察函数的基本性质，本题处理的方法如果不同，那么本题侧重的知识点就有所不同，但本质上都是围绕着函数的对称性进行问题的求解。

黑龙江省哈尔滨市高三上学期数学9月第一次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共4题；共8分)1. （2分）(2016·天津模拟) 已知条件p：|x+1|＞2，条件q：|x|＞a，且￢p是￢q的必要不充分条件，则实数a的取值范围是（）A . 0≤a≤1B . 1≤a≤3C . a≤1D . a≥32. （2分） (2015高二下·金台期中) 设有一个容积V一定的铝合金盖的圆柱形铁桶，已知单位面积铝合金的价格是铁的3倍，当总造价最少时，桶高为（）A .B .C . 2D . 23. （2分） (2019高二下·鹤岗月考) 已知函数，，若存在，使得，则的取值范围是（）A .B .C .D .4. （2分） (2019高三上·上海月考) 数学中有许多形状优美、寓意美好的曲线，曲线C：就是其中之一（如图）.给出下列三个结论：①曲线C恰好经过6个整点（即横、纵坐标均为整数的点）；②曲线C上任意一点到原点的距离都不超过；③曲线C所围成的“心形”区域的面积小于3.其中，所有正确结论的序号是A . ①B . ②C . ①②D . ①②③二、填空题 (共12题；共12分)5. （1分） (2016高一上·清河期中) 设全集U={0，1，2，3，4}，集合A={0，1，2，3}，B={2，3，4}，则（∁UA）∪B=________．6. （1分） (2020高二上·吉林期末) 命题若，则”的逆命题是________．7. （1分）若函数的定义域为，则的定义域为________．8. （1分） (2016高一上·黑龙江期中) 设函数f（x）= ，若f（x0）＞1，则x0的取值范围是________．9. （1分）(2017·长宁模拟) 若函数f（x）=log2（x+1）+a的反函数的图象经过点（4，1），则实数a=________．10. （1分） (2016高一上·桐乡期中) 函数f（x）= ，x∈[2，4]的最小值是________．11. （1分）关于x的不等式ax2+ax+3＜0的解集是∅，则a的取值范围是________．12. （1分） (2016高一下·岳池期末) 设变量x，y满足约束条件，则目标函数z=4x+2y的最大值为________．13. （1分）(2018·南宁月考) 已知函数，，若存在，使得，则实数b的取值范围是（）A .B .C .D .14. （1分） (2019高一上·山西月考) 设，是关于的方程的两个实根，则的最小值是________．15. （1分） (2016高一上·金华期末) 已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=2x﹣x2 ，若存在实数a，b，使f（x）在[a，b]上的值域为[ ， ]，则ab=________．16. （1分） (2019高三上·上海月考) 设是定义在上的两个周期函数，的周期为4，的周期为2，且是奇函数.当时，，，其中 .若在区间上，关于的方程有8个不同的实数根，则的取值范围是________.三、解答题 (共5题；共60分)17. （10分） (2018高一下·鹤岗期末) 如图，在四棱锥中，底面是菱形，，且侧面平面，点是的中点（1）求证:（2）若，求证:平面平面18. （10分）(2020·海南模拟) 设函数 .（1）若实数满足，求实数的取值范围；（2）记函数的最小值为，若不等式对恒成立，求实数的取值范围.19. （10分） (2017高一下·龙海期中) 某食品厂定期购买面粉．已知该厂每天需用面粉6t，每吨面粉的价格为1800元，面粉的保管等其他费用为平均每吨每天3元，购面粉每次需支付运费900元．（1）求该厂多少天购买一次面粉，才能使平均每天所支付的总费用最少？（2）若提供面粉的公司规定：当一次购买面粉不少于210t时，其价格可享受9折优惠（即原价的90%），问该厂是否考虑利用此优惠条件？请说明理由．20. （15分） (2019高一上·大连月考) 已知函数是定义在上的奇函数，且.（1）确定函数的解析式；（2）用定义证明函数在上是减函数；（3）若实数满足，求的取值范围.21. （15分） (2019高一上·绵阳期中) 已知函数f（x）=logm （m＞0且m≠1），（I）判断f（x）的奇偶性并证明；（II）若m= ，判断f（x）在（3，+∞）的单调性（不用证明）；（III）若0＜m＜1，是否存在β＞α>0，使f（x）在[α，β]的值域为[logmm（β-1）， ]？若存在，求出此时m的取值范围；若不存在，请说明理由．参考答案一、单选题 (共4题；共8分)1-1、2-1、3-1、4-1、二、填空题 (共12题；共12分)5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共5题；共60分) 17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、20-3、21-1、第11 页共11 页。

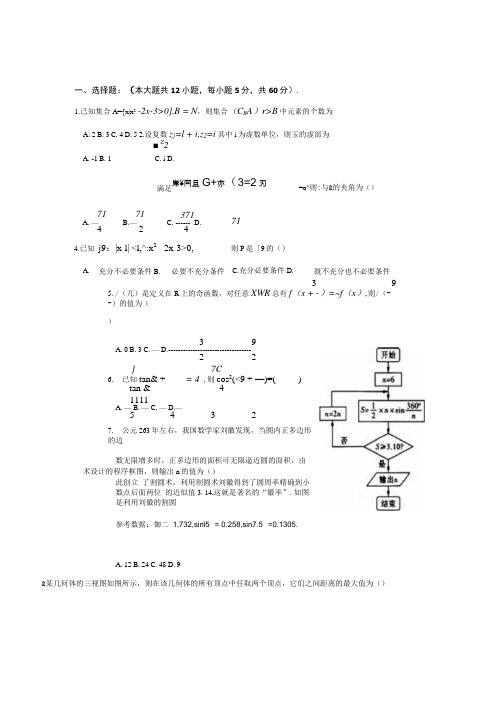
一、选择题：（本大题共12小题，每小题5分，共60分）.1.己知集合A={x|x 2 -2x-3>0],B = N ，则集合（C R A ）r>B 中元素的个数为A. 2B. 3C. 4D. 5 2.设复数z }=l + i,z 2=i 其中i 为虚数单位，则玉的虚部为■ Z 23 95. /（兀）是定义在R 上的奇函数，对任意XWR 总有f （x + -）=~f （x ）,则/（--）的值为（）3 9 A. 0 B. 3 C. — D. ---------------------------------- 2 2]7C 6.已知tan& + ------ = 4 ,则cos 2(<9 + —)=( ) tan & 4 1111 A. — B. — C. — D.— 5 4 3 2 7. 公元263年左右，我国数学家刘徽发现，当圆内正多边形的边数无限增多时，正多边形的面积可无限逼近圆的面积，由此创立 了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位 的近似值3. 14,这就是著名的“徽率”.如图是利用刘徽的割圆参考数据：御二 1,732,sinl5° = 0.258,sin7.5° =0.1305.A. 12B. 24C. 48D. 9&某几何体的三视图如图所示，则在该几何体的所有顶点中任取两个顶点，它们之间距离的最大值为（） A. -1 B. 1 C. i D.满足 岸¥冃且G+亦（3=2刃 =o^则:与&的夹角为（）71 71 A. — B.— 4 2 4.已知 j9：|x-l| <l,^:x 2 - 2x-3>0, 371 C. ------ D. 4 71则P 是「9的（）A. 充分不必要条件B. 必要不充分条件C.充分必要条件D.既不充分也不必要条件 术设计的程序框图，则输出n 的值为（）9. 设有下面四个命题：① “若a>0,则:与忌与的夹角为锐角”及它的逆命题均为真命题② 若 R,2X > 0,则—\p : 3x 0 e R,2X ° < 0③ “ ab<l ”是“ Q W1或b<l ff 的充分不必要条件④ 命题“ AABC 中，若A>B ,则sin A > sin B "的逆命题为真命题其中正确命题的个数是（）A. 3B. 2C. 1D. 010. 已知定义在7?上的函数/（x-1）的图像关于兀=1对称，且当兀〉0时，/（兀）单调递减，若 a = f(logQ 5 3),Z? = /(0.5-13),c = /(0.76)则 a.b.c 的大小关系是()二、填空题：（本大题共4小题，每小题5分，共20分）.14.在正方体ABCD-A.B.C.D.中，对角线AC ；与底面ABCD 所成角的正弦值为.侧视图A . c> a> bB . b> a> c c. a> c>b D . c>b> a 又AD DC = 0,则BD 的最大值为（ D . 2A /212.己知函数y (x ) = -- — ax' XX e （0,+8）,当%2 >%!时，不等式丿凶 无2 也。

2018-2019学年度上学期九月高三考试（文科）数学试题一．选择题（共12小题）1．已知集合A={x|x﹣1≥0}，B={0，1，2}，则A∩B=（）A．{0}B．{1}C．{1，2}D．{0，1，2}2．函数f（x）=lnx+2x﹣1零点的个数为（）A．4 B．3 C．2 D．13．若a=30.4，b=0.43，c=log0.43，则（）A．b＜a＜c B．c＜a＜b C．a＜c＜b D．c＜b＜a4．已知α为第二象限的角，且tanα=﹣，则sinα+cosα=（）A．﹣ B．﹣ C．﹣ D．5．若sinα=，且α为第二象限角，则tanα的值等于（）A．B．﹣C．D．﹣6．若tanα=1，则sin2α﹣cos2α的值为（）A．1 B．C．D．7．已知函数（x∈R），下列说法错误的是（）A．函数f（x）最小正周期是πB．函数f（x）是偶函数C．函数f（x）在上是增函数D．函数f（x）图象关于对称8．已知a∈R，则“a＞1”是“＜1”的（）A．充分非必要条件 B．必要非充分条件C．充要条件D．既非充分又非必要条件9．函数f（x）=的图象大致为（）10．若函数f（x）=ax2+1图象上点（1，f（1））处的切线平行于直线y=2x+1，则a=（）A．﹣1 B．0 C．D．111．已知平面向量=（1，1），=（x，﹣3），且⊥，则|2+|=（）A． B．C．D．12．在如图所示的平面直角坐标系中，向量的坐标是（）A．（2，2） B．（﹣2，﹣2）C．（1，1） D．（﹣1，﹣1）第Ⅱ卷（非选择题）二．填空题（共4小题）13．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜）的部分图象如图所示，则φ=；ω=．14．=．15．如图函数f（x）的图象在点P处的切线为：y=﹣2x+5，则f（2）+f′（2）=．16．已知向量，，若，则实数t=．三．解答题（共6小题）17．已知α∈（0，π）且cos（α﹣）=．求cosα18．已知函数f（x）=2sinxcosx﹣sin2x+cos2x．（x∈R）．（1）求f（x）的最小值及取得最小值时所对应的x的值；（2）求f（x）的单调递增区间．19．已知向量=（，=（cosx，cosx），x∈R，设f（x）=．（1）求函数f（x）的解析式及单调递增区间；（2）在△ABC中，a，b，c分别为内角A，B，C的对边，且a=1，b+c=2．f（A）=1，求△ABC的面积．20．在△ABC中，角A，B，C的对边分别为a，b，c，且（2a﹣b）•cosC=c•cosB．（1）求角C的大小；（2）若c=2，△ABC的面积为，求该三角形的周长．21．已知函数，x∈R．（1）求函数f（x）的最大值和最小正周期；（2）设△ABC的内角A，B，C的对边分别a，b，c，且c=3，f（C）=0，若sin（A+C）=2sinA，求a，b的值．22．已知函数f（x）=﹣x+alnx．（1）讨论f（x）的单调性；（2）若f（x）存在两个极值点x1，x2，证明：＜a﹣2．参考答案与试题解析一．选择题（共12小题）C D D C D B C A B D A D二．填空题（共4小题）13．﹣；．14．﹣15．如图函数f（x）的图象在点P处的切线为：y=﹣2x+5，则f（2）+f′（2）=﹣1．16．已知向量，，若，则实数t=．三．解答题（共6小题）17．已知α∈（0，π）且cos（α﹣）=．求cosα【解答】解：∵α∈（0，π），∴，又，∴，∴=．18．已知函数f（x）=2sinxcosx﹣sin2x+cos2x．（x∈R）．（1）求f（x）的最小值及取得最小值时所对应的x的值；（2）求f（x）的单调递增区间．【解答】解：函数f（x）=2sinxcosx﹣sin2x+cos2x=sin2x+cos2x=2sin（2x+）（1）当2x+=﹣时，即x=，k∈Z．函数f（x）取得最小值为﹣2，（2）当（2x+）≤，k∈Z．函数f（x）单调递增，得：≤x≤，k∈Z．∴f（x）的单调递增区间为[，]，k∈Z．19．已知向量=（，=（cosx，cosx），x∈R，设f（x）=．（1）求函数f（x）的解析式及单调递增区间；（2）在△ABC中，a，b，c分别为内角A，B，C的对边，且a=1，b+c=2．f（A）=1，求△ABC的面积．【解答】解：（1）向量=（，=（cosx，cosx），x∈R，f（x）=．=，=，=，令：（k∈Z），解得：（k∈Z），故函数的单调递增区间为：（k∈Z）．（2）在△ABC中，a，b，c分别为内角A，B，C的对边，f（A）=1，则：（0＜A＜π），解得：A=，利用余弦定理：，a2=b2+c2﹣2bccosA，且a=1，b+c=2．解得：bc=1所以△ABC的面积为：．20．在△ABC中，角A，B，C的对边分别为a，b，c，且（2a﹣b）•cosC=c•cosB．（1）求角C的大小；（2）若c=2，△ABC的面积为，求该三角形的周长．【解答】解：（1）在△ABC中，由正弦定理知===2R，又因为（2a﹣b）•cosC=c•cosB，所以2sinAcosC=sinBcosC+cosBsinC，即2sinAcosC=sinA；………………（4分）∵0＜A＜π，∴sinA＞0；∴cosC=；………………（6分）又0＜C＜π，∴C=；………………（8分）（2）∵S=absinC=ab=，△ABC∴ab=4 ………………（10分）又c2=a2+b2﹣2abcosC=（a+b）2﹣3ab=4，∴（a+b）2=16，∴a+b=4；∴周长为6．………………（14分）21．已知函数，x∈R．（1）求函数f（x）的最大值和最小正周期；（2）设△ABC的内角A，B，C的对边分别a，b，c，且c=3，f（C）=0，若sin（A+C）=2sinA，求a，b的值．【解答】解：（1）…．（3分）∵，∴，∴f（x）的最大值为0，最小正周期是…（6分）（2）由，可得∵0＜C＜π，∴0＜2C＜2π，∴∴，∴∵sin（A+C）=2sinA，∴由正弦定理得①…（9分）由余弦定理得∵c=3∴9=a2+b2﹣ab②由①②解得，…（12分）22．已知函数f（x）=﹣x+alnx．（1）讨论f（x）的单调性；（2）若f（x）存在两个极值点x1，x2，证明：＜a﹣2．【解答】解：（1）函数的定义域为（0，+∞），函数的导数f′（x）=﹣﹣1+=﹣，设g（x）=x2﹣ax+1，当a≤0时，g（x）＞0恒成立，即f′（x）＜0恒成立，此时函数f（x）在（0，+∞）上是减函数，当a＞0时，判别式△=a2﹣4，①当0＜a≤2时，△≤0，即g（x）＞0，即f′（x）＜0恒成立，此时函数f（x）在（0，+∞）上是减函数，②当a＞2时，x，f′（x），f（x）的变化如下表：），综上当a≤2时，f（x）在（0，+∞）上是减函数，当a＞2时，在（0，），和（，+∞）上是减函数，则（，）上是增函数．（2）由（1）知a＞2，0＜x1＜1＜x2，x1x2=1，则f（x1）﹣f（x2）=（x2﹣x1）（1+）+a（lnx1﹣lnx2）=2（x2﹣x1）+a（lnx1﹣lnx2），则=﹣2+，则问题转为证明＜1即可，即证明lnx1﹣lnx2＞x1﹣x2，则lnx1﹣ln＞x1﹣，即lnx1+lnx1＞x1﹣，即证2lnx1＞x1﹣在（0，1）上恒成立，设h（x）=2lnx﹣x+，（0＜x＜1），其中h（1）=0，求导得h′（x）=﹣1﹣=﹣=﹣＜0，则h（x）在（0，1）上单调递减，∴h（x）＞h（1），即2lnx﹣x+＞0，故2lnx＞x﹣，则＜a﹣2成立．（2）另解：注意到f（）=x﹣﹣alnx=﹣f（x），即f（x）+f（）=0，由韦达定理得x1x2=1，x1+x2=a＞2，得0＜x1＜1＜x2，x1=，可得f（x2）+f（）=0，即f（x1）+f（x2）=0，要证＜a﹣2，只要证＜a﹣2，即证2alnx2﹣ax2+＜0，（x2＞1），构造函数h（x）=2alnx﹣ax+，（x＞1），h′（x）=≤0，∴h（x）在（1，+∞）上单调递减，∴h（x）＜h（1）=0，∴2alnx﹣ax+＜0成立，即2alnx2﹣ax2+＜0，（x2＞1）成立．即＜a﹣2成立．。

2018-2019学年度上学期九月高三考试（理科）数学试题-、选择题（每题5分，合计60分）1、设全集—3、下列函数小，既是偶函数乂是在区间I 氏］—t 上单调递增的函数是（）.A.4.不等式（”一2）d —1）20 （辺〈0）的解集为（ ）1 2 1 A. - B. - C. —-D. 1 6.由曲线y=心,直线y=x~2及y 轴所围成的图形的面积为()10 16 A. — B. 4 C. — D. 67. 已知下列命题： ① 命题“3%丘/?,兀2+1>3兀”的否定是“色€/?,兀2+1<3兀”；② “ a > 2 ”是“ a 〉5 ”的充分不必要条件；③ “若小=0，则兀=0且y = 0”的逆否命题为真命题；④ 已知为两个命题，若“ 2 q ”为假命题，贝”为真命题.其中真命题的个数为（ ）A. 3 个B. 2 个C. 1 个D. 0A ・丨因一十 B.［因一十 C.丨因一十 D.|因 …9. 在△肋C 屮，内角B, Q 的对边分别为曰，b, c,若c=2日，力=4, cos 〃=+则c 的值 为（）D.因一亘号则比皿述勺大小关系是（ B •国二 ). D .|凶—b"2 2、 ( 2 A. 1 B. b 一 C ・ 一 I - .日丿 目」U [1, +°°) D. (—8, 1] U +°° 。

卜£，°丘（一才，0）则cos^ a —的值是（ ）8、对任意实数世若不等式「因 ------|恒成立, 则实数旦的取值范闱是（） 2、 B. A .5. 已知sin|10.已知函数f\x) =^x —2x +3/77, ［o, +°°),若f(x)+520恒成立，则实数加的取值范闱是()12. 己知于(兀)是定义在R 上的奇函数，当兀>0时,畑“-4兀,则不等式 W )> 0的解集 为( )A. (-00, -4) (4,4-oo)B. (-4,0) (4,+8)C. (―口―4) (0,4)D. (-4,4)二、填空题：本大题共4小题，每小题5分，共20分.把答案填在题中横线上.13. 已知函数f(x)=F+/ + 3/—9,若A--3是函数fd)的一个极值点，则实数a=14. 已知奇函数/(兀)满足/U+2) = -/(%),当"(0,1)时,f(x) = 2X f 则/(_4.5)的值为15. 函数f\x) =e v -Xe 为自然对数的底数)在区间［一1, 1］上的最大值是 _________ ・ 16. 在厶ABC 111,角B, Q 所对的边分别为 by c, JI $=2, cos C=_*, 3sin J=2sin B,则 c= _________ •三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤. 17. (10分)若/!= {” 一3W/W4}, 〃= {”2刃一刃+1}, BQ A t 求实数刃的取值范围. A. 4B. 2C. 5D. 617A.百，+ooB. 停+°°C. (一8, 2]D. (一8, 2)11. 已知函数f(0=sin( e>0)的最小正周期为 则该函数的图象( A.关于直线/=丁对称 B. 关于点(*, 0)对称C.关于直线x=—石对称D.关于点(*, 0)对称18.设函数f3 =3sin(Qx+wJ (。

2019高三数学9月月考试题 文一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的1.已知集合{|||2}A x x =<，{1,0,1,2,3}B =-，则A B =I （ ） A.{0,1} B.{0,1,2} C.{1,0,1}- D.{1,0,1,2}- 2．设复数12i z =-（i 是虚数单位），则z z +的值为（ ）A ．32B ．2C ．1D ．223.设命题p ：2,2nn N n ∃∈>，则p ⌝为( )（A ）2,2n n N n ∀∈> （B ）2,2nn N n ∃∈≤ （C ）2,2n n N n ∀∈≤ （D ）2,=2nn N n ∃∈4.已知函数1()3()3x xf x =-，则()f x（A ）是奇函数，且在R 上是增函数 （B ）是偶函数，且在R 上是增函数 （C ）是奇函数，且在R 上是减函数 （D ）是偶函数，且在R 上是减函数 5．设a b <，函数()()2y x a x b =--的图象可能是（ ）A. B ．C ．D ．6．如右图，网格纸上小正方形的边长为1，下图为某几何体的三视图，则该几何体的表面积为（ ） A ．16B ．842+C ．12D ．482+7.已知函数()y f x =在0x x =处的导数为11,则()()000lim x f x x f x x∆→-∆-=∆ ( )A. 11B. -11C.111 D. 111-8．已知函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭，若将它的图象向右平移6π个单位长度，得到函数()g x 的图象，则函数()g x 图象的一条对称轴方程为（ ） A ．12x π=B ．4x π=C ．3x π=D ．3x 2π=9．我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问塔底几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的底层共有灯（ ） A ．3盏 B ．9盏 C ．192盏 D ．9384盏10.已知ABC ∆中, ,,A B C ∠∠∠的对边分别是2=,3,,,3ABC a A b b c S π∆==1,,则2=sin sin 2sin a b cA B C+-+-A. 393B. 393C. 27D. 4711.已知函数()()sin f x x ωϕ=A +（A ，ω，ϕ均为正的常数）的最小正周期为π，当23x π=时，函数()f x 取得最小值，则下列结论正确的是（） （A ）()()()220f f f <-<（B ）()()()022f f f <<- （C ）()()()202f f f -<<（D ）()()()202f f f <<-12.已知方程23ln 02x ax -+=有4个不同的实数根,则实数a 的取值范围是( ) A. 2,3e ⎛⎫-∞ ⎪⎝⎭ B. 22e ⎛⎫∞ ⎪⎝⎭-，C. 20,3e ⎛⎫ ⎪⎝⎭D. 20,2e ⎛⎫ ⎪⎝⎭二、填空题：本大题共4小题，每小题5分．13．已知a r =（1,2m —1），b r =（2—m,—2），若向量a r //b r，则实数m 的值为_________．14.在ABC △中，4a =，5b =，6c =，则sin 2sin AC= ．15已知函数()4121x f x x -=-, 则12201320142015201520152015f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++⋅⋅⋅++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭=_________ 16．如图所示，正方体1111ABCD A B C D -的棱长为1，线段11B D 上有两个动点E F 、，则下列结论中正确结论的序号是__________ ①AC BE ⊥；②直线AE 与平面11DBB D 所成角的正弦值为定值13； ③当EF 为定值，则三棱锥E ABF -的体积为定值； ④异面直线AE ，BF 所成的角的余弦值为定值63． 三、解答题：解答应写出文字说明、证明过程或演算步骤．17．（10分）已知向量cos ,12x m =-u r （），2(3sin ,cos )22x x n =r ，设函数()1f x m n =•+u r r 。

选择题：本大题共12个小题，每小题5分，共60分•在每小题给出的四个选项中，只有一项是 符合题目要求的.1. 已知集合 A=[x-1 <x<2) B=<x<3)» 贝ij AU B=() A. (-1, 3) B. (-1, 0) C. (0, 2) D. (2, 3)2、 复数错误!未找到引用源。

在复平面上对应的点位于()A.笫一象限B.第二象限C.第三象限D.笫四象限\(兀 3. ------------------------------------ 己知 cos a =—,则 sin 2a 34. 设D, E, F 分别为AABC 的三边BC, CA, AB 的中点，则错误!未找到引用源。

()A.错误!未找到引用源。

B.错误!未找到引用源。

C.错误!未找到引用源。

D.错误!未找到引用源。

5. 已知点P 是抛物线/ =4兀上的一点，F 为抛物线的焦点,若|PF| = 5,则点P 的横坐标为( )A. 1B. 2C. 3D.4 6. 如图，网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图，则该多面体的表面 积为( ) A. 18 + 36^5 B. 54+18舲 C. 90 D. 819. 设函数/(x),g(x)的定义域为H/W 是奇函数，g(x)是偶函数，则下列结论正确的、71 D.4^2~9~) 10. 下边程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”，执行该 稈序框图，若输入的a, b 分别为14, 18,则输出的a =()A. 0B. 2C. 4D. 1411.己知M(3,O)是圆X 2+/-8X -2J + 1O =()内一点，则过M 点最长的弦所在的直线方程 是( )A.兀+歹—3 = 0 B ・ x — y — 3 = 0 C ・ 2x —y —6 = 0 D. 2兀+y —6 = 0 12. 设/(x) = |lgx|,若函数g(x) = f(x)-ax 在区间(0,4)上有三个零点，则实数a 的取值 范围是 金］订竽判 c 罗)屮詈)第II 卷(共90分)填空题(每题5分，满分20分，将答案填在答题纸上)JT jr13. 将函数/(x) = sin(x + ^), (0<^<一)的周期缩小到原来的一半，再向左平移上个单 2 8 位，所得到的函数图象关于y 轴对称，则©的取值为—14. 己知三棱锥P-ABC 的三条侧棱两两互相垂直，且AB = y/5f BC 二护,AC = 2｝则此 三棱锥的外接球的体积为 _________15. 在△八BC 中，b = 2, cosC=-, Z\ABC 的面积为则 a 二是(4 416.甲、乙、丙三位同学，其屮一位是班长，一位是体育委员，一位是学习委员，已知丙的年龄比学委的大，甲与体委的年龄不同，体委比乙年龄小•据此推断班长是 _________三、解答题(本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤•)17.(本小题12分)已知｛匕｝是公差不为零的等差数列，满足冬=7,且色、偽、坷成等比数列(1)•求数列｛色｝的通项公式18.(本小题12分)如图，三棱柱ABC—AiB.Ci的侧棱Ah丄底面ABC, ZACB = 90° , E是棱CG 的中点,F是AB的中点，AC=BC=1, AA)=2(1)求证：CF//平面ABE；(2)求点C到平面ABE的距离。

黑龙江省数学高三上学期文数9月月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分） (2019高一上·兴义期中) 已知全集，则）等于（）A . {2，4，6}B . {1，3，5}C . {2，4，5}D . {2，5}2. （2分）函数的定义域为（）A . (e，+∞）B . [e，+∞)C .D . (-∞，e]3. （2分）(2018·衡阳模拟) 下列说法正确的是（）A . 命题“若，则.”的否命题是“若，则.”B . 是函数在定义域上单调递增的充分不必要条件C .D . 若命题，则4. （2分）设集合则“”是“”的（）A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件5. （2分）已知函数,又数列满足，且，则正实数a的取值范围是（）A .B .C .D .6. （2分） (2016高一上·温州期末) 存在函数f（x）满足：对任意x∈R都有（）A . f（|x|）=xB . f（|x|）=x2+2xC . f（|x+1|）=xD . f（|x+1|）=x2+2x7. （2分） (2019高一上·普宁期中) 当时，函数的值域为（）A .B .C .D .8. （2分）函数y=的单调减区间为（）A . RB . （﹣∞，0）∪（0，+∞）C . （﹣∞，0），（0，+∞）D . （0，+∞）9. （2分）已知函数f（x）=，则y=f（2﹣x）的大致图象是（）A .B .C .D .10. （2分） (2018高三上·福建期中) 已知f（x）是定义在R上的奇函数，且当x≥0时，f（x）=x2 ，对任意的x∈[t，t+2]不等式f（x+t）≥2f（x）恒成立，那么实数t的取值范围是（）A . [ ，+∞）B . [2，+∞）C . （0， ]D . [0， ]11. （2分）下列函数中既不是奇函数也不是偶函数的是（）A .B .C .D .12. （2分） (2020高一上·赣县期中) 已知函数，若，则（）．A .B .C .D .二、填空题 (共4题；共4分)13. （1分） (2020高一上·吴江期中) 命题“ ，”的否定为________.14. （1分） (2019高一上·项城月考) 若函数在上的最大值比最小值大，则a的值为________.15. （1分） (2019高一上·长春期中) 已知函数在区间上单调递减，则的取值范围是________.16. （1分） (2019高一下·上海期末) 关于的方程只有一个实数根，则实数 ________．三、解答题 (共6题；共60分)17. （10分） (2019高一上·重庆月考) 求值：（1）；（2） .18. （10分） (2019高一上·吐鲁番月考) 设函数，且 .（1）求的值；（2）当x∈[2,14]时，求的值域．19. （10分） (2016高一上·苏州期中) 已知函数f（x）=x2+ ．（1）求证：f（x）是偶函数；（2）判断函数f（x）在（0，）和（，+∞）上的单调性并用定义法证明．20. （10分） (2019高一下·岳阳月考) 已知函数f（x）=x2-2|x|-1。

13x的图象是(＜φ＜）的最小正周期为π，将该函数的A.关于点（，0）对称 B.关于直线x=对称2019届高三数学9月月考试题文一、选择题（本题共12道小题，每小题5分，共60分）1.复数z=2-i2+i（i为虚数单位）在复平面内对应的点所在象限为()A．第一象限B．第二象限C．第三象限D．第四象限2.已知集合A={x|x2﹣x﹣6≥0}，B={x|﹣3≤x≤3}，则A∩B等于（）A．[﹣3，﹣2]B．[2，3]C．[﹣3，﹣2]∪{3}D．[2，3]∪{﹣3}3.已知命题p：∀x∈[1,2]，使e x-a≥0.若⌝p是假命题，则实数a的取值范围为（）A.（-∞，e2]B.（-∞，e]C.[e，+∞）D.[e2，+∞）4.下列命题正确的是（）A．命题“若α=β，则sinα=sinβ”的逆否命题为真命题B．命题“若a<b，则ac2≤bc2”的逆命题为真命题C．命题“∀x>0,5x>0”的否定是“∃x≤0,5x0≤0”D．“x<-1”是“ln(x+2)<0”的充分不必要条件15.设a=log3，b=()0.2，c=23，则（）12A．a<b<c B．c<b<a C．c<a<b D．b<a<c6.函数y=x ln x)A B C D7.已知函数f（x）=sin（ωx+φ）（w＞0，-ππ22图象向左平移π6个单位后，得到的图象对应的函数为奇函数，则f（x）的图象是（）π5π1212，0）对称 D.关于直线 x = 对称8.要想得到函数 y = sin 2 x + ⎪ 的图象，只需将 y = sin 2 x + ⎪ 的图像()π ⎫ C.向右平移 个单位D.向右平移 个单位，则 tan - 2θ ⎪ = ( )7D. - ⎛ 3 ⎫3 3 ⎫ 3 0, 3 ⎪ ⎛ 3 ⎫ ) ⋃ 0, ⎪ ,0) ⋃ ,+∞ ⎪⎪ A. (-∞,B ． (- C. D ． 3 ⎪ 3 ⎪ ⎝ ⎝ 3 3 3 ⎝ 3 A ． -5照此规律，第五个不等式为.2 ) 的部分图象如图所示，则C.关于点（5π12π12⎛ ⎛ π ⎫ ⎝ 3 ⎭ ⎝6 ⎭A.向左平移 π6个单位B.向左平移π12个单位π6π129.已知 tan θ =1 ⎛ π ⎫2 ⎝ 4 ⎭A.7B. －7C. 11710.函数 y = 3x 2 - 2 ln x 的单调增区间为（）⎛ ⎛ ⎫ ,+∞ ⎪⎪⎝ ⎭⎭4x + a11. 已知函数 f ( x ) = 是奇函数，则 f (a) 的值为（）2x5 33B ．C ． -D ．222 212. 设函数 f ′(x )是奇函数 f （x ）（x ∈R ）的导数，f （-1）=0，当 x ＞0 时，xf ′(x )-f （x ）＜0，则使得 f （x ）＞0 成立的 x 的取值范围是（）A.（－∞, －1）∪（0,1）B.（－1,0）∪（1，+∞）C.（－∞，－1）∪（－1,0）D.（0,1）∪（1，+∞）二、填空题（本题共 4 道小题，每小题 5 分，共 20 分）13.观察下列不等式1 + 122 <3 21 +1 + 1 1 5 + < ， 22 33 3 1 1 1 5 + + <22 32 42 3……．．．14.若函数 y = A s in(ωx + ϕ)( A > 0,ω > 0, ϕ <该函数解析式是 .π．15.已知函数 f ( x ) = xe x + 2 ，则曲线 y = f ( x ) 在点 (0, f (0)) 处的切线方程为16 关于函数 f （x ）=4sin （2x+ ），（x ∈R ）有下列结论：①y=f（x ）是以 π 为最小正周期的周期函数；②y=f（x ）可改写为 y=4cos （2x ﹣③y=f（x ）的最大值为 4；）；④y=f（x ）的图象关于直线 x=对称；则其中正确结论的序号为．三、解答题（本题共 2 道小题,第 1 题 0 分,第 2 题 0 分,共 0 分）17 已知函数 f ( x ) =3 sin 2 x - 2cos 2 x - 1, x ∈ R .(Ⅰ) 求函数 f ( x) 的最小正周期和最小值；(Ⅱ) 在 ∆ABC 中, A, B, C 的对边分别为 a, b , c ,若 c =求 a, b 的值.3, f (C ) = 0,sin B = 2sin A ，18.已知△ABC 的内角 A , B , C 的对边分别为 a , b , c ,且 2c ⋅ cos B - b = 2a .（Ⅰ）求角 C 的大小；（Ⅱ）设角 A 的平分线交 BC 于 D ，且 AD = 3 ，若 b = 2 ，求△ABC 的面积 .1 9.如图，在半径为 30cm 的半圆形铁皮上截取一块矩形材料 A （点 A ，B 在直径上，点 C ，D在半圆周上），并将其卷成一个以 AD 为母线的圆柱体罐子的侧面（不计剪裁和拼接损耗）（1）若要求圆柱体罐子的侧面积最 大，应如何截取？（2）若要求圆柱体罐子的体积最大，应如何截取？20.已知函数 f (x )= 23ax 3 + x 2 + x - 1.[e 在直角坐标系 xOy 中,曲线 C 的参数方程为 ⎨ ⎪ y =sin α 2坐标方程为 ρcos θ + ⎪ = -2 2 .（ I ）当 a = -的取值范围.12 时，求 f (x )的单调区间； （Ⅱ）若函数 f (x )在 1,3]上单调递增，试求出 a21.已知函数 f （x ）= kx 2 x（k ＞0）．（1）求函数 f （x ）的单调区间；（2）当 k=1 时，若存在 x ＞0，使 lnf （x ）＞ax 成立，求实数 a 的取值范围．（二）选考题：共 10 分。

2018-2019 学年度上学期九月高三考试（理科）数学试题一、选择题（每题 5 分，合计 60 分）1、设全集，集合，则（）A.B.C.D.2、设,,,则 , , 的大小关系是( ).A.B.C.D.3、下列函数中,既是偶函数又是在区间上单调递增的函数是( ).A.B.C.D.4．不等式(ax－2)(x－1)≥0(a<0)的解集为( )A.2a，1B.1，2a C.－∞，2a∪[1，＋∞) D．(－∞，1]∪2a，＋∞5. 已知 sinπ2 ＋α＝12，α∈－π2 ，0，则 cosα－π3 的值是()1 A. 22 B. 31 C．－2D．16.由曲线 y＝ x，直线 y＝x－2 及 y 轴所围成的图形的面积为( )A.130 B．4 C.136D．67.已知下列命题：①命题“ x  R, x2 1  3x ”的否定是“ x  R, x2 1  3x ”；②“ a  2 ”是“ a  5 ”的充分不必要条件；③“若 xy  0 ,则 x  0 且 y  0”的逆否命题为真命题；④已知 p, q 为两个命题，若“ p  q ”为假命题，则“ p  q ”为真命题．其中真命题的个数为（ ）A.3 个 B.2 个 C.1 个 D.08、对任意实数 ,若不等式恒成立,则实数 的取值范围是( )A.B.C.D.9．在△ABC 中，内角 A，B，C 的对边分别为 a，b，c，若 c＝2a，b＝4，cos B＝14.则 c 的值为( )-1-A．4 B．2 C．5 D．6 10．已知函数 f(x)＝13x3－2x2＋3m，x∈[0，＋∞)，若 f(x)＋5≥0 恒成立，则实数 m 的取值范围是( )A.197，＋∞ B.197，＋∞ C．(－∞，2] D．(－∞，2)11．已知函数 f(x)＝sinωx＋π3 (ω>0)的最小正周期为 π，则该函数的图象()A．关于直线 x＝π3 对称B．关于点π3 ，0对称C．关于直线 x＝－π6 对称D．关于点π6 ，0对称12.已知 f (x) 是定义在 R 上的奇函数，当 x  0 时， f (x)  x2  4x ，则不等式 xf (x)  0 的解集为（ ）A. (, 4) U(4, )B. (4,0) U(4, )C. (, 4) U(0, 4)D. (4, 4)二、填空题：本大题共 4 小题，每小题 5 分，共 20 分．把答案填在题中横线上．13．已知函数 f(x)＝x3＋ax2＋3x－9，若 x＝－3 是函数 f(x)的一个极值点，则实数 a＝________．14.已知奇函数 f (x) 满足 f (x  2)   f (x) ，当 x (0,1) 时， f (x)  2x ，则 f (4.5) 的值为___________. 15.函数 f(x)＝ex－x(e 为自然对数的底数)在区间[－1,1]上的最大值是________． 16．在△ABC 中，角 A，B，C 所对的边分别为 a，b，c，且 a＝2，cos C＝－14，3sin A＝2sin B，则 c＝________.-2-三、解答题：本大题共 6 小题，共 70 分．解答应写出文字说明、证明过程或演算步骤． 17．(10 分)若 A＝{x|－3≤x≤4}，B＝{x|2m－1≤x≤m＋1}，B⊆ A，求实数 m 的取值范围．18．设函数 f(x)＝3sinωx＋π6 (ω>0，x∈R)的最小正周期为π2 .(1)求 f(x)的解析式； (2)已知 fα4 ＋π 12＝95，求 cos α 的值．19．在△ABC 中，角 A，B，C 的对边分别为 a，b，c，已知 2bcos C＝acos C＋ccos A. (1)求角 C 的大小； (2)若 b＝2，c＝ 7，求 a 及△ABC 的面积．-3-20．已知函数 f(x)＝4cos ωx·sinωx＋π6 ＋a(ω>0)图象上最高点的纵坐标为 2，且图象上 相邻两个最高点的距离为 π.(1)求 a 和 ω 的值； (2)求函数 f(x)在[0，π]上的单调递减区间．21．已知函数 f(x)＝ex(ax＋b)－x2－4x，曲线 y＝f(x)在点(0，f(0))处的切线方程为 y＝4x ＋4. (1)求 a，b 的值； (2)讨论 f(x)的单调性，并求 f(x)的极大值．-4-22．已知函数 f(x)＝lnx x＋ax，x>1. (1)若 a＝2，求函数 f(x)的极小值． (2)若 f(x)在(1，＋∞)上单调递减，求实数 a 的取值范围；-5-2018-2019 学年度上学期九月高三考试（理科）数学试题答案 一、选择题（每题 5 分，合计 60 分） 1.D 2.D 3.D 4.A 5.C 6.C 7.C 8.A 9.A 10.A 11.B 12.A 二、填空题13.5 14.三、解答题 17.15.e-1 16.418.（1） （2） 19.-6-20.21.22.-7--8-。