中考数学复习第四单元图形的初步认识与三角形第15讲等腰三角形练习

等腰三角形练习题(含答案)等腰三角形第1课时：等腰三角形的性质1.已知等腰三角形的一个底角为50°，则其顶角为80°。

2.如图，△ABC中，AB=AC，BC=6cm，AD平分∠BAC，则BD=3cm。

3.如图，△ABC中，AB=AC，D为BC中点，∠BAD=35°，则∠C的度数为45°。

4.已知等腰三角形的一个内角为50°，则这个等腰三角形的顶角为80°。

5.如图，在△ABC中，D是BC边上一点，且AB=AD=DC，∠BAD=40°，求∠C的度数为100°。

6.如图，△ABC中，AB=AC，D是BC的中点，E，F分别是AB，AC上的点，且AE=AF。

证明：DE=DF。

第2课时：等腰三角形的判定1.在△ABC中，∠A=40°，∠B=70°，则△ABC为钝角三角形。

2.已知△ABC中，∠B=50°，∠A=80°，AB=5cm，则AC=5cm。

3.如图，在△ABC中，AD⊥BC于点D，且BD=DC，则△ABC为等腰三角形。

4.如图，已知△ABC中，∠A=36°，AB=AC，BD为∠ABC的平分线，则图中共有2个等腰三角形。

5.如图，D是△XXX的BC边上的中点，DE⊥AC，DF⊥AB，垂足分别是E，F，且DE=DF。

证明：AB=AC。

6.如图，AB∥CD，直线l交AB于点E，交CD于点F，FG平分∠EFD交直线AB于点G。

证明：△EFG是等腰三角形。

等边三角形第1课时：等边三角形的性质与判定1.如图，a∥b，等边△ABC的顶点B，C在直线b上，则∠1的度数为60°。

2.在△ABC中，∠A=60°，现有下面三个条件：①AB=AC；②∠B=∠C；③∠A=∠B。

能判定△ABC为等边三角形的有条件①、②、③。

3.如图，在等边△ABC中，BD⊥AC于D，若AB=4，则AD=2.4.如图，△ABC是等边三角形，∠CBD=90°，BD=BC，连接AD交BC于点E，求∠BAD的度数为75°。

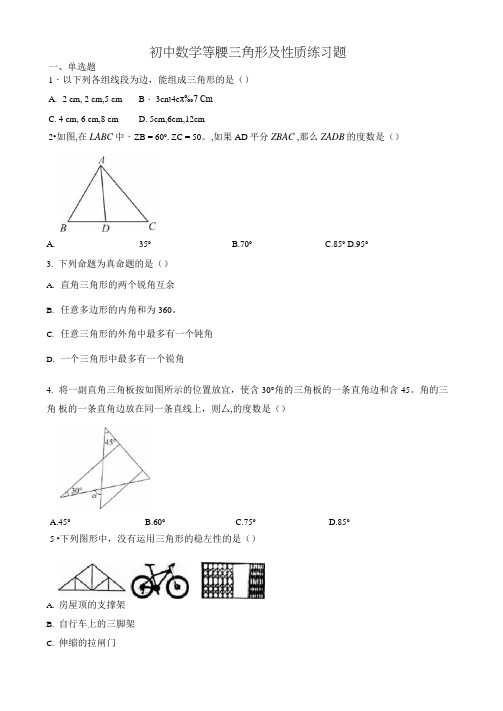
初中数学等腰三角形及性质练习题一、单选题1・以下列各组线段为边，能组成三角形的是（）A. 2 cm, 2 cm,5 cm B ・ 3cn ι4c π‰7 CmC. 4 cm, 6 cm,8 cmD. 5cm,6cm,12cm2•如图,在LABC 中・ZB = 60o . ZC = 50。

,如果AD 平分ZBAC ,那么ZADB 的度数是（）A. 35oB.70oC.85oD.95o 3. 下列命题为真命题的是（）A. 直角三角形的两个锐角互余B. 任意多边形的内角和为360。

C. 任意三角形的外角中最多有一个钝角D. 一个三角形中最多有一个锐角4. 将一副直角三角板按如图所示的位置放宜，使含30°角的三角板的一条直角边和含45。

角的三角 板的一条直角边放在同一条直线上，则厶,的度数是（）A. 房屋顶的支撑架B. 自行车上的三脚架C. 伸缩的拉闸门A.45oB.60oC.75o 5 •下列图形中，没有运用三角形的稳左性的是（）D.85oD.在木门上钉一根木条6 •如图AB// DF, AC丄BC于C, BC与DF交于点E ,若ZA = 20°,则ZCEF等于（）A.IlO oB.100oC.80oD.70o7.如图，在ZvlBC中，AB = AC, AQ平分ABAC, DE丄AB，DF丄AC, E,F分别为垂足，则下列四个结论：（I）ZDEF = ZDFE ；（2） AE = AFX⑶AD平分ZEDF ；⑷AD垂直平分矿.其中正确的有（）A.1个B.2个C.3个D.4个&如图BF = £CZB = ZE请问添加下而哪个条件不能判断AABC ^DEF（）A. ZA = ZD B・ AB = ED C. DF//AC D. AC = DF9.如图，点P为ZAOB内一点,分别作点P关于04,03的对称点P l,P2,连接人,出交OA于M,交OB于N,若∕>Λ=6,则APMN的周长为（）10•如图,在正五边形ABa）E中,连接BE侧ZABE的度数为（）A.30oB.36°C.54oD.72°11・已知点P(-1-2<Λ5)关于x轴的对称点和点Q(3,b)关于y轴的对称点相同，则点Aab)关于X轴对称的点的坐标为()A.(l,-5)B.(l,5)C. (-1,5)D.(-l,-5)12.在正方形网格中，ZAoB的位宜如图所示,到ZAoB两边距离相等的点是()A.M点B.N点、C.P点 D・Q点二S解答题E如图所示，ZA = 27。

安徽省2017年中考数学总复习第一轮中考考点系统复习第四单元图形的初步认识与三角形第15讲等腰三角形与直角三角形第2课时能力提升试题编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（安徽省2017年中考数学总复习第一轮中考考点系统复习第四单元图形的初步认识与三角形第15讲等腰三角形与直角三角形第2课时能力提升试题）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为安徽省2017年中考数学总复习第一轮中考考点系统复习第四单元图形的初步认识与三角形第15讲等腰三角形与直角三角形第2课时能力提升试题的全部内容。

第2课时能力提升1．(2016·滨州)如图，△ABC中，D为AB上一点，E为BC上一点，且AC＝CD＝BD＝BE,∠A＝50°，则∠CDE的度数为( D )A．50° B．51° C．51.5° D．52.5°2．（2016·陕西)如图,在△ABC中，∠AB C＝90°，AB＝8,BC＝6，若DE是△ABC的中位线,延长DE交△ABC的外角平分线于点F，则线段DF的长为( B )A．7 B．8 C．9 D．103．（2016·马鞍山和县一模)如图，等边三角形ABC边AB上一点P，作PE⊥AC于点E，Q为BC 延长线上一点，当PA＝CQ时，连接PQ交AC于点D，下列结论中不一定正确的是( D ) A．PD＝DQ B．DE＝错误!AC C．AE＝错误!CQ D．PQ⊥AB提示：过点P作PF∥BC，则△APF为等边三角形，△PDF≌△QDC。

4．(2016·连云港）如图1,分别以直角三角形三边为边向外作等边三角形，面积分别为S1,S2，S3;如图2，分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形，面积分别为S4，S5,S6。

中考数学复习----《等腰三角形》知识点总结与专项练习题（含答案解析）知识点总结1.等腰三角形的定义：有两条边相等的三角形叫做等腰三角形。

其中相等的两边叫做腰，另一边叫做底。

两腰构成的夹角叫做顶角，腰与底构成的夹角叫做底角。

2.等腰三角形的性质：①等腰三角形的两腰相等。

②等腰三角形的两底角相等。

（简称“等边对等角”）③等腰三角形底边的中线、高线以及顶角平分线相互重合。

（简称底边上三线合一）3.等腰三角形的判定：①有两条边相等的三角形是等腰三角形。

②有两个底角相等的三角形是等腰三角形。

（等角对等边）③若一个三角形某一边上存在“三线合一”，则三角形是等腰三角形。

练习题1、（2022•黑龙江）如图，△ABC中，AB＝AC，AD平分∠BAC与BC相交于点D，点E是AB的中点，点F是DC的中点，连接EF交AD于点P．若△ABC的面积是24，PD＝1.5，则PE的长是（）A．2.5 B．2 C．3.5 D．3【分析】如图，过点E作EG⊥AD于G，证明△EGP≌△FDP，得PG＝PD＝1.5，由三角形中位线定理可得AD的长，由三角形ABC的面积是24，得BC的长，最后由勾股定理可得结论．【解答】解：如图，过点E作EG⊥AD于G，∵AB＝AC，AD平分∠BAC，∴AD⊥BC，BD＝CD，∴∠PDF＝∠EGP＝90°，EG∥BC，∵点E是AB的中点，∴G是AD的中点，∴EG＝BD，∵F是CD的中点，∴DF＝CD，∴EG＝DF，∵∠EPG＝∠DPF，∴△EGP≌△FDP（AAS），∴PG＝PD＝1.5，∴AD＝2DG＝6，∵△ABC的面积是24，∴•BC•AD＝24，∴BC＝48÷6＝8，∴DF＝BC＝2，∴EG＝DF＝2，由勾股定理得：PE＝＝2.5．故选：A．2、（2022•淄博）某城市几条道路的位置关系如图所示，道路AB∥CD，道路AB与AE的夹角∠BAE＝50°．城市规划部门想新修一条道路CE，要求CF＝EF，则∠E的度数为（）A．23°B．25°C．27°D．30°【分析】先根据平行线的性质，由AB∥CD得到∠DFE＝∠BAE＝50°，根据等腰三角形的性质得出∠C＝∠E，再根据三角形外角性质计算∠E的度数．【解答】解：∵AB∥CD，∴∠DFE＝∠BAE＝50°，∵CF＝EF，∴∠C＝∠E，∵∠DFE＝∠C+∠E，∴∠C＝∠DFE＝×50°＝25°，故选：B．3、（2022•鞍山）如图，在△ABC中，AB＝AC，∠BAC＝24°，延长BC到点D，使CD＝AC，连接AD，则∠D的度数为（）A．39°B．40°C．49°D．51°【分析】利用等边对等角求得∠B＝∠ACB＝78°，然后利用三角形外角的性质求得答案即可．【解答】解：∵AB＝AC，∠BAC＝24°，∴∠B＝∠ACB＝78°．∵CD＝AC，∠ACB＝78°，∠ACB＝∠D+∠CAD，∴∠D＝∠CAD＝∠ACB＝39°．故选：A．4、（2022•荆州）如图，直线l1∥l2，AB＝AC，∠BAC＝40°，则∠1+∠2的度数是（）A．60°B．70°C．80°D．90°【分析】过点C作CD∥l1，利用平行线的性质可得∠1+∠2＝∠ACB，再由等腰三角形的性质可得∠ACB＝∠ABC，从而可求解．【解答】解：过点C作CD∥l1，如图，∵l1∥l2，∴l1∥l2∥CD，∴∠1＝∠BCD，∠2＝∠ACD，∴∠1+∠2＝∠BCD+∠ACD＝∠ACB，∵AB＝AC，∴∠ACB＝∠ABC，∵∠BAC＝40°，∴∠ACB＝（180°﹣∠BAC）＝70°，∴∠1+∠2＝70°．故选：B．5、（2022•台湾）如图，△ABC中，D点在AB上，E点在BC上，DE为AB的中垂线．若∠B＝∠C，且∠EAC＞90°，则根据图中标示的角，判断下列叙述何者正确？（）A．∠1＝∠2，∠1＜∠3 B．∠1＝∠2，∠1＞∠3C．∠1≠∠2，∠1＜∠3 D．∠1≠∠2，∠1＞∠3【分析】根据线段垂直平分线的性质，等腰三角形的性质解答即可．【解答】解：∵DE为AB的中垂线，∴∠BDE＝∠ADE，BE＝AE，∴∠B＝∠BAE，∴∠1＝∠2，∵∠EAC＞90°，∴∠3+∠C＜90°，∵∠B+∠1＝90°，∠B＝∠C，∴∠1＞∠3，∴∠1＝∠2，∠1＞∠3，故选：B．6、（2022•宜宾）如图，在△ABC中，AB＝AC＝5，D是BC上的点，DE∥AB交AC于点E，DF∥AC交AB于点F，那么四边形AEDF的周长是（）A．5 B．10 C．15 D．20【分析】由于DE∥AB，DF∥AC，则可以推出四边形AFDE是平行四边形，然后利用平行四边形的性质可以证明▱AFDE的周长等于AB+AC．【解答】解：∵DE∥AB，DF∥AC，∴四边形AFDE是平行四边形，∠B＝∠EDC，∠FDB＝∠C∵AB＝AC，∴∠B＝∠C，∴∠B＝∠FDB，∠C＝∠EDC，∴BF＝FD，DE＝EC，∴▱AFDE的周长＝AB+AC＝5+5＝10．故选：B．7、（2022•宿迁）若等腰三角形的两边长分别是3cm和5cm，则这个等腰三角形的周长是（）A．8cm B．13cm C．8cm或13cm D．11cm或13cm 【分析】题目给出等腰三角形有两条边长为3cm和5cm，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．【解答】解：当3cm是腰长时，3，3，5能组成三角形，当5cm是腰长时，5，5，3能够组成三角形．则三角形的周长为11cm或13cm．故选：D．8、（2022•天津）如图，△OAB的顶点O（0，0），顶点A，B分别在第一、四象限，且AB ⊥x轴，若AB＝6，OA＝OB＝5，则点A的坐标是（）A．（5，4）B．（3，4）C．（5，3）D．（4，3）【分析】根据等腰三角形的性质求出AC，根据勾股定理求出OC，根据坐标与图形性质写出点A的坐标．【解答】解：设AB与x轴交于点C，∵OA＝OB，OC⊥AB，AB＝6，∴AC＝AB＝3，由勾股定理得：OC＝＝＝4，∴点A的坐标为（4，3），故选：D．9、（2022•泰安）如图，l1∥l2，点A在直线l1上，点B在直线l2上，AB＝BC，∠C＝25°，∠1＝60°．则∠2的度数是（）A．70°B．65°C．60°D．55°【分析】利用等腰三角形的性质得到∠C＝∠BAC＝25°，利用平行线的性质得到∠BEA＝95°，再根据三角形外角的性质即可求解．【解答】解：如图，∵AB＝BC，∠C＝25°，∴∠C＝∠BAC＝25°，∵l1∥l2，∠1＝60°，∴∠BEA＝180°﹣60°﹣25°＝95°，∵∠BEA＝∠C+∠2，∴∠2＝95°﹣25°＝70°．故选：A．10、（2022•自贡）等腰三角形顶角度数比一个底角度数的2倍多20°，则这个底角的度数是（）A．30°B．40°C．50°D．60°【分析】设底角的度数是x°，则顶角的度数为（2x+20）°，根据三角形内角和是180°列出方程，解方程即可得出答案．【解答】解：设底角的度数是x°，则顶角的度数为（2x+20）°，根据题意得：x+x+2x+20＝180，解得：x＝40，故选：B．11、（2022•广安）若（a﹣3）2+5−b＝0，则以a、b为边长的等腰三角形的周长为．【分析】先求a，b．再求第三边c即可．【解答】解：∵（a﹣3）2+＝0，（a﹣3）2≥0，≥0，∴a﹣3＝0，b﹣5＝0，∴a＝3，b＝5，设三角形的第三边为c，当a＝c＝3时，三角形的周长＝a+b+c＝3+5+3＝11，当b＝c＝5时，三角形的周长＝3+5+5＝13，故答案为：11或13．12、．（2022•岳阳）如图，在△ABC中，AB＝AC，AD⊥BC于点D，若BC＝6，则CD＝．【分析】根据等腰三角形的性质可知D是BC的中点，即可求出CD的长．【解答】解：∵AB＝AC，AD⊥BC，∴CD＝BD，∵BC＝6，∴CD＝3，故答案为：3．13、（2022•苏州）定义：一个三角形的一边长是另一边长的2倍，这样的三角形叫做“倍长三角形”．若等腰△ABC是“倍长三角形”，底边BC的长为3，则腰AB的长为．【分析】由等腰△ABC是“倍长三角形”，可知AB＝2BC或BC＝2AB，若AB＝2BC＝6，可得AB的长为6；若BC＝3＝2AB，因1.5+1.5＝3，故此时不能构成三角形，这种情况不存在；即可得答案．【解答】解：∵等腰△ABC是“倍长三角形”，∴AB＝2BC或BC＝2AB，若AB＝2BC＝6，则△ABC三边分别是6，6，3，符合题意，∴腰AB的长为6；若BC＝3＝2AB，则AB＝1.5，△ABC三边分别是1.5，1.5，3，∵1.5+1.5＝3，∴此时不能构成三角形，这种情况不存在；综上所述，腰AB的长是6，故答案为：6．14、（2022•云南）已知△ABC是等腰三角形．若∠A＝40°，则△ABC的顶角度数是．【分析】分∠A是顶角和底角两种情况讨论，即可解答．【解答】解：当∠A是顶角时，△ABC的顶角度数是40°；当∠A是底角时，则△ABC的顶角度数为180°﹣2×40°＝100°；综上，△ABC的顶角度数是40°或100°．故答案为：40°或100°．15、（2022•滨州）如图，屋顶钢架外框是等腰三角形，其中AB＝AC，立柱AD⊥BC，且顶角∠BAC＝120°，则∠C的大小为．【分析】根据等腰三角形的性质和三角形内角和得到∠B＝∠C＝30°．【解答】解：∵AB＝AC且∠BAC＝120°，∴∠B＝∠C＝（180°﹣∠BAC）＝×60°＝30°．故答案为：30°．11。

河北省2019届中考数学系统复习第四单元图形的初步认识与三角形第15讲等腰三角形（8年真题训练）练习编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（河北省2019届中考数学系统复习第四单元图形的初步认识与三角形第15讲等腰三角形（8年真题训练）练习）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为河北省2019届中考数学系统复习第四单元图形的初步认识与三角形第15讲等腰三角形（8年真题训练）练习的全部内容。

第15讲等腰三角形命题点1 等腰三角形的性质与判定1．（2018·河北T8·3分)已知，如图,点P在线段AB外,且PA＝PB，求证：点P在线段AB的垂直平分线上．在证明该结论时，需添加辅助线，则作法不正确的是(B)A．作∠APB的平分线PC交AB于点CB．过点P作PC⊥AB于点C且AC＝BCC．取AB中点C，连接PCD．过点P作PC⊥AB，垂足为C2．(2017·河北T10·3分）如图,码头A在码头B的正西方向，甲、乙两船分别从A，B同时出发,并以等速驶向某海域，甲的航向是北偏东35°，为避免行进中甲、乙相撞，则乙的航向不能是（D)A．北偏东55° B．北偏西55°C．北偏东35° D．北偏西35°3．（2013·河北T8·3分）如图，一艘海轮位于灯塔P的南偏东70°方向的M处，它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处，则N处与灯塔P的距离为（D)A．40海里B．60海里C．70海里 D．80海里命题点2 等边三角形的性质与判定4．（2016·河北T16·2分)如图，∠AOB＝120°，OP平分∠AOB,且OP＝2.若点M，N分别在OA，OB上,且△PMN为等边三角形，则满足上述条件的△PMN有(D)A．1个B．2个C．3个D．3个以上5．（2011·河北T17·3分）如图1，两个等边△ABD,△CBD的边长均为1，将△ABD沿AC方向向右平移到△A′B′D′的位置，得到图2,则阴影部分的周长为2.图1 图2重难点1 等腰三角形的性质与判定在△ABC中，AC＝BC，∠ACB＝120°，点D是线段AB上一动点（D不与A，B重合)．(1)如图1，当点D为AB的中点,过点B作BF∥AC交CD的延长线于点F,求证：AC＝BF；（2）连接CD。

等腰三角形练习题一、计算题：1. 如图，△ABC 中，AB=AC,BC=BD,AD=DE=EB 求∠A 的度数2.如图，CA=CB,DF=DB,AE=AD 求∠A 的度数3、AB 于⊥AB 于E ，DF ⊥BC 交AC 于点F ，若∠EDF=70°，求∠AFD 的度数CFDA4. 如图，△ABC 中，AB=AC,BC=BD=ED=EA 求∠A 的度数5. 如图，△ABC 中，AB=AC ，D 在BC 上, ∠BAD=30°,在AC 上取点E ，使AE=AD, 求∠EDC 的度数6. 如图，△ABC 中，∠C=90°，D 为AB 上一点，作DE ⊥BC 于E ，若BE=AC,BD=21,DE+BC=1,求∠ABC 的度数BBDC7. 如图，△ABC 中，AD 平分∠BAC ，若AC=AB+BD 求∠B ：∠C 的值二、证明题：8. 如图，△DEF 中，∠EDF=2∠E ，FA ⊥DE 于点A ，问：DF 、AD 、AE 间有什么样的大小关系9. 如图，△ABC 中，∠B=60°，角平分线AD 、CE 交于点O求证：AE+CD=ACABCDAD FEABCDE12. 如图,△ABC 中,AB=AC,D 为△ABC 外一点，且∠ABD=∠ACD =60° 求证：CD=AB-BD13.已知：如图，AB=AC=BE ，CD 为△ABC 中AB 边上的中线求证：CD=21CE14. 如图，△ABC 中，∠1=∠2，∠EDC=∠BAC 求证：BD=EDECA BDE1 2 ABCD15. 如图，△ABC 中，AB=AC,BE=CF,EF 交BC 于点G 求证：EG=FG16. 如图，△ABC 中，∠ABC=2∠C ，AD 是BC 边上的高，B 到点E ，使BE=BD求证：AF=FC17. 如图，△ABC 中，AB=AC,AD 和BE 两条高，交于点H ，且AE=BE 求证：AH=2BDABDFECBD18. 如图，△ABC 中，AB=AC, ∠BAC=90°,BD=AB, ∠ABD=30° 求证：AD=DC19. 如图，等边△ABC 中，分别延长BA 至点E ，延长BC 至点D ，使AE=BD 求证：EC=ED20. 如图，四边形ABCD 中，∠BAD+∠BCD=180°，AD 、BC 的延长线交于点F ，DC 、AB 的延长线交于点E ，∠E 、∠F 的平分线交于点H 求证：EH ⊥FHBCDHABDCEF一、计算题：1. 如图，△ABC中，AB=AC,BC=BD,AD=DE=EB求∠A的度数设∠ABD为x,则∠A为2x由8x=180°得∠A=2x=45°2.如图，CA=CB,DF=DB,AE=AD求∠A的度数设∠A为x,由5x=180°得∠A=36°3. 如图，△ABC中，AB=AC，D在BC上，DE⊥AB于E，DF⊥BC交AC于点F，若∠EDF=70°，求∠AFD的度数∠AFD=160°FDAB4. 如图，△ABC中，AB=AC,BC=BD=ED=EA求∠A的度数设∠A为x∠A=71805. 如图，△ABC中，AB=AC，D在BC上, ∠BAD=30°,在AC上取点E，使AE=AD, 求∠EDC的度数设∠ADE为x∠EDC=∠AED－∠C=15°B2x6. 如图，△ABC 中，∠C=90°，D 为AB 上一点，作DE ⊥BC 于E ，若BE=AC,BD=21,DE+BC=1,求∠ABC 的度数 延长DE 到点F,使EF=BC 可证得:△ABC ≌△BFE 所以∠1=∠F 由∠2+∠F=90°, 得∠1+∠F=90°在Rt △DBF 中, BD=21,DF=1所以∠F =∠1=30°7. 如图，△ABC 中，AD 平分∠BAC ，若AC=AB+BD 求∠B ：∠C 的值在AC 上取一点E,使AE=AB 可证△ABD ≌△ADE 所以∠B=∠AEDFAE由AC=AB+BD,得DE=EC,所以∠AED=2∠C 故∠B ：∠C=2:1 二、证明题：8. 如图，△ABC 中，∠ABC,∠CAB 的平分线交于点P ，过点P 作DE ∥AB ，分别交BC 、AC 于点D 、E 求证：DE=BD+AE 证明△PBD 和△PEA 是等腰三角形9. 如图，△DEF 中，∠EDF=2∠E ，FA ⊥DE 于点A ，问：DF 、AD 、AE 间有什么样的大小关系 DF+AD=AE在AE 上取点B,使AB=AD10. 如图，△ABC 中，∠B=60°，角平分线AD 、CE 交于点O 求证：AE+CD=AC 在AC 上取点F,使AF=AE 易证明△AOE ≌△AOF, 得∠AOE=∠AOF由∠B=60°，角平分线AD 、CE,CBAD EPAD FEBOABCDEF得∠AOC=120°所以∠AOE=∠AOF=∠COF=∠COD=60°故△COD ≌△COF,得CF=CD所以AE+CD=AC11. 如图，△ABC 中，AB=AC, ∠A=100°，BD 平分∠ABC,求证：BC=BD+AD延长BD 到点E,使BE=BC,连结CE在BC 上取点F,使BF=BA易证△ABD ≌△FBD,得AD=DF再证△CDE ≌△CDF,得DE=DF故BE=BC=BD+AD也可:在BC 上取点E,使BF=BD,连结DF在BF 上取点E,使BF=BA,连结DE先证DE=DC,再由△ABD ≌△EBD,得AD=DE,最后证明DE=DF 即可 12. 如图,△ABC 中,AB=AC,D 为△ABC 外一点，且∠ABD=∠ACD =60° 求证：CD=AB-BD在AB 上取点E ，使BE=BD ，在AC 上取点F ，使CF=CD得△BDE 与△CDF 均为等边三角形，只需证△ADF ≌△AED AC FA C E F A BCDE F13.已知：如图，AB=AC=BE ，CD 为△ABC 中AB 边上的中线求证：CD=21CE 延长CD 到点E,使DE=CD.连结AE 证明△ACE ≌△BCE14. 如图，△ABC 中，∠1=∠2，∠EDC=∠BAC求证：BD=ED在CE 上取点F,使AB=AF易证△ABD ≌△ADF,得BD=DF,∠B=∠AFD 由∠B+∠BAC+∠C=∠DEC+∠EDC+∠C=180°所以∠B=∠DEC所以∠DEC=∠AFD所以DE=DF,故BD=ED15. 如图，△ABC 中，AB=AC,BE=CF,EF 交BC 于点G求证：EG=FGE C A B D E 1 2 F16. 如图，△ABC 中，∠ABC=2∠C ，AD 是BC 边上的高，B 到点E ，使BE=BD 求证：AF=FC17. 如图，△ABC 中，AB=AC,AD 和BE 两条高，交于点H ，且AE=BE 求证：AH=2BD 由△AHE ≌△BCE,得BC=AH18. 如图，△ABC 中，AB=AC, ∠BAC=90°,BD=AB,∠ABD=30°求证：AD=DC作AF ⊥BD 于F,DE ⊥AC 于E可证得∠DAF=DAE=15°,所以△ADE ≌△ADF得AF=AE,由AB=2AF=2AE=AC,所以AE=EC,因此DE 是AC 的中垂线,所以AD=DCA B DFE C B D19. 如图，等边△ABC 中，分别延长BA 至点E ，延长BC 至点D ，使AE=BD 求证：EC=ED延长BD 到点F,使DF=BC,可得等边△BEF,只需证明△BCE ≌△FDE 即可20. 如图，四边形ABCD 中，∠BAD+∠BCD=180°，AD 、BC 的延长线交于点F ，DC 、AB 的延长线交于点E ，∠E 、∠F 的平分线交于点H求证：EH ⊥FH延长EH 交AF 于点G由∠BAD+∠BCD=180°,∠DCF+∠BCD=180°得∠BAD=∠DCF,由外角定理,得∠1=∠2,故△FGM 是等腰三角形 由三线合一,得EH ⊥附录资料：不需要的可以自行删除生活中的物理知识大全厨房中的物理知识我们认真观察厨房里燃料、炊具，做饭、做菜等全部过程，回忆厨房中发生的一系列变化，会看到有关的物理现象。

初中数学：等腰三角形练习（含答案）一、选择题1、等腰三角形一底角为50°,则顶角的度数为（）A、65B、70C、80D、40【答案】C【解析】试题分析：根据三角形的内角和定理求解.解：等腰三角形的顶角度数=180°-50°-50°=80°.故应选C考点：等腰三角形的性质2、如图,在△ABC中,AB=AC,∠A=36°,BD,CE分别为∠ABC,∠ACB的角平分线,则图中等腰三角形共有（）A． 5个B． 6个C．7个D．8个【答案】D【解析】试题分析：根据等腰三角形两底角相等和∠A=36°,求出∠ABC和∠ACB的度数,再根据角平分线的定义求出∠ABD、∠CBD、∠ACE、∠BCE的度数,利用三角形外角定理求出∠BOE、∠COD的度数,根据等角对等边进行判断.解：如下图所示,∵AB=AC,∠A=36°,∴∠ABC=∠ACB=72°,∵BD平分∠ABC,CE平分∠ACB,∴∠ABD=∠C BD=∠ACE=∠BCE=∠A=36°,∴△ABD、△BCD、△ACE、△BCE、△OBC是等腰三角形；∴∠BEC=∠A+∠ACE=72°,∠BOE=∠BCE+∠CBD=72°,∴∠BEC=∠BOE,同理可得：∠CDO=∠COD,∴△BOE、△COD是等腰三角形；又△ABC是等腰三角形,∴共有8个等腰三角形.故应选D.考点：1.等腰三角形的性质；2.等腰三角形的判定3、下列条件中不能确定是等腰三角形的是（）A．三条边都相等的三角形B．一条中线把面积分成相等的两部分的三角形C．有一个锐角是45°的直角三角形D．一个外角的平分线平行于三角形一边的三角形【答案】D【解析】试题分析：根据等腰三角形的定义和等腰三角形的判定定理进行判断.解：A选项、三条边都相等的三角形是特殊的等腰三角形,故A选项正确；B选项、三角形任何一条边上的中线都能把三角形分成面积相等的两个三角形,故B选项错误；C选项、有一个锐角是45°的直角三角形的另一个锐角也是45°,根据等角对等边可得这是一个等腰三角形,故C选项正确；D选项、如果一个外角的平分线平行于三角形一边,利用平行线的性质可证三角形的两个角相等,根据等角对等边可证这是一个等腰三角形,故D选项正确.故应选B考点：等腰三角形的判定4、下列能断定△ABC为等腰三角形的是（）A．∠A=30°,∠B=60°B．∠A=50°,∠B=80°C． AB=AC=2,BC=4 D．AB=3,BC=7,周长为13【答案】B【解析】试题分析：根据等腰三角形的判定定理进行判断.解：A选项、若∠A=30°,∠B=60°,则∠C=90°,不能判定△ABC为等腰三角形；B选项、若∠A=50°,∠B=80°,则∠C=50°,根据等角对等边能判定△ABC为等腰三角形；C选项、若AB=AC=2,BC=4,因为2+2=4,所以不能构成三角形；D选项、若AB=3,BC=7,周长为13,则AC=3,因为3+3<7,所以不能构成三角形.故应选B.考点：等腰三角形的判定5、已知下列各组数据,可以构成等腰三角形的是（）A． 1,2,1 B．2,2,1 C． 1,3,1 D．2,2,5【答案】B【解析】试题分析：根据三角形三边的关系进行判断.解：A选项、因为1+1=2,所以不能构成三角形；B选项、因为2+1>2,能构成三角形,所以可以构成等腰三角形；C选项、因为1+1<3,所以不能构成三角形；D选项、因为2+2<5,所以不能构成三角形.故应选B.考点：三角形三边关系6、小明将两个全等且有一个角为60°的直角三角形拼成如图所示的图形,其中两条较长直角边在同一直线上,则图中等腰三角形的个数是（）Ａ．4 Ｂ．3 Ｃ．2 Ｄ．1【答案】B【解析】试题分析：根据直角三角形的性质求出各角的度数,根据等角对等边进行判断. 解：∵∠B=∠E=60°,∴∠A=∠D=30°,∴△MAD是等腰三角形；∵∠EMG-∠A+∠D=60°,∴△EGM是等腰三角形；同理可证△BHM是等腰三角形.∴共有三个等腰三角形.故应选B考点：1.直角三角形的性质；2.等腰三角形的判定二、填空题7、一个等腰三角形的两边分别为3cm和4cm,则它的周长为_________；【答案】10cm或11cm【解析】试题分析：根据三角形的周长公式分情况进行计算.解：当三角形三边分别是3cm、3cm、4cm时,三角形的周长是3+3+4=10cm；当三角形三边分别是3cm、4cm、4cm时,三角形的周长是3+4+4=11cm.故答案是10cm或11cm.考点：等腰三角形的性质8、在方格纸上有一个△ABC,它的顶点位置如图所示,则这个三角形是三角形.【答案】等腰【解析】试题分析：根据点A在BC的垂直平分线上,可证AB=AC,所以这个三角形是等腰三角形.解：∵点A在BC的垂直平分线上,∴AB=AC,∴△ABC是等腰三角形.故答案是等腰.考点：1.线段垂直平分线的性质；2.等腰三角形的定义9、如果一个三角形有两个角分别为80°,50°,则这个三角形是_________三角形．【答案】等腰【解析】试题分析：根据三角形内角和求出三角形的另一个内角,根据等角对等边进行判断.解：∵第三个角=180°-50°-80°=50°.∴这个三角形是等腰三角形.故答案是等腰.考点：等腰三角形的判定10、用若干根火柴（不折断）紧接着摆成一个等腰三角形,一边用了10根火柴,则至少还要用_________根火柴．【答案】11【解析】试题分析：根据用10根火柴组成的边是等腰三角形的底边和腰,分两种情况进行讨论.解：当用10根火柴组成的边是等腰三角形的底边时,则每个腰上至少用6根火柴棍,∴共需要12根火柴棍；当用10根火柴组成的边是等腰三角形的腰时,则另一个腰上需要用10根火柴棍,底边至少用1根火柴,∴共需要11根火柴棍.∴至少还要用11根火柴.故答案是11.考点：1.等腰三角形的定义；2.三角形三边关系11、如图,△ABC是等腰三角形,且AB=AC,BM,CM分别平分∠ABC,∠ACB,DE 经过点M,且DE∥BC,则图中有_________个等腰三角形．【答案】5【解析】试题分析：根据等腰三角形的性质可得∠ABC=∠ACB,根据平行线的性质可证∠ADE=∠AED,根据角平分线的性质可证∠DBM=∠MBC=∠DMB=∠EMC=∠ECM=∠BCM,根据等角对等边进行证明.解：∵△ABC是等腰三角形,∴∠ABC=∠ACB,∵DE∥BC,∴∠ADE=∠AED,∴△ADE是等腰三角形；∵BM平分∠ABC,∴∠DBM=∠CBM,∵BC∥DE,∴∠DMB=∠CBM,∴∠DBM=∠DMB,∴△DBM是等腰三角形,同理可得△EMC是等腰三角形；又∵∠ABC=∠ACB,∴∠MBC=∠MCB,∴△MBC是等腰三角形.∵△ABC是等腰三角形.∴共有5个等腰三角形.故答案是5.考点：1.等腰三角形的性质；2.等腰三角形的判定三、解答题12、已知：如图,OA平分∠BAC,∠1=∠2．求证：△ABC是等腰三角形．【答案】证明见解析【解析】试题分析：首先过点O作OE⊥AB于E,OF⊥AC于F,根据角平分线的性质可证OE=OF,根据HL可证Rt△OBE≌Rt△OCF,利用全等三角形的性质可证∠5=∠6,所以可证∠ABC=∠ACB,根据等角对等边可证结论成立.证明：如下图所示,过点O作OE⊥AB于E,OF⊥AC于F,∵AO平分∠BAC,∴OE=OF（角平分线上的点到角两边的距离相等）．∵∠1=∠2,∴OB=OC．∴Rt△OBE≌Rt△OCF（HL）．∴∠5=∠6．∴∠1+∠5=∠2+∠6．即∠ABC=∠ACB．∴AB=AC．∴△ABC是等腰三角形．考点：1.角平分线的性质；2.等腰三角形的判定定理；3.全等三角形的判定和性质13、如图,△ABC中,∠A=36°,AB=AC,CD平分∠ACB,试说明△BCD是等腰三角形．【答案】证明见解析【解析】试题分析：根据等腰三角形的性质求出∠B=∠ACB=72°,根据角平分线的定义可以求出∠ACD=∠A=36°,根据三角形外角的性质可以求出∠ADB=72°,再根据等角对等边可证结论成立.证明：∵∠A=36°,AB=AC,∴∠B=∠ACB=72°,∵CD平分∠ACB,∴∠ACD=∠A=36°,∴∠BDC=∠A+∠ACD,∴∠BDC=∠B=72°,∴△BCD是等腰三角形．考点：1.等腰三角形的性质；2.等腰三角形的判定14、如图,ABC△中,∠ABC、∠ACB的平分线交于点F,过点F作DE∥BC分别交AB、AC于D、E,已知△ADE的周长为20cm,且BC=12cm,求△ABC的周长【答案】32cm.【解析】试题分析：首先根据角平分线的性质可证∠DBF=∠FBC,根据平行线的性质可证∠DFB=∠DBF,所以可证BD=DF,同理可证EC=EF,所以可证AD+AE+DF+EF=20cm,再根据BC的长度求出△ABC的周长.解：∵∠ABC、∠ACB的平分线交于点F,∴∠DBF=∠FBC,又∵DE∥BC,∴∠DFB=∠FBC,∴∠DFB=∠DBF,∴BD=DF,同理EC=EF,∵△ADE的周长为20cm,∴AD+AE+DF+EF=20cm,∴AD+AE+BD+EC=AB+AC=20cm又∵BC=12cm,∴AB+AC+BC=32cm即△ABC的周长为32cm.考点：1.等腰三角形的判定；2.等腰三角形的性质。

第十五讲等腰三角形与直角三角形宜宾中考考情与预测宜宾考题感知与试做1.（xx·宜宾中考）如图，在Rt△ABC中，∠B＝90°，AB＝3，BC＝4，将△ABC折叠，使点B恰好落在边AC上，与点B′重合，AE为折痕，则EB′＝ 1.5 .2.（宜宾中考）如图，在△ABC中，AD⊥BC于点D.请你再添加一个条件，就可以确定△ABC是等腰三角形.你添加的条件是答案不唯一，如BD＝CD Ｗ.宜宾中考考点梳理等腰三角形及其性质和判定1.等腰三角形概念有两条边相等的三角形叫做等腰三角形，相等的两边都叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角性质（1）等腰三角形两腰相等（如AB＝AC）；（2）等腰三角形的两底角相等（简写成“等边对等角”，如∠B＝∠C）；（3）等腰三角形底边上的高、中线及顶角的平分线互相重合（简称“三线合一”）；（4）等腰三角形是轴对称图形，有一条对称轴；（5）面积： S△ABC＝12BC·AD判定如果一个三角形有两个角相等，那么这两个角所对的边相等（简写成“等角对等边”）2.定义三条边都相等的三角形称为等边三角形（或正三角形）性质（1）等边三角形三边相等（如AB＝BC＝AC）；（2）等边三角形的各个角都相等，并且每一个角都等于60°（如∠A＝∠B＝∠C＝60°）；（3）等边三角形的内、外心重合；（4）等边三角形是轴对称图形，有三条对称轴；（5）面积：S△ABC＝12BC·AD＝34AB2判定（1）三条边都相等的三角形是等边三角形；（2）三个角都相等的三角形是等边三角形；（3）有一个角等于60°的等腰三角形是等边三角形直角三角形及其性质和判定3.直角三角形4.定义顶角为90°的等腰三角形是等腰直角三角形性质等腰直角三角形的顶角是直角，两底角都为45°判定（1）用定义判定；（2）有两个角为45°的三角形线段的垂直平分线和角平分线定义有一个角是直角的三角形叫做直角三角形性质（1）直角三角形的两个锐角互余；（2）直角三角形斜边上的中线等于斜边的一半（如CD＝12AB）；（3）在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半（如AC＝12AB）；（4）勾股定理：直角三角形两直角边的平方和等于斜边的平方（如a2＋b2＝c2）；（5）在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°；（6）面积：S△ABC＝12ab＝12ch（h为斜边c上的高）判定（1）有一个角是直角的三角形是直角三角形；（2）有两个角互余的三角形是直角三角形；（3）一条边的中线等于这条边的一半的三角形是直角三角形；（4）勾股定理的逆定理：如果三角形三边长a、b、c有关系a2＋b2＝c2，那么这个三角形是直角三角形，且边c所对的角为直角5.线段的垂直平分线（1）性质定理：线段垂直平分线上的点到线段两端的距离相等.如图，若OP垂直平分AB，则PA＝PB.（2）判定（性质定理的逆定理）：到线段两端距离相等的点在线段的垂直平分线上.6.角平分线（1）性质定理：角平分线上的点到角两边的距离相等.如图，若∠1＝∠2，PA⊥OA，PB⊥OB，则PA＝PB.（2）判定（性质定理的逆定理）：角的内部到角两边距离相等的点在角的平分线上.1.到三角形三个顶点的距离都相等的点是这个三角形的（D）A.三条高的交点B.三条角平分线的交点C.三条中线的交点D.三条边的垂直平分线的交点2.如图，在△ABC中，AB＝AC，∠A＝30°，AB的垂直平分线l交AC于点D，则∠CBD的度数为（B）A.30°B.45°C.50°D.75°（第2题图）（第3题图）3.如图，在△ABC中，AB＝AC，D为BC上一点，且DA＝DC，BD＝BA，则∠B的大小为（B）A.40°B.36°C.30°D.25°4.已知一个等腰三角形的两边长分别为2和4，则该等腰三角形的周长是10 Ｗ.5.在△ABC中，若∠C＝90°，∠A＝30°，AC＝5，则AB＝1033Ｗ.6.含30°角的直角三角板与直线l1、l2的位置关系如图所示，已知l1∥l2，∠1＝60°，以下三个结论中正确的是 ②③ （写出所有正确结论的序号）.①AC ＝2BC ；②△B CD 为正三角形；③AD＝BD.7.如图，在Rt △ABC 中，∠ACB ＝90°，CD 是AB 边上的中线，ED ⊥AB 于点D ，交AC 于点E.（1）若BC ＝3，AC ＝4，求CD 的长；（2）求证：∠1＝∠2.（1）解：∵∠ACB＝90°，BC ＝3，AC ＝4，∴AB ＝AC 2＋BC 2＝5.∵CD 是AB 边上的中线，∴CD ＝12AB ＝2.5； （2）证明：∵∠ACB＝90°，∴∠A ＋∠B＝90°.∵ED ⊥AB ，∴∠A ＋∠1＝90°，∴∠B ＝∠1.∵CD 是AB 边上的中线，∴BD ＝CD ，∴∠B ＝∠2，∴∠1＝∠2.8.如图，在△ABC 中，AB ＝AC ，CD 是∠ACB 的平分线，DE ∥BC ，交AC 于点E.（1）求证：DE ＝CE ；（2）若∠CDE＝35°，求∠A 的度数.（1）证明：∵CD 是∠ACB 的平分线，∴∠BCD ＝∠ECD.∵DE ∥BC ，∴∠EDC ＝∠BCD，∴∠EDC ＝∠ECD，∴DE ＝CE ；（2）解：∵∠ECD＝∠EDC＝35°，∴∠ACB ＝2∠ECD＝70°.∵AB ＝AC ，∴∠ABC ＝∠ACB＝70°，∴∠A ＝180°－70°－70°＝40°.中考典题精讲精练等腰三角形的性质和判定【典例1】如图，已知点D 为△ABC 内一点，CD 平分∠ACB，BD ⊥CD ，∠A ＝∠ABD，若AC ＝6，BC ＝4，求BD 的长.【解析】延长BD 与AC 交于点E ，由题意可推出BE ＝AE ，依据等角的余角相等，即可得等腰三角形BCE ，可推出BC ＝CE ，AE ＝BE ＝2BD ，根据AC ＝6，BC ＝4，即可求出BD 的长.【解答】解：延长BD 与AC 交于点E.∵∠A ＝∠ABD，∴BE ＝AE.∵BD ⊥CD ，∴BE ⊥CD.∵CD 平分∠ACB，∴∠BCD ＝∠ECD，∴∠EBC ＝∠BEC，∴BC ＝CE.∵BE⊥CD，∴2BD ＝BE.∵AC＝6，BC ＝4，∴CE ＝4，∴AE ＝AC －EC ＝6－4＝2，∴BE ＝2，∴BD ＝1.直角三角形的性质和判定【典例2】如图1，△ABC 中，CD 、BE 分别是AB 、AC 边上的高，M 、N 分别是线段BC 、DE 的中点.（1）求证：MN⊥DE；（2）连结DM 、ME ，猜想∠A 与∠DME 之间的关系，并写出推理过程；（3）若将锐角△ABC 变为钝角△ABC，如图2，上述（1）（2）中的结论是否都成立？若结论成立，直接回答，不需证明；若结论不成立，说明理由.图1 图2【解析】（1）连结DM 、EM ，根据“直角三角形斜边上的中线等于斜边的一半”可得DM ＝12BC ，EM ＝12BC ，从而得到DM ＝ME ，再根据等腰三角形的“三线合一”可得结论；（2）根据三角形的内角和定理可得∠ABC＋∠ACB＝180°－∠A，再根据“等腰三角形两底角相等”表示出∠BMD＋∠CME，然后根据“平角等于180°”表示出∠DME，整理即可得解；（3）根据三角形的内角和定理可得∠ABC＋∠ACB＝180°－∠BAC，再根据“等腰三角形两底角相等及三角形的一个外角等于与它不相邻的两个内角的和”表示出∠BME＋∠CMD，然后根据“平角等于180°”表示出∠DME，整理即可得解.【解答】（1）证明：连结DM 、EM.∵CD 、BE 分别是AB 、AC 边上的高，点M 是BC 的中点，∴DM ＝12BC ，ME ＝12BC ， ∴DM ＝EM.又∵点N 为DE 的中点，∴MN ⊥DE ；（2）解：在△ABC 中，∠ABC ＋∠ACB＝180°－∠A.∵DM ＝EM ＝BM ＝CM ，∴∠BMD ＋∠CME＝（180°－2∠ABC ）＋（180°－2∠ACB）＝360°－2（∠ABC＋∠ACB）＝360°－2（180°－∠A）＝2∠A，∴∠DME ＝180°－2∠A；（3）解：（1）中的结论成立，（2）中的结论不成立.理由：在△ABC 中，∠ABC ＋∠ACB＝180°－∠BAC.∵DM＝EM ＝BM ＝CM ，∴∠BME ＋∠CMD＝2∠ACB＋2∠ABC＝2（180°－∠BAC）＝360°－2∠BAC， ∴∠DME ＝180°－（360°－2∠BAC）＝2∠BAC－180°.线段中垂线定理及其逆定理【典例3】如图，在△ABC 中，AD 平分∠BAC，DE∥AC，EF ⊥AD 交BC 的延长线于点F.求证：∠FAC ＝∠B.【解析】根据角的平分线的定义和平行线的性质，可得AE ＝DE ，则EF 是AD 的垂直平分线，又∠FAD＝∠CAD＋∠FAC，∠FDA ＝∠B＋∠BAD，即可得证.【解答】证明：∵AD 平分∠BAC，∴∠BAD ＝∠CAD.∵DE ∥AC ，∴∠EDA ＝∠CAD.∴∠EDA ＝∠BAD，∴AE ＝ED.又∵EF⊥AD，∴EF 是AD 的垂直平分线，∴AF ＝DF ，∴∠FAD ＝∠FDA.又∵∠FAD＝∠CAD＋∠FAC，∠FDA ＝∠B＋∠BAD，∴∠FAC ＝∠B.1.如图，在△ABC 中，AD 平分∠BAC，BE ⊥AD ，BE 交AD 的延长线于点E ，点F 在AB 上，且EF∥AC.求证：点F 是AB 的中点.证明：∵AD 平分∠BAC，∴∠BAE ＝∠CAE.∵EF ∥AC ，∴∠AEF ＝∠CAE，∴∠AEF ＝∠BAE，∴AF ＝EF.又∵BE⊥AD，∴∠BAE ＋∠ABE＝90°，∠BEF ＋∠AEF ＝90°，∴∠ABE ＝∠BEF，∴BF ＝EF ，∴AF ＝BF ，∴点F 为AB 的中点.2.如图，∠AOP ＝∠BOP＝15°，PC ∥OA ，PD ⊥OA ，垂足为D ，若PC ＝10，则PD 等于（ C ）A .10B .5 3C .5D .2.53.如图，∠ABC ＝∠ADC＝90°，M 、N 分别是AC 、BD 的中点.求证：MN⊥BD.证明：连结BM 、DM.∵∠ABC ＝∠ADC＝90°，M 是AC 的中点，∴BM ＝DM ＝12AC. ∵N 是BD 的中点，∴MN ⊥BD.4.在△ABC 中，MP 、NO 分别垂直平分AB 、A C.（1）若BC ＝10 cm ，试求出△PAO 的周长；（2）若AB ＝AC ，∠BAC ＝110°，试求∠PAO 的度数；（3）在（2）中，若无“AB＝AC”的条件，你能求出∠PAO 的度数吗？若能，请求出来；若不能，请说明理由.解：（1）∵MP、NO 分别垂直平分AB 、AC ，∴AP ＝BP ，AO ＝CO ，∴△PAO 的周长＝AP ＋PO ＋AO ＝BP ＋PO ＋CO ＝BC ，∵BC ＝10 cm ，∴△PAO 的周长为10 cm ；（2）∵AB＝AC ，∠BAC ＝110°，∴∠B ＝∠C＝12（180°－110°）＝35°. ∵MP 、NO 分别垂直平分AB 、AC ，∴AP＝BP，AO＝CO，∴∠BAP＝∠B＝35°，∠CAO＝∠C＝35°，∴∠PAO＝∠BAC－∠BAP－∠CAO＝110°－35°－35°＝40°；（3）能.∵∠BAC＝110°，∴∠B＋∠C＝180°－110°＝70°.∵MP、NO分别垂直平分AB、AC，∴AP＝BP，AO＝CO，∴∠BAP＝∠B，∠CAO＝∠C，∴∠PAO＝∠BAC－∠BAP－∠CAO＝∠BAC－（∠B＋∠C）＝110°－70°＝40°.。

EDC A B F1.等腰三角形练习题(第一课时)一、选择题1．等腰三角形的对称轴是（ ）A ．顶角的平分线B ．底边上的高C ．底边上的中线D ．底边上的高所在的直线2．等腰三角形有两条边长为4cm 和9cm ，则该三角形的周长是（ ） A ．17cm B ．22cm C ．17cm 或22cm D ．18cm3．等腰三角形的顶角是80°，则一腰上的高与底边的夹角是（ ） A ．40° B ．50° C ．60° D ．30° 4．等腰三角形的一个外角是80°，则其底角是（ ）A ．100°B ．100°或40°C ．40°D ．80°5．如图，C 、E 和B 、D 、F 分别在∠GAH 的两边上，且AB=BC=CD=DE=EF ，若∠A=18°，则∠GEF 的度数是（ ）A ．80°B ．90°C ．100°D ．108°EDCABHFG二、填空题6．等腰△ABC 的底角是60°，则顶角是________度． 7．等腰三角形“三线合一”是指___________．8．等腰三角形的顶角是n °，则两个底角的角平分线所夹的钝角是_________． 9．如图，△ABC 中AB=AC ，EB=BD=DC=CF ，∠A=40°，则∠EDF•的度数是_____． 10．△ABC 中，AB=AC ．点D 在BC 边上（1）∵AD 平分∠BAC ，∴_______=________；________⊥_________； （2）∵AD 是中线，∴∠________=∠________；________⊥________； （3）∵AD ⊥BC ，∴∠________=∠_______；_______=_______． 三、解答题11．已知△ABC 中AB=AC ，AD ⊥BC 于D ，若△ABC 、△ABD 的周长分别是20cm 和16cm ，•求AD 的长．12．如图，在四边形ABCD 中，AB=AD ，CB=CD ，求证：∠ABC=∠ADC.DCAB13．已知△ABC 中AB=AC ，点P 是底边的中点，PD ⊥AB ，PE ⊥AC ，垂足分别是D 、E ，• 求证：PD=PE.四、探究题14．如图，CD 是△ABC 的中线，且CD=12AB ，你知道∠ACB 的度数是多少吗？由此你能得到一个什么结论？请叙述出来与你的同伴交流．DCAB答案:1．D 2．B 3．A 4．C 5．B 6．607．等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合 8．（90+12n ）° 9．70° 10．略 11．6cm 12．连接BD ，∵AB=AD ，∴∠ABD=∠ADB ．∵CB=CD ，∴∠CBD=∠CDB ．∴∠ABC=∠ADC 13．连接AP ，证明AP 平分∠BAC ．14．∠ACB=90°．结论：若一个三角形一条边上的中线等于这条边的一半，那么这个三角形是直角三角形练习题(第二课时)一、选择题1．如图1，已知OC 平分∠AOB ，CD ∥OB ，若OD=3cm ，则CD 等于（ ）A ．3cmB ．4cmC ．1.5cmD ．2cmD C A BE D ABFEDCABH F（1） (2) (3)2．△ABC 中AB=AC ，∠A=36°，BD 平分∠ABC 交AC 于D ，则图中的等腰三角形有（ ） A ．1个 B ．2个 C ．3个 D ．4个3．如图2，△ABC 中，∠ABC 与∠ACB 的平分线交于点F ，过点F 作DE ∥BC 交AB 于点D ，交AC 于点E ，那么下列结论：①△BDF 和△CEF 都是等腰三角形；②DE=BD+CE ；•③△ADE 的周长等于AB 与AC 的和；④BF=CF ．其中正确的有（ ） A ．①②③ B ．①②③④ C ．①② D ．①4．如图3，Rt △ABC 中，CD 是斜边AB 上的高，角平分线AE 交CD 于H ，EF ⊥AB 于F ，则下列结论中不正确的是（ ）A ．∠ACD=∠B B ．CH=CE=EFC ．CH=HD D ．AC=AF 二、填空题5．△ABC 中，∠A=65°，∠B=50°，则AB ：BC=_________．6．已知AD 是△ABC 的外角∠EAC 的平分线，要使AD•∥BC ，•则△ABC•的边一定满足________． 7．△ABC 中，∠C=∠B ，D 、E 分别是AB 、AC 上的点，•AE=•2cm ，•且DE•∥BC ，•则AD=________． 8．一灯塔P 在小岛A 的北偏西25°，从小岛A 沿正北方向前进30海里后到达小岛，•此时测得灯塔P 在北偏西50°方向，则P 与小岛B 相距________． 三、解答题 9．如图，已知AB=AC ，E 、D 分别在AB 、AC 上，BD 与CE 交于点F ，•且∠ABD=•∠ACE ， 求证：BF=CF ．E D CA BF10．如图，△ABC 中BA=BC ，点D 是AB 延长线上一点，DF ⊥AC 于F 交BC 于E ，• 求证：△DBE 是等腰三角形．ED CABF四、探究题11．如图，AF 是△ABC 的角平分线，BD ⊥AF 交AF 的延长线于D ，DE ∥AC•交AB 于E ， 求证：AE=BE ．ECABF答案:1．A 2．C 3．A 4．C 5．1 6．AB=AC 7．2cm 8．30海里9．连接BC ，∵AB=AC ，∴∠ABC=∠ACB ，又∵∠ABD=∠ACE ，∴∠FBC=∠FCB ，∴FB=FC 10．证明∠D=∠BED11．证明∠EAD=∠EDA ，∠EBD=∠EDB 分别得到AE=DE ，BE=DE。