2006年中考二次函数试题精选(1)_3

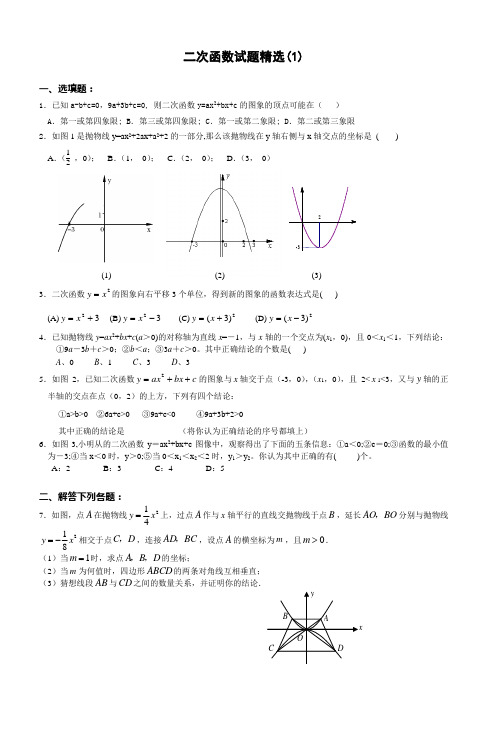
一、选填题：1．已知a-b+c=0，9a+3b+c=0, 则二次函数y=ax 2+bx+c A ．第一或第四象限; B ．第三或第四象限; C 2．如图1是抛物线y=ax 2+2ax+a 2+2的一部分,( ) A ．（12，0）； B ．（1， 0）； C ．（2， 0）； D ．（3，(1) (2) (3) 3．二次函数2x y =的图象向右平移3个单位，得到新的图象的函数表达式是( ) (A)32+=x y (B)32-=x y (C)2)3(+=x y(D)2)3(-=x y4．已知抛物线y =ax 2+bx +c (a ＞0)的对称轴为直线x =－1，与x 轴的一个交点为(x 1，0)，且0＜x 1＜1，下列结论：①9a －3b ＋c ＞0；②b ＜a ；③3a ＋c ＞0。

其中正确结论的个数是( ) A 、0 B 、1 C 、3 D 、3 5．如图2，已知二次函数c bx ax y ++=2的图象与x 轴交于点（-3，0），（x 1，0），且2<x 1<3，又与y 轴的正半轴的交点在点（0，2）的上方，下列有四个结论： ①a>b>0 ②6a+c>0 ③9a+c<0 ④9a+3b+2>0其中正确的结论是_____________（将你认为正确结论的序号都填上）6．如图3,小明从的二次函数y ＝ax 2+bx+c 图像中，观察得出了下面的五条信息：①a ＜0;②c ＝0;③函数的最小值为－3;④当x ＜0时，y ＞0;⑤当0＜x 1＜x 2＜2时，y 1＞y 2。

你认为其中正确的有( )个。

A ：2 B ：3 C ：4 D ：5二、解答下列各题：7．如图，点A 在抛物线214y x =上，过点A 作与x 轴平行的直线交抛物线于点B ，延长AO BO ，分别与抛物线218y x =-相交于点C D ，，连接AD BC ，，设点A 的横坐标为m ，且0m >．（1）当1m =时，求点AB D ，，的坐标； （2）当m 为何值时，四边形ABCD 的两条对角线互相垂直； （3）猜想线段AB 与CD 之间的数量关系，并证明你的结论．8．如图，抛物线y ＝－12x 2＋52x －2与x 轴相交于点A 、B ，与y 轴相交于点C ． （1）求证：△AOC ∽△COB ；（2）过点C 作CD ∥x 轴交抛物线于点D ．若点P 在线段AB 上以每秒1个单位的速度由A 向B 运动，同时点Q 在线段CD 上也以每秒1个单位的速度由D 向C 运动，则经过几秒后，PQ ＝AC ．9．如图，P 为抛物线4123432+-=x x y 上对称轴上右侧的一点，且点P 在x 轴上方，过点P 作P A 垂直x 轴与点A ，PB 垂直y 轴于点B ，得到矩形P AOB ．若AP =1，求矩形P AOB 的面积．10．如图①，正方形ABCD 的顶点A 、B 的坐标分别为（0，10）、（8，4），顶点C 、D 在第一象限．点P 从点A 出发，沿正方形按逆时针方向匀速运动，同时，点Q 从点E （4，0）出发，沿x 轴正方向以相同速度运动．当点P 到达点C 时，P 、Q 两点同时停止运动，设运动的时间为t 秒．（1）求正方形ABCD 的边长．（2）当点P 在AB 边上运动时，△OPQ 的面积S (平方单位)与时间t (秒)之间的函数图象为抛物线的一部分（如图②所示），求P 、Q 两点的运动速度．（3）求（2）中面积S (平方单位)与时间t (秒)的函数关系式及面积S 最大值时点P 的坐标．（4分）（4）若点P 、Q 保持（2）中的速度不变，则点P 沿着AB 边运动时，∠OPQ 的大小随着时间t 的增大而增大；沿着BC 边运动时，∠OPQ 的大小随着时间t 的增大而减小．当点P 沿着这两边运动时，使∠OPQ =90o 的点P 有__________个．（抛物线)0(2≠++=a c bx ax y 的顶点坐标是(a b 2-，ab ac 442-)．）图① 图②11．如图，足球场上守门员在O 处开出一高球，球从离地面1米的A 处飞出（A 在y 轴上），运动员乙在距O 点6米的B 处发现球在自己头的正上方达到最高点M ，距地面约4米高，球落地后又一次弹起．据实验，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半． （1）求足球开始飞出到第一次落地时，该抛物线的表达式． （2）足球第一次落地点C距守门员多少米？（取7=）（3）运动员乙要抢到第二个落点D，他应再向前跑多少米？（取5=）12.如图11，已知抛物线32++-=mx x y 与x 轴的一个交点A （3，0）.(1)你一定能分别求出这条抛物线与x 轴的另一个交点B 及与y 轴的交点C 的坐标，试试看；（2）设抛物线的顶点为D ，请在图中画出抛物线的草图. 若点E （－2，n ）在直线BC 上，试判断E 点是否在经过D 点的反比例函数的图象上，把你的判断过程写出来； (3)请设法求出tan ∠DAC 的值.13．已知：半径为1的⊙O 1与X 轴交于A 、B 两点，圆心O 1的坐标为（2, 0)，二次函数y=-x 2+bx+c 的图象经过A 、B 两点，其顶点为F.（1）求 b 、c 的值及二次函数顶点F 的坐标；（2）写出将二次函数y=-x 2+bx+c 的图象向下平移1个单位再向左平移2个单位的图象的函数表达式；（3）经过原点O 的直线l 与⊙O 相切，求直线l 的函数表达式.14．一条隧道的截面如图所示，它的上部是一个以AD 为直径的半圆O ，下部是一个矩形ABCD . ⑴当AD=4米时，求隧道截面上部半圆O 的面积；⑵已知矩形ABCD 相邻两边之和为8米，半圆O 的半径为r 米.①求隧道截面的面积S （米2）关于半径r （米）的函数关系式（不要求写出r 的取值范围）； ②若2米≤CD ≤3米，利用函数图象求S 的最大值（π取3.14，结果精确到0.1米）15．已知P(m,a)是抛物线y=ax 2上的点，且点P 在第一象限. (1)求m 的值；(2)直线y=kx+b 过点P ，交x 轴的正半轴于点A,交抛物线于另一点M. ①当b=2a 时，∠OPA=90°是否成立？如果成立，请证明；如果不成立，举出一个反例说明；②当b=4时，记△MOA 的面积为S ，求1S 的最大值.16.已知:AC 是⊙O`的直径,点A 、B 、C 、O 在⊙O`上OA=2.建立如图11所示的直角坐标系.∠ACO=∠ACB=60°.D(1)求点B 关于x 轴对称的点D 的坐标;(2)求经过三点A 、B 、O 的二次函数的解析式;(3)该抛物线上是否存在在点P,使四边形PABO 为梯形?若存在,请求出P 点的坐标;若不存在,请说明理由.17．已知抛物线c bx x y ++=221经过点(1，－1)和C(0，－1)，且与x 轴交于A 、B 两点(A 在B 左边)，直线x = m (m > 0)与x 轴交于点D 。

2006年深圳市中考试题：二次函数篇【教学目标】结合实例掌握二次函数综合题中存在的问题的解法．【重难点】1．（泰州市，2001）如图所示，已知二次函数()62222-+-+-=k k kx x y ，k 为正整数，它的图像与x 轴交于点A 、B ，且点A 在原点左边，点B 在原点右边．（1）求这个二次函数的解析式．（2）直线n mx y +=过点A 且与y 轴的正半轴交于点C ，与抛物线交于第一象限内的点D ，过点D 作x DE ⊥轴于点E ，已知1:3:=∆∆ACO EDB S S ．①求直线的解析式；②若点O 1是ABD ∆的外接圆的圆心，求1tan ADO ∠；③设抛物线交y 轴于点F ，问点F 是否在ABD ∆的外接圆上，请证明你的结论．2．如图所示，抛物线c bx ax y ++=2与x 轴有两个不同的交点()()()21210,,0,x x x B x A <，与y 轴的正半轴交于点C,已知该抛物线顶点横坐标为1,A 、B 两点间的距离为4,ABC ∆的面积是6． （1）求这条抛物线的解析式；（2）求ABC ∆的外接圆的圆心M 的坐档；（3）在抛物线上是否存在一点P ，使BPD ∆（PD 垂直x 轴，垂足为D ）被直线BM 分成的面积比为1:2两部分？若存在，请求出P 点坐标，若不存在，请说明理由．3．已知抛物线134312++=x x y 与x 轴的交点从左到右依次为A 、B ，与y 轴的交点为C ．（1）通过配方，求抛物线的对称轴；（2）试求ABC ∆的外接圆的圆心M 的坐标；（3）设（2）中的⊙M 与y 轴的另一个交点为N ，直线AN 与抛物线的另一个交点为P ，试问在过P 点且平行于x 轴的直线上是否存在一点D ，使得点D 到⊙M 的切线长最小？若存在，求出点D 的坐标；若不存在，请说明理由．4．如图所示，抛物线c bx ax y ++=2经过点A （1,0），B(4,0)，C(0,2)．（1）求抛物线的解析式及顶点坐标；（2）在对称轴右侧的抛物线上是否存在点P ，使P A C ∆为直角三角形？若存在，求出所有符合条件的点P 的坐标，并判断PAC ∆是否与COA ∆相似；荐不存在，请说明理由．n ,) x5．已知：如图所示，抛物线c bx ax y ++=2与x 轴交于A 、B 两点，它们的横坐标分别为-1和3，与y 轴交点C 的纵坐标为3，ABC ∆的外接圆的圆心点M ．（1）求这条抛物线的解析式；（2）求图像经过M ，A 两点的一次函数解析式；（3）在（1）中的抛物线上是否存在点P ，使过P ，M 两点的直线与ABC ∆的两边AB 、BC 的交点E 、F 和点B 所组成的BEF ∆与ABC ∆相似？若存在，求出点P 的坐标；若不存在，请说明理由．。

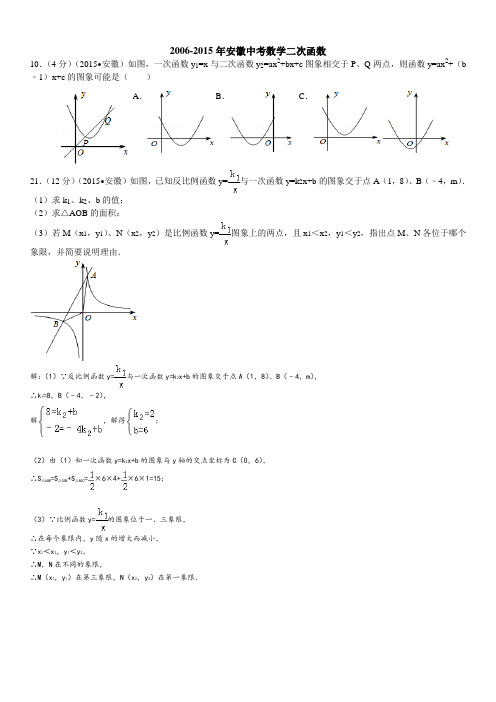
2006-2015年安徽中考数学二次函数10．（4分）（2015•安徽）如图，一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点，则函数y=ax2+（b ﹣1）x+c的图象可能是（）A．B．C．21．（12分）（2015•安徽）如图，已知反比例函数y=与一次函数y=k2x+b的图象交于点A（1，8）、B（﹣4，m）．（1）求k1、k2、b的值；（2）求△AOB的面积；（3）若M（x1，y1）、N（x2，y2）是比例函数y=图象上的两点，且x1＜x2，y1＜y2，指出点M、N各位于哪个象限，并简要说明理由．解：（1）∵反比例函数y=与一次函数y=k2x+b的图象交于点A（1，8）、B（﹣4，m），∴k1=8，B（﹣4，﹣2），解，解得；（2）由（1）知一次函数y=k2x+b的图象与y轴的交点坐标为C（0，6），∴S△AOB=S△COB+S△AOC =×6×4+×6×1=15；（3）∵比例函数y=的图象位于一、三象限，∴在每个象限内，y随x的增大而减小，∵x1＜x2，y1＜y2，∴M，N在不同的象限，∴M（x1，y1）在第三象限，N（x2，y2）在第一象限．22．（12分）（2015•安徽）为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m 的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等．设BC 的长度为xm ，矩形区域ABCD 的面积为ym 2．（1）求y 与x 之间的函数关系式，并注明自变量x 的取值范围； （2）x 为何值时，y 有最大值？最大值是多少？解（1）∵三块矩形区域的面积相等， ∴矩形AEFD 面积是矩形BCFE 面积的2倍， ∴AE=2BE ， 设BE=a ，则AE=2a ， ∴8a+2x=80，∴a=﹣x+10，2a=﹣x+20，∴y=（﹣x+20）x+（﹣x+10）x=﹣x 2+30x ， ∵a=﹣x+10＞0， ∴x ＜40，则y=﹣x 2+30x （0＜x ＜40）；（2）∵y=﹣x 2+30x=﹣（x ﹣20）2+300（0＜x ＜40），且二次项系数为﹣＜0， ∴当x=20时，y 有最大值，最大值为300平方米9．（4分）（2014•安徽）如图，矩形ABCD 中，AB=3，BC=4，动点P 从A 点出发，按A →B →C 的方向在AB 和BC 上移动，记PA=x ，点D 到直线PA 的距离为y ，则y 关于x 的函数图象大致是（ ）12．（5分）（2014•安徽）某厂今年一月份新产品的研发资金为a 元，以后每月新产品的研发资金与上月相比增长率都是x ，则该厂今年三月份新产品的研发资金y （元）关于x 的函数关系式为y= _________ ． 22．（12分）（2014•安徽）若两个二次函数图象的顶点、开口方向都相同，则称这两个二次函数为“同簇二次函数”． （1）请写出两个为“同簇二次函数”的函数；（2）已知关于x 的二次函数y 1=2x 2﹣4mx+2m 2+1和y 2=ax 2+bx+5，其中y 1的图象经过点A （1，1），若y 1+y 2与y 1为“同簇二次函数”，求函数y 2的表达式，并求出当0≤x ≤3时，y 2的最大值．解：（1）设顶点为（h ，k ）的二次函数的关系式为y=a （x ﹣h ）2+k ，A ．B ．C ．当a=2，h=3，k=4时，二次函数的关系式为y=2（x﹣3）2+4．∵2＞0，∴该二次函数图象的开口向上．当a=3，h=3，k=4时，二次函数的关系式为y=3（x﹣3）2+4．∵3＞0，∴该二次函数图象的开口向上．∵两个函数y=2（x﹣3）2+4与y=3（x﹣3）2+4顶点相同，开口都向上，∴两个函数y=2（x﹣3）2+4与y=3（x﹣3）2+4是“同簇二次函数”．∴符合要求的两个“同簇二次函数”可以为：y=2（x﹣3）2+4与y=3（x﹣3）2+4．（2）∵y1的图象经过点A（1，1），∴2×12﹣4×m×1+2m2+1=1．整理得：m2﹣2m+1=0．解得：m1=m2=1．∴y1=2x2﹣4x+3=2（x﹣1）2+1．∴y1+y2=2x2﹣4x+3+ax2+bx+5=（a+2）x2+（b﹣4）x+8∵y1+y2与y1为“同簇二次函数”，∴y1+y2=（a+2）（x﹣1）2+1=（a+2）x2﹣2（a+2）x+（a+2）+1．其中a+2＞0，即a＞﹣2．∴．解得：．∴函数y2的表达式为：y2=5x2﹣10x+5．∴y2=5x2﹣10x+5=5（x﹣1）2．∴函数y2的图象的对称轴为x=1．∵5＞0，∴函数y2的图象开口向上．①当0≤x≤1时，∵函数y2的图象开口向上，∴y2随x的增大而减小．∴当x=0时，y2取最大值，最大值为5（0﹣1）2=5．②当1＜x≤3时，∵函数y2的图象开口向上，∴y2随x的增大而增大．∴当x=3时，y2取最大值，最大值为5（3﹣1）2=20．综上所述：当0≤x≤3时，y2的最大值为20．9.（2013·安徽）图1所示矩形ABCD 中，BC=x ，CD=y ，y 与x 满足反比例函数关系式如图2所示，等腰直角三角形AEF 的斜边EF 过C 点，M 为EF 的中点，则下列结论正确的是（ ）A.当x =3时，EC<EMB.当y =9时，EC>EMC.当x 增大时，EC CF ⋅的值增大D.当y 增大时，BE DF ⋅的值不变16.（2013·安徽）已知二次函数的顶点坐标为(1,1)-，且经过原点(0,0)，求该函数的解析式。

2006~2017年南京市中考数学-----二次函数汇编（2006年，26题，8分）西瓜经营户以2元/千克的价格购进一批小型西瓜，以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价O.1元/千克，每天可多售出40千克.另外，每天的房租等固定成本共24元.该经营户要想每天盈利2O0元，应将每千克小型西瓜的售价降低多少元?（2007年，25题，7分）某农场去年种植了10亩地的南瓜，亩产量为2000kg ，根据市场需要，今年该农场扩大了种植面积，并且全部种植了高产的新品种南瓜，已知南瓜种植面积的增长率是亩产量的增长率的2倍，今年南瓜的总产量为60 000kg ，求南瓜亩产量的增长率．（2008年，25题，7分）某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2:1．在温室内，沿前侧内墙保留3m 宽的空地，其它三侧内墙各保留1m 宽的通道．当矩形温室的长与宽各为多少时，蔬菜种植区域的面积是2288m ？（第25题）（2008年，26题，8分）已知二次函数2y x bx c =++中，函数y 与自变量x 的部分对应值如下表：（1）求该二次函数的关系式；（2）当x 为何值时，y 有最小值，最小值是多少？（3）若1()A m y ，，2(1)B m y +，两点都在该函数的图象上，试比较1y 与2y 的大小．（2009年，24题，10分）如图，已知二次函数221y x x =--的图象的顶点为A ．二次函数2y ax bx=+的图象与x 轴交于原点O 及另一点C ，它的顶点B 在函数221y x x =--的图象的对称轴上． （1）求点A 与点C 的坐标；（2）当四边形AOBC 为菱形时，求函数2y ax bx =+的关系式．（1）用含a的代数式表示b；（2）如果该二次函数的图像与x轴只有一个交点，求这个二次函数的图像的顶点坐标。

（2010年，27题，8分）某批发商以每件50元的价格购进800件T恤，第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件，批发商为增加销售量，决定降价销售，根据市场调查，单价每降低1元，可多售出10件，但最低单价应高于购进的价格；第二个月结束后，批发商将对剩余的T恤一次性清仓销售，清仓是单价为40元，设第二个月单价降低x元。

2006《二次函数图像与性质》中考题集锦（二）第31题（2006济宁课改）二次函数26y x x =+-的图象与x 轴交点的横坐标是（ ）A ．2和3-B ．2-和3C ．2和3D ．2-和3-答案：A第32题（2006荆州课改）已知y 关于x 的函数：()()22211y k x k x k =---++中满足3k ≤．（1）求证：此函数图象与x 轴总有交点． （2）当关于z 的方程2233z kz z -=+--有增根时，求上述函数图象与x 轴的交点坐标． 答案：（1）当2k =时，函数为23y x =-+，图象与x 轴有交点． 当2k ≠时，()()()241421412k k k k =---+=-+△ 当3k ≤时，0△≥，此时抛物线与x 轴有交点．因此，3k ≤时，y 关于x 的函数()()22211y k x k x k =---++的图象与x 轴总有交点．（2）关于z 的方程去分母得：226z k z -=+-，4k z =-． 由于原分式方程有增根，其根必为3z =．这时1k =（6分）这时函数为22y x =-+．它与x 轴的交点是()和)第33题（2006苏州课改）抛物线2245y x x =++的对称轴是x =______．答案：1-第34题. （2006安徽课改）抛物线2(1)y x m x m =-+-+与y 轴交于（1）求出m 的值并画出这条抛物线；（2）求它与x 轴的交点和抛物线顶点的坐标； （3）x 取什么值时，抛物线在x 轴上方？（4）x 取什么值时，y 的值随x 值的增大而减小？ 【解】答案：解：（1）由抛物线2(1)y x m x m =-+-+与y 轴交于(03)，，得：m =∴抛物线为223y x x =-++．图象略．（2）由2230x x -++=，得1213x x =-=，． ∴抛物线与x 轴的交点为(10)(30)-，，，．2223(1)4y x x x =-++=--+， ∴抛物线顶点坐标为(14)，．（3）由图象可知：当13x -<<时，抛物线在x 轴上方． （4）由图象可知：当1x >时，y 的值随x 值的增大而减小．第35题（2006贺州课改）已知抛物线268y ax x =+-与直线3y x =-相交于点(1)A m ，．（1）求抛物线的解析式；（2）请问（1）中的抛物线经过怎样的平移就可以得到2y ax =的图象？（3）设抛物线2y ax =上依次有点1234P P P P ，，，，…，其中横坐标依次是2468，，，，…，纵坐标依次为1234n n n n ，，，，…，试求31003n n -的值． 答案：解：（1）点(1)A m ，在直线3y x =-上，313m ∴=-⨯=-．把13x y ==-，代入268y ax x =+-， 得683a +-=-．求得1a =-．∴抛物线的解析式是268y x x =-+-．（2）2268(3)1y x x x =-+-=--+．∴顶点坐标为(31)，．∴把抛物线268y x x =-+-向左平移3个单位长度得到21y x =-+的图象，再把21y x =-+的图象向下平移1个单位长度得到2y x =-的图象．（3）由题意知，123P P P ，，，…的横坐标是连续偶数，所以n P 的横坐标是2n ，纵坐标为31003n n ，所对应的纵坐标依次是2262006--，．(20066)(20066)4024000=+-=．第36题.（2006湖南永州非课改）观察下列四个函数的图象（ ）A B C D 第37题（2006沈阳非课改）抛物线()2361y x =-+-的对称轴是直线（ ）①② ③ ④Ａ．6x =- Ｂ．1x =- Ｃ．1x =Ｄ．6x =答案：Ａ第38题（2006兰州A 课改）请选择一组你喜欢的a b c ，，的值，使二次函数2(0)y ax bx c a =++≠的图象同时满足下列条件：①开口向下，②当2x <时，y 随x 的增大而增大；当2x >时，y 随x 的增大而减小．这样的二次函数的解析式可以是 ．答案：答案不唯一，只要满足对称轴是2x =，0a <．第39题（2006兰州A 课改）已知22y x =的图象是抛物线，若抛物线不动，把x 轴，y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是（ ）． Ａ．22(2)2y x =-+ Ｂ．22(2)2y x =+-Ｃ．22(2)2y x =--Ｄ．22(2)2y x =++答案：Ｂ第40题.（2006兰州A 课改）已知二次函数2y ax bx c =++的图象如图所示，对称轴是1x =，则下列结论中正确的是（ ）． Ａ．0ac > Ｂ．0b < Ｃ．240b ac -<Ｄ．20a b +=答案：Ｄ第41题.（2006辽宁十一市课改）已知二次函数2(0)y ax bx c a =++≠，其中a b c ，，满足0a b c ++=和930a b c -+=，则该二次函数图象的对称轴是直线 ． 答案：1x =-第42题（2006辽宁十一市非课改）如图，已知抛物线2(0)y ax bx c a =++≠经过(20)(04)A B --，，，，(24)C -，三点，且与x 轴的另一个交点为E ．（1）求抛物线的解析式；（2）用配方法求抛物线的顶点D 的坐标和对称轴； （3）求四边形ABDE 的面积．答案：解：（1）抛物线2y ax bx c =++经过(20)(04)(24)A B C ---，，，，，三点4204424a b c c a b c -+=⎧⎪∴=-⎨⎪++=-⎩解得1214a b c ⎧=⎪⎪=-⎨⎪=-⎪⎩OA B C D OExyA BCDOE xy∴抛物线解析式：2142y x x =--． （2）221194(1)222y x x x =--=-- ∴顶点坐标912D ⎛⎫- ⎪⎝⎭，，对称轴：1x =．（3）连结OD ，对于抛物线解析式2142y x x =-- 当0y =时，得2280x x --=，解得：12x =-，24x =42915AOB BOD EOD ABDE S S S S ∴=++=++=△△△四边形．第43题. （2006 浙江湖州课改）已知二次函数()2111y x bx b =-+-≤≤，当b 从1-逐渐变化到1的过程中，它所对应的抛物线位置也随之变动．下列关于抛物线的移动方向的描述中，正确的是（ ）Ａ．先往左上方移动，再往左下方移动 Ｂ．先往左下方移动，再往左上方移动 Ｃ．先往右上方移动，再往右下方移动 Ｄ．先往右下方移动，再往右上方移动答案：Ｃ第44题. （2006 江西课改）二次函数223y x x =--的最小值是 ．答案：4-第45题（2006长春课改）如图，P 为抛物线2331424y x x =-+上对称轴右侧的一点，且点P 在x 轴上方，过点P 作PA 垂直x 轴于点A ，PB 垂直y 轴于点B ，得到矩形PAOB ．若1AP =，求矩形PAOB 的面积．答案：PA x ⊥轴，1AP =，∴点P 的纵坐标为1．当1y =时，23311424x x -+=，即2210x x --=．解得121212x x =+=-，．抛物线的对称轴为1x =，点P 在对称轴的右侧，12x ∴=+．∴矩形PAOB 的面积为()12+个平方单位．第46题（2006山西非课改）二次函数()20y ax bx c a =++≠的图象如图所示．有下列结论：①240b ac -<；②0ab >；③0a b c -+=；④40a b +=；⑤当2y =时，x 只能等于0．其中正确的是（ ）Ａ．①④ Ｂ．③④ Ｃ．②⑤ Ｄ．③⑤答案：Ｂ第47题（2006威海非课改）抛物线2=y ax bx c ++(0)a ≠过点(13)(33)(15)A B C ---，，，，，，顶点为M 点．（1）求该抛物线的解析式．（2）试判断抛物线上是否存在一点P ，使∠POM ＝90˚． 若不存在，说明理由；若存在，求出P 点的坐标．（3）试判断抛物线上是否存在一点K ，使∠OMK ＝90˚， 说明理由． 答案：解：（1）根据题意，得33935a b c a b c a b c -=++⎧⎪-=++⎨⎪=-+⎩，，．解，得 140a b c =⎧⎪=-⎨⎪=⎩，，．∴ 抛物线的解析式为24y x x =-． （2）抛物线上存在一点P ，使∠POM ＝90˚．x =2242=--=-a b ，4416442-=-=-=a b ac y . ∴ 顶点M 的坐标为(24)-，．设抛物线上存在一点P ，满足OP ⊥OM ，其坐标为2(4)a a a -，． 过P 点作PE ⊥y 轴，垂足为E ；过M 点作MF ⊥y 轴，垂足为F ．则 ∠POE ＋∠MOF ＝90˚，∠POE ＋∠EPO ＝90˚． ∴ ∠EPO ＝∠FOM ．∵ ∠OEP ＝∠MFO ＝90˚， ∴ Rt △OEP ∽Rt △MFO ． ∴ OE ∶MF=EP ∶OF ． 即2(4)24a a a -=::． 解，得10a =（舍去），292a =． ∴ P 点的坐标为9924⎛⎫ ⎪⎝⎭，．（3）过顶点M 作MN ⊥OM ，交y 轴于点N ．则 ∠FMN ＋∠OMF ＝90˚． ∵ ∠MOF ＋∠OMF ＝90˚， ∴ ∠MOF ＝∠FMN ．又∵ ∠OFM ＝∠MFN ＝90˚，∴ △OFM ∽△MFN ．∴ OF ∶MF ＝MF ∶FN ． 即 4∶2＝2∶FN ．∴ FN ＝1． ∴ 点N 的坐标为（0，-5）． 设过点M ，N 的直线的解析式为y kx b =+．425k b b -=+⎧⎨-=⎩， 解，得125k b ⎧=⎪⎨⎪=-⎩，．直线的解析式为521-=x y ． ∴ ⎪⎩⎪⎨⎧-=-=②①，.45212x x y x y 把①代入②，得 05292=+-x x ． 2981145200244⎛⎫∆=--⨯=-=> ⎪⎝⎭．∴ 直线MN 与抛物线有两个交点（其中一点为顶点M ）．∴ 抛物线上必存在一点K ，使∠OMK ＝90˚．第48题（2006资阳课改）已知函数222y x x =--的图象如图3所示，根据其中提供的信息，可求得使1y ≥成立的x 的取值范围是（ ） Ａ．13x -≤≤ Ｂ．31x -≤≤Ｃ．3x -≥Ｄ．1x -≤或3x ≥答案：Ｄ第49题（2006安徽非课改）请你写出一个b 的值，使得函数22y x bx =+在第一象限内y 的值随着x 的值增大而增大，则b 可以是．答案：答案不唯一，如0；1；2等第50题（2006南充课改）二次函数2y ax bx c =++中，2b ac =，且0x =时4y =-，则（ ） A ．4y =-最大B ．4y =-最小C ．3y =-最大D ．3y =-最小答案：C第51题(2006徐州非课改)下表给出了代数式2x bx c ++与x 的一些对应值：（1）请在表内的空格中填入适当的数；（2）设2y x bx c =++，则当x 取何值时，0y >？（3）请说明经过怎样平移函数2y x bx c =++的图象得到函数2y x =的图象． 答案：（1）0，0；（2）当1x <或3x >时，0y >．（写出1x <或3x >中的一个得1分）（用1x <和3x >中的特殊值说明得1分，只用1x <或3x >中的特殊值说明不得分） （3）由（1）得243y x x =-+，即2(2)1y x =--，将抛物线243y x x =-+先向左平移2个单位（1分），再向上平移1个单位（1分）即得抛物线2y x =．（配方正确，并说明将抛物线243y x x =-+的顶点移到原点得2分；不配方，但说明将抛物线243y x x =-+的顶点(21)-，移到原点得2分；不配方，只说明将抛物线的顶点移到原点不得分）第52题（2006龙岩三县非课改）已知抛物线2(1)(0)y a x h a =-+≠与x 轴交于1(0)(30)A x B ，，，两点，则线段AB 的长度为（ ）Ａ．1 Ｂ．2Ｃ．3Ｄ．4答案：Ｄ第53题（2006岳阳课改）小明从右边的二次函数2y ax bx c =++图象中，观察得出了下面的五条信息：①0a <，②0c =，③函数的最小值为3-，④当0x <时，0y >，⑤当1202x x <<<时，12y y >．你认为其中正确的个数为（ ） Ａ．2 Ｂ．3Ｃ．4Ｄ．5答案：Ｃ。

图14大连中考二次函数26题1、（2006年中考）25．如图14，抛物线E ：y ＝x 2＋4x ＋3交x 轴于A 、B 两点，交y 轴于M 点，抛物线E 关于y 轴对称的抛物线F 交x 轴于C 、D 两点。

（1）求F 的解析式；（2）在x 轴上方的抛物线F 或E 上是否存在一点N ，使以A 、C 、N 、M 为顶点的四边形是平行四边形。

若存在，求点N 的坐标；若不存在，请说明理由；（3）若将抛物线E 的解析式改为y ＝ax 2＋bx ＋c ，试探索问题（2）。

2、（2007年中考）26．（1）如图13，直线A B 交x 轴于点(20)A ，，交抛物线2y ax =于点(1B ，点C 到O A B △各顶点的距离相等，直线A C 交y 轴于点D ．当0x >时，在直线O C 和抛物线2y ax =上是否分别存在点P 和点Q ，使四边形DOPQ 为特殊的梯形？若存在，求点P Q ，的坐标；若不存在，说明理由．（2）附加题：在第26题中，抛物线的解析式和点D 的坐标不变（如图14）．当0x >，在直线(01)y kx x =<<和这条抛物线上，是否分别存在点P 和点Q ，使四边形DOPQ 为以O D 为底的等腰梯形．若存在，求点P Q ，的坐标；若不存在，说明理由．图143、（2008年中考）26．如图18，点C 、B 分别为抛物线C 1：121+=x y ，抛物线C 2：22222c x b x a y ++=的顶点．分别过点B 、C 作x 轴的平行线，交抛物线C 1、C2于点A 、D ，且AB = BD ． ⑴求点A 的坐标；⑵如图19，若将抛物线C 1：“121+=x y ”改为抛物线“11212c x b x y ++=”．其他条件不变，求CD 的长和2a 的值．附加题：如图19，若将抛物线C 1：“121+=x y ”改为抛物线 “11211c x b x a y ++=”，其他条件不变，求b b +的值．3、（2009年中考模拟）25．如图14，平移抛物线F 1：y ＝x 后得到抛物线F 2．已知抛物线F 2经过抛物线F 1的顶点M和点A （2，0），且对称轴与抛物线F 1交于点B ，设抛物线F 2的顶点为N ．⑴探究四边形ABMN 的形状及面积（直接写出结论）⑵若将已知条件中的“抛物线F 1：y ＝x 2”改为“抛物线F 1：y ＝ax 2”（如图15），“点A （2，0）”改为“点A （m ，0）”，其它条件不变，探究四边形ABMN 的形状及其面积，并说明理由． ⑶若将已知条件中的“抛物线F 1：y ＝x 2”改为“抛物线F 1：y ＝ax 2＋c ，”（如图16），“点A （2，0）”改为“点A （m ，c ）”其它条件不变，求直线AB 与y 轴的交点C 的坐标（直接写出结论）图 14 图 15图 164、（2009年中考）26．如图18，抛物线F：c+y+=2的顶点为P，抛物线：与y轴交于点A，axbx与直线OP交于点B．过点P作PD⊥x轴于点D，平移抛物线F使其经过点A、D得到抛物线F′：xby2，抛物线F′与x轴的另一个交点为C．xa''=c++'6、（2010年中考）26.如图17，抛物线F ：2(0)y ax bx c a =++>与y 轴相交于点C ，直线1L 经过点C 且平行于x 轴，将1L 向上平移t 个单位得到直线2L ，设1L 与抛物线F 的交点为C 、D ，2L 与抛物线F 的交点为A 、B ，连接AC 、BC （1）当12a =，32b =-，1c =，2t =时，探究△ABC 的形状，并说明理由；（2）若△ABC 为直角三角形，求t 的值（用含a 的式子表示）；（3）在（2）的条件下，若点A 关于y 轴的对称点A ’恰好在抛物线F 的对称轴上，连接A ’C ，BD ，求四边形A ’CDB 的面积（用含a 的式子表示）7、（2011年中考模拟）26.如图，抛物线y= ax2+bx+c 经过A （-3,0）、B （1,0）、C （0，-3）三点； ⑴求抛物线的解析式；⑵设抛物线的顶点为D ，y 轴上的点E 坐标为（0,1），连接DC 、EB ，试探索抛物线上是否存在一点P ，使△PDC 和△PBE 的面积相等，若存在，求出点P 的坐标，并直接写出三角形面积的值，若不存在，说明理由；10、（2012年中考模拟）26、如图14，点A（—2，0）、B（4，0）、C（3，3）在抛物线y=ax2＋bx＋c 上，点D在y轴上，且DC⊥BC，∠BCD绕点C顺时针旋转后两边与x轴、y轴分别相交于点E、F. （1）求抛物线的解析式；（2）CF能否经过抛物线的顶点？若能，求出此时点E的坐标，若不能，说明理由；（3）若△FDC是等腰三角形，求点E的坐标.11、（2012年中考模拟）26、如图13，在平面直角坐标系中，点A的坐标为(1,3)⊥轴，垂足-，AB x为B，将线段A B绕点O顺时针旋转90︒，得到线段C D（其中点A、B的对应点分别为点C、D）。

2006年中考试题分类汇编—函数1.（2006²梅列区）函数y = 3x+1 中自变量x 的取值范围是 .x ≠-12.（2006²梅列区）有一个函数的图象经过点（1，2），且y 随x 的增大而减小，则这个函数的解析式可以是 （任写出一个）.如：y=-x+33.（2006²梅列区）夏令营组织学员到某一景区游玩，老师交给同学一张画有直角坐标系和标有A 、B 、C 、D 四个景点位置的地图，指出：今天我们游玩的景点E 是新开发的，地图上还没来得及标注，但已知这个景点E 满足：①与景点A 、C 和景点B 、D 所在的两条直线等距离；②到B 、C 两景点等距离。

请你在平面直角坐标系中，画出景点E 的位置，并标明坐标（用整数表示）。

4.（2006²梅列区）如图,函数y=kx （x ﹥0）与y=4x的图象交于A 、B 两点，过A 、B 点分别作x 轴和y 轴作垂线垂足为D 、E ，两线相交于C 点。

求S △ABC 5．（2006²湖州市）反比例函数()0ky k x=≠的图像经过点（1，－3），则k 的值为（ A ）A 、－3B 、3C 、13D 、－136．（2006²湖州市）已知一次函数y=kx+b （k 、b 是常数，且k ≠0），x 与y 的部分对应值如下表所示，那么不等式kx+b<0的解集是（ D ） A 、x<0 B 、x>0C、x<1 D 、x>1 7．（2006²湖州市）已知二次函数y=x 2－bx+1（－1≤b ≤1），当b 从－1逐渐变化到1的过程中，它所对应的抛物线位置也随之变动。

下列关于抛物线的移动方向的描述中，正确的是（ C ）A.先往左上方移动，再往左下方移动;B.先往左下方移动，再往左上方移动;C.先往右上方移动，再往右下方移动;D.先往右下方移动，再往右上方移动 8．（ 2006²湖州市） 为了鼓励小强勤做家务，培养他的劳动意识，小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的。

2006《二次函数图像与性质》中考题集锦（二）第31题（2006济宁课改）二次函数26y x x =+-的图象与x 轴交点的横坐标是（ ）A ．2和3-B ．2-和3C ．2和3D ．2-和3-答案：A第32题（2006荆州课改）已知y 关于x 的函数：()()22211y k x k x k =---++中满足3k ≤．（1）求证：此函数图象与x 轴总有交点． （2）当关于z 的方程2233z kz z -=+--有增根时，求上述函数图象与x 轴的交点坐标．答案：（1）当2k =时，函数为23y x =-+，图象与x 轴有交点． x路过··走过···需要的时候记得回来看看····因为容易得到所以得不到大家的珍惜·即使这样我们也要答案：解：（1）由抛物线2(1)y x m x m =-+-+与y 轴交于(03)，，得：3m =． ∴抛物线为223y x x =-++．图象略． （2）由2230x x -++=，得1213x x =-=，． ∴抛物线与x 轴的交点为(10)(30)-，，，． 2223(1)4y x x x =-++=--+ ， ∴抛物线顶点坐标为(14)，． （3）由图象可知：当13x -<<时，抛物线在x 轴上方． （4）由图象可知：当1x >时，y 的值随x 值的增大而减小．第35题（2006贺州课改）已知抛物线268y ax x =+-与直线3y x =-相交于点(1)A m ，．（1）求抛物线的解析式；（2）请问（1）中的抛物线经过怎样的平移就可以得到2y ax =的图象？（3）设抛物线2y ax =上依次有点1234P P P P ，，，，…，其中横坐标依次是2468，，，，…，纵坐标依次为1234n n n n ，，，，…，试求31003n n -的值．答案：解：（1） 点(1)A m ，在直线3y x =-上， 313m ∴=-⨯=-．把13x y ==-，代入268y ax x =+-， 得683a +-=-．求得1a =-．∴抛物线的解析式是268y x x =-+-．（2）2268(3)1y x x x =-+-=--+ ．∴顶点坐标为(31)，．路过··走过···需要的时候记得回来看看····因为容易得到所以得不到大家的珍惜·即使这样我们也要∴把抛物线268y x x =-+-向左平移3个单位长度得到21y x =-+的图象，再把21y x =-+的图象向下平移1个单位长度得到2y x =-的图象．（3）由题意知，123P P P ，，，…的横坐标是连续偶数，所以n P 的横坐标是2n ，纵坐标为31003n n ，所对应的纵坐标依次是2262006--，． 22310036(2006)n n ∴-=---增大而增大；当2x >时，y 随x 的增大而减小．这样的二次函数的解析式可以是 ．答案：答案不唯一，只要满足对称轴是2x =，0a <．路过··走过···需要的时候记得回来看看····因为容易得到所以得不到大家的珍惜·即使这样我们也要第39题（2006兰州A 课改）已知22y x =的图象是抛物线，若抛物线不动，把x 轴，y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是（ ）． Ａ．22(2)2y x =-+ Ｂ．22(2)2y x =+-Ｃ．22(2)2y x =--Ｄ．22(2)2y x =++答案：Ｂ第40题.（2006兰州A 课改）已知二次函数y ax =所示，对称轴是1x =，则下列结论中正确的是（ Ａ．0ac > Ｂ．0b < Ｃ．240b ac -<Ｄ．20a b +=答案：Ｄ第41题.（2006辽宁十一市课改）已知二次函数2(0)y ax bx c a =++≠，其中a b c ，，满足0a b c ++=和930a b c -+=，则该二次函数图象的对称轴是直线 ． 答案：1x =-第42题（2006辽宁十一市非课改）如图，已知抛物线2(0)y ax bx c a =++≠经过(20)(04)A B --，，，，(24)C -，三点，且与x 轴的另一个交点为E ． （1）求抛物线的解析式；（2）用配方法求抛物线的顶点D 的坐标和对称轴； （3）求四边形ABDE 的面积．答案：解：（1） 抛物线2y ax bx c =++经过(20)(04)(24)A B C ---，，，，，三点 xAB CDOExy4204424a b c c a b c -+=⎧⎪∴=-⎨⎪++=-⎩解得1214a b c ⎧=⎪⎪=-⎨⎪=-⎪⎩∴抛物线解析式：2142y x x =--．（2）221194(1)222y x x x =--=-- ∴顶点坐标912D ⎛⎫- ⎪⎝⎭，，对称轴：1x =． （3）连结OD ，对于抛物线解析式2142y x x =-- 当0y =时，得2280x x --=，解得：12x =-，24x = (40)4E OE ∴=，，42915AOB BOD EOD ABDE S S S S ∴=++=++=△△△四边形．第43题. （2006 浙江湖州课改）已知二次函数()2111y x bx b =-+-≤≤，当b 从1-逐渐变化到1的过程中，它所对应的抛物线位置也随之变动．下列关于抛物线的移动方向的描述中，正确的是（ ）Ａ．先往左上方移动，再往左下方移动 Ｂ．先往左下方移动，再往左上方移动 Ｃ．先往右上方移动，再往右下方移动 Ｄ．先往右下方移动，再往右上方移动答案：Ｃ第44题. （2006 江西课改）二次函数223y x x =--的最小值是 ．答案：4-第45题（2006长春课改）如图，P 为抛物线2331424y x x =-+上对称轴右侧的一点，且点P 在x 轴上方，过点P 作PA 垂直x 轴于点A ，PB 垂直y 轴于点B ，得到矩形ABCDOExy路过··走过···需要的时候记得回来看看····因为容易得到所以得不到大家的珍惜·即使这样我们也要答案：PA x ⊥ 轴，1AP =，∴点P 的纵坐标为1． 当1y =时，23311424x x -+=，即2210x x --=．解得1211x x ==．抛物线的对称轴为1x =，点P 在对称轴的右侧，1x ∴=∴矩形PAOB的面积为(1+个平方单位．第46题（2006山西非课改）二次函数()20y ax bx c a =++≠的图象如图所示．有下列结论：①240b ac -<；②0ab >；③0a b c -+=；④40a b +=；⑤当2y =时，x 只能等于0．其中正确的是（ ）Ａ．①④Ｂ．③④Ｃ．②⑤Ｄ．③⑤答案：Ｂ第47题（2006威海非课改）抛物线2=y ax bx c ++(0)a ≠过点(13)(33)A B C ---，，，，，，顶点为M 点．（1）求该抛物线的解析式．（2）试判断抛物线上是否存在一点P ，使∠POM ＝90˚． 若不存在，说明理由；若存在，求出P 点的坐标．（3）试判断抛物线上是否存在一点K ，使∠OMK ＝90˚， 说明理由．答案：解：（1）根据题意，得0 2 5 x2y路过··走过···需要的时候记得回来看看····因为容易得到所以得不到大家的珍惜·即使这样我们也要33935a b c a b c a b c -=++⎧⎪-=++⎨⎪=-+⎩，，．解，得 140a b c =⎧⎪=-⎨⎪=⎩，，．∴ 抛物线的解析式为24y x x =-． （2）抛物线上存在一点P ，使∠POM ＝90˚．x =2242=--=-a b ，4416442-=-=-=a b ac y .∴ 顶点M 的坐标为(24)-，． 设抛物线上存在一点P ，满足OP ⊥OM ，其坐标为(a ，过P 点作PE ⊥y 轴，垂足为E ；过M 点作MF ⊥y 则 ∠POE ＋∠MOF ＝90˚，∠POE ＋∠EPO ＝90˚． ∴ ∠EPO ＝∠FOM ．∵ ∠OEP ＝∠MFO ＝90˚， ∴ Rt △OEP ∽Rt △MFO ． N ．则 ∠FMN ＋∠OMF ＝90˚． ．∴ FN ＝1． ∴ 点N 的坐标为（0，-5）． 设过点M ，N 的直线的解析式为y kx b =+．425k b b -=+⎧⎨-=⎩， 解，得125k b ⎧=⎪⎨⎪=-⎩，．直线的解析式为521-=x y ．路过··走过···需要的时候记得回来看看····因为容易得到所以得不到大家的珍惜·即使这样我们也要∴ ⎪⎩⎪⎨⎧-=-=②①，.45212x x y x y 把①代入②，得 05292=+-x x ．2981145200244⎛⎫∆=--⨯=-=> ⎪⎝⎭．∴ 直线MN 与抛物线有两个交点（其中一点为顶点M ）．∴ 抛物线上必存在一点K ，使∠OMK ＝90˚．第48题（2006资阳课改）已知函数222y x x =--的图象如图3所示，根据其中提供的信息，可求得使1y ≥成立的x 的取值范围是（ ） Ａ．13x -≤≤ Ｂ．31x -≤≤Ｃ．3x -≥Ｄ．1x -≤或3x ≥答案：Ｄ第49题（2006安徽非课改）请你写出一个b 的值，使得函数22y x bx=+（1）请在表内的空格中填入适当的数；（2）设2y x bx c =++，则当x 取何值时，0y >？（3）请说明经过怎样平移函数2y x bx c =++的图象得到函数2y x =的图象．路过··走过···需要的时候记得回来看看····因为容易得到所以得不到大家的珍惜·即使这样我们也要答案：（1）0，0；（2）当1x <或3x >时，0y >．（写出1x <或3x >中的一个得1分）（用1x <和3x >中的特殊值说明得1分，只用1x <或3x >中的特殊值说明不得分） （3）由（1）得243y x x =-+，即2(2)1y x =--，将抛物线243y x x =-+先向左平移2个单位（1分），再向上平移1个单位（1分）即得抛物线2y x =．（配方正确，并说明将抛物线243y x x =-+的顶点移到原点得2分；不配方，但说明将抛物线243y x x =-+的顶点(21)-，移到原点得2分；不配方，只说明将抛物线的顶点移到原点不得分）第52题（2006龙岩三县非课改）已知抛物线2(1)(0)y a x h a =-+≠与x 轴交于1(0)(30)A x B ，，，两点，则线段AB 的长度为（ ）Ａ．1 Ｂ．2Ｃ．3Ｄ．4答案：Ｄ第53题（2006岳阳课改）小明从右边的二次函数2y ax bx c =++图象中，观察得出了下面的五条信息：①0a <，②0c =，③函数的最小值为3-，④当0x <时，0y >，⑤当1202x x <<<时，12y y >．你认为其中正确的个数为（ ） Ａ．2 Ｂ．3Ｃ．4Ｄ．5答案：Ｃ路过··走过···需要的时候记得回来看看····因为容易得到所以得不到大家的珍惜·即使这样我们也要。