当前位置：文档之家 › 圆的切线性质定理优秀课件

圆的切线性质定理优秀课件

  • 格式：ppt
  • 大小：292.00 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

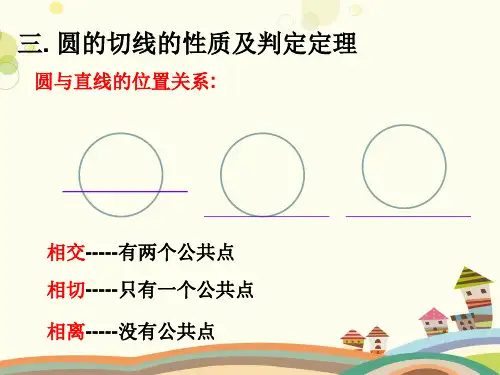
圆的切线的性质及判定定理完整版课件

圆的切线的性质及判定定理完整版课件

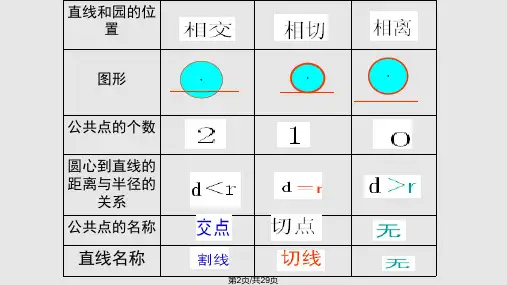
证明:连接OD. ∵BD=CD,OA=OB,
∴OD是△ABC的中位线,
C
∴OD//AC.
又∵∠DEC=90º ∴∠ODE=90º 又∵D在圆周上,
∴DE是⊙O是切线..
E D
B
A
O
例2 如图. AB为⊙O的直径,C为⊙O上一点,AD和 过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
证明:连接OC, ∵CD是⊙O的切线,
C
2.已知:OA和OB是⊙O的半径,并且OA⊥OB,P是OA 上任意一点,BP的延长线交⊙O于Q.过Q作⊙O的切 线交OA的延长线于R,.
求证:RP=RQ
B
PA
O
R
Q
∠AQO= ∠APQ
3.AB是⊙O的直径,BC是⊙O的切线,切点为B,OC 平行于弦AD. 求证:DC是⊙O的切线.
C
D
3
1
42
A
∴OC⊥CD.
又∵AD⊥CD, ∴OC//AD.由此得 ∠ACO=∠CAD. ∵OC=OA. ∴ ∠CAO=∠ACO.
D C
A
O
B
∴ ∠CAD=∠CAO. 故AC平分∠DAB.
习题2.3
1.如图,△ABC为等腰三角形,O是底边BC的中点, ⊙O与腰AB相切于点D.
求证:AC与⊙O相切.
A
E D
B
O
推论2: 经过切点且垂直于切线的直线必经过圆心.
思考: 切线的性质定理逆命题是否成立?
切线的判定定理: 经过半径的外端并且垂直于这条半径的直线是圆的切线.
在直线上任取异于A的点B.
l
A
B
连OB.
则在Rt△ABO中
OB>OA=r

切线长定理PPT课件

切线长定理PPT课件
求AF、BD、CE的长.
解: ∵ ⊙O与△ABC的三边都相切
∴AF＝AE,BD＝BF,CE＝CD
设AF=x(cm), BD=y(cm),CE＝z(cm)
x＋y＝9
x＝4
则有 y＋z＝14 解得 y＝5
x＋z＝13
z＝9
∴ AF=4(cm), BD=5(cm), CE=9(cm).
第十七页，共26页。
F
设AD= x , BE= y ,CE＝ r
D O·
则有
x＋r＝b y＋r＝a x＋y＝c
解得
r＝
a＋b－c
2
C
E
B
设Rt△ABC的直角边为a、b，斜边为c，则Rt△ABC的
内切圆的半径 r＝ a＋b－c或r＝
2 第十八页，共26页。
ab
a＋b＋c
思考：如图，AB是⊙O的直径，
AD、DC、BC是切线，点A、E、B 为切点，若BC=9，AD=4，求OE的长.
AL
B
补充：圆的外切四边形的两组对边的和相等．
第十五页，共26页。
想一想
A
反思：在解决有关圆的
切线长问题时，往往需
。
要我们构建基本图形。 O
P
B
（1）分别连结圆心和切点 （2）连结两切点
（3）连结圆心和圆外一点
第十六页，共26页。
例题3
例3 △ABC的内切圆⊙O与BC、CA、AB分别相切于
点D、E、F，且AB=9cm，BC=14cm，CA=13cm，
C E
C E
D
D
F
A
·O
B
A
O
B
第十九页，共26页。
例题讲解
例1、已知：P为⊙O外一点，PA、PB为⊙O的 切线，A、B为切点，BC是直径。

2.3 圆的切线的性质及判定定理 课件(人教A选修4-1)

2.3 圆的切线的性质及判定定理 课件(人教A选修4-1)
1．切线的性质 (1)性质定理：圆的切线垂直于经 过 切点的半径． 如图，已知AB切⊙O于A点，则 OA ⊥AB.
(2)推论1：经过圆心且 垂直于切线 的直线必经过切点．
(3)推论2：经过切点且 垂直于切线 的直线必经过圆心．
2．圆的切线的判定方法 (1)定义：和圆只有一个公共点的直线是圆的切线．
利用圆的切线的性质来证明或进行有关的计算有时需
添加辅助线，其中连接圆心和切点的半径是常用辅助线， 从而可以构造直角三角形，利用直角三角形边角关系求解， 或利用勾股定理求解，或利用三角形相似求解等．
1. AB是圆O的直径，D为圆O上一点， 过D作圆O的切线交AB的延长线于点C，
若DA＝DC，求证：AB＝2BC.
∠BOD 是 BD 所对的圆心角，
∠BCD＝45° ， ∴∠BOD＝90° . ∵∠ADB 是△BCD 的一个外角， ∴∠DBC＝∠ADB－∠ACB ＝60° －45° ＝15° ， ∴∠DOC＝2∠DBC＝30° ， 从而∠BOC＝120° ， ∵OB＝OC，∴∠OBC＝∠OCB＝30° .
在△OEC 中，因为∠EOC＝∠ECO＝30° ， ∴OE＝EC， 在△BOE 中，因为∠BOE＝90° ，∠EBO＝30° . ∴BE＝2OE＝2EC， CE CD 1 ∴BE＝DA＝ ， 2 ∴AB∥OD，∴∠ABO＝90° ， 故 AB 是△BCD 的外接圆的切线．
交⊙O于点E，PA＝AO＝OB＝1. (1)求∠P的度数； (2)求D切点，∴OC⊥PC，△POC 为直角三角形． ∵OC＝OA＝1，PO＝PA＋AO＝2， OC 1 ∴sin ∠P＝ PO＝ .∴∠P＝30° . 2 (2)∵BD⊥PD，∴在 Rt△PBD 中， 由∠P＝30° ，PB＝PA＋AO＋OB＝3， 3 得 BD＝ . 2 连接 AE.则∠AEB＝90° ，∴AE∥PD. ∴∠EAB＝∠P＝30° ，∴BE＝ABsin 30° ＝1， 1 ∴DE＝BD－BE＝ . 2

圆的切线的性质及判定定理 课件

圆的切线的性质及判定定理 课件

【典例训练】
1.在Rt△ABC中，∠C=90°，AC=3 cB的关系为( )
(A)相切
(B)相离
(C)相交
(D)无法判断
2.如图所示，CB为⊙O的直径，P是CB的延
长线上一点，且OB=BP，∠AOC=120°，
则PA与⊙O的位置关系是_____.
圆的切线的性质
圆的切线的性质 (1)已知一条直线是圆的切线时,常作出过切点的半径,则该半 径垂直于切线,从而出现了直角. (2)从圆外一点引圆的两条切线,这点与圆心的连线平分这两条 切线的夹角,这点到切点的切线长相等. (3)连接圆的两条平行切线的切点的线段是圆的直径.
【典例训练】 1.如图所示，DB，DC是⊙O的两条切线，A是圆上一点，已知 ∠D=46°，则∠A=_____.
DO AD
AD
2.如图，已知EB是半圆O的直径，A是BE延长线上的一点，AC是 半圆O的切线，D为切点，BC⊥AC于C，若BC=6，AC=8，则 AE=_______.
【解析】1.如图所示，连接OB，OC，
则OB⊥BD，OC⊥CD，
则∠DBO+∠DCO=90°+90°=180°，
则四边形OBDC内接于一个圆，
则有∠BOC=180°-∠D=180°-46°=134°，
【解析】连接OC，∵OA=OB,AC=CB,OC=OC, ∴△OAC≌△OBC, ∴∠OCA=∠OCB=90°, ∴直线AB与⊙O相切. 答案：相切
1.圆的切线的其他相关性质 (1)切线和圆只有一个公共点; (2)切线和圆心的距离等于圆的半径; (3)过圆心且过切点的直线与过该点的切线垂直.
2.切线的判定定理 在切线的判定定理中要分清定理的题设和结论，“经过半径外 端”和“垂直于这条半径”这两个条件缺一不可，否则就不是 圆的切线，如图①②中的例子就不同时满足这两个条件，所以 都不是圆的切线.

切 线+++第1课时 圆的切线的判定与性质++课件++2024—2025学年华东师大版数学九年级下册

切 线+++第1课时 圆的切线的判定与性质++课件++2024—2025学年华东师大版数学九年级下册

证明：连接DE，过点D作DF⊥OB于点F. ∵OA切⊙D于点E，∴DE⊥OA. 又∵DF⊥OB，D是∠AOB平分线上一点， ∴DE＝DF，∴OB与⊙D相切．
知识点2：切线的性质
3．(长春中考)如图，AB是⊙O的直径，BC是⊙O的切线，若∠BAC＝35
°，则∠ACB的度数为
（C ）
A．35°
B．45°
(2)解：在Rt△EOF中，设半径为r，即OE＝OB＝r，则OF＝r＋1， 4 OE r
∵sin∠AFE＝5＝OF＝r＋1， ∴r＝4，∴AB＝2r＝8， 在Rt△ABC中， sin∠ABC＝AACB＝sin∠AFE＝45，AB＝8， ∴AC＝45×8＝352，∴BC＝ AB2－AC2＝254.
的延长线于点 D.若⊙O 的半径为 1，则 BD 的长为
（D ）
A．1
B．2
C. 2
D. 3
8．如图，AB 为⊙O 的直径，C 为⊙O 上一点，AD 和过点 C 的切线互相垂 直，垂足为 D. (1)求证：AC 平分∠DAB；
3 (2)若 AD＝8，tan∠CAB＝4，求边 AC 及 AB 的长．
如图，△ABC中，AB＝AC，以AB为直径作⊙O，与BC交于点D，过D作 AC的垂线，垂足为点E. (1)求证：点D是BC的中点； (2)求证：DE是⊙O切线． 【思路分析】(1)根据“三线合一”证明； (2∵AB是直径，∴AD⊥BC， 又∵AB＝AC，∴BD＝CD, ∴点D是BC的中点． (2)连接OD，∵AO＝BO, BD＝CD， ∴OD∥AC，又∵DE⊥AC， ∴DE⊥OD，∴DE是⊙O的切线． 【名师支招】切线的判定方法2，3的选择标准是看直线与圆的公共点是 否已知，若已知公共点，则连圆心与公共点，证垂直；若公共点未知， 则过圆心作垂线，证d＝r.

圆的切线课件

圆的切线课件

通过圆上一点作切线
总结词
通过圆上一点作切线需要利用半径垂直于切线的性质。
详细描述
选取圆上任意一点，然后通过这一点作一条直线与圆相切，即为切线。这种方法 需要利用圆的性质，即半径垂直于切线。
通过圆外一点作切线
总结词
通过圆外一点作切线需要利用垂径定 理和切线的性质。
详细描述
选取圆外任意一点，然后通过这一点 作一条直线与圆相切，即为切线。这 种方法需要利用垂径定理和切线的性 质，即半径与切线垂直且半径长度等 于圆心到切点的距离。
判定方法三
利用圆的性质，通过观察 圆心到直线的距离是否等 于半径来判断是否为切线 。
02 圆的切线的性质定理
切线与半径垂直
切线与经过切点的半径垂直， 这是切线的基本性质。
在几何学中，这一性质用于证 明切线的其他性质和定理。
在实际应用中，这一性质可用 于确定某直线是否为圆的切线 。
切线长定理
切线长定理：从圆外一点引圆的两条切线，它们的切线长相等。 这一性质在几何作图和证明中非常有用，特别是在解决与圆和切线相关的问题时。
05 圆的切线的相关定理和推论
切线与半径之间的夹角定理
总结词
切线与半径之间的夹角定理描述了切线与半径之间的角度关系。
详细描述
切线与半径之间的夹角是直角，即切线与半径垂直。这个定理是圆的基本性质之一，是证明其他切线定理的基础 。
切线长定理的推论
总结词
切线长定理的推论给出了切线长度与半径之间的关系。
圆的切线ppt课件
目录
Contents
• 圆的切线的基本概念 • 圆的切线的性质定理 • 圆的切线的应用 • 圆的切线的作法 • 圆的切线的相关定理和推论
01 圆的切线的基本概念

圆的切线的性质和判定定理省名师优质课赛课获奖课件市赛课一等奖课件


切线旳鉴定定理 过半径外端且与这条 半径垂直旳直线是圆旳切线
切线旳性质定理 圆旳切线垂直于经过 切点旳半径
例1、如图，已知P为⊙O外一点，以PO 为直径作⊙M，⊙M与⊙O交于点A、B， 求证：PA、PB是⊙O旳切线
A
O
··
·
M
P
B
例2、如图，从圆外一点P引⊙O旳两条 切线PA、PB，点A、B为切点。
圆旳切线旳性质和鉴定定理
直线与圆旳位置关系有几种?
当直线与圆有两个公共点时，直线与圆
相交 当直线与圆有且只有一种公共点时，直
线与圆相切 当直线与圆没有公共点时，直线与圆相
离
判断直线与圆旳位置关系有哪些措施？
设⊙O旳半径为r，直线l与圆心O旳距离
为d
d＞r 直线与圆相离
d＝r d＜r
直线与圆相切 直线与圆相交
求证：（1）PO平分∠APB
（2）PO垂直平分线段AB
※结论能够直接用
A
O
P
·
B 切线长定理 从圆外一点引圆旳两条
切线，切线长相等
例3、如图，⊙O和⊙O′外切于点P，一 条外公切线切两圆于点A、B，求证：∠APB ＝90°
A B
Q
O
·O
·P
′
从一点向一条直线作垂线，垂足就称为
这点在这条直线上旳射影
CD2＝AD·BD
A
DB
例4、试用直角三角形射影定理证明勾股 定理
已知：如图，Rt△ABC中， ∠C=90° 求证：AC2＋BC2＝AB2
C
A
D
B
例5、如图，Rt△ABC中， ∠C=90°， AC＞BC，CD⊥AB于点D，若CD＝4，AB＝10， 求AC及BC

圆的切线PPT课件


如上图：直线l与⊙O相切，直线l叫做⊙O切线 ，点D叫做切点。
第3页/共29页
活动二:探究切线的判定
问题：过已知一个圆和圆上的一个点，怎样过该 点作圆的切线？
已知：⊙O和⊙O上的一点D，如何过点D 画⊙O的切线？
下面我们共同完成作图后,再回答问 题:
（1）任意画一个半径为r的⊙O。 （2）任意画⊙O的一条半径OD。 （3）过D作直线l⊥OD。
若直线满足②， 而不满足①。
第6页/共29页
例题欣赏
例1：如图，直线AB经过⊙O上的 点C，并且OA＝OB, CA＝CB, 求证：直线AB是⊙O的切线。
证明：连接OC ∵OA=OB ∴ABC是等腰三角形 ∵CA=CB ∴OC⊥AB ∵OC为半径 ∴AB为⊙O的切线
第7页/共29页
2 、如图，以O为圆心，OA为半 径的圆交OB于C，若OA=3，AB=4， BC=2，则AB是⊙O的切线吗？
如果不相切，请说明理由？ ②，若CD与⊙O相切，且∠D＝30，BD＝ 10，求⊙O的半径。
第26页/共29页
练习引入： 如图，已知在△ABC中，∠BAC＝ 120°,AB＝AC,AB＝4,以A为圆心，2 为半径，做⊙A,试问直线BC与⊙A的 相切吗？说明原因 ？
答：相切 ∵D＝2＝r
第27页/共29页
第23页/共29页
A
O
B
D C
（2），如图，AB为非直径的弦， 且∠CAE＝∠B, 求证：直线EF是⊙O的切线。
第24页/共29页
1，AD为等腰△ ABC的高，E、F分别为AB、AC的中点，
则以EF为直径的圆与BC的位置关系是
（C）
A.
相离
B、相切
C、 相交
D、以上都有可能

人教版数学九年级上册24.2.2切线的判定与性质课件(共24张PPT)


知识回顾
直线与圆相切的判定： 1.利用定义判定：直线和圆只有一
个公共点时，直线与圆相切. 2.利用直线与圆心距离判定：当圆
心与直线的距离等于该圆的半径时，直 线与圆相切.
O
l
O d=r
l
新知探究
知识点1 切线的判定
思考：如图，在⊙O中，经过半径OA 的外端点 A 作直线 l⊥OA. （1）圆心O到直线 l 的距离是多少？
l
∴OA⊥l
ห้องสมุดไป่ตู้ 反证法证明切线的性质
如图，直线CD与⊙O相切，求证：⊙O的半径OA
与直线CD垂直.
证明：（1）假设AB与CD不垂直，过
B
点O作一条直线垂直于CD，垂足为M；
（2）则OM＜OA，即圆心到直线CD的
O
距离小于⊙O的半径，因此，CD与⊙O
相交.这与已知条件“直线与⊙O相切”相 C 矛盾；
A MD
证明：连接OA,OD,作OE⊥AC 于E . ∵ ⊙O与AB相切于E, ∴OD⊥AB.
又∵△ABC为等腰三角形，
O是底边BC的中点，
B
A D
1
O
E C
∴AO平分∠BAC,
∴OD=OE ，即OE是⊙O半径.
∴AC是⊙O的切线. 方法总结：无交点，作垂直，证半径.
随堂练习
1.如图，已知⊙O的直径AB与弦AC的夹角为31°，
d l
A
3.判定定理：经过半径的外端并且垂直于
O
这条半径的直线是圆的切线.
l
A
已 知 ： 直 线 AB 经 过 ⊙ O 上 的 点 C ， 并 且 OA=OB ，
CA=CB.求证：直线AB是⊙O的切线.
证明：连接OC.

圆的切线性质定理市公开课一等奖百校联赛获奖课件

老师提醒:
依据“经过半径外端且垂直于这条半径直线是圆切线” 只要连结OA,过点A作OA垂线即可.
第14页
练习与巩固：
1、如图，A、B是⊙O上两点，AC是⊙O切线，∠B=70°，则 ∠BAC等于（ ） A. 70° B. 35° C. 20° D. 10°
O O
B
A
C
（1）
（2）
B A
（3）
2、如图,在△ABC中,AB=AC,∠BAC=120°,⊙A与BC相切于 点D,与AB相交于点E,则∠ADE等于___ _度.
圆， 内内切心，
．I
E
F
它是三角形
交点。
三条角平分线
图2
3. 三角形内切圆能作____1个,圆外切三角形有_____ 无个,数三角形内心在三角形_______. 内部
第26页
探究：三角形内切圆作法
思索以下问题：
1．如图，若⊙O与∠ABC 两边相切，那么圆心O位置 有什么特点？
圆心0在∠ABC平分线上。 B 2．如图2，假如⊙O与 △ABC内角∠ABC两边相切， 且与内角∠ACB两边也相切， 那么此⊙O圆心在什么位置？
2.三角形内心在三角形角平分线上；
A
D
r
C
O
E F
B
第30页
分别作出锐角三角形,直角三 角形,钝角三角形内切圆,并说明
与它们内心位置情况? A A A
●
●
B
C
┐ B
●
C
B
C
提醒:先确定圆心和半径,尺规 作图要保留作图痕迹.
第31页
A
1.如图1，△ABC是⊙O 内接三角形。
⊙ O是△ABC 外接圆，
A
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

已知：如图，AB 是⊙O的直径， AC、BD是⊙O的切线.
A
C
求证: AC∥BD
证明：如图，
O
AC、BD是⊙O的切线 AB 是⊙O的直径
B
D
AB⊥AC AB⊥BD
AC∥BD
O
A
L
O
MA
L
性质3：圆的切线垂直于过切点的半径。
∵ 直线L是圆O的切线∴ OA ⊥ L
练习与巩固：
1、如图，A、B是⊙O上的两点，AC是⊙O的切线， ∠B=70°，则∠BAC等于（ ） A. 70° B. 35° C. 20° D. 10°
O
B
A
C
（1）
A E
B
D
（2）
O
C
A
B
（3）
2、如图,在△ABC中,AB=AC,∠BAC=120°,⊙A与 BC相切于点D,与AB相交于点E,则∠ADE等于___ _ 度.
B，且AB=2 ，弦BC∥OA，则BC的长为
。
A
B
D CB
A C
O A
C
B
7、如图,AB为⊙O的直径，C为⊙O上一点，AD和过 C点的切线互相垂直，垂足为D，求证：AC平分 ∠DAB。
DC
D
C
A OB
（7）
AO
B
（8）
8、如图,AB为⊙O的直径，BC是⊙O的切线， 切点为B，OC平行于弦AD，求证：CD是⊙O 的切线。
3、如图,在△OAB中,OB：AB=3：2 , 0B=6，⊙O与
AB相切于点A, 则⊙O的直径为
。
4、如图,PA、PB是⊙O的切线,切点分别为A、B,且
∠APB=50°,点C是优弧上的一点,则∠ACB=___.
A
C
COP来自AOBP
B
（4）
（5）
5、如图，⊙O的直径AB与弦AC的夹角为30°，过C
点的切线PC与AB的延长线交于P，PC=5，则⊙O的
练习 A
如图，在⊙O中，AB为直
径， AD为弦， 过B点的切 线与AD的延长线交于点C，
D
O
且AD=DC
求∠ABD的度数.
C
解： AB为直径
∠ABC=90°
B
BC为切线
∠ADB=90°
△ABC为直角三角形
AD=DB
AD=DC ∠ADB=90°
△ABD为等腰直角三角形
∠ABD=45°
练习 求证：经过直径两端点的切线互相平行
半径为（ ）
53
53
A辅. 助3线的作B法. ：作6 过切C点. 的10半径D. 5
6、在△ABC中，AB=2，以A为圆心，1为半径的圆
与边BC相切于点D ，则BD的长为
。
变式一：在△ABC中，AB=2，AC= ，以A为圆心，1为
半径的圆与边BC相切 ，则BC的长为
。
变式二：如图，点A是圆O外一点，OA=4，AB与圆相切于点
将上述判定1、2反过来，得到的是一个什么样 的命题？结论是否还成立呢？
切线的性质：
1、圆的切线与圆只有一个交点。
2、切线与圆心的距离等于半径。
如果直线L是圆O的切线，切点为A，那么半径 OA与直线L是不是垂直呢？
分析：假设OA与L不垂直，过点 作OM⊥L，垂足为M。 根据垂 线段最短的性质，有OM﹤OA， 这说明圆心O到直线L的距离小 于半径OA，于是直线L就要与圆 相交，而这与直线L是圆O的切 线相矛盾。因此，OA与直线L垂 直。
圆的切线性质定理优秀课件
切线的判定：
1、直线与圆交点的个数：只有一个交点。
2、圆心到直线的距离与半径的大小关系， 即d=r。
3、经过半径外端且垂直于这条半径的直 线是圆的切线。
切线的判定： 1、直线与圆交点的个数：只有一个交点。 2、圆心到直线的距离与半径的大小关系，即 d=r。 3、经过半径外端且垂直于这条半径的直线是 圆的切线。