微生物分析测量不确定度评定
- 格式:doc
- 大小:118.00 KB
- 文档页数:3

微生物法测定婴幼儿配方乳粉中叶酸含量的不确定度评定高利海,陈秋明,钟燕华(精益和泰质量检测股份有限公司,广东广州 510700)摘 要:目的:评估微生物法测定婴幼儿配方乳粉中叶酸含量的测量不确定度。
方法:依据《食品微生物定量检测的测量不确定度评估指南》(RB/T 151—2016)及《食品安全国家标准食品中叶酸的测定》(GB 5009.211—2022)评估测试过程中各主要因素引入的相对标准不确定度分量,进而对其进行合成与扩展。
结果:当试样叶酸含量为66.1 μg/100 g时,其扩展不确定度为5.2 μg/100 g,包含因子k=2,置信概率95%。
结论:重复性测量、标准物质称量、标准溶液配制及系列管制备、标准曲线拟合等测量不确定度分量对检测结果的影响较大。
关键词:微生物法;婴幼儿配方乳粉;叶酸;测量不确定度Uncertainty Evaluation for the Determination of Folic Acid in Infant Formula Milk Powder by Microbiological MethodGAO Lihai, CHEN Qiuming, ZHONG Yanhua(Jingyihetai Quality Testing Co., Ltd., Guangzhou 510700, China)Abstract: Objective: To establish an uncertainty evaluation method for the determination of folic acid in infant formula milk powder by microbiological method. Method: According to RB/T 151—2016 and GB 5009.211—2022, the components of measurement uncertainty generated in the process of determining folic acid content in infant formula milk powder by microbiological method were analyzed, and the combined standard uncertainty and expanded uncertainty of measurement results were calculated. Result: When the folic acid content of the sample was 66.1 μg/100 g, with an expanded uncertainty was 5.2 μg/100 g, with a coverage factor of k=2 and a confidence probability of 95%. Conclusion: The uncertainty components such as repeatability measurement, standard substance weighing, standard solution preparation and serial tube preparation, and standard curve fitting have a great impact on the test results.Keywords: microbiological method; infant formula milk powder; folic acid; uncertainty evaluation叶酸是一种水溶性维生素,又名蝶酰谷氨酸,在自然界主要以蝶啶、对氨基苯甲酸和谷氨酸3种成分结合成母体化合物而存在[1]。


方法验证及不确定度评定
报告
方法名称:
方法依据:
分析项目:
报告编写:日期:
报告审核:日期:
报告批准:日期:
1 方法原理(或适用范围)
2 主要人员、仪器设备及试剂耗材
样品处理,方法适用性等等,复现整个验证过程
4 验证报告结果
4.1精密度
描述精密度试验过程(同一个样品重复测量或同一产品多个样品平行测量)
表4 重复测量检测结果
4.2结果质量控制(阴性,阳性,环境监控)
5不确定度分析
从方法步骤可知,不确定度来源主要是由样品中微生物分布的均匀性和重复测量带来。
5.1检测结果:详见表4;
5.2取对数lgX ,得到对数后lgX = ; 5.3求残差lgX-X lg ; 5.4求残差平方和
210
1
)lgX (lg ∑=-
i X
=
5.5求平均值的标准不确定度
)
1(n )
lg lg (U 1
2
lgx --=∑=n X X n
i )
(
5.6求扩展不确定度
若取包含因子k=2,故)
(lgx kU U == 由于lgx 与x 之间属于非线性关系,不能直接求扩展不确定度U 的反对数,因此首先确定lgx 的取值范围:**≤lgx≤**
取反对数得:** ≤x≤ **
则本次测量结果的取值区间为** ≤x≤ **(置信概率95%)
6结论
由上述方法验证实验可知,实验室已满足方法要求的条件(包括人员资历、仪器设备、试剂、精密度等),适合在本实验室开展。


食品中菌落总数的测定和不确定度分析一、引言食品中菌落总数的测定和不确定度分析是食品卫生检测中的重要一环。
菌落总数是指食品样品中各类菌落的总数,反映了食品样品的卫生质量和微生物状态。
通过对食品中菌落总数的测定和不确定度分析,可以评估食品样品中微生物的数量,并确定分析结果的准确度和可靠性。
二、测定方法食品中菌落总数的测定通常使用平皿计数法。
具体步骤如下:1. 准备样品:取食品样品适量,保持其完整性和天然状态。
2. 消毒处理:将样品进行消毒处理,通常采用酒精灼烧或辐射灭菌等方法,以确保样品中的微生物数量符合测定要求。
3. 取样:采用无菌技术,将样品取适量均匀地涂于含有营养物质的琼脂平板上。
4. 培养:将平板培养基斜放于培养箱中,控制培养环境的温度和湿度,使菌落得以生长。
5. 记录和计数:在培养一定时间后,观察平板上菌落的生长情况,并且根据菌落的形状、颜色、大小等特征进行记录和计数。
6. 计算菌落总数:统计记录的菌落数量,并根据实验过程中相应的计算公式计算出食品中菌落总数。
三、不确定度分析不确定度是对测量结果的可靠性和准确度的度量。
在食品中菌落总数的测定过程中,存在多个可能影响结果的因素,如样品的不均匀性、菌落的形状和大小的主观判断等。
通过不确定度的分析,可以评估测定结果的可靠性,并确保实验数据的准确度。
不确定度的分析可以通过以下步骤进行:1. 确定测定结果的标准偏差:通过进行多次实验测定,计算出测定结果的标准偏差。
标准偏差可以反映出数据的离散程度和测定的精确性。
2. 估计不确定度的类型:根据测定过程中存在的因素和误差来源,估计可能的不确定度类型,如随机误差和系统误差等。
3. 计算不确定度的组成:根据不确定度类型,分别计算出每个不确定度源的贡献度,并进行数值上的组合和求和。
4. 定量表示不确定度:通过数值表示不确定度的大小,常用表示形式包括标准不确定度和扩展不确定度。
5. 不确定度扩展:在测定过程中,不确定度可能会随着操作过程的复杂性而增加。

食品中菌落总数的测定和不确定度分析食品中的菌落总数是指在食品中的菌落总数,它是食品卫生领域中Non-pathogenic微生物检验的必要项目。
在食品中检测菌落总数可以评估食品的卫生状况,并确定食品是否符合卫生标准。
测定方法:菌落总数检验通常采用平板计数法和过滤计数法这两种方法进行测定,平板法是最常见的方法。
概括来说,这种方法就是将食品样品分离在富营养培养基上,并在恰当的温度下进行培养,然后通过肉眼或显微镜观察并计数可见的生长菌落。
不确定度分析:测量不确定度是在测量过程中存在的不确定性,其中一些无法避免。
菌落总数测定中的不确定度可以分为A类和B类两种不确定度。
A类不确定度是指在测量期间,当反复进行同一测量时,由于所测参数的波动而导致的不一致性,它是由各种不确定性的数据分析计算而得出的。
B类不确定度是指测量时间和测量地点产生的未考虑到的因素所导致的不确定性。
测量不确定度的计算:对于菌落总数的测定,测量精度可以通过以下方法计算:1.重复性不确定度(uR): 通过重复不同时间进行5次测量获得结果,计算相对标准偏差,进而计算得到uR。
2.内部准确度不确定度(Ua):通过定量生产的标准菌落悬浮液,在重复测量时计算得到悬浮液的标准差,插入扩展系数得到Ua.3.标准偏差(Sn):根据测试结果计算标准差。
B类不确定度取决于测量环境和工具的水平,所以不是固定的。
但是,它可以通过历史数据、生物学和化学知识、经验和文献资料进行评估。
估计它的常用方法是使用方程式(1):uB = k·C (1)其中,C是不确定度的测量范围,k是扩展的覆盖因子。
通过方程式(2)计算得到:U总= √(uA2 + uB2)(2)其中,uA是A类不确定度,uB是B类不确定度。
通过菌落总数检验评估食品卫生状况的过程涉及到测量不确定度的计算。
A和B这两个不确定度的估计可以使用不同的方法,但都必须要被考虑进来才能得出真实的分析结论。
最终,这种分析过程有助于识别食品检验过程中存在的问题,并且使公众更好地了解食品的安全问题,并对其进行评估。

微生物检测领域中测量不确定度的研究进展综述测量不确定度在微生物检测领域的运用。
方法根据菌落总数、大肠菌群、金黄色葡萄球菌定量检验分析不确定度方面发表的论文,阐述了测量不确定度作为科学的统计手段,合理地表征了被测量值的分散性,是定量说明测量结果质量的一个重要参数,已经逐渐在微生物检测领域开始应用。
结果与结论综述了近年来测量不确定度在微生物定量检测领域的菌落总数、a大肠菌群、金黄色葡萄球菌上的研究进展,阐述了测量不确定度的评定方法和意义,为更好不确定度应用于微生物定量检测领域提供理论参考。
标签:测量不确定度;定量检测;菌落总数;大肠菌群;金黄色葡萄球菌1 概述测量不确定度应用统计分析原理,以具体数值的形式科学评判检验结果的可信度[1]。
不确定越低则对应实验室的检测能力越高。
GB/T 27025-2008《检验和校准实验室能力的通用要求》中:当不确定度和测量结果的有效性或者应用有关CNAS-CL 07:2011《测量不确定度评估和报告通用要求》中规定实验室进行定量检验时,具备同时进行测量结果不确定度评估的能力。
进行不确定度评定:第一,不确定度来源分析;第二,不确定度分量计算;第三,合成标准不确定度;第四计算扩展不确定度;最终以不确定度分析检验结果的可信度。
现如今,检验机构已经陆续通过或正在申请实验室国家认可,国家认可是第三方检验机构对外出具检验报告的资质证明。
其中,实验室认可途径:一,通过官方机构认可的能力验证;二,实验室的结果报告量值可追溯到国际单位制和出具结果的不确定度[2]。
随着微生物检测领域的发展,其检验方法和技术不断完善,所以为保证结果的科学有效,引进了对实验室数据不确定度评估。
对微生物检测领域的不同定量检测项目:菌落总数、大肠菌群计数、金黄色葡萄球菌计数;不同检验方法:平板计数法、MPN计数法的测量结果的不确定度评定的国内研究进展进行了综述。
2 微生物定量检验的不确定度评定的研究进展2.1 菌落计数菌落总数为待检样品10倍系列稀释后,取2~3个适宜稀释度的样品匀液进行接种,倾注平板计数琼脂培养后肉眼观察或者使用放大镜或者菌落计数器进行菌落计数,报告结果。

食品中大肠菌群MPN 法结果不确定度的评定卢春凤 邢荣花 史方 河南出入境检验检疫局技术中心安阳分中心 455000摘要: 通过分析影响食品中大肠菌群多管发酵法结果的不确定度来源,建立一种简单的大肠菌群多管发酵法不确定度评定方法。
结果表明,影响食品中大肠菌群多管发酵法结果不确定度的主要因素为取样量的不确定度、稀释倍数的不确定度、加样体积的不确定度、月桂基硫酸盐胰蛋白胨(LST)肉汤和煌绿乳糖胆盐(BGLB)肉汤管产气比例产生的不确定度,其中后两者产生的不确定度所占分量比较大。
关键词:食品;大肠菌群;MPN 法;不确定度 1 检验方法依据《GB 4789.3-2010 食品卫生微生物学检验大肠菌群计数》中第一法大肠菌群MPN 法进行检验,流程如下:25g 样品+225ml 无菌生理盐水+1ml 稀释过的大肠埃希氏菌液 — 10倍系列稀释 — LST 肉汤36o C 培养48h — BGLB 肉汤36o C 培养48h — 计数产气数,查MPN 表报告结果。
2 各分量的不确定度2.1样品制备称量过程中引入的不确定度(A 类)无菌条件下用精度为0.1g 的电子天平称取样品25.0g ,用250ml 的量筒量取225ml 无菌生理盐水加入,根据电子天平检定证书给出的最大允差为0.1,量筒按JJG196-2006常用玻璃量器的容量允差为5ml ,由于按级使用的数字式仪表、测量仪器最大允差误差导致的不确定度属于矩形(均匀)分布,则天平和玻璃容器的标准不确定度分别为: μ(m 样)=31.0g =0.0577gμ(v 样)=30.2m l =1.1547ml相应地它们的相对不确定度分别为: U (m 样)=样样)μ(m m =25gg0577.0=0.0023U (v 样)=样样)μ(v v =225ml g1547.1=0.0051 则该步产生的相对标准不确定度:U (取样)= 22m 样样+V U U =220051.00023.0+=0.0056 2.2样品稀释过程中引入的不确定度(A 类)样品10倍系列梯度稀释采用1ml 和10ml 量出式分度吸量管进行。

菌落总数不确定度菌落总数不确定度评定食品的质量直接关系到消费者的身体健康,食品中微生物的测量是食品质量优劣的重要卫生指标之一,因此对食品中菌落总数进行测量不确定度的评定非常有必要。
目前《GB 4789.2-2010 食品安全国家标准食品微生物学检验菌落总数测定》是食品中菌落总数测定的标准方法。
我们对食品样品营养包进行卫生微生物菌落总数检测后进行不确定度的评定。
1.材料与方法 1.1材料1.1.1 样品:婴幼儿辅食营养包。
1.1.2 培养基:平板计数琼脂培养基。
1.1.3 主要仪器设备:立式高压蒸汽灭菌锅、鼓风电热恒温干燥器、电热恒温培养箱、超净工作台、恒温水浴锅。
1.2.检验方法1.2.1依据《 GB 4789.2-2010 食品安全国家标准食品微生物学检验菌落总数测定》进行测定。
1.2.2检验过程:25g 样品+225mL 稀释液,均质→ 10倍系列稀释→选择2-3个适宜的样品匀液,各取1mL 分别加入无菌培养皿内→ 每皿加入15-20mL 平板计数琼脂培养基,混匀→ 培养→ 计数各平板菌落数→ 计算菌落总数1.2.3 建立数学模型:设菌落总数为A ,试验结果为X ,则A=Xcfu/g ,最佳∑===nii x n X A 111.2.4 不确定度来源及分析,见图1:不确定度的因果关系图2.结果与分析2.1试样在称重时天平带来的不确定度本实验中称取样品25.0g ,0.1g 天平的最大允许误差为±0.1g ,可认为服从均匀分布,则其导致的不确定度:u rel (m )=0.1/﹙25×3﹚=0.002309 2.2 稀释和取样过程中导致的不确定度本实验中计数的稀释度为2个梯度,因此不确定度主要是由250mL 量筒、10mL 和1mL 刻度吸管的容量允许误差,容器和溶液温度与校准时温度不同引起的。
根据JJG196-1990《常用玻璃量器》检定规程规定,20℃时250mL 量筒的允许误差为±2.0mL ,10mL 刻度吸管的允许误差为±0.05mL ,1mL 刻度吸管的允许误差为±0.008mL ,取均匀分布,由容量允许差引入测定温度培养时间培养温度重复性样品均匀性取样重复性V 样品修约V 稀释培养时间允差时间培养温度允差培养条件样品保存条件温度ΔV 稀释稀释体积温度取样体积取样ΔV 样品温度菌落总数的不确定度:①由250mL量筒引入的不确定度:u rel(V1)=2/(225×3)=0.005132②由10mL刻度吸管引入的不确定度:u rel(V2)=0.05/(9×3)=0.003208③由1mL刻度吸管引入的不确定度:u rel(V3)=0.008/(1×3)=0.0046192.3 样品的均匀性引入的不确定度本实验将样品充分混合后随机取样,可认为样品是均匀的,具代表性,由此所致的不确定度可忽略不计。

微生物检验中菌落总数的不确定度如何评定在ISO/IEC17025《校准和检测实验室能力的通用要求》中明确指
出实验室出具的检测报告应包含有关评定校准或测试结果的不确定度说明,故对测量结果进行不确定度的评定成为检测实验室的重要内容。
下面是yjbys 小编为大家带来的关于微生物检验中菌落总数的不确定度如
何评定的知识,欢迎阅读。
1 .检验方法
依据GB 4789.2-2010 《食品安全国家标准食品微生物学检验菌落总数测定》中要求以无菌操作取检样25 g(ml)剪碎放于含有225 ml 灭菌生理盐水或磷酸盐缓冲液中,经振摇或研磨做成1︰10 的均匀稀释样液,按照标准要求制备10 倍系列稀释样品匀液。
根据污染情况的估计,选择2~3 个稀释度,每个稀释度作2 个平皿,每个平皿注入培养
基约15~20 ml,并转动培养皿使混合均匀,待琼脂凝固后,翻转平板,置36℃±1℃温箱内培养48 h±2 h。
计数后以同稀释度的各平板平均菌落总数报告。
2. 数学模型
设菌落总数为A,检测结果为X,则A=X CFU/g(ml)。
3 .计算不确定度
3.1 在微生物检验中,样品中细菌分布的均匀性和重复测量带来的不确定度是影响检验结果准确度的主要原因,而B 类不确定度分量对合成不确定度影响较少。
按GB 4789.2-2010 《食品安全国家标准食品微生物学检验菌落总数测定》中方法,同一样品每个稀释度作两个平衡样,因此可以采用合并样本标准差求检测结果的不确定度见表1。
3.2 从检验结果可知,如直接用贝塞尔公式计算合并样本标准。
微生物问题汇总1、标准菌株纯度和活性作为实验室应该怎么验证?关于微生物菌种这类的标准还没有,每位专家、检验员都有自己的理解。
但是可以明确一下,对于定量试验中的对照菌种,比如总数、霉菌和酵母、乳酸菌、金葡等,必须进行活度的测定,而其他定性试验的菌种,只需进行纯度的验证即可。
首先,对于商品话的的菌种冻存管来说,纯度是没必要验证的,因为随菌附的菌种证明材料就是很好的证实。
而对于野生菌株来说,需要对纯度进行验证,建议采用平板分离纯化,挑取完全单菌落,进行生化试验确证,可保证菌种的纯度。
其次,对于活度的监控需要从菌株保存的一开始就要进行监控,最简单的是刚开始买回来的菌株,活化之后保存10管,一个月之后分别接种10管中的菌,若10管全部存活,则活度为100%。
活度一般应大于90%。
你下面说的这些均是对培养基的验证方法。
也可以侧面反映菌落活性的大小,采用复合验收程序的培养基,对菌种的活性进行验证,仅仅是针对特定的一管菌。
并不是计算活度的方法。
若要准确的计算活性,必须制备已知浓度的菌悬液,涂布平板,进行培养,计算真实浓度和理论浓度差异。
一般记录纯度和存活度就好了。
①目标菌纯度,先活化菌株,在进行平板计数法,选择菌落数最少的平板上的菌全部进行生化鉴定。
②目标菌活性,在做培养基验证时,根据G值来观察,G值越大,说明其活性越好。
③非目标菌纯度,需要验证吗?例如表皮葡萄球菌。
我认为非目标菌只是用来和目标菌进行菌落形态进行对比的,没有必要验证。
如果需要验证,是否可以在营养平板或者TSA平板上进行划线,观察菌落形态是否一致,或有无杂菌。
④非目标菌活性验证,是否可以用该菌的工作菌悬液在TSA 或者营养平板上划16条线,根据G值判断,G值越大,说明其活性越好?2、非常规项目质量控制计划如何做?此部分的控制,建议采用人为污染样品,对方法的灵敏性和稳定性进行验证,从而达到质控的目的。
①蜡样芽胞杆菌:对蜡样芽胞杆菌标准菌株活化,然后对菌悬液做平板计数(定量确定各个稀释度的菌浓度),选择适当浓度的菌悬液的稀释度作为工作菌悬液,然后吸取1ml污染阴性样品为阳性,在按照蜡样芽胞杆菌的国标方法检验,对添加量和检验结果进行比对。
582020/12中国食品工业安全与检测SAFETY AND TESTING肖 炜 伊犁州检验检测认证研究院 新疆伊犁 835000食品中两类致病微生物检测结果不确定度评定用外行话说,不确定度额定值是指不可靠的程度,主要用来表示实验测量结果的可行性程度。
它可以用来测试参与实验的人员、适用的测量仪器和设备、以及具体的实验环境条件等因素对测量能力的水平进行量化。
1实验材料与实验方法1.1材料实验食品从2018年至2019年随机抽检的236批蛋糕和肉制品中抽取。
实验中涉及的食物主要有火腿、烤鸡、蛋糕等不同种类。
[1]BP 计数琼脂:用北京路桥有限公司提供的培养基按照说明书配制培养液,将配制好的培养液倒在平板上。
脑心提取肉汤(BHI)、兔血浆、小斜营养琼脂均由北京路桥有限公司提供,直接用于实验。
生理盐水缓冲液由伊犁州产品质量检验所食品室配制而成。
1.2检测方法1.2.1分析培养基增菌技术目前,在我国食品微生物检测过程中,主要采用选择性培养基和显色培养基两种技术来实现培养基的生长[2]。
值得注意的是,虽然选择性培养基常用于区分不同类型的细菌,但检测结果不能用于准确识别细菌类型,只有通过分型鉴定等方式才能确定是否有相应菌株的存在。
1.2.2沙门氏菌检验在食品病原微生物实验室检测过程中,微生物检测能力的高低直接影响检测结果的可靠性和准确性,是检测质量控制的关键[3-4]。
长期以来,中国食品药品检验所等机构一直以实验室比对计划的形式开展沙门氏菌检测能力验证活动。
在具体的验证过程中,盲样检测过程主要采用《食品安全国家标准 食品微生物学检验 沙门氏菌检验》(GB4789.4-2016)。
1.2.3金黄色葡萄球菌检验在食品微生物检测过程中,日常采用《食品微生物学检验 金黄色葡萄球菌检验》(GB4789.10-2016)作为检测方法,包括预富集培养、分离培养、菌落形态观察、血浆凝固酶实验等多个实验步骤。
然而,在传统的检测过程中,检测的具体摘要:不确定度评定是测量不确定度的缩写,包括综合标准不确定度、A 类标准不确定度和标准不确定度等多个不确定度。
食品中菌落总数的测定和不确定度分析一、引言食品安全是人们生活中不可忽视的一个重要问题,食品安全直接关系到人们的身体健康。
而食品中的微生物污染是导致食品安全问题的重要原因之一。
在食品生产和加工过程中,微生物总数是一个重要的指标,可以反映出食品中微生物的污染情况。
对食品中微生物总数的测定和不确定度分析具有重要的意义。
二、食品中微生物总数的测定方法测定食品中微生物总数的常用方法有两种:一种是菌落计数法,另一种是细菌总数法。
菌落计数法是指通过分次稀释的方法,将食品样品接种在富含营养物质的琼脂平板上,培养一段时间后,观察和计算形成的菌落数,从而推算出原始食品样品中的微生物总数。
这种方法简单易行,不需要高端的设备,因此在实际的食品检测中应用较为广泛。
而细菌总数法则是通过显微镜观察食品样品中的微生物数量,计算出微生物总数。
这种方法相对复杂,需要一定的实验技术和显微镜设备,因此在实际应用中较为少见。
由于菌落计数法简单易行,并且结果可靠,因此在食品中微生物总数的测定中常常采用菌落计数法。
下面将对菌落计数法的步骤进行详细介绍。
菌落计数法的步骤如下:1. 准备琼脂平板,将琼脂平板装入培养皿中,待琼脂凝固后,将培养皿反面标上编号,以便于后续操作。
2. 将食品样品加入适量的生理盐水中,制成稀释液。
3. 取适量的稀释液,通过分次稀释的方法,制成不同浓度的稀释液。
4. 取适量的每种浓度的稀释液,将其分别加入琼脂平板上,用灭菌的玻璃棒均匀涂抹。
5. 将培养皿反面朝上,置于恒温箱内进行培养。
6. 培养一定时间后,观察培养皿上的菌落情况,根据不同浓度的稀释液,选择菌落数较适宜计算的培养皿。
7. 使用计算器计算出原始食品样品中的微生物总数。
通过上述步骤,即可完成对食品中微生物总数的测定工作。
三、菌落计数法的不确定度分析菌落计数法是一种间接测定方法,因此在测定的过程中难免会产生一定的误差。
为了能够更加准确地反映出食品中微生物总数的真实情况,需要对菌落计数法的不确定度进行分析和评价。
微生物分析之量测不确定度评估1、引言:由于微生物检测的特殊性,因此该例只讨论了单一样品重复测定菌落总数不确定度的评估。
2、技术说明:该技术说明简单描述了菌落总数测定过程以及单一样品重复测试与其他所依赖的参数的关系。
测定过程;检样做成几个适当倍数的稀释液选择2—3个适宜稀释度,各以1ml分别加入灭菌平皿内每皿内加入适量营养琼脂(36±1°C、48±2h)菌落计数报告计算;做平板菌落计数时,用肉眼观察,在记下平板的菌落数后,求出稀释度的各平板平均菌落总数。
3、不确定度来源和量化;校准(1ml移液管):根据标准查到A级1ml±0.007 ml移液管的不确定度(假设三角形分布)0.007 ml/√6=0.0028 ml由于该例是同一样品单一重复测试的结果,而由于培养引起的不确定度因素在此忽略。
由于微生物的称量是粗称,故由称量引起的不确定度在此也忽略。
由稀释起的不确定度分量与计数相比在此贡献较小故也忽略。
稀释和培养称量一个样品经过微生物测试后得到下列结果:3.3×1049.8×10³3.0×105 2.0×105 6.5×1049.6×10³5.0×1048.8×1049.0×10³3.5×105由微生物学的角度来看,这些结果的差异性并不大。
然而将这些数值平均后发现会产生以105为单位之不合理偏差。
算术平均值及log平均值所表示出的不同结果如表1所列:表 1由以上数值可得到开log后的平均值等于4.7225 具体计算如表2所列;表 2n (xi-x)2使用公式S=[ ∑]1/2 (1)i=1 (n-1)3.35166S=√ =0.610310-1查表得知于95%信赖区间时t=2.26。
此微生物测试以log的方式表示,2.26×0.6其结果= 4.7225±= 4.7225±0.4361√10这说此结果分布于4.2864及5.1586之间。
微生物检验中菌落总数的不确定度如何评定微生物检验中菌落总数的不确定度如何评定在ISO/IEC17025《校准和检测实验室能力的通用要求》中明确指出实验室出具的检测报告应包含有关评定校准或测试结果的不确定度说明,故对测量结果进行不确定度的评定成为检测实验室的重要内容。
下面是yjbys店铺为大家带来的关于微生物检验中菌落总数的不确定度如何评定的知识,欢迎阅读。
1 .检验方法依据 GB 4789.2-2010 《食品安全国家标准食品微生物学检验菌落总数测定》中要求以无菌操作取检样25 g(ml)剪碎放于含有225 ml 灭菌生理盐水或磷酸盐缓冲液中,经振摇或研磨做成1︰10的均匀稀释样液,按照标准要求制备10倍系列稀释样品匀液。
根据污染情况的估计,选择2~3个稀释度,每个稀释度作2个平皿,每个平皿注入培养基约15~20 ml,并转动培养皿使混合均匀,待琼脂凝固后,翻转平板,置36℃±1℃温箱内培养48 h±2 h。
计数后以同稀释度的各平板平均菌落总数报告。
2. 数学模型设菌落总数为A,检测结果为X,则A=X CFU/g(ml)。
3 .计算不确定度3.1 在微生物检验中,样品中细菌分布的均匀性和重复测量带来的不确定度是影响检验结果准确度的主要原因,而B类不确定度分量对合成不确定度影响较少。
按 GB 4789.2-2010 《食品安全国家标准食品微生物学检验菌落总数测定》中方法,同一样品每个稀释度作两个平衡样,因此可以采用合并样本标准差求检测结果的不确定度见表1。
3.2 从检验结果可知,如直接用贝塞尔公式计算合并样本标准差,由于数据的散发性较大,计算出的合并样本标准差很大,当样本均值较小时其不确定度则会过大,此时可以对上述数据取对数后,计算出样本检验结果对数值的均值和残差,将中间计算结果见表2。
根据贝赛尔公式,可计算出检测结果对数值的合并样本标准差:取置信水平P=95%,自由度ν=19,查t分布表得:分布于X±0.043之间。
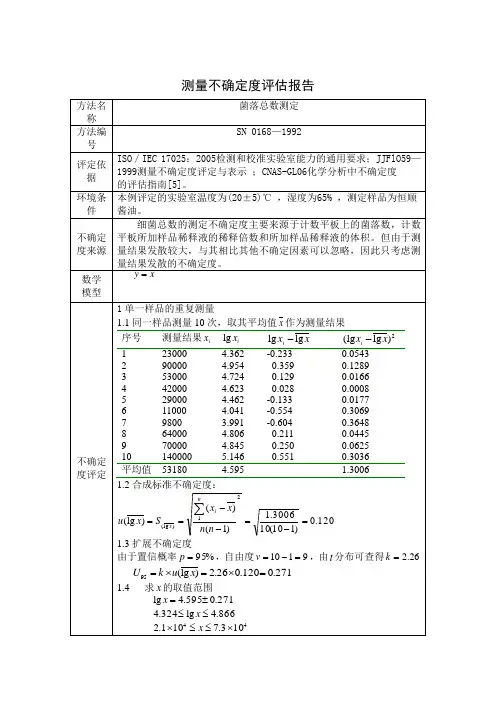
微生物分析测量不确定度评定
一、 概 述
与通常的测量相比较,微生物测量的特点是测量结果相差极大。
与平均值之偏差高达105。
因此用常规的直接根据平均值得到标准偏差的方法显得有些不合理。
通常的做法是取对数以后进行计算。
同样情况可能会出现在增益和衰减的测量不确定度评定中。
由于微生物分析测量结果散发极大,因此本例仅考虑由散发引起的测量不确定度,其它不确定度来源均可以忽略不计。
二、 数学模型
测量是直接数微生物菌落总数,所以数学模型为
y =x (12.18.1)
【例1】单一样品重复测量 1 测量结果
对同一样品重复测量10次,测量结果列于表12.18.1,取10次测量的平均值作为最后测量结果。
2计算过程
(1) 列出测量结果x i 。
(2) 取对数log x i ,得到对数log x i 的平均值为log 4.72245x =。
(3) 求残差log log i x x -(i =1,2,…,10)。
(4) 求残差平方和10
21(log log ) 3.35169i i x x =-=∑。
(5)
求平均值的实验标准差(log )0.1930s x ==
=。
(6) 求平均值的标准不确定度
平均值的标准不确定度等于一倍平均值的实验标准差,所以(log )(log )0.1930u x s x ==。
(7) 求扩展不确定度
如前所述,全部测量过程只有一项不确定度,所以直接由平均值的标准不确定度给出测量结果的扩展不确定度。
取置信概率p =95%,根据自由度ν=9,由t 分布表得到包含因子k =2.26。
于是得到扩展不确定度
U 95=k ×u (x log )=2.26×0.193=0.4361
(8) 取反对数,由log x 坐标换算回x 坐标
由于log x 与x 之间的非线性关系,不能直接求扩展确定度U 95的反对数。
因此首先应确定log x 的取值
范围为
x log =4.7224±0.4361
4.2864≤x log ≤
5.1536
再取反对数后,得测量结果x 分布区间为
1.9×104≤x ≤1.4×105
(9) 测量结果报告
由于测量结果散发极大,不能准确报告测量结果和测量不确定度。
通常以测量结果取值区间的形式报告测量结果。
微生物菌落总数测量结果的取值区间为1.9×104≤x ≤1.4×105,提供95%的置信概率。
表12.18.1 单一样品重复测量的计算过程
【例2】一组样品的重复测量
同一产品准备15份微生物含量可能不同的样品,通过对15份样品的检测,估算每一样品的微生物含量。
每一样品由不同人员进行测量,同一样品由同一人员测量两次,x 1和x 2为两次测量结果。
第i 个样品测量结果x 1i 和x 2i 。
1 测量结果
由不同人员对15个样品分别测量2次,测量结果列于表12.18.2。
2 计算过程:
(1) 列出每一样品的两次测量结果x 1i 和x 2i 。
(2) 对测量结果取对数,得到每一样品的log x 1i 和log x 2i 及两次测量的平均值i x log 。
(3) 对每一样品分别求残差平方和2
21(log log )(1,2,...,15)ij i j x x i =-=∑。
(4) 由各样品的残差平方和,计算其15个样品的合并样本方差s p (log x ij )
p (log )0.0554()ij j j s x s x ====
(5) 每一样品测量两次,因此平均值的实验标准差为
(log )
(log )
i s x s x (6) 求平均值的标准不确定度
平均值的标准不确定度等于一倍平均值的实验标准差,所以有
(log )(log )0.0392i i u x s x ==
(7) 求扩展不确定度
如前所述,全部测量过程只有一项不确定度,所以直接由平均值的标准不确定度给出测量结果的扩展不确定度。
取置信概率p =95%,根据自由度ν=15,由t 分布表得到包含因子k =2.13。
于是得到扩展不确定度
U 95=k ×u (log i x )=2.13×0.0392=0.0835
【注】U 95=0.0835不用于最后报告,所以保留了3位有效数字。
(8) 以区间形式表示每一样品的测量结果
95log i x U -≤log i x ≤95log i x U + log 0.0835i x -≤log i x ≤log 0.0835i x +
(9) 测量结果报告
根据每一样品log i x 的取值范围,由反对数得到每一样品微生物含量x 的取值范围,如表12.18.2所示(保留2位有效数字)。
表12.18.2 同一产品15个样品的重复测量结果。