测量不确定度评估报告

混凝土抗压强度测量结果不确定度评定报告咱们这次聊的事儿，听起来是不是有点高大上？其实说白了，就是咱们在做混凝土强度测试的时候，怎么评估测量数据的准确性和可靠性。

这事儿啊，稍微不小心就容易弄得一团乱麻，不过不用担心，今天我给大家拆解拆解，把这事儿说得清清楚楚，大家看完一定会豁然开朗。

首先呢，说到混凝土抗压强度，大家别以为只是一个简单的数字。

这可关系到建筑物的安全，桥梁、公路、房子，哪个不是靠这块儿来保证稳稳的呢？你想啊，万一测得不准确，拿个低强度的混凝土去盖大楼，那可就麻烦大了。

为了避免这类事情发生，我们就得给测量结果加个“帽子”，就是评定不确定度。

什么意思呢？就是说，咱们测试出的数字背后，还有个不确定的范围，这个范围要搞清楚，否则拿到的数据只是一张“面子”的数据，缺了真凭实据。

怎么搞清楚这些不确定度呢？首先得考虑测量时的各种因素。

举个例子，你是不是觉得混凝土每次搅拌、浇筑、养护的状态都一样？哼哼，那可就太天真了。

每次的气温、湿度、砂石的粒径，甚至混凝土的配比，都会影响最终的强度。

就像做饭一样，你每次放点盐的量不一样，做出来的味道肯定不一样。

测量的时候，咱们得把这些变量统统考虑进去，不然出来的结果准不准，谁也不敢保证。

我们还得考虑设备的误差。

说白了，就是你拿的那个试验机是不是“好状态”。

有时候设备老化了，传感器可能不准，导致测出来的值就有点偏差。

你看，像我们有时候手机的电池用久了，明明充电器插着，结果电量还一直往下掉，咋整？所以设备也得定期校准，才能保证它的精准度。

再说了，咱们试验员也是人，手抖、没睡好觉，都可能影响结果。

所以呀，在评定不确定度的时候，除了机械问题，我们还得考虑操作过程中的人为因素。

如何评定不确定度呢？这就有点技术含量了。

说白了，就是要通过统计学方法，估算出结果的可靠性。

我们可以用标准差来表示测量结果的波动范围。

换句话说，就是给测量结果加上一条“保护线”，告诉大家，原来这个结果有个大致的误差范围。

测量不确定度评估报告测量不确定度评估报告1.识别测量不确定度的来源在医学实验室中构成测量不确定度的4个主要分量主要包括“检验过程不精密度”、“校准品赋值的不确定度”、“样品影响分量”和“其它检验影响分量”。

我们参考CNAS-GL05：2011《测量不确定度要求的实施指南》和CNAS-TRL-001：2012《医学实验室―测量不确定度的评定与表达》的要求，制定了测量不确定度评定程序，评估了本科室申报的定量项目的测量不确定度。

由于在医学实验室中“样品影响分量”和“其它检验影响分量”的不确定度难以估计，故我们只评估了前两个分量的不确定度。

2.目标不确定度2.1 确定的检验程序在正式启用前，实验室应为每个测量程序确定目标不确定度，即规定每个测量程序的测量不确定度性能要求。

2.2 检验科每个测量程序的目标不确定度由各实验室确定。

2.3 各实验室在确定目标不确定度时可以基于生物变异、国内外专家组的建议、管理准则或当地医学界的判断。

根据应用要求，对不同水平的测量结果可以确定一个或多个目标不确定度。

2.4目标不确定度如下：2.4.1临床化学项目将TEa(国家标准(GB/T20470-2006)、卫生部临床检验中心室间质量评价标准)作为目标扩展不确定度。

2.4.2血液学项目，将TEa（行业标准WS/T406-2012）指标作为目标扩展不确定度。

3.确立输出量与输入量之间的数学模型若输出量为Y（被测量值），输入量X的估计值为xi，则被测量与各输入量之间的函数关系为Y=f（x1，x2，x3，x4…）；由于在医学实验室中“样品影响分量”和“其它检验影响分量”的不确定度难以估计，故只对前两个分量的不确定进行评估。

4测量不确定度的计算4.1 A类评估：检验过程不精密度评估样本使用高低2个水平的室内质控品作为实验用样本。

计算本室2水平质控品的日间精密度。

计算批间变异系数CV。

=批间u 批间CV4.2 B 类评估：校准品赋值的不确定度评估信息来源于厂商提供的校准品溯源性文件。

01通常的测量不确定度报告一般应包含如下信息：a）阐明根据实验观测值和输入量到测量结果及其不确定度的方法；b）列出全部不确定度分量，并给出它们是如何评估的；c）数据的分析方法；d）给出分析中使用的全部修正因子和常数及其来源；e）给出被测量的估计值及测量不确定度适宜的报告表示。

02重要的测量不确定度报告一般应包括如下信息：a）被测量Y的明确定义；b）输出量与输入量之间的函数关系及灵敏度系数；c）给出每个输入量的估计值、标准不确定度，并列出表格；d）给出所有相关输入量的协方差或相关系数及得到的方法；e）给出被测量的估计值、合成标准不确定度或扩展不确定度及计算过程；f）对扩展不确定度应给出包含因子、置信水平；g）修正值和常数的来源及其不确定度；h）用Y=y±U表示测量结果并有适当的单位。

03报告日常检测结果的测量不确定度报告日常检测结果时，一般情况下，仅给出被测量的估计值、标准不确定度、扩展不确定度的数值和k值就足够了。

04报告测量不确定度的表达形式报告被测量的测量不确定度时，可以报告其测量结果的标准不确定度；也可以报告其测量结果的扩展不确定度；报告测量结果应尽可能多地提供有关不确定评估的信息；不确定度也可以用相对形式来报告。

05报告测量结果的标准不确定度报告测量结果的标准不确定度时，推荐采用：测量结果（单位），加上标准不确定度（单位）。

例如：盐酸标准溶液浓度c（HCI）的平均值为0.05046mol/L，其合成标准不确定度Uc（HCl）为0.00008mol/L，可表示为：盐酸标准溶液浓度C（HCI）=0.05046mol/L标准不确定度Uc（HCl）=0.00008mol/L当使用标准不确定度时，建议不使用±符号。

因为该符号通常与高置信水平的区间有关。

06报告测量结果的扩展不确定度在检验中一般使用扩展不确定度U＝kuc（y）表示结果的测量不确定度。

完整的测量结果应含有两个基本量，一是被测量的最佳估计值y，一般由数据测量列的算术平均值给出，另一个是描述该测量结果分散性的测量不确定度。

不确定度评定报告1、测量方法由标准晶振输出频标信号,输入到通用计数器中,在通用计数器上显示读数。

2、数学模型 数学模型A=A S +δ式中：A —频率计上显示的频率值A S —参考频率标准值；δ—被测与参考频标频率的误差。

3、输入量的标准不确定度3.1 标准晶振引入的标准不确定度()s A u ，用B 类标准不确定度评定。

标准晶振的频率准确度为±2×10-10，即当被测频率为10MHz 时，区间半宽为a ＝10×106×2×10-9＝2×10-2Hz ，在区间内认为是均匀分布，则标准不确定度为()s A u ＝a/k ＝1.2×10-2Hz()=rel s A u 1.2×10-2/107=1.2×10-93.2被测通用计数器的测量重复性引入的标准不确定度分量u(δ2)u(δ2)来源于被测通用计数器的测量重复性，可通过连续测量得到测量列，采用A 类方式进行评定。

对一台通用计数器10MHz 连续测量10次，得到测量列9999999.6433、9999999.6446、9999999.6448、9999999.6437、9999999.6435、9999999.6428、9999999.6446、9999999.6437、9999999.6457、9999999.6451Hz 。

由测量列计算得算术平均值 ∑==ni i f n f 11=9999999.6442Hz,标准偏差 ()Hz n ffs ni i00091.0121=--=∑=标准不确定度分量u(δ3)=0.00091/=0.00029Hzu(δ3)rel =2.9×10-114 合成标准不确定度评定 主要标准不确定度汇总表不确定度来源（i x ）i a i k ()i u x标准晶振引入的标准不确定度()rel s A u 2×10-3Hz 31.2×10-10 通用计数器引入的标准不确定度分量()1δu2.5×10-2Hz31.5×10-9被测石英晶体振荡器测量重复性()rel u 2δ0.00091Hz 12.9×10-11输入量A S 、δ1、δ2相互独立，所以合成标准不确定度为u c (A)= 922212105.1)()()(-⨯=++δδu u A u S5 扩展不确定度评定 取k=2，则 扩展不确定度为U rel ＝k ×u c ＝2×1.5×10-9＝3×10-96测量不确定度报告f ＝f 0（1±3×10-9）Hz ，k=2不确定度评定报告1、测量方法由标准晶振输出频标信号,输入到通用计数器中,在通用计数器上显示读数。

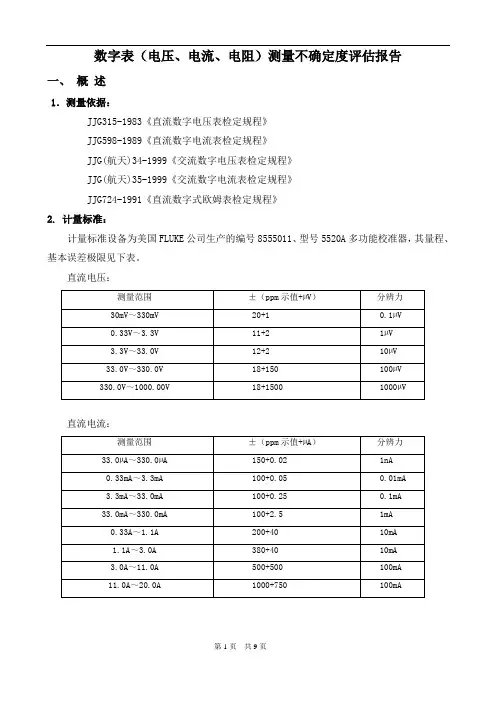
数字表（电压、电流、电阻）测量不确定度评估报告一、概述1．测量依据：JJG315-1983《直流数字电压表检定规程》JJG598-1989《直流数字电流表检定规程》JJG(航天)34-1999《交流数字电压表检定规程》JJG(航天)35-1999《交流数字电流表检定规程》JJG724-1991《直流数字式欧姆表检定规程》2. 计量标准：计量标准设备为美国FLUKE公司生产的编号8555011、型号5520A多功能校准器，其量程、基本误差极限见下表。

直流电压：直流电流：第1页共9页交流电流:交流电压:阻：电3．测量环境条件：温度：20.5℃，相对湿度：50.5%。

4.被测对象：选用美国FLUKE公司生产的编号86770198、型号F189数字万用表，其量程、基本误差极限见下表。

交流电压：交流电流：5. 测量方法：5.1直流电压表：依据规程JJG315-1983第7.1条“直流标准电压发生器检定方法”。

设多功能校准器输出标准设定电压UN ，被校表的显示读数Ux，每个设定值测量一次，则被校表的误差为Δ=U x-U N 。

5.2直流电流表：依据规程JJG598-1989第10.1条“直流标准电流源检定方法”。

设多功能校准器输出标准设定电流IN ，被校表的显示读数Ix，每个设定值测量一次，则被校表的误差为Δ=Ix-IN。

5.3交流电压表：依据规程JJG(航天)34-1999第5.2.3.3条“交流标准源检定方法”。

设多功能校准器输出标准设定电压UN ，被校表的显示读数Ux，每个设定值测量一次，则被校表的误差为Δ=U x-U N 。

5.4交流电流表：依据规程JJG(航天)35-1999第5.2.3.2条“标准源测量法”，设多功能校准器输出标准设定电流IN ，被校表的显示读数Ix，每个设定值测量一次，则被校表的误差为Δ=Ix-IN。

5.5直流欧姆表：依据规程JJG724-1991第9.2条“电阻校准仪法”，设多功能校准器输出标准设定电阻R N，被校表的显示读数R x，每个设定值测量一次，则被校表的误差为Δ=R x-R N 。

第 1 页 共 2 页指示表示值误差测量结果不确定度评定1. 概述1.1 测量依据：JJG 34-2008《指示表（指针式、数显式）检定规程》。

1.2 环境条件：温度(20 ±10) ℃，每小时温度变化不大于 2℃。

1.3 测量标准：光栅式指示表检定仪。

1.4 被测对象：指针式千分表（制造厂家：三和，型号规格： (0 ~ 1)mm ，编号：3533）。

1.5 测量方法：千分表的示值误差是采用指示表检定仪进行校准。

校准时，先将检定仪和千分表分别对好 零位， (0 ~ 1)mm 千分表示值误差是在正行程的方向上每隔0.05mm 个分度进行校准。

由正行程校准得到的最大误差与最小误差之差值为千分表的示值误差。

2. 数学模型e = L d - L s + L d ⋅ a d ⋅ ∆d - L s ⋅ a s ⋅ ∆t s式中： L d -千分表的示值（20℃条件下）；L s -检定仪的示值（20℃条件下）；a d , a s -分别为千分表和检定仪的线胀系数；∆t d , ∆t s -分别为千分表和检定仪偏离温度 20℃时的数值。

3. 计算分量标准不确定度3.1 测量重复性引入的不确定度分量u 1在相同的条件下，千分表中1mm 点重复测量10 次，得到示值误差如下第 2 页 共 2 页αa b 经计算得出单次测量实验标准差： s = 0.2μm , 则u 1 = s = 0.2μm 。

3.2 指示表检定仪不确定度引起的不确定度分量u 2根据证书指示表检定仪任意1mm 示值误差为0.7μm ，按均匀分布，则： u 2 == 0.41μm3.3 千分表和检定仪线胀系数给出的不确定度分量u 3δ 的界限为± 2×10-6 。

C -1 ，按均匀分布。

则： u = 2 ⨯10-6 。

C -1 = 1.15⨯10-6 。

C -1若 L = 1mm ， ∆t = 10。

C ，则u = 11.5⨯10-6 。

不确定度评定报告1、测量方法由标准晶振输出频标信号,输入到通用计数器中,在通用计数器上显示读数。

2、数学模型 数学模型A=A S +δ式中：A —频率计上显示的频率值A S —参考频率标准值；δ—被测与参考频标频率的误差。

3、输入量的标准不确定度3.1 标准晶振引入的标准不确定度()s A u ，用B 类标准不确定度评定。

标准晶振的频率准确度为±2×10-10，即当被测频率为10MHz 时，区间半宽为a ＝10×106×2×10-9＝2×10-2Hz ，在区间内认为是均匀分布，则标准不确定度为()s A u ＝a/k ＝1.2×10-2Hz()=rel s A u 1.2×10-2/107=1.2×10-93.2被测通用计数器的测量重复性引入的标准不确定度分量u(δ2)u(δ2)来源于被测通用计数器的测量重复性，可通过连续测量得到测量列，采用A 类方式进行评定。

对一台通用计数器10MHz 连续测量10次，得到测量列9999999.6433、9999999.6446、9999999.6448、9999999.6437、9999999.6435、9999999.6428、9999999.6446、9999999.6437、9999999.6457、9999999.6451Hz 。

由测量列计算得算术平均值 ∑==ni i f n f 11=9999999.6442Hz,标准偏差 ()Hz n ffs ni i00091.0121=--=∑=标准不确定度分量u(δ3)=0.00091/=0.00029Hzu(δ3)rel =2.9×10-114 合成标准不确定度评定 主要标准不确定度汇总表不确定度来源（i x ）i a i k ()i u x标准晶振引入的标准不确定度()rel s A u 2×10-3Hz 31.2×10-10 通用计数器引入的标准不确定度分量()1δu2.5×10-2Hz31.5×10-9被测石英晶体振荡器测量重复性()rel u 2δ0.00091Hz 12.9×10-11输入量A S 、δ1、δ2相互独立，所以合成标准不确定度为u c (A)= 922212105.1)()()(-⨯=++δδu u A u S5 扩展不确定度评定 取k=2，则 扩展不确定度为U rel ＝k ×u c ＝2×1.5×10-9＝3×10-96测量不确定度报告f ＝f 0（1±3×10-9）Hz ，k=2不确定度评定报告1、测量方法由标准晶振输出频标信号,输入到通用计数器中,在通用计数器上显示读数。

测量不确定度评定报告1、评定目的
2、评定依据
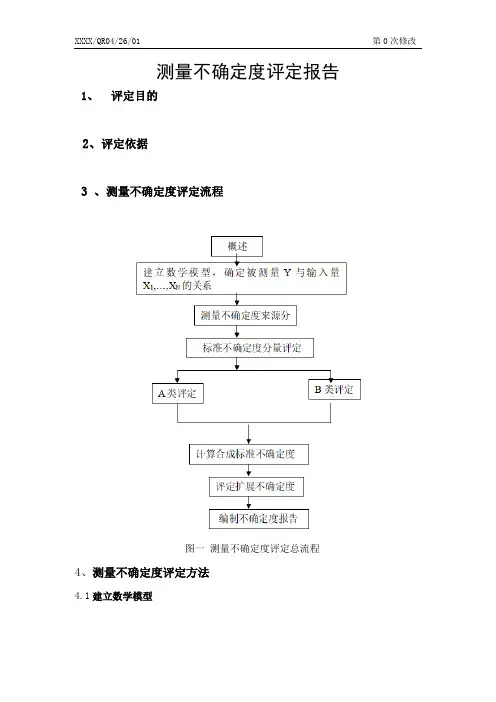
3 、测量不确定度评定流程
图一测量不确定度评定总流程4、测量不确定度评定方法
4.1建立数学模型
4.2不确定度来源分析
测量过程中引起不确定度来源，可能来自于：
a、对被测量的定义不完整；
b、复现被测量定义的方法不理想；
c、取样的代表性不够，即被测量的样本不能完全代表所定义的被测量；
d、对测量过程受环境影响的认识不周全或对环境条件的测量和控制不完善；
e、对模拟式仪器的读数存在人为偏差（偏移）；
f、测量仪器的计量性能（如灵敏度、鉴别力阈、分辨力、死区及稳定性等）的
局限性；
g、赋予计量标准的值或标准物质的值不准确；
h、引入的数据和其它参量的不确定度；
i、与测量方法和测量程序有关的近似性和假定性；
j、在表面上完全相同的条件下被测量在重复观测中的变化。

4.3标准不确定度分量评定
4.3.1 A 类评定
4.3.2 标准不确定度的B类评定
4.4合成不确定度U c(y)的计算
4.5扩展不确定度U 的计算
4.6 测量不确定报告
编制人：
批准人：
日期：。

测量不确定度实验报告测量不确定度实验报告引言：在科学研究和实验中，测量是一项重要的工作。

然而，由于各种因素的干扰，任何测量都存在一定的误差和不确定度。

因此，准确地评估测量结果的可靠性和可信度就显得尤为重要。

本实验旨在通过测量不确定度的方法，探讨测量结果的精确性和可靠性。

材料与方法：本实验使用了一台电子天平和一组重量标准。

首先，将电子天平校准至零点。

然后，使用重量标准分别测量了五个物体的质量，并记录下测量结果。

在每次测量之前，确保物体的表面干净，并放置在天平的中央位置。

每个物体的测量重复三次，以减小随机误差的影响。

结果与讨论：通过对测量结果的分析，我们可以得到每个物体的平均质量和标准偏差。

平均质量是通过将三次测量结果相加并除以三得到的。

标准偏差则是测量结果的离散程度的一种度量。

它可以帮助我们评估测量的精确性和可靠性。

在本实验中，我们发现每个物体的平均质量都非常接近于其已知质量。

这表明电子天平的测量结果是准确的。

然而，通过计算标准偏差，我们发现测量结果之间存在一定的离散程度。

这可能是由于天平的精确度限制、操作者的误差以及环境因素等因素所导致的。

为了更准确地评估测量结果的可靠性，我们还计算了不确定度。

不确定度是一个测量结果的范围，用于表示测量结果的可信度。

在本实验中，我们使用了合成不确定度的方法。

合成不确定度是通过将各种误差的不确定度进行合成计算得到的。

在这个过程中，我们考虑了天平的分辨率、重复测量的误差以及环境因素的影响。

通过计算，我们得到了每个物体测量结果的不确定度。

这些不确定度可以帮助我们判断测量结果的可靠性。

如果不确定度较小，说明测量结果较为可信。

反之，如果不确定度较大，说明测量结果的可靠性较低。

结论：通过本实验，我们学习了测量不确定度的方法，并评估了测量结果的精确性和可靠性。

实验结果表明，电子天平的测量结果是准确的，但存在一定的离散程度。

通过计算不确定度，我们得到了测量结果的可靠性评估。

这对于科学研究和实验具有重要意义，可以帮助我们更准确地理解和解释测量结果，并提高实验的可靠性和准确性。

测量不确定度报告导言在科学和工程领域中，精确测量是至关重要的。

然而，任何测量都会存在一定的不确定性，即测量结果与真实值之间的差异。

为了准确评估测量数据的可靠性，测量不确定度报告在实验和研究中扮演着重要的角色。

本文将探讨测量不确定度报告的概念、意义以及其中的关键要素。

一、测量不确定度的定义测量不确定度指的是测量结果和预期真实值之间的范围，它是一种对测量结果的估计，表明该结果附近可能存在的误差。

不确定度的大小反映了测量结果的可靠性和精确性。

二、数据收集与处理在进行测量实验时，数据的收集和处理环节决定了最终的测量不确定度。

数据采集要确保足够的重复性和可重复性，通过多次实验取得一系列测量数据。

然后，需要对数据进行处理，例如计算平均值和标准偏差，以提供更准确的测量结果。

三、类型和来源测量不确定度可以分为两种类型：随机误差和系统误差。

随机误差是由于测量条件的不确定性引起的，如仪器的精确度和环境条件的变化。

系统误差是由于仪器的固有偏差、操作者偏差或方法的局限性等引起的。

这两种不确定度来源需要被合理评估和记录。

四、表达和计算测量不确定度通常用标准差或扩展不确定度来表示。

标准差是一种衡量数据分散程度的统计指标，通过对数据的方差进行开方计算得到。

扩展不确定度考虑了其他因素的贡献，例如系统误差和不确定度分量之间的相互关系。

计算测量不确定度时，应使用适当的数学模型和统计方法。

五、报告的要素一份完整的测量不确定度报告应包括以下要素：1. 实验目的和背景：说明进行该实验的目的以及背景知识和相关研究。

2. 测量方法：详细描述实验过程、使用的仪器和设备。

3. 数据处理和不确定度评估：展示数据处理的步骤，计算不确定度，并解释评估方法。

4. 结果与讨论：提供最终的测量结果以及与其他研究或标准值的比较，在结果的讨论中，解释不确定度对结果的影响。

5. 结论：总结实验结果，强调测量不确定度对结果的重要性。

六、应用与影响测量不确定度报告在科学和工程领域中有广泛的应用。

输入功率测量不确定度评估报告1.目的:本报告旨在说明本实验室依照CNAS量测不确定度表示指引，分析评估本实验室依照测试法规执行贮热式室内加热器的输入功率之量测不确定度的分析方法与评估结果。

2.测量不确定度评估的标准依据：GB 4706.44-2005 《家用和类似用途电器的安全贮热式室内加热器的特殊要求》；GB 4706.1-2005 《家用和类似用途电器的安全第1部分：通用要求》JJF1059.1-2012: 《测量不确定度的评定与表示》；3.适用范围：适用于贮热式室内加热器的输入功率的不确定度评定。

4.试验环境：a).大气压力：86kPa--106kPa;b).环境温度：23℃±2℃，且试验室内无气流及热辐射影响；c).相对湿度：45%--75%RH;d).电源电压：（220V±1%），频率为（50Hz±0.5），电源总谐波失真不大于5%；e).不存在影响测量的机械振动与电磁5.试验仪器设备：6.试验方法：6.1 输入功率测量：用温度功率记录集成系统，并用10KW变压器将输入电压控制在220V±0.5V，贮6.各输入量的标准不确定度分析：6.1 输入量P1 的不确定度u1(P1)的评定输入量P1 标准不确定度的来源主要有:6.1.1 由重复性测量引入的标准不确定度u1(t1)的评定由重复性测量引入的标准不确定度,根据贝塞尔公式计算：这里x—表示n次测量的算术平均值，这里n=6。

因此u1(P1)= 1.732W/正态分布=1.732W6.1.2.由电子计时器示值误差引入的标准不确定度u4(t1)的评定查找电子计时器说明书知，对于大于48小时的时间而言，人为读数的时间误差为1/3600=0. 028%，对仪表的误差，取其极限误差1s/h, 服从均匀分布。

所以电子计时器最大示值误差引人的标准不确定度u4(t1)6.1.3.由数字功率分析仪的最大允许示值误差引入的标准不确定度u5(E1)的评定查数字功率分析仪的使用说明书：电压：0.5%（300V），电流：0.5%（5A），功率：0.5%（1.0kW），电能：0.5%；时间t：0.01s：故本身仪器最大允许示值误差的不确定度u5(E1)，服从均匀分布。

外径千分尺测量阀杆Ø35外径不确定度评定报告1.概述1.1测量依据：按图PFF78-35-02阀杆尺寸进行测量。

1.2环境条件：常温，相对湿度<35%RH 。

1.3测量设备：（25-50）mm 外径千分尺，在其测量范围内最大示值误差为±0.004mm 。

1.4被测对象：外径为025.0087.035－－mm 的阀杆。

材料为12Cr13，α1=10.3×10-6/℃。

1.5测量方法：用外径千分尺直接测量。

2. 测量模型：由于对象内径值可以直接在内径千分尺上直接测量 故：L=L S －L S (δα·Δt ＋αs ·δt)L---被测内孔的测定内径；L S ---内径千分尺对内孔内径的测量值。

δα—被测内孔线膨胀系数与内径千分尺线膨胀系数之差。

Δt — 被测内孔温度对参考温度20℃的偏差，取±10℃。

αs — 内径千分尺线膨胀系数，取11.5×10-6/℃。

δt — 被测内孔温度与内径千分尺温度之差，取±1℃。

3.灵敏系数该数学模型是透明箱模型，必须逐一计算灵敏系数：1 ≈ ∂ ∂)Δ1(=t s t αD S δαδLs f C －－＝ ;t S s αδD s αf C －== ∂ ∂=－35×1㎜℃=－3.5×104µm ℃；δαD f C S t t －=Δ=Δ ∂ ∂=－35×1×10－6㎜/℃=－0.035µm/℃δαf C δα ∂ ∂/==－Ds Δt=－35×10㎜℃=－3.5×105µm ℃ t δf C t δ ∂ ∂/==－Ds αs=－35×11.5×10－6㎜/℃=－0.402µm /℃4.计算各分量标准不确定度4.1外径千分尺示值误差引入的分量u(L S )根据外径千分尺检定规程，在其测量范围内最大示值误差e=±0.004mm在半宽度为区间内，以均匀分布，则u(L S)= 4/1.732 =2.4μm;4.2被测主轴线膨胀系数不准确引入的分量u(αS)由于被测主轴线膨胀系数α1＝ 10.4×10-6/℃是给定的，是一个常数，故 u(αS)= 0 ，4.3测量环境偏离标准温度20℃引入的分量u(Δt)测量环境偏离标准温度20℃的偏差为±10℃，在半宽为10℃范围内，以等概率分布（均匀分布）。

测量不确定度评定报告一、引言二、测量方法和装置本次测量使用的方法是直线测量法，采用直尺和游标卡尺进行测量。

直线测量法是一种简单有效的测量方法，在工程和科学领域得到广泛应用。

1.人为误差测量1：30.2cm测量2：30.1cm测量3：30.3cm根据三次测量结果的平均值，得到被测量值为30.2cm。

通过测量结果的离散程度，可评估人为误差的大小。

2.仪器误差仪器误差是由于测量仪器本身的不准确性而引起的。

在使用直尺和游标卡尺进行测量时，需要考虑到仪器的刻度精度和读数精度。

本次测量中，直尺和游标卡尺的刻度间距分别为0.1cm和0.01cm。

根据仪器的刻度间距，可以评估测量结果在刻度内的不确定度。

例如，如果测量结果位于两个刻度之间，不确定度可以评估为刻度间距的一半。

3.环境影响环境因素如温度、湿度等的变化会对测量结果产生一定的影响。

在本次测量中，环境温度保持相对稳定，湿度变化较小，因此可以忽略环境影响对测量结果的不确定度。

四、测量不确定度评定五、灵敏度分析和建议灵敏度分析用于评估测量结果对误差的敏感程度，从而提供改进测量方法和装置的建议。

1.人为误差的影响2.仪器误差的影响根据前述的仪器误差评估，本次测量结果对仪器误差的敏感程度较高。

为了减小仪器误差对测量结果的影响，可以考虑使用更精密的测量仪器，如数字卡尺等，降低仪器误差。

六、结论本次测量的不确定度评定结果为0.1cm。

测量结果对人为误差的敏感程度较低，对仪器误差的敏感程度较高。

改进测量方法和装置可降低仪器误差对测量结果的影响。

浙江富春江水电设备股份有限公司关键测量项目不确定度评定汇编编制部门：品管部编制时间：2008年12月金属材料强度测量不确定度评定0011 概述1.1 测试依据：GB/T 228-2002《金属材料 室温拉伸试验方法》。

1.2 环境条件：10℃～35℃。

1.3 测量设备：1.3.1屏显式液压万能试验机，测量范围：（0～1000）kN, 准确度等级：1.0级。

1.3.2 游标卡尺，测量范围：（0～200 ）mm ，最大允许误差：±0.02mm 。

1.4 测量对象: 各种金属材料。

1.5 测量方法：在规定的条件下用屏显式液压万能试验机测试金属试样的抗拉强度和屈服强度。

1.6使用范围：在满足以上条件的金属材料抗拉强度和屈服强度测定过程中均可采用本不确定度评定，在此报告中选取金属材料抗拉强度测量进行不确定度分析。

2 数学模型2.1抗拉强度可表示为：ba Fb Fm S Fb Fm Rm b •==)()()(0σ 式中： )(b Rm σ——试样的强度,MPa 或N/mm 2； )(Fb Fm ——试样承受的最大负荷，N ；S 0 ——试样标距部分原始的最小横截面积，mm 2；a ——试样标距部分原始的最小宽度，mm ；b ——试样标距部分原始的最小长度，mm 。

3 不确定度来源分析根据数学模型，若不考虑试验温度效应所引起的不确定度分量，抗拉强度测量不确定度将取决于输入量Fm ，S 0的标准不确定度u(a)和u(b) 。

在本报告中选取同种规格型号的金属材料进行抗拉强度的测量不确定度评定。

3.1输入量Fm 的标准不确定度u(Fm )的评定当试样拉断时承受的最大负荷为164kN 时,而本实验为破坏性试验，不考虑重复性试验带来的不确定度分量。

因此输入量Fm 的标准不确定度u(Fm )由仪器自身误差引起。

万能试验机的测量范围为（0～1000）kN, 准确度等级为 1.0级，则其最大允许误差为：1000kN ×1%=10kN ，其半宽a=10kN ，采用B 类评定，估计其服从均匀分布，k=3， 则u(Fm )=301kN =5780N估计其不可靠性为5%，则，根据公式2)Fm ()Fm (21-⎥⎦⎤⎢⎣⎡∆=u u v Fm，其自由度为200。

电压（电流）测量结果的不确定度评定1．概述在23条件下，开机2小时候后，选取适当的量程，在测量用设备处于统计控制的情况下时，电路中通以恒流（压）源，测量电路中电流（电压）。

并给出测量结果的不确定度。

使用设备：安捷伦数字万用表（34405A）直流电压VDC(V) 直流电流IDC(A)交流电压V AC(V)交流电流IAC(A)量程10V 100mA 1kHz 100V 1kHz 1A最大允许误差（读数+量程）%0.0035+0.0005 0.050+0.005 0.06+0.03 0.10+0.04被测量电源：直流标称电压10V，电流50mA；交流标称电压50.0V，电流0.5A。

2．测量模型在本试验中输入量X即为输出量Y。

因为此有数学公式：Y(I) = X(I)+和Y(V) = X(V)+X(I)：为被测电流值平均值X(V)：为被测电压值平均值：为仪器修正值3．不确定度来源分析根据JJG124-2005《电流表，电压表，功率表，电阻表》以及设备仪器使用说明书。

万用表误差来自于以下最大允许误差，修正值（偏离零位），以及测试重复性和设备仪器分辨率这几个方面分量。

序号引起不确定度u（y）的中的各来源标准偏差分量使用评定方法1 由测量本身的重复性引起的偏差，其不确定度为u1。

使用A类方法评定2 由测试设备的最大允许误差引起偏差，其不确定度为u2。

使用B类方法评定3 由测试设备自身灵敏度引起的偏差，其不确定度为u3。

使用B类方法评定4 由测试设备的修正值（偏离零位）引起的不确定度为u4。

使用B类方法评定4．标准不确定度的评定4.1测量重复性引起的标准不确定度采用A类方法进行评定。

对每一样品重复测量10次。

标准差按贝塞尔公式计算：序号直流电压VDC(V)直流电流IDC(mA)交流电压V AC(V)交流电流IAC(A)1 9.9992 49.999 49.969 0.499792 9.9994 49.998 49.977 0.499883 9.9997 50.001 49.968 0.499814 9.9989 49.997 49.971 0.499835 9.9996 50.001 49.966 0.499916 9.9991 49.997 49.979 0.499767 9.9986 50.003 49.983 0.499868 9.9993 49.998 49.987 0.499909 9.9984 50.003 49.989 0.4998410 9.9989 50.000 49.992 0.49994平均值x9.99911 49.9997 49.9781 0.499852标准偏差s0.000418 0.00226 0.00942 0.0000567其中测量结果的算术平均值作为输入量的无偏估计值，其不确定度u1的计算公式如下u 1=u()=s()=直流电压VDC(V) 直流电流IDC(mA)交流电压V AC(V)交流电流IAC(A)标准不确定度u10.000132 0.00071 0.00298 0.00001794.2由测试设备自身最大允许误差引入的不确定度采用B类方法进行评定。