平面连杆机构分析与综合(曹惟庆)思维导图

定义：全部用转动副相连的平面四杆机构。
机架
组成: 连架杆
连杆
分类:
整转副 机架 曲柄
摆动副
摇杆
三种基本型式：曲柄摇杆机构、双曲柄机构、 双摇杆机构
3
2020/11/17
第2章 平面连杆机构
§2-1 平面四杆机构的基本类型及其应用 1. 曲柄摇杆机构
定义：在两连架杆中，一个为曲柄，另一个为摇杆。
运动特点：
2020/11/17
两个特性 ：
①两曲柄同速同向转动；
②连杆作平动。
12
第2章 平面连杆机构
§2-1 平面四杆机构的基本类型及其应用
反平行四边形机构—两个曲柄 反向回转。
应用实例：车门启闭机构
反平行四边形机构
平行四边形机构在四杆
(或铰链)共线位置出现运
动不确定。
13
2020/11/17
第2章 平面连杆机构
风扇摇头机构
汽车转向机构
B’ C’
B
C
A
D
2020/11/17
C 电机
蜗轮 BBA
D D
A
D 蜗杆
C C
风扇座
第2章 平面连杆机构
A A E E B B
17
§2-1 平面四杆机构的基本类型及其应用 铰链四杆机构的演化
演化常用的方式: ①改变运动副类型； ②选不同构件作机架； ③改变相对杆长。
2020/11/17
2020/11/17
第2章 平面连杆机构
24
§2-1 平面四杆机构的基本类型及其应用
② 双滑块机构：椭圆仪机构(延长点的运动轨迹为椭圆)
2 1 4
3
椭圆仪机构

2019/11/7
49
三、压力角和传动角
1、压力角与传动角
压力角 从动杆(运动输出件)受力作用点的力作用线与速 度方位线所夹锐角. (不考虑摩擦)
有效力Ft=FCOS ，越大越好，因此越小越好。
传动角 压力角的余角. (连杆轴线与从动杆轴线所夹锐角)

F

d
V
d
d
180 d
传动不利，设计时规定 min 4050
传动角 的大小随机构位置的不同而变化， min在哪？
2019/11/7
50
2、最小传动角 min
2
BD
a2d22adcosj
b
2
BD
b2c22bccosd
B
co sdb2c22adco sja2d2
2bc
a
j
A
分析： j =0 cos j =1 cos d d min j =180° cos j =–1 cos d d max
d min 或 d max 可能最小
传动角最小的位置 ：
主动件与机架共线
C
d c
d
D
2019/11/7
51
三、 死点
2、平面连杆机构
3、铰链四杆机构
二、平面连杆机构的特点和应用
1、特点 优点：
(1)面接触低副，压强小，便于润滑，磨损轻，寿命长，传递动力大
(2)低副易于加工，可获得较高精度，成本低
(3)杆可较长，可用作实现远距离的操纵控制
(4)可实现转动、移动等基本运动规律和运动轨迹
缺点：
(1)低副中存在间隙，精度低
20
二、铰链四杆机构的演化

第3章 平面连杆机构
3.1
运动副及平面机构运动简图 铰链四杆机构
3.2
3.3
牛头刨床传动机构设计
3.1 运动副及平面机构运动简图
3.1.1 机构和运动副 3.1.2 机构运动简图 3.1.3 平面机构的自由度
3.1.1 机构和运动副
1．机构
机构是由两个或两个以上构件通过活动连接形成的构件系统。一 个机器中通常包含多种不同类型的机构，每个机构可以实现不同的 运动功能。机构可以按照以下原则进行分类。 ① 按组成的各构件间相对运动形式的不同，机构可分为平面机构（ 如平面连杆机构、圆柱齿轮机构等）和空间机构（如空间连杆机构 、蜗轮蜗杆机构等）。 ② 按结构特征可分为连杆机构、齿轮机构、棘轮机构等。 ③ 按所转换的运动或力的特征可分为匀速和非匀速转动机构、直线 运动机构、换向机构、间歇运动机构等。 ④ 按功用可分为安全保险机构、联锁机构、擒纵机构等。 ⑤ 按运动副类别可分为低副机构（如连杆机构等）和高副机构（如 凸轮机构等）。
（1）电动机经皮带轮和齿轮传动，带动曲柄2和固结在 其上的凸轮8。 （2）刨床工作时，由导杆机构1-2-3-4-5-6带动刨头6和刨 刀做往复运动。 （3）刨头右行时，刨刀进行切削加工，称为工作行程， 要求速度较低且均匀，以减小电机容量并提高切削质 量。 （4）刨头左行时，刨刀不进行切削加工，称为空回行程 ，要求速度较高，以提高产率。因此，刨床上通常采 用具有急回特性的导杆机构。 （5）刨刀每完成一次切削加工，利用空回行程的时间， 凸轮8通过四杆机构1-9-10-11与棘轮带动螺旋机构（图 中未绘出）使工作台连同工件做进给运动，以便切削 加工继续进行。
从以上分析不难得知，这种主动件做等 速运动，从动件空回行程平均速度大于 工作行程平均速度的特性，称为连杆机 构的急回特性。 牛头刨床、往复式运输机等机械就是利 用这种急回特性来缩短非生产时间，提 高生产效率的。

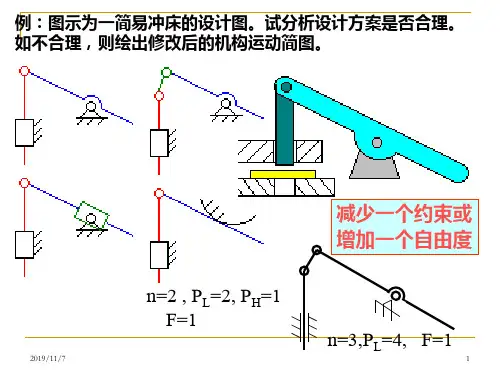
(2)函数生成机构综合 该综合要求 连杆机构的输入和输出构件间的位移 关系满足预先给定的函数关系。
(3)轨迹生成机构综合 该综合要 求机构中连杆上某点沿给定的轨迹运 动。
如图所示轧辊机构
连杆机构综合所用的方法有解析法和几何法。解析法根据运动学 原理建立设计方程，然后解析求解或用计算机求数值解。几何法应 用运动几何学的原理作图求解。
示刚体上一个矢量由位置v1，绕原点旋转a角到位置v2 。两者的关系为
由于Z轴不变,上式写成矩阵
简化记为:
前面公式的意义:在于知道刚体第一个位置的坐标后，可以用第一 个位置的坐标和转角，来表示刚体转动后的坐标。
二，刚体平面运动的一般情况（转动+移动）
如图所示，平面上某刚体由初始位置 运动
到末位置 。该一般位移可以分解为随同基点的
例5-1 已知连杆的三个位置，即连杆上P点的三个位置及连杆的两个转角:
=
试综合该四杆导引机构。 素.
cos0
D12 sin0
0
sin0 cos0
0
2 cos0 1sin0 0.5sin0 1cos0
1
10 1 0 1 0.5
00 1
cos0
D12 sin0
0
sin 0 cos0
0
2cos0 1sin0 0.5sin0 1cos0
曲柄存在准则：最短杆与最长杆之和≤其余两 杆长度之和；
在此条件下，取最短杆或与最短杆相邻接的构 件作机架，必有曲柄。 （2）运动连续性准则
(3)运动的顺序准则
平面机构运动综合中,应符合规 定的运动顺序要求。
（4）传力准则
机构的最小传动角≥40°。
5-2 刚体位移矩阵
一、刚体绕坐标原点的旋转矩阵 刚体上的一个矢量就能完全确定此刚体在平面中的位置。图5-3表

第6章 平面连杆机构
本章重点: 本章重点:
四杆机构的基本型式及其应用 曲柄摇杆机构的主要特性 平面连杆机构的设计
本章难点: 本章难点:
平面连杆机构的设计
6-1 连杆机构及其传动特点
平面连杆机构: 用低副连接而成的平面机构。
一、主要优点：
1、能实现多种运动形式。如：转动，摆动，移动，平面运动 2、运动副为低副： 面接触： ①承载能力大；②便于润滑。寿命长 几何形状简单——便于加工，成本低。 3、利用连杆曲线，可满足不同轨迹的要求。 4、原动件的运动规律不变，可通过改变从动件的长度 得到不同的运动规律。
1、图解法，2、解析法，3、图谱法，4实验法
一、按K设计四杆机构
1. 曲柄摇杆机构 2. 曲柄滑块机构 3. 导杆机构
图解法设计
已知：摇杆CD长度，摆角，K, 设计此机构（确定曲柄和连杆长）
二、按给定连杆位置
图解法设计
1、已知B，C及连杆的三个位置，设计该铰链四杆机构。 若知2个位置，无穷解。 2*、已知A，D，连杆的三个位置，设计铰链四杆机构。
输送机
刮雨器
飞剪
2、双曲柄机构
升降台-平行四杆 绘图仪-平行四边形 开门机构-反平行四边形
3、双摇杆机构
汽车转向-双摇杆 起重机-双摇杆
二、四杆机构的演化
1、转动副转化成移动副
3 C 2 B A 1 4 3 1 D 3 C e B 2 1 A 4 A 1 B 2 4 C 3 A D B 2 K角θ
其值与构件尺寸有关， 可能<90°，>90°
2 =180 θ
从动件慢行程 从动件快行程
1 →t1
2 →t2
2.行程速度变化系数
ψ
t2

§3-5 平面四杆机构的设计
当机构处于死点位置（ g=0°）时，机构发生自锁或 运动不确定。
消除死点的方法： 1）对曲柄施加外力。 2）利用构件自身或飞轮的惯性，使机构顺利通过死 点。 3）采用联动的两相同机构，使两机构的死点错开。
死点的利用： 1）飞机起落架 2）快速夹具
死点的利用： 1）飞机起落架
2）快速夹具
3）折叠靠椅
2）当最短杆+最长杆＞其余两杆之和 无论固定哪个构件，都为双摇杆机构
例：
例：在铰链四杆机构中，已知l2= 30mm，l3=35mm， l4=50mm，构件AD为机架，试问：
1）若此机构为曲柄摇杆机构，且构件AB为曲柄，求 l1min ；
2）若此机构为双曲柄机构，求l1max ； 3）若此机构为双摇杆机构，求l1的数值
解：由式得 lmax+lmin≤l余1+l余2 1) 若此机构为曲柄摇杆机构，且构件AB为曲柄， 当l4为最长杆时，应满足：
l2+l4≤l1+l3 l1≥l4+l2–l3=50+30-35=45mm 当l1为最长杆时，应满足： l1+l2≤l3+l4 l1≤l3+l4–l2=50+35–30=55mm ∴45mm≤l1≤55mm时，该机构为曲柄摇杆机构。 Lmin=45mm。
传动角g ——压力角的余角。
所以，压力角越小、传动角越大，机构的传力性能越 好，传动效率越高。
一般机械：
aa g g m a5 x;0m in 40
大功率机械：
aa g g m a4 x;0m in 50
三、死点位置
对曲柄摇杆机构，当摇杆为主动件时，从动件曲柄与 连杆在一条线上时，会出现死点。此时曲柄不转动。

工程应用前景
分析优化后机构在工程应用中的前景，为实 际应用提供指导。
05
平面连杆机构的未来发展
新材料的应用
轻质材料
01
采用轻质材料如碳纤维、玻璃纤维等，降低机构重量，提高运
动性能。
高强度材料
02
选用高强度材料如钛合金、超高强度钢等，提高机构承载能力
。
复合材料
03
利用复合材料的各向异性特点，优化机构性能，实现多功能化
遗传算法
利用遗传算法对平面连杆机构进行优化，通 过不断迭代和选择，寻找最优解。
约束处理
在优化过程中，需要特别注意处理各种约束 条件，如几何约束、运动约束等。
优化实例
曲柄摇杆机构优化
以曲柄摇杆机构为例，通过优化算法找到最优 的设计参数，使得机构的运动性能达到最佳。
双曲柄机构优化
对双曲柄机构进行优化，改善机构的运动平稳 性和精度。
平面连杆机构系列优化
对一系列平面连杆机构进行优化，比较不同机构的性能特点，为实际应用提供 参考。
优化效果评估
性能指标
通过性能指标来评估优化效果，如运动精度 、运动范围、刚度等。
经济性评估
评估优化后机构的经济效益，包括制造成本 、运行成本等。
实验验证
通过实验验证优化的有效性，对比优化前后 的性能差异。
。
新工艺的探索
精密铸造
通过精密铸造技术，提高 零件的精度和表面质量， 减少加工余量。
激光切割
利用激光切割技术，实现 零件的高精度、高效率加 工。
3D打印
利用3D打印技术，快速制 造复杂结构零件，缩短产 品研发周期。
新技术的应用
智能控制
有限元分析
引入智能控制技术，实现机构的高精 度、高效率运动控制。

-4
-6
a (ms2)
80
40
0 -40
60º120º180º240º300º360º
-80
-120
(三) 实现轨迹运动
搅拌机机构 曲柄摇杆机构
摄影机抓片机构 曲柄摇杆机构
鹤式起重机 双摇杆机构
契贝谢夫四足步行机构 多杆机构
Multi-bar linkage
(四) 导引刚体实现一定的位置姿态要求
连杆机构中，常用传动角的大小及变化情况来衡量机 构传力性能的优劣。
传动角出现极值的位置及计算
传动角总取锐角
C2
2 b
C1
1 c
B2
Aa
D
B1 d

min为1和2中的较小值者。
为保证机构具有良好的传力性能，设计时通常min 40º
；高速和大功率传动机械，min 50º。
雷达天线俯仰机构 曲柄摇杆机构
颚式破碎机 曲柄摇杆机构
3. 往复运动→转动
往复摆动转换为转 动 缝纫机踏板机构
往复移动转换为转 动
内燃机曲柄滑块机构
4. 摆动→摆动
电风扇摇头机构 双摇杆机构
汽车转向机构 双摇杆机构
(二) 实现运动规律的变换与运动函数的再现 机构中任意两构件的位置、速度和加速度存在着一一对 应的函数关系。
应用举例：鹤式起重机
平面连杆机构的类型
特例：等腰梯形机构—— 汽车转向机构
平面连杆机构
四杆机构
铰链四杆机构
曲柄摇杆机构 双曲柄机构 双摇杆机构
2.1.2 平面四杆机构的演化型式 (1) 将转动副演化成移动副
平面连杆机构的类型
曲柄摇杆机构
偏心曲柄滑块机构↓ ∞