高一数学函数的表示法

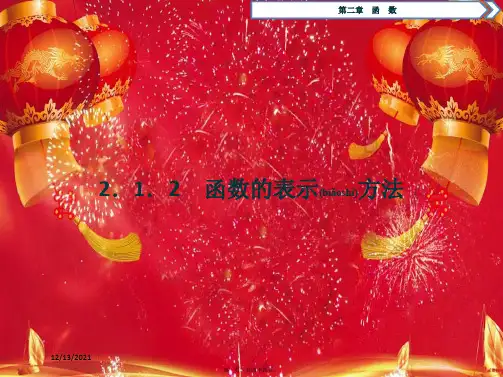
函数的表示方法(一)1、列表法：通过列出自变量与对应的函数值的表来表达函数关系的方法叫列表法2、图像法：如果图形F 是函数)(x f y =的图像，则图像上的任意点的坐标满足函数的关系式，反之满足函数关系的点都在图像上.这种由图形表示函数的方法叫做图像法.3、如果在函数)(x f y =)(A x ∈中，)(x f 是用代数式来表达的，这种方法叫做解析法4、讨论分别用a x -，a y -分别替换函数)(x f y =中的x ，y 以后函数的图像会发生哪些变化？5、讨论分别用x -，y -分别替换函数)(x f y =中的x ，y 以后函数的图像会发生哪些变化？6、讨论分别用ax ，by 分别替换函数)(x f y =中的x ，y 以后函数的图像会发生哪些变化？7、讨论分别用||x ，|)(|x f 分别替换函数)(x f y =中的x ，)(x f 以后函数的图像会发生哪些变化？8、试作出下列函数的图像： （1）43-+=x x y （2）11-=x y11、若)3()3(x f x f +=-，那么函数)(x f 的图像有何性质？ 12、)3(x f y -=与)3(x f +的图像之间有何关系函数的表示方法(二)1．例题：例1．（1）已知一次函数()f x 满足(0)5f =，图象过点(2,1)-，求()f x ；（2）已知二次函数()h x 与x 轴的两交点为(2,0)-，(3,0)，且(0)3h =-，求()h x ； （3）已知二次函数()F x ，其图象的顶点是(1,2)-，且经过原点，()F x ．例2．（1）已知2()43f x x x =-+，(1)f x +； （2）已知2(1)2f x x x +=-，求()f x ．例3．函数在闭区间[1,2]-例4．某人开汽车以60/km h 的速度从A 地到150km 远处的B 地，在B 地停留1h 后，再以50/km h 的速度返回A 地，把汽车离开A 地的路程()x km 表示为时间()t h （从A 地出发是开始）的函数，并画出函数的图象；再把车速v /km h 表示为时间()t h 的函数，并画出函数的图象．例5．已知一个函数的解析式为22y x x =-，它的值域为[1,3]-，这样的函数有多少个？试写出其中两个函数．2．练习：（1）练习：（1）已知2(3)21f x x =-，求()f x ； （答案：22()19f x x =-）（2）已知2211()1f x x xx-=++，求()f x ．（答案：2()3f x x =+）3．小结：1．已知函数类型，求函数解析式，常用待定系数法；它的基本步骤是：设出函数的一般式（或顶点式等），代入已知条件，通过解方程（组）确定未知系数； 2．已知()f x 的解析式，求[()]f g x 时，把x 用()g x 代替；已知[()]f g x 的解析式，求()f x 时，常用配凑法或换元法；3．在解决实际问题时，求出函数解析式后，一定要写出定义域。

疱丁巧解牛知识·巧学·升华 一、函数的表示方法表示函数常用的三种方法是解析法、图象法、列表法 . 1.解析法（公式法）用数学表达式表示两个变量之间的对应关系，这个表达式叫做函数的解析表达式，这种表达函数的方法叫做解析法.如y=2x-1，y=x 2-2x-3，y=12-+x x 等. 解析法的优点在于：一是从“数”的方面简明、全面地概括了变量间的数量关系；二是可以通过解析式求出任意一个自变量的值所对应的函数值.解析法是表示函数的一种最重要的方法.但并不是所有的函数都能用解析法去表示. 2.图象法通过函数图象表示两个变量之间的关系的方法.图象法的优点是能够直观形象地表示自变量的变化，相应的函数值的变化趋势也一目了然.可以通过图象来研究函数的某些性质，它从“形”的方面刻画了函数关系.函数的图象不一定是一条连续的曲线，也可以由一些孤立的点、线段等图形构成. 3.列表法通过列出自变量与对应函数值来表达函数关系的方法叫做列表法.例如，火车站的列车时刻表，银行发行的利率表，工厂中每月的产值及利润报表，甚至我们历次考试的成绩一览表等.又例如，新中国成立后共进行了五次人口普查，各次普查得到的人口数据如下表所示.这张表清楚地表达了年份与当年我国总人口（单位：亿）的函数值域为{5.9，6.9，10.1，11.0，12.1}.利用列表法表示的函数也可解决相应的数学问题.列表法也是表示函数的一种方法，它常适合于定义域是有限集的函数，列表时要注意自变量与函数值应对应，所列图表是否是函数的唯一依据仍然是函数的定义. 列表法是表示函数的一种方法，此法的优点是不需计算就可以直接看出与自变量的值相对应的函数值. 二、分段函数 函数⎩⎨⎧>-<<-11,44,110,622x x x 的表达式是分段表示的，即函数与自变量的关系不是只满足一个式子，而是在不同范围内有不同的对应关系，这样的函数关系是分段函数.分段函数是一个函数而不是几个函数.如教材中例5、例6所体现变量之间的函数关系都是分段函数. 分段函数的定义域应为各段上自变量取值的并集，这一点与函数y=x x ++-11的定义域的求法不相同，如函数y=⎪⎩⎪⎨⎧≥<<1,,10,1x x x x的定义域为{x|0＜x ＜1}∪{x|x ≥1}={x|x ＞0}.作分段函数的图象时，特别注意接点处点的虚实，如函数y=⎪⎩⎪⎨⎧<-=>0,1,0,0,0,1x x x 的图象为（见右上图）：分段函数的表示法是解析法的一种形式.函数y=⎩⎨⎧≥-<<-11,44,110,622x x x 不能写成y=22-6x ，0＜x ＜11或y=-44，x ≥11.要点提示 注意此处空半格注意写分段函数定义域时，区间端点应不重不漏.理解分段函数是一种函数，而不是几个函数. 三、函数的图象对于函数y=f （x ）（x ∈A ），定义域内每一个x 值都有唯一的y 值与它对应，把这两个对应的数构成的有序实数对（x ，y ）作为点P 的坐标，记作P （x ，y ），则所有这些点的集合F 叫做函数y=f （x ）的图象. 1.作函数图象的基本步骤 （1）先求函数定义域；（2）化简函数解析式；（3）列表；（4）描点；（5）连线.作图时，应注意抓住函数的特征，如抓住定义域的分界值，图象上的特征点（与x 轴、y 轴的交点等），图象随x 增大的趋势等来辅助作图. 2.带绝对值号的简单函数的图象作该类函数图象的基本方法是：先求函数的定义域，然后化简函数解析式，就是去绝对值号.（1）带一个绝对值号的函数，根据绝对值的意义去绝对值号，如 y=|x-1|=⎩⎨⎧<--≥-.1,1,1,1x x x x（2）带两个或两个以上绝对值号的问题，常用“零点分段法”去绝对值号，从而把函数写成分段函数的形式，然后作图. 如作函数y=|x-1|+|x+2|的简图.令x-1=0，得x=1；令x+2=0，得x=-2.∴-2和1把数轴分成三部分.当x ≤-2时，y=-2x-1；当-2＜x ＜1时，y=3； 当x ＞1时，y=2x+1.所以，⎪⎩⎪⎨⎧>+<<--≤--1,12,12,3,2,12x x x x x 的图象如右图.要点提示 注意此处空半格(1)绝对值的意义：|a|=⎪⎩⎪⎨⎧<-=>.0,,0,0,0,a a a a a (2)所谓“零点”是指令每一个绝对值分别等于0，求得相应的x 值. (3)可借助函数的图象分析这个函数的性质，例如这个函数的最小值为3. 四、映射一般地，我们有：设A 、B 是两个非空的集合，如果按某一个确定的对应关系f ，使对于集合A 中的任意一个元素x ，在集合B 中都有唯一确定的元素y 与之对应，那么就称对应f ：A →B 为从集合A 到集合B 的一个映射.由映射的定义可知，上图中（1）（3）两个对应是集合A 到集合B 的映射;（2）不是集合A 到集合B 的映射，因为A 中元素a 在B 中有两个元素e 、g 与之对应，不符合定义中“唯一性”的要求;（4）也不是A 到B 的映射，因为集合A 中的元素b 在集合B 中没有元素与之对应.对于映射f ：A →B 来说，与集合A 中的元素x 对应的集合B 中的元素y 叫做x 的象，x 叫做y 的原象.那么，怎样由对应法则找到它的象与原象呢？对于A 到B 的映射而言，集合A 中的每一个元素在集合B 中都有唯一元素与之对应，集合A 中不同的元素在集合B 中可以对应相同的元素，集合B 中的元素可以在A 中有一个或多个元素与之对应，也可无元素与之对应.要点提示 注意此处空半格(1)映射是特殊的对应，对应是两个集合元素之间的一种关系，对应关系可用图示的方法或文字描述等来表示. (2)常选择椭圆内加上元素直观体现f 下元素的对应关系.(3)集合A 到B 的映射，A 、B 必须是非空集合（可以是数集，也可以是其他集合）. (4)对应关系有“方向性”，即强调从集合A 到集合B 的对应，它与从集合B 到集合A 的对应关系一般是不同的.(5)A 中元素的象是集合B 的子集. 问题·思路·探究问题 表示函数常用的解析法、列表法、图象法三种方法的优缺点是什么? 思路:考虑三种方法的含义,可通过举例比较.探究: (1)用解析式表示函数关系的优点是：函数关系清楚，容易从自变量的值求出其对应的函数值，便于用解析式来研究函数的性质.中学里研究的函数主要是用解析式表示的函数.缺点是:有些函数很难用解析式表示.(2)用列表法表示函数关系的优点是：不必通过计算就知道当自变量取某些值时函数的对应值.缺点是:函数解析式的体现有时不明显.(3)用图象法表示函数关系的优点是：能直观形象地表示出函数的变化情况.更能体现数形结合的思想.缺点是:变量的值依赖于图象的精度.不利于精确计算. 典题·热题·新题例1 将长为a 的铁丝折成矩形，求此矩形面积y 关于一边长x 的函数关系式，并求定义域和值域，作出函数的图象.思路解析：解此题的关键是先把实际问题转化成数学问题，即把面积y 表示为x 的函数，用数学的方法解决，再回到实际中去. 解：设矩形一边长为x ，则另一边长为21（a-2x ），面积为y=21（a-2x ）·x=-x 2+21ax.又⎩⎨⎧>->,02,0x a x 得0＜x ＜2a .由于y=-（x-4a ）2+161a 2≤161a 2， 故函数的解析式为y=-x 2+21ax ，定义域为（0，2a ），值域为（0，161a 2）.图象如右图所示.深化升华 注意此处空半格解析式是用自变量的多项式来表示因变量的，函数解析式由定义域和对应法则确定，因此，求解析式的关键是明确对应法则，选好自变量.解决此类问题的关键是首先建立目标函数，确定函数的定义域.若是实际问题，除了考虑函数解析式自身的限制条件外，还要考虑到它的实际意义.例 2 据报道，我国目前已成为世界上受荒漠化危害最严重的国家之一，左下图表示我国土地沙化总面积在上个世纪五六十年代、七八十年代、九十年代的变化情况，由图中的相关信息，可将上述有关年代中我国年平均土地沙化面积在右下图中示为_____________.思路解析：本题涉及的数学点只是平均数，事实上，图形上的数据是连续的，而连续的数据的平均数在中学里未学过，要求我们在新情景下获取相关图表中的信息和进行数形转换. 解：分别计算出1950年到1970年，1970年到1990年及1990年到2000年的平均值，只需对两个端点的数据进行计算即可.考虑单位后，则平均值分别为16，21.25，并在上图中表示.如右图：深化升华 注意此处空半格用图象法表示一个函数是数形结合的基础.判断一个图形是不是函数图象的依据仍旧是函数的定义.函数图象的形状与定义域、对应法则有关.定义域确定变量的分布范围，对应法则确定形状.如何从图象中提取有用的信息，把“形”转化成“数”是解决问题的关键. 例3 （经典回放）《中华人民共和国个人所得税法》规定，公民全月工资、薪金所得不超过800元的部分不必纳税，超过800元的部分为全月应纳税所得额，此项税款按下表分段累加进行计算：某人一月份应交纳此税款26.78元，则他的当月工资、薪金所得介于（ ） A.800—900元 B.900—1 200元 C.1 200—1 500元 D.1 500—2 800元思路解析：本题是一道适用列表法表示函数关系的题目，解决此题首先要理解题意，能计算出相应工资的税款的算法，列出分段函数，找到函数值26.78所在的某段函数，求出自变量.本题作为选择题，亦可采用估算法求解. 解法一：（估算法）依题意知，当工人工资为1 300元时，应交税金（1 300-800）×5%=25（元），而该工人实际交税金26.78元＞25元，知其工资应超过1 300元.又26.78-25=1.78元，知该工资仅比1 300元多一点，但不会超过1 500元，从而可估算选C. 解法二：（列出分段函数）依题意知，应交税金y 与实际工资x 的函数关系式为y=⎪⎩⎪⎨⎧≤<⨯-+⨯≤<⨯-≤<28001300%,15)1300(%5500,1300800%,5)800(,8000,0x x x x x =⎪⎩⎪⎨⎧≤<-≤<-≤<28001300,1051.0,1300800,4005.0,8000,0x x x x x 即当y=26.78时，有26.78=0.1x-105.∴x=1 317.8元. 答案：C误区警示 注意此处空半格本题中实际问题的数学模型是分段函数，它的对应法则在不同的区间内可能不同，要注意找好不同区间内的解析式.从作出的图象看，它是一个阶梯函数.例4 已知 f （x ）=⎪⎩⎪⎨⎧<=>,0,0,0,1,0,2x x x x (1)画出函数的图象；(2)根据已知条件分别求f(1)、f(-4)、f[f(-4)]和f[f[f(-4)]]的值.思路解析：题设中给出的函数是分段函数，注意在不同的区间应用不同的关系式.本题中的关系式都是常见的初等函数的关系式，因而可以利用常见函数的图象知识来作图. 解：(1)函数的图象如右图所示：（2）f(1)=12=1； f(-4)=0；f[f(-4)]=f(0)=1； f[f[f(-4)]]=f(1)=12=1.例5 作出下列各函数的图象： （1）y=1-x ，x ∈Z ；（2）y=2x 2-4x-3，0≤x ＜3； （3）y=|1-x|；（4）y=⎩⎨⎧<≤-+≤≤.01,1,10,2x x x x思路解析：（1）定义域为Z ，所以图象为离散的点.（2）定义域不是R ，因此图象不是完整的抛物线，而是从上面截取的一部分.（3）先根据绝对值的定义去掉绝对值号，写成y=⎩⎨⎧<-≥-.11,11x xx x （4）这个函数图象由两部分组成.当0≤x ≤1时，为抛物线y=x 2的一段；当-1≤x ＜0时，为直线y=x+1上的一段. 答案：深化升华 注意此处空半格作函数图象，首先要明确函数定义域，其次明确函数图象是点、线段或直线，体会定义域对图象的控制作用.处理好端点处或x=0时的情况.作图时，先不受定义域限制作出完整图象，然后再截取.例6 设f ：A →B 是A 到B 的一个映射，其中A=B={（x ，y ）|x ，y ∈R }，f ：（x ，y ）→（x-y ，x+y ），求A 中元素（-1，2）的象和B 中元素（-1，2）的原象.思路解析：这是一个映射的问题，由已知（x ，y ）的象为（x-y ，x+y ），即确定了对应法则. 解：先求A 中元素（-1，2）的象.令x=-1，y=2，由题意得x-y=-1-2=-3， x+y=-1+2=1，所以（-1，2）的象为（-3，1）；再求B 中元素（-1，2）的原象.令⎩⎨⎧=+-=-,2,1y x y x 解得⎪⎪⎩⎪⎪⎨⎧==.23,21y x所以（-1，2）的原象是（21，23）. 深化升华 注意此处空半格映射是一种特殊的对应，函数是一种特殊的映射. 例7 下列对应是A 到B 的映射的是（ ） A.A=N *，B=N *，f ：x →|x-3|B.A=N *，B={-1，1，-2}，f ：x →（-1）x xC.A=Z ，B=Q ，f ：x →x3 D.A=N *，B=R ，f ：x →x 的平方根思路解析：判定一个对应是否是映射，关键是看是否符合映射的定义，若要判定不是映射只要举一反例即可.对于A ，由于A 中元素3在法则f 作用下其与3的差的绝对值，在B 中找不到元素与之对应.对于B ，对任意的正整数x ，所得（-1）x 均为1或-1；都在集合B 中有唯一的1或-1与之对应，符合映射定义.对于C ，0在f 下无意义.对于D ，对正整数，在实数集R 中有两个平方根与之对应，不满足映射概念，所以该对应不是映射. 答案：B。

高一数学必修1 函数的三种表示法介绍
教学目的
知识与技能
掌握函数的三种表示法：列表法、图像法、解析法，体会三种表示法的特点。

过程与方法
（1）能根据实际问题情境选择恰当方法表示一个函数以获取有用信息，培养学生的灵活运用知识的能力。

（2）初步体会运用函数知识解决实际问题地方法。

（3）体会数形结合思想在理解函数概念中的重要作用，在图形的变化中感受直观美。

情感、态度与价值观
培养学生重要数学思想方法——数形结合，分类讨论
重点难点
重点：函数的三种表示及恰当选择一个函数表示实际问题。

难点：恰当选择一个函数表示实际问题。

教法学法：探讨研究
教学用具：多媒体
教学过程
板书设计
教学反思。

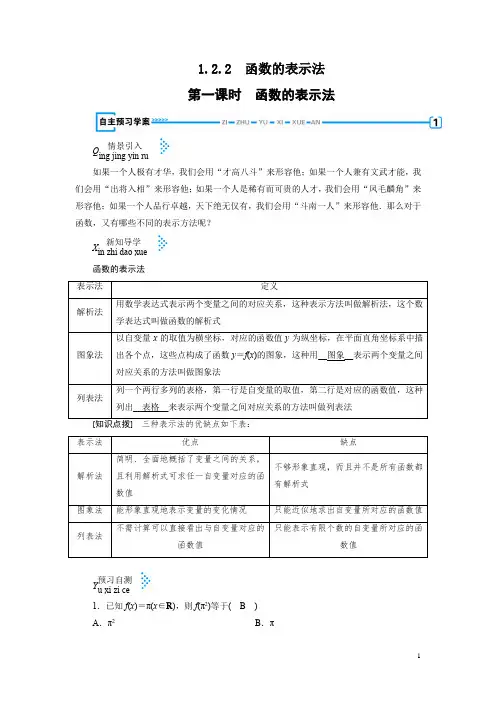
1.2.2 函数的表示法第一课时函数的表示法Q 情景引入ing jing yin ru如果一个人极有才华，我们会用“才高八斗”来形容他；如果一个人兼有文武才能，我们会用“出将入相”来形容他；如果一个人是稀有而可贵的人才，我们会用“凤毛麟角”来形容他；如果一个人品行卓越，天下绝无仅有，我们会用“斗南一人”来形容他．那么对于函数，又有哪些不同的表示方法呢？X 新知导学in zhi dao xue 函数的表示法Y 预习自测u xi zi ce1．已知f(x)＝π(x∈R)，则f(π2)等于(B) A．π2B．πC．πD．不确定[解析]因为π2∈R，所以f(π2)＝π.2．某同学在一学期的5次大型考试中的数学成绩(总分120分)如下表所示：A．成绩y不是考试次数x的函数B．成绩y是考试次数x的函数C．考试次数x是成绩y的函数D．成绩y不一定是考试次数x的函数[解析]把考试次数组成的集合看作A＝{1,2,3,4,5}，成绩组成的集合看作B＝{90,102,105,106}，∴集合A中的任一个数在集合B中有唯一一个数与之对应，∴成绩y是考试次数x的函数．3．已知函数y＝f(x)的图象如图，则f(x)的定义域是(C)A．(－∞，1)∪(1，＋∞)B．RC．(－∞，0)∪(0，＋∞)D．(－1,0)[解析]由图象，知x≠0，即x∈(－∞，0)∪(0，＋∞)．4．如图，函数f(x)的图象是曲线OAB，其中点O，A，B的坐标分别为(0,0)，(1,2)，(3,1)，则f[f(3)]的值等于__2__.[解析]据图象，知f(3)＝1，所以f[f(3)]＝f(1)＝2.H 互动探究解疑u dong tan jiu jie yi命题方向1 ⇨函数的三种表示方法典例1 某商场新进了10台彩电，每台售价3 000元，试求售出台数x 与收款数y 之间的函数关系，分别用列表法、图象法、解析法表示出来．[思路分析] 函数的定义域是{1,2,3，…，10}，值域是{3 000，6 000,9 000，…，30 000}，可直接列表、画图表示．分析题意得到表达y 与x 关系的解析式，注意定义域．[解析] (1)列表法：(3)解析法：y ＝3 000x ，x ∈{1,2,3，…，10}．『规律方法』 列表法、图象法和解析法是从三个不同的角度刻画自变量与函数值的对应关系，同一个函数可以用不同的方法表示．在应用三种方法表示函数时要注意：(1)解析法：必须注明函数的定义域；(2)列表法：选取的自变量要有代表性，应能反映定义域的特征； (3)图象法：是否连线． 〔跟踪练习1〕将一条长为10 cm 的铁丝剪成两段，并以每一段铁丝的长度为周长各做一个正方形．试用多种方法表示两个正方形的面积之和S 与其中一段铁丝长x 的函数关系．(x 属于正整数集)[解析] (1)解析法：S ＝(x4)2＋(10－x 4)2.将上式整理得S ＝18x 2－54x ＋254，x ∈{x |1≤x <10，x ∈N *}．(2)列表法：命题方向2 ⇨与函数图象有关的问题典例2 作出下列函数的图象并求出其值域．(1)y ＝2x ＋1，x ∈[0,2]；(2)y ＝2x ，x ∈[2，＋∞)；(3)y ＝x 2＋2x ，x ∈[－2,2]．[思路分析] (1)画函数的图象时首先要注意的是什么？ (2)所给三个函数的大致图象分别是什么形式的？ [解析] (1)列表：当x ∈[0,2][1,5]．(2)列表当x ∈[2，＋∞)，图象是反比例函数y ＝2x的一部分，观察图象可知其值域为(0,1]．(3)列表由图可得函数的值域是[－1,8]．『规律方法』 (1)常见函数图象的特征： ①一次函数y ＝kx ＋b (k ≠0)是一条直线； ②y ＝kx (k ≠0)是与坐标轴无限接近的双曲线；③y ＝ax 2＋bx ＋c (a ≠0)是顶点为(－b 2a ，4ac －b 24a )，对称轴为x ＝－b 2a的抛物线． (2)作函数图象时应注意以下几点： ①在定义域内作图；②图象是实线或实点，定义域外的部分有时可用虚线来衬托整个图象；③要标出某些关键点，例如图象的顶点、端点与坐标轴的交点等．要分清这些关键点是实心点还是空心点．〔跟踪练习2〕作出下列函数的图象，并指出其值域． (1)y ＝x 2＋x (－1≤x ≤1)； (2)y ＝2x(－2≤x ≤1，且x ≠0)．[解析] (1)用描点法可以作出函数的图象如图． 由图可知y ＝x 2＋x (－1≤x ≤1)的值域为[－14，2]．(2)用描点法可以作出函数的图象如图．由图可知y ＝2x (－2≤x ≤1，且x ≠0)的值域为(－∞，－1]∪[2，＋∞)．Y 易混易错警示i hun yi cuo jing shi换元求解析式时忽略自变量的取值范围致误典例3 已知f (x －1)＝3－x ，求f (x )的解析式．[错解] 令x －1＝t ，则x ＝t 2＋1，所以f (t )＝3－(t 2＋1)＝2－t 2，即有f (x )＝2－x 2.[错因分析] 本例的错误是由于忽视了已知条件中“f ”作用的对象“x －1”是有范围限制的．利用换元法求函数的解析式时，一定要注意换元后新元的限制条件．[正解] 令x －1＝t ，则t ≥0，且x ＝t 2＋1，所以f (t )＝3－(t 2＋1)＝2－t 2(t ≥0)，即f (x )＝2－x 2(x ≥0)．[警示] 利用换元法求函数解析式时，一定要注意保持换元前后自变量的范围不变． X 学科核心素养ue ke he xin su yang 求函数解析式的常用方法1．待定系数法已知函数类型(如一次、二次、正比例、反比例函数等)，可先设出函数解析式，再依据所给条件，确定待定系数．典例4 已知f (x )为二次函数，其图象的顶点坐标为(1,3)，且过原点，求f (x )的解析式．[思路分析] 已知二次函数f (x )的顶点坐标，可设顶点(配方)式，再利用其他条件确定待定系数．[解析] 由于函数图象的顶点坐标为(1,3)，则设f (x )＝a (x －1)2＋3(a ≠0)． ∵函数图象过原点(0,0)，∴a ＋3＝0，∴a ＝－3. 故f (x )＝－3(x －1)2＋3. 即f (x )＝－3x 2＋6x .『规律方法』 (1)一次函数可设为y ＝kx ＋b (k ≠0)，正比例函数可设为y ＝kx (k ≠0)；反比例函数可设为y ＝kx (k ≠0)；已知二次函数f (x )的顶点或对称轴、最值时，可设顶点式f (x )＝a (x ＋m )2＋n ；已知二次函数与x 轴两交点坐标时，常设分解(标根)式f (x )＝a (x －x 1)(x －x 2)．已知f (x )的图象过某三点时，常设一般式f (x )＝ax 2＋bx ＋c ；(2)凡是已知函数(或方程、不等式等)的形式时，常用待定系数法求解． 2．恒成立的应用一般地，若f (x )与g (x )是同类型的函数(或具有相同的表达式)，f (x )＝g (x )恒成立，则f (x )与g (x )的对应项系数相等．典例5 已知f (x )是一次函数，且满足3f (x ＋1)－2f (x －1)＝2x ＋17，求f (x )．[解析] 由题意可设f (x )＝ax ＋b (a ≠0)，则3f (x ＋1)－2f (x －1)＝3ax ＋3a ＋3b －2ax ＋2a －2b ＝ax ＋b ＋5a ＝2x ＋17，∴⎩⎪⎨⎪⎧a ＝2b ＋5a ＝17，∴a ＝2，b ＝7.∴f (x )＝2x ＋7. 典例6 已知f (x )＋2f (－x )＝x ＋1，求f (x )的解析式．[思路分析] 这是关于x 的一个恒等式，由于x ∈R ，∴对任意x ∈R ，此等式都成立，当x ∈R 时，－x ∈R ，因此上述等式对－x 也成立．用－x 代替原等式中的x ，可构造关于f (x )与f (－x )的方程组求解．[解析] 因为f (x )＋2f (－x )＝x ＋1，对任意x ∈R 都成立，所以用－x 替换x ，得f (－x )＋2f (x )＝－x ＋1，由以上两式可解得f (x )＝－x ＋13.K 课堂达标验收e tang da biao yan shou1．如图，函数f (x )的图象是折线段，其中点A ，B ，C 的坐标分别是(0,4)，(2,0)，(6,4)，则f [f (2)]＝( C )A ．0B ．2C ．4D ．6[解析] 由图象可得f [f (2)]＝f (0)＝4.2．函数y ＝x 2－2x 的定义域为{0,1,2,3}，那么其值域为( A ) A ．{－1,0,3} B ．{0,1,2,3} C ．{y |－1≤y ≤3}D ．{y |0≤y ≤3} [解析] 把x ＝0,1,2,3分别代入y ＝x 2－2x 中得y 的值共三个为－1,0,3，故值域为{－1,0,3}．3．某人开车去某地旅行，先沿直线匀速前行了a km ，到达目的地后游玩了一段时间，又原路返回匀速行驶了b km(b <a )，再折回匀速前进c km ，则此人距起点的距离s 与时间t 的关系示意图正确的是( C )[解析] 注意理解两坐标轴s ，t 的含义，这里s 是指距起点的距离，不是路程的累加，结合题意可知C 符合．故选C ．4．一个面积为100 cm 2的等腰梯形，上底长为x cm ，下底长为上底长的3倍，则它的高y 与x 的函数关系为__y ＝50x(x ＞0)__. [解析] 由梯形的面积公式有100＝(x ＋3x )2·y ，得y ＝50x(x >0)．5．已知函数f (x )＝ax ＋b ，且f (－1)＝－4，f (2)＝5， 求：(1)a ，b 的值；(2)f (0)的值．[解析] (1)由⎩⎨⎧f (－1)＝－4f (2)＝5，得⎩⎪⎨⎪⎧－a ＋b ＝－42a ＋b ＝5，解得a ＝3，b ＝－1.(2)由(1)知f (x )＝3x －1，所以f (0)＝－1.一、选择题1．已知函数f (x )由下表给出，则f (3)等于( C )A ．1 C ．3D ．不存在[解析] ∵2<x ≤4时， f (x )＝3，∴f (3)＝3，故选C ．2．已知y 与x 成反比，且当x ＝2时，y ＝1，则y 关于x 的函数关系式为( C ) A ．y ＝1xB ．y ＝－1xC ．y ＝2xD ．y ＝－2x[解析] 设y ＝k x ，由1＝k2得，k ＝2，因此，y 关于x 的函数关系式为y ＝2x.3．一等腰三角形的周长是20，底边长y 是关于腰长x 的函数，则它的解析式为( D ) A ．y ＝20－2xB ．y ＝20－2x (0＜x ＜10)C ．y ＝20－2x (5≤x ≤10)D ．y ＝20－2x (5＜x ＜10)[解析] 由题意得y ＋2x ＝20，∴y ＝20－2x .又∵2x ＞y ，∴2x ＞20－2x ，即x ＞5.由y ＞0，即20－2x ＞0得x ＜10，∴5＜x ＜10.故选D ．4．若f (x )＝2x ＋3，g (x ＋2)＝f (x )，则g (x )的表达式为( B ) A ．g (x )＝2x ＋1 B ．g (x )＝2x －1 C ．g (x )＝2x －3D ．g (x )＝2x ＋7[解析] ∵g (x ＋2)＝f (x )＝2x ＋3， 令x ＋2＝t ，∴x ＝t －2， ∴g (t )＝2(t －2)＋3＝2t －1， ∴g (x )＝2x －1. 5．观察下表：则f [g (3)－f A ．3 B ．4 C ．－3D ．5[解析] 由题表知，g (3)－f (－1)＝－4－(－1)＝－3， ∴f [g (3)－f (－1)]＝f (－3)＝4.6．若f (1x )＝x1－x ，则当x ≠0，且x ≠1时，f (x )＝( B )A ．1xB ．1x －1C ．11－xD ．1x－1[解析] f (1x )＝x 1－x ＝11x －1∴f (x )＝1x －1，故选B ．二、填空题7．已知函数f (x )是反比例函数，且f (－1)＝2，则f (x )＝__－2x __.[解析] 设f (x )＝kx (k ≠0)，∴f (－1)＝－k ＝2，∴k ＝－2， ∴f (x )＝－2x.8．已知g (x )＝1－2x ，f [g (x )]＝1－x 2x 2(x ≠0)，则f (12)等于__15__.[解析] 令g (x )＝1－2x ＝12，∴x ＝14，∴f (12)＝f [g (14)]＝1－(14)2(14)2＝15.三、解答题9．作出下列函数的图象． (1)y ＝x2＋1，x ∈{1,2,3,4,5}；(2)y ＝2x 2－4x －3(0≤x <3)．[解析] (1)函数y ＝x 2＋1，x ∈{1,2,3,4,5}是由(1，32)，(2,2)，(3，52)，(4,3)，(5，72)五个孤立的点构成，如图．(2)因为0≤x <3，所以这个函数的图象是抛物线y ＝2x 2－4x －3介于0≤x <3之间的一段曲线，且y ＝2x 2－4x －3＝2(x －1)2－5，当x ＝0时，y ＝－3；当x ＝3时，y ＝3，如图所示．10．已知函数f (x )＝xax ＋b (a ，b 为常数，且a ≠0)满足f (2)＝1，且f (x )＝x 有唯一解，求函数y ＝f (x )的解析式和f [f(－3)]的值．[解析] 因为f (2)＝1，所以22a ＋b ＝1，即2a ＋b ＝2，①又因为f (x )＝x 有唯一解，即xax ＋b＝x 有唯一解，所以ax 2＋(b －1)x ＝0有两个相等的实数根，所以Δ＝(b －1)2＝0，即b ＝1.代入①得a ＝12.所以f (x )＝x 12x ＋1＝2xx ＋2，所以f (－3)＝2×(－3)－3＋2＝6，所以f [(f (－3)]＝f (6)＝2×66＋2＝32.。

高一数学函数的表示法知识点导言：函数是数学中的一个重要概念，它描述了不同变量之间的关系。

在高一数学课程中，学生需要掌握函数的表示法知识点，包括函数的定义域、值域、图像等。

本文将从不同角度介绍这些知识点，以帮助读者更好地理解和应用函数的表示法。

一、函数的定义域：函数的定义域是指函数输入值的集合，也就是使函数有意义的取值范围。

在表示法上，常用的方式是用一个或多个不等式来描述定义域。

例如，对于一个简单的一次函数 y = 2x + 3，它的定义域可以表示为 x≥ -∞。

这意味着这个函数在实数集的所有值上都有定义。

但是，并不是所有函数都能在整个实数集上定义。

例如，一个分式函数 f(x) = 1 / (x - 2) 在定义域时需要排除使分母为零的情况，所以它的定义域可以表示为x ≠ 2。

这样，函数就在实数集中的所有值上有定义，除了 x = 2。

在求定义域时，我们还需要考虑根式函数的取值范围。

以一个简单的二次函数y = √x 为例，要使函数有意义，我们需要保证x ≥ 0，所以它的定义域可以表示为x ≥ 0。

二、函数的值域：函数的值域是函数输出值的集合，也叫做函数的取值范围。

在表示法上，我们可以用一个或多个不等式来描述值域。

例如，对于一个简单的一次函数 y = 2x + 3，它的值域可以表示为 y ∈ (-∞, +∞)。

这意味着这个函数在实数集的所有值上都有取值。

对于一个分式函数 f(x) = 1 / (x - 2)，我们可以通过分析分数的性质来确定它的值域。

当 x 趋近于正无穷时，分母接近于正无穷小，所以函数的值趋近于0。

同理，当x 趋近于负无穷时，函数的值也趋近于0。

因此，这个函数的值域可以表示为y ≠ 0。

三、函数的图像：函数的图像是函数在平面直角坐标系中的表示。

它反映了函数输入值和输出值的对应关系，帮助我们更直观地理解函数的性质。

在表示函数图像时，我们通常使用曲线来表示。

对于一个简单的一次函数 y =2x + 3，它的图像是一条直线。

高一数学必修一函数的表示法（完整）1.2函数及其表示§1.2.2函数的表示法1教学目的：1．掌握函数的解析法、列表法、图象法三种主要表示方法．2．培养数形结合、分类讨论的数学思想方法，掌握分段函数的概念教学重点：解析法、图象法．教学难点：作函数图象教学过程：一、复习引入：1．函数的定义是什么？函数的图象的定义是什么？2．在中学数学中，画函数图象的基本方法是什么？3．用描点法画函数图象，怎样避免描点前盲目列表计算？怎样做到描最少的点却能显示出图象的主要特征？二、讲解新课：函数的表示方法表示函数的方法，常用的有解析法、列表法和图象法三种.⑴解析法：就是把两个变量的函数关系，用一个等式表示，这个等式叫做函数的解析表达式，简称解析式.222例如，=60t，A=r，S=2rl,y=a某+b某+c(a0),y=某2(某2)等等都是用解析式表示函数关系的.优点：一是简明、全面地概括了变量间的关系；二是可以通过解析式求出任意一个自变量的值所对应的函数值.中学阶段研究的函数主要是用解析法表示的函数.⑵列表法：就是列出表格来表示两个变量的函数关系.D优点：不需要计算就可以直接看出与自变量的值相对应的函数值.⑶图象法：就是用函数图象表示两个变量之间的关系.C例如，气象台应用自动记录器描绘温度随时间变化的曲线，课本中我国人口出生率变化的曲线，工厂的生产图象，股市走向图等都是用图象法表示函数B关系的.优点：能直观形象地表示出自变量的变化，相应的函数值变化的趋势，这A样使得我们可以通过图象来研究函数的某些性质.三、例题讲解例1某种笔记本每个5元，买某{1,2,3,4}个笔记本的钱数记为y （元），试写出以某为自变量的函数y的解析式，并画出这个函数的图像解：这个函数的定义域集合是{1,2,3,4}，函数的解析式为y=5某，某{1,2,3,4}.它的图象由4个孤立点A(1，5)B(2，10)C(3，15)D(4，20)组成，如图所示例2国内投寄信函（外埠），每封信函不超过20g付邮资80分，超过20g而不超过40g付邮资160分，依次类推，每封某g(0320,某(60,80],400,某(80,100].这个函数的图象是5条线段（不包括左端点），都平行于某轴，如图所示.这一种函数我们把它称为分段函数4003202401608020406080100某某例3画出函数y=|某|=某某0,的图象.某0.解：这个函数的图象是两条射线，分别是第一象限和第二象限的角平分线，如图所示.说明：①再次说明函数图象的多样性；y②从例4和例5看到，有些函数在它的定义域中，对于自变量某的不同取值范围，对应法则不同，这样的函数通常称为分段函数.注意某某0分段函数是一个函数，而不是几个函数.y=1某<0某③注意：并不是每一个函数都能作出它的图象，如狄利克雷{（Dirichlet）函数D(某)=1，某是有理数，.0，某是无理数,我们就作不出它的图象.某例4作出分段函数y某1某2的图像解：根据“零点分段法”去掉绝对值符号，即：y某2(2某1)3y某1某2=2某12某1某1作出图像如下例5作出函数y某列表描点：K'L'M'N'G'O'P'Q'(-5.0，-5.2)(-4.0，-4.3)(-3.0，-3.3)(-2.0，-2.5)(-1.0，-2.0)(-0.4，-3.0)(-0.3，-4.0)(-0.2，-5.0)QPOGNMLK(0.2，5.0)(0.3，4.0)(0.4，3.0)(1.0，2.0)(2.0，2.5)(3.0，3.3)(4.0，4.3)(5.0，5.2)某1的图象某2补充：1．作函数y=|某-2|(某＋1)的图像分析显然直接用已知函数的解析式列表描点有些困难，除去对其函数性质分析外，我们还应想到对已知解析式进行等价变形．解：(1)当某≥2时，即某-2≥0时，1086Q4KLMGNPO2-10-5510-2N'M'L'K'G'O'-4P'Q'-619y(某2)(某1)某2某2(某)224当某＜2时，即某-2＜0时，-10-5864251019y(某2)(某1)某2某2(某)2.24219某2某24∴y219某2某24-2-4-665432这是分段函数，每段函数图象可根据二次函数图象作出-6-4-2124682．作出函数y|某2某3|的函数图像解：y2-1-2-3-4某2某32(某2某3)22某2某302某2某302步骤：（1）作出函数y=某2某3的图象（2）将上述图象某轴下方部分以某轴为对称轴向上翻折（上方部分不变），即得y=|某2某3|的图象23四、课后练习一、选择题1.已知一次函数的图象过点(1,0)和(0,1)，则此一次函数的解析式为()＝－某＝某＋12＝某－1＝－某＋12.已知函数f(某－1)＝某－3，则f(2)的值为()A.－2B.6C.1D.03.已知f(某)＝2，g(某)＝某＋1，则f(g(某))的表达式是()某－12某＋2某某2某＋2某f(1)＝0f(n＋1)＝f(n)＋3，n∈N2某2某－11某－1224.已知函数y＝某，则f(3)等于()D.二、填空题5.已知函数f(某)的图象如图所示，则此函数的定义域是，值域是.6.已知f(某)与g(某)分别由下表给出某f(某)14233241某g(某)13213442那么f(g(3))＝.4三、解答题7.解答下列问题：2(1)若f(某＋1)＝2某＋1，求f(某)；某(2)若函数f(某)＝，f(2)＝1，又方程f(某)＝某有唯一解，求f(某).a某＋b8.作下列各函数的图象：(1)y＝2某2－4某－3(0≤某＜3)；9.已知函数2某，(某≤－1)f(某)＝1，(－1＜某≤1)－2某，(某＞1)(1)求f(某)的定义域、值域；.＝|某－1|；作出这个函数的图象.5(2)y(2)课后作业参考答案一、选择题1.112.B3.A[f(g(某))＝＝2.]4.f(2)＝f(1＋1)＝f(1)＋3＝0＋3＝3，2(某＋1)－1某＋2某∴f(3)＝f(2＋1)＝f(2)＋3＝3＋3＝6.选二、填空题5.［-3,3］［-2,2］6.【答案】1由表可得g(3)＝4，∴f(g(3))＝f(4)＝1.三、解答题7.【解析】(1)令t＝某＋1，则某＝t－1，∴f(t)＝2(t－1)＋1＝2t －4t＋3.∴f(某)＝2某－4某＋3.2(2)由f(2)＝1得＝1，即2a＋b＝2；2a＋b某11－b由f(某)＝某得＝某变形得某(－1)＝0，解此方程得：某＝0或某＝.又因为方程有唯a某＋ba某＋ba1－b1一解，所以＝0，解得b＝1，代入2a＋b＝2得a＝，a22某所以所求解析式为f(某)＝.某＋28.【解析】(1)∵0≤某＜3，∴这个函数的图象是抛物线2y＝2某－4某－3介于0≤某＜3之间的一段弧(如图(1)).某－1某≥1(2)所给函数可写成分段函数y＝1－某某＜1222是端点为(1,0)的两条射线(如图(2)).9.【解析】(1)f(某)的定义域为{某|某≤－1}∪{某|－1＜某≤1}∪{某|某＞1}＝{某|某≤－1或－1＜某≤1或某＞1}＝R，f(某)的值域为{y|y≤－2}∪{1}∪{y|y＜－2}＝{y|y≤－2或y＝1}，∴f(某)的定义域为R，值域为{y|y≤－2或y＝1}.(2)根据解析式分段作图如图6。

高一数学函数的表示法（一）（一）函数的三种表示方法：1、解析法：就是用数学表达式表示两个变量之间的对应关系 优点：简明扼要；给自变量求函数值。

图象法：就是用图象表示两个变量之间的对应关系，如1.2.1的实例（2）； 优点：直观形象，反映两个变量的变化趋势。

2、列表法：就是列出表格来表示两个变量之间的对应关系，如1.2.1的实例（3）； 优点：不需计算就可看出函数值，如股市走势图； 列车时刻表；银行利率表等。

例1．某种笔记本的单价是2元，买x (x ∈{1，2，3，4，5})个笔记本需要y 元．试用三种表示法表示函数y=f(x) ．例2：下表是某校高一（1）班三位同学高一六次数学测试成绩及班级平均分表：（二）分段函数的定义：在函数的定义域内，对于自变量x 的不同取值范围，有着不同的对应法则，这样的函数通常叫做分段函数。

说明：（1）．分段函数是一个函数而不是几个函数，处理分段函数问题时，首先要确定自变量的数值属于哪个区间段，从而选取相应的对应法则；画分段函数图象时，应根据不同定义域上的不同解析式分别作出；（2）．分段函数只是一个函数，只不过x 的取值范围不同时，对应法则不相同。

例3：某市出租车：（1）5公里内（含5公里），票价2元；（2）5公里以上，每增加5公里，票价增加1元（不足5公里的俺公里计算）。

如果某条线路的总里程为20公里，请根据题意，写出票价与里程之间的函数解析式，并画出函数的图象。

例4．已知f(x)＝⎩⎨⎧+∞∈+-∞∈+),0[,12)0,(,322x x x x ，求f(0)、f[f(-1)]的值（三）课堂练习：1．作业本每本0.3元，买x 个作业本的钱数y （元）。

试用三种方法表示此实例中的函数。

2．某水果批发店，100kg 内单价1元／kg ，500kg 内、100kg 及以上0.8元／kg ，500kg 及第一次 第二次 第三次 第四次 第五次 第六次 甲 98 87 91 92 88 95 乙 90 76 88 75 86 80 丙 68 65 73 72 75 82 班平均分88．278．385．480．375．782．6以上0.6元／kg 。