分数除法的意义和整数除以分数练习题
- 格式:doc
- 大小:96.00 KB
- 文档页数:2

六年级上册的分数除法主要涉及以下几个知识点:
1. 分数的除法概念:理解分数除法的意义和定义,即将一个分数(被除数)平均分成几等份,每份是多少(除数),求解每份的结果(商)。
2. 整数除以分数:将整数除以分数的情况转化为乘法,并进行简化计算。
例如,计算4 ÷1/2,可以转化为4 × 2 = 8的形式。
3. 分数除以整数:将分数除以整数的情况转化为乘法,并进行简化计算。
例如,计算3/4 ÷2,可以转化为3/4 ×1/2 = 3/8的形式。
4. 分数除以分数:将分数除以分数的情况转化为乘法,并进行简化计算。
需要注意分子与分子相乘,分母与分母相乘。
例如,计算2/3 ÷1/4,可以转化为2/3 ×4/1 = 8/3的形式。
5. 分数除法的混合运算:在分数除法的题目中,可能会涉及到加减乘除的混合运算。
需要按照运算的优先级进行计算,或者使用括号来改变运算顺序。
在学习分数除法时,建议学生掌握分数的基本概念和运算规则,
理解除法的概念和意义。
同时进行大量的练习,熟练掌握各种情况下的计算方法和技巧。
通过实际问题的应用,培养学生解决实际问题的能力。

4÷2
5 克,得出三道分数乘、除法算式。
×3=(千克)÷3=(千克)÷3=3(盒)
(4)通过整数题组和分数题组的对照,小组讨论后得出:分数除法的意义与整数除法相同,都是已知两个因数的积与其中一个因数,求另个一个因数。
都是乘法的逆运算。
2、巩固分数除法意义的练习:P28“做一做”
3、学习例
(1)拿出课前准备好的纸,小组讨论操作,如何把这张纸的平均分成2份,并通过操作得出每份是这张纸的几分之几。
(2)小组汇报操作过程,得出:将一张纸的平均分成2份,每份是这张纸的。
(3)数形结合,对照不同的折法,说出两
种不同的计算方法。
A 、÷2=,每份就是2个。
B 、÷2=×=,每份就是的。
1011031031011035
4545
254525
154542152542
1。


人教版六上3.2分数整数除以分数课课练一.填空题1.甲数是24,乙数是甲数的,乙数是;甲数是24,相当于乙数的,乙数是.2.1÷的意义是.3.若a×=b÷=c(a,b,c均不为0),则a、b、c中最大的数是.4.++++=×.×==÷==.5.34里面有个,吨的是24吨.二.选择题6.五(1)班男生人数占全班人数的,女生人数就相当于男生人数的()A.B.C.1D.7.已知:a×=b×1=c÷,且a、b、c中最大的数是()A.a B.b C.c8.一个数的是,求这个数的算式是.()A.×B.÷C.÷D.×9.如果a是一个大于1的任意自然数,那么下面各式中得数最大的是()A.B.C.10.一个数(0除外)除以,这个数就()A.扩大到原来的3倍B.缩小到原来的倍C.无法判断三.判断题11.A和B都是自然数,如果A÷=B×,那么A>B.()12.整数除以分数可以转化为乘这个分数的倒数.()13.18除以,可以表示为,已知一个数的是18,求这个数()14.一个数除以,就是把这个数扩大8倍.()15.一个不等于0的数除以真分数,商一定比这个数大.()四.解答题16.直接写得数===========17.填得数18.先算一算,再观察发现规律÷=÷=0÷=÷5=0÷=÷3=(1)计算上面各题.(2)仔细观察,再比较商与被除数的大小,你发现了:.。
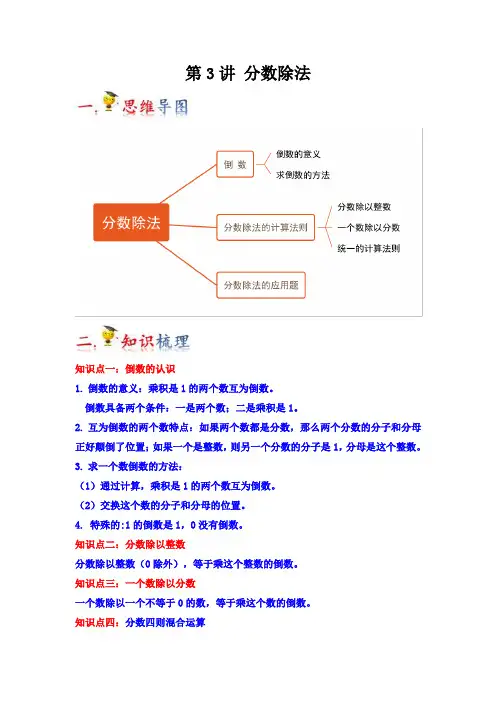
第3讲分数除法知识点一:倒数的认识1.倒数的意义:乘积是1的两个数互为倒数。
倒数具备两个条件:一是两个数;二是乘积是1。
2.互为倒数的两个数特点:如果两个数都是分数,那么两个分数的分子和分母正好颠倒了位置;如果一个是整数,则另一个分数的分子是1,分母是这个整数。
3.求一个数倒数的方法:(1)通过计算,乘积是1的两个数互为倒数。
(2)交换这个数的分子和分母的位置。
4. 特殊的:1的倒数是1,0没有倒数。
知识点二:分数除以整数分数除以整数(0除外),等于乘这个整数的倒数。
知识点三:一个数除以分数一个数除以一个不等于0的数,等于乘这个数的倒数。
知识点四:分数四则混合运算1. 只有乘、除法,按照从左到右的顺序依次进行计算。
2. 在没有括号的算式里,既有加、减法又有乘、除法,要先算乘、除法,再算加、减法。
3. 在一个有小括号的算式里,应该先算小括号里面的,后算小括号外面的。
知识点五:已知一个数的几分之几是多少求这个数解决“已知一个数的几分之几是多少,求这个数”的问题,一般方法:方程法:1.找出单位“1”,设未知量为x;2.找出题中的等量关系式;3.列出方程并解答;4.检验并写出答案。
知识点六:已知一个数比另一个数多(少)几分之几求这个数“已知比一个数多(少)几分之几的数是多少,求这数”的问题的解法:方程法:根据题中的等量关系:“单位‘1’的量×(1±几分之几)=已知量”或“单位‘1’的量±单位‘1’的量×几分之几=已知量”,设单位“1”的量为 x,列方程解答。
知识点七:分数除法之和倍、差倍问题已知两个量的和(差),其中一个量是另一个量的几分之几,求这两个量的问题的解法:有两个量都是未知的,先把谁看作单位“1”都可以,设其中一个量为未知数x,用这个量表示另一个量,然后找出等量关系,列方程解答出一个量,再解答第二个量。
知识点八:工程问题1.利用抽象的“1”解决实际问题:工程问题是分数问题的特例,工作总量与工作效率都不是具体的数,而是用抽象的分数来表示。


分数除法同步练习(一)班级________ 姓名________一、直接写出得数。
35÷2019= 37×2= 12÷3= 910÷35= 415÷45= 920÷34= 二、填空。
1、40的58是( )。
2、一个数的58是25,这个数是( )。
3、45分=( )时 20分=( )时 2019千克=( )吨 32分=( )元4、一批货物的23是180吨,这批货物有( )吨。
5、已知a ×34=45×b=c ×56,并且a 、b 、c 都不等于0.那么,a 、b 、c 按从小到大的顺序排列是( )。
6、有2吨货物,甲车每次运12,乙车每次运12吨。
若单独运完这些货物,甲车需运( )次,乙车需运( )次。
7、小红走56千米要用43小时,她平均每小时走( )千米,她每走1千米要( )小时。
三、计算下面各题。
45÷[8×(12-25)] [1-(14+38)]÷14四、下面各题怎样算简便就怎样算。
(35-14)×53(78+1316)÷131667×111-17÷11五、选择。
(把正确答案的序号填在括号里)1、电扇厂原计划生产电扇100万台,现在生产了120万台,增产了几分之几?列式是()。
A.120÷100-1 B.1-100÷12 C.(120-100) ÷120 D.(120-100) ÷1002、一根绳子长4米,比另一根短14米,另一根绳子长()。
A.154米 B.174米 C.3米 D.165米六、解方程。
9 10x-2=35x÷25=3825+35x=182534x-13x=10七、解决实际问题。
1、一根电线杆全长的27是2米,这根电线杆全长多少米?露出地面的部分占全长的57,露出地面的部分是几米?2、某乡去年绿色蔬菜的总产量比今年少111,去年比今年少110吨,今年的产量是多少吨?3、学校新购进了一些球,新购进的足球占购球总数的3,新购5进的足球有60个,学校新购进了多少个球?(用算术和方程两种方法解答)4、一项工程,甲、乙两队合作需要12天完成,乙、丙两队合作需要15天完成,甲丙两队合作需要20天完成。

分数除法的意义和计算法则第一课时教学内容分数除法的意义和分数除以整数(教科书第25页——26页的例1,练习七第1——7题)。
教学要求使用学生理解分数除法的意义,掌握分数除以整数的计算方则,并正确计算分数除以整数。
教学重点分数除以整数的计算方法。
教学难点除转化为乘和道理。
教学过程一、复习1口答下面各题的倒数。
2 、、1、、1、0.42根据一个乘法算式写出两个除法算式。
3×15=45 125×8=10003口述下面各式的意义。
×416××2二、新授揭示课题:分数除法1分数除法的意义和计算法则(1)出示25页的月饼图。
(2)引导学生回答问题:1)每人吃半块月饼。
4个人一共吃多少块?怎样列式?得多少?板书:×4=2 (块)2)再看把两块月饼平均分给4个人,每人分得几块?怎样列式?得多少?板书:2÷4=(块)3)如果把两块月饼平均分给每个人半块,可以分给几人?怎样列式?得多少?板书:2÷=4(人)(3)让学生观察比较(板书的)3个式子的已知数和得数。
明确:第一个算式是已知两个因数(和4)求它们的积(2),用乘法计算。
第二算式是已知两个因数的积2与其中一个因数4,求一个因数,用除法计算。
第三算式是已知两个因数的积2与其中一个因数,求一因数4,用除法计算。
小结:分数除法的意义。
强调:分数除法的意义和整数除法的意义相同。
(4)练习:教科书第25页"做一做。
2、分数除以整数的计算方法。
(1)出示例子:把米铁丝平均分成2段,每段长多少米?(2)启发学生分析数量关系。
(画线段图表示)米是1米的,把1米平均分成7份,表示其中的6份。
6份是,再加上米米里面有6个米,要把米平均分成2段实质就是把6个米平均分成2份,每份是3个米,就是米。
板书解法1:÷2==(米)使学生明白:1)分数除以整数,可以把分数的分子除以整数作分子,分母不变。
2)这种计算方法有限制条件的,分子必须能被整数整除。

六年级分数除法练习题班次 姓名一、分数除以整数53÷3= 74÷2= 72÷3= 52÷2=103÷6= 65÷4= 107÷7= 101÷2=73÷4= 85÷5= 119÷6= 65÷10=98÷12= 31÷2= 75÷15= 95÷5=1211÷11= 31÷3= 54÷4= 53÷9=21÷4= 74÷8= 145÷5= 1310÷1=二、整数除以分数6÷72= 4÷158= 5÷21= 6÷43=8÷2516=7÷83= 36÷4027= 6÷65= 7÷57=4÷52= 24÷98= 3÷75= 12÷2516=9÷91= 2÷101= 3÷57= 1÷54=11÷1211= 5÷1415= 4÷74= 4÷47=10÷1310= 36÷49= 5÷52=三、分数除以分数185÷185= 98÷2710= 49÷23= 87÷43=51÷32= 74÷47= 21÷113= 31÷32=65÷85= 107÷65= 75÷65= 98÷72=2516÷98= 51÷41= 72÷75= 61÷3619=158÷2516= 1514÷1415= 1310÷95= 34÷2516=三、分数混合运算1-21×31 41×51÷41×51 113×(43-43) 31+32-31+321÷75-1÷65 0×72+1×53 107-72-75 (21-31)÷65+3187+32×101+81 85×41+41×83 247÷154×0.32 6-2.4÷9810-(1-21)÷21 (32-0.4)÷(61+0.5) 54×(65-43)-15143×91+158÷2516 (5-43÷83)×3619(0.75+61)÷1011÷0.4×8541×0.8+21÷43-0.8 0.25÷(1-95)+83 97÷1514+92×1415513217247⎛⎫++÷⨯⎪⎝⎭51216436⎛⎫-⨯÷ ⎪⎝⎭ 311314162020⎡⎤⎛⎫⎛⎫÷+⨯÷⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦417×(125 × 34)555748681216⎛⎫⨯+-- ⎪⎝⎭ 5751681224⎛⎫+-÷⎪⎝⎭ 200720062008÷111129999999999233333++++ 58738574÷+⨯⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+÷⨯314314839 415313534÷⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-- 661631÷÷⨯⎥⎦⎤⎢⎣⎡÷⎪⎭⎫ ⎝⎛-÷85218554 973297÷÷ ⎪⎭⎫ ⎝⎛-÷⨯5415133261⎪⎭⎫ ⎝⎛+÷544153 ⎪⎭⎫ ⎝⎛--÷138135341 715871156÷+⨯0.75×75+72×0.75 4151÷÷ 434358.43442.2÷+⨯+÷)]512.1(75.3[43-⨯÷ 1146.04326.160÷-⨯ ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-÷⨯5410914.5 1357251375⨯+÷⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯÷8373562100 107523221÷⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--15132=-x x 7221321=⨯+x 6.3)521(=-÷x 604316=-x125655=-x 310855=-x 35425=÷x 613243=+x x1012831÷=⎪⎭⎫ ⎝⎛-⨯x3121465÷=+x 87165=+x x 762175=-x x1096552=+x x-85=109 12x=109815 X +512 X = 57 X ÷35 = 512 ×815 3X +1335 = 57四、列式计算⒈ 一个数的32是64,这个数的85是多少? 2。

新苏教版六年级上册数学-分数除法知识题型归纳总结分数除法(一)知识梳理1、分数除法的意义:分数除法的意义与整数除法的意义相同,都是已知两个因数的积与其中一个因数,求另一个因数的运算。
2、分数除法的计算法则:甲数除以乙数(除外),等于甲数乘乙数的倒数。
模块一分数除以整数例1:一个货物有48吨,每次运走40吨,运了5次,还剩下53吨,问平均每次运走这堆货物的几分之几?照这样计算,14次一共运走这堆货物的几分之几?例2:小明用6分钟从1楼跑到6楼,问小明平均每上一层楼需要几分钟?例3:一块菜地有7公顷,现在要将这块菜地平均分成4份种不同的蔬菜,每种蔬菜占地多少公顷,列式是(12÷4)=3,每种蔬菜占地3公顷。
变式2:一个正方体的棱长总和是12米,这个正方体的棱长是多少米?设正方体的棱长为x,则有4x=12,x=3,所以正方体的棱长是3米。
变式1:如果m、n都是不为0的自然数,请比较(m÷n)和(n÷m)的大小。
因为(m÷n)×(n÷m)=1,所以(m÷n)和(n÷m)互为倒数,由于倒数的大小关系与原数的大小关系相反,所以当m(n÷m);当m>n时,有(m÷n)<(n÷m)。
模块二整数除以分数例4:一台拖拉机每小时耕地2公顷,要耕完2公顷地需要(2÷2)=1小时。
某工程队30天修了一段地铁的(30÷5)=6次,平均每天修(5÷6)=5/6次,(5÷6)天可以修完。
例5:某化工厂生产了25吨化肥,如果每1吨装一袋,这些化肥能装多少袋?25÷1×20=500,这些化肥能装500袋。
例6:一个同学在做题时,粗心大意,把除数看成35,得到的商是18,那么正确的商是多少?由于商和除数的乘积等于被除数,所以正确的商是53÷35=1余18.变式4:食堂运来6吨煤,每天要用(6÷5)=1.2吨,可以用几天?可以用5天。
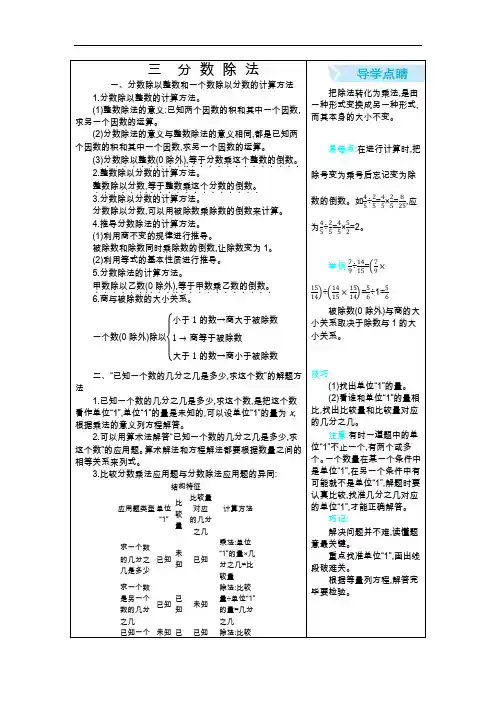
.............把除法转化为乘法,是由一种形式变换成另一种形式,而其本身的大小不变。
易错点:在进行计算时,把除号变为乘号后忘记变为除数的倒数。
如45÷25=45×25=825,应为45÷25=45×52=2。
举例:79÷1415=(79×1514)÷(1415×1514)=56÷1=56被除数(0除外)与商的大小关系取决于除数与1的大小关系。
技巧:(1)找出单位“1”的量。
(2)看谁和单位“1”的量相比,找出比较量和比较量对应的几分之几。
注意:有时一道题中的单位“1”不止一个,有两个或多个。
一个数量在某一个条件中是单位“1”,在另一个条件中有可能就不是单位“1”,解题时要认真比较,找准几分之几对应的单位“1”,才能正确解答。
巧记:解决问题并不难,读懂题意最关键。
重点找准单位“1”,画出线段破难关。
根据等量列方程,解答完毕要检验。
数的几分之几是多少,求这个数知量÷几分之几=单位“1”的量方程:单位“1”的量×几分之几=比较量三、分数连除和乘除混合运算1.乘除混合运算的计算方法。
计算分数乘除混合运算时,先把其中的除法转化为乘法,再按照分数连乘的方法进行计算。
2.连除运算的计算方法。
计算分数连除时.......,.先把其中的除法转化为乘法............,.再按照分....数连乘的方法进行计算。
...........四、比的意义1.比的意义及各部分名称。
(1)比的意义:两个数相除又叫作两个数的比。
..............(2)比的读、写方法。
“比”可以用比号“∶”来代替,也可以写成分数的形式,两种形式的比都读“几比几”。
如3 比2,写作3∶2或32,读作3比2。
(3)比的各部分名称。
(4)比是有序的。
求一个量和另一个量的比,则前一个量是比的前项,后一个量是比的后项。
2.比值的意义和求法。
问题生成单(学生姓名: )A 类基标类检测单预习内容分数除法的意义和整数除以分数1、计算题76÷3 21÷3 1615÷20 85÷535÷10139÷62、“一桶油的3/4重6千克”,是把( )看作单位“1”, 数量关系式是,( )×3/4 = 6千克3、“男生占全班人数的5/9”,是把( )看作单位“1”, 数量关系式是: 全班人数×5/9=( )4、“鸭只数的2/7等于鸡的只数”, 是把( )看作单位“1”,数量关系式是( )×2/7=( )5、“一桶油,用去2/7”,是把( )看作单位“1”, 数量关系式是:( )×2/7 =( )6、“梨重量的3/4与桃一样多”,是把( )看作单位“1”, 数量关系式是:( )×3/4=( )7、美术班有男生20人,是女生人数的5/6, 女生有多少人?我会预习一、复习 1、51×343×3283×3894×43121×6 115×51二、探索新知1、认真阅读,仔细观察例1,想一想左右两边的题组有什么不同?___________________________________________________ 右边的题组是怎样得来的?_________________________________________________ 2、讨论:右边的两个分数除法算式是怎样求出得数的?____________________ _______ 思考:分数除法的意义是什么?_____________________________________________ ☆友情小提示:分数除法的意义与整数除法相同,都是已知两个因数的积与其中一个因数,求另个一个因数。
(都是乘法的逆运算。
)3、巩固分数除法意义的练习:P28“做一做”4、阅读例2题目,自己拿出一张纸试着折一折,涂一涂,看你能够想到几种不同的折法?对照不同的折法,列式计算,注意它们的计算过程以及算理。
1. 已知一箱苹果需要4次运走这堆苹果的
27
, (1)平均每次运走这堆苹果的几分之几? (2)那么7次可以运走这堆苹果的几分之几? 解: (1)
214714
÷= 答:平均每次运走这堆苹果的1
14
(3)117142
⨯
= 答:那么7次可以运走这堆苹果的12
分数除以整数法则:
(1)分数除以整数,可以先转化为乘法计算; (2)分数除以整数,等于这个分数乘这个整数的倒数。
3.一辆汽车行
2
千米用汽油25
升。
行1千米用汽油多少升?1升汽油可以行多少千米? 解:33225225÷= 33252252
÷=
10 分数除以整数与一个数除以分数
答;行1千米用汽油2
25
升,1升汽油可以行
25
2
千米。
分数除以分数法则:
(1)分数除以分数,可以先转化为乘法计算;
(2)分数除以分数,等于分数乘这个分数的倒数。
总结:若甲数除以乙数(0除外),等于甲数乘乙数的倒数。
A.B.C.D.15
5.=10______
1.________的等于40.
=30(个)
甲比丙多加工:30×(30-12)
=30×18
=540(个)
答:甲比丙多加工540个。
【点睛】本题主要考查工程问题,先求出甲、乙、丙三人的效率比,是解答此题的关键。
1。
五年级下册数学分数与除法习题1. 分数的基本概念和表示方法数学中我们会遇到一种特殊的数,叫做分数。
分数由一个分子和一个分母组成,分子表示被分成的份数,分母表示每份的份数。
例如,1/2表示将一个单位分成两份,每份为1/2。
2. 分数的相等和约简(a) 分数的相等:两个分数的值相等,当且仅当它们的分子和分母成比例。
例如,1/2和2/4是相等的分数。
(b) 分数的约简:一个分数可以通过约简来使其分子和分母不再有公因子。
例如,2/4可以约简为1/2。
3. 分数的大小比较(a) 分数相等:两个分数相等的条件已经在前面提到过。
(b) 分数的大小比较:我们可以通过比较两个分数的大小关系来判断它们的大小。
若两个分数的分母相同,则分子较大的分数较大;若两个分数的分子相同,则分母较小的分数较大;其他情况下,可以通分后再进行比较。
4. 分数的基本运算(a) 分数的加法:当两个分数的分母相同,我们只需要将分子相加即可;当分母不同,我们需要找到它们的最小公倍数,然后通分后再相加。
(b) 分数的减法:同样需要找到最小公倍数,通分后再进行相减。
(c) 分数的乘法:将两个分数的分子相乘,分母相乘,得到的积即为结果。
(d) 分数的除法:将两个分数的分子和分母互换位置,然后使用乘法的规则进行计算。
5. 分数的混合运算和应用问题(a) 分数的混合运算:分数可以与整数进行混合运算,我们需要注意将整数转化为分数。
(b) 分数的应用问题:分数在日常生活中有广泛的应用,例如计算物体的重量、长度或者交通工具的速度等。
总结:数学中的分数和除法是我们在五年级下册学习的重点内容。
通过学习分数的基本概念和表示方法,我们能够准确地理解分数的含义;掌握分数的相等和约简,可以方便地进行分数的比较和运算;同时,了解分数的混合运算和应用问题,能够将分数知识运用到实际生活中。
通过不断练习分数与除法习题,我们能够更加熟练地运用这些知识,提高数学解题的能力。