高数多元函数微分法及其应用
- 格式:ppt
- 大小:1.22 MB
- 文档页数:22



第八章 多元函数微分法及其应用第一讲 多元函数的基本概念授课题目:§8.1多元函数的基本概念教学目的与要求:1、理解多元函数的概念.2、了解二元函数的极限与连续性的概念,以及有界闭区域上连续函数的性质.教学重点与难点:重点:多元函数的概念、二元函数的极限和连续的概念. 讲授内容:一、平面点集 n 维空间1、平面点集平面上一切点的集合称为二维空间, 记为R 2 即R 2=R ⨯R={(x , y ):x , y ∈R }坐标平面上具有某种性质P 的点的集合, 称为平面点集,记作E ={(x , y ):(x , y )具有性质P }.例如,平面上以原点为中心、r 为半径的圆内所有点的集合是C ={(x , y ):x 2+y 2<r 2}.如果我们以点P 表示(x , y ), 以|OP |表示点P 到原点O 的距离, 那么集合C 可表成C ={P :|OP |<r }.回顾数轴上点的邻域。
邻域:设P 0(x 0, y 0)是xOy 平面上的一个点,δ是某一正数,与点P 0(x 0, y 0)距离小于δ的点P (x , y )的全体,称为点P 0的δ邻域,记为U (P 0, δ),即}||{),(00δδ<=PP P P U :或 })()(),{(),(20200 y y x x y x P U δδ<-+-=:. 点P 0的去心δ邻域, 记作) ,(0δP U ,即 }||0{),(00δδ<<=P P P P U :.如果不需要强调邻域的半径δ, 则用U (P 0)表示点P 0的某个邻域, 点P 0的去心邻域记作)(0P U..点与点集之间的关系:任意一点P ∈R 2与任意一个点集E ⊂R 2之间必有以下三种关系中的一种:(1)内点:如果存在点P 的某一邻域U (P ), 使得U (P )⊂E , 则称P 为E 的内点.(2)外点:如果存在点P 的某个邻域U (P ), 使得U (P )⋂E =∅, 则称P 为E 的外点.(3)边界点:如果点P 的任一邻域内既有属于E 的点, 也有不属于E 的点, 则称P 点为E 的边点.E 的边界点的全体, 称为E 的边界, 记作∂E .E 的内点必属于E ; E 的外点必定不属于E ; 而E 的边界点可能属于E , 也可能不属于E .(4)聚点:如果对于任意给定的δ>0, 点P 的去心邻域),(δP U 内总有E 中的点, 则称P 是E 的聚点.由聚点的定义可知, 点集E 的聚点P 本身, 可以属于E , 也可能不属于E .例如, 设平面点集E ={(x , y )|1<x 2+y 2≤2}.,则满足1<x 2+y 2<2的一切点(x , y )都是E 的内点;满足x 2+y 2=1的一切点(x , y )都是E 的边界点;它们都不属于E ;满足x 2+y 2=2的一切点(x , y )也是E 的边界点;它们都属于E ;点集E 以及它的界边∂E 上的一切点都是E 的聚点.开集:如果点集E 的点都是内点, 则称E 为开集.闭集:如果点集的余集E c 为开集, 则称E 为闭集.例如,E ={(x , y )|1<x 2+y 2<2}是开集;E ={(x , y )|1≤x 2+y 2≤2}是闭集; 集合{(x , y )|1<x 2+y 2≤2}既非开集, 也非闭集.连通性:如果点集E 内任何两点, 都可用折线连结起来, 且该折线上的点都属于E , 则称E 为连通集.区域(或开区域):连通的开集称为区域或开区域.例如,E ={(x , y )|1<x 2+y 2<2}是区域.闭区域:开区域连同它的边界一起所构成的点集称为闭区域. 例如,E = {(x , y )|1≤x 2+y 2≤2}.有界集:对于平面点集E , 如果存在某一正数r ,使得E ⊂U (O , r ),其中O 是坐标原点, 则称E 为有界点集.无界集:一个集合如果不是有界集,就称这集合为无界集.例如,集合{(x , y )|1≤x 2+y 2≤2}是有界闭区域;集合{(x , y )| x +y >1}是无界开区域;集合{(x , y )| x +y ≥1}是无界闭区域..2.n 维空间设n 为取定的一个自然数,我们用表示n 元有序数组(x 1, x 2, ⋅ ⋅ ⋅ , x n )的全体所构成的集合记为R n ,即R n =R ⨯R ⨯⋅ ⋅ ⋅⨯R ={(x 1, x 2, ⋅ ⋅ ⋅ , x n ):x i ∈R ,i =1, 2, ⋅ ⋅ ⋅, n }.这样定义了线性运算的集合R n 称为n 维空间.R n 中点x =(x 1, x 2, ⋅ ⋅ ⋅ , x n )与点y =(y 1, y 2, ⋅ ⋅ ⋅ , y n )之间的距离,记作ρ(x , y ), 规定2222211)( )()(),(n n y x y x y x -+⋅⋅⋅+-+-=y x ρ.R n 中元素x =(x 1, x 2, ⋅ ⋅ ⋅ , x n )与零元0之间的距离ρ(x , 0)记作||x ||(在R 1、R 2、R 3中,通常将||x ||记作|x |), 即22221 ||||nx x x ⋅⋅⋅++=x . 采用这一记号,结合向量的线性运算, 便得),()( )()(||||2222211y x y x ρ=-+⋅⋅⋅+-+-=-n n y x y x y x .二、多元函数概念回顾一元函数的概念。





第八章 偏导数与全微分一、选择题1.若u=u(x, y)是可微函数,且,1),(2==x y y x u ,2x xuxy =∂∂=则=∂∂=2x y y u [A ] A. 21-B. 21C. -1D. 12.函数62622++-+=y x y x z [ D ]A. 在点(-1, 3)处取极大值B. 在点(-1, 3)处取极小值C. 在点(3, -1)处取极大值D. 在点(3, -1)处取极小值3.二元函数(),f x y 在点()00,x y 处的两个偏导数()()0000,,,x y f x y f x y 存在是函数f 在该点可微的 [ B ]A. 充分而非必要条件B.必要而非充分条件C.充分必要条件D.既非充分也非必要条件4. 设u=2x +22y +32z +xy+3x-2y-6z 在点O(0, 0, 0)指向点A(1, 1, 1)方向的导数=∂∂lu[ D ] A.635 B.635- C.335 D. 335- 5. 函数xy y x z 333-+= [ B ]A. 在点(0, 0)处取极大值B. 在点(1, 1)处取极小值C. 在点(0, 0), (1, 1)处都取极大值 D . 在点(0, 0), (1, 1)处都取极小值 6.二元函数(),f x y 在点()00,x y 处可微是(),f x y 在该点连续的[ A ] A. 充分而非必要条件 B.必要而非充分条件 C.充分必要条件D.既非充分也非必要条件 7. 已知)10(0sin <<=--εεx y y , 则dxdy= [ B ] A. y cos 1ε+ B.y cos 11ε- C. y cos 1ε- D. ycos 11ε+8. 函数yx xy z 2050++= (x>0,y>0)[ D ] A. 在点(2, 5)处取极大值 B. 在点(2, 5)处取极小值C.在点(5, 2)处取极大值D. 在点(5, 2)处取极小值9.二元函数(),f x y 在点()00,x y 处连续的是(),f x y 在点()00,x y 处可微的 [A ] A. 必要而非充分条件 B. 充分而非必要条件 C.充分必要条件 D.既非充分也非必要条件 10. 曲线x=t, y=2t -, z=3t 所有切线中与平面x+2y+z=4平行的切线有 [ B ] A. 1 条 B.2条 C. 3条 D.不存在 11.设22(,)xy f x y y x =-,则(,)x yf y x= B A. 42xyy x - B. 2244x y y x - C. 2244x y y x +- D. 2244y x y x --12.为使二元函数(,)x yf x y x y+=-沿某一特殊路径趋向(0,0)的极限为2,这条路线应选择为 B A.4x y = B. 3x y = C. 2x y = D. 23x y = 13.设函数(,)z f x y =满足222zy∂=∂,且(,1)2f x x =+,(,1)1y f x x '=+,则(,)f x y =BA.2(1)2y x y +++ B. 2(1)2y x y +-+ C. 2(1)2y x y +-- D. 2(1)2y x y ++- 14.设(,)32f x y x y =+,则(,(,))f xy f x y = CA.344xy x y ++B. 2xy x y ++C. 364xy x y ++D. 346xy x y ++15.为使二元函数222(,)xy f x y x y=+在全平面连续,则它在(0,0)处应被补充定义为 B A.-1 B.0 C.1 D. 16.已知函数22(,)f x y x y x y +-=-,则(,)(,)f x y f x y x y∂∂+=∂∂ C A.22x y - B. 22x y + C. x y + D. x y -17.若()yf x=(0)x >,则()f x =BB. C.xD.18.若xz y =,则在点 D 处有z z y x∂∂=∂∂ A.(0,1) B.(,1)e C.(1,)e D. (,)e e19.设2y z x =,则下列结论正确的是 AA.220z z x y y x ∂∂-=∂∂∂∂ B. 220z zx y y x ∂∂->∂∂∂∂ C.220z zx y y x∂∂-<∂∂∂∂ D.两者大小无法确定 20.函数0,0(,)11sin sin ,0xy f x y x y xy y x =⎧⎪=⎨+≠⎪⎩,则极限00lim (,)x y f x y →→ ( C ). (A) 等于1 (B) 等于2 (C) 等于0 (D) 不存在 21.函数z xy =在点(0,0) ( D ).(A) 有极大值 (B) 有极小值 (C) 不是驻点 (D) 无极值 22.二元函数z =在原点(0,0)处( A ).(A) 连续,但偏导不存在 (B) 可微(C) 偏导存在,但不连续 (D) 偏导存在,但不可微23.设()u f r =,而r =()f r 具有二阶连续导数,则222222u u ux y z∂∂∂++=∂∂∂( B ).(A) 1''()'()f r f r r +(B) 2''()'()f r f r r+ (C) 211''()'()f r f r r r + (D) 212''()'()f r f r r r+24.函数(,)z f x y =在点00(,)x y 处连续是它在该点偏导存在的( D ). (A) 必要而非充分条件 (B) 充分而非必要条件(C) 充分必要条件 (D) 既非充分又非必要条件 25.函数221z x y =--的极大值点是 ( D ).(A) (1,1) (B) (1,0) (C) (0,1) (D) (0,0)26.设(,)f x y =(2,1)x f '=(B ).(A)14 (B) 14- (C) 12 (D) 12-27.极限24200lim x y x yx y →→+( B ).(A) 等于0 (B) 不存在 (C) 等于12 (D) 存在且不等于0及1228.(,)z f x y =若在点000(,)P x y 处的两个一阶偏导数存在,则(B ). (A) (,)f x y 在点0P 连续 (B) 0(,)z f x y =在点0x 连续 (C) 00||P P z zdz dx dy x y ∂∂=⋅+⋅∂∂ (D) A,B,C 都不对 29. 设函数y x z =,则z d =( A ). (A).y x x x yxy y d ln d 1+- (B).y x x yx y y d d 1+-(C).y x x x x yy d ln d + (D).y y x x yxy y d ln d 1+-30. 已知=∂∂===y zxy v y x u v u z 则 ,,,ln 2( C )(A )y x xy y x 3232ln 2+ (B )y xxy y x 3232ln 2-(C )y x xy y x 3232ln 2+- (D )y x xy y x 22ln 2+31.函数z=22y x 1--的定义域是( D ) (A.) D={(x,y)|x 2+y 2=1}(B.)D={(x,y)|x 2+y 2≥1}(C.) D={(x,y)|x 2+y 2<1}(D.)D={(x,y)|x 2+y 2≤1}32.设22),(yx xyy x f +=,则下列式中正确的是( C );)A ( ),(,y x f x y x f =⎪⎭⎫⎝⎛; )B (),(),(y x f y x y x f =-+;)C ( ),(),(y x f x y f =; )D ( ),(),(y x f y x f =-33.设e cos xz y =,则=∂∂∂yx z2( D );)A ( e sin x y ; )B ( e e sin x x y +;)C ( e cos xy -; )D ( e sin xy -34.已知22),(y x y x y x f -=-+,则x f ∂∂=∂∂+yf ( C ); )A ( y x 22+; )B ( y x -; )C ( y x 22- )D ( y x +.35. 设y xy x z 2232-+=,则=∂∂∂y x z( B )(A )6 (B )3 (C )-2 (D )2.36.设()=∂∂=⎪⎭⎫ ⎝⎛x zy x y x f z 00, ,,则( B )(A )()()x y x f y y x x f x ∆-∆+∆+→∆00000,,lim(B )()()x y x f y x x f x ∆-∆+→∆0000,,lim(C )()()x y x f y x x f x ∆-∆+→∆00000,,lim(D )()x y x x f x ∆∆+→∆000,lim37. 设由方程0=-xyz e z确定的隐函数()=∂∂=x z y x f z 则,,( B )(A )z z+1 (B )()1-z x z (C )()z x y +1 (D )()z x y -138. 二次函数 11)4ln(2222-++--=y x y x z 的定义域是( D )A. 1 < 22y x + ≤ 4;B. –1 ≤ 22y x + < 4; C. –1 ≤ 22y x + ≤ 4; D. 1 < 22y x + < 4。

第五章多元函数微分法及其应用1、多元函数极限存在的条件极限存在是指P(x,y)以任何方式趋于P0(x0,y0)时,函数都无限接近于A,如果P(x,y)以某一特殊方式,例如沿着一条定直线或定曲线趋于P0(x0,y0)时,即使函数无限接近某一确定值,我们还不能由此断定函数极限存在。
反过来,如果当P(x,y)以不同方式趋于P0(x0,y0)时,函数趋于不同的值,那么就可以断定这函数的极限不存在。
例如函数:f(x,y)={0(xy)/(x^2+y^2)x^2+y^2≠02、多元函数的连续性定义设函数f(x,y)在开区域(或闭区域)D内有定义,P0(x0,y0)是D的内点或边界点且P0∈D,如果lim(x→x0,y→y0)f(x,y)=f(x0,y0)则称f(x,y)在点P0(x0,y0)连续。
性质(最大值和最小值定理)在有界闭区域D上的多元连续函数,在D上一定有最大值和最小值。
性质(介值定理)在有界闭区域D上的多元连续函数,如果在D上取得两个不同的函数值,则它在D上取得介于这两个值之间的任何值至少一次。
3、多元函数的连续与可导如果一元函数在某点具有导数,则它在该点必定连续,但对于多元函数来说,即使各偏导数在某点都存在,也不能保证函数在该点连续。
这是因为各偏导数存在只能保证点P沿着平行于坐标轴的方向趋于P0时,函数值f(P)趋于f(P0),但不能保证点P按任何方式趋于P0时,函数值f(P)都趋于f(P0)。
4、多元函数可微的必要条件一元函数在某点的导数存在是微分存在的充分必要条件,但多元函数各偏导数存在只是全微分存在的必要条件而不是充分条件,即可微=>可偏导。
5、多元函数可微的充分条件定理(充分条件)如果函数z=f(x,y)的偏导数存在且在点(x,y)连续,则函数在该点可微分。
6.多元函数极值存在的必要、充分条件定理(必要条件)设函数z=f(x,y)在点(x0,y0)具有偏导数,且在点(x0,y0)处有极值,则它在该点的偏导数必为零。

多元函数微分法及其应用设函数y = f(x)在x0的邻域内有定义,x0及x0 + Δx在此区间内。
如果函数的增量Δy = f(x0 + Δx) - f(x0)可表示为Δy = AΔx + o(Δx)(其中A是不依赖于Δx的常数),而o(Δx)是比Δx高阶的无穷小(注:o读作奥密克戎,希腊字母)那么称函数f(x)在点x0是可微的,且AΔx称作函数在点x0相应于自变量增量Δx的微分,记作dy,即dy = AΔx。
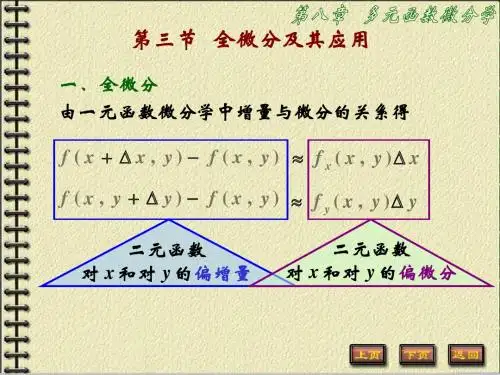
如sinx的微分可写作为dsinx=cosxdx设有二元函数z=f(x,y),点(x0,y0)是其定义域D内一点.把y固定在y0而让x在x0有增量△x,相应地偏导数函数z=f(x,y)有增量(称为对x的偏增量)△z=f(x0+△x,y0)-f(x0,y0)。
如z=sinxy对x的偏导数为dz/dx=y*cosxy前者是微分,后者是偏微分。
求微分原则一样的,后者一般会出现在二元函数或者以上的函数求微分中1.偏导数不存在,全微分就不存在2.全微分若存在,偏导数必须存在3.有偏导数存在,全微分不一定存在微分是函数改变量的线性主要部分,导数是微积分中的重要基础概念。
当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数。
导数:一般指一元函数而言,对只有一个自变量x的函数y,则对函数y求导得到导数y',称之为函数y的导数。
偏导数:一般是针对多元函数而言,例如对有两个自变量x,y的函数z,则求z对y的导数,即为z对y的偏导数,书写为:z'y。
微分:存在一元微分和偏微分两种类型,与导数和偏导数的区别,只是书写的不同。
例如,对一元函数而言,y的微分书写为:dy=y'dx;对有两个自变量x,y的函数z,则求z对y的导数,z对y的偏微分,书写为:のz=z'yのy。
二元函数的微分与导数区别是什么呢?_作业帮微分一般指全微分或者全导数,在这个方面就没有区别,如果是偏导数就有区别了.例如u=x^2y他的全微分或者全导数一般写成:du=2ydx+x^2dy但对x 的偏导数=2y,对y的偏导数=x^2.多元函数微积分里,那两个的区别,不懂,求大神指导定积分的几何意义是曲边梯形的面积.而情形2中阴影部分面积正好是两个曲边梯形面积之差,加上绝对值就是看哪条曲线在上面,总是用上面的曲边梯形减去下面的曲边梯形才能保证结果是面积.否则积分值可能为负.【二元函数与一元函数求微分的区别是多求一个变量的导数?】大概可以这样说,但表述不同,一元中,我们称为求微分,二元中,我们称为求偏微分而且一元中中微分存在,原函数就可以说明连续了,但二元中是不能这样说的,必须偏微分存在且连续.不知道我的表述你可不可以接受,而且,你的问题有点大,如果可以具体点,我也可以更具体的告诉你.高数,一元函数微分,这两个式子区别在哪? 意思是上面个求的极限在下面个式子的无穷小的位置,如果函数连续,两个式子的值是相等的【多元函数:偏导数存在、可微分、连续!请一定用通俗的话给我讲讲:1、多元函数可微分到底是什么意思?可微分代表什么?2.偏导数存在、可微分、连续他们的关系是什么?为什么什么是这样的】1.一元函数可微分与可求导比较接近二元函数的话,你想象一张平面,在上面任何一个方向都可以求导,就接近可微分了; 而偏导数存在仅仅是某几个方向可以求导2.可微分->偏导数存在可微分->连续偏导数存在(比如x、y方向可偏导)->x、y方向函数连续,其他方向不一定。