华师版初一数学平行线测试题
- 格式:pdf
- 大小:147.40 KB
- 文档页数:12

华东师大版七年级数学上册第五章相交线与平行线单元测试题一.选择题(每小题4分,共40分)1 •下列图形可以由一个图形经过平移变换得到的是( )3•对于命题“若a 2>b\则a>b\下而四组关于g 方的值中,能说明这个命题是假命题的是()A.B.D.A ・ “=3, b=2 B. a — - 3, b=2C ・“=3, b= - 1 D. a=・ 1, b=34•如图,下列判断中错误的是( )A.ZA 与Z1是同位角 C. Z4与Z1是内错角5. 如图,ZBAC=9O% AD 丄BC 于点 D, A.点C 到AB 的垂线段是线段ACC.线段AB 的长度是点B 到AC 的距离B.ZA 与ZB 是同旁内角 D.Z1与Z3是同位角则下列结论中错误的是()B.点A 到BC 的距离是线段AD 的长度 D •线段AB 是点B 到的距离D.B DCB第4题图6. 如图,给岀了过直线外一点作已知直线的平行线的方法,英依据是() A.同位角相等,两直线平行 B.内错角相等,两直线平行 C.同旁内角互补,两直线平行 D.两直线平行,同位角相等7. 下列说法正确的个数是()①同位角相等;②过一点有且只有一条直线与已知直线垂直:③过一点有且只有一条直线与已知直线平行:④三条直线两两相交,总有三个交点; ⑤若 a//b> b//c> 则 a//c.A ・1个 B.2个 C.3个 D.4个8. 如图,ABCD 为一长方形纸带,AB//CD.将ABCD 沿EF 折,爪D 两点分别与从 D 对应,若Z1 = 2Z2,则ZAEF 的度数为()9. 如图,Zl=68。
,直线“平移后得到直线6则Z2- Z3的度数为()10. 如图,AB//CD,则下列各式中正确的是() A.Zl = 180°-Z3二.填空题(每小题4分,共24分)11. 直线,松、CD 相交于点O,若ZJOC= 50% 12. 如图,测量运动员跳远成绩选取的是AB 的长度,其依据是.A .60°B.65°C. 72°D. 75°B.Z1 = Z3-Z2C.Z2+Z3=180°-ZlD. Z2+Z3 = 180°+Zl则 ZBOD= 第12題图13 •若直线a丄S b丄g则直线。

第五章 5.2.2平行线的判定同步测试题一、选择题1.如图是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.两直线平行,同位角相等D.两直线平行,内错角相等2.如图所示,下列条件:①∠1=∠3;②∠2=∠3;③∠4=∠5;④∠2+∠4=180°.不能判断直线l1∥l2的是()A.①②B.②③ C.④ D.②3.如图,若∠1与∠2互补,∠2与∠3互补,则一定有( )A.l1∥l2 B.l3∥l4C.l1∥l4 D.l2∥l44.如图所示,若∠1=50°,当∠2=()时,AB∥CD.A.50°B.60° C.70° D.80°5.如图,在四边形ABCD中,已知∠B=60°,∠C=2∠B,由这些条件你能判断平行的两条直线是().A.AB∥CD B.AD∥BCC.AC∥BD D.AD∥AB二、填空题6.如图,∠1=50°,∠2=50°,则a,b的位置关系是______.7.如图,要使AC∥BD,则需______=______或______=______.8.如图所示,用两个相同的三角形按照如图方式作平行线,能解释其中道理的定理是______9.如图,已知∠2=∠3,则______.10.如图,一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD,是根据______11.已知a,b,c为平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是______.12.如图,在下列条件中:①∠DAC=∠ACB;②∠BAC=∠ACD;③∠BAD+∠ADC=180°;④∠BAD+∠ABC=180°.其中能使直线AB∥CD成立的是______.(填序号)三、解答题13.根据图形填空:(1)∵∠1=∠2(已知),∴______∥______;(2)∵∠3+∠4=180°(已知),∴______∥______;(3)∵∠4+∠5=180°(已知),∴______∥______;(4)∵∠2=∠4(已知),∴______∥______.14.如图,AB⊥AC,EF⊥AC,∠1=∠2,那么AB与CD是否平行?填空注明推理的依据.解:∵AB⊥AC,EF⊥AC(______),∴AB∥EF(______).∵∠1=∠2(______),∴EF∥DC(______).∴AB∥CD(______).15.如图,已知∠B=∠1,∠ECD+∠1=180°,试说明:AB∥CD,BF∥CE.16.如图,直线AB,CD被EF所截,∠3=∠4,∠1=∠2,EG⊥FG.试说明:AB∥CD.17.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中∠A=60°,∠D=30°,∠E=∠B=45°):(1)①若∠DCE=45°,则∠ACB的度数为______;②若∠ACB=140°,求∠DCE的度数;(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由;(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE度数所有可能的值(不必说明理由);若不存在,请说明理由.参考答案一、选择题1.如图是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是(A)A.同位角相等,两直线平行B.内错角相等,两直线平行C.两直线平行,同位角相等D.两直线平行,内错角相等2.如图所示,下列条件:①∠1=∠3;②∠2=∠3;③∠4=∠5;④∠2+∠4=180°.不能判断直线l1∥l2的是(D)A.①②B.②③ C.④ D.②3.如图,若∠1与∠2互补,∠2与∠3互补,则一定有(B)A.l1∥l2 B.l3∥l4C.l1∥l4 D.l2∥l44.如图所示,若∠1=50°,当∠2=( A )时,AB∥CD.A.50°B.60° C.70° D.80°5.如图,在四边形ABCD中,已知∠B=60°,∠C=2∠B,由这些条件你能判断平行的两条直线是( A).A.AB∥CD B.AD∥BCC.AC∥BD D.AD∥AB二、填空题6.如图,∠1=50°,∠2=50°,则a,b的位置关系是a∥b.7.如图,要使AC∥BD,则需∠A=∠B或∠C=∠D.8.如图所示,用两个相同的三角形按照如图方式作平行线,能解释其中道理的定理是内错角相等,两直线平行.9.如图,已知∠2=∠3,则AD∥BC.10.如图,一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD,是根据同旁内角互补,两直线平行.11.已知a,b,c为平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是a∥c.12.如图,在下列条件中:①∠DAC=∠ACB;②∠BAC=∠ACD;③∠BAD+∠ADC=180°;④∠BAD+∠ABC=180°.其中能使直线AB∥CD成立的是②③.(填序号)三、解答题13.根据图形填空:(1)∵∠1=∠2(已知),∴CF∥AD;(2)∵∠3+∠4=180°(已知),∴CF∥AD;(3)∵∠4+∠5=180°(已知),∴BC∥DE;(4)∵∠2=∠4(已知),∴BC∥DE.14.如图,AB⊥AC,EF⊥AC,∠1=∠2,那么AB与CD是否平行?填空注明推理的依据.解:∵AB⊥AC,EF⊥AC(已知),∴AB∥EF(在同一平面内,垂直于同一条直线的两条直线平行).∵∠1=∠2(已知),∴EF∥DC(内错角相等,两直线平行).∴AB∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行).15.如图,已知∠B=∠1,∠ECD+∠1=180°,试说明:AB∥CD,BF∥CE.解:∵∠B=∠1,∴AB∥CD.∵∠1=∠2,且∠ECD+∠1=180°,∴∠ECD+∠2=180°.∴BF∥CE.16.如图,直线AB,CD被EF所截,∠3=∠4,∠1=∠2,EG⊥FG.试说明:AB∥CD.解:∵EG⊥FG,∴∠G=90°.∴∠1+∠3=90°.∵∠1=∠2,∠3=∠4,∴∠1+∠2+∠3+∠4=180°,即∠EFD+∠BEF=180°.∴AB∥CD.17.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中∠A=60°,∠D=30°,∠E=∠B=45°):(1)①若∠DCE=45°,则∠ACB的度数为135°;②若∠ACB=140°,求∠DCE的度数;(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由;(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE度数所有可能的值(不必说明理由);若不存在,请说明理由.解:(1)②∵∠ACB=140°,∠ACD=90°,∴∠DCB=140°-90°=50°.∴∠DCE=90°-50°=40°.(2)∠ACB+∠DCE=180°.理由:∵∠ACB=∠ACD+∠DCB=90°+∠DCB,∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+90°=180°.(3)存在.当∠ACE=30°时,AD∥BC;当∠ACE=45°时,AC∥BE;当∠ACE=120°时,AD∥CE;当∠ACE=135°时,BE∥CD;当∠ACE=165°时,BE∥AD.。
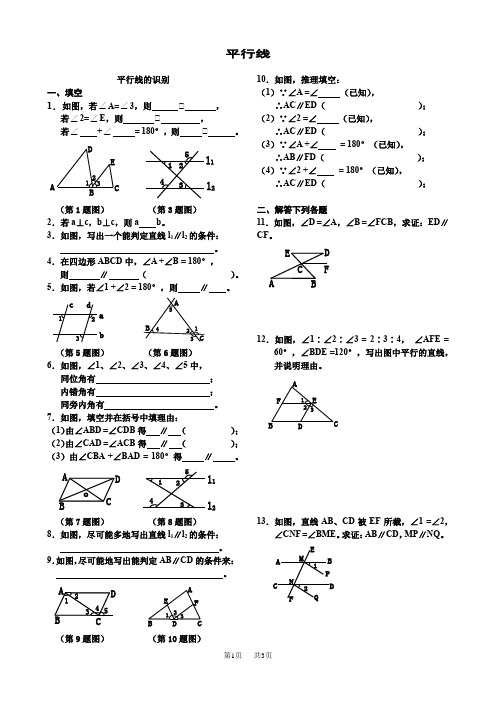
平行线平行线的识别一、填空1.如图,若∠A=∠3,则 ∥ , 若∠2=∠E ,则 ∥ ,若∠ +∠ = 180°,则 ∥ 。
ABCDE12354321l 2l 1 (第1题图) (第3题图) 2.若a ⊥c ,b ⊥c ,则a b 。
3.如图,写出一个能判定直线l 1∥l 2的条件: 。
4.在四边形ABCD 中,∠A +∠B = 180°,则 ∥ ( )。
5.如图,若∠1 +∠2 = 180°,则 ∥ 。
ab cd12345123ABC (第5题图) (第6题图) 6.如图,∠1、∠2、∠3、∠4、∠5中, 同位角有 ; 内错角有 ; 同旁内角有 。
7.如图,填空并在括号中填理由: (1)由∠ABD =∠CDB 得 ∥ ( ); (2)由∠CAD =∠ACB 得 ∥ ( ); (3)由∠CBA +∠BAD = 180°得 ∥ 。
o ABCDl 1l245123(第7题图) (第8题图) 8.如图,尽可能多地写出直线l 1∥l 2的条件: 。
9.如图,尽可能地写出能判定AB ∥CD 的条件来: 。
ABCD 45123123A FE(第9题图) (第10题图)10.如图,推理填空:(1)∵∠A =∠ (已知),∴AC ∥ED ( ); (2)∵∠2 =∠ (已知),∴AC ∥ED ( ); (3)∵∠A +∠ = 180°(已知), ∴AB ∥FD ( ); (4)∵∠2 +∠ = 180°(已知), ∴AC ∥ED ( );二、解答下列各题11.如图,∠D =∠A ,∠B =∠FCB ,求证:ED ∥CF 。
C D E F12.如图,∠1∶∠2∶∠3 = 2∶3∶4, ∠AFE =60°,∠BDE =120°,写出图中平行的直线,并说明理由。
A B C123FE13.如图,直线AB 、CD 被EF 所截,∠1 =∠2,∠CNF =∠BME 。

华师大版七年级上册数学第5章相交线与平行线含答案一、单选题(共15题,共计45分)1、如图,能得到AB∥CD的条件是()A.∠B=∠DB.∠B+∠D+∠E=180°C.∠B+∠D=180°D.∠B+∠D=∠E2、如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=()A.40°B.50°C.60°D.70°3、如图,将直尺与含30°角的三角尺放在一起,若∠1=25°,则∠2的度数是()A.30°B.45°C.55°D.60°4、如图,在平行线a,b之间放置一块直角三角板,三角板的顶点A,B分别在直线a,b上,则∠1+∠2的值为()A.90°B.85°C.80°D.60°5、如图,AB∥CD,DA⊥CE于点A.若∠EAB=55°,则∠D的度数为()A.25°B.35°C.45°D.55°6、下列语句:①同一平面上,三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行,其中()A.①、②是正确的命题B.②、③是正确命题C.①、③是正确命题D.以上结论皆错7、如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为( )A.7B.8C.9D.108、直线AB∥CD,∠B=23°,∠D=42°,则∠E=()A.23°B.42°C.65°D.19°9、如图,直线//b,下列各角中与相等的是()A. B. C. D.10、如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=40°,则∠2等于()A.130°B.140°C.150°D.160°11、下列四个图形中,不能推出与相等的是()A. B. C. D.12、如图,△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论错误的是()A. BF= DFB.∠1=∠ EFDC. BF> EFD. FD∥ BC13、下列命题中,是真命题的是()A.同位角相等B.邻补角一定互补C.相等的角是对顶角D.有且只有一条直线与已知直线垂直14、如图所示,下列说法正确的是()A.若AB CD,则∠A+∠ABC=180°B.若AD BC,则∠C+∠ADC=180° C.若∠1=∠2,则AB CD D.若∠3=∠4,则AD BC15、如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于()A.42°B.44°C.46°D.48°二、填空题(共10题,共计30分)16、如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程,请你帮他在括号内填上推导依据或内容.证明:∵∠1+∠2﹦180(已知)∠1﹦∠4 (________)∴∠2﹢________﹦180°.∴EH∥AB(________)∴∠B﹦∠EHC(________)∵∠3﹦∠B(已知)∴∠3﹦∠EHC(________)∴ DE∥BC(________)17、如图,AB∥CD ,以点A为圆心,小于AC长为半径作圆弧,分别交AB ,AC于E , F两点,再分别以E , F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P ,作射线AP ,交CD于点M .若∠ACD=114°,则∠MAB的度数为________°.18、已知点P的坐标为(m﹣1,m2﹣2m﹣3),则点P到直线y=﹣5的最小值为________.19、将一副三角板如图放置,使点A在DE上,BC∥DE,则∠AFC的度数为________ .20、如图,AB∥FC,E是DF的中点,若AB=30,CF=17,则BD=________.21、如图,已知,,所以与重合的理由是:________.22、如图,已知点B在点A的北偏东32°,点C在点B的北偏西58°,CB=12,AB=9,AC=15,则△ABC的面积为________.23、如图,直线a∥b,直线c,d与直线b相交于点A,∠3=∠4,设∠1为α度,则∠2=________度(用含有α的代数式表示).24、在同一平面内,∠A的两边分别与∠B的两边平行,且∠A比∠B的3倍少40°,则∠A =________25、在平面内,若直线a与b没有公共点,则称a与b________ ,记作________ .三、解答题(共5题,共计25分)26、如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,AB=6,FC=4,求线段DB的长.27、如图,AB⊥ BC,BC⊥ CD,且∠ 1=∠ 2,那么EB∥ CF吗?为什么?28、完成下面的证明:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.证明:∵DE∥AB(已知),∴∠A=∠CED(________)又∵∠BFD=∠CED(已知),∴∠A=∠BFD(________)∴DF∥AE(________)∴∠EGF+∠AEG=180°(________)29、阅读下列文字,并完成证明;已知:如图,∠1=∠4,∠2=∠3,求证:AB∥CD;证明:如图,延长CF交AB于点G∵∠2=∠3∴BE∥CF()∴∠1=()又∠1=∠4∴∠4=()∴AB∥CD()30、如图,已知∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.证明:∵DE⊥BC,AB⊥BC(已知)∴∠DEC=∠ABC=90°(________)∴DE∥AB(________)∴∠2=________(________)∠1=________ (________)又∵∠1=∠2(________)∴∠A=∠3(________)参考答案一、单选题(共15题,共计45分)1、D2、B3、C4、A6、A7、D8、C9、C10、D11、B12、B13、B14、B15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、27、28、29、30、。

七年级数学上册《第五章平行线的判定》同步练习题及答案(华东师大版)班级姓名学号一、选择题1.如图,直线a、b被直线c所截,下列条件能使a∥b的是()A.∠1=∠6B.∠2=∠6C.∠1=∠3D.∠5=∠72.如图,直线a、b被直线c所截,互为同旁内角的是()A.∠4和∠6B.∠2和∠7C.∠4和∠5D.∠4和∠63.如图,AB∥CD,EF∥GH,且∠1=50°,下列结论错误的是( )A.∠2=130°B.∠3=50°C.∠4=130°D.∠5=50°4.如图,直线a,b被直线c所截,下列条件能判断a∥b的是( )A.∠1=∠2B.∠1=∠4C.∠3+∠4=180°D.∠2=30°,∠4=35°5.同一平面内有四条直线a、b、c、d,若a∥b,a⊥c,b⊥d,则c、d的位置关系为( )A.互相垂直B.互相平行C.相交D.没有确定关系6.如图,下列条件中不能判断直线a∥b的是( )A.∠1=∠2B.∠3=∠4C.∠2=∠3D.∠5+∠6=180°7.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是()A.第一次右拐50°,第二次左拐130°B.第一次左拐50°,第二次右拐50°C.第一次左拐50°,第二次左拐130°D.第一次右拐50°,第二次右拐50°8.若两条平行线被第3条直线所截,则一组同位角的平分线互相()A.垂直B.平行C.重合D.相交二、填空题9.如图,已知AB与CF相交于点E,∠AEF=80°,要使AB∥CD,需要添加的一个条件是.10.如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是.11.如图:已知:∠1=105°,∠2=105°,则_____∥_____.12.如图,∠B=∠D=∠E,那么图形中的平行线有___________________________理由是_________________________________________。

第5章 相交线与平行线检测题(本检测题满分:100分,时间:90分钟)一、选择题(每小题3分,共30分)1.如图,已知点是直线外的一点,点在直线上,且,垂足为,,则下列语句错误的是( ) A.线段的长是点到直线的距离B.三条线段中,最短C.线段的长是点到直线的距离D.线段的长是点到直线的距离2.在一个平面内,任意四条直线相交,交点的个数最多为( ) A.7 B.6 C.5 D.43.如图,将含有30°角的三角板的直角顶点放在相互平行的两条直线中的一条上,若∠1=35°,则∠2的度数为( ) A.10°B.20°C.25°D.30°4.(2016·福州中考)如图,直线a ,b 被直线c 所截,∠1与∠2的位置关系是( )A.同位角B.内错角C.同旁内角D.对顶角AB ∥EF ,CD ⊥EF ,∠BAC =50°,则∠ACD =( )A.120°B.130°C.140°D.150°第4题图第5题图6.如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.两直线平行,同位角相等 D.两直线平行,内错角相等7.(2016·陕西中考)如图,AB∥CD,AE平分∠CAB交CD于点E.若∠C=50°,则∠AED=( )A.65°B.115°C.125°D.130°第7题图8.某商品的商标可以抽象为如图所示的三条线段,其中∥,∠°,则∠的度数是()A.30°B.45°C.60°D.75°9.(2015·湖北宜昌中考)如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是()A.60°B.50°C.40°D.30°第9题图10.下列说法正确的个数为()(1)如果,那么、∠2与∠3互为补角;(2)如果,那么是余角;(3)互为补角的两个角的平分线互相垂直;(4)有公共顶点且又相等的角是对顶角;(5)如果两个锐角相等,那么它们的余角也相等.A.1B.2C.3D.4二、填空题(每小题3分,共24分)11.已知a,b,c为平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是.12.将一副直角三角板ABC和EDF如图放置(其中∠A=60°,∠F=45°),使点E落在AC边上,且ED∥BC,则∠CEF的度数为______.13.如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为______.14.如图,与∠1构成同位角的是______,与∠2构成内错角的是______.15.如图,已知∠1=∠2,∠B=40°,则∠3=_____.16.(2016·浙江金华中考)如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED 的度数是.第16题图17.上午九点时分针与时针互相垂直,再经过分钟后分针与时针第一次成一条直线.18.(2016·吉林中考)如图,AB∥CD,直线EF分别交AB,CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放.若∠EMB=75°,则∠PNM等于度.三、解答题(共46分)19.(6分)如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,求∠ADE的度数.20.(8分)小明到工厂去进行社会实践活动时,发现工人师傅生产了一种如图所示的零件,工人师傅告诉他:AB∥CD,∠BAE=45°,∠1=60°, 小明马上运用已学的数学知识得出∠ECD的度数.你能求出∠ECD的度数吗?如果能,请写出理由.21.(6分)如图,要测量两堵墙所形成的∠的度数,但人不能进入围墙,如何测量?请你写出两种不同的测量方法,并说明其几何道理.22.(6分)如图,直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.第18题图23.(6分)如图,∠1和∠2是哪两条直线被哪一条直线所截形成的?它们是什么角?∠1和∠3是哪两条直线被哪一条直线所截形成的?它们是什么角?24. (8分)将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.(1)求证:CF∥AB;(2)求∠DFC的度数.25.(6分)如图,直线AB∥CD,直线EF分别交AB、CD于点M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.第5章相交线与平行线检测题参考答案1.C 解析:因为P A⊥PC,所以线段P A的长是点A到直线PC的距离,选项C错误.2.B 解析:在平面上画出4条直线,当这4条直线经过同一个点时,有1个交点;当3条直线经过同一个点,第4条直线不经过该点时,有4个交点;当4条直线不经过同一点时,有6个交点.3.C 解析:如图,作一直线平行于已知两直线.由平行线的性质得∠1=∠3,∠2=∠4.又∠3+∠4=60°,所以∠1+∠2=60°,所以∠2=60°-∠1=60°-35°=25°.4.B 解析:∠1和∠2两个角都在被截直线a和b之间,并且在第三条直线c(截线)的两旁,故∠1和∠2是直线a,b被直线c所截而成的内错角.5.C 解析:如图,过点C作CM∥AB,∴ 50∠=∠=︒.ACM BAC∵ AB∥EF, ∴ CM∥EF.∵ CD EF⊥,∴ CD CM⊥,∠=︒∴, 第5题答图MCD90∴ 5090140∠=∠+∠=+=︒︒︒.ACD ACM MCD点拨:本题考查了平行线的性质:(1)两直线平行,同位角、内错角分别相等,同旁内角互补;(2)如果一条直线垂直于两条平行线中的一条,那么也垂直于另一条直线.6.A 解析:∵∠DPF=∠BAF,∴AB∥PD(同位角相等,两直线平行).故选A.7.B解析:∵AB∥CD,∴∠CAB+∠C=180°,∠BAE+∠AED=180°.∵∠C=50°,∴∠CAB=180°-50°=130°.∵AE平分∠CAB,∴∠BAE=∠CAB=×130°=65°.∴∠AED=180°-65°=115°.故选B.规律:在解题过程中常常由直线的位置关系得到不共顶点的角的数量关系(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补),从而将已知与未知建立联系.8.B 解析:因为∠,所以.因为∥,所以,所以.9.C 解析:因为FE⊥DB,所以∠FED=90°.由∠1=50°可得∠FDE=90°-50°=40°.因为AB∥CD,由两直线平行,同位角相等,可得∠2=∠FDE=40°.10.A 解析:(1)互为补角的应是两个角而不是三个角,故此说法错误;(2)应改为∠是∠的余角,故此说法错误;(3)互为邻补角的两个角的平分线互相垂直,故此说法错误; (4)根据对顶角的定义可判断此说法错误;(5)相等锐角的余角相等,故正确.综上可得只有一个正确.11.平行 解析:根据在“同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行”可得答案.12.15° 解析:∵ ED ∥BC ,∴ ∠DEC =∠ACB =30°, ∴ ∠CEF =∠DEF -∠DEC =45°-30°=15°. 13.65° 解析:∵ ∠1=155°,∴ ∠EDC =180°-∠1=25°. ∵ DE ∥BC ,∴ ∠C =∠EDC =25°.在△ABC 中,∵ ∠A =90°,∴ ∠B +∠C =90°,∴ ∠B =90°-∠C =90°-25°=65°. 14.∠∠解析:根据同位角、内错角的定义,与∠1构成同位角的是∠,与∠2构成内错角的是∠.15.40° 解析:因为∠1=∠2,所以AB ∥CE ,所以∠3=∠B .又∠B =40°,所以∠3=40°. 16.80° 解析:如图,延长DE 交AB 于点F .第16题答图∵ BC ∥DE ,∴ ∠AFE =∠B . ∵ AB ∥CD ,∴ ∠B +∠C =180°.∵ ∠C =120°,∴ ∠AFE =∠B =60°.∵ ∠A =20°,∴ ∠AEF =180°-∠A -∠AFE =100°. ∴∠AED =180°-∠AEF =80°.17.11416解析:分针每分钟转动6°,时针每分钟转动0.5°,设再经过分钟后分针与时针第一次成一条直线,则有,解得11416.18.30 解析:∵ AB ∥CD ,∴ ∠EMB =∠END =75°.又∵ ∠PND =45°,∴ ∠PNM =∠END -∠PND =75°-45°=30°.19.解:∵∠B =46°,∠C =54°,∴ ∠BAC =180°-∠B -∠C =180°-46°-54°=80°.∴ ∠BAD =12∠BAC = 12×80°=40°.∵ DE ∥AB ,∴ ∠ADE =∠BAD =40°. 20.解:∠ECD =15°.理由:如图,过点E 作EF ∥AB , 由平行线的性质定理,得 ∠BAE =∠AEF ,∠ECD =∠FEC,从而∠ECD =∠1-∠BAE =60°-45°=15°.21.解:方法1:延长到,测量,利用邻补角的数量关系求.所以. 方法2:延长到,延长到,测量,利用对顶角相等求.所以.22.解:因为 ∠FOC =90°,∠1=40°,AB 为直线,所以∠3+∠FOC +∠1=180°,所以∠3=180°-90°-40°=50°. 因为∠3与∠AOD 互补,所以∠AOD =180°-∠3=130°. 因为OE 平分∠AOD ,所以∠2=21∠AOD =65°. 23.解:∠1和∠2是直线被直线所截形成的同位角,∠1和∠3是直线被直线所截形成的同位角.24.(1)证明:∵ CF 平分∠DCE ,∴ ∠1=∠2=12∠DCE . ∵ ∠DCE =90°,∴ ∠1=45°. ∵ ∠3=45°,∴ ∠1=∠3.∴ AB ∥CF (内错角相等,两直线平行). (2)解:∵ ∠D =30°,∠1=45°, ∴ ∠DFC =180°-30°-45°=105°.25.解:∵∠EMB=50°,∴∠BMF=180°-∠EMB=130°.∵MG平分∠BMF,∴∠BMG=12∠BMF=65°.∵AB∥CD,∴∠1=∠BMG=65°.【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
华师大新版七年级上学期《5.2 平行线》2019年同步练习卷一.选择题(共23小题)1.下列说法:①用两根钉子固定一根木条,体现数学事实是两点之间线段最短;②射线AB与射线BA表示同一条射线;③若AB=BC,则B为线段AC的中点;④不相交的两条直线叫做平行线;⑤过一点有且只有一条直线与已知直线垂直,其中正确的有()A.0个B.1个C.2个D.3个2.下列说法中,正确的有()①过两点有且只有一条直线;②有AB=MA+MB,AB<NA+NB,则点M在线段AB上,点N在线段AB外;③一条射线把一个角分成两个角,这条射线叫这个角的平分线;④40°50′=40.5°;⑤不相交的两条直线叫做平行线.A.1个B.2个C.3个D.4个3.下列说法中,正确的是()A.两条不相交的直线叫做平行线B.一条直线的平行线有且只有一条C.在同一平面内,若直线a∥b,a∥c,则b∥cD.若两条线段不相交,则它们互相平行4.下列说法正确的有()①两点之间的所有连线中,线段最短;②相等的角叫对顶角;③过一点有且只有一条直线与已知直线平行;④过一点有且只有一条直线与已知直线垂直;⑤两点之间的距离是两点间的线段;⑥在同一平面内的两直线位置关系只有两种:平行或相交.A.1个B.2个C.3个D.4个5.如图,直线a、b被直线c所截,下列条件中,不能判定a∥b的是()A.∠2=∠4B.∠4=∠5C.∠1=∠3D.∠1+∠4=180°6.如图,下列条件中,能判断直线a∥b的有()个.①∠1=∠4;②∠3=∠5;③∠2+∠5=180°;④∠2+∠4=180°A.1B.2C.3D.47.平面上五条直线l1,l2,l3,l4和l5相交的情形如图所示,根据图中标出的角度,下列叙述正确的是()A.l1和l3不平行,l2和l3平行B.l1和l3不平行,l2和l3不平行C.l1和l3平行,l2和l3平行D.l1和l3平行,l2和l3不平行8.如图,点E在延长线上,下列条件中不能判定BD∥AC的是()A.∠1=∠2B.∠3=∠4C.∠5=∠C D.∠C+∠BDC=180°9.下列结论正确的是()A.同位角相等B.同一平面内,不相交的两条直线叫做平行线C.过一点有且只有一条直线与已知直线平行D.垂直于同一条直线的两条直线互相平行10.如图,在下列四组条件中,不能判断AB∥CD的是()A.∠1=∠2B.∠3=∠4C.∠ABD=∠BDC D.∠ABC+∠BCD=180°11.如图,点E在AC的延长线上,下列条件能判断AB∥CD的是()A.∠1=∠2B.∠3=∠4C.∠D=∠DCE D.∠D+∠ACD=180°12.下列叙述,其中不正确的是()A.过一点有且只有一条直线与已知直线平行B.同角(或等角)的余角相等C.两点确定一条直线D.两点之间的所有连线中,线段最短13.下列说法中①过一点有且只有一条直线与已知直线平行;②在同一平面内,过一点有且只有一条直线与已知直线垂直;③两直线平行,同旁内角互补;④直线外一点到已知直线的垂线段就是点到直线的距离,其中正确的有()个A.4个B.3个C.2个D.1个14.下列说法正确的是()A.经过已知一点有且只有一条直线与已知直线平行B.两个相等的角是对顶角C.互补的两个角一定是邻补角D.直线外一点与直线上各点连接的所有线段中,垂线段最短15.下列结论中,不正确的是()A.两点确定一条直线B.两点之间,直线最短C.等角的余角相等D.过直线外一点,有且只有一条直线与已知直线平行16.下列说法错误的是()A.两点之间线段最短B.在同一平面内,过一点有且只有一条直线与已知直线垂直C.同角的余角相等D.过一点有且只有一条直线与已知直线平行17.下列说法正确的是()A.两点之间的直线最短B.当时钟指向3:30时,时针与分针的夹角是90°C.平面内,过一点有且只有一条直线与已知直线垂直D.平面内,过一点有且只有一条直线与已知直线平行18.已知直线m∥n,将一块含30°角的直角三角板ABC,按如图所示方式放置,其中A、B两点分别落在直线m、n上,若∠1=25°,则∠2的度数是()A.25°B.30°C.35°D.55°19.如图,AB∥DC,点E在BC上,且∠D=∠CED,∠D=74°,则∠B的度数为()A.68°B.32°C.22°D.16°20.如图,AB∥CD,CB∥DE,点A、B、E在DC同侧,若∠B=71°,则∠D的度数为()A.71°B.109°C.119°D.142°21.如图,直线a与直线b被直线c所截,b⊥c,垂足为A,∠1=69°,若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转()A.69°B.49°C.31°D.21°22.如图,把一张长方形的纸按如图所示那样折叠,B、C两点分别落在B′,C′点处,若∠AOB′=70°,则∠B′OG的度数为()A.50°B.55°C.60°D.65°23.在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c 的距离为1cm,则a与c的距离为()A.1cm B.3cm C.5cm或3cm D.1cm或3cm 二.填空题(共7小题)24.在同一平面内,若a⊥b,b⊥c,则a与c的位置关系是.25.因为AB∥CD,EF∥AB,根据,所以.26.因为AB∥CD,EF∥CD,所以∥,理由是.27.如图,平行线a、b被直线c所截,∠1=50°,则∠2=°.28.如图,把一张长方形纸片沿AB折叠后,若∠1=48°,则∠2的大小为度.29.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和直线b之间的距离为.30.(1)如图1,在长方形ABCD中,AB=3cm,BC=2cm,则AB与CD之间的距离为cm;(2)如图2,若∠=∠,则AD∥BC;(3)如图3,DE∥BC,CD是∠ACB的平分线,∠ACB=50°,则∠EDC=度;三.解答题(共20小题)31.如图,∠ABC=∠ADC,BF,DE分别是∠ABC,∠ADC的角平分线,∠1=∠2,求证:DC∥AB.32.如图,∠5=∠CDA=∠ABC,∠1=∠4,∠2=∠3,∠BAD+∠CDA=180°,填空:证明:∵∠5=∠CDA(已知)∴∥(内错角相等两直线平行)∵∠5=∠ABC(已知)∴∥(同位角相等,两直线平行)∵∠2=∠3(已知)∴∥(内错角相等两直线平行)∵∠BAD+∠CDA=180°(已知)∴∥(同旁内角互补,两直线平行)∵∠5=∠CDA(已知),又∵∠5与∠BCD互补(邻补角的定义)∠CDA与互补(邻补角定义)∴∠BCD=∠6(等量代换)∴∥.33.如图所示,AB⊥BC,BC⊥CD,BF和CE是射线,并且∠1=∠2,试说明BF∥CE.34.如图,如果CD∥AB,CE∥AB,那么C,D,E三点是否共线?你能说明理由吗?35.如图,已知OA∥CD,OB∥CD,那么∠AOB是平角,为什么?36.a,b,c不在同一平面内,a∥b,b∥c,那么a∥c是真命题吗?37.阅读下面的证明过程,指出其错误.已知△ABC.求证:∠A+∠B+∠C=180度.证明:过A作DE∥BC,且使∠1=∠C∵DE∥BC(画图)∴∠2=∠B(两直线平行,内错角相等)∵∠1=∠C(画图)∴∠B+∠C+∠3=∠2+∠1+∠3=180°即∠BAC+∠B+∠C=180°.38.(1)如图1,点E是AB,CD之间的一点且AB∥CD,试说明:∠BED=∠B+∠D;(2)如图2,点E是AB,CD外一点且AB∥CD,结论有什么变化?39.如图所示,修高速公路需要开山洞,为节省时间,要在山两面A,B同时开工,在A处测得洞的走向是北偏东76°12′,那么在B处应按什么方向开口,才能使山洞准确接通,请说明其中的道理.40.已知:如图,BE∥GF,∠1=∠3,∠DBC=70°,求∠EDB的大小.阅读下面的解答过程,并填空(理由或数学式)解:∵BE∥GF(已知)∴∠2=∠3()∵∠1=∠3()∴∠1=()()∴DE∥()()∴∠EDB+∠DBC=180°()∴∠EDB=180°﹣∠DBC(等式性质)∵∠DBC=()(已知)∴∠EDB=180°﹣70°=110°41.如图,∠E=52°,∠BAC=52°,∠D=110°,求∠ABD的度数.请完善解答过程,并在括号内填写相应的理论依据.解:∵∠E=52°,∠BAC=52°,(已知)∴∠E=.(等量代换)∴∥.()∴+∠D=180°()∵∠D=110°,(已知)∴∠ABD=70°.(等式的性质)42.如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.请完善解答过程,并在括号内填写相应的理论依据.解:∵∠E=50°,∠BAC=50°,(已知)∴∠E=(等量代换)∴∥.()∴∠ABD+∠D=180°.()∴∠D=110°,(已知)∴∠ABD=70°.(等式的性质)43.【感知】如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BEE+∠DCE=∠AEC.下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式):解:如图①,过点E作EF∥AB∴∠BAE=∠1()∵AB∥CD()∴CD∥EF()∴∠2=∠DCE∴∠BAE+∠DCE=∠1+∠2()∴∠BAE+∠DCE=∠AEC【探究】当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠FGC+∠DCE=360°;【应用】点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③.若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG=°.44.如图,在四边形ABCD中,E、F分别是CD、AB延长线上的点,连结EF,分别交AD、BC于点G、H.若∠1=∠2,∠A=∠C,试说明AD∥BC和AB∥CD.请完成下面的推理过程,并填空(理由或数学式):∵∠1=∠2()∠1=∠AGH()∴∠2=∠AGH()∴AD∥BC()∴∠ADE=∠C()∵∠A=∠C()∴∠ADE=∠A∴AB∥CD()45.如图,在下列解答中,填写适当的理由或数学式:(1)∵∠ABD=∠CDB,(已知)∴∥()(2)∵∠ADC+∠DCB=180°,(已知)∴∥()(3)∵AD∥BE,(已知)∴∠DCE=∠()(4)∵∥,(已知)∴∠BAE=∠CFE.()46.如图,如果AB∥CD,∠B=37°,∠D=37°,那么BC与DE平行吗?完成下面解答过中的填空或填写理由.解:∵AB∥CD(已知),∴∠B=()∵∠B=∠D=37°(已知)∴=∠D(等量代换)∴BC∥DE().47.如图,直线a∥b,直线AB与a,b分别相交于点A,B,AC⊥AB,AC交直线b于点C.(1)若∠1=60°,求∠2的度数;(2)若AC=3,AB=4,BC=5,求a与b的距离.48.如图,长方形ABCD中,AB=6cm,长方形的面积为24cm2,求AB与CD之间的距离.49.已知直线a,b,a平行于b,过直线a上任意两点A,B分别向直线b作垂线,交直线b于点C,D.(1)线段AC,BD所在的直线有怎样的位置关系?(2)比较线段AC,BD的长短.50.如图,已知S△ABC=S△ABD,求证:AB∥CD.华师大新版七年级上学期《5.2 平行线》2019年同步练习卷参考答案与试题解析一.选择题(共23小题)1.下列说法:①用两根钉子固定一根木条,体现数学事实是两点之间线段最短;②射线AB与射线BA表示同一条射线;③若AB=BC,则B为线段AC的中点;④不相交的两条直线叫做平行线;⑤过一点有且只有一条直线与已知直线垂直,其中正确的有()A.0个B.1个C.2个D.3个【分析】根据平行线、相交线等相关知识解答.【解答】解:①用两根钉子固定一根木条,体现数学事实是两点确定一条直线,此结论错误;②射线AB与射线BA的起点不同、方向不同,不是同一射线,此结论错误;③若AB=BC,则B不一定是线段AC的中点,此结论错误;④同一平面内不相交的两条直线叫做平行线,此结论错误;⑤同一平面内,过一点有且只有一条直线与已知直线垂直,此结论错误;故选:A.【点评】本题主要考查了射线,垂线与平行线,解题的关键是熟记平行线与射线的定义及垂线的性质.2.下列说法中,正确的有()①过两点有且只有一条直线;②有AB=MA+MB,AB<NA+NB,则点M在线段AB上,点N在线段AB外;③一条射线把一个角分成两个角,这条射线叫这个角的平分线;④40°50′=40.5°;⑤不相交的两条直线叫做平行线.A.1个B.2个C.3个D.4个【分析】利用直线的性质,度分秒的换算,以及角平分线定义判断即可.【解答】解:①过两点有且只有一条直线,正确;②有AB=MA+MB,AB<NA+NB,则点M在线段AB上,点N在线段AB外,正确;③在角的内部,一条射线把一个角分成两个角,这条射线叫这个角的平分线,错误;④40°50′=40.83°,错误;⑤在一个平面内,不相交的两条直线叫做平行线,错误.故选:B.【点评】此题考查了平行线,直线的性质,度分秒的换算,以及角平分线定义,熟练掌握各自的性质是解本题的关键.3.下列说法中,正确的是()A.两条不相交的直线叫做平行线B.一条直线的平行线有且只有一条C.在同一平面内,若直线a∥b,a∥c,则b∥cD.若两条线段不相交,则它们互相平行【分析】根据平行线的定义、性质、判定方法判断,排除错误答案.【解答】解:A、平行线的定义:在同一平面内,两条不相交的直线叫做平行线.故错误;B、过直线外一点,有且只有一条直线与已知直线平行.故错误;C、在同一平面内,平行于同一直线的两条直线平行.故正确;D、根据平行线的定义知是错误的.故选:C.【点评】本题考查平行线的定义、性质及平行公理,熟练掌握公理和概念是解决本题的关键.4.下列说法正确的有()①两点之间的所有连线中,线段最短;②相等的角叫对顶角;③过一点有且只有一条直线与已知直线平行;④过一点有且只有一条直线与已知直线垂直;⑤两点之间的距离是两点间的线段;⑥在同一平面内的两直线位置关系只有两种:平行或相交.A.1个B.2个C.3个D.4个【分析】①根据两点之间线段最短判断.②对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.③根据平行公理进行判断.④根据垂线的性质进行判断.⑤距离是指的长度.⑥根据在同一平面内,两条不重合的直线的位置关系.【解答】解:①两点之间的所有连线中,线段最短,故①正确.②相等的角不一定是对顶角,故②错误.③经过直线外一点有且只有一条直线与已知直线平行,故③错误.④同一平面内,过一点有且只有一条直线与已知直线垂直,故④错误.⑤两点之间的距离是两点间的线段的长度,故⑤错误.⑥在同一平面内,两直线的位置关系只有两种:相交和平行,故⑥正确.综上所述,正确的结论有2个.故选:B.【点评】本题主要考查对平行线的定义,两点间的距离,相交线等知识点的理解和掌握,能熟练地运用性质进行说理是解此题的关键.5.如图,直线a、b被直线c所截,下列条件中,不能判定a∥b的是()A.∠2=∠4B.∠4=∠5C.∠1=∠3D.∠1+∠4=180°【分析】根据平行线的判定定理,对各选项进行判断即可.【解答】解:若∠2=∠4,则a∥b,故A选项能判定a∥b;若∠4=∠5,则a∥b,故B选项能判定a∥b;若∠1=∠3,则不能得到a∥b,故C选项不能判定a∥b;若∠1+∠4=180°,则a∥b,故D选项能判定a∥b;故选:C.【点评】本题考查了平行线的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.6.如图,下列条件中,能判断直线a∥b的有()个.①∠1=∠4;②∠3=∠5;③∠2+∠5=180°;④∠2+∠4=180°A.1B.2C.3D.4【分析】根据平行线的判定方法,对各选项分析判断后利用排除法求解.【解答】解:∵∠1=∠4,∴a∥b;∵∠3=∠5,∴a∥b,∵∠2+∠5=180°,∴a∥b,∴能判断直线a∥b的有3个,故选:C.【点评】本题考查了平行线的判定,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行,解题时要认准各角的位置关系.7.平面上五条直线l1,l2,l3,l4和l5相交的情形如图所示,根据图中标出的角度,下列叙述正确的是()A.l1和l3不平行,l2和l3平行B.l1和l3不平行,l2和l3不平行C.l1和l3平行,l2和l3平行D.l1和l3平行,l2和l3不平行【分析】直接利用平行线的判定方法分别判断得出答案.【解答】解:由题意可得:∠1=88°,利用同位角相等,两直线平行可得l2和l3平行,∵92°+92°≠180°,∴l1和l3不平行.故选:A.【点评】此题主要考查了平行线的判定,正确掌握判定方法是解题关键.8.如图,点E在延长线上,下列条件中不能判定BD∥AC的是()A.∠1=∠2B.∠3=∠4C.∠5=∠C D.∠C+∠BDC=180°【分析】根据平行线的判定方法直接判定即可.【解答】解:选项A中,∠1与∠2是直线AC、BD被AD所截形成的内错角,因为∠1=∠2,所以应是AC∥BD,故A选项不合题意.选项B中,∵∠3=∠4,∴AB∥CD(内错角相等,两直线平行),不能判定BD∥AC,所以B选项符合题意;选项C中,∵∠5=∠C,∴BD∥AC(内错角相等,两直线平行),所以C选项不合题意;选项D中,∵∠C+∠BDC=180°,∴BD∥AC(同旁内角互补,两直线平行),所以D选项不合题意;故选:B.【点评】本题主要考查了平行线的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.9.下列结论正确的是()A.同位角相等B.同一平面内,不相交的两条直线叫做平行线C.过一点有且只有一条直线与已知直线平行D.垂直于同一条直线的两条直线互相平行【分析】根据平行线的定义、性质,即可解答.【解答】解:A、两直线平行,同位角相等,故错误;B、同一平面内,不相交的两条直线叫做平行线,正确;C、过直线外一点有且只有一条直线与这条直线平行,故错误;D、在同一平面内,垂直于同一直线的两条直线互相平行,故错误;故选:B.【点评】本题考查了平行线,解决本题的关键是熟记相关性质,注意强调同一平面内.10.如图,在下列四组条件中,不能判断AB∥CD的是()A.∠1=∠2B.∠3=∠4C.∠ABD=∠BDC D.∠ABC+∠BCD=180°【分析】根据各选项中各角的关系,利用平行线的判定定理,分别分析判断AB、CD是否平行即可.【解答】解:A、∵∠1=∠2,∴AD∥BC(内错角相等,两直线平行),故A不能判断;B、∵∠3=∠4,∴AB∥CD(内错角相等,两直线平行),故B能判断;C、∵∠ABD=∠BDC,∴AB∥CD(内错角相等,两直线平行),故C能判断;D、∵∠ABC+∠BCD=180°,∴AB∥CD(同旁内角互补,两直线平行),故D能判断;故选:A.【点评】本题考查了平行线的判定.掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行是解题的关键.11.如图,点E在AC的延长线上,下列条件能判断AB∥CD的是()A.∠1=∠2B.∠3=∠4C.∠D=∠DCE D.∠D+∠ACD=180°【分析】根据平行线的判定定理即可直接作出判断.【解答】解:A.根据内错角相等,两直线平行即可证得AB∥BC;B.根据内错角相等,两直线平行即可证得BD∥AC,不能证AB∥CD;C.根据内错角相等,两直线平行即可证得BD∥AC,不能证AB∥CD;D.根据同旁内角互补,两直线平行,即可证得BD∥AC,不能证AB∥CD.故选:A.【点评】本题考查了平行线的判定定理,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.12.下列叙述,其中不正确的是()A.过一点有且只有一条直线与已知直线平行B.同角(或等角)的余角相等C.两点确定一条直线D.两点之间的所有连线中,线段最短【分析】根据平行公理,线段的性质,直线的性质,余角的性质,可得答案.【解答】解:A、过直线外一点有且只有一条直线与已知直线平行,错误;B、同角(或等角)的余角相等,正确;C、两点确定一条直线,正确;D、两点之间的所有连线中,线段最短,正确;故选:A.【点评】本题考查平行线的判定定理以及平行线的性质.注意过直线外一点有且只有一条直线与已知直线平行.13.下列说法中①过一点有且只有一条直线与已知直线平行;②在同一平面内,过一点有且只有一条直线与已知直线垂直;③两直线平行,同旁内角互补;④直线外一点到已知直线的垂线段就是点到直线的距离,其中正确的有()个A.4个B.3个C.2个D.1个【分析】根据平行公理,平行线的性质,点到直线的距离判断即可.【解答】解:①在同一平面内,过一点有且只有一条直线与已知直线平行;错误;②在同一平面内,过一点有且只有一条直线与已知直线垂直;正确;③两直线平行,同旁内角互补;正确;④直线外一点到已知直线的垂线段的长度就是点到直线的距离,错误;故选:C.【点评】本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.14.下列说法正确的是()A.经过已知一点有且只有一条直线与已知直线平行B.两个相等的角是对顶角C.互补的两个角一定是邻补角D.直线外一点与直线上各点连接的所有线段中,垂线段最短【分析】根据平行公理,对顶角的定义,邻补角的定义,以及垂线段最短的性质对各选项分析判断后利用排除法求解.【解答】解:A、应为在同一平面内,经过直线外一点有且只有一条直线与已知直线平行,故本选项错误;B、对顶角相等,但相等的两个角不一定是对顶角,故本选项错误;C、邻补角互补,但互补的两个角不一定是邻补角,故本选项错误;D、直线外一点与直线上各点连接的所有线段中,垂线段最短,故本选项正确.故选:D.【点评】本题考查了平行公理,对顶角的定义,邻补角的定义,垂线段最短,是基础概念题.15.下列结论中,不正确的是()A.两点确定一条直线B.两点之间,直线最短C.等角的余角相等D.过直线外一点,有且只有一条直线与已知直线平行【分析】分别利用平行公理以及直线的性质和线段的性质、互为余角的性质分别分析得出答案.【解答】解:A、两点确定一条直线,正确,不合题意;B、两点之间,线段最短,故此选项错误,符合题意;C、等角的余角相等,正确,不合题意;D、过直线外一点,有且只有一条直线与已知直线平行,正确,不合题意;故选:B.【点评】此题主要考查了平行公理以及直线的性质和线段的性质、互为余角的性质,正确把握相关性质是解题关键.16.下列说法错误的是()A.两点之间线段最短B.在同一平面内,过一点有且只有一条直线与已知直线垂直C.同角的余角相等D.过一点有且只有一条直线与已知直线平行【分析】直接利用线段的性质以及互余的性质和垂线等知识,分析得出答案.【解答】解:A、两点之间线段最短,正确,不合题意;B、在同一平面内,过一点有且只有一条直线与已知直线垂直,正确,不合题意;C、同角的余角相等,正确,不合题意;D、过直线外一点有且只有一条直线与已知直线平行,故此选项错误.故选:D.【点评】此题主要考查了平行公理、线段的性质以及互余的性质和垂线,正确把握相关定义是解题关键.17.下列说法正确的是()A.两点之间的直线最短B.当时钟指向3:30时,时针与分针的夹角是90°C.平面内,过一点有且只有一条直线与已知直线垂直D.平面内,过一点有且只有一条直线与已知直线平行【分析】根据平行线,垂线,钟面角等知识依次进行判断.【解答】解:A、两点之间的线段最短,错误;B、3:30时,时针与分针之间有2.5个大格,每个大格是30°,故时针与分针的夹角是30°×2.5=75°,错误;C、正确;D、应强调过直线外一点,错误.故选:C.【点评】本题考查了平行线,垂线,钟面角等概念,熟练掌握各个知识点是解本题的关键.18.已知直线m∥n,将一块含30°角的直角三角板ABC,按如图所示方式放置,其中A、B两点分别落在直线m、n上,若∠1=25°,则∠2的度数是()A.25°B.30°C.35°D.55°【分析】根据平行线的性质即可得到∠3的度数,再根据三角形内角和定理,即可得到结论.【解答】解:∵直线m∥n,∴∠3=∠1=25°,又∵三角板中,∠ABC=60°,∴∠2=60°﹣25°=35°,故选:C.【点评】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.19.如图,AB∥DC,点E在BC上,且∠D=∠CED,∠D=74°,则∠B的度数为()A.68°B.32°C.22°D.16°【分析】根据三角形内角和定理和等腰三角形性质求出∠C,根据平行线性质得出∠B=∠C,代入求出即可.【解答】解:∵∠D=∠CED,∠D=74°,∴∠DEC=∠D=74°,∴∠C=180°﹣74°﹣74°=32°,∵AB∥CD,∴∠B=∠C=32°,故选:B.【点评】本题考查了两直线平行,内错角相等的性质,等腰三角形两底角相等的性质,熟记性质是解题的关键.20.如图,AB∥CD,CB∥DE,点A、B、E在DC同侧,若∠B=71°,则∠D的度数为()A.71°B.109°C.119°D.142°【分析】直接利用平行线的性质,两直线平行内错角相等,得出∠C的度数,进而得出∠D 的度数.【解答】解:∵AB∥CD,∴∠B=∠C=71°,∵CB∥DE,∴∠D+∠C=180°,∴∠D=109°.故选:B.【点评】此题主要考查了平行线的性质,正确把握平行线的性质是解题关键.21.如图,直线a与直线b被直线c所截,b⊥c,垂足为A,∠1=69°,若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转()A.69°B.49°C.31°D.21°【分析】先根据b⊥c得出∠2的度数,再由平行线的性质定理即可得出结论.【解答】解:∵b⊥c,∴∠2=90°.∵∠1=69°,a∥b,∴直线b绕着点A顺时针旋转的度数=90°﹣69°=21°.故选:D.【点评】本题考查的是平行线的性质定理,熟知两直线平行,同位角相等是解答此题的关键.22.如图,把一张长方形的纸按如图所示那样折叠,B、C两点分别落在B′,C′点处,若∠AOB′=70°,则∠B′OG的度数为()A.50°B.55°C.60°D.65°【分析】根据折叠的性质可得出∠BOG=∠B′OG,再根据∠AOB′=70°,由平角的定义即可得出∠B′OG的度数.【解答】解:∵B、C两点落在B′、C′点处,∴∠BOG=∠B′OG,∵∠AOB′=70°,∴∠B′OG=(180°﹣∠AOB′)=×(180°﹣70°)=55°.故选:B.【点评】本题考查了角的计算以及翻折变换,注意翻折前后不变的边和角,是解此题的关键.23.在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c 的距离为1cm,则a与c的距离为()A.1cm B.3cm C.5cm或3cm D.1cm或3cm【分析】分类讨论:当直线c在a、b之间或直线c不在a、b之间,然后利用平行线间的距离的意义分别求解.【解答】解:当直线c在a、b之间时,∵a、b、c是三条平行直线,而a与b的距离为4cm,b与c的距离为1cm,∴a与c的距离=4﹣1=3(cm);当直线c不在a、b之间时,∵a、b、c是三条平行直线,而a与b的距离为4cm,b与c的距离为1cm,∴a与c的距离=4+1=5(cm),综上所述,a与c的距离为5cm或3cm.故选:C.【点评】本题考查了平行线之间的距离,从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离.平行线间的距离处处相等.注意分类讨论.二.填空题(共7小题)24.在同一平面内,若a⊥b,b⊥c,则a与c的位置关系是a∥c.【分析】根据在同一平面内,垂直于同一条直线的两条直线互相平行即可求解.【解答】解:∵a⊥b,b⊥c,∴a∥c.故答案为a∥c.【点评】本题考查了平行线的判定:在同一平面内,垂直于同一条直线的两条直线互相平行.25.因为AB∥CD,EF∥AB,根据两条直线都与第三条直线平行,所以这两条直线也互相平行CD∥EF.【分析】根据平行公理的推论“如果两条直线都和第三条直线平行,那么这两条直线平行”进行分析,得出正确答案.【解答】解:因为AB∥CD,EF∥AB,所以CD∥EF,依据为:如果两条直线都和第三条直线平行,那么这两条直线平行.【点评】本题考查的重点是平行公理的推论:如果两条直线都和第三条直线平行,那么这两条直线平行.26.因为AB∥CD,EF∥CD,所以AB∥EF,理由是如果两条直线都与同一条直线平行,那么这两条直线也平行.【分析】根据如果两条直线都与同一条直线平行,那么这两条直线也平行,即可得到AB∥EF.【解答】解:∵AB∥CD,EF∥CD,∴AB∥EF.。
平行线的性质(30分钟50分)一、选择题(每小题4分,共12分)1. 如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于()A.50°B.60°C.65°D.90°2. 如图,AB∥CD,DB⊥BC,∠1=40°,则∠2的度数是()A.40°B.50°C.60°D.140°3.如图,若∠DAC=∠ECA,∠ADB=35°,B在CE上,则∠DBE=()A.35°B.135°C.145°D.大小不能确定二、填空题(每小题4分,共12分)4.如图,∠1=∠2,∠3=110°,则∠4=__________度.5.(2012·长沙中考)如图,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=________度.6.珠江流域某江段江水流向经过B,C,D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE=____________度.三、解答题(共26分)7.(8分)已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AGE=50°,求∠BHF的度数.8.(9分)已知,如图所示,∠BAE+∠AED=180°,∠M=∠N.试说明∠1=∠2.【拓展延伸】9.(9分)如图,AB∥CD.完成填空,探索各图中标有数字的角之间存在的关系,并把发现的规律用符号语言表示.(1)∠1=∠2.(2)∠1+____=____.(3)____+____=∠2+____.(4)____+____+____=____+____.…(2013)____+____+…+____=____+____+…+____.答案解析1.【解析】选C.∵AB∥CD,∴∠BEF+∠1=180°,∠2=∠BEG.∵∠1=50°,∴∠BEF=130°.∵EG平分∠BEF,∴∠BEG=∠BEF=65°,∴∠2=∠BEG=65°.2.【解析】选B.如图,∵DB⊥BC,∠1=40°,∴∠3=180°-90°-∠1=180°-90°-40°=50°.∵AB∥CD,∴∠2=∠3=50°.3.【解析】选C.∵∠DAC=∠ECA,∴AD∥CE,∴∠DBC=∠AD B.∵∠ADB=35°,B在CE上,∴∠DBC=35°,∴∠DBE=145°.4.【解析】∵∠2=∠5,∠1=∠2,∴∠1=∠5,∴l1∥l2,∴∠3=∠6,∠3=110°,∴∠6=110°.∵∠4+∠6=180°,∴∠4=180°-110°=70°.答案:705.【解析】∵AB∥CD∥EF,∴∠BAC+∠ACD=180°,∠DCE+∠CEF=180°,∴∠BAC+∠ACE+∠CEF=∠BAC+∠ACD+∠DCE+∠CEF=180°+180°=360°.答案:3606.【解析】如图,过点C作CF∥AB,∴∠B CF+∠ABC=180°,∴∠BCF=60°,∴∠DCF=20°.由题意得AB∥DE,∴CF∥DE,∴∠CDE=∠DCF=20°.答案:207.【解析】∵AB∥CD,∴∠BHF+∠HFD=180°,∠CFG=∠AGE=50°,∴∠GFD=130°.又FH平分∠EFD,∴∠HFD=∠EFD=65°,∴∠BHF=180°-∠HFD=115°.8.【解析】∵∠BAE+∠AED=180°(已知),∴AB∥CD(同旁内角互补,两直线平行),∴∠BAE=∠AEC(两直线平行,内错角相等).又∵∠M=∠N(已知),∴AN∥ME(内错角相等,两直线平行),∴∠N AE=∠MEA(两直线平行,内错角相等),∴∠BAE-∠NAE=∠AEC-∠MEA(等式性质),即∠1=∠2.【归纳整合】1.由平行线的性质可知,如果两直线平行,那么同位角的平分线互相平行;内错角的平分线互相平行;同旁内角的平分线互相垂直.2.判断两个角相等关系的依据有互余角的性质;互补角的性质;对顶角的性质及平行线的性质等.3.如果同位角相等,那么必定有内错角相等,同旁内角互补,这三者之间可以互相转化;如果三者之中有其一不成立,那么另外两个结论均不成立.9.【解析】分别过折点作AB(或CD)的平行线,根据平行线的性质从中发现规律,奇数角之和等于偶数角之和.(2)∠1+∠3=∠2,(3)∠1+∠3=∠2+∠4,(4)∠1+∠3+∠5=∠2+∠4 …(2013)∠1+∠3+…+∠2013 =∠2+∠4+…+∠2014.。
华东师大版七年级数学上册《4.2.2平行线的判定》同步测试题及答案学校:___________班级:___________姓名:___________考号:___________一、单选题1.如图,AC 与BD 交于点O ,下列条件中①12∠=∠;①34∠∠=;①256∠+∠=∠;①23180DAB ∠+∠+∠=︒,能判断AD BC ∥的有( )A .1个B .2个C .3个D .4个2.如图,下列条件中不能判定AB FD ∥的是( )A .14∠=∠B .3A ∠=∠C .2180A ∠+∠=︒D .1A ∠=∠3.如图,能判定AB //CE 的条件是( )A .B DCE ∠=∠ B .A DCE ∠=∠C .B ACE ∠=∠D .A ACD ∠=∠4.如图,下列条件中能判断AD BC ∥是 ( )A .12∠=∠B .14∠=∠C .23∠∠=D .B D ∠=∠5.如图,直线a b ,被直线c 所截,下列条件不能判断ab 的是( )A .14∠=∠B .24∠∠=C .23180∠+∠=︒D .34180∠+∠=︒6.如图,下列四个条件中能判定AD BC ∥的有( )①12∠=∠;①34∠=∠;①5DCE ∠=∠;①180BCD D ∠+∠=︒ A .①①B .①①C .①①D .①①7.直线1l 和2l ,被直线3l 所截,形成的夹角如图所示,那么添加下列哪个条件后,可判定1l 2l ∥的是( )A .12∠=∠B .13180∠+∠=︒C .12180∠+∠=︒D .15180∠+∠=︒8.如图,已知190∠=︒,为保证两条铁轨平行,添加的下列条件中,正确的是( )A .290∠=︒B .390∠=︒C .490∠=︒D .590∠=︒二、填空题9.如图,已知线段AC 和DE .点B 为DE 上一点,连接AB 、CD 相交于点O 、请添加一个条件 (只填一个即可).使AC DE ∥.10.如图,下列条件能判定AB CD ∥的是 . ①12∠=∠ ①180BAD ADC ∠+∠=︒ ①3ABC ∠=∠ ①3ADC ∠=∠11.如图所示,过点P 画直线a 的平行线b 的作法的依据是 .12.如图,请添加一个条件 ,可得AD BC ∥.13.如图,只需添加一个条件,即可以证明AB CD ∥,这个条件可以是 .(写出一个即可)三、解答题14.如图,直线AB CD ,与EF 交于M ,N 两点12∠=∠,且MQ 平分EMB ∠,NP 平分MND ∠,求证:直线AB CD ∥.15.如图,AC ①AE ,BD ①BF ,①1=35°,①2=35°.AC 与BD 平行吗?AE 与BF 平行吗?16.如图1,点A 、B 在直线1l 上,点C 、D 在直线2l 上,AE 平分BAC ∠,CE 平分ACD ∠,90EAC ACE ∠∠+=︒.判断1l 与2l 的位置关系并说明理由.17.如图,把含30︒角的直角三角尺()30FGE ∠=︒的两个顶点分别放在纸片ABCD 的两条边上,测得25FEA ∠=︒,65FGC ∠=︒直线AD 与BC 平行吗?为什么?题号 1 2 3 4 5 6 7 8 答案 CDACD ACC1.C【分析】根据平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行进行分析即可. 【详解】①12∠=∠①AD BC ∥ 故①符合题意; ①3=4∠∠ ①AB CD ∥ 故①不符合题意;①256∠+∠=∠ 156∠+∠=∠ ①12∠=∠ ①AD BC ∥ 故①符合题意;①23180DAB ∠+∠+∠=︒ ①180DAB ABC ∠+∠=︒ ①AD BC ∥ 故①符合题意;综上:可以判断AD BC ∥的有①①①; 故选:C .【点睛】本题考查了平行线的判定,正确掌握平行线的判定方法,找出被截直线是解题的关键. 2.D【分析】本题考查了平行线的判定定理,解题的关键是正确识别“三线八角”中的同位角、内错角、同旁内角,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行. 根据平行线的判定定理,对各项逐一进行判断即可.【详解】解:A 14∠=∠根据内错角相等,两直线平行可判定AB FD ∥,故此选项不符合题意;B 、3A ∠=∠根据同位角相等,两直线平行可判定AB FD ∥,故此选项不符合题意;C 、2180A ∠+∠=︒根据同旁内角互补,两直线平行可判定AB FD ∥,此选项不符合题意; D 、1A ∠=∠可判定AC DE ∥,无法判定AB FD ∥,故此选项符合题意; 故选:D . 3.A【分析】根据平行线的判定方法对各选项进行判断.【详解】解:当①B =①DCE 时AB ①CE ; 当①A =①ACE 时AB ①CE . 当①B +①BCE =180°时AB ①CE . 故答案选:A .【点睛】本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行. 4.C【分析】本题考查了平行线的判定.熟练掌握平行线的判定是解题的关键. 根据平行线的判定定理求解作答即可.【详解】解:A 中12∠=∠不能判断AD BC ∥,故不符合要求; B 中14∠=∠可得AB CD ∥,不能判断AD BC ∥,故不符合要求; C 中23∠∠=能判断AD BC ∥,故符合要求; D 中B D ∠=∠不能判断AD BC ∥,故不符合要求; 故选:C . 5.D【分析】本题考查的是平行线的判定,用到的知识点为:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行. 根据平行线的判定定理对各选项进行逐一判断即可. 【详解】解:A 14∠=∠同位角相等可以判定a b ;B 24∠∠=内错角相等可以判定ab ;C 23180∠+∠=︒同旁内角互补能判断直线a b ;D 34180∠+∠=︒不能判定a b ;故选D . 6.A【分析】本题主要考查了平行线的判定定理,运用“内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行”逐项分析判断即可,灵活运用平行线的判定定理是解题的关键.【详解】解:①1∠ 2∠是AD ,BC 被直线AC 所截的内错角,故12∠=∠可判定AD BC ∥,符合题意;①3∠,4∠是AB ,CD 被直线AC 所截的内错角,故3=4∠∠可判定AB CD ∥,但不能判定AD BC ∥,不符合题意;①DCE ∠,5∠是AB ,CD 被直线BE 所截的同位角,故5DCE ∠=∠可判定AB CD ∥,但不能判定AD BC ∥,不符合题意;①BCD ∠,D ∠是AD ,BC 被直线CD 所截的同旁内角,故180BCD D ∠+∠=︒可判定AD BC ∥,符合题意;①能判定AD BC ∥的有①① 故选:A . 7.C【分析】根据平行线的判定定理逐项分析即可.【详解】解:A .由12∠=∠不能判定12l l ∥,不符合题意; B .由13180∠+∠=︒不能判定12l l ∥,不符合题意;C .由12180∠+∠=︒可得2∠与1∠的对顶角的和是180︒,根据同旁内角互补,两直线平行可判定12l l ∥,符合题意;D .由15180∠+∠=︒不能判定12l l ∥,不符合题意; 故选:C .【点睛】本题考查了平行线的判定,熟知同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行是解题的关键. 8.C【分析】根据平行线的判定方法进行判断即可.【详解】解:A.①1与①2是邻补角,无法判断两条铁轨平行,故此选项不符合题意; B. ①1与①3与两条铁轨平行没有关系,故此选项不符合题意;C. ①1与①4是同位角,且①1=①4=90°,故两条铁轨平行,所以该选项正确;D. ①1与①5与两条铁轨平行没有关系,故此选项不符合题意; 故选:C .【点睛】本题主要考查了平行线的判定,熟练掌握平行线的判定是解答本题的关键. 9.C D ∠=∠(答案不唯一)【分析】根据平行线的判定条件即可得到答案. 【详解】解:因为C D ∠=∠,内错角相等,两直线平行所以,AC DE ∥ 故答案为:C D ∠=∠.【点睛】本题考查了平行线的判定,熟练掌握平行线的判定条件是解题关键. 10.①①①【分析】本题考查了平行线的判定,熟练掌握平行线的判定定理是解题的关键.由同位角,内错角相等及同旁内角互补等,判定两直线平行. 【详解】解:①、12∠=∠能判定AB CD ∥; ①、180BAD ADC ∠+∠=︒能判定AB CD ∥; ①、3ABC ∠=∠能判定AB CD ∥;①、3ADC ∠=∠能判定AD CB ∥,不能判定AB CD ∥; 故答案是:①①①11.内错角相等,两直线平行【分析】根据平行线的判定方法解决问题即可. 【详解】解:由作图可知12∠=∠12∠=∠a //b ∴(内错角相等两直线平行)故答案为:内错角相等,两直线平行.【点睛】本题考查作图,平行线的判定等知识,熟练掌握平行线的判定定理是解题的关键,属于中考常考题型. 12.5B ∠=∠(案不唯一)【分析】本题考查平行线的判定,关键是掌握平行线的判定方法. 由平行线的判定方法,即可得到答案. 【详解】解:①5B ∠=∠AD BC ∴∥∴添加一个条件5B ∠=∠,可得AD BC ∥.故答案为:5B ∠=∠(案不唯一)13.BAC ACD ∠=∠(答案不唯一) 【分析】根据平行线的判定即可求解. 【详解】解:①BAC ACD ∠=∠ ①AB CD ∥故答案为:BAC ACD ∠=∠(答案不唯一).【点睛】本题考查了平行线的判定,熟练掌握平行线的判定是解题的关键. 14.证明见解析【分析】本题主要考查了平行线的判定,角平分线的定义,只需要根据角平分线的定义和已知条件证明EMB MND ∠=∠,即可证明AB CD ∥. 【详解】证明:①MQ 平分EMB ∠,NP 平分MND ∠,求 ①2121EMB MND ∠=∠∠=∠, 又①12∠=∠ ①EMB MND ∠=∠ ①AB CD ∥.15.平行,,平行,理由见解析【分析】根据平行线的判定可得出AC BD ,再根据已知条件可得出EAC FBD ∠=∠,即可得出AE BF .【详解】解:AC BD ,AE BF 理由如下:135235,∠=︒∠=︒AC BD ∴(同位角相等,两直线平行)又AC AE ,BD BF ⊥⊥90EAC FBD ∴∠=∠=︒ 12EAC FBD ∴∠+∠=∠+∠AE BF ∴(同位角相等,两直线平行).【点睛】本题考查了平行线的判定,解题的关键是掌握平行线的判定的方法. 16.12l l ∥,理由见解析.【分析】先利用角平分线的定义可得2BAC EAC ∠=∠,2ACD ACE ∠=∠从而可得180BAC ACD ∠+∠=︒,然后利用平行线的判定,即可解答.【详解】解:12l l ∥,理由如下:第 11 页 共 11 页 理由:AE 平分BAC ∠,CE 平分ACD ∠2BAC EAC ∴∠=∠ 2ACD ACE ∠=∠90EAC ACE ∠+∠=︒180BAC ACD ∴∠+∠=︒12l l ∴∥.【点睛】本题考查了平行线的判定,角平分线的定义,熟知同旁内角互补,两直线平行是解题的关键.17.平行;理由见解析【分析】求出35AEG FEG FEA ∠=∠-∠=︒ 653035EGC FGC FGE ∠=∠-∠=︒-︒=︒从而得出EGC AEG ∠=∠,根据平行线的判定得出AD BC ∥.【详解】解:平行;理由如下:①30FGE ∠=︒①903060FEG ∠=︒-︒=︒①25FEA ∠=︒①35AEG FEG FEA ∠=∠-∠=︒①65FGC ∠=︒①653035EGC FGC FGE ∠=∠-∠=︒-︒=︒①EGC AEG ∠=∠①AD BC ∥.【点睛】本题主要考查了平行线的判定,三角板中的角度计算,解题的关键是熟练掌握内错角相等,两直线平行.。
七年级上学期数学《平行线》同步练习《平行线》一、选择题1.在同一平面内,两条不重合的直线的位置关系是()A.平行B.相交C.相交或平行D.垂直2.下列表示方法正确的是()A.a∥A B.AB∥cd C.A∥B D.a∥b3.P,Q都是直线l外的点,下列说法正确的是()A.连结PQ,则PQ一定与直线l垂直B.连结PQ,则PQ一定与直线l平行C.连结PQ,则PQ一定与直线l相交D.过点P只能画一条直线与直线l平行4.如图1所示,将一张长方形纸片对折三次,产生的折痕与折痕之间的位置关系是()图1A.平行B.垂直C.平行或垂直D.无法确定5.已知直线m及一点P,若过点P作一直线与m平行,那么这样的直线()A.有且只有一条B.有两条C.不存在D.不存在或只有一条6.小明与小刚就作直线的垂线与平行线讨论时有如下对话:小明:过一点A,有且只有一条直线与已知直线m平行;小刚:过一点A有且只有一条直线与已知直线m垂直.你认为他们的说法谁是正确的?()A.小明B.小刚C.都正确D.都不正确7.在同一平面内,下列判断:①过两点有且只有一条直线;②两条不同的直线有且只有一个公共点;③过一点有且只有一条直线与已知直线垂直;④过一点有且只有一条直线与已知直线平行.其中正确的有()A.1个B.2个C.3个D.4个二、填空题8.在同一平面内,与已知直线a平行的直线有_______________________条,而经过直线a外一点P,与已知直线a平行的直线有且只有________条.9.同一平面内有三条直线,如果其中只有两条直线平行,那么它们有________个交点.10.如图2,在4×6的网格中,点A,B,C,D,E,F都在格点上,连结C,D,E,F中任意两点得到的所有线段中,与线段AB平行的线段是________.图211.同一平面内的三条直线最多可将平面划分成________个部分,最少可将平面划分成________个部分.12.如图3所示是一个长方体,用平行或垂直符号表示下列两棱的位置关系:AB________A1B1,AD______BC,AA1______A1B1,CC1________C1D1.图313.如图4,图中不相交的线都是平行的,则此图中共有________组平行线段.图4三、解答题14.在如图5所示的图形中,过点M作PQ∥AB.图515.如图6,直线l1∥l2,l3与l1,l2都相交,分别按下列要求画直线l4,并回答相应的问题(在横线上填上答案即可).图6(1)在图①中画直线l4,使l4∥l1,且图中增加1个交点,则图中的同位角有________对;(2)在图②中画直线l4,使l4∥l3,且图中增加2个交点,则图中的内错角有________对;(3)在图③中画直线l4,使l4与l1,l3都不平行,且图中增加3个交点,则图中的同旁内角有________对.16.按要求画图.(1)点A,B在直线a上,点C在直线a外,画直线AC,再过点B画直线BD,使BD∥AC;(2)画∠AOB的平分线OC,在OC上取一点P,过点P画PE∥OA,交OB于点E,过点P画PF∥OB,交OA于点F;(3)画直线l1∥l2,直线l3⊥l1于点M,交l2于点N.17.在“武广高铁”的修建中,铁路路基要通过一平地上的点E,如图7,AB,CD是一河流的两岸,并且AB∥CD,E为直线AB外一点,现在要使铁路路基过点E且与岸CD平行.建筑工人在修建时过点E,修建路基EF,使EF∥AB,请说明这种作法的理由.链接听课例3归纳总结图7《平行线的判定》一、选择题1.2017·山西如图1,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是()图1A.∠1=∠3 B.∠2+∠4=180° C.∠1=∠4 D.∠3=∠42.如图2,下列说法正确的是()图2A.因为∠2=∠4,所以AD∥BCB.因为∠BAD+∠D=180°,所以AD∥BCC.因为∠1=∠3,所以AD∥BCD.因为∠BAD+∠B=180°,所以AB∥CD3.如图3,能判定EB∥AC的条件是()图3A.∠C=∠ABE B.∠A=∠EBAC.∠C+∠ABC=180°D.∠A+∠DBA=180°4.如图4,下列能判定AB∥CD的条件有()(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.图4A.1个B.2个C.3个D.4个5.如图5,∠A=70°,O是AB上一点,∠BOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转()图5A.8°B.10°C.12°D.18°6.以下四种沿AB折叠的方法中,不一定能判定两条边a,b互相平行的是()图6A.如图①,展开后测得∠1=∠2B.如图②,展开后测得∠1=∠2且∠3=∠4C.如图③,测得∠1=∠2D.如图④,展开后测得∠1+∠2=180°二、填空题7.把含30°角的三角尺按图7所示放置,要使AC∥BD,则∠DBC=______°.图78.如图8,如果∠1=65°,∠C=65°,∠D=120°,那么平行的直线是______________(用平行符号表示).图89.如图9,小明利用两块相同的三角尺分别沿三角尺的边缘画两平行直线AB和CD,这是根据____________,两直线平行.图910.如图10所示,木工师傅用角尺画出工件边缘的两条垂线,这两条垂线是否平行.______(填“是”或“否”).图1011.如图11,要判定DE∥BC,图11(1)有三条截线可以考虑,它们分别是AB,________和________;(2)当考虑截线AB时,只需同位角∠ADE与________相等,或同旁内角________与∠B互补,就能判定DE∥BC.三、解答题12.如图12,已知∠1=∠A,∠2=∠B,试说明MN∥EF.请完善解答过程,并在括号内填上相应依据.图12解:∵∠1=∠A(已知),∴______∥______().∵∠2=∠B(已知),∴______∥______(),∴MN∥EF().13.如图13是一个“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.图1314.如图14,直线AB过点C,∠2=80°,∠D=50°,∠1=∠3,AB∥DE吗?为什么?图1415.如图15所示,已知EF⊥PQ,GM⊥PQ,垂足分别为E,G,∠1=35°,∠2=35°,EF与GM平行吗?AB与CD平行吗?为什么?图15《平行线的性质》一、选择题1.2017·海南如图1,直线a∥b,c⊥a,则c与b相交所形成的∠1的度数为()图1A.45°B.60°C.90°D.120°2.如图2,已知∠1=60°,CD∥BE,那么∠B的度数为()图2A.70°B.100°C.110°D.120°3.如图3,把一块含有30°角的三角尺的两个顶点放在一把直尺的对边上.如果∠1=25°,那么∠2的度数为()图3A.25°B.35°C.45°D.55°4.如图4,已知直线AB∥CD,BE平分∠ABC,交CD于点D.若∠CDE=150°,则∠C的度数为()图4A.150°B.130°C.120°D.100°5.如图5,AB∥CD,BC平分∠ABD,已知∠C=50°,则∠D的度数为()图5A.85°B.80°C.65°D.60°6.如图6,把长方形纸片ABCD沿EF对折后使两部分重合.若∠1=50°,则∠AEF的度数为()图6A.110°B.115°C.120°D.130°7.如图7,AB∥EF,CD⊥EF于点D.若∠ABC=40°,则∠BCD等于()图7A.140°B.130°C.120°D.110°二、填空题8.如图8,直线CD∥EF,直线AB与CD,EF分别相交于点M,N.若∠1=30°,则∠2=________°.图89.如图9,AC∥BD,AE平分∠BAC交BD于点E.若∠1=64°,则∠2=________°.图910. 如图10所示,直线a∥b,直线c与直线a,b分别相交于点A,B,AM⊥b,垂足为M.若∠1=58°,则∠2=________°.图1011.把一张宽度相等的纸条按如图11所示的方式折叠,则∠1=________°.图1112.如图12,在△ABC中,∠C=90°.若BD∥AE,∠DBC=22°,则∠CAE的度数是________.图12三、解答题13.如图13,已知∠1=∠2,∠A=∠F,试说明:∠C=∠D.请补充说明过程,并在括号内填上相应理由.图13解:∵∠1=∠2(已知),∠1=∠3(____________),∴∠2=∠3(__________),∴BD∥________(____________________________),∴∠FEM=∠D(________________________).∵∠A=∠F(已知),∴AC∥________(______________________),∴∠C=∠FEM(___________________________________).又∵∠FEM=∠D(已证),∴∠C=∠D(等量代换).14.如图14,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4的度数.图1415.如图15,已知AB∥CE,∠A=∠E.试说明:∠CGD=∠FHB.图1516.如图16所示,在△ABC中,∠1∶∠2∶∠3=2∶3∶4,DE∥AB.若∠C=40°,求∠A和∠B 的度数.图1617.在三角形中,每两边所组成的角叫三角形的内角,如图17,在三角形ABC中,∠A,∠B 和∠C是它的三个内角.在学习了平行线的性质以后,我们可以用几何推理的方法说明“三角形的内角和等于180°”.已知三角形ABC,试说明∠A+∠B+∠C=180°.图17《平行线》参考答案1.C2.D3.D.4.C5.D6.B7.B8.无数一9.210.DF11.7412.∥∥⊥⊥13.914.解:如图所示.15.解:(1)l4如图①.12(2)l4如图②.8(3)l4如图③.1616.略17.解:因为EF∥AB,AB∥CD,所以EF∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行).《平行线的判定》参考答案1.D2.C3.B4.C5.C6.C7.60.8.AB∥CD9.内错角相等10.是11.(1)AC DC(2)∠B∠BDE12.MN AB内错角相等,两直线平行EF AB同位角相等,两直线平行平行于同一条直线的两直线平行13.解:OA∥BC,OB∥AC.理由:∵∠1=50°,∠2=50°,∴∠1=∠2,∴OB∥AC.∵∠2=50°,∠3=130°,∴∠2+∠3=180°,∴OA∥BC.14.解:AB∥DE.理由如下:∵∠2=80°,∠1=∠3(已知),∠1+∠2+∠3=180°(平角的定义),∴∠1=∠3=50°.又∵∠D=50°(已知),∴∠1=∠D(等量代换),∴AB∥DE(内错角相等,两直线平行).15.解:EF∥GM,AB∥CD.理由:∵EF⊥PQ,GM⊥PQ,∴∠FEP=∠MGE=90°,∴EF∥GM.又∵∠1=∠2,∴∠FEP-∠1=∠MGE-∠2,即∠AEP=∠CGE,∴AB∥CD(同位角相等,两直线平行).《平行线是性质》参考答案1.C2.D3.B.4.C.5.B.6.B7.B.8.309.122.10.3211.6512.68°13.对顶角相等等量代换CE同位角相等,两直线平行两直线平行,同位角相等DF 内错角相等,两直线平行两直线平行,内错角相等14.解:因为∠1=∠2,所以AB ∥CD(同位角相等,两直线平行),所以∠3=∠4(两直线平行,内错角相等),所以∠4=75°.15.解:∵AB ∥CE ,∴∠E =∠BFH. ∵∠A =∠E , ∴∠A =∠BFH , ∴AD ∥EF ,∴∠CGD =∠EHC. 又∵∠FHB =∠EHC ,∴∠CGD =∠FHB.16.解:因为∠1∶∠2∶∠3=2∶3∶4, 且∠1+∠2+∠3=180°,所以∠1=180°×29=40°,∠2=180°×39=60°,∠3=180°×49=80°.又因为∠C =40°,所以∠1=∠C ,所以EF ∥BC(同位角相等,两直线平行), 所以∠2=∠EDC(两直线平行,内错角相等),所以∠EDC =60°.因为DE ∥AB ,所以∠A =∠3=80°, ∠B =∠EDC =60°(两直线平行,同位角相等).17.作BC 的延长线CD ,过点C 作CE ∥AB ,如图所示.因为CE ∥AB(已作),所以∠A =∠ACE(两直线平行,内错角相等),∠B =∠ECD(两直线平行,同位角相等).又因为∠ACB +∠ACE +∠ECD =180°(平角的定义),所以∠A +∠B +∠ACB =180°.。