巧用Matlab进行主成分降维

使用Matlab进行数据降维数据降维是一种在数据分析和机器学习领域中广泛应用的技术。

它可以帮助我们从高维数据中提取出最为关键的特征，以便更好地进行数据分析和模型建立。

在这篇文章中，我们将探讨使用Matlab进行数据降维的方法和步骤，以及一些常用的降维算法。

首先，让我们引入一个简单的例子来说明数据降维的概念和应用。

假设我们有一个包含1000个样本和100个特征的数据集。

这个数据集可能来自于某个实验，记录了不同因素对结果的影响。

然而，由于每个样本具有过多的特征，我们很难直接观察和分析数据。

因此，我们希望通过数据降维的方式，找出最能代表原始数据的特征。

在Matlab中，我们可以使用主成分分析（Principal Component Analysis，PCA）算法来进行数据降维。

PCA是一种常用的线性降维方法，通过线性变换将高维数据映射到低维空间，保留大部分的信息。

在Matlab中，我们可以使用“pca”函数来实现PCA降维。

下面是一个简单的PCA降维示例代码：```matlabdata = load('data.mat'); % 加载数据[mapped_data, ~, latent] = pca(data); % 进行PCA降维explained_variance = cumsum(latent) / sum(latent); % 计算解释方差比例```在上面的代码中，我们首先使用“load”函数加载了一个名为"data.mat"的数据文件。

接下来，我们使用“pca”函数对数据进行降维。

函数返回了降维后的映射数据“mapped_data”，以及每个主成分的累计方差“latent”。

最后，我们通过计算累计方差的比例，来衡量每个主成分所解释的数据方差比例。

除了PCA之外，Matlab还提供了其他一些常用的降维算法，如多维尺度(Multidimensional Scaling，MDS)、线性判别分析(Linear Discriminant Analysis，LDA)等。

主成分分析类型：一种处理高维数据的方法.降维思想：在实际问题的钻研中,往往会涉及众多有关的变量.但是,变 量太多不但会增加计算的复杂性,而且也会给合理地分析问题和解释问题 带来困难.一般说来,虽然每个变量都提供了一定的信息,但其重要性有 所不同,而在很多情况下,变量间有一定的相关性,从而使得这些变量所 提供的信息在一定程度上有所重叠.因而人们盼望对这些变量加以“改造〞, 用为了数极少的互补相关的新变量来反映原变量所提供的绝大局部信息,通 过对新变量的分析到达解决问题的目的.、总体主成分1.1 定义J (3)P p =E[(X -E(X))(X -E(X))T ],Y p =l p X 刁心辰乂2 l pp X那么有Var(YJ =Var(l ：X) =l 上,,i =1,2,... Cov(Y j ,Y j ) =Cov(L TX,l T X) = l TE l j , j =1,2,..., p.第i 个主成分: 般地,在约束条件l ：l i =1Cov(Y j ,Y k )=『叫=0,k = 1,2,...,i 一1.设X i,X 2,…,X p 为了某实际问题所涉及的 P 个随机变量 X=(X i, X 2,…,Xp)T ,其协方差矩阵为了它是一个P阶非负定矩阵.设/TY 1 = l T X Y 2 = l ； X--= I II X I l“X 2 fp X p=»1 I 22X 2l 2p X p111(1)(2)下,求"使Var(Y i)到达最大,由此1,所确定的丫二l：X称为了X i, X2,…,X p的第i个主成分.1.2 总体主成分的计算设£是X =(X i,X2,..,X p)T的协方差矩阵,Z的特征值及相应的正交单位化特征向量分别为了‘1 - 2 - - p-0及e i,e2,...,e p,那么X的第i个主成分为了丫=q T X *1X1+42X2+ Mp X p,i =1,2,..., p, (3)此时Var(Y i)=eWe i = ",i =1,2,..., p,Cov(Y i,Y k)=eWe k =0,i =k.1.3 总体主成分的性质1.3.1 主成分的协方差矩阵及总方差记Y =(Y1,Y2,...,Y p)T为了主成分向量,贝U Y=P T X,其中P = (e1q,..,e p),且Cov(Y) =Cov(P T X) = P T EP =A = Diag( 1, 2,..., p),由此得主成分的总方差为了p p pVar(YJ = ' L=tr(P T E P) =tr(E PP T) =tr G)= Var(X i), i d i =1 i =1'、'即主成分分析是把p个原始变量Xj X2,…,X p的总方差p' Var(X j ) i =1mviy ,它说明前m 个主成分丫1, 丫2,…,ii dY m 综合提供Xj X 2,…,X p 中信息的水平 1.3.2主成分Y i 与变量X j 的相关系数由于Y=P T X ,故X=PY,从而Xj = e i j Y ie2 j Y 2Cov(Y i ,X j)= "e j .由此可得丫与X j 的相关系数为了篇'沿=.'：j j1.4 标准化变虽的主成分在实际问题中,不同的变量往往有不同的量纲,由于不同的量纲会引起各变量取值的分散程度差异较大,这时总体方差那么主要受方差较大的变 量的控制.为了了消除由于量纲的不同可能带来的影响,常采用变量标准化 的方法,即令分解成p 个互不相关变量丫1, 丫2,…,Y p 的方差之和,即p、Var(Y i )i」而 Var(YQ = k .第k 个主成分的奉献率:-p )二■■ ii =4前m 个主成分累计奉献率:x ： = Xi ", V CT ii1,2,..., p,(5)其中 f =E(X j),% =Var(X) 这时= (X1,X2,...,X p)T的协方差矩阵便是= (X i,X2,...,X p)T的相关矩阵P=(R j)p"其中Cov(X i,X j)："E(XiXj)= ' / (6) 利用X的相关矩阵p作主成分分析,有如下结论:* * *2 ,..=(X I,X2,...,X；)T为了标准化的随机向量,其协方差矩阵(即X的相关并且其中*Y iP,那么X*的第i个主成分为了* T * * X i -口i * X2 - 2= (e.) X =如1一1条一2 -\ '、- 22,i=1,2,..., p. (7)的正交单位特征向量. 第i个主成分的奉献率:p p* *' Var(Y i )=' "i =1 i=1p.—*厂Var(X,= p,(8)P的特征值, e；=(e：i,e；2,..,e；p)T为了相应于特征值前m个主成分的累计奉献率: m J; pY；与X*的相关系数为了“X; =屁*j.、样本主成分的,需要通过样本来估计.设,,, x ip ) ,i = 1,2,..., n. 为了取白X =(X i ,X 2,...,X p )T的简洁随机样本,那么样本协方差矩阵及样本相关矩阵分别_1 /Ts =(§j )p p(X k-x)(X k -x),n -1 k 」其中-_ __ . _1Ix =(X 1,X 2,..., X p ) , X jX ij , j =1,2,..., p,n i d1 ,§j—(易 - X i )( X kjn -1 kj作为了 £和P 的估计,然后按总体主成分分析的方法作样本主成分分析前面讨论的是总体主成分,但在实际问题中,一舟Z （或P ）是未知X = (Xi, Xi2,.的一个容量为了 R=(r ‘j )ppS j/SiiS jj分别以二、例题某市为了了全面分析机械类个企业的经济效益,选择了8个不同的利润指标,14企业关于这8个指标的统计数据如下表所示,试进行主成分分析c表1 14家企业的利润指标的统计数据解：样本均值向量为了：x =(27.979 10.950 9.100 8.543 11.064 14.614 1.552 14.686)T,样本协方差矩阵为了：-168.333 60.357 45.757 41.215 57.906 71.672 8.602 101.620〕37.207 16.825 15.505 23.535 29.029 4.785 44.02324.843 24.335 36.478 49.278 3.629 39.410Q —24.423 36.283 49.146 3.675 38.718S —56.046 75.404 5.002 59.723103.018 6.821 74.5231.137 6.722102.707168.33 60.357 45.758 41.216 57.906 71.672 8.602 101.62 60.357 37.20716.82515.505 23.535 29.029 4.7846 44.023 45.75816.825 24.843 24.335 36.478 49.278 3.629 39.4141.21615.505 24.335 24.423 36.283 49.146 3.6747 38.718 S =57.906 23.535 36.478 36.283 56.046 75.404 5.0022 59.723 71.672 29.02949.278 49.146 75.404103.02 6.8215 74.5238.602 4.7846 3.629 3.6747 5.0022 6.82151.137 6.7217 101.62 44.023 39.41 38.718 59.723 74.523 6.7217102.71由于S 中主对角线元素差异较大,因此我们样本相关矩阵 R 出发进行 主成分分析.样本相关矩阵R 为了:0.62202 1矩阵的特征值及相应的特征向量分别为了:一1 0.76266 0.70758 0.64281 0.59617 0.54426 10.55341 0.51434 0.51538 0.46888 0.62178 0.772850.73562 0.712140.98793 0.9776 0.97409 0.68282 0.780190.98071 0.9798 0.69735 0.773060.992350.62663 0.7871810.6303 0.72449前3个标准化样本主成分类及奉献率已到达95.184% ,故只需取前三个主成分即可前3个标准化样本主成分中各标准化变量x； = (i =1,2,...,8)前的系数即为了对应特征向量,由此得到3个标准化样本主成分为了y1= 0.32113x1 +0.29516x2+0.38912x3 +0.38472x4 +0.37955x5 +0.37087又+0.31996又+0.35546x8,y2 = -0.4151x1 -0.59766x2 +0.22974x3+0.27869x4+0.31632x5 +0.37151x6 -0.27814x7 -0.15684x8 y3 = -0.45123x1 +0.10303x^-0.039895x3 +0.053874x4-0.037292x5 +0.075186x6 +0.77059x^-0.42478x8注意到,y i近似是8个标准化变量x* = (i = 1,2,...,8)的等权重之和,是反映各企业总效应大小的综合指标,y i的值越大,那么企业的效益越好.由于y i的奉献率高达76.708%,故假设用y i的得分值对各企业进行排序,能从整体上反映企业之间的效应差异.将S中8^的值及x中各x i的值以及各企业关于X i的观测值代入y i的表达式中,可求得各企业y i的得分及其按其得分由大到小的排序结果.所以,第9家企业的效益最好,第12家企业的效益最差.Matlab 程序:[coeff,score,latent]=princomp(X)注：该函数使用协方差阵作主成分分析.主成分分析程序a=[];b=corrcoef(zscore(a))% 计算相关系数矩阵D=tril(b)% 得到三角矩阵[d,v]=eig(b)% 计算特征值和特征向量[f1,i1]=sort(y4); [f2,i2]=sort(i1);[flipud(i1),flipud(f1),f2]% 第 si 主成分得分排序y5=zscore(a)*d(:,3)% 计算第一主成分数值[f1,i1]=sort(y1); [f2,i2]=sort(i1);[flipud(i1),flipud(f1),f2]%第一主成分得分排序y=y5*(0.64/(0.64+0.84+1.04+1.17+2.36))+y4*(0.84/(0.64+0.84+1.04+1.17+2.36))+y3*(1.04/(0.64 +0.84+1.04+1.17+2.36))+y2*(1.17/(0.64+0.84+1.04+1.17+2.36))+y1*(2.36/(0.64+0.84+1.04+1.17+ 2.36)) [f1,i1]=sort(y); [f2,i2]=sort(i1);[flipud(i1),flipud(f1),f2]%y1=zscore(a)*d(:,7)% [f1,i1]=sort(y1); [f2,i2]=sort(i1); [flipud(i1),flipud(f1),f2]%y2=zscore(a)*d(:,6)%[f1,i1]=sort(y2); [f2,i2]=sort(i1); [flipud(i1),flipud(f1),f2]% y3=zscore(a)*d(:,5)% [f1,i1]=sort(y3); [f2,i2]=sort(i1); [flipud(i1),flipud(f1),f2]% y4=zscore(a)*d(:,4)% 计算第一主成分数值第一主成分得分排序计算第二主成分数值 第二主成分得分排序 计算第三主成分数值 第三主成分得分排序 计算第三主成分数值综合主成分得分排序。

主成分分析方法在许多实际问题中,多个变量之间就是具有一定的相关关系的。

因此,我们就会很自然地想到,能否在各个变量之间相关关系研究的基础上,用较少的新变量代替原来较多的变量,而且使这些较少的新变量尽可能多地保留原来较多的变量所反映的信息？事实上,这种想法就是可以实现的,这里介绍的主成分分析方法就就是综合处理这种问题的一种强有力的方法。

一、主成分分析的基本原理主成分分析就是把原来多个变量化为少数几个综合指标的一种统计分析方法,从数学角度来瞧,这就是一种降维处理技术。

假定有n 个地理样本,每个样本共有p 个变量描述,这样就构成了一个n×p 阶的地理数据矩阵:111212122212p p n n np x x x x x x X x x x ⎧⎪⎪=⎨⎪⎪⎩L L L L L LL (1)如何从这么多变量的数据中抓住地理事物的内在规律性呢？要解决这一问题,自然要在p 维空间中加以考察,这就是比较麻烦的。

为了克服这一困难,就需要进行降维处理,即用较少的几个综合指标来代替原来较多的变量指标,而且使这些较少的综合指标既能尽量多地反映原来较多指标所反映的信息,同时它们之间又就是彼此独立的。

那么,这些综合指标(即新变量)应如何选取呢？显然,其最简单的形式就就是取原来变量指标的线性组合,适当调整组合系数,使新的变量指标之间相互独立且代表性最好。

如果记原来的变量指标为x 1,x 2,…,x p ,它们的综合指标——新变量指标为z 1,z 2,…,zm(m≤p)。

则11111221221122221122,,.........................................,p p p p m m m mp p z l x l x l x z l x l x l x z l x l x l x =+++⎧⎪=+++⎪⎨⎪⎪=+++⎩L L L (2)在(2)式中,系数l ij 由下列原则来决定:(1)z i 与z j (i≠j ;i,j=1,2,…,m)相互无关;(2)z 1就是x 1,x 2,…,x p 的一切线性组合中方差最大者;z 2就是与z 1不相关的x 1,x 2,…,x p 的所有线性组合中方差最大者;……;z m 就是与z 1,z 2,……z m-1都不相关的x 1,x 2,…,x p 的所有线性组合中方差最大者。

matlab主成分-回复关于MATLAB主成分分析的介绍、原理和实现主成分分析（Principal Component Analysis, PCA）是一种经典的线性降维方法，用于在高维数据中找到主要的特征，以实现数据的降维和可视化。

在MATLAB中，PCA是一种强大的功能，可以帮助我们快速而准确地实现主成分分析，并处理大量的数据。

本文将围绕MATLAB主成分分析展开，一步一步地回答关于主题的问题，以帮助读者更好地了解和使用PCA。

第一部分：MATLAB中的主成分分析介绍1. 什么是主成分分析？主成分分析是一种无监督的降维技术，通过将高维数据映射到低维空间中，找到最能代表原始数据信息的特征向量，从而减少数据的维度。

2. 为什么要使用主成分分析？主成分分析能够帮助我们发现数据中的结构和模式，并用较少的维度进行表示。

这对于数据的可视化、数据预处理和机器学习等任务非常有用。

3. MATLAB中如何实现主成分分析？在MATLAB中，可以使用内置的函数pca来实现主成分分析。

该函数可以直接对矩阵数据进行处理，返回主成分分析的结果。

第二部分：MATLAB主成分分析的原理和步骤1. 主成分分析的原理是什么？主成分分析的核心思想是找到能够最大程度解释数据变异性的主成分。

这些主成分是原始数据的线性组合，通过对数据的协方差矩阵进行特征值分解得到。

2. MATLAB主成分分析的步骤是什么？主成分分析的步骤主要包括数据预处理、计算协方差矩阵、进行特征值分解和选择主成分。

2.1 数据预处理：在进行主成分分析之前，通常需要对数据进行预处理，如去除均值、归一化等操作，以提高数据的稳定性和准确性。

2.2 计算协方差矩阵：通过使用MATLAB内置的cov函数，可以计算出数据的协方差矩阵。

协方差矩阵描述了数据中各个变量之间的相关性。

2.3 进行特征值分解：通过使用MATLAB内置的eig函数，可以对协方差矩阵进行特征值分解，得到特征值和特征向量。

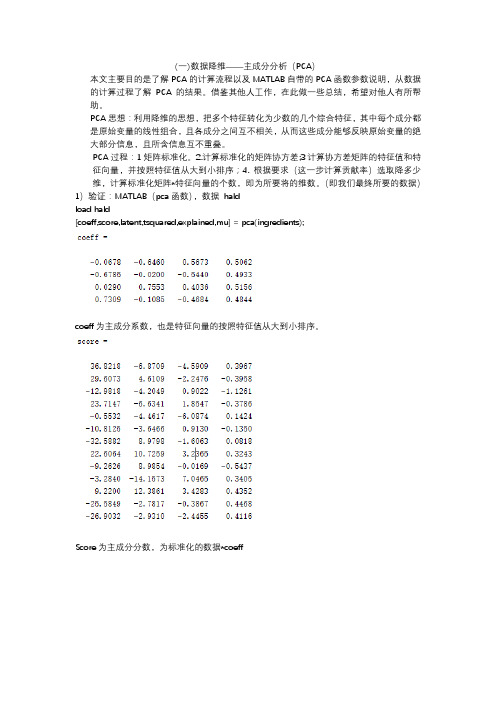
(一)数据降维——主成分分析（PCA）本文主要目的是了解PCA的计算流程以及MATLAB自带的PCA函数参数说明，从数据的计算过程了解PCA的结果。

借鉴其他人工作，在此做一些总结，希望对他人有所帮助。

PCA思想：利用降维的思想，把多个特征转化为少数的几个综合特征，其中每个成分都是原始变量的线性组合，且各成分之间互不相关，从而这些成分能够反映原始变量的绝大部分信息，且所含信息互不重叠。

PCA过程：1矩阵标准化。

2.计算标准化的矩阵协方差;3计算协方差矩阵的特征值和特征向量，并按照特征值从大到小排序；4.根据要求（这一步计算贡献率）选取降多少维，计算标准化矩阵*特征向量的个数，即为所要将的维数。

（即我们最终所要的数据）1）验证：MATLAB（pca函数），数据haldload hald[coeff,score,latent,tsquared,explained,mu] = pca(ingredients);coeff为主成分系数，也是特征向量的按照特征值从大到小排序。

Score为主成分分数，为标准化的数据*coeffLatent为主成分方差，即为从大到小排列的特征值。

Tsquared为H otelling’s T-Squared Statistic,标准化的score的平方和（每一行）Explained每个主成分的贡献率，我们可以看出前两个加在一起，一共97%多，即前两个成分都能表示数据的大部分信息。

Mu：X的每一列的均值。

以上是MATLAB自带的函数。

接下来进行验证。

数据ingredient中心化计算得分：我们发现score=F，表明能反推到原始数据（注意此结果不是唯一，接下来会表明）；至此，那么什么数据是我们想要的呢？我们知道我们要前两个主成分。

最终的结果是score的前两列就可以了（这才是我们进行PCA主要的目的）。

2）我们重新编写程序，看看有何差异1.数据中心化，我们得到X；2.计算协方差；3.计算协方差的特征值和特征向量并对特征值从大到小排序问题来了，我们发现特征值在V中从小到大排序，对特征值从大到小排序，并保持为列向量（latent），使用fliplr对U进行左右翻转，我们发现第二主成分与coeff中第二主成分的值相反，其他一致（如果维度更高的话，相反的列更多），不要着急。

主成分分析法(PCA)在实际问题中.我们经常会遇到研究多个变量的问题.而且在多数情况下.多个变量之间常常存在一定的相关性。

由于变量个数较多再加上变量之间的相关性.势必增加了分析问题的复杂性。

如何从多个变量中综合为少数几个代表性变量.既能够代表原始变量的绝大多数信息.又互不相关.并且在新的综合变量基础上.可以进一步的统计分析.这时就需要进行主成分分析。

I. 主成分分析法(PCA)模型（一）主成分分析的基本思想主成分分析是采取一种数学降维的方法.找出几个综合变量来代替原来众多的变量.使这些综合变量能尽可能地代表原来变量的信息量.而且彼此之间互不相关。

这种将把多个变量化为少数几个互相无关的综合变量的统计分析方法就叫做主成分分析或主分量分析。

主成分分析所要做的就是设法将原来众多具有一定相关性的变量.重新组合为一组新的相互无关的综合变量来代替原来变量。

通常.数学上的处理方法就是将原来的变量做线性组合.作为新的综合变量.但是这种组合如果不加以限制.则可以有很多.应该如何选择呢？如果将选取的第一个线性组合即第一个综合变量记为1F .自然希望它尽可能多地反映原来变量的信息.这里“信息”用方差来测量.即希望)(1F Var 越大.表示1F 包含的信息越多。

因此在所有的线性组合中所选取的1F 应该是方差最大的.故称1F 为第一主成分。

如果第一主成分不足以代表原来p 个变量的信息.再考虑选取2F 即第二个线性组合.为了有效地反映原来信息.1F 已有的信息就不需要再出现在2F 中.用数学语言表达就是要求0),(21 F F Cov .称2F 为第二主成分.依此类推可以构造出第三、四……第p 个主成分。

（二）主成分分析的数学模型 对于一个样本资料.观测p 个变量p x x x ,,21.n 个样品的数据资料阵为：⎪⎪⎪⎪⎪⎭⎫⎝⎛=np n n p p x x x x x x x x x X 212222111211()p x x x ,,21=其中：p j x x x x nj j j j ,2,1,21=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=主成分分析就是将p 个观测变量综合成为p 个新的变量（综合变量）.即⎪⎪⎩⎪⎪⎨⎧+++=+++=+++=ppp p p p pp p p x a x a x a F x a x a x a F x a x a x a F 22112222121212121111 简写为：p jp j j j x x x F ααα+++= 2211p j ,,2,1 =要求模型满足以下条件：①j i F F ,互不相关（j i ≠.p j i ,,2,1, =） ②1F 的方差大于2F 的方差大于3F 的方差.依次类推 ③.,2,1122221p k a a a kp k k ==+++于是.称1F 为第一主成分.2F 为第二主成分.依此类推.有第p 个主成分。

在Matlab中进行数据降维的技术实现随着科学技术和计算能力的快速发展，人们能够从各种来源获取到海量的数据。

然而，对于这些数据进行处理和分析的过程常常面临一个难题：高维问题。

高维数据不仅在存储空间上占用较大，而且难以进行可视化和分析。

因此，数据降维成为了解决高维问题的一种重要手段。

数据降维是指将高维数据映射到低维空间的过程，通过这个过程可以保留数据间的重要关系和结构信息。

在Matlab中，有多种方法可以实现数据降维，下面将介绍其中几种常用的技术。

一、主成分分析（Principal Component Analysis，PCA）主成分分析是一种常用的数据降维方法。

其基本思想是通过线性变换将原始特征映射到新的坐标系中，使得映射后的特征具有最大的方差。

Matlab中的pca函数可以直接应用主成分分析算法进行数据降维。

例如，我们有一组高维数据X，其中每一行表示一个样本，每一列表示一个特征。

我们可以使用以下代码将数据降至二维：```[coeff,score,latent] = pca(X);Y = X * coeff(:,1:2);```代码中，coeff表示主成分的系数矩阵，score表示映射后的特征矩阵，latent表示每个主成分的方差。

通过选择合适的主成分数，我们可以将数据降维到任意维度。

二、独立成分分析（Independent Component Analysis，ICA）独立成分分析是一种非线性的数据降维方法，它假设高维数据是由多个相互独立的信号混合而成的。

通过ICA算法，我们可以将这些信号分离出来，从而达到数据降维的目的。

在Matlab中，可以使用ica函数进行独立成分分析。

以下是一个简单的示例：```[A, S] = ica(X, 'approach', 'symm', 'g', 'tanh');Y = A * X;```代码中，A表示分离矩阵，S表示分离后的独立成分。

使用Matlab进行高维数据降维与可视化的方法数据降维是数据分析和可视化中常用的技术之一，它可以将高维数据映射到低维空间中，从而降低数据的维度并保留数据的主要特征。

在大数据时代，高维数据的处理和分析变得越来越重要，因此掌握高维数据降维的方法是一项关键技能。

在本文中，我们将介绍使用Matlab进行高维数据降维与可视化的方法。

一、PCA主成分分析主成分分析（Principal Component Analysis，PCA）是一种常用的降维方法，它通过线性变换将原始数据映射到新的坐标系中。

在新的坐标系中，数据的维度会减少，从而方便进行可视化和分析。

在Matlab中，PCA可以使用`pca`函数来实现。

首先，我们需要将数据矩阵X 传递给`pca`函数，并设置降维后的维度。

`pca`函数将返回一个降维后的数据矩阵Y和对应的主成分分析结果。

```matlabX = [1 2 3; 4 5 6; 7 8 9]; % 原始数据矩阵k = 2; % 降维后的维度[Y, ~, latent] = pca(X, 'NumComponents', k); % PCA降维explained_variance_ratio = latent / sum(latent); % 各主成分的方差解释比例```通过这段代码，我们可以得到降维后的数据矩阵Y，它的维度被减少为k。

我们还可以计算出每个主成分的方差解释比例，从而了解每个主成分对数据方差的贡献程度。

二、t-SNE t分布随机邻域嵌入t分布随机邻域嵌入（t-distributed Stochastic Neighbor Embedding，t-SNE）是一种非线性的高维数据降维方法，它能够有效地保留数据样本之间的局部结构关系。

相比于PCA，t-SNE在可视化高维数据时能够更好地展现不同类别之间的差异。

在Matlab中，t-SNE可以使用`tsne`函数来实现。

我们同样需要将数据矩阵X 传递给`tsne`函数，并设置降维后的维度。

matlab中的pca降维处理Matlab中的PCA降维处理PCA(Principal Component Analysis)，主成分分析，是一种常用的数据降维方法。

在Matlab中，有多种方法可以实现PCA降维处理。

本文将详细介绍在Matlab中如何进行PCA降维处理的一步一步操作。

1. 数据准备首先，需要准备要进行PCA降维处理的数据集。

假设我们有一个m行n列的数据矩阵X，其中m是样本数目，n是每个样本的特征数。

在Matlab中，可以使用二维矩阵来表示数据集。

例如，我们使用以下代码生成一个5行3列的数据矩阵X：matlabX = [1 2 3; 4 5 6; 7 8 9; 10 11 12; 13 14 15];2. 数据标准化在进行PCA降维处理之前，通常需要对数据进行标准化，使得每个特征具有相同的尺度。

一种常用的数据标准化方法是将每个特征减去其均值，然后除以其标准差。

在Matlab中，可以使用`zscore` 函数来实现数据标准化。

以下代码演示了如何对数据矩阵X进行标准化：matlabX_std = zscore(X);3. 计算协方差矩阵PCA的核心是计算数据的协方差矩阵。

在Matlab中，可以使用`cov` 函数来计算协方差矩阵。

以下代码演示了如何计算数据矩阵X的协方差矩阵：matlabcov_matrix = cov(X_std);4. 计算特征值和特征向量根据协方差矩阵，我们可以计算特征值和特征向量。

特征值表示数据在对应特征向量方向上的方差，而特征向量则表示数据在对应方向上的投影。

在Matlab中，可以使用`eig` 函数来计算特征值和特征向量。

以下代码演示了如何计算协方差矩阵cov_matrix的特征值和特征向量：matlab[eig_vectors, eig_values] = eig(cov_matrix);需要注意的是，特征值和特征向量的顺序是按照特征值的大小从大到小排列的。

使用MATLAB进行数据降维的最佳实践引言：数据降维是在现代数据分析和机器学习中非常重要的一项技术，主要用于减少特征维度、压缩数据和提高算法效率。

在大数据时代，如何在信息丰富的数据集中找到最具代表性的特征向量成为了一个挑战。

这篇文章将介绍如何使用MATLAB 进行数据降维的最佳实践。

一、数据降维概述数据降维是指将高维数据转化为低维数据的过程，同时保留原始数据的重要信息。

高维数据往往包含大量冗余特征，因此进行降维可以提高计算效率、减少存储空间和消除特征之间的相关性。

常用的降维方法包括主成分分析（PCA）和线性判别分析（LDA）等。

在使用这些方法时，MATLAB提供了丰富的函数和工具箱，方便我们进行高效的数据降维分析。

二、数据准备与预处理在进行数据降维之前，首先需要对原始数据进行准备和预处理。

对于数值型数据，可以进行缺失值处理、标准化和归一化等操作。

对于类别型数据，可以进行独热编码或者使用数值代替进行处理。

在使用MATLAB进行数据预处理时，可以使用函数如preprocess和normalize等进行相应操作，确保数据的一致性和准确性。

三、主成分分析（PCA）主成分分析（PCA）是常用的一种降维方法，通过线性变换将原始数据映射到新的坐标系上，使得降维后的数据保留了最大方差。

在MATLAB中，可以使用函数pca进行主成分分析。

通过设置参数，我们可以选择保留的主成分个数，从而实现数据降维。

同时，MATLAB还提供了绘制主成分分析结果的函数，如biplot和scatter等，便于我们直观地分析降维后的数据分布。

四、线性判别分析（LDA）与PCA不同，线性判别分析（LDA）是一种监督式的降维方法，主要用于分类问题。

LDA通过找到最佳投影方向，使得同一类样本的投影尽可能接近，不同类样本的投影尽可能远离。

这样可以使得样本之间的区分度最大化。

在MATLAB 中，可以使用函数classify进行LDA分类，同时也提供了lda函数用于进行降维分析。