基于matlab的龙格库塔法求解布拉修斯方程

MATLAB是一种用于算法开发、数据分析、可视化和数值计算的高级技术计算语言和交互式环境。

作为一个强大的工具，MATLAB提供了许多数值计算方法，其中4级4阶Runge-Kutta方法就是其中之一。

1. Runge-Kutta方法简介Runge-Kutta方法是求解常微分方程（ODE）的数值方法之一。

在MATLAB中，用户可以使用内置的ode45函数来调用4级4阶Runge-Kutta方法。

具体来说，4级4阶Runge-Kutta方法是一种单步迭代方法，通过在每个步骤中计算斜率来逐步逼近解析解。

它的优点是数值稳定性好，适用于多种类型的微分方程。

2. Runge-Kutta方法的公式4级4阶Runge-Kutta方法的一般形式如下：$$k_1 = hf(t_n, y_n)$$$$k_2 = hf(t_n + \frac{1}{2}h, y_n + \frac{1}{2}k_1)$$$$k_3 = hf(t_n + \frac{1}{2}h, y_n + \frac{1}{2}k_2)$$$$k_4 = hf(t_n + h, y_n + k_3)$$$$y_{n+1} = y_n + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4)$$其中，$t_n$是当前的独立变量值，$y_n$是当前的解向量，h是步长，$f(t_n, y_n)$是给定点$(t_n, y_n)$处的斜率。

通过不断迭代上述公式，可以逐步求解微分方程的数值解。

3. MATLAB中的4级4阶Runge-Kutta方法的应用在MATLAB中，用户可以使用ode45函数调用4级4阶Runge-Kutta方法来求解常微分方程。

使用ode45函数的基本语法如下：```matlab[t, y] = ode45(odefun, tspan, y0)```其中，odefun是用户定义的ODE函数句柄，tspan指定了求解的时间范围，y0是初始条件。

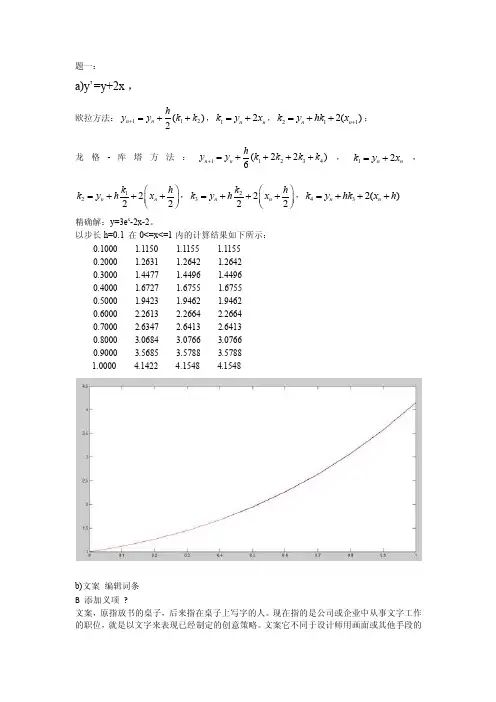
题一：a)y’=y+2x ， 欧拉方法：112()2n n h y y k k +=++，12n n k y x =+，2112()n n k y hk x +=++； 龙格-库塔方法：11234(22)6n n h y y k k k k +=++++，12n n k y x =+，12222n n k h k y h x ⎛⎫=+++ ⎪⎝⎭，23222n n k h k y h x ⎛⎫=+++ ⎪⎝⎭，432()n n k y hk x h =+++ 精确解：y=3e x -2x-2。

以步长h=0.1 在0<=x<=1内的计算结果如下所示：0.1000 1.1150 1.1155 1.11550.2000 1.2631 1.2642 1.26420.3000 1.4477 1.4496 1.44960.4000 1.6727 1.6755 1.67550.5000 1.9423 1.9462 1.94620.6000 2.2613 2.2664 2.26640.7000 2.6347 2.6413 2.64130.8000 3.0684 3.0766 3.07660.9000 3.5685 3.5788 3.57881.0000 4.1422 4.1548 4.1548b)文案 编辑词条B 添加义项 ?文案，原指放书的桌子，后来指在桌子上写字的人。

现在指的是公司或企业中从事文字工作的职位，就是以文字来表现已经制定的创意策略。

文案它不同于设计师用画面或其他手段的表现手法，它是一个与广告创意先后相继的表现的过程、发展的过程、深化的过程，多存在于广告公司，企业宣传，新闻策划等。

基本信息中文名称文案外文名称Copy目录1发展历程2主要工作3分类构成4基本要求5工作范围6文案写法7实际应用折叠编辑本段发展历程汉字"文案"(wén àn)是指古代官衙中掌管档案、负责起草文书的幕友,亦指官署中的公文、书信等;在现代，文案的称呼主要用在商业领域，其意义与中国古代所说的文案是有区别的。

龙格-库塔方法及其matlab实现摘要：本文的目的数值求解微分方程精确解，通过龙格-库塔法，加以利用matlab为工具达到求解目的。

龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法，用于数值求解微分方程。

MatLab软件是由美国Mathworks公司推出的用于数值计算和图形处理的科学计算系统环境。

MatLab是英文MATrix LABoratory（矩阵实验室）的缩写。

在MratLab环境下，用户可以集成地进行程序设计、数值计算、图形绘制、输入输出、文件管理等各项操作。

关键词：龙格-库塔 matlab 微分方程1.前言1.1：知识背景龙格－库塔法（Runge-Kutta）是用于非线性常微分方程的解的重要的一类隐式或显式迭代法。

这些技术由数学家卡尔·龙格和马丁·威尔海姆·库塔于1900年左右发明。

通常所说的龙格库塔方法是相对四阶龙格库塔而言的，成为经典四阶龙格库塔法。

该方法具有精度高，收敛，稳定，计算过程中可以改变步长不需要计算高阶导数等优点，但是仍需计算在一些点上的值，比如四阶龙格-库塔法没计算一步需要计算四步，在实际运用中是有一定复杂性的。

Matlab是在20世纪七十年代后期的事：时任美国新墨西哥大学计算机科学系主任的Cleve Moler教授出于减轻学生编程负担的动机，为学生设计了一组调用LINPACK和EISPACK库程序的“通俗易用”的接口，此即用FORTRAN编写的萌芽状态的MATLAB。

经几年的校际流传，在Little的推动下，由Little、Moler、Steve Bangert合作，于1984年成立了MathWorks公司，并把MATLAB正式推向市场。

从这时起，MATLAB的内核采用C语言编写，而且除原有的数值计算能力外，还新增了数据图视功能。

MATLAB以商品形式出现后，仅短短几年，就以其良好的开放性和运行的可靠性，使原先控制领域里的封闭式软件包（如英国的UMIST，瑞典的LUND和SIMNON，德国的KEDDC）纷纷淘汰，而改以MATLAB为平台加以重建。

函数功能编辑本段回目录ode是专门用于解微分方程的功能函数，他有ode23,ode45,ode23s等等，采用的是Runge-Kutta算法。

ode45表示采用四阶，五阶runge-kutta单步算法,截断误差为(Δx)³。

解决的是Nonstiff(非刚性)的常微分方程.是解决数值解问题的首选方法,若长时间没结果,应该就是刚性的,换用ode23来解.使用方法编辑本段回目录[T,Y] = ode45(odefun,tspan,y0)odefun 是函数句柄,可以是函数文件名,匿名函数句柄或内联函数名tspan 是区间[t0 tf] 或者一系列散点[t0,t1,...,tf]y0 是初始值向量T 返回列向量的时间点Y 返回对应T的求解列向量[T,Y] = ode45(odefun,tspan,y0,options)options 是求解参数设置,可以用odeset在计算前设定误差,输出参数,事件等[T,Y,TE,YE,IE] =ode45(odefun,tspan,y0,options)在设置了事件参数后的对应输出TE 事件发生时间YE 事件解决时间IE 事件消失时间sol =ode45(odefun,[t0 tf],y0...)sol 结构体输出结果应用举例编辑本段回目录1 求解一阶常微分方程程序:一阶常微分方程odefun=@(t,y) (y+3*t)/t^2; %定义函数tspan=[1 4]; %求解区间y0=-2; %初值[t,y]=ode45(odefun,tspan,y0);plot(t,y) %作图title('t^2y''=y+3t,y(1)=-2,1<t<4')legend('t^2y''=y+3t')xlabel('t')ylabel('y')% 精确解% dsolve('t^2*Dy=y+3*t','y(1)=-2')% ans =一阶求解结果图% (3*Ei(1) - 2*exp(1))/exp(1/t) - (3*Ei(1/t))/exp(1/t)2 求解高阶常微分方程关键是将高阶转为一阶,odefun的书写.F(y,y',y''...y(n-1),t)=0用变量替换,y1=y,y2=y'...注意odefun方程定义为列向量dxdy=[y(1),y(2)....]程序:function Testode45tspan=[3.9 4.0]; %求解区间y0=[2 8]; %初值[t,x]=ode45(@odefun,tspan,y0);plot(t,x(:,1),'-o',t,x(:,2),'-*')legend('y1','y2')title('y'' ''=-t*y + e^t*y'' +3sin2t')xlabel('t')ylabel('y')function y=odefun(t,x)y=zeros(2,1); % 列向量y(1)=x(2);y(2)=-t*x(1)+exp(t)*x(2)+3*sin(2*t);endend高阶求解结果图相关函数编辑本段回目录ode23, ode45, ode113, ode15s, ode23s, ode23t, ode23tbMatlab中龙格-库塔(Runge-Kutta)方法原理及实现(自己写的，非直接调用)龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。

用Matlab 软件：4阶经典Runger-kutta 格式解常微分方程考虑一阶常微分方程初值问题00)(),(y x y y x f y =='由Lagrange 微分中值定理知道，存在),(1+∈n n x x ε使得：⇒-='+hx y x y y n n )()()(1ε， *++='+=K h x y y h x y x y n n n *)()(*)()(1ε 其中))(,()(*εεεy f y K ='=称为)(x y 在],[1+n n x x 上的平均斜率现在问题转化为如何对*K 进行数值计算，可取)(x y 在],[1+n n x x 若干个点的斜率，或预报斜率值r K K K ⋅⋅⋅21,的加权平均∑=r i i i K a 1 （∑==ri i a 11）作为*K 的近似值。

设计],[1+n n x x 上若干个点斜率值或预报斜率值 及加权系数r K K K ⋅⋅⋅21,使得差分格式 ∑=++=ri i i n n K a h x y x y 11*)()(达到r 阶，称为r 阶Runge-kutta 格式。

由此导出四阶经典Runge-kutta 格式：)*2/,()*2/,()*2/,()()22(*6/32/1422/1312/12143211K h y x f K K h y x f K K h y x f K y x f K K K K K h y y n n n n n n n n n n +=+=+=+=++++=++++程序：(1)调用函数程序：function [x,y]=nark4(dyfun,xspan,y0,h)%用途：四阶经典Runge-Kutta 格式解常微分方程y'=f(x,y),y(x0)=y0;%格式：[x,y]=nark4(dyfun,xspan,y0,h)%dyfun 为函数f （x,y ）,xspan 为求解区间[x0,xN],y0为初始值y （x0）,h 为步长，x 返回节点，y 返回函数值解x=xspan(1):h:xspan(2);y(1)=y0;for n=1:length(x)-1k1=feval(dyfun,x(n),y(n));k2=feval(dyfun,x(n)+h/2,y(n)+h/2*k1);k3=feval(dyfun,x(n)+h/2,y(n)+h/2*k2);k4=feval(dyfun,x(n+1),y(n)+h*k3);y(n+1)=y(n)+h*(k1+2*k2+2*k3+k4)/6;endx=x';y=y';编写程序：>> dyfun=inline('y-2*x/y');>> [x,y]=nark4(dyfun,[0,1],1,0.1);plot(x,y,'-r') >> hold on>> grid on>> [x,y]=nark4(dyfun,[0,1],1,0.05);>> plot(x,y,'-g')>> hold on>> [x,y]=nark4(dyfun,[0,1],1,0.2);plot(x,y,'-b')。

matlab四阶龙格库塔法解方程组摘要：一、引言二、龙格库塔法介绍1.龙格库塔法的基本原理2.龙格库塔法的发展历程三、MATLAB 实现四阶龙格库塔法1.MATLAB 中龙格库塔法的函数2.四阶龙格库塔法的MATLAB 实现四、龙格库塔法解方程组的应用1.线性方程组的求解2.非线性方程组的求解五、结论正文：一、引言在数学领域，求解方程组是一项基本任务。

龙格库塔法作为高效数值求解线性方程组的方法，被广泛应用于各个领域。

MATLAB 作为一款强大的数学软件，可以方便地实现龙格库塔法求解方程组。

本文将介绍MATLAB 中四阶龙格库塔法解方程组的原理、实现与应用。

二、龙格库塔法介绍1.龙格库塔法的基本原理龙格库塔法（Runge-Kutta method）是一种求解常微分方程初值问题的数值方法。

它通过求解一组线性方程来逼近微分方程的解，具有较高的数值稳定性和精度。

龙格库塔法可以分为四阶、五阶等多种形式，其中四阶龙格库塔法是较为常用的一种。

2.龙格库塔法的发展历程龙格库塔法由德国数学家卡尔·龙格（Carl Runge）和英国数学家詹姆斯·库塔（James Kutta）分别在1900 年和1901 年独立发现。

自那时以来，龙格库塔法在数学、物理、工程等领域得到了广泛应用，并发展出了多种改进和扩展。

三、MATLAB 实现四阶龙格库塔法1.MATLAB 中龙格库塔法的函数在MATLAB 中，可以使用内置函数ode45、ode23、ode113 等实现龙格库塔法求解常微分方程。

这些函数分别对应四阶、五阶和三阶龙格库塔法。

2.四阶龙格库塔法的MATLAB 实现以下是一个使用MATLAB 实现四阶龙格库塔法求解方程组的示例：```matlabfunction [x, status] = solve_system_with_ode45(A, B, x0)% 定义方程组func = @(t, x) A * x + B;% 初始条件x0 = [1; 2];% 时间区间tspan = [0, 10];% 求解[x, status] = ode45(func, tspan, x0);end```四、龙格库塔法解方程组的应用1.线性方程组的求解线性方程组在数学、物理、工程等领域具有广泛应用。

龙格库塔法（Runge-Kutta method）和欧拉法（Euler's method）是两种常用的数值求解常微分方程的方法。

这里分别给出它们的MATLAB实现：1. 龙格库塔法（Runge-Kutta method）：```matlabfunction [y, t] = runge_kutta(f, y0, t0, tf, h)% f: 微分方程函数，输入为[y, t]，输出为dy/dt% y0: 初始值% t0: 初始时间% tf: 结束时间% h: 步长N = round((tf - t0) / h); % 计算迭代次数t = zeros(1, N + 1); % 初始化时间向量y = zeros(size(y0), N + 1); % 初始化解向量t(1) = t0;y(:, 1) = y0;for i = 1:Nk1 = h * f(y(:, i), t(i));k2 = h * f(y(:, i) + k1 / 2, t(i) + h / 2);k3 = h * f(y(:, i) + k2 / 2, t(i) + h / 2);k4 = h * f(y(:, i) + k3, t(i) + h);y(:, i + 1) = y(:, i) + (k1 + 2 * k2 + 2 * k3 + k4) / 6;t(i + 1) = t(i) + h;endend```2. 欧拉法（Euler's method）：```matlabfunction [y, t] = euler_method(f, y0, t0, tf, h)% f: 微分方程函数，输入为[y, t]，输出为dy/dt% y0: 初始值% t0: 初始时间% tf: 结束时间% h: 步长N = round((tf - t0) / h); % 计算迭代次数t = zeros(1, N + 1); % 初始化时间向量y = zeros(size(y0), N + 1); % 初始化解向量t(1) = t0;y(:, 1) = y0;for i = 1:Ny(:, i + 1) = y(:, i) + h * f(y(:, i), t(i));t(i + 1) = t(i) + h;endend```使用这两个函数时，需要定义一个表示微分方程的函数`f`，例如：```matlabfunction dydt = my_ode(y, t)dydt = -y; % 一个简单的一阶线性微分方程：dy/dt = -yend```然后调用相应的求解函数，例如：```matlaby0 = 1; % 初始值t0 = 0; % 初始时间tf = 5; % 结束时间h = 0.1; % 步长[y_rk, t_rk] = runge_kutta(@my_ode, y0, t0, tf, h);[y_euler, t_euler] = euler_method(@my_ode, y0, t0, tf, h);```。

Runge —Kutta 法求解布拉修斯解摘要薄剪切层方程主要有三种解法，即相似解，非相似条件下对偏微分方程组的数值解和近似解。

布拉修斯解是布拉修斯于1908年求出的，它是零攻角沿平板流动的相似解。

本文用四阶Runge —Kutta 法求解高阶微分方程的方法，并用matlab 编程实现，求得了与实际层流边界层相符合的数值解。

关键词：布拉修斯解，相似解，Runge —Kutta 法，数值解。

1 布拉修斯近似解方程二维定常不可压缩层流边界层的方程为：0=∂∂+∂∂yvx u （1）22yuv dx d y u v x u u u u e e ∂∂+=∂∂+∂∂（2）边界条件为:0=y )(,0x v u v w ==:δ=y )(x u u e =将式（1）和式（2）进行法沃克纳—斯坎变换（简称F —S 变换），将边界层方程无量纲化，即设（3）y x v u e 5.0⎪⎪⎭⎫⎝⎛=η（4）x x =得出F —S 变换后的动量方程（5）()[]()[]⎪⎭⎫ ⎝⎛∂∂''-∂'∂'='-+''++'''+x f f xf f x f m f f m f t k221211其中k 为流动类型指标，横曲率项t 为（6）212120cos 211⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛++-=ηφe u vxL r L t m 是量纲一的压力梯度参数，定义为（7）xd du u x m ee =其边界条件变为:0=η0='f:∞=η1='f 对于二维平面实壁流动（）可以忽略横曲率项t 的轴对称流动，式（5）成:0=η0=w f 为（8）()[]⎪⎭⎫ ⎝⎛∂∂''-∂'∂'='-+''++'''x f f xf f x f m f f m f 2121根据相似解的定义，方程（8）中的函数f 若式相似的，则它应只与η有关而与x 无关，即对x 的偏导数应为零。

三阶、四阶龙格库塔函数m a t l a b代码本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March三阶龙格—库塔法的计算公式为： )4(6)2,()2,2(),(3211213121K K K h y y hK hK y h x g K K h y h x g K y x g K i i i i i i i i +++=+-+=++==+ 三阶龙格—库塔公式的Matlab 程序代码：function y = DELGKT3_kuta(f, h,a,b,y0,varvec)format long;N = (b-a)/h;y = zeros(N+1,1);y(1) = y0;x = a:h:b;var = findsym(f);for i=2:N+1K1 = Funval(f,varvec,[x(i-1) y(i-1)]);K2 = Funval(f,varvec,[x(i-1)+h/2 y(i-1)+K1*h/2]);K3 = Funval(f,varvec,[x(i-1)+h y(i-1)-h*K1+K2*2*h]);y(i) = y(i-1)+h*(K1+4*K2+K3)/6;endformat short;DELGKT3_kuta函数运行时需要调用下列函数：function fv=Funval(f, varvec, varval)var= findsym(f);if length(var)<4if var(1)==varvec(1)fv=subs(f,varvec(1),varval(1));elsefv=subs(f,varvec(2),varval(2));endelsefv=subs(f,varvec,varval);end三阶龙格—库塔求解一阶常微分方程应用实例。

用三阶龙格—库塔法求下面常微分方程的数值解。

资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载龙格库塔方法及其matlab实现地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容龙格-库塔方法及其matlab实现摘要：本文的目的数值求解微分方程精确解，通过龙格-库塔法，加以利用matlab为工具达到求解目的。

龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法，用于数值求解微分方程。

MatLab软件是由美国Mathworks公司推出的用于数值计算和图形处理的科学计算系统环境。

MatLab 是英文MATrix LABoratory（矩阵实验室）的缩写。

在MratLab环境下，用户可以集成地进行程序设计、数值计算、图形绘制、输入输出、文件管理等各项操作。

关键词：龙格-库塔 matlab 微分方程前言1.1：知识背景龙格－库塔法（Runge-Kutta）是用于非线性常微分方程的解的重要的一类隐式或显式迭代法。

这些技术由数学家卡尔·龙格和马丁·威尔海姆·库塔于1900年左右发明。

通常所说的龙格库塔方法是相对四阶龙格库塔而言的，成为经典四阶龙格库塔法。

该方法具有精度高，收敛，稳定，计算过程中可以改变步长不需要计算高阶导数等优点，但是仍需计算在一些点上的值，比如四阶龙格-库塔法没计算一步需要计算四步，在实际运用中是有一定复杂性的。

Matlab是在20世纪七十年代后期的事：时任美国新墨西哥大学计算机科学系主任的Cleve Moler教授出于减轻学生编程负担的动机，为学生设计了一组调用LINPACK和EISPACK库程序的“通俗易用”的接口，此即用FORTRAN编写的萌芽状态的MATLAB。

经几年的校际流传，在Little的推动下，由Little、Moler、Steve Bangert合作，于1984年成立了MathWorks公司，并把MATLAB正式推向市场。

matlab中rungekutta方法的用法在MATLAB中，Runge-Kutta方法可以通过ode45函数实现。

ode45函数是用于求解初值问题的常微分方程组的函数，它使用了4阶和5阶的Runge-Kutta方法来计算微分方程的数值解。

下面是在MATLAB中使用ode45函数的基本语法：[t,y] = ode45(odefun,tspan,y0)其中：* odefun：函数句柄，它描述了微分方程组。

odefun应该接受两个输入参数（t和y），并返回一个列向量，该列向量包含y的每个分量的导数。

* tspan：时间跨度，它是一个包含起始时间和结束时间的向量，例如[t0 tf]。

如果省略tf，则默认为Inf。

tspan也可以是一个包含多个时间点的向量，例如[t0,t1,...,tf]。

在这种情况下，ode45将在指定的时间点返回解。

* y0：初始条件向量，它包含了在tspan起始时间点的y的值。

ode45函数返回两个输出：* t：一个列向量，包含了ode45计算解的时间点。

* y：一个矩阵，每一行包含了对应时间点t的y的值。

例如，如果我们有一个简单的微分方程组 dy/dt = -2.3y，我们可以使用以下代码在MATLAB中使用ode45函数求解：首先定义odefun函数：function dy = odefun(t,y)dy = -2.3 * y;end然后在MATLAB命令窗口中输入以下代码：tspan = [0 10]; % 时间跨度为0到10y0 = 1; % 初始条件为1[t,y] = ode45(@odefun,tspan,y0); % 使用ode45函数求解微分方程组。

佛山科学技术学院实 验 报 告课程名称 数值分析 实验项目 常微分方程问题初值问题数值解法 专业班级 姓 名 学 号 指导教师 陈剑 成 绩 日 期一. 实验目的1、理解如何在计算机上实现用Euler 法、改进Euler 法、Runge －Kutta 算法求一阶常微分方程初值问题⎩⎨⎧=∈='1)(],[),,()(y a y b a x y x f x y 的数值解。

2、利用图形直观分析近似解和准确解之间的误差。

二、实验要求（1） 按照题目要求完成实验内容； （2） 写出相应的Matlab 程序；（3） 给出实验结果(可以用表格展示实验结果)； （4） 分析和讨论实验结果并提出可能的优化实验。

（5） 写出实验报告。

三、实验步骤1、用Matlab 编写解常微分方程初值问题的Euler 法、改进Euler 法和经典的四阶Runge-Kutta 法。

2、给定初值问题⎪⎩⎪⎨⎧=≤≤-=;1)1(,21,1')1(2y x xy x y⎪⎩⎪⎨⎧=≤≤++-=31)0(10,25050')2(2y x x x y y 要求：（a ）用Euler 法和改进的Euler 法(步长均取h=0.05)及经典的四阶Runge-Kutta 法(h=0.1)求（1）的数值解，并打印)10,....2,1,0(1.01=+=i i x 的值。

(b) 用经典的四阶Runge-Kutta 方法解(2)，步长分别取h=0.1, 0.05,0.025,计算并打印)10,....2,1,0(1.0==i i x 个点的值，与准确解25031)(x e x y x +=-比较，并列表写出在x=0.2,0.5,0.8处，对于不同步长h 下的误差，讨论同一节点处，误差随步长的变化规律。

（c ）用Matlab 绘图函数绘制（2）的精确解和近似解的图形。

四、实验结果 %Euler.mfunction y = Euler(x0,xn,y0,h) %Euler 法解方程f_xy ； %x0,y0为初始条件； %x0,xn 为求值区间； %h 为步长； %求区间个数： n = (xn-x0)/h;%矩阵x 存储n+1个节点： x = [x0:h:xn]';%矩阵y 存储节点处的值： y = [y0;zeros(n,1)];%矩阵y_存储节点处导数值： y_(1)= f_xy(x0,y0); y_ = [y_(1);zeros(n,1)];%进行迭代（欧拉法迭代；求导数）： for i = 2:n+1y (i) = y(i-1)+h*y_(i-1); y_(i) = f_xy(x(i),y(i)); end%Imp_Euler.mfunction y = Imp_Euler(x0,xn,y0,h)%改进的Euler法解方程f_xy；%x0,y0为初始条件；%x0,xn为求值区间；%h为步长；%求区间个数：n = (xn-x0)/h;%矩阵x存储n+1个节点：x = [x0:h:xn]';%矩阵y存储节点处的值：y = [y0;zeros(n,1)];%矩阵y_存储节点处导数值：y_(1)= f_xy(x0,y0);y_ = [y_(1);zeros(n,1)];%使用改进Euler法求值（欧拉法求近似；近似点导数；梯形校正；求导）：for i = 2:n+1y_l = y(i-1) + h*y_(i-1);y_l = f_xy(x(i),y_l);y(i) = y(i-1) + (h/2)*(y_(i-1)+y_l);y_(i)= f_xy(x(i),y(i));end%R_Kutta4.mfunction y = R_Kutta4(x0,xn,y0,h)%Runger_Kutta法解方程f_xy；%x0,y0为初始条件；%x0,xn为求值区间；%h为步长；%求区间个数：n = (xn-x0)/h;%矩阵x存储n+1个节点：x = [x0:h:xn]';%矩阵y存储节点处的值：y = [y0;zeros(n,1)];%矩阵k1,k2,k3,k4存储各节点（中点）数值：k1(1)= f_xy(x0,y0);k1 = [k1(1);zeros(n,1)];k2(1)= f_xy(x0+h/2,y0+h*k1(1)/2);k2 = [k2(1);zeros(n,1)];k3(1)= f_xy(x0+h/2,y0+h*k2(1)/2);k3 = [k3(1);zeros(n,1)];k4(1)= f_xy(x0+h,y0+h*k3(1));k4 = [k4(1);zeros(n,1)];for i= 2:n+1y(i) = y(i-1)+(h/6)*(k1(i-1)+2*k2(i-1)+2*k3(i-1)+k4(i-1));k1(i)= f_xy(x(i),y(i));k2(i)= f_xy(x(i)+h/2,y(i)+h*k1(i)/2);k3(i)= f_xy(x(i)+h/2,y(i)+h*k2(i)/2);k4(i)= f_xy(x(i)+h,y(i)+h*k3(i));end（a）：%f_xy.mfunction y_=f_xy(x,y)%求解第五次作业第一题的点（x,y）处的导数；y_ = 1/(x^2) - y/x;%run521.mclc,clear;x0 = 1;xn = 2;h = 0.05;y0 = 1;%便于显示出x，与y对应：x = [x0:h:xn]';y = Euler(x0,xn,y0,h);YE =[x,y];y = Imp_Euler(x0,xn,y0,h); YIE= [x,y];h = 0.1;x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); YRK= [x,y];(b)： %f_xy.mfunction y_=f_xy(x,y) %求第二个方程的导数： y_ = -50*y+50*(x^2)+2*x;%run522.mclc,clear; x0 = 0; xn = 1; y0 = 1/3; %步长0.1： h = 0.1; x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); y_r= f_Real(x); Y1 = [x,y,y_r];%步长0.05： h = 0.05; x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); y_r= f_Real(x); Y2 = [x,y,y_r]; %步长0.025： h = 0.025; x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); y_r= f_Real(x); Y3 = [x,y,y_r];五、讨论分析(a)从结果可以看出使用RK 方法，步长较大但是结果也更加精确； (b)分析求值结果的误差，可以发现当步长取0.1时，误差是超级大的（10^8数量级），但是当步长缩小一半取0.05时，误差就很小了，再缩小一半，误差就更小了。

一、介绍Matlab作为一种强大的科学计算软件，提供了众多函数和工具来解决微分方程组。

其中，四阶龙格库塔函数是一种常用的数值方法，用于求解常微分方程组。

本文将介绍如何使用Matlab中的四阶龙格库塔函数来求解微分方程组，并对该方法的原理和实现进行详细说明。

二、四阶龙格库塔方法四阶龙格库塔方法是一种常用的数值方法，用于求解常微分方程组。

它是一种显式的Runge-Kutta方法，通过逐步逼近微分方程的解，在每一步使用多个中间值来计算下一步的解。

该方法通过四个中间值来计算下一步的状态，并且具有较高的精度和稳定性。

三、在Matlab中使用四阶龙格库塔方法求解微分方程组在Matlab中，可以使用ode45函数来调用四阶龙格库塔方法来解决微分方程组的问题。

ode45函数是Matlab提供的用于求解常微分方程组的函数，可以通过指定微分方程组以及初值条件来调用四阶龙格库塔方法来进行求解。

1. 定义微分方程组我们需要定义要求解的微分方程组。

可以使用Matlab中的匿名函数来定义微分方程组，例如：```matlabf = (t, y) [y(2); -sin(y(1))];```其中，f是一个匿名函数，用于表示微分方程组。

在这个例子中，微分方程组是y' = y2, y2' = -sin(y1)。

2. 指定初值条件和求解区间接下来，我们需要指定微分方程组的初值条件和求解区间。

初值条件可以通过指定一个初始时刻的状态向量来完成，例如：```matlabtspan = [0, 10];y0 = [0, 1];```其中，tspan表示求解区间，y0表示初值条件。

3. 调用ode45函数进行求解我们可以通过调用ode45函数来求解微分方程组的数值解。

具体的调用方式如下：```matlab[t, y] = ode45(f, tspan, y0);```其中，t和y分别表示求解的时间点和对应的状态值。

四、示例下面我们通过一个具体的例子来演示如何使用Matlab中的四阶龙格库塔方法来求解微分方程组。

如何用matlab求解非线性微分方程组（基于龙格库塔的数值微分算法）？例如要求解下面这个含时间的线性微分方程组，如下图所示其中：这里的tau_q，g_f，w0都是不含时间的常数：初始条件为：归一化条件：通过观察以上方程组，可以看到：每个方程等式里面并没有u（t）*v（t）这样的交叉项形式，也就是没有非线性项。

因此，用龙格库塔的数值微分算法，可以有两种思路，一种思路是利用哈密顿量矩阵去算，另外一种思路是用列向量去算。

两种代码如下解析：（1）利用哈密顿量矩阵的思路先构建一个子程序m文件，文件名为：coupled_differential_equation.m这里.m文件写入以下代码：function[U,Er,U_condition,TEST]=coupled_differential_equation(rho_0,T,L,w 0,g_f,tau_q)t=linspace(0,T,L);%最终演化时间T就等于每一个tau_qh=T/L;%h这是步长和精度，不同的tau_q，精度应该不一样C{1}=rho_0; %演化矩阵的初态for x=1:1:LTEST(1:2,x)=C{1};%这里的测试代码时用，没有其他用途，以下才是龙格库塔算法 k1=master(t(1,x),C{1},w0,g_f,tau_q);k2=master(t(1,x)+h/2,C{1}+h*k1/2,w0,g_f,tau_q);k3=master(t(1,x)+h/2,C{1}+h*k2/2,w0,g_f,tau_q);k4=master(t(1,x)+h,C{1}+h*k3,w0,g_f,tau_q);C{1}=C{1}+(k1+2*k2+2*k3+k4)*h/6;U=C{1};endEr=w0*(abs(U(2,1)))^2-(w0*g_f^2)/4*(abs(U(1,1)+U(2,1)))^2-(w0*sqr t(1-g_f^2)-w0)/2;%这是根据Er公式算写的，U（1,1）和U（2,1）就是演化到每一个最终时间T=tau_q时的解u（tau_q）和v（tau_q）解。

【SOS】在matlab中四阶Runge-Kutta法求解常微分方程匚悬赏分：150 -解决时间：2008-9-16 10:19【SOS】在matlab中四阶Runge-Kutta法求解常微分方程dx1/dt=x2 x1(0)=1e-8dx2/dt=x3 x2(0)=0dx3/dt=x4 x3(0)=0dx4/dt=f(t,x1,x2,x3,x4) x4(0)=0求解区间［0,1e-6］，在matlab中用四阶Runge-Kutta法求解，怎么用从一阶循环到四阶？有没有类似的具体算例？最好能帮小弟写个子程序希望各路高人出手相助，关乎小弟能否明年一月份顺利毕业，在此先多谢各位高人了。

提问者：zhihaikou -三级最佳答案没试过matlab，算这玩意太慢了，有fortran版的要不，有兴趣的话可以参考一下。

代码:SUBROUTINE run ge_kutta()!关于Runge-Kutta方法，该方法是用来解形如y'=f(t,y)的常微分方程的!经典的4阶R-K方法的公式如下：! Yn+1 = Yn + h/6 * (K1+2K2+2K3+K4)!其中! K仁f(Tn,Yn)! K2=f(T n+h/2,Y n+h/2*K1)! K3=f(T n+h/2,Y n+h/2*K2)! K4=f(T n+h,Y n+h*K3)type( no de_fish),po in ter :: pi7HO!S%（『!）siuo!」inu% 厂u 人 NOa%（r!）siuau;nu%r u 人NOd%（『!）siuo!」inu% 厂 u 人t7HN%（『!）siuo!」inu% 厂 u 人£ON%（『!）siuo!」inu%厂u 人（（>HO!S%lueu;nu _U!UJ >（ NOa%lueu;nu _u!iu > （ NOd%lueu;nu _u!iu >（ >HN%lueu;nu _U!UJ > eON%lueu;nu _u!iu >WW : >d31S -一ii（W+£>k0N+Z>k0N+"）*（09dois —|j ） + u 人二厂u 人L+u 人直具 *-以吐u 人甲：ed3丄S-—一ii（e>i*de;s -p+u 人'dois —：M+iuaurK ）—：|j ）uo!Qun 厂 |E 」60屮!=厂》£>UL|+u 人 POM u人'u+l DOMfeJB來：kSd3丄S ------- i（2>1*（0S/deis _p ）+UA 10S/deis _p+juajjno _p ）uo!pun4_|ej6aju!=e>j◊u ⑵q ）+u 人［1 變歪 u 人'乙/i|+i pOMfeJB Ux 來：c sd3丄s ------------- i（L>1*（0S/deis _|j ）+UA 107/deis _p+juajjno _p ）uo!pun4_|ej6aju!=3>j以*⑵L|）+u 人 H 變歪U 人'乙/1|+1 POMHB 辽X 來：2 2 C □丄s --------- i（uA^uejjno-pJuoipunPie 」6。

实验二 常微分方程数值解一、火箭飞行器㈠问题描述小型火箭初始质量为1400kg ，其中包括1080kg 燃料，火箭竖直向上发射时燃料燃烧率为18kg/s ，由此产生32000N 的推力，火箭引擎在燃料用尽时关闭，设火箭上升时空气阻力正比于速度的平方，比例系数为0.4kg/m ，求引擎关闭瞬间火箭的高度，速度，加速度及火箭达到最高点时的高度和加速度，并画出高度、速度、加速度随时间变化的图形。

㈡方法与公式1、简要分析本题的求解需要用到常微分方程，而整个过程又被分为两个阶段：火箭加速上升阶段和燃料燃尽后减速的阶段。

由题目易知第一个阶段持续时间T 1=108018=60s 列出第一阶段的方程组：设M0为火箭本身质量，m 为燃料质量，g 为重力加速度 = 9.8m/s 2,燃料燃烧率为a ，空气阻力的比例系数为k ，F 为推进力。

M0 = 1400-1080 = 320kg; v̇=F−kv 2−(M0+m )g M0+mm =−a初值v̇=0，m =1080。

由以上各式可以求出t=T 1时火箭的速度。

再求解第二阶段：v̇=−kv 2−M0g M0m =0可以求出火箭速度降为0的时刻。

将整个过程中的时间向量以及速度向量联合起来，利用第三章所学插值与数值积分的方法可以求得任意时刻火箭的近似高度。

2、方法求解常微分方程时，我分别采用了自己编写的欧拉公式、改进欧拉公式、4级4阶龙格-库塔公式，以及MATLAB自带的龙格-库塔方法，求解数值积分时采用辛普森公式。

由于Matlab自带的Simpson公式是自适应的，因此需要使用自己在上一次实验时所编的Simpson公式。

㈢结果与分析1、各种公式的对比首先，我作出了各种不同公式计算得到的火箭速度随时间变化的图像，图如下：从图中可以看出，各种公式计算得到的结果基本一致，为确定其区别，将图像放大，放大约2000 倍后，得到下图：分析：从图中可以看出，自编欧拉公式距离MATLAB 自带龙格-库塔公式最远，精度最差；自编的改进欧拉公式和自编的龙格-库塔公式结果基本一致，两者中自编龙格-库塔公式距MATLAB 自带龙格-库塔公式的结果稍近。