生活中的等腰三角形图片
- 格式:pptx
- 大小:1.82 MB
- 文档页数:11

等腰三角形和等边三角形的性质等腰三角形和等边三角形是基础的几何形状,它们有着特殊的性质和特点。
在本文中,我们将一起探讨等腰三角形和等边三角形的性质,并分析它们在几何学中的重要性。
一、等腰三角形的性质等腰三角形是指具有两条边相等的三角形。
以下是等腰三角形的主要性质:1. 两底角相等:等腰三角形的底边是两边相等的边,因此,其对应的底角相等。
即∠A = ∠C,其中A、C为等腰三角形的两个底角。
2. 顶角平分底角:等腰三角形的顶角恰好平分了底角。
也就是说,等腰三角形的顶角∠B恰好等于底角∠A和∠C的一半。
3. 等腰三角形的高线:等腰三角形的高线是连接顶点与底边垂直的线段。
在等腰三角形ABC中,高线BD垂直于底边AC,并且BD是AC的中线(即BD=DC)。
4. 等腰三角形的中线:等腰三角形中线是分别连接底边中点与顶点的线段。
在等腰三角形ABC中,中线BE与底边AC相等(即BE=EC)。
二、等边三角形的性质等边三角形是指三条边相等的三角形。
以下是等边三角形的主要性质:1. 三个内角相等:等边三角形的三个内角都相等,即∠A = ∠B =∠C = 60°。
2. 三条高线重合:等边三角形的三条高线分别由顶点向底边上的三个顶点所引。
这三条高线相交于同一个点,也就是等边三角形的垂心。
3. 等边三角形的中线:等边三角形的中线是分别连接底边中点与顶点的线段,也就是等边三角形的高线。
由于等边三角形的三边相等,中线也为等边三角形三边的中线。
三、等腰三角形和等边三角形的重要性等腰三角形和等边三角形在几何学中具有重要的应用和特点。
以下是它们的一些重要性:1. 判定等腰三角形:利用等腰三角形的性质,我们可以通过两条边的长度相等来判定一个三角形是否为等腰三角形。
2. 判定等边三角形:等边三角形的三条边相等,因此,我们可以通过三条边的长度相等来判定一个三角形是否为等边三角形。
3. 等腰三角形的应用:等腰三角形的性质常常应用在各类数学问题中,如三角函数、三角恒等式、三角面积等计算中。


等腰直角三角形中斜边等于根号二直角边等腰直角三角形是指有两条边长度相等的直角三角形。
在等腰直角三角形中,斜边等于直角边乘以根号二。
这个主题是关于三角形的特殊性质,对于数学和几何知识有很大的重要性。
下面我们将通过深入的讨论和详细的介绍来帮助你更好地理解这个主题。
一、等腰直角三角形的定义1.1 什么是等腰直角三角形等腰直角三角形是指两个直角边相等的直角三角形。
它是直角三角形中的特殊情况,具有一些独特的性质。
1.2 等腰直角三角形的性质在等腰直角三角形中,直角边和斜边之间存在一个特殊的关系,即斜边等于直角边乘以根号二。
这个性质是等腰直角三角形中特别重要的一个特征。
二、斜边等于根号二直角边的证明2.1 斜边和直角边的关系在等腰直角三角形中,根据勾股定理,直角边和斜边的关系可以用数学公式表示为:斜边的平方等于直角边的平方和。
即c² = a² + b²。
2.2 斜边等于根号二直角边的证明我们可以利用勾股定理来推导出斜边等于直角边乘以根号二的结论。
根据勾股定理的公式c² = 2a²,通过开方运算可得c = a√2。
这就证明了斜边等于直角边乘以根号二。
三、等腰直角三角形的应用3.1 等腰直角三角形在几何图形中的应用等腰直角三角形的性质和特点在几何图形中有着广泛的应用。
通过这个性质,我们可以计算三角形的各边长度和角度,从而解决各种几何问题。
3.2 等腰直角三角形在实际生活中的应用等腰直角三角形的性质也经常在实际生活中被应用。
例如在建筑工程中,利用等腰直角三角形的原理可以计算建筑结构的支撑和稳定性。
四、总结和回顾在本篇文章中,我们深入探讨了等腰直角三角形中斜边等于根号二直角边的性质,并给出了相应的证明和应用。
通过对这个主题的深入理解,我们可以更好地掌握等腰直角三角形的特点和应用。
希望通过这篇文章的阐述,你对等腰直角三角形中斜边等于根号二直角边的性质有了更清晰的认识。


生活中的图形——三角形一、知识点梳理1、定义2、分类3、关系4、常见的公式1、定义定义定义:由不在同一条直线上的三条线段首尾顺次连接所组成的图形叫做三角形注意:1、不在同一直线2、首尾顺次连接welcome to use these PowerPoint templates, New锐角三角形不等边三角形Content design, 10 years experience按角度直角三角形按边长钝角三角形等腰三角形(等边三角形)①三边之间的关系三角形任意两边之和大于第三边,任意两边之差小于第三边。
②三角之间的关系三角形三个内角之和为180°4、常见公式1、周长公式:C=a+b+c2、面积公式:S=(底*高)/2二、案例分析例1、一个三角形的两边长为2和9,第三边为奇数,则此三角形的周长是多少?分析:根据三边之间的关系,可以得出第三边的范围为7~11,而在7~11这个范围内的奇数只有9,所以第三条边为9,那么根据周长公式可知三角形周长为:2+9+9=20。
针对性练习:若一个等腰三角形的周长为17cm,一边长为3cm,则它的另一边长为分析:根据三边关系和等腰三角形的性质,可以分两种情况讨论①腰长为3cm,则另一腰长也为3cm,那么底边长为11cm,根据三边之间的关系可得无法组成三角形②底边长3cm,则腰长为(17-3)/2=7cm,即三边分别为7、7、3,根据三边关系判断可以构成三角形综上,另一边长为7cm。
三、课后练习21有下列长度的三条线段,能组成三角形的是A. 1,2,3 B. 1,2,4 C. 2,3,4 D. 2,3,6已知等腰三角形的两边长为3和6,则它的周长为()A. 9B. 12C. 15D. 12或15跟踪联系:已知等腰三角形的两边长为3和5,则它的周长为()A. 8B. 11C. 13D. 11或13谢谢。
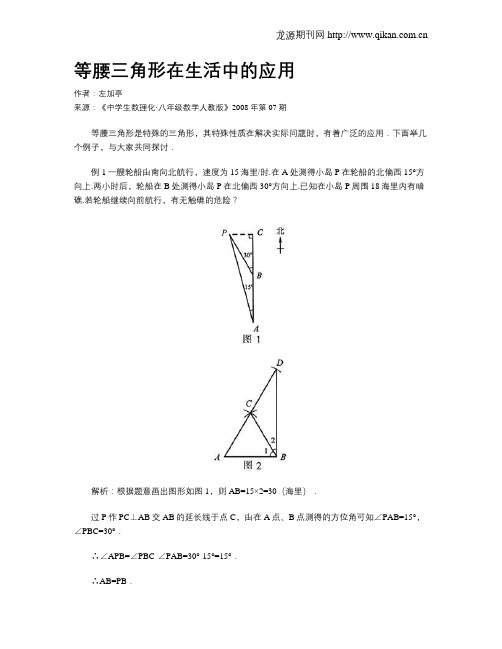
等腰三角形在生活中的应用作者:左加亭来源:《中学生数理化·八年级数学人教版》2008年第07期等腰三角形是特殊的三角形,其特殊性质在解决实际问题时,有着广泛的应用.下面举几个例子,与大家共同探讨.例1一艘轮船由南向北航行,速度为15海里/时.在A处测得小岛P在轮船的北偏西15°方向上.两小时后,轮船在B处测得小岛P在北偏西30°方向上.已知在小岛P周围18海里内有暗礁.若轮船继续向前航行,有无触礁的危险?解析:根据题意画出图形如图1,则AB=15×2=30(海里).过P作PC⊥AB交AB的延长线于点C,由在A点、B点测得的方位角可知∠PAB=15°,∠PBC=30°.∴∠APB=∠PBC-∠PAB=30°-15°=15°.∴AB=PB.在Rt△BCP中,∵∠PBC=30°,∴PC=1/2PB=1/2AB=15(海里).即点C距小岛P的距离只有15海里,而小岛周围18海里内有暗礁,所以该船继续向北航行有触礁的危险.规律总结:解此类问题,应首先正确画出图形,然后将实际问题转化成数学问题.作垂线是解这类题常用的方法之一.例2某中学学生在工厂学习时,看到工人师傅在材料的边角处画直角采用“三弧法”.如图2所示,(1)画线段AB,分别以A、B为圆心,AB长为半径画弧,相交于点C;(2)以C 为圆心,仍以AB长为半径画弧,交AC的延长线于D;(3)连接DB,则∠ABD为直角.这是为什么呢?解析:易知△ABC为等边三角形,△BCD是等腰三角形,进而可得一方程,解出即可.由画法可知,AB=AC=BC=CD.∵ AC=BC,∴∠A=∠1.∵CB=CD,∴∠D=∠2.∵∠A+∠1+∠2+∠D=180°,∴2∠1+2∠2=180°,∠1+∠2=90°,即∠ABD=90°.规律总结:在三角形中求角的度数,有时还可借助于“等边三角形的每个角都是60°”来解决.比如本题,可知∠1=60°.又△BCD为等腰三角形,且易知∠BCD=120°,故∠2=30°.相加即得结论.例3东风汽车公司冲压汽车零件后剩余的废料都是形状为等腰三角形的小钢板,如图3,其中AB=AC.该厂为了降低生产成本,变废为宝,把这些废料加工成红星农业机械厂粉碎机上的零件,销售给红星农业机械厂,但要求零件的形状都要是矩形.现在要求把如图3所示的等腰三角形钢板切割后再焊接成两种不同规格的矩形,每种矩形的面积正好等于该三角形的面积,每个钢板切割的次数最多为两次(切割的损失忽略不计).(1)请你设计两种不同的切割焊接方案,并用简要的文字加以说明.(2)若该三角形废料切割后能焊接成正方形零件(要求只切割一次),则该三角形应满足什么条件?解析:等腰三角形切割后焊接成矩形的方法很多,但解此题时要注意切割次数最多为两次的条件.(1)方案一:如图4所示.方案二:如图5所示(虚线为切割线,M、N分别为AB、AC中点,MP⊥BC).(2)若要把三角形废料只切割一次后焊接成正方形零件,则三角形应为等腰直角三角形.规律总结:应用几何知识设计图形,要勤于动脑,可能的情况下要善于动手操作.。
等腰三角形底角角平分线定理1. 引言说到三角形,大家都不会陌生吧?无论是课堂上那一张张透光的图纸,还是生活中形形色色的标志和建筑,三角形总是出现在我们眼前。
今天我们要聊的是等腰三角形中的一个小秘密——底角角平分线定理。
乍一听,这个名字好像挺高深的,其实嘛,它就像是一个温暖的朋友,轻松易懂,能带你了解三角形的一些小妙招。
2. 等腰三角形的基本概念2.1 什么是等腰三角形?等腰三角形,顾名思义,就是那种两边相等的三角形。
想象一下,你的两个手指头并排站在一起,像极了等腰三角形的两条边。
而那根连接指尖的手指,就是它的底边。
等腰三角形的一个特别之处在于,它的底角相等,简直是数学界的双胞胎!而这些底角的大小,跟它的角平分线可是有着千丝万缕的联系哦。
2.2 底角角平分线的定义那什么是底角角平分线呢?简单来说,底角角平分线就是把底角分成两个相等角度的那条线。
想象一下,假如你有一块美味的蛋糕,切蛋糕的时候,如果从中心切下去,那块蛋糕就会被分成两个一模一样的部分,这就像是底角角平分线在等腰三角形里的作用。
真是好比“分蛋糕”的哲学,讲究的是公平与美味。
3. 底角角平分线定理的内容3.1 定理的具体内容底角角平分线定理告诉我们,当你在等腰三角形中画出底角的角平分线时,这条线会把对边分成两段,使得这两段的长度相等。
也就是说,如果你把等腰三角形的两个底角用一条线分开,那么这条线会把对边切得刚刚好,真是“分道扬镳”的绝佳示范!所以,掌握这个定理,不仅能在数学考试中加分,还能在生活中增添不少趣味。
3.2 生活中的应用想象一下,你在家里做手工,准备剪一张纸成一个等腰三角形。
你心里想着要把角分得好看,这时候,你可以利用这个定理,确保纸张被剪得“公平公正”。
另外,在一些建筑设计中,等腰三角形的结构也是常见的,底角的角平分线帮助设计师保持对称美感,真是实用至极!4. 小结在这个数学的小世界里,底角角平分线定理不仅仅是一个公式,它更像是一把钥匙,能打开等腰三角形的神秘大门。