1第二讲古代希腊数学恩格斯（德，1820－1895年）指出：“没有希腊的文化和罗马帝国奠定的基础，就没有现代的欧洲。
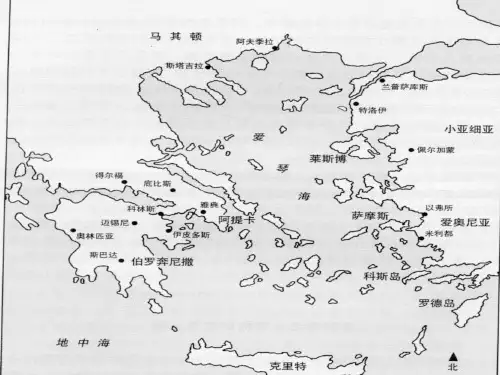
”背景：古希腊的变迁。
1、古典时期的希腊数学公元前600－前300年。
1.1爱奥尼亚学派（米利都学派）泰勒斯（公元前625－前547年），被称为“希腊哲学、科学之父”。
哲学：水生万物，万物复归于水。
数学：创数学命题逻辑证明之先河，希腊几何学的鼻祖，最早留名于世的数学家，测量过金字塔的高度，预报了公元前585年的一次日食。
1.2毕达哥拉斯学派毕达哥拉斯（约公元前560－前480年），在萨摩斯岛建立了具有宗教、哲学、科学性质的学派，致力于哲学和数学的研究，繁荣兴旺达一个世纪以上。
哲学：万物皆为数。
数学：数学研究抽象概念的认识归功于毕达哥拉斯学派，毕达哥拉斯定理，完全数、亲和数，正五角星作图与“黄金分割”，发现了“不可公度量”。
1.3伊利亚学派芝诺（约公元前490－前430年）悖论：运动不存在、阿基里斯、飞矢不动。
芝诺的功绩在于把动和静的关系、无限和有限的关系、连续和离散的关系以非数学的形态提出，并进行了辩证的考察。
1.4诡辩学派（智人学派）活跃于公元前5世纪下半叶的雅典城，代表人物均以雄辩著称，故亦称智人学派。
安蒂丰（约公元前480－前411年）的“穷竭法”。
古典几何三大作图问题：三等分任意角、化圆为方、倍立方。
1.5柏拉图学派柏拉图（约公元前427－前347年）对于欧洲的哲学乃至整个文化的发展，有着深远的影响。
柏拉图说：“不懂几何者免进”，认为打开宇宙之迷的钥匙是数与几何图形，发展了用演绎逻辑方法系统整理零散数学知识的思想。
2柏拉图不是数学家，却赢得了“数学家的缔造者”的美称，创办雅典学院（前387－公元529），讲授哲学与数学。
1.6亚里士多德学派（吕园学派）亚里士多德（公元前384－前322年）是古希腊最著名的哲学家、科学家。
集古希腊哲学之大成，把古希腊哲学推向最高峰，堪称“逻辑学之父”，为欧几里得演绎几何体系的形成奠定了方法论的基础，被后人奉为演绎推理的圣经。
