高三人教B文科数学一轮复习课时作业基本算法语句

课时作业(一)A[第1讲集合及其运算](时间：35分钟分值：80分)基础热身1．[2012·潍坊月考] 设集合A＝{x|2x－2<1}，B＝{x|1－x≥0}，则A∩B等于()A．{x|x≤1} B．{x|1≤x<2}C．{x|0<x≤1} D．{x|0<x<1}2．[2012·商丘模拟] 设全集U＝{1，2，3，4，5，6，7，8}，集合A＝{1，2，3，5}，B ＝{2，4，6}，则图K1－1中的阴影部分表示的集合为()图K1－1A．{2} B．{4，6}C．{1，3，5} D．{4，6，7，8}3．设非空集合M，N满足：M＝{x|f(x)＝0}，N＝{x|g(x)＝0}，P＝{x|f(x)g(x)＝0}，则集合P恒满足的关系为()A．P＝M∪N B．P⊆(M∪N)C．P≠∅D．P＝∅4．[2012·上海卷] 若集合A＝{x|2x－1>0}，B＝{x||x|<1}，则A∩B＝________．能力提升5．已知集合A＝{x|x2－4x－12<0}，B＝{x|x<2}，则A∪(∁R B)＝()A．{x|x<6} B．{x|－2<x<2}C．{x|x>－2} D．{x|2≤x<6}6．设集合A＝{1，2}，则满足A∪B＝{1，2，3}的集合B的个数为()A．1 B．3C．4 D．87．[2012·开封模拟] 设全集U＝{x|x≤7，x∈N*}，集合A＝{1，3}，B＝{2，6}，则∁U(A∪B)＝()A．{2，3，6} B．{1，2，7}C．{2，5，7} D．{4，5，7}8．[2012·北京卷] 已知集合A＝{x∈R|3x＋2>0}，B＝{x∈R|(x＋1)(x－3)>0}，则A∩B ＝()A ．(－∞，－1) B.⎝⎛⎭⎫－1，－23 C.⎝⎛⎭⎫－23，3 D ．(3，＋∞)9．已知集合A ＝{(x ，y )|x ，y 为实数，且x 2＋y 2＝1}，B ＝{(x ，y )|x ，y 为实数，且y ＝x }，则A ∩B 的元素个数为________．10．集合A ＝{x |ax －1＝0}，B ＝{x |x 2－3x ＋2＝0}，且A ∪B ＝B ，则实数a 的值为________．11．已知x ∈R ，y >0，集合A ＝{x 2＋x ＋1，－x ，－x －1}，集合B ＝－y ，－y2，y ＋1，若A ＝B ，则x 2＋y 2的值为____________________．12．(13分)集合A ＝{x |x 2－ax ＋a 2－19＝0}，B ＝{x |x 2－5x ＋6＝0}，C ＝{x |x 2＋2x －8＝0}，满足A ∩B ≠∅，A ∩C ＝∅，求实数a 的值．难点突破13．(12分)集合A ＝{x |－2≤x ≤5}，B ＝{x |m ＋1≤x ≤2m －1}． (1)若B ⊆A ，求实数m 的取值范围；(2)当x ∈Z 时，求A 的非空真子集的个数；(3)当x ∈R 时，若A ∩B ＝∅，求实数m 的取值范围．课时作业(一)B [第1讲 集合及其运算](时间：35分钟 分值：80分)基础热身1．S ＝{y |y ＝3x ，x ∈R }，T ＝{y |y ＝x 2－1，x ∈R }，则S ∩T 是( ) A ．S B ．TC ．∅D ．有限集 2．[2012·浙江卷] 设全集U ＝{1，2，3，4，5，6}，集合P ＝{1，2，3，4}，Q ＝{3，4，5}，则P ∩(∁U Q )＝( )A ．{1，2，3，4，6}B ．{1，2，3，4，5}C ．{1，2，5}D ．{1，2}3．若集合A ＝⎩⎨⎧⎭⎬⎫x ⎪⎪log 12x ≥12，则∁R A ＝( ) A.⎣⎡⎭⎫22，＋∞ B.⎝⎛⎭⎫22，＋∞ C ．(－∞，0]∪⎣⎡⎭⎫22，＋∞D ．(－∞，0]∪⎝⎛⎭⎫22，＋∞4．[2012·淮阴模拟] 已知全集U＝{1，2，3，4，5}，集合A＝{x|x2－3x＋2＝0}，B＝{x|x ＝2a，a∈A}，则集合∁U(A∪B)＝________．能力提升5．[2012·驻马店模拟] 集合A＝{x|x2－2x＋a>0}，1∉A，则实数a的取值范围是() A．(－∞，0] B．[0，＋∞)C．[1，＋∞) D．(－∞，1]6．定义集合运算：A⊙B＝{z|z＝xy(x＋y)，x∈A，y∈B}，设集合A＝{0，1}，B＝{2，3}，则集合A⊙B的所有元素之和为()A．0 B．6C．12 D．187．已知A，B均为集合U＝{1，3，5，7，9}的子集，且A∩B＝{3}，(∁U B)∩A＝{9}，则A等于()A．{1，3} B．{3，7，9}C．{3，5，9} D．{3，9}8．已知集合A，B，A＝{x|－2≤x<2}，A∪B＝A，则集合B不可能．．．为() A．∅B．{x|0≤x≤2}C．{x|0<x<2} D．{x|0≤x<2}9．已知集合M＝{(x，y)|x＋y＝1}，N＝{(x，y)|x－y＝1}，则M∩N＝________．10．设集合A＝{5，log2(a＋3)}，B＝{a，b}，若A∩B＝{2}，则A∪B＝________．11．集合A＝{(x，y)|y＝1－x2}，B＝{(x，y)|y＝x＋b}，若A∩B的子集有4个，则b 的取值范围是________．12．(13分)设关于x的不等式x(x－a－1)<0(a∈R)的解集为M，不等式x2－2x－3≤0的解集为N.(1)当a＝1时，求集合M；(2)若M⊆N，求实数a的取值范围．难点突破13．(1)(6分)[2012·北京西城区模拟] 已知集合A＝{a1，a2，…，a20}，其中a k>0(k＝1，2，…，20)，集合B＝{(a，b)|a∈A，b∈A，a－b∈A}，则集合B中的元素至多有() A．210个B．200个C．190个D．180个(2)(6分)[2012·北京朝阳区模拟] 已知集合A＝{(x，y)|x2＋y2≤4}，集合B＝{(x，y)|y≥m|x|，m为正常数}．若O为坐标原点，M，N为集合A所表示的平面区域与集合B所表示的平面区域的边界的交点，则△MON的面积S与m的关系式为________．课时作业(二)[第2讲简单的逻辑联结词、全称量词与存在量词](时间：35分钟分值：80分)基础热身1．已知命题p：∀x∈R，x>sin x，则命题p的否定形式为()A．∃x0∈R，x0<sin x0B．∀x∈R，x≤sin xC．∃x0∈R，x0≤sin x0D．∀x∈R，x<sin x2．[2012·乌鲁木齐模拟] 已知α，β是两个不重合的平面，l是空间一条直线，命题p：若α∥l，β∥l，则α∥β；命题q：若α⊥l，β⊥l，则α∥β.对以上两个命题，下列结论中正确的是()A．命题“p∧q”为真B．命题“p∨q”为假C．命题“p∨q”为真D．命题“(綈p)∧(綈q)”为真3．[2012·河北五校联考] 下列结论错误的是()A．命题“若x2－3x＋2＝0，则x＝2”的逆否命题为“若x≠2，则x2－3x＋2≠0”B．命题“存在x为实数，x2－x>0”的否定是“任意x是实数，x2－x≤0”C．“ac2>bc2”是“a>b”的充分不必要条件D．若p且q为假命题，则p，q均为假命题4．[2012·河南四校联考] 命题“∀x∈R，都有|x－1|－|x＋1|≤3”的否定是________________________________________________________________________．能力提升 5．[2012·黄冈中学月考] 命题“∀x ∈[1，2]，x 2－a ≤0”为真命题的一个充分不必要条．．．．．．件．是( ) A ．a ≥4 B ．a ≤4 C ．a ≥5 D ．a ≤5 6．[2013·德州重点中学月考] 下列有关命题的说法正确的是( ) A ．命题“若xy ＝0，则x ＝0”的否命题为：“若xy ＝0，则x ≠0” B ．“若x ＋y ＝0，则x ，y 互为相反数”的逆命题为真命题C ．命题“∃x 0∈R ，使得2x 20－1<0”的否定是：“∀x ∈R ，均有2x 2－1<0”D ．命题“若cos x ＝cos y ，则x ＝y ”的逆否命题为真命题7．[2012·东北三校联考] 已知命题p ：∃x 0∈0，π2，sin x 0＝12，则綈p 为( )A ．∀x ∈0，π2，sin x ≠12B ．∀x ∈0，π2，sin x ＝12C ．∃x 0∈0，π2，sin x 0≠12D ．∃x 0∈0，π2，sin x 0>128．[2012·大庆模拟] 已知命题p ：∃x 0∈(－∞，0)，2x 0<3x 0，命题q ：∀x ∈0，π2，tan x >sin x ，则下列命题为真命题的是( )A ．p ∧qB ．p ∨(綈q )C ．(綈p )∧qD ．p ∧(綈q )9．在“綈p ”“p ∧q ”“p ∨q ”形式的命题中，“p ∨q ”为真，“p ∧q ”为假，“綈p ”为真，那么p ，q 的真假为p ________，q ________．10．[2012·宁德质检] 若“∀x ∈R ，(a －2)x ＋1>0”是真命题，则实数a 的取值集合是________．11．下列四个命题：①∀x ∈R ，x 2＋x ＋1≥0；②∀x ∈Q ，12x 2＋x －13是有理数；③∃α，β∈R ，使sin(α＋β)＝sin α＋sin β； ④∃x ，y ∈Z ，使3x －2y ＝10. 所有真命题的序号是________． 12．(13分)[2012·吉林模拟] 已知p ：f (x )＝x 3－ax 在(2，＋∞)上为增函数，q ：g (x )＝x 2－ax ＋3在(1，2)上为减函数，若p 或q 为真命题，p 且q 为假命题，求a 的取值范围．难点突破13．(12分)已知p：方程a2x2＋ax－2＝0在[－1，1]上有解；q：只有一个实数x满足不等式x2＋2ax＋2a≤0，若“p或q”是假命题，求实数a的取值范围．课时作业(三)[第3讲命题及其关系、充分条件、必要条件](时间：35分钟分值：80分)基础热身1．[2012·重庆卷] 命题“若p，则q”的逆命题是()A．若q，则pB．若綈p，则綈qC．若綈q，则綈pD．若p，则綈q2．[2012·佛山模拟] 已知非零向量a，b，则“a＋b＝0”是“a∥b”的()A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分又不必要条件3．下列命题中为真命题的是()A．命题“若x>y，则x>|y|”的逆命题B．命题“若x>1，则x2>1”的否命题C．命题“若x＝1，则x2＋x－2＝0”的否命题D．命题“若x2>0，则x>1”的逆否命题4．[2013·扬州中学月考] 已知a，b，c∈R，命题“若a＋b＋c＝3，则a2＋b2＋c2≥3”的否命题是________________________．能力提升5．“a＝2”是“函数f(x)＝x a－12为偶函数”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件6．下列有关命题的说法中，正确的是()A．命题“若x2>1，则x>1”的否命题为“若x2>1，则x≤1”B．“x>1”是“x2＋x－2>0”的充分不必要条件C．命题“∃x0∈R，使得x20＋x0＋1<0”的否定是“∀x∈R，都有x2＋x＋1>0”D．命题“若α>β，则tanα>tanβ”的逆命题为真命题7．下列命题中，真命题的个数是()①x，y∈R，“若x2＋y2＝0，则x，y全为0”的逆命题；②“若a＋b是偶数，则a，b都是偶数”的否命题；③“若x＝3或x＝7，则(x－3)(x－7)＝0”的逆否命题．A．0 B．1C．2 D．38．[2012·郑州模拟] 设p：|2x＋1|>a，q：x－12x－1>0，使p是q的必要不充分条件的实数a 的取值范围是()A．(－∞，0) B．(－∞，－2]C．[－2，3] D．(－∞，3]9．[2012·焦作质检] 写出一个使不等式x2－x<0成立的充分不必要条件________．10．已知命题“若a>b，则ac2>bc2”，则命题的原命题、逆命题、否命题和逆否命题中正确命题的个数是________．11．“x＝2”是“向量a＝(x＋2，1)与向量b＝(2，2－x)共线”的________条件．12．(13分)π为圆周率，a，b，c，d∈Q，已知命题p：若aπ＋b＝cπ＋d，则a＝c且b＝d.(1)写出命题p的否定并判断真假；(2)写出命题p的逆命题、否命题、逆否命题并判断真假；(3)“a＝c且b＝d”是“aπ＋b＝cπ＋d”的什么条件？并证明你的结论．难点突破13．(12分)已知集合A＝y错误!y＝x2－错误!x＋1，x∈错误!，2，B＝{x|x＋m2≥1}．条件p：x∈A，条件q：x∈B，并且p是q的充分条件，求实数m的取值范围．课时作业(四)A [第4讲 函数的概念及其表示](时间：35分钟 分值：80分)基础热身 1．[2012·石家庄质检] 下列函数中与函数y ＝x 相同的是( )A ．y ＝|x |B ．y ＝1xC ．y ＝x 2D ．y ＝3x 3 2．[2012·郑州质检] 函数f (x )＝2x －1log 2x的定义域为( ) A ．(0，＋∞) B ．(1，＋∞)C ．(0，1)D ．(0，1)∪(1，＋∞)3．下列函数中，值域为[0，3]的函数是( ) A ．y ＝－2x ＋1(－1≤x ≤0) B ．y ＝3sin xC ．y ＝x 2＋2x (0≤x ≤1)D ．y ＝x ＋34．[2012·陕西卷] 设函数f (x )＝⎩⎪⎨⎪⎧x ，x ≥0，⎝⎛⎭⎫12x，x ＜0，则f (f (－4))＝________．能力提升5．[2013·浙江重点中学联考] 已知f (x ＋1)＝－f (x )，且f (x )＝⎩⎪⎨⎪⎧1（－1<x <0），0（0≤x ≤1），则f (3)＝( )A ．－1B ．0C ．1D ．1或0 6．若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“孪生函数”，例如解析式为y ＝2x 2＋1，值域为{9}的“孪生函数”三个：(1)y ＝2x 2＋1，x ∈{－2}；(2)y ＝2x 2＋1，x ∈{2}；(3)y ＝2x 2＋1，x ∈{－2，2}．那么函数解析式为y ＝2x 2－1，值域为{－1，5}的“孪生函数”共有( )A ．5个B ．4个C ．3个D ．2个 7．[2012·唐山模拟] 函数y ＝1－lg （x ＋2）的定义域为( ) A ．(0，8] B ．(－2，8] C ．(2，8] D ．[8，＋∞)8．已知f ⎝⎛⎭⎫12x －1＝2x ＋3，f (m )＝6，则m 等于( )A.14 B ．－14 C.32 D ．－329．[2012·汕头质检] 已知f (x )＝⎩⎪⎨⎪⎧sin πx ，x ≤0，f （x －1）＋1，x >0，则f ⎝⎛⎭⎫56的值为________． 10．已知f (x )＝⎩⎪⎨⎪⎧1，x ≥0，0，x <0，则不等式xf (x )＋x ≤2的解集是________．11．已知g (x )＝1－2x ，f (g (x ))＝1－x 2x2(x ≠0)，那么f ⎝⎛⎭⎫12＝________． 12．(13分)图K4－1是一个电子元件在处理数据时的流程图：图K4－1(1)试确定y ＝f (x )的函数关系式； (2)求f (－3)，f (1)的值； (3)若f (x )＝16，求x 的值．难点突破13．(12分)已知二次函数f(x)有两个零点0和－2，且f(x)的最小值是－1，函数g(x)与f(x)的图象关于原点对称．(1)求f(x)和g(x)的解析式；(2)若h(x)＝f(x)－λg(x)在区间[－1，1]上是增函数，求实数λ的取值范围．课时作业(四)B[第4讲函数的概念及其表示](时间：35分钟分值：80分)基础热身1．下列是映射的是()图K4－2A ．(1)(2)(3)B ．(1)(2)(5)C ．(1)(3)(5)D ．(1)(2)(3)(5)2．[2012·江西师大附中月考] 已知函数f (x )＝⎩⎪⎨⎪⎧1－x ，x ≤0a x ，x >0，若f (1)＝f (－1)，则实数a 的值等于( )A ．1B ．2C ．3D ．43．[2012·马鞍山二模] 已知函数f (x )＝⎩⎪⎨⎪⎧2x ，x >0，x ＋1，x ≤0，若f (a )＋f (1)＝0，则实数a 的值等于( )A ．－3B ．－1C ．1D ．34．函数y ＝x －x 的值域是________．能力提升5．已知f (x )的图象恒过点(1，2)，则f (x ＋3)的图象恒过点( ) A ．(－3，1) B ．(2，－2) C ．(－2，2) D ．(3，5)6．[2012·肇庆一模] 已知函数f (x )＝lg x 的定义域为M ，函数y ＝⎩⎪⎨⎪⎧2x ，x >2，－3x ＋1，x <1的定义域为N ，则M ∩N ＝( )A ．(0，1)B ．(2，＋∞)C ．(0，＋∞)D ．(0，1)∪(2，＋∞)7．已知函数y ＝⎩⎪⎨⎪⎧x 2＋1，x ≤0，－2x ，x >0，则使函数值为5的x 的值是( )A ．－2B ．2或－52C ．2或－2D ．2或－2或－528．[2012·石家庄质检] 设集合A ＝⎣⎡⎭⎫0，12，B ＝⎣⎡⎦⎤12，1，函数f (x )＝⎩⎪⎨⎪⎧x ＋12，x ∈A ，2（1－x ），x ∈B ，若x 0∈A 且f (f (x 0))∈A ，则x 0的取值范围是( )A.⎝⎛⎦⎤0，14B.⎝⎛⎭⎫14，12C.⎝⎛⎦⎤14，12D.⎣⎡⎦⎤0，38 9．[2012·四川卷] 函数f (x )＝11－2x的定义域是________．(用区间表示)10．已知f (x )＝⎩⎨⎧ln 1x，x >0，1x，x <0，则f (x )＞－1的解集为____________________．11．函数f (x )＝⎩⎪⎨⎪⎧x 2－x ＋1，x <1，1x ，x >1的值域是________．12．(13分)(1)求函数f (x )＝lg （x 2－2x ）9－x 2的定义域；(2)已知函数f (x )的定义域为[0，1]，求下列函数的定义域：①f (x 2)，②f (x －1)； (3)已知函数f (lg(x ＋1))的定义域是[0，9]，求函数f (2x )的定义域．难点突破13．(12分)已知f (x )是定义在[－6，6]上的奇函数，它在[0，3]上是一次函数，在[3，6]上是二次函数，且当x ∈[3，6]时，f (x )≤f (5)＝3，f (6)＝2，求f (x )的解析式．课时作业(五) [第5讲 函数的单调性与最值](时间：45分钟 分值：100分)基础热身 1．下列函数中，满足“对任意x 1，x 2∈(0，＋∞)，当x 1<x 2时，都有f (x 1)>f (x 2)”的是( )A ．f (x )＝1xB ．f (x )＝(x －1)2C ．f (x )＝e xD ．f (x )＝ln(x ＋1)2．函数f (x )＝1－1x在[3，4)上( )A ．有最小值无最大值B ．有最大值无最小值C ．既有最大值又有最小值D ．最大值和最小值皆不存在 3．[2012·天津卷] 下列函数中，既是偶函数，又在区间(1，2)内是增函数的为( ) A ．y ＝cos2x ，x ∈RB ．y ＝log 2|x |，x ∈R 且x ≠0C ．y ＝e x －e －x2，x ∈RD ．y ＝x 3＋1，x ∈R4．函数f (x )＝xx ＋1的最大值为________．能力提升 5．[2012·宁波模拟] 已知函数f (x )为R 上的减函数，则满足f (|x |)<f (1)的实数x 的取值范围是( )A ．(－1，1)B ．(0，1)C ．(－1，0)∪(0，1)D ．(－∞，－1)∪(1，＋∞) 6．[2012·商丘三模] 设f (x )＝x 2－2x －3(x ∈R )，则在区间[－π，π]上随机取一个实数x ，使f (x )＜0的概率为( )A.1πB.2πC.3πD.32π 7．[2012·哈尔滨师范大学附中期中] 函数y ＝⎝⎛⎭⎫121x 2＋1的值域为( )A ．(－∞，1) B.⎝⎛⎭⎫12，1 C.⎣⎡⎭⎫12，1 D.⎣⎡⎭⎫12，＋∞ 8．[2013·惠州二调] 已知函数f (x )＝e x －1，g (x )＝－x 2＋4x －3，若有f (a )＝g (b )，则b 的取值范围为( )A ．(2－2，2＋2)B ．[2－2，2＋2]C ．[1，3]D ．(1，3)9．[2012·长春外国语学校月考] 已知函数f (x )＝⎩⎪⎨⎪⎧a x （x <0），（a －3）x ＋4a （x ≥0）满足对任意的实数x 1≠x 2都有f （x 1）－f （x 2）x 1－x 2<0成立，则实数a 的取值范围是( )A ．(3，＋∞)B ．(0，1)C.⎝⎛⎦⎤0，14 D ．(1，3) 10．若函数y ＝f (x )的值域是⎣⎡⎦⎤12，3，则函数F (x )＝f (x )＋1f （x ）的值域是________． 11．若在区间⎣⎡⎦⎤12，2上，函数f (x )＝x 2＋px ＋q 与g (x )＝x ＋1x在同一点取得相同的最小值，则f (x )在该区间上的最大值是________．12．函数y ＝xx ＋a 在(－2，＋∞)上为增函数，则a 的取值范围是________．13．函数y ＝ln 1＋x1－x的单调递增区间是________．14．(10分)试讨论函数f (x )＝xx 2＋1的单调性．15．(13分)已知函数f(x)＝a－1|x|.(1)求证：函数y＝f(x)在(0，＋∞)上是增函数；(2)若f(x)<2x在(1，＋∞)上恒成立，求实数a的取值范围．难点突破16．(12分)已知函数f(x)＝x2x－2(x∈R，且x≠2)．(1)求f(x)的单调区间；(2)若函数g(x)＝x2－2ax与函数f(x)在x∈[0，1]上有相同的值域，求a的值．课时作业(六)A [第6讲 函数的奇偶性](时间：35分钟 分值：80分)基础热身1．下列函数中，在其定义域内既是奇函数又是减函数的是( ) A ．y ＝－x 3，x ∈R B ．y ＝sin2x ，x ∈RC ．y ＝2x ，x ∈RD ．y ＝－⎝⎛⎭⎫13x ，x ∈R2．函数f (x )＝a 2x －1ax (a >0，a ≠1)的图象( )A ．关于原点对称B ．关于直线y ＝x 对称C ．关于x 轴对称D ．关于y 轴对称 3．[2012·哈尔滨师范大学附中月考] 设f (x )是定义在R 上的奇函数，当x ≤0时，f (x )＝2x 2－x ，则f (1)＝( )A ．－3B ．－1C ．1D ．3 4．[2012·上海卷] 已知y ＝f (x )是奇函数，若g (x )＝f (x )＋2且g (1)＝1，则g (－1)＝________．能力提升5．设f (x )是周期为2的奇函数，当0≤x ≤1时，f (x )＝x ，则f ⎝⎛⎭⎫－134＝( ) A.32 B ．－32C.12 D ．－12 6．[2012·长春外国语学校月考] 已知函数f (x )是定义在R 上的奇函数，且f (x ＋2)＝－f (x )，若f (1)＝1，则f (3)－f (4)＝( )A ．－1B ．1C ．－2D ．27．[2013·保定摸底] 若函数f (x )＝|x －2|＋a 4－x 2的图象关于原点对称，则f a2＝( )A.33 B ．－33C ．1D ．－1 8．已知定义在R 上的奇函数f (x )是一个减函数，若x 1＋x 2＜0，x 2＋x 3＜0，x 3＋x 1＜0，则f (x 1)＋f (x 2)＋f (x 3)的值( )A ．大于0B ．小于0C ．等于0D ．以上都有可能 9．[2013·银川一中月考] 已知f (x )是定义在R 上的函数，且满足f (x ＋1)＋f (x )＝3，当x ∈[0，1]时，f (x )＝2－x ，则f (－2 005.5)＝________．10．[2013·南昌一中、十中联考] 函数f (x )是定义在R 上的奇函数，下列结论中，正确结论的序号是________．①f (－x )＋f (x )＝0；②f (－x )－f (x )＝－2f (x )；③f (x )f (－x )≤0；④f （x ）f （－x ）＝－1.11．[2012·南京三模] 若函数f (x )＝⎩⎪⎨⎪⎧x 2－2x ，x ≥0，－x 2＋ax ，x <0是奇函数，则满足f (x )>a 的x 的取值范围是________．12．(13分)[2012·衡水中学一调] 已知函数f (x )＝x m －2x 且f (4)＝72.(1)求m 的值；(2)判定f (x )的奇偶性；(3)判断f (x )在(0，＋∞)上的单调性，并给予证明．难点突破13．(12分)已知定义域为R 的函数f (x )＝－2x ＋b2x ＋1＋a是奇函数．(1)求a ，b 的值；(2)若对任意的t ∈R ，不等式f (t 2－2t )＋f (2t 2－k )<0恒成立，求k 的取值范围．课时作业(六)B [第6讲 函数的奇偶性](时间：35分钟 分值：80分)基础热身 1．[2012·佛山质检] 下列函数中既是奇函数，又在区间(－1，1)上是增函数的为( ) A ．y ＝|x | B ．y ＝sin xC ．y ＝e x ＋e －x D ．y ＝－x 32．已知f (x )＝ax 2＋bx 是定义在[a －1，2a ]上的偶函数，那么a ＋b 的值是( )A ．－13 B.13 C.12 D ．－123．已知f (x )＝⎩⎪⎨⎪⎧x 2－x ＋1（x >0），－x 2－x －1（x <0），则f (x )为( )A ．奇函数B ．偶函数C ．非奇非偶函数D ．不能确定奇偶性 4．[2012·浙江卷] 设函数f (x )是定义在R 上的周期为2的偶函数，当x ∈[0，1]时，f (x )＝x ＋1，则f ⎝⎛⎭⎫32＝________．能力提升5．[2012·郑州模拟] 设函数f (x )＝⎩⎪⎨⎪⎧2x，x <0，0，x ＝0，g （x ），x >0，且f (x )为奇函数，则g (3)＝( )A ．8 B.18 C ．－8 D ．－186．已知y ＝f (x )是定义在R 上的偶函数，且f (x )在(0，＋∞)上是增函数，如果x 1<0，x 2>0，且|x 1|<|x 2|，则有( )A ．f (－x 1)＋f (－x 2)>0B ．f (x 1)＋f (x 2)<0C ．f (－x 1)－f (－x 2)>0D ．f (x 1)－f (x 2)<0 7．[2012·石嘴山二联] 已知函数f (x )是(－∞，＋∞)上的偶函数，若对于x ≥0，都有f (x ＋2)＝f (x )，且当x ∈[0，2)时，f (x )＝log 2(x ＋1)，则f (－2 012)＋f (2 011)的值为( )A ．1B ．2C ．－2D ．－1 8．[2013·忻州一中月考] 命题p ：∀x ∈R ，3x >x ；命题q ：若函数y ＝f (x －1)为奇函数，则函数y ＝f (x )的图象关于点(1，0)成中心对称．以下说法正确的是( ) A ．p ∨q 真 B ．p ∧q 真 C ．綈p 真 D ．綈q 假9．函数f (x )对于任意实数x 满足条件f (x ＋2)f (x )＝1，若f (1)＝－5，则f (－5)＝________． 10．[2011·广东卷] 设函数f (x )＝x 3cos x ＋1.若f (a )＝11，则f (－a )＝________．11．设定义在[－2，2]上的奇函数f (x )在[0，2]上单调递减，若f (3－m )≤f (2m 2)，则实数m 的取值范围是________．12．(13分)已知函数f (x )＝lg 1＋x1－x.(1)求证：对于f (x )的定义域内的任意两个实数a ，b ，都有f (a )＋f (b )＝f ⎝ ⎛⎭⎪⎫a ＋b 1＋ab ； (2)判断f (x )的奇偶性，并予以证明．难点突破13．(12分)函数f (x )的定义域为D ＝{x |x ≠0}，且满足对于任意x 1，x 2∈D ，有f (x 1·x 2)＝f (x 1)＋f (x 2)．(1)求f (1)的值；(2)判断f (x )的奇偶性并证明你的结论； (3)如果f (4)＝1，f (3x ＋1)＋f (2x －6)≤3，且f (x )在(0，＋∞)上是增函数，求x 的取值范围．课时作业(七)[第7讲二次函数](时间：45分钟分值：100分)基础热身1．已知二次函数y＝x2－2ax＋1在区间(2，3)内是单调函数，则实数a的取值范围是() A．a≤2或a≥3B．2≤a≤3C．a≤－3或a≥－2D．－3≤a≤－22．函数y＝(cos x－a)2＋1，当cos x＝a时有最小值，当cos x＝－1时有最大值，则a的取值范围是()A．[－1，0] B．[－1，1]C．(－∞，0] D．[0，1]3．[2012·长春外国语学校月考] 若函数f(x)＝(m－1)x2＋(m2－1)x＋1是偶函数，则f(x)在区间(－∞，0]上是()A．增函数B．减函数C．常数D．增函数或常数4．[2011·陕西卷] 设n∈N＋，一元二次方程x2－4x＋n＝0有整数．．根的充要条件是n＝________．能力提升5．函数f (x )＝4x 2－mx ＋5在区间[－2，＋∞)上是增函数，则f (1)的取值范围是( ) A ．f (1)≥25 B ．f (1)＝25 C ．f (1)≤25 D ．f (1)>256．已知函数f (x )＝－x 2＋4x ＋a ，x ∈[0，1]，若f (x )有最小值－2，则f (x )的最大值为( ) A ．－1 B ．0 C ．1 D ．27．[2012·昆明模拟] 若函数y ＝ax 与y ＝bx在(0，＋∞)上都是减函数，则y ＝ax 2＋bx 在(－∞，0)上是( )A ．增函数B ．减函数C ．先增后减D ．先减后增8．若f (x )＝x 2－x ＋a ，f (－m )＜0，则f (m ＋1)的值为( ) A ．正数 B ．负数C ．非负数D ．与m 有关 9．[2012·牡丹江一中期中] 如图K7－1是二次函数f (x )＝x 2－bx ＋a 的图象，其函数f (x )的导函数为f ′(x )，则函数g (x )＝ln x ＋f ′(x )的零点所在的区间是( )图K7－1A.⎝⎛⎭⎫14，12B.⎝⎛⎭⎫12，1 C ．(1，2) D ．(2，3)10．函数f (x )＝⎩⎪⎨⎪⎧x 2＋2x －3（－2≤x <0），x 2－2x －3（0≤x ≤3）的值域是________．11．方程|x 2－2x |＝a 2＋1(a ∈(0，＋∞))的解的个数是________．12．若x ≥0，y ≥0，且x ＋2y ＝1，那么2x ＋3y 2的最小值为________． 13．[2012·北京卷] 已知f (x )＝m (x －2m )(x ＋m ＋3)，g (x )＝2x －2，若∀x ∈R ，f (x )<0或g (x )<0，则m 的取值范围是________．14．(10分)[2012·正定月考] 已知f (x )＝2x 2＋bx ＋c ，不等式f (x )<0的解集是(0，5)． (1)求f (x )的解析式；(2)对于任意x ∈[－1，1]，不等式f (x )＋t ≤2恒成立，求t 的范围．15．(13分)设f(x)是定义在R上的偶函数，当0≤x≤2时，y＝x，当x>2时，y＝f(x)的图象是顶点为P(3，4)，且过点A(2，2)的抛物线的一部分．(1)求函数f(x)在(－∞，－2)上的解析式；(2)在下面的直角坐标系中直接画出函数f(x)的草图；(3)写出函数f(x)的值域．图K7－2难点突破16．(12分)[2013·衡水中学一调] 已知对于函数f(x)，若存在x0∈R，使f(x0)＝x0，则称x0是f(x)的一个不动点，已知函数f(x)＝ax2＋(b＋1)x＋(b－1)(a≠0)．(1)当a＝1，b＝－2时，求函数f(x)的不动点；(2)对任意实数b，函数恒有两个相异的不动点，求a的取值范围；(3)在(2)的条件下，若y＝f(x)的图象上A，B两点的横坐标是f(x)的不动点，且A，B两点关于直线y＝kx＋12a2＋1对称，求b的最小值．课时作业(八)A [第8讲 指数与对数的运算](时间：35分钟 分值：80分)基础热身1．2log 510＋log 50.25＝( ) A ．0 B ．1 C ．2 D ．42．下列等式能够成立的是( )A.⎝⎛⎭⎫n m 5＝m 15n 5B.12（－2）4＝3－2C.4x 3＋y 3＝(x ＋y )34D.39＝333．在对数式b ＝log (a －2)(5－a )中，实数a 的取值范围是( ) A ．a >5或a <2 B ．2<a <5C ．2<a <3或3<a <5D ．3<a <44．[2012·正定中学月考] 计算lg 14－lg25100－12＝________．能力提升5．若log 2log 3log 4x ＝log 3log 4log 2y ＝log 4log 2log 3z ＝0，则x ＋y ＋z 的值为( ) A ．50 B ．58 C ．89 D ．1116．[2012·武汉调研] 若x ＝log 43，则(2x －2－x )2＝( ) A.94 B.54 C.34 D.43 7．[2012·重庆卷] 已知a ＝log 23＋log 23，b ＝log 29－log 23，c ＝log 32，则a ，b ，c 的大小关系是( )A ．a ＝b <cB ．a ＝b >cC ．a <b <cD ．a >b >c8．若lg(x －y )＋lg(x ＋2y )＝lg2＋lg x ＋lg y ，则xy＝( )A ．2B ．3 C.12 D.139．[2012·海南五校联考] x >0，则(2x 14＋332)(2x 14－332)－4x －12(x －x 12)＝________．10．[(1－log 63)2＋log 62·log 618]÷log 64＝________．11．[2012·上海卷] 方程4x －2x ＋1－3＝0的解是________．12．(13分)设x >1，y >1，且2log x y －2log y x ＋3＝0，求T ＝x 2－4y 2的最小值．难点突破13．(12分)已知f (x )＝e x －e －x ，g (x )＝e x ＋e －x .(1)求[f (x )]2－[g (x )]2的值；(2)若f (x )·f (y )＝4，g (x )·g (y )＝8，求g （x ＋y ）g （x －y ）的值．课时作业(八)B [第8讲 指数与对数的运算](时间：35分钟 分值：80分)基础热身1．下列命题中，正确命题的个数为( ) ①na n ＝a ；②若a ∈R ，则(a 2－a ＋1)0＝1； ③3x 4＋y 6＝x 43＋y 2；④5－3＝10（－3）2.A ．0B ．1C ．2D ．32．化简：（log 23）2－4log 23＋4＋log 213＝( )A ．2B ．2－2log 23C ．－2D ．2log 23－23．log(n ＋1＋n )(n ＋1－n )＝( ) A ．1 B ．－1 C ．2 D ．－24．已知a 12＝49，则log 23a ＝________．能力提升5．若10x ＝2，10y ＝3，则103x －y2＝( ) A.263 B.63 C.233D.366．函数y ＝x 2＋2x ＋1＋3x 3－3x 2＋3x －1的图象是( ) A ．一条直线 B ．两条射线 C ．抛物线 D ．半圆7．若a >1，b >0，且a b ＋a －b ＝22，则a b －a －b 的值等于( ) A. 6 B ．2或－2 C ．2 D ．－28．[2012·唐山模拟] 已知3x ＝4y ＝12，则1x ＋1y＝( )A. 2 B ．1 C.12D ．2 9．设f (x )＝⎩⎪⎨⎪⎧2－x ，x ∈（－∞，1]，log 81x ，x ∈（1，＋∞），则满足f (x )＝14的x 值为________．10．[2012·福州质检] 化简：lg2＋lg5－lg8lg50－lg40＝________．11．方程log 2(x 2＋x )＝log 2(2x ＋2)的解是________．12．(13分)已知x 12＋x －12＝3，求x 2＋x －2－2x 32＋x －32－3的值．难点突破13．(12分)设a ，b ，c 均为正数，且满足a 2＋b 2＝c 2.(1)求证：log 2⎝⎛⎭⎫1＋b ＋c a ＋log 2⎝⎛⎭⎫1＋a －c b ＝1；(2)若log 4⎝⎛⎭⎫1＋b ＋c a ＝1，log 8(a ＋b －c )＝23，求a ，b ，c 的值．课时作业(九) [第9讲 指数函数、对数函数、幂函数](时间：45分钟 分值：100分)基础热身1．[2012·西安质检] 已知a ＝32，函数f (x )＝a x ，若实数m ，n 满足f (m )>f (n )，则m ，n满足的关系为( )A ．m ＋n <0B ．m ＋n >0C ．m >nD ．m <n 2．[2012·梅州中学月考] 若函数y ＝f (x )是函数y ＝a x (a >0，且a ≠1)的反函数，其图象经过点(a ，a )，则f (x )＝( )A ．log 2xB ．log 12xC.12x D ．x 2 3．[2012·四川卷] 函数y ＝a x －a (a >0，且a ≠1)的图象可能是( )图K9－14．[2012·南通模拟] 已知幂函数f (x )＝k ·x α的图象过点⎝⎛⎭⎫12，22，则k ＋α＝________．能力提升 5．[2012·汕头测评] 下列各式中错误．．的是( ) A ．0.83>0.73 B ．log 0.50.4>log 0.50.6C ．0.75－0.1<0.750.1 D ．lg1.6>lg1.46．若集合A ＝{y |y ＝x 13，－1≤x ≤1}，B ＝y⎪⎪⎪ )y ＝⎝⎛⎭⎫12x ，x ≤0，则A ∩B ＝( ) A ．(－∞，1) B ．[－1，1] C ．∅ D ．{1}7．[2012·南昌调研] 函数f (x )＝log 22x 2＋1的值域为( )A ．[1，＋∞)B ．(0，1]C ．(－∞，1]D ．(－∞，1)8．[2012·三明联考] 已知函数y ＝f (x )是奇函数，当x >0时，f (x )＝lg x ，则f ⎝⎛⎭⎫f ⎝⎛⎭⎫1100的值等于( )A.1lg2 B ．－1lg2 C ．lg2 D ．－lg29．[2012·全国卷] 已知x ＝ln π，y ＝log 52，z ＝e －12，则( )A ．x <y <zB ．z <x <yC ．z <y <xD ．y <z <x10．已知函数f (x )＝⎩⎪⎨⎪⎧log 3x ，x >0，3x ，x <0，则满足f (a )<13的a 的取值范围是________．11．若函数f (x )＝a |2x －4|(a >0，且a ≠1)，满足f (1)＝19，则f (x )的单调递减区间是________．12．[2013·河北五校联盟调研] 已知函数f (x )＝⎩⎪⎨⎪⎧log 2x ，（x >0），2x ，（x ≤0）且关于x 的方程f (x )＋x－a ＝0有且只有一个实根，则实数a 的取值范围是________．13．[2012·长春外国语学校月考] 关于函数f (x )＝lg x 2＋1|x |(x ≠0)，有下列命题：①其图象关于y 轴对称； ②f (x )的最小值是lg2；③当x >0时，f (x )是增函数；当x <0时，f (x )是减函数； ④f (x )在区间(－1，0)，(2，＋∞)上是增函数； ⑤f (x )无最大值，也无最小值．其中所有正确结论的序号是________．14．(10分)设a >0，f (x )＝e x a ＋aex 是R 上的偶函数．(1)求a 的值；(2)证明f (x )在(0，＋∞)上是增函数； (3)解方程f (x )＝2. 15．(13分)已知函数f (x )＝log a (x ＋1)(a >1)，且函数y ＝g (x )图象上任意一点P 关于原点的对称点Q 的轨迹恰好是函数f (x )的图象．(1)写出函数g (x )的解析式；(2)当x ∈[0，1)时总有f (x )＋g (x )≥m 成立，求m 的取值范围．难点突破16．(12分)已知函数f (x )＝log 4(ax 2＋2x ＋3)． (1)若f (1)＝1，求f (x )的单调区间；(2)是否存在实数a ，使f (x )的最小值为0？若存在，求出a 的值；若不存在，说明理由．课时作业(十) [第10讲 函数的图象与性质的综合](时间：45分钟 分值：100分)基础热身1．函数f (x )＝1x＋2x 的图象关于( )A ．y 轴对称B ．直线y ＝－x 对称C ．坐标原点对称D ．直线y ＝x 对称2．为了得到函数y ＝3⎝⎛⎭⎫13x 的图象，可以把函数y ＝⎝⎛⎭⎫13x 的图象( )A ．向左平移3个单位长度B ．向右平移3个单位长度C ．向左平移1个单位长度D ．向右平移1个单位长度3．下列四个函数中，图象如图K10－1所示的只能是( )图K10－1A．y＝x＋lg x B．y＝x－lg xC．y＝－x＋lg x D．y＝－x－lg x4．[2012·开封质检] 把函数y＝f(x)＝(x－2)2＋2的图象向左平移1个单位，再向上平移1个单位，所得图象对应的函数的解析式是________________________________________________________________________．能力提升5．在函数y＝|x|(x∈[－1，1])的图象上有一点P(t，|t|)，此函数与x轴、直线x＝－1及x ＝t围成图形(如图K10－2阴影部分)的面积为S，则S与t的函数关系图象可表示为()图K10－2图K10－36．已知图K10－4①中的图象对应的函数为y＝f(x)，则图K10－4②中的图象对应的函数为()图K10－4A．y＝f(|x|) B．y＝|f(x)|C．y＝f(－|x|) D．y＝－f(|x|)7．[2012·郑州调研] 已知曲线如图K10－5所示：图K10－5以下为编号为①②③④的四个方程：①x－y＝0；②|x|－|y|＝0；③x－|y|＝0；④|x|－y＝0.请按曲线A，B，C，D的顺序，依次写出与之对应的方程的编号为()A．④②①③B．④①②③C．①③④②D．①②③④8．函数f(x)＝1＋log2x与g(x)＝21－x在同一直角坐标系下的图象大致是()图K10－69．已知函数f(x)＝e x，其反函数为y＝f－1(x)，则函数g(x)＝|f－1(1－x)|的大致图象是()图K10－710．将函数y ＝2x ＋1的图象按向量a 平移得到函数y ＝2x ＋1的图象，则a ＝________．11．[2012·海淀一模] 函数f (x )＝x ＋1x图象的对称中心为________．12．设函数f (x )＝|x ＋1|＋|x －a |的图象关于直线x ＝1对称，则a 的值为________．13．[2012·唐山二模] 奇函数f (x )、偶函数g (x )的图象分别如图K10－8(1)，K10－8(2)所示，方程f (g (x ))＝0，g (f (x ))＝0的实根个数分别为a ，b ，则a ＋b ＝________．图K10－814．(10分)设函数f (x )＝x ＋1x的图象为C 1，C 1关于点A (2，1)对称的图象为C 2，C 2对应的函数为g (x )．求g (x )的解析式．15．(13分)已知f (x )＝log a x (a >0且a ≠1)，如果对于任意的x ∈⎣⎡⎦⎤13，2都有|f (x )|≤1成立，试求a 的取值范围．难点突破16．(12分)(1)已知函数y ＝f (x )的定义域为R ，且当x ∈R 时，f (m ＋x )＝f (m －x )恒成立，求证y ＝f (x )的图象关于直线x ＝m 对称；(2)若函数y ＝log 2|ax －1|的图象的对称轴是x ＝2，求非零实数a 的值．课时作业(十一)[第11讲函数与方程](时间：45分钟分值：100分)基础热身1．[2013·安庆四校联考] 图K11－1是函数f(x)的图象，它与x轴有4个不同的公共点．给出下列四个区间之中，存在不能用二分法求出的零点的区间是()图K11－1A．[－2.1，－1] B．[1.9，2.3]C．[4.1，5] D．[5，6.1]2．[2012·唐山期末] 设f (x )＝e x＋x －4，则函数f (x )的零点位于区间( ) A ．(－1，0) B ．(0，1) C ．(1，2) D ．(2，3)3．若x 0是方程lg x ＋x ＝2的解，则x 0属于区间( ) A ．(0，1) B ．(1，1.25)C ．(1.25，1.75)D ．(1.75，2)4．已知函数f (x )＝⎩⎪⎨⎪⎧2x －1，x >0，－x 2－2x ，x ≤0，若函数g (x )＝f (x )－m 有3个零点，则实数m 的取值范围是________．能力提升5．函数y ＝f (x )在区间(－2，2)上的图象是连续的，且方程f (x )＝0在(－2，2)上仅有一个实根0，则f (－1)·f (1)的值( )A ．大于0B ．小于0C ．等于0D ．无法确定6．[2013·诸城月考] 设函数y ＝x 2与y ＝⎝⎛⎭⎫12x －2的图象的交点为(x 0，y 0)，则x 0所在的区间是( )A ．(0，1)B ．(1，2)C ．(2，3)D ．(3，4)7．已知定义在R 上的函数f (x )＝(x 2－3x ＋2)g (x )＋3x －4，其中函数y ＝g (x )的图象是一条连续曲线，则方程f (x )＝0在下面哪个范围内必有实数根( )A ．(0，1)B ．(1，2)C ．(2，3)D ．(3，4) 8．[2011·陕西卷] 方程|x |＝cos x 在(－∞，＋∞)内( ) A ．没有根 B ．有且仅有一个根C ．有且仅有两个根D ．有无穷多个根9．[2012·石家庄质检] 已知函数f (x )＝⎝⎛⎭⎫12x －sin x ，则f (x )在[0，2π]上的零点个数为( )A ．1B ．2C ．3D ．410．若方程2ax 2－x －1＝0在(0，1)内恰有一解，则a 的取值范围是________．11．若函数f (x )＝x 2＋ax ＋b 的两个零点是－2和3，则不等式af (－2x )>0的解集是________．12．[2012·盐城二模] 若y ＝f (x )是定义在R 上的周期为2的偶函数，当x ∈[0，1]时，f (x )＝2x －1，则函数g (x )＝f (x )－log 3|x |的零点个数为________．13．[2013·扬州中学月考] 已知函数f (x )＝|x 2－1|x －1－kx ＋2恰有两个零点，则k 的取值范围是________．14．(10分)已知函数f (x )＝4x ＋m ·2x ＋1有且仅有一个零点，求m 的取值范围，并求出该零点．15．(13分)已知二次函数f (x )＝ax 2＋bx ＋1(a ，b ∈R ，a >0)，设方程f (x )＝x 的两个实数根为x 1和x 2.(1)如果x 1<2<x 2<4，设函数f (x )的对称轴为x ＝x 0，求证：x 0>－1； (2)如果|x 1|<2，|x 2－x 1|＝2，求b 的取值范围．难点突破16．(12分)已知函数f (x )＝⎩⎪⎨⎪⎧2x （0≤x ≤1），－25x ＋125（1<x ≤5）.(1)若函数y ＝f (x )的图象与直线kx －y －k ＋1＝0有两个交点，求实数k 的取值范围； (2)试求函数g (x )＝xf (x )的值域．课时作业(十二)[第12讲函数模型及其应用](时间：45分钟分值：100分)基础热身图K12－11．“红豆生南国，春来发几枝？”，图K12－1给出了红豆生长时间t (月)与枝数y (枝)的散点图，那么红豆生长时间与枝数的关系用下列哪个函数模型拟合最好？( )A ．y ＝t 2B ．y ＝log 2tC ．y ＝2tD ．y ＝2t 22．等边三角形的边长为x ，面积为y ，则y 与x 之间的函数关系式为( )A ．y ＝x 2B ．y ＝12x 2C ．y ＝32x 2D ．y ＝34x 23．某工厂第三年的产量比第一年的产量增长44%，若每年的平均增长率相同(设为x )，则以下结论正确的是( )A ．x >22%B ．x <22%C ．x ＝22%D ．x 的大小由第一年的产量确定4．某种储蓄按复利计算利息，若本金为a 元，每期利率为r ，存期是x ，本利和(本金加利息)为y 元，则本利和y 随存期x 变化的函数关系式是________．能力提升5．某电视新产品投放市场后第一个月销售100台，第二个月销售200台，第三个月销售400台，第四个月销售790台，则下列函数模型中能较好地反映销量y 与投放市场的月数x 之间关系的是( )A ．y ＝100xB ．y ＝50x 2－50x ＋100C ．y ＝50×2xD ．y ＝100log 2x ＋100 6．[2012·华南师大附中模拟] 在股票买卖过程中，经常用到两种曲线，一种是即时价格曲线y ＝f (x )，一种是平均价格曲线y ＝g (x )(如f (2)＝3表示开始交易后第2小时的即时价格为3元；g (2)＝4表示开始交易后两个小时内所有成交股票的平均价格为4元)．下面所给出的四个图象中，实线表示y ＝f (x )，虚线表示y ＝g (x )，其中可能正确的是( )图K12－27．[2012·商丘一模] 某公司在甲、乙两地销售一种品牌车，利润(单位：万元)分别为L 1＝5.06x －0.15x 2和L 2＝2x ，其中x 为销售量(单位：辆)．若该公司在这两地共销售15辆车，则能获得的最大利润为( )A ．45.606万元B ．45.6万元C ．45.56万元D ．45.51万元 8．[2013·荆州中学一检] 下列所给4个图象中，与所给3件事吻合最好的顺序为( ) (a)我离开家不久，发现自己把作业本忘在家里了，于是立刻返回家里取了作业本再上学； (b)我骑着车一路以常速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间； (c)我出发后，心情轻松，缓缓行进，后来为了赶时间开始加速．图K12－3A ．(1)(2)(4)B ．(4)(2)(3)C ．(4)(1)(3)D ．(4)(1)(2)9．某车间分批生产某种产品，每批的生产准备费用为800元．若每批生产x 件，则平均仓储时间为x8天，且每件产品每天的仓储费用为1元．为使平均到每件产品的生产准备费用与仓储费用之和最小，每批应生产产品( )A ．60件B ．80件C ．100件D ．120件图K12－410．一位设计师在边长为3的正方形ABCD 中设计图案，他分别以A ，B ，C ，D 为圆心，以b ⎝⎛⎭⎫0<b ≤32为半径画圆，由正方形内的圆弧与正方形边上线段(圆弧端点在正方形边上的连。

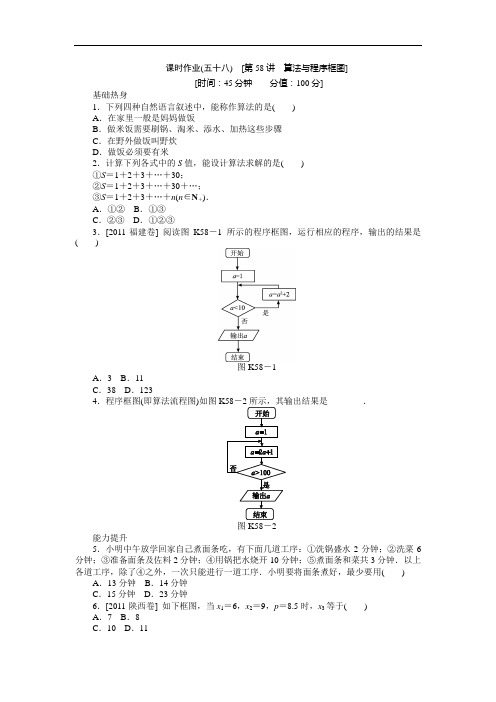
课时作业(五十八)[第58讲算法与程序框图][时间：45分钟分值：100分]基础热身1．下列四种自然语言叙述中，能称作算法的是()A．在家里一般是妈妈做饭B．做米饭需要刷锅、淘米、添水、加热这些步骤C．在野外做饭叫野炊D．做饭必须要有米2．计算下列各式中的S值，能设计算法求解的是()①S＝1＋2＋3＋ (30)②S＝1＋2＋3＋…＋30＋…；③S＝1＋2＋3＋…＋n(n∈N＋)．A．①②B．①③C．②③D．①②③3．[2011·福建卷] 阅读图K58－1所示的程序框图，运行相应的程序，输出的结果是()图K58－1A．3 B．11C．38 D．1234．程序框图(即算法流程图)如图________．图K58－2能力提升5．小明中午放学回家自己煮面条吃，有下面几道工序：①洗锅盛水2分钟；②洗菜6分钟；③准备面条及佐料2分钟；④用锅把水烧开10分钟；⑤煮面条和菜共3分钟．以上各道工序，除了④之外，一次只能进行一道工序．小明要将面条煮好，最少要用() A．13分钟B．14分钟C．15分钟D．23分钟6．[2011·陕西卷] 如下框图，当x1＝6，x2＝9，p＝8.5时，x3等于()A．7 B．8C．10 D．11图K58－3图K58－47．[2011·天津卷] 阅读程序框图K58－4，运行相应的程序，则输出i的值为() A．3 B．4C．5 D．68．如果执行程序框图K58－5，输入n＝6，m＝4，那么输出的p等于()A．720 B．360C．240 D．120K58－5图K58－69．执行如图K58－6所示的程序框图，若输出的结果为S＝105，则判断框中应填入() A．i<6 B．i<7C．i<9 D．i<1010．为确保信息安全，信息需加密传输，发送方由明文→密文(加密)，接收方由密文→明文(解密)，已知加密规则如图K58－7所示，例如，明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28．图K58－7图K58－811．对任意非零实数a，b，若a b的运算原理如图K58－8程序框图所示，则32＝________.12．[2011·浙江卷] 某程序框图如图K58－9所示，则该程序运行后输出的k的值是________．图K58－9图K58－1013．[2011·山东卷] 执行图K58－10所示的程序框图，输入l＝2，m＝3，n＝5，则输出的y的值是________．14．(10分)画出求坐标平面内两点A(a，b)，B(c，d)之间距离的程序框图．15．(13分)为了加强居民的节水意识，某市制定了以下生活用水收费标准：每户每月用水未超过7立方米时，每立方米收费1.0元，并加收0.2元的城市污水处理费；超过7立方米的部分，每立方米收费1.5元，并加收0.4元的城市污水处理费．设某户每月用水量为x 立方米，应交纳水费y元，请你设计一个输入用水量、输出应交水费额的算法，画出程序框图．难点突破16．(12分)一企业生产的某产品在不做电视广告的前提下，每天销售量为b件．经市场调查后得到如下规律：若对产品进行电视广告的宣传，每天的销售量S(件)与电视广告每天的播放量n(次)的关系可用如图K58－11所示的程序框图来体现．(1)试写出该产品每天的销售量S(件)关于电视广告每天的播放量n(次)的函数关系式；(2)要使该产品每天的销售量比不做电视广告时的销售量至少增加90%，则每天电视广告的播放量至少需多少次？课时作业(五十八)【基础热身】1．B[解析] 算法是做一件事情或解决一个问题等的程序或步骤，故选B.2．B[解析] ②为求无限项的和，而算法要求必须在有限步之内完成．3．B[解析] 该程序框图是当型循环结构，由程序框图可知，第一次循环，a＝12＋2＝3；第二次循环，a＝32＋2＝11；当a＝11时，a<10不成立，输出a＝11，故选B.4．127[解析] 由程序框图知，循环体被执行后的值依次为3、7、15、31、63、127，故输出的结果是127.【能力提升】5．C [解析] ①洗锅盛水2分钟＋④用锅把水烧开10分钟(同时②洗菜6分钟＋③准备面条及佐料2分钟)＋⑤煮面条和菜共3分钟＝15分钟．6．B [解析] 因为x 1＝6，x 2＝9，p ＝8.5，p ＝x 1＋x 22或p ＝x 2＋x 32，当p ＝x 1＋x 22时，p ＝7.5，与p ＝8.5不符，不合题意，故p ＝x 2＋x 32＝8.5，得x 3＝8，故答案为B. 7．B [解析] i ＝1时，a ＝1×1＋1＝2；i ＝2时，a ＝2×2＋1＝5；i ＝3时，a ＝3×5＋1＝16；i ＝4时，a ＝4×16＋1＝65>50，∴输出i ＝4，故选B.8．B [解析] p ＝1×3×4×5×6＝360.9．C [解析] ∵105＝1×3×5×7，∴由程序框图可知结果应是由1×3×5×7得到的，故应填i <9.10．6,4,1,7 [解析] 4d ＝28⇒d ＝7,2c ＋3d ＝23⇒c ＝1，2b ＋c ＝9⇒b ＝4，a ＋2b ＝14⇒a ＝6.11．2 [解析] ∵a ＝3，b ＝2，a >b ，∴输出a ＋1b ＝3＋12＝2. 12．5 [解析] k ＝3时，a ＝43＝64，b ＝34＝81，a <b ；k ＝4时，a ＝44＝256，b ＝44＝256，a ＝b ；k ＝5时，a ＝45＝256×4，b ＝54＝625，a >b ，输出k ＝5.13．68 [解析] 把l ＝2，m ＝3，n ＝5代入y ＝70l ＋21m ＋15n 得y ＝278，此时y ＝278>105，第一次循环y ＝278－105＝173，此时y ＝173>105，再循环，y ＝173－105＝68<105，输出68，结束循环．14．[解答]15．[解答] y 与xy ＝⎩⎪⎨⎪⎧ 1.2x (0≤x ≤7)，1.9x －4.9(x >7)， 算法设计如下：第一步，输入每月用水量x ；第二步，判断输入的x 是否超过7；若x >7，则应交水费y ＝1.9x －4.9；否则应交水费y ＝1.2x ；第三步，输出应交水费y .程序框图如图所示．【难点突破】16．[解答] (1)设电视广告播放量为每天i 次时，该产品的销售量为S i (0≤i ≤n ，i ∈N *)．由题意S i ＝⎩⎪⎨⎪⎧b ，i ＝0，S i －1＋b 2i，1≤i ≤n ，i ∈N *， 于是当i ＝n 时，S n ＝b ＋⎝⎛⎭⎫b 2＋b 22＋…＋b 2n ＝b ⎝⎛⎭⎫2－12n (n ∈N *)，所以，该产品每天销售量S (件)与电视广告播放量n (次/天)的函数关系式为：S ＝b ⎝⎛⎭⎫2－12n ，n ∈N *. (2)由题意，有b ⎝⎛⎭⎫2－12n ≥1.9b ⇒2n ≥10⇒n ≥4(n ∈N *)． 所以，要使该产品的销售量比不做电视广告时的销售量至少增加90%，则每天广告的播放量至少需4次．。

第36讲 等差数列的概念及基本运算1．已知数列{a n }是等差数列，且a 7－2a 4＝6，a 3＝2，则公差d ＝(B)A ．2 2B ．4C ．8D ．16因为a 7－2a 4＝a 7－(a 1＋a 7)＝－a 1＝6，所以a 1＝－6.又a 3＝2，所以公差d ＝a 3－a 13－1＝2－(－6)2＝4. 2．(2018·武汉二月调研)在等差数列{a n }中，前n 项和S n 满足S 7－S 2＝45，则a 5＝(B)A ．7B ．9C ．14D ．18因为S 7－S 2＝a 3＋a 4＋a 5＋a 6＋a 7＝45，所以5a 5＝45，所以a 5＝9.3．已知正项数列{a n }中，a 1＝1，a 2＝2,2a 2n ＝a 2n ＋1＋a 2n －1(n ≥2)，则a 6等于(D) A ．16 B ．8C ．2 2D ．4由2a 2n ＝a 2n ＋1＋a 2n －1可知数列{a 2n }是等差数列，且首项为a 21＝1，公差d ＝a 22－a 21＝4－1＝3.所以{a 2n }的通项a 2n ＝1＋3(n －1)＝3n －2， 所以a n ＝3n －2.所以a 6＝3×6－2＝4.4．(2018·汕头模拟)记S n 为等差数列{a n }的前n 项和，S 5＝15a 5，S 5－S 2＝18，则3a 3－a 4的值为(A)A ．21B ．24C ．27D ．30因为{a n }是等差数列，由等差数列的性质和前n 项和公式及S 5＝15a 5，得a 3＝3a 5，①又因为S 5－S 2＝18，得a 3＋a 4＋a 5＝3a 4＝18，得a 4＝6，且a 4＝a 3＋d ，a 4＋d ＝a 5，②由①②得 a 4－d ＝3(a 4＋d )，解得a 4＝－2d ＝6，所以d ＝－3，则3a 3－a 4＝3(a 4－d )－a 4＝2a 4－3d ＝2×6－3×(－3)＝12＋9＝21.5．(2018·北京卷)设{a n }是等差数列，且a 1＝3，a 2＋a 5＝36，则{a n }的通项公式为__a n ＝6n －3__.(方法一)设公差为d .因为a 2＋a 5＝36，所以(a 1＋d )＋(a 1＋4d )＝36，所以2a 1＋5d ＝36.因为a 1＝3，所以d ＝6，所以通项公式a n ＝a 1＋(n －1)d ＝6n －3.(方法二)设公差为d ，因为a 2＋a 5＝a 1＋a 6＝36，a 1＝3，所以a 6＝33，所以d ＝a 6－a 15＝6. 因为a 1＝3，所以通项公式a n ＝6n －3.6．设S n 是数列{a n }的前n 项和，且a 1＝－1，a n ＋1＝S n S n ＋1，则S n ＝ －1n. 由已知得a n ＋1＝S n ＋1－S n ＝S n ＋1·S n ，两边同除以S n ＋1·S n ，得1S n ＋1－1S n＝－1， 故数列⎩⎨⎧⎭⎬⎫1S n 是以－1为首项，－1为公差的等差数列， 所以1S n ＝－1－(n －1)＝－n ，所以S n ＝－1n. 7．(2018·全国卷Ⅱ)记S n 为等差数列{a n }的前n 项和，已知a 1＝－7，S 3＝－15.(1)求{a n }的通项公式；(2)求S n ，并求S n 的最小值．(1)设{a n }的公差为d ，由题意得3a 1＋3d ＝－15.由a 1＝－7得d ＝2.所以{a n }的通项公式为a n ＝a 1＋(n －1)d ＝2n －9.(2)由(1)得S n ＝a 1＋a n 2·n ＝n 2－8n ＝(n －4)2－16. 所以当n ＝4时，S n 取得最小值，最小值为－16.8．(2018·郑州市二模)设数列{a n }满足：a 1＝1，a 2＝3，且2na n ＝(n －1)a n －1＋(n ＋1)a n ＋1，则a 20的值是(D)A ．415B ．425C ．435D ．445由2na n ＝(n －1)a n －1＋(n ＋1)a n ＋1，得na n －(n －1)a n －1＝(n ＋1)a n ＋1－na n ，又因为1×a 1＝1,2×a 2－1×a 1＝5，所以数列{na n }为首项为1，公差为5的等差数列，则20a 20＝1＋19×5＝96，解得a 20＝245. 9．数列{a n }是等差数列，且a 1＋a 2＋…＋a 10＝10，a 11＋a 12＋…＋a 20＝20，则a 41＋a 42＋…＋a 50＝ 50 .因为A 1＝S 10，A 2＝S 20－S 10，A 3＝S 30－S 20，…，数列{A n }构成等差数列，其中A 1＝S 10＝10，公差d ＝10，所以a 41＋a 42＋…＋a 50＝A 5＝A 1＋(5－1)×d＝10＋4×10＝50.10．已知数列{a n }中，a 1＝5且a n ＝2a n －1＋2n －1(n ≥2且n ∈N *)．(1)求证数列⎩⎨⎧⎭⎬⎫a n －12n 为等差数列； (2)求数列{a n }的通项公式．(1)(方法一：构造法)因为a 1＝5且a n ＝2a n －1＋2n －1，所以当n ≥2时，a n －1＝2(a n －1－1)＋2n ，所以a n －12n ＝a n －1－12n －1＋1， 所以a n －12n －a n －1－12n －1＝1， 所以⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n －12n 是以a 1－12＝2为首项，以1为公差的等差数列． (方法二：代入法)因为a 1＝5，n ≥2时，所以a n －12n －a n －1－12n －1＝(2a n －1＋2n －1)－12n －a n －1－12n －1＝1， 所以⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n －12n 是以a 1－12＝2为首项，以1为公差的等差数列． (2)由(1)知a n －12n ＝2＋(n －1)×1＝n ＋1， 所以a n ＝(n ＋1)2n ＋1.。

第3课 算法语句（1）【考点导读】会用伪代码表述四种基本算法语句：输入输出语句，赋值语句，条件语句和循环语句.会用上述基本语句描述简单问题的算法过程.高考要求对算法语句有最基本的认识，并能解决相关的简单问题.【基础练习】1 .下列赋值语句中，正确的是 （1） .(1)3x ← (2)3x ← (3)30x -← (4)30x -←2．条件语句表达的算法结构为 ② . ①．顺序结构 ②．选择结构 ③．循环结构 ④．以上都可以解析：条件语句典型的特点是先判断再执行，对应的是选择结构. 3．关于for 循环说法错误的是 ④ .①．在for 循环中，循环表达式也称为循环体②．在for 循环中，步长为1，可以省略不写，若为其它值，则不可省略 ③．使用for 循环时必须知道终值才可以进行④．for 循环中end 控制结束一次循环，开始一次新循环解析：for 循环中end 是指整个循环结束，而不是一次循环结束4.阅读下面的算法，说明该算法的处理功能 输出X ，Y 两个值中较大的一个值 . R ead X I f X >Y then P rint X E lse P rint Y E nd if 【范例解析】例1．试写出解决求函数y =⎩⎨⎧x 2-1(x <2)-x 2+1(x ≥2)的函数值这一问题的伪代码．解： R ead xI f x <2 T heny ← x 2-1E lsey ← -x 2+1E nd I f P rint y点评 分段函数问题是考查If 语句一个重要的载体，因此，我们要注意此类问题可以先根据语言叙说，让学生先列出函数关系式，再写出相应的伪代码．例2.已知S ＝5+10+15+…+1500，请用流程图描述求S 的算法并用伪代码表示.解 流程图如下图所示：结束从流程图可以看出这是一个循环结构，我们可以运用循环语句来实现. S ←5 F or I from 10 to 1500 step 5 S ←S +I E nd F or P rint S点评 在准确理解算法的基础上，学会循环语句的使用.循环语句包括for 循环、While 循环.解题时要根据需要灵活运用.循环语句包括if …then ，if …then …else ，并且if …then …else 可以嵌套，解题时要根据需要灵活运用. 例3. 青年歌手大奖赛有10名选手参加，并请了12名评委.为了减少极端分数的影响，通常去掉一个最高分和一个最低分后再求平均分.请用算法语句表示：输入12名评委所打的分数a i ，用函数Max(a 1,a 2,…,a 12)和Min (a 1,a 2,…,a 12) 分别求出中a i (i =1,2,…,12)的最大值和最小值，最后输出该歌手的成绩.解 S ←0F or I from 1 to 12 R ead a i S ←S +a i E nd F orG ←(S - Max (a 1,a 2,…,a 12)- Min (a 1,a 2,…,a 12))/10 P rint G 【反馈演练】1.阅读下列伪代码，并指出当3,5a b ==-时的计算结果：⑴read a, b (2) read a, b (3) read a, b x←a+b a←a+b a←a+b y ←a-b b←a -b b←a -ba←(x+y )/2 a ←(a+b )/2 a ←(a-b )/2 b ←(x-y )/2 b ←(a-b )/2 b ←(a+b )/2 P rint a, b P rint a, b P rint a, ba = 3 ，b = -5 a = 1/2 ，b = -5/4 a = -5/2 ，b = 1/4 2.下图中程序执行后输出的结果是_____7___________.3．已知菲波那契数列：1,1,2,3,5,8,…（从第三项起每一项都是其前两项的和）.用For 语句给 出求第20项的一个算法：其中A 可以是：（1） （2）（3） （4）其中正确的序号是 （3）（4） .4.写出下面流程图所表述的算法的功能并用伪代码表示.开始结束答案：解：输出两个不同的数中小的一个数.用伪代码表示为R ead a ，b I f a >b then P rint b E lse P rint a E nd if5.写出计算1+2+3+4+…+100之和的伪代码.答案：此问题可以用循环语句表示为 S ←1F or I from 2 to 100 S ←S +II ←1F or n from 1 to 11 step 2 I ←2I+1I f I >20 Then I ←I －20 E nd if E nd for Print I （第2题）a b b a +b b a +b a b m b b a +b a m m a + ba b b mE ndF or P rint S6.求1－21+31－41+…+91－101的值. 解：算法分析：第一步是选择一个变量S 表示和，并赋给初值0，再选一个变量H ，并赋给初值0； 第二步开始进入for 循环语句，首先设i 为循环变量，并设初值、步长、终值； 第三步为循环表达式（循环体）；第四步用“end for ”控制一次循环，开始一次新的循环. 伪代码如下： S ←0 H ←0For i from 1 to 10 H ←（－1）i +1/iS ←S +HE nd forP rint S7.依次将十个数输入，要求将其中最大的数打印出来.试用流程图和伪代码表示问题的算法.解：用伪代码设计算法如下：R ead Xmax ←XF or I from 2 to 10R ead XI f X >max then max ←X E nd ifE nd for P rint max8. 判断某年份是否为闰年，要看此年份数能否被4整除.若不能被4整除，则是平年，2月是28天；若能被4整除，但不能被100整除，则为闰年，2月是29天；若能被4整除，又能被100整除，还要看能否被400整除，若能则为闰年，否则也为平年.画出上述算法的流程图，并写出伪代码.结束解：用伪代码设计算法如下：Array Read yMod y≠thenIf (,4)0Print y 是平年Mod y≠then Else If (,100)0Print y是润年Mod y=then Else If (,400)0Print y是润年ElsePrint y是平年Else If。

第21课时基本算法语句【考点点知】知己知彼，百战不殆基本算法语句与排序问题是新课标增加的内容，是数学及其应用的重要组成部分，新课标高考对本部分的考查可能与代数、几何中的有关知识结合，以客观题的形式考查对几种基本算法语句的理解与应用．复习时应理解5种基本算法语句的表示方法、结构和用法．对算法思想要有深层次的体会和理解．考点一:条件语句1.条件语句是表达选择结构最常用的语句,主要是针对所给条件进行判断,根据条件的真假决定执行下一步的任务.实际上,如图的流程图都可以用条件语句进行表示.2.条件语句的一般形式如下:if <条件>then<语句1>else<语句2>end if3.条件语句是表达选择结构的最常用语句.其含义是，如果条件成立，执行语句1，否则，执行语句2.“语句1”和“语句2”表示当条件成立时和不成立分别要执行语句. 用一句表达，就是：如果条件成立（也称条件为真），那么程序执行“语句1”中的语句，否则（条件为假）程序执行“语句2”的语句．这就是if...else语句.考点二:循环语句算法中的循环结构在程序设计语言中由循环语句来表达．对应算法中的两种循环结构，一般程序设计语言中也有当型（while型）和直到型（until型）两种语句结构，即WHILE 语句和UNTIL语句．1.WHILE语句(当型)循环语句(1)WHILE语句的一般格式是：WHILE 条件循环体END WHILE(2)当计算机遇到WHILE语句时，首先判断条件的真假，如果条件符合，就执行HILE 与END之间的循环体；然后再检查上述条件，如果条件仍符合，再次执行循环体，这个过程反复进行，直到某一次条件不符合为止．这时，计算机将不执行循环体，直接跳到END 语句后，接着执行END语句之后的语句．2.UNTIL语句(直到型)语句(1)UNTIL语句的一般格式是：DO循环体UNTIL 条件END DO(2)当计算机遇到UNTIL语句时，先执行一次循环体，然后对条件进行判断，如果条件不符合，就再一次执行循环体，然后再对条件进行判断，如果条件仍然符合，那么再一次执行循环体，这个过程反复进行，直到某一次条件符合为止．这时，计算机将不执行循环体，而直接跳到UNTIL 语句后，接着执行UNTIL 语句之后的语句．【小题热身】明确考点，自省反思1.计算机执行下面的程序段后，输出的结果是 .1a =3b =a ab =+b a b =-PRINT a ，b2.下列程序运行结果是 .3. 下列程序运行结果是 .【考题点评】分析原因，醍醐灌顶例1.(广东滕州模)为了在运行右边的程序之后得到输出16=y ，键盘输入x 应该是 .思路透析:程序是已知一个分段函数22(1),0()(1),0x x f x x x ⎧+<=⎨-≥⎩， 当0x <时, 由2(1)16x +=, 可解得5x =-;当0x >时, 由2(1)16x -=, 可解得5x =.∴键盘输入x 应该是5-或5．点评: 条件结构是处理算法的流程中，根据条件是否成立而有不同的流向的处理步骤．本题出错的多数情形是解方程出错或出现漏解.例2.当2=x 时，下面的程序段结果是 .思路透析:第一次循环:0211,2s i =⨯+==第二次循环:1213,3s i =⨯+==,第三次循环:3217,4s i =⨯+==,第四次循环:72115,5s i =⨯+==,此时退出循环,输出的15s =,点评:应用WHILE 语句描述算法比流程图表示算法要简单的多了,流程图需要将算法的各个细节都要考虑在内,要考虑如何设计循环起止点,让流程线正确带领程序运行.而用WHILE 语句时这些问题均不用多考虑, 只需要将循环体用变量赋值或其它的形式语句表示出来就行了.例3.求小于100的所有正偶数的和，设计一个算法的程序.思路透析:小于100的所有的正偶数的和为2+4+6+8+…+98,用Do 语句可以直接编写. S ←2 , i ← 4 ;DOs ←s +i ;i ←i +2 ;UNTIL i ≥100 ;END DO输出 s .点评:本例也可以用for 语句可以描述为:s ←0 ,for i from 1 to 49 dos ←s +2；end for输出a .由这两个语句有同一算法中的比较可得, for 语句表示循环结构必须知道运行次数,而do 语句表示则必须知道循环终止条件,不同的条件下选择不同的语句,可以灵活求解此类问题.例4某地电信部门规定：拨打市内电话时，如果通话时间不超过3 min ，则收取通话费0.22元；如果通话时间超过3 min ，则超过部分按每分钟0.1元收取通话费，不足1 min 按1 min 计.设通话时间为t （min ），通话费用为y （元），如何设计一个计算通话费用的算法?编写一个程序.．思路透析:实际上y 是关于t 的分段函数，关系式为y =0.22(03),0.220.1(3)(3,),0.220.1([3]1)(3,).t t t t t t t <≤⎧⎪+->∈⎨⎪+-+>∉⎩Z Z［t －3］表示取不大于t －3的整数部分.其算法的程序框图是这里应用的是条件结构，在程序语言中应用复合if条件语句来表达.输入“请输入通话时间（分钟）：”；tif t<=3 ,then y←0.22 ;else if t是整数,then y←0.22+0.1×（t－3）;else y←0.22+0.1×（INT（t－3）+1）;输出“通话时间为（分钟）：”；t输出“通话费用为（元）：”；y .点评:取整函数在程序中用INT（）来表示，如：INT（2.5）=2，INT（3）=3，INT （－3.5）=－4. 若t是整数，则INT（t）=t，若t不是整数，则INT（t）< >t.当t－3不是整数时，计费时间应该是t－3的整数部分加1..分段函数的形式.类似的实际问题，乘飞机按年龄分：12岁以下买半票，12岁以上买全票，无免票.这里有两个条件结构，要分清各自的控制条件.条件语句嵌套分别用END if结束.程序结束用END结束.在程序中要区分开END IF 与END的作用.【即时测评】学以致用，小试牛刀1.下列程序运行结果是()A. 10B. -10C. 190D.1002.下面程序运行后，输出的值是( )i←0DOi←i+1UNTIL i*i>=2000END DOi←i 1PRINT iA. 43B. 44C. 45D. 463.下面程序执行后输出的结果是( )第3题图 第4题图A. 2B. 3C. 4D. 54.上面的程序运行后输出的结果为( ) A.20,20- B. 22,22- C. 22,22- D. 20,20-【课后作业】学练结合，融会贯通一、填空题:1. 在until 语句的一般形式中有“until A ”,其中A 是 .2. 当3=a 时，下面的程序段输出的结果是 .3.把求!1234n n =⨯⨯⨯⨯⋅⋅⋅⨯的程序补充完整第3题图 第4题图 第5题图4.上面程序运行后输出的结果为 .5.上面的算法语句所表示的程序运行后实现的功能为_______________ 二、解答题:6. 求方程x 2+ax +b =0的解的过程的算法流程图,并用条件语句表示.7. 试用算法语句表示：寻找满足1357_____10000⨯⨯⨯⨯⨯> 的最小整数的算法．8第21课时 基本算法语句参考答案【小题热身】1. 4,12. 13. 25【即时测评】1. A2. B3. A4. B【课后作业】一、填空题:1. 终止条件为真2. 63. INPUT ，WHILE ，END WHILE4. 65. 06. 将,,a b c 按从大到小的顺序排列后再输出二、解答题:6.解析:其程序流程图如图所示.用复合if 语句来描述这个算法如下:输入 ,a b ;2:4a b ∆=-;if 0∆<,then 输出方程无解;else if 0∆=,then :2a x =-, 输出x ;else 1:2a x -+=, 2:2a x -∆=; 输出 12,x x .end ifend if7. 解析: 循环的次数不定，因此可用“While 循环”语句，具体描述如下：8.1S ← 1I ← While S ≤10000 2I I =+ *S S I ←End While Print IEnd。

高三文科数学一轮复习 基本算法语句 算法案例 (必修3 选修1-2)- 153 -基本算法语句 算法案例【知识要点】1． 输入语句的格式：INPUT “提示内容”； 变量. 例如： INPUT “x =”； 2． 输出语句的一般格式：PRINT “提示内容”；表达式. 例如：PRINT “S=”；S 3．赋值语句的一般格式：变量=表达式. 赋值语句中的“＝”称作赋值号赋值语句左边只能是变量名字，而不是表达式，右边表达式可以是一个常量、变量 或含变量的运算式。

不能利用赋值语句进行代数式的演算。

4．条件语句 5．循环语句6.求最大公约数:（1）辗转相除法;（2）更相减损术7.秦九韶算法用秦九韶算法求一般多项式f(x)= a n x n +a n-1x n-1+….+a 1x+a 0当x=x 0时的函数值, 递推公式：v 0=a n ,v k =v k －1+a n －k (k=1,2,…n) 8.进位制(1)一般地，若k 是一个大于一的整数，那么以k 为基数的k 进制可以表示为：110()110...(0,0,...,,)n n k n n a a a a a k a a a k --<<≤<，如34(5)表示5进制数。

(2)进位制间的转换:非十进制数转换为十进制数:0111011.........)(.....a k a k a k a k a a a a n n n n n n +⨯++⨯+⨯=---; 十进制数转换成非十进制数 :“除k 取余法”。

【典例解析】 例1:右边程序运行结果为( ) A ．7 B ．6 C ．5 D ．4【巩固练习】（1）“IF —THEN —ELSE ”语句 格式： IF 条件 THEN 语句1 ELSE 语句2 END IF(2）“IF —THEN ”语句格式： IF 条件 THEN 语句 END IF （1）当型循环语句 当型（WHILE 型）语句的一般格式为：WHILE 条件 循环体WEND（2）直到型循环语句 直到型（UNTIL 型）语句的一般格式为： DO 循环体LOOP UNTIL 条件高三文科数学一轮复习 基本算法语句 算法案例 (必修3 选修1-2)- 154 - 一选择题：1.如果以下程序运行后s 值是336，那么在程序中until 后面的条件应为 （ ）i=8 s=1 Do s ←s ×i i = i -1Loop UntilA. 6>iB. 7>iC. 6<iD. 7<i2.用秦九韶算法求多项式a x a x a x f n n +++=-11)(时，求)( x f 需要算乘方、乘法、加 法的次数分别为 A.n n n n ,),1(21+ B.n n n ,2, C.n n ,2,0 D. n n ,,0 ( )二．填空题:3. (2)1011的十进制数：_______________；十进制数250的二进制数为：____________.4.5.用秦九韶算法求1510105)(2+++++=x x x x x x f 当2-=x 的值时. 4v = 三．解答题6.:现将某科的成绩分为3个等级：不低于80分为A ，低于60分为C ，其余为B ，试用 语句表示输出学生相应的成绩等级的算法语句。