沪教版2016八年级数学期末难题压轴题

沪教版八年级上册压轴题数学数学模拟试题一、压轴题1．（概念认识）如图①，在∠ABC 中，若∠ABD ＝∠DBE ＝∠EBC ，则BD ，BE 叫做∠ABC 的“三分线”．其中，BD 是“邻AB 三分线”，BE 是“邻BC 三分线”．（问题解决）（1）如图②，在△ABC 中，∠A ＝70°，∠B ＝45°，若∠B 的三分线BD 交AC 于点D ，则∠BDC ＝ °；（2）如图③，在△ABC 中，BP 、CP 分别是∠ABC 邻AB 三分线和∠ACB 邻AC 三分线，且BP ⊥CP ，求∠A 的度数；（延伸推广）（3）在△ABC 中，∠ACD 是△ABC 的外角，∠B 的三分线所在的直线与∠ACD 的三分线所在的直线交于点P ．若∠A ＝m°，∠B ＝n°，直接写出∠BPC 的度数．（用含 m 、n 的代数式表示）2．某校八年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究．（1）如图1，在△ABC 中，∠ABC 与∠ACB 的平分线交于点P ，∠A ＝64°，则∠BPC ＝ ；（2）如图2，△ABC 的内角∠ACB 的平分线与△ABC 的外角∠ABD 的平分线交于点E ．其中∠A ＝α，求∠BEC ．（用α表示∠BEC ）；（3）如图3，∠CBM 、∠BCN 为△ABC 的外角，∠CBM 、∠BCN 的平分线交于点Q ，请你写出∠BQC 与∠A 的数量关系，并证明．3．已知，在平面直角坐标系中，(42,0)A ，(0,42)B ，C 为AB 的中点，P 是线段AB 上一动点，D 是线段OA 上一点，且PO PD =，DE AB ⊥于E ．（1）求OAB ∠的度数；（2）当点P 运动时，PE 的值是否变化？若变化，说明理由；若不变，请求PE 的值． （3）若45OPD ∠=︒，求点D 的坐标．4．已知在△ABC 中，AB ＝AC ，射线BM 、BN 在∠ABC 内部，分别交线段AC 于点G 、H ． （1）如图1，若∠ABC ＝60°，∠MBN ＝30°，作AE ⊥BN 于点D ，分别交BC 、BM 于点E 、F ．①求证：∠1＝∠2；②如图2，若BF ＝2AF ，连接CF ，求证：BF ⊥CF ；（2）如图3，点E 为BC 上一点，AE 交BM 于点F ，连接CF ，若∠BFE ＝∠BAC ＝2∠CFE ，求ABFACF S S 的值．5．阅读下面材料，完成(1)-(3)题．数学课上，老师出示了这样一道题：如图1，已知等腰△ABC 中，AB ＝AC ，AD 为BC 边上的中线，以AB 为边向AB 左侧作等边△ABE ，直线CE 与直线AD 交于点F ．请探究线段EF 、AF 、DF 之间的数量关系，并证明． 同学们经过思考后，交流了自已的想法：小明：“通过观察和度量，发现∠DFC 的度数可以求出来．”小强：“通过观察和度量，发现线段DF 和CF 之间存在某种数量关系．”小伟：“通过做辅助线构造全等三角形，就可以将问题解决．”......老师：“若以AB 为边向AB 右侧作等边△ABE ，其它条件均不改变，请在图2中补全图形,探究线段EF 、AF 、DF 三者的数量关系，并证明你的结论．”（1）求∠DFC 的度数；（2）在图1中探究线段EF 、AF 、DF 之间的数量关系，并证明；（3）在图2中补全图形，探究线段EF 、AF 、DF 之间的数量关系，并证明．6．学习了三角形全等的判定方法（即“SAS ”、“ASA ”、“AAS ”、“SSS ”）和直角三角形全等的判定方法（即“HL ”）后，我们继续对“两个三角形满足两边的其中一边的对角对应相等”的情形进行研究．（初步思考）我们不妨将问题用符号语言表示为：在△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，然后，对∠B 进行分类，可分为“∠B 是直角、钝角、锐角”三种情况进行探究．（深入探究）第一种情况：当∠B 是直角时，△ABC ≌△DEF ．（1）如图①，在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ＝90°，根据______，可以知道Rt △ABC ≌Rt △DEF ．第二种情况：当∠B 是钝角时，△ABC ≌△DEF ．（2）如图②，在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，且∠B 、∠E 都是钝角．求证：△ABC ≌△DEF ．第三种情况：当∠B 是锐角时，△ABC 和△DEF 不一定全等．（3）在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，且∠B 、∠E 都是锐角．请你用直尺在图③中作出△DEF ，使△DEF 和△ABC 不全等，并作简要说明．7．如图所示，在平面直角坐标系xOy 中，已知点A 的坐标(3,2)-，过A 点作AB x ⊥轴，垂足为点B ，过点(2,0)C 作直线l x ⊥轴，点P 从点B 出发在x 轴上沿着轴的正方向运动．（1）当点P 运动到点O 处，过点P 作AP 的垂线交直线l 于点D ，证明AP DP =，并求此时点D 的坐标；（2）点Q 是直线l 上的动点，问是否存在点P ，使得以P C Q 、、为顶点的三角形和ABP ∆全等，若存在求点P 的坐标以及此时对应的点Q 的坐标，若不存在，请说明理由．8．如图，在等边ABC ∆中，线段AM 为BC 边上的中线．动点D 在直线AM 上时，以CD 为一边在CD 的下方作等边CDE ∆，连结BE ．（1）求CAM ∠的度数；（2）若点D 在线段AM 上时，求证：ADC BEC ∆≅∆；（3）当动点D 在直线AM 上时，设直线BE 与直线AM 的交点为O ，试判断AOB ∠是否为定值？并说明理由．9．如图，ABC ∆在平面直角坐标系中，60BAC ∠=︒，()0,43A ，8AB =，点B 、C 在x 轴上且关于y 轴对称．（1）求点C的坐标；（2）动点P以每秒2个单位长度的速度从点B出发沿x轴正方向向终点C运动，设运动时间为t秒，点P到直线AC的距离PD的长为d，求d与t的关系式；∠的平分（3）在（2）的条件下，当点P到AC的距离PD为33时，连接AP，作ACB线分别交PD、PA于点M、N，求MN的长．10．已知ABC，P 是平面内任意一点（A、B、C、P 中任意三点都不在同一直线上）．连接 PB、PC，设∠PBA＝s°，∠PCA＝t°，∠BPC＝x°，∠BAC＝y°．（1）如图，当点 P 在ABC 内时，①若 y＝70，s＝10，t＝20，则 x＝；②探究 s、t、x、y 之间的数量关系，并证明你得到的结论．（2）当点 P 在ABC 外时，直接写出 s、t、x、y 之间所有可能的数量关系，并画出相应的图形．11．如图，以直角三角形AOC的直角顶点O为原点，以OC，OA所在直线为轴和轴建立平--=．面直角坐标系，点A（0，a），C（b，0a6b80（1）a= ；b= ；直角三角形AOC的面积为．（2）已知坐标轴上有两动点P，Q同时出发，P点从C点出发以每秒2个单位长度的速度向点O匀速移动，Q点从O点出发以每秒1个单位长度的速度向点A匀速移动，点P到达O点整个运动随之结束．AC的中点D的坐标是（4，3），设运动时间为t秒．问：是否存在这样的t，使得△ODP与△ODQ的面积相等？若存在，请求出t的值；若不存在，请说明理由．（3）在（2）的条件下，若∠DOC=∠D CO，点G是第二象限中一点，并且y轴平分∠GOD．点E是线段OA上一动点，连接接CE交OD于点H，当点E在线段OA上运动的过程中，探究∠GOD，∠OHC，∠ACE之间的数量关系，并证明你的结论(三角形的内角和为180)．12．某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究．（1）如图1，在△ABC 中，∠ABC 与∠ACB 的平分线交于点P ，∠A ＝64°，则∠BPC ＝ ；（2）如图2，△ABC 的内角∠ACB 的平分线与△ABC 的外角∠ABD 的平分线交于点E ．其中∠A ＝α，求∠BEC ．（用α表示∠BEC ）；（3）如图3，∠CBM 、∠BCN 为△ABC 的外角，∠CBM 、∠BCN 的平分线交于点Q ，请你写出∠BQC 与∠A 的数量关系，并说明理由；（4）如图4，△ABC 外角∠CBM 、∠BCN 的平分线交于点Q ，∠A=64°，∠CBQ ，∠BCQ 的平分线交于点P ，则∠BPC= ゜，延长BC 至点E ，∠ECQ 的平分线与BP 的延长线相交于点R ，则∠R= ゜．13．已知：如图1，直线//AB CD ，EF 分别交AB ，CD 于E ，F 两点，BEF ∠，DFE ∠的平分线相交于点K ．（1）求K ∠的度数；（2）如图2，BEK ∠，DFK ∠的平分线相交于点1K ，问1K ∠与K ∠的度数是否存在某种特定的等量关系？写出结论并证明；（3）在图2中作1BEK ∠，1DFK ∠的平分线相交于点2K ，作2BEK ∠，2DFK ∠的平分线相交于点3K ，依此类推，作n BEK ∠，n DFK ∠的平分线相交于点1n K +，请用含的n 式子表示1n K ∠+的度数．（直接写出答案，不必写解答过程）14．小敏与同桌小颖在课下学习中遇到这样一道数学题：“如图（1），在等边三角形ABC 中，点E 在AB 上，点D 在CB 的延长线上，且ED EC =，试确定线段AE 与DB 的大小关系，并说明理由”．小敏与小颖讨论后，进行了如下解答：（1）取特殊情况，探索讨论：当点E 为AB 的中点时，如图（2），确定线段AE 与DB 的大小关系，请你写出结论：AE _____DB （填“>”，“<”或“=”），并说明理由．（2）特例启发，解答题目：解：题目中，AE 与DB 的大小关系是：AE _____DB （填“>”，“<”或“=”）．理由如下：如图（3），过点E 作EF ∥BC ，交AC 于点F ．（请你将剩余的解答过程完成） （3）拓展结论，设计新题：在等边三角形ABC 中，点E 在直线AB 上，点D 在直线BC 上，且ED EC =，若△ABC 的边长为1，2AE =，求CD 的长（请你画出图形，并直接写出结果）．15．在△ABC 中，已知∠A ＝α．（1）如图1，∠ABC 、∠ACB 的平分线相交于点D ．求∠BDC 的大小（用含α的代数式表示）；（2）如图2，若∠ABC 的平分线与∠ACE 的平分线交于点F ，求∠BFC 的大小（用含α的代数式表示）；（3）在（2）的条件下，将△FBC 以直线BC 为对称轴翻折得到△GBC ，∠GBC 的平分线与∠GCB 的平分线交于点M （如图3），求∠BMC 的度数（用含α的代数式表示）．16．如图，在ABC 中，D 为AB 的中点，10AB AC cm ==，8BC cm =．动点P 从点B 出发，沿BC 方向以3/cm s 的速度向点C 运动；同时动点Q 从点C 出发，沿CA 方向以3/cm s 的速度向点A 运动，运动时间是ts ．（1）在运动过程中，当点C 位于线段PQ 的垂直平分线上时，求出t 的值；（2）在运动过程中，当BPD CQP ≌时，求出t 的值；（3）是否存在某一时刻t ，使BPD CPQ ≌？若存在，求出t 的值；若不存在，请说明理由．17．（1）如图1，ABC 和DCE 都是等边三角形，且B ，C ，D 三点在一条直线上，连接AD ，BE 相交于点P ，求证：BE AD =．（2）如图2，在BCD 中，若120BCD ∠<︒，分别以BC ，CD 和BD 为边在BCD 外部作等边ABC ，等边CDE △，等边BDF ，连接AD 、BE 、CF 恰交于点P ． ①求证：AD BE CF ==；②如图2，在（2）的条件下，试猜想PB ，PC ，PD 与BE 存在怎样的数量关系，并说明理由．18．已知AB //CD ，点E 是平面内一点，∠CDE 的角平分线与∠ABE 的角平分线交于点F ． （1）若点E 的位置如图1所示．①若∠ABE =60°，∠CDE =80°，则∠F = °；②探究∠F 与∠BED 的数量关系并证明你的结论；（2）若点E的位置如图2所示，∠F与∠BED满足的数量关系式是．（3）若点E的位置如图3所示，∠CDE为锐角，且1452E F∠≥∠+︒，设∠F=α，则α的取值范围为．19．（1）探索发现：如图1，已知Rt△ABC中，∠ACB＝90°，AC＝BC，直线l过点C，过点A作AD⊥l，过点B作BE⊥l，垂足分别为D、E．求证：AD＝CE，CD＝BE．（2）迁移应用：如图2，将一块等腰直角的三角板MON放在平面直角坐标系内，三角板的一个锐角的顶点与坐标原点O重合，另两个顶点均落在第一象限内，已知点M的坐标为（1，3），求点N的坐标．（3）拓展应用：如图3，在平面直角坐标系内，已知直线y＝﹣3x+3与y轴交于点P，与x轴交于点Q，将直线PQ绕P点沿逆时针方向旋转45°后，所得的直线交x轴于点R．求点R的坐标．20．在等边△ABC的顶点A、C处各有一只蜗牛，它们同时出发，分别以每分钟1米的速度由A向B和由C向A爬行，其中一只蜗牛爬到终点时，另一只也停止运动，经过t分钟后，它们分别爬行到D、E处，请问：（1）如图1，在爬行过程中，CD和BE始终相等吗，请证明？（2）如果将原题中的“由A向B和由C向A爬行”，改为“沿着AB和CA的延长线爬行”，EB与CD交于点Q，其他条件不变，蜗牛爬行过程中∠CQE的大小保持不变，请利用图2说明：∠CQE=60°；（3）如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行，连接DE交AC于F”，其他条件不变，如图3，则爬行过程中，证明：DF=EF【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）85或100；（2）45°；（3）23m 或13m 或23m ＋13n 或13m －13n 或13n －13m 【解析】【分析】（1）根据题意可得B 的三分线BD 有两种情况，画图根据三角形的外角性质即可得BDC ∠的度数；（2）根据BP 、CP 分别是ABC ∠邻AB 三分线和ACB ∠邻AC 三分线，且BP CP ⊥可得135ABC ACB ，进而可求A ∠的度数；（3）根据B 的三分线所在的直线与ACD ∠的三分线所在的直线交于点P ．分四种情况画图：情况一：如图①，当BP 和CP 分别是“邻AB 三分线”、“邻AC 三分线”时；情况二：如图②，当BP 和CP 分别是“邻BC 三分线”、“邻CD 三分线”时；情况三：如图③，当BP 和CP 分别是“邻BC 三分线”、“邻AC 三分线”时；情况四：如图④，当BP 和CP 分别是“邻AB 三分线”、“邻CD 三分线”时，再根据A m ∠=︒，B n ∠=︒，即可求出BPC ∠的度数．【详解】解：（1）如图，当BD 是“邻AB 三分线”时，701585BD C； 当BD 是“邻BC 三分线”时，7030100BD C； 故答案为：85或100；（2）BP CP ， 90BPC ∴∠=︒，90PBC PCB ， 又BP 、CP 分别是ABC ∠邻AB 三分线和ACB ∠邻AC 三分线， 23PBC ABC ，23PCB ACB ∠=∠， ∴229033ABC ACB ， 135ABC ACB ，在ABC ∆中，180A ABC ACB ∠+∠+∠=︒ 180()45A ABCACB ． （3）分4种情况进行画图计算：情况一：如图①，当BP 和CP 分别是“邻AB 三分线”、“邻AC 三分线”时，2233BPC A m ； 情况二：如图②，当BP 和CP 分别是“邻BC 三分线”、“邻CD 三分线”时，1133BPC A m ；情况三：如图③，当BP 和CP 分别是“邻BC 三分线”、“邻AC 三分线”时， 21213333BPC A ABC m n ； 情况四：如图④，当BP 和CP 分别是“邻AB 三分线”、“邻CD 三分线”时，①当m n >时，11113333BPC A ABC m n ∠=∠-∠=-； ②当m n <时，11113333P ABC A n m ∠=∠-∠=-． 【点睛】 本题考查了三角形的外角性质，解决本题的关键是掌握三角形的外角性质．注意要分情况讨论． 2．（1）∠BPC ＝122°；（2）∠BEC ＝2a ；（3）∠BQC ＝90°﹣12∠A ，证明见解析 【解析】【分析】（1）根据三角形的内角和化为角平分线的定义；（2）根据三角形的一个外角等于与它不相邻的两个内角的和，用∠A 与∠1表示出∠2，再利用∠E 与∠1表示出∠2，于是得到结论；（3）根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠EBC 与∠ECB ，然后再根据三角形的内角和定理列式整理即可得解．解：（1）BP 、CP 分别平分ABC ∠和ACB ∠， 12PBC ABC ∴∠=∠，12PCB ACB ∠=∠， 180()BPC PBC PCB ∴∠=︒-∠+∠11180()22ABC ACB =︒-∠+∠， 1180()2ABC ACB =︒-∠+∠， 1(180180)2A =︒-︒-∠， 1180902A =-︒+︒∠， 9032122=︒+=︒，故答案为：122︒；（2）CE 和BE 分别是ACB ∠和ABD ∠的角平分线，112ACB ∴∠=∠，122ABD ∠=∠， 又ABD ∠是ABC ∆的一外角，ABD A ACB ∴∠=∠+∠，112()122A ABC A ∴∠=∠+∠=∠+∠， 2∠是BEC ∆的一外角，112111222BEC A A α∴∠=∠-∠=∠+∠-∠=∠=； （3）1()2QBC A ACB ∠=∠+∠，1()2QCB A ABC ∠=∠+∠， 180BQC QBC QCB ∠=︒-∠-∠，11180()()22A ACB A ABC =︒-∠+∠-∠+∠， 11180()22A A ABC ACB =︒-∠-∠+∠+∠， 结论：1902BQC A ∠=︒-∠．本题考查了三角形的外角性质与内角和定理，熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键．3．（1）45°；（2）PE 的值不变，PE=4，理由见详解；（3）D(8，0)．【解析】【分析】（1）根据A，B ，得△AOB 为等腰直角三角形，根据等腰直角三角形的性质，即可求出∠OAB 的度数；（2）根据等腰直角三角形的性质得到∠AOC=∠BOC=45°，OC ⊥AB ，再证明△POC ≌△DPE ，根据全等三角形的性质得到OC=PE ，即可得到答案；（3）证明△POB ≌△DPA ，得到PA=OB=DA=PB ，进而得OD 的值，即可求出点D 的坐标．【详解】（1）A，B ，∴OA=OB=∵∠AOB=90°，∴△AOB 为等腰直角三角形，∴∠OAB=45°；（2）PE 的值不变，理由如下：∵△AOB 为等腰直角三角形，C 为AB 的中点，∴∠AOC=∠BOC=45°，OC ⊥AB ，∵PO=PD ，∴∠POD=∠PDO ，∵D 是线段OA 上一点，∴点P 在线段BC 上，∵∠POD=45°+∠POC ，∠PDO=45°+∠DPE ，∴∠POC=∠DPE ，在△POC 和△DPE 中，90POC DPE OCP PED PO PD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩， ∴△POC ≅△DPE(AAS)，∴OC=PE ，∵OC=12AB=12×， ∴PE=4；（3）∵OP=PD ，∴∠POD=∠PDO=(180°−45°)÷2=67.5°，∴∠APD=∠PDO−∠A=22.5°，∠BOP=90°−∠POD=22.5°，∴∠APD=∠BOP ，在△POB 和△DPA 中，OBP PAD BOP APD OP PD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△POB ≌△DPA(AAS)，∴PA=OB=42，DA=PB ， ∴DA=PB=42×2-42=8-42，∴OD=OA−DA=42-(8-42)=828-，∴点D 的坐标为(828-，0)．【点睛】本题主要考查等腰直角三角形的性质，三角形全等的判定与性质定理，图形与坐标，掌握等腰直角三角形的性质，是解题的关键．4．（1）①见解析；②见解析；（2）2【解析】【分析】（1）①只要证明∠2+∠BAF ＝∠1+∠BAF ＝60°即可解决问题；②只要证明△BFC ≌△ADB ，即可推出∠BFC ＝∠ADB ＝90°；（2）在BF 上截取BK ＝AF ，连接AK ．只要证明△ABK ≌CAF ，可得S △ABK ＝S △AFC ，再证明AF ＝FK ＝BK ，可得S △ABK ＝S △AFK ，即可解决问题；【详解】（1）①证明：如图1中，∵AB ＝AC ，∠ABC ＝60°∴△ABC 是等边三角形，∴∠BAC ＝60°，∵AD ⊥BN ，∴∠ADB ＝90°，∵∠MBN ＝30°，∠BFD ＝60°＝∠1+∠BAF ＝∠2+∠BAF ，∴∠1＝∠2②证明：如图2中，在Rt △BFD 中，∵∠FBD ＝30°，∴BF ＝2DF ，∵BF ＝2AF ，∴BF ＝AD ，∵∠BAE ＝∠FBC ，AB ＝BC ，∴△BFC ≌△ADB ，∴∠BFC ＝∠ADB ＝90°，∴BF ⊥CF（2）在BF 上截取BK ＝AF ，连接AK ．∵∠BFE ＝∠2+∠BAF ，∠CFE ＝∠4+∠1，∴∠CFB ＝∠2+∠4+∠BAC ，∵∠BFE ＝∠BAC ＝2∠EFC ，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB ＝AC ，∴△ABK ≌CAF ，∴∠3＝∠4，S △ABK ＝S △AFC ，∵∠1+∠3＝∠2+∠3＝∠CFE ＝∠AKB ，∠BAC ＝2∠CEF ，∴∠KAF ＝∠1+∠3＝∠AKF ，∴AF ＝FK ＝BK ，∴S △ABK ＝S △AFK ， ∴ABF AFCS 2S ∆∆=． 【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、等腰三角形的判定和性质、直角三角形30度角性质等知识，解题的关键是能够正确添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．5．（1）60°；（2）EF=AF+FC，证明见解析；（3）AF=EF+2DF，证明见解析．【解析】【分析】（1）可设∠BAD＝∠CAD＝α，∠AEC＝∠ACE＝β，在△ACE中，根据三角形内角和可得2α＋60＋2β＝180°，从而有α＋β＝60°，即可得出∠DFC的度数；（2）在EC上截取EG＝CF，连接AG，证明△AEG≌△ACF，然后再证明△AFG为等边三角形，从而可得出EF＝EG＋GF＝AF＋FC；（3）在AF上截取AG＝EF，连接BG，BF，证明方法类似（2），先证明△ABG≌△EBF，再证明△BFG为等边三角形，最后可得出结论．【详解】解：（1）∵AB=AC，AD为BC边上的中线，∴可设∠BAD＝∠CAD＝α，又△ABE为等边三角形，∴AE=AB=AC，∠EAB=60°，∴可设∠AEC＝∠ACE＝β，在△ACE中，2α＋60°＋2β＝180°，∴α＋β＝60°，∴∠DFC=α＋β＝60°；（2）EF=AF+FC，证明如下：∵AB=AC，AD为BC边上的中线，∴AD⊥BC，∴∠FDC=90°，∵∠CFD＝60°，则∠DCF=30°，∴CF＝2DF，在EC上截取EG＝CF，连接AG，又AE=AC，∴∠AEG=∠ACF，∴△AEG≌△ACF（SAS）,∴∠EAG＝∠CAF，AG＝AF，又∠CAF=∠BAD，∴∠EAG=∠BAD，∴∠GAF＝∠BAD+∠BAG=∠EAG+∠BAG=∠60°，∴△AFG为等边三角形，∴EF＝EG＋GF＝AF＋FC，即EF=AF+FC；（3）补全图形如图所示，结论：AF=EF+2DF．证明如下：同（1）可设∠BAD＝∠CAD＝α，∠ACE＝∠AEC＝β，∴∠CAE＝180°－2β，∴∠BAE＝2α＋180°－2β＝60°，∴β－α＝60°，∴∠AFC=β－α＝60°，又△ABE为等边三角形，∴∠ABE=∠AFC=60°，∴由8字图可得：∠BAD＝∠BEF，在AF上截取AG＝EF，连接BG，BF，又AB=BE，∴△ABG≌△EBF（SAS），∴BG＝BF，又AF垂直平分BC，∴BF=CF，∴∠BFA=∠AFC=60°，∴△BFG为等边三角形，∴BG=BF，又BC⊥FG，∴FG=BF=2DF，∴AF＝AG＋GF＝BF＋EF＝2DF＋EF．【点睛】本题考查了全等三角形的判定和性质、等边三角形的性质、等腰三角形的性质等知识，解决问题的关键是常用辅助线构造全等三角形，属于中考常考题型．6．（1）HL；（2）见解析；（3）如图②，见解析；△DEF就是所求作的三角形，△DEF和△ABC不全等．【解析】【分析】（1）根据直角三角形全等的方法“HL”证明；（2）过点C作CG⊥AB交AB的延长线于G，过点F作FH⊥DE交DE的延长线于H，根据等角的补角相等求出∠CBG=∠FEH，再利用“角角边”证明△CBG和△FEH全等，根据全等三角形对应边相等可得CG=FH，再利用“HL”证明Rt△ACG和Rt△DFH全等，根据全等三角形对应角相等可得∠A=∠D，然后利用“角角边”证明△ABC和△DEF全等；（3）以点C为圆心，以AC长为半径画弧，与AB相交于点D，E与B重合，F与C重合，得到△DEF与△ABC不全等；（4）根据三种情况结论，∠B不小于∠A即可．【详解】（1）在直角三角形中一条斜边和一条直角边对应相等的两个直角三角形全等运用的是HL．（2）证明：如图①，分别过点C、F作对边AB、DE上的高CG、FH，其中G、H为垂足．∵∠ABC、∠DEF都是钝角∴G、H分别在AB、DE的延长线上．∵CG⊥AG，FH⊥DH，∴∠CGA＝∠FHD＝90°．∵∠CBG＝180°－∠ABC，∠FEH＝∠180°－∠DEF，∠ABC＝∠DEF，∴∠CBG＝∠FEH．在△BCG和△EFH中，∵∠CGB＝∠FHE，∠CBG＝∠FEH，BC＝EF，∴△BCG≌△EFH．∴CG＝FH．又∵AC＝DF．∴Rt△ACG≌△DFH．∴∠A＝∠D．在△ABC和△DEF中，∵∠ABC＝∠DEF，∠A＝∠D，AC＝DF，∴△ABC≌△DEF．（3）如图②，△DEF就是所求作的三角形，△DEF和△ABC不全等．【点睛】本题是三角形综合题，主要考查了全等三角形的判定与性质，应用与设计作图，熟练掌握三角形全等的判定方法是解题的关键，阅读量较大，审题要认真仔细．7．（1）证明见解析；(2,3)D ；（2）存在，(0,0)P ，(2,3)Q 或(0,0)P ，(2,3)Q -或(4,0)P ，(2,7)Q 或(4,0)P ，(2,7)Q -或1(,0)2P -，(2,2)Q -或1(,0)2P -，(2,2)Q -．【解析】【分析】（1）通过全等三角形的判定定理ASA 证得△ABP ≌△PCD ，由全等三角形的对应边相等证得AP ＝DP ，DC ＝PB ＝3，易得点D 的坐标；（2）设P （a ，0），Q （2，b ）．需要分类讨论：①AB ＝PC ，BP ＝CQ ；②AB ＝CQ ，BP ＝PC ．结合两点间的距离公式列出方程组，通过解方程组求得a 、b 的值，得解．【详解】（1）AP PD ⊥90APB DPC ∴∠+∠=AB x ⊥轴90A APB ∴∠+∠=A DPC ∴∠=∠在ABP ∆和PCD ∆中A DPC AB PCABP PCD ∠=∠⎧⎪=⎨⎪∠=∠⎩()ABP PCD ASA ∴∆≅∆AP DP ∴=，3DC PB ==(2,3)D ∴（2）设(,0)P a ，(2,)Q b①AB PC =，BP CQ =223a a b ⎧-=⎪⎨+=⎪⎩，解得03a b =⎧⎨=±⎩或47a b =⎧⎨=±⎩ (0,0)P ∴，(2,3)Q 或(0,0)P ，(2,3)Q -或(4,0)P ，(2,7)Q 或(4,0)P ，(2,7)Q - ②AB CQ =，BP PC =，322a a b +=-⎧⎨=⎩，解得122a b ⎧=⎪⎨⎪=±⎩ 1(,0)2P ∴-，(2,2)Q -或1(,0)2P -，(2,2)Q - 综上：(0,0)P ，(2,3)Q 或(0,0)P ，(2,3)Q -或(4,0)P ，(2,7)Q 或(4,0)P ，(2,7)Q -或1(,0)2P -，(2,2)Q -或1(,0)2P -，(2,2)Q - 【点睛】考查了三角形综合题．涉及到了全等三角形的判定与性质，两点间的距离公式，一元一次绝对值方程组的解法等知识点．解答（2）题时，由于没有指明全等三角形的对应边（角），所以需要分类讨论，以防漏解．8．（1）30°；（2）证明见解析；（3）AOB ∠是定值，60AOB ∠=︒.【解析】【分析】（1）根据等边三角形的性质可以直接得出结论；（2）根据等边三角形的性质就可以得出AC AC =，DC EC =，，60ACB DCE ∠=∠=︒，由等式的性质就可以BCE ACD ∠=∠，根据SAS 就可以得出ADC BEC ∆≅∆；（3）分情况讨论：当点D 在线段AM 上时，如图1，由（2）可知ACD BCE ≅∆∆，就可以求出结论；当点D 在线段AM 的延长线上时，如图2，可以得出ACD BCE ≅∆∆而有30CBE CAD ∠=∠=︒而得出结论；当点D 在线段MA 的延长线上时，如图3，通过得出ACD BCE ≅∆∆同样可以得出结论．【详解】（1）ABC ∆是等边三角形，60BAC ∴∠=︒．线段AM 为BC 边上的中线，12CAM BAC ∴∠=∠， 30CAM ∴∠=︒．（2）ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，ACD DCB DCB BCE ∴∠+∠=∠+∠，ACD BCE ∠∠∴=．在ADC ∆和BEC ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩， ()ACD BCE SAS ∴∆≅∆；（3）AOB ∠是定值，60AOB ∠=︒，理由如下：①当点D 在线段AM 上时，如图1，由（2）可知ACD BCE ≅∆∆，则30CBE CAD ∠=∠=︒，又60ABC ∠=︒，603090CBE ABC ∴∠+∠=︒+︒=︒，ABC ∆是等边三角形，线段AM 为BC 边上的中线AM ∴平分BAC ∠，即11603022BAM BAC ∠=∠=⨯︒=︒ 903060BOA ∴∠=︒-︒=︒．②当点D 在线段AM 的延长线上时，如图2，ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，ACB DCB DCB DCE ∴∠+∠=∠+∠，ACD BCE ∠∠∴=，在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩， ()ACD BCE SAS ∴∆≅∆，30CBE CAD ∴∠=∠=︒，同理可得：30BAM ∠=︒，903060BOA ∴∠=︒-︒=︒．③当点D 在线段MA 的延长线上时，ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，60ACD ACE BCE ACE ∴∠+∠=∠+∠=︒，ACD BCE ∠∠∴=，在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩， ()ACD BCE SAS ∴∆≅∆，CBE CAD ∴∠=∠，同理可得：30CAM ∠=︒150CBE CAD ∴∠=∠=︒30CBO ∴∠=︒，∵30BAM ∠=︒，903060BOA ∴∠=︒-︒=︒．综上，当动点D 在直线AM 上时，AOB ∠是定值，60AOB ∠=︒．【点睛】此题考查等边三角形的性质，全等三角形的判定及性质，等边三角形三线合一的性质，解题中注意分类讨论的思想解题.9．（1）C （4，0）；（2）433d t =；（3）103MN =【解析】【分析】（1）根据对称的性质知ABC ∆为等边三角形，利用直角三角形中30度角的性质即可求得答案；（2）利用面积法可求得AC PD PC OA ⋅=⋅，再利用坐标系中点的特征即可求得答案； （3）利用(2)的结论求得2BP =，利用角平分线的性质证得ABO CBQ ∆∆≌，求得43CQ AO ==43QN =，再利用直角三角形中30度角的性质即可求得答案．【详解】（1）∵点B 、C 关于y 轴对称， ∴12OB OC BC ==， ∴AB AC =，∵60BAC ∠=︒，∴ABC ∆为等边三角形，∴8AB BC AC ===， ∴142OC BC ==， ∴点C 的坐标为：()4,0C ；（2）连接AP ，∵1122APC S AC PD PC OA ∆=⋅=⋅， ∴AC PD PC OA ⋅=⋅，∵()0,43A ，∴43OA =，∵2BP t =，∴82PC t =-，∵8AC =，∴433PC OA PD t AC⋅==-， 即：433d t =-；（3）∵点P 到AC 的距离为33，∴43333d t =-=，∴1t =，∴2BP =，延长CN 交AB 于点Q ，过点N 作NE x ⊥轴于点E ，连接PQ 、BN ，∵CQ 为ACB ∠的角平分线，ABC ∆为等边三角形，∴1302BCQ ACB ∠=∠=︒，CQ AB ⊥， ∵1302BAO BAC ∠=∠=︒，AB BC =， ∴ABO CBQ ∆∆≌，∴CQ AO ==设2QN a =，在Rt CNE ∆中，30QCB ∠=︒，∴112)22NE CN a a ===， ∵ABP ABN BPN S S S ∆∆∆=+， ∴111222BP OA AB QN BP NE ⋅=⋅+⋅，∴1112822)222a a ⨯⨯=⨯⨯+⨯⨯，∴7a =，∴QN =， ∵60ACB ∠=︒，90PDC ∠=︒，∴30DPC ∠=︒，∵30BCQ ∠=︒，∴PM CM =，在Rt CDM ∆中，90MDC ∠=︒，30MCD ∠=︒， ∴12MD MC =，∴12MD PM =，PD =∴PM CM ==∴77MN CQ QN CM =--=-=．【点睛】本题是三角形综合题，涉及的知识有：含30度直角三角形的性质，全等三角形的判定与性质，外角性质，角平分线的性质，等边三角形的判定和性质，坐标与图形性质，熟练掌握性质及定理、灵活运用面积法求线段的长是解本题的关键．10．（1）①100；②x=y+s+t；（2）见详解．【解析】【分析】（1）①利用三角形的内角和定理即可解决问题；②结论：x=y+s+t．利用三角形内角和定理即可证明；（2）分6种情形分别求解即可解决问题．【详解】解：（1）①∵∠BAC=70°，∴∠ABC+∠ACB=110°，∵∠PBA=10°，∠PCA=20°，∴∠PBC+∠PCB=80°，∴∠BPC=100°，∴x=100，故答案为：100．②结论：x=y+s+t．理由：∵∠A+∠ABC+∠ACB=∠A+∠PBA+∠PCA+∠PBC+∠PCB=180°，∠PBC+∠PCB+∠BPC=180°，∴∠A+∠PBA+∠PCA=∠BPC，∴x=y+s+t．（2）s、t、x、y之间所有可能的数量关系：如图1：s+x=t+y；如图2：s+y=t+x；如图3：y=x+s+t；如图4：x+y+s+t=360°；如图5：t=s+x+y；如图6：s=t+x+y；【点睛】本题考查三角形的内角和定理，三角形的外角的性质等知识，解题的关键是学会用分类讨论的思想思考问题．t 时，使得△ODP与△ODQ的面积相等；（3）11．（1）6；8；24；（2）存在 2.4∠GOD+∠ACE=∠OHC，见解析【解析】【分析】（1）利用非负性即可求出a，b即可得出结论,即可求出△ABC的面积；（2）先表示出OQ ，OP ，利用那个面积相等，建立方程求解即可得出结论；（3）先判断出∠OAC=∠AOD ，进而判断出OG ∥AC ，即可判断出∠FHC=∠ACE ，同理∠FHO=∠GOD ，即可得出结论．【详解】解：(1) 解：（1）∵a 6b 80-+-=， ∴a-6=0，b-8=0，∴a=6，b=8，∴A （0，6），C （8，0）；∴S △ABC=6×8÷2=24,故答案为（0，6），（8，0）； 6；8；24(2) ∵114222ODQ D S OQ x t t ∆=⋅=⋅⋅= 11(82)312322ODP D S OP y t t ∆=⋅=⋅-⋅=- 由2123t t =-时, 2.4t =∴存在 2.4t =时,使得△ODP 与△ODQ 的面积相等(3) ）∴2∠GOA+∠ACE=∠OHC ，理由如下：∵x 轴⊥y 轴，∴∠AOC=∠DOC+∠AOD=90°∴∠OAC+∠ACO=90°又∵∠DOC=∠DCO∴∠OAC=∠AOD∵y 轴平分∠GOD∴∠GOA=∠AOD∴∠GOA=∠OAC∴OG ∥AC ，如图，过点H 作HF ∥OG 交x 轴于F ，∴HF ∥AC∴∠FHC=∠ACE同理∠FHO=∠GOD ，∵OG ∥FH ，∴∠GOD=∠FHO ，∴∠GOD+∠ACE=∠FHO+∠FHC即∠GOD+∠ACE=∠OHC ，∴2∠GOA+∠ACE=∠OHC ．∴∠GOD+∠ACE=∠OHC ．【点睛】此题是三角形综合题，主要考查了非负性的性质，三角形的面积公式，角平分线的定义，平行线的性质，正确作出辅助线是解本题的关键．12．（1） 122°；（2）12BEC α∠=；（3）01902BQC A ；（4）119，29 ； 【解析】【分析】（1）根据三角形的内角和角平分线的定义；（2）根据三角形的一个外角等于与它不相邻的两个内角的和，用A ∠与1∠表示出2∠，再利用E ∠与1∠表示出2∠，于是得到结论；（3）根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出EBC ∠与ECB ∠，然后再根据三角形的内角和定理列式整理即可得解；（4）根据（1），（3）的结论可以得出∠BPC 的度数；根据（2）的结论可以得到∠R 的度数．【详解】解：（1）BP 、CP 分别平分ABC ∠和ACB ∠，12PBC ABC ∴∠=∠，12PCB ACB ∠=∠， 180()BPC PBC PCB ∴∠=︒-∠+∠11180()22ABC ACB =︒-∠+∠， 1180()2ABC ACB =︒-∠+∠， 1(180180)2A =︒-︒-∠， 1180902A =-︒+︒∠， 9032122，故答案为：122︒；（2）如图2示，CE 和BE 分别是ACB ∠和ABD ∠的角平分线，112ACB ∴∠=∠，122ABD ∠=∠，又ABD ∠是ABC ∆的一外角，ABD A ACB ∴∠=∠+∠， 112()122A ABC A ∴∠=∠+∠=∠+∠， 2∠是BEC ∆的一外角，112111222BEC A A α∴∠=∠-∠=∠+∠-∠=∠=； （3）1()2QBC A ACB ∠=∠+∠，1()2QCB A ABC ∠=∠+∠， 180BQC QBC QCB ∠=︒-∠-∠，11180()()22A ACB A ABC =︒-∠+∠-∠+∠， 11180()22A A ABC ACB =︒-∠-∠+∠+∠， 结论1902BQC A ∠=︒-∠． （4）由（3）可知，119090645822BQCA ， 再根据（1），可得180()BPCPBC PCB 1118022QBC QCB 1180902Q 118090582119； 由（2）可得：11582922R Q ;故答案为：119，29．【点睛】本题考查了三角形的外角性质与内角和定理，熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键．13．（1）90︒；（2）12K K ∠∠=，证明见解析；（3）111902n n K ∠++=⨯︒【解析】【分析】（1） 过 K 作KG ∥AB ，交 EF 于 G ，证出//AB CD ∥KG ，得到BEK EKG ∠∠=，GKF KFD ∠∠=，根据角平分线的性质及平行线的性质得到()2180BEK DFK ∠∠+=，即可得到答案；（2）根据角平分线的性质得到1112BEK KEK KEB ∠∠∠==，1112KFK DFK DFK ∠∠∠==，根据90BEK KFD ∠∠+=求出1145KEK KFK ∠∠+=，根据()()111180K KEF EFK KEK KFK ∠∠∠∠∠=-+-+求出答案；（3）根据（2）得到规律解答即可.【详解】（1） 过 K 作KG ∥AB ，交 EF 于 G ，∵//AB CD ，∴//AB CD ∥KG ，BEK EKG ∠∠∴=，GKF KFD ∠∠=，EK ，FK 分别为BEF ∠与EFD ∠的平分线， BEK FEK ∠∠∴=，EFK DFK ∠∠=，∵//AB CD ，180BEK FEK EFK DFK ∠∠∠∠∴+++=，()2180BEK DFK ∠∠∴+=，90BEK DFK ∠∠∴+=，则 90EKF EKG GKF ∠∠∠=+=；（2） 12K K ∠∠=，理由为：BEK ∠，DFK ∠的平分线相交于点1K ，1112BEK KEK KEB ∠∠∠∴==，1112KFK DFK DFK ∠∠∠==， 180BEK FEK EFK DFK ∠∠∠∠+++=，即 ()2180BEK KFD ∠∠+=， 90BEK KFD ∠∠∴+=，1145KEK KFK ∠∠∴+=，()()11118045K KEF EFK KEK KFK ∠∠∠∠∠∴=-+-+=，12K K ∠∠∴=；（3）由（2）知90K ∠=；1119022K K ∠∠==⨯ 同理可得2112K K ∠∠==14K ∠1904=⨯， ∴111902n n K ∠++=⨯. 【点睛】此题考查平行线的性质：两直线平行，内错角相等；平行公理的推论：平行于同一直线的两直线平行；角平分线的性质；(3)是难点，注意总结前两问的做题思路得到规律进行解答.14．（1）AE DB =，理由详见解析；（2）AE DB =，理由详见解析；（3）3或1【解析】【分析】（1）根据等边三角形的性质、三线合一的性质证明即可；（2）根据等边三角形的性质，证明△EFC ≌△DBE 即可；（3）注意区分当点E 在AB 的延长线上时和当点E 在BA 的延长线上时两种情况，不要遗漏．【详解】解：（1）AE DB =，理由如下： ED EC =，EDC ECD ∴∠=∠∵△ABC 是等边三角形，60ACB ABC ∠=∠=︒∴，点E 为AB 的中点，1302ECD ACB ∴︒∠=∠=，30EDC ∠=︒∴，30D DEB ∠=∠=︒∴， DB BE ∴=，AE BE =，AE DB ∴=；故答案为：=；（2）AE DB =，理由如下：如图3：∵△ABC 为等边三角形，且EF ∥BC ，60AEF ABC ∠=∠=︒∴，60AFE ACB ∠=∠=︒，FEC ECB ∠=∠；120EFC DBE ∠=∠=︒∴；ED EC =，D ECB ∴∠=∠，D FEC ∠=∠，在△EFC 与△DBE 中，FEC D EFC DBE EC DE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△EFC ≌△DBE （AAS ），EF DB ∴=60AEF AFE ∠=∠=︒，∴△AEF 为等边三角形，AE EF ∴=，AE BD ∴=．（3）①如图4，当点E 在AB 的延长线上时，过点E 作EF ∥BC ，交AC 的延长线于点F ：则DCE CEF ∠=∠，DBE AEF ∠=∠；ABC AEF ∠=∠，ACB AFE ∠=∠；∵△ACB 为等边三角形，60ABC ACB ∴∠=∠=︒，60AEF AFE ∴∠=∠=︒，60DBE ABC ∠=∠=︒， DBE EFC ∴∠=∠；而ED EC =，D DCE ∴∠=∠，D CEF ∠=∠；在△FEC 和△BDE 中，FEC D EFC DBE EC DE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△FEC ≌△BDE （AAS ），EF BD ∴=；∵△AEF 为等边三角形，2AE EF ∴==，2BD EF ==，123CD ∴=+=；②如图5，当点E 在BA 的延长线上时，过点E 作EF ∥BC ，交CA 的延长线于点F ：类似上述解法，同理可证：2DB EF ==，1BC =，211CD =-=∴．【点睛】本题考查等边三角形的性质、全等三角形的判定和性质．熟练掌握等边三角形的性质，构造合适的全等三角形是解题的关键．15．（1）∠BDC ＝90°+2α；（2）∠BFC ＝2α；（3）∠BMC ＝90°+4α． 【解析】【分析】（1）由三角形内角和可求∠ABC +∠ACB ＝180°﹣α，由角平分线的性质可求∠DBC +∠BCD ＝12（∠ABC +∠ACB ）＝90°﹣2α，由三角形的内角和定理可求解； （2）由角平分线的性质可得∠FBC ＝12∠ABC ，∠FCE ＝12∠ACE ，由三角形的外角性质可求解；（3）由折叠的性质可得∠G ＝∠BFC ＝2α，方法同（1）可求∠BMC ＝90°+2G ∠，即可求解.【详解】解：（1）∵∠A ＝α，∴∠ABC +∠ACB ＝180°﹣α，∵BD 平分∠ABC ，CD 平分∠ACB ，∴∠DBC ＝12∠ABC ，∠BCD ＝12∠ACB ， ∴∠DBC +∠BCD ＝12（∠ABC +∠ACB ）＝90°﹣2α， ∴∠BDC ＝180°﹣（∠DBC +∠BCD ）＝90°+2α； （2）∵∠ABC 的平分线与∠ACE 的平分线交于点F ，∴∠FBC ＝12∠ABC ，∠FCE ＝12∠ACE ，。

⊥，点G是1．已知：如图，在△ABC中，AD、BE是高，F是AB的中点，FG DE垂足．求证：点G是DE的中点．2．如图，在△OBC中，点O为坐标原点，点C坐标为（4，0），点B坐标为（2，23），A B y⊥轴，点A为垂足，BCOH⊥，点H为垂足．动点P、Q分别从点O、A同时出发，点P沿线段OH向点H运动，点Q沿线段AO向点O运动，速度都是每秒1个单位长度．设点P的运动时间为t秒．=；（1）求证：OB CB（2）若△OPQ的面积为S，求S与t之间的函数关系式及定义域；⊥（垂足为点M）时，求五边形ABHPQ的面积的值.（3）当PQ OB3.如图，在△ABC 中，AB=AC ，点P 是BC 边上的一点，PD ⊥AB 于D ，PE ⊥AC 于E ，CM ⊥AB 于M ，试探究线段PD 、PE 、CM 的数量关系，并说明理由。

B4. 如图，R t △ABC 中，AB=AC ，︒=∠90A ，O 为BC 中点。

（1） 写出点O 到△ABC 三个顶点的距离之间的关系；（2） 如果点M 、N 分别在边AB 、AC 上移动，且保持AN=BM 。

请判断△OMN 的形状，并证明你的结论。

5．如图，点A 的坐标为（3,0），点C 的坐标为（0,4），OABC 为矩形，反比例函数xky =的图像过AB 的中点D ，且和BC 相交于点E ，F 为第一象限的点，AF =12,CF =13. （1）求反比例函数xky =和直线OE 的函数解析式； （2）求四边形OAFC 的面积．_6．已知：如图，正比例函数的图象与反比例函数的图象交于点（1）试确定上述正比例函数和反比例函数的表达式；（2）根据图象回答，在第一象限内，当取何值时，反比例函数的值大于正比例函数的值？ （3）是反比例函数图象上的一动点，其中过点作直线轴，交轴于点；过点作直线轴交轴于点，交直线于点．当四边形的面积为6时，请判断线段与的大小关系，并说明理由．7．已知：如图，在⊿ABC 中，∠C=90°，∠B=30°，AC =6，点D 在边BC 上，AD 平分∠CAB ，E 为AC 上的一个动点（不与A 、C 重合），EF ⊥AB ，垂足为F ． （1）求证：AD=DB ；（2）设CE=x ，BF=y ，求y 关于x 的函数解析式； （3）当∠DEF =90°时，求BF 的长.第26题图FE D CBA压轴题答案1．证明： 联结EF 、DF ．……………………………1分∵AD 是高， ∴AD BC ⊥，∴90ADB ∠=．………………………1分 又∵F 是AB 的中点， ∴12DF AB =(直角三角形斜边上的中线等于斜边的一半) ．……2分 同理可得：12EF AB =．……………………………………………1分∴EF DF =．…………………………………………………………1分 又∵FG DE ⊥，…………………………………………………………1分 ∴DG EG =．…………………………………………………………1分 即：点G 是DE 的中点．2．解：（1）∵4OB ==………………………………………………1分4CB ==………………………………………1分∴OB CB = ………………………………………………………………1分 （2）易证：△OBC 为等边三角形． ∵BC OH ⊥，∴30BOH HOC ∠=∠=．………………1分 ∴30AOB ∠=．过点P 作PE OA ⊥垂足为点E ． 在Rt △PEO 中，30EPO ∠=,PO t =， ∴122tEO PO ==，由勾股定理得：2PE =．…………………………1分 又∵OQ AO AQ t =-=，………………………………………………1分∴()211363232224t t S OQ PE t t -==-=．………………………1分 即：232S t =+（320<<t ）．……………………………………1分 【说明】最后1分为定义域分数．（3）易证Rt △OAB ≌Rt △OHB ≌Rt △OHC ，GFEDCBA∴2OABH 4OAB OHBOHB OHCOBCS S SSSSOC =+=+===四边形1分 易证△OPQ 为等边三角形， ∴OQ OP =，即：t t =，解得 t =1分∴244OPQSOP =⨯=．…………………………………………………1分∴ABHPQ 4OPQOABH S S S =-==五边形四边形1分 3. 解：PD+PE=CM ， 证明：连接AP ，∵AB=AC， ∴S △ABC =S △ABP +S △ACP =AB ×PD+AC ×PE=×AB ×（PD+PE ）， ∵S △ABC =AB ×CM， ∴PD+PE=CM。

1．已知：如图，在△ABC 中， AD 、 BE 是高， F 是 AB 的中点， FG DE ，点 G 是垂足．求证：点G 是 DE 的中点．2 OBC中，点O为坐标原点，点C坐标为（4 0 B坐标为（2，23 ），．如图，在△，），点AB轴，点A为垂足，OH BC ，点 H 为垂足．动点 P、 Q分别从点O 、A 同时y出发，点 P 沿线段 OH 向点 H 运动，点Q沿线段 AO 向点 O 运动，速度都是每秒 1 个单位长度．设点 P 的运动时间为 t 秒．（1）求证：OB CB；（2）若△OPQ的面积为S，求S与t之间的函数关系式及定义域；（3）当PQ OB （垂足为点M ）时，求五边形ABHPQ 的面积的值.yA BQ M HPOC x3.如图，在△ ABC中， AB=AC，点 P是 BC边上的一点， PD⊥AB 于 D，PE⊥ AC于 E，CM⊥AB于M，试探究线段 PD、PE、 CM的数量关系，并说明理由。

AMEDB P C4. 如图， Rt △ ABC中， AB=AC， A 90 ，O为BC中点。

（1）写出点 O到△ ABC三个顶点的距离之间的关系；（2）如果点 M、N分别在边 AB、AC上移动，且保持 AN=BM。

请判断△ OMN的形状，并证明你的结论。

CONA M B5．如图，点 A 的坐标为（3,0 ），点 C 的坐标为（ 0,4 ）， OABC 为矩形，反比例函数k yx的图像过 AB 的中点 D，且和 BC 相交于点 E， F 为第一象限的点， AF=12, CF =13.k和直线 OE 的函数解析式；（1）求反比例函数yx（2）求四边形 OAFC 的面积．yFC BEDOA x_6．已知：如图，正比例函数的图象与反比例函数的图象交于点（1）试确定上述正比例函数和反比例函数的表达式；（2）根据图象回答，在第一象限内，当取何值时，反比例函数的值大于正比例函数的值？（ 3）是反比例函数图象上的一动点，其中过点作直线轴，交轴于点；过点作直线轴交轴于点，交直线于点．当四边形的面积为 6 时，请判断线段与的大小关系，并说明理由．7．已知：如图，在⊿ ABC 中，∠ C= 90°，∠ B= 30°， AC=6，点 D 在边 BC 上， AD 平分∠CAB ， E 为 AC 上的一个动点（不与 A、C 重合）， EF ⊥ AB，垂足为 F ．（1）求证： AD=DB ；（2）设 CE=x ，BF=y ，求 y 关于 x 的函数解析式；（3）当∠ DEF =90°时，求 BF 的长 .AFEC D B第 26题图答案1． 明：EF 、 DF ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分A∵ AD 是高，∴ ADBC ，E FG∴ ADB 90o ．⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分又∵ F 是 AB 的中点，BDC∴ DF1AB (直角三角形斜 上的中 等于斜 的一半)．⋯⋯ 2 分2同理可得： EF1AB ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分2∴ EF DF ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分 又∵ FG DE ，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分 ∴ DGEG ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分即：点 G 是 DE 的中点．2． 解：（ 1）∵ OB222 324 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分22CB 2 42 3 4 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分 ∴ OB CB ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分（2）易 ：△ OBC 等 三角形．y∵ OHBC ，AB∴ BOHHOC 30o ．⋯⋯⋯⋯⋯⋯ 1 分∴ AOB 30 o ．Q H点 P 作 PEOA 垂足 点 E ．EP在 Rt △ PEO 中， EPO 30o, PO t ，OCx∴ EO1PO t，由勾股定理得： PE3t ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分2 22又∵ OQ AO AQ 2 3 t ，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分 ∴ S1OQgPE 1 2 3 t g 3 t 6t 3t 2 ．⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分22 2 4即： S3t 23t （ 0t2 3 ）．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分42【 明】最后1 分 定 域分数．（3）易 Rt △ OAB ≌Rt △ OHB ≌ Rt △ OHC ，∴ S四边形OABH S VOAB S VOHB S VOHB S VOHC S V OBC 3OC 2 4 3 ．1分4易△ OPQ 等三角形，∴OQ OP ，即： 2 3 t t ，解得t 3 ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分∴SVOPQ 3 OP 2 3 3．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分4 4 ∴S五边形ABHPQ S四边形 OABHSV OPQ4 33 3133 ．⋯⋯⋯⋯⋯1分4 43.解： PD+PE=CM ，明：接 AP ，∵ AB=AC ，∴ S△ABC=S △ABP+S △ACP= AB× PD+ AC× PE=× AB×（PD+PE），∵ S△ABC= AB× CM，∴ PD+PE=CM。

四边形综合题1、已知：在矩形ABCD 中，AB =10，BC =12，四边形EFGH 的三个顶点E 、F 、H 分别在矩形ABCD 边AB 、BC 、DA 上，AE =2.（1）如图①，当四边形EFGH 为正方形时，求△GFC 的面积； （2）如图②，当四边形EFGH 为菱形，且BF = a 时，求△GFC 的面积.（用含a 的代数式）2、已知点E 是正方形ABCD 外的一点，EA=ED ，线段BE 与对角线AC 相交于点F ， （1）如图1，当BF=EF 时，线段AF 与DE 之间有怎样的数量关系？并证明；（2）如图2，当△EAD 为等边三角形时，写出线段AF 、BF 、EF 之间的一个数量关系，并证明．D(图1)FD CA BE(图2)FHG图1图23、如图，直线y =+与x 轴相交于点A，与直线y =相交于点P . (1) 求点P 的坐标.(2) 请判断△OPA 的形状并说明理由.(3) 动点E 从原点O 出发，以每秒1个单位的速度沿着O P A →→的路线向点A 匀速运动（E 不与点O 、A 重合），过点E 分别作EF x ⊥轴于F ，EB y ⊥轴于B .设运动t 秒时，矩形EBOF 与△OPA 重叠部分的面积为S .求S 与t 之间的函数关系式.4、如图，在平面直角坐标中，四边形OABC 是等腰梯形，CB ∥OA ，OC=AB=4，BC=6，∠COA=45°,动点P 从点O 出发，在梯形OABC 的边上运动，路径为O →A →B →C ，到达点C 时停止．作直线CP. （1）求梯形OABC 的面积；（2）当直线CP 把梯形OABC 的面积分成相等的两部分时，求直线CP 的解析式； （3）当∆OCP 是等腰三角形时，请写出点P 的坐标（不要求过程，只需写出结果）O ABC Pxy五、27．如图，已知在梯形ABCD 中，AD // BC ，AB = CD ，BC = 8，60B ∠=︒，点M 是边BC 的中点，点E 、F 分别是边AB 、CD 上的两个动点（点E 与点A 、B 不重合，点F 与点C 、D 不重合），且120EMF ∠=︒． （1）求证：ME = MF ；（2）试判断当点E 、F 分别在边AB 、CD 上移动时，五边形AEMFD 的面积的大小是否会改变，请证明你的结论；（3）如果点E 、F 恰好是边AB 、CD 的中点，求边AD的长．A B C DM E F （第27题图） A BCD ME F （备用图）3（1）求点A 和点B 的坐标；（2）过点A 作AC ⊥y 轴于点C ，过点B 作直线l ∥y 轴．动点P 从点O 出发，以每秒1个单位长的速度，沿O ﹣C ﹣A 的路线向点A 运动；同时直线l 从点B 出发，以相同速度向左平移，在平移过程中，直线l 交x 轴于点R ，交线段BA 或线段AO 于点Q ．当点P 到达点A 时，点P 和直线l 都停止运动．在运动过程中，设动点P 运动的时间为t 秒)0( t ．①当t 为何值时，以A 、P 、R 为顶点的三角形的面积为8？②是否存在以A 、P 、Q 为顶点的三角形是QA=QP 的等腰三角形？若存在，求t 的值；若不存在，请说明理由．3∴y ＝－x +7，0＝x +7，∴x ＝7，∴B 点坐标为：（7，0），----------------------------1分 ∵y ＝－x +7＝x 34，解得x ＝3，∴y ＝4，∴A 点坐标为：（3，4）；-------------------1分 （2）①当0＜t ＜4时，PO ＝t ，PC ＝4－t ，BR ＝t ，OR ＝7－t ，--------------1分 过点A 作AM ⊥x 轴于点M∵当以A 、P 、R 为顶点的三角形的面积为8，∴S 梯形ACOB －S △ACP －S △POR －S △ARB ＝8， ∴21（AC +BO ）×CO －21AC ×CP －21PO ×RO －21AM ×BR ＝8， ∴（AC +BO ）×CO －AC ×CP －PO ×RO －AM ×BR ＝16，∴（3+7）×4－3×（4－t ）－t ×（7－t ）－4t ＝16，∴t 2－8t +12＝0. -----------------1分 解得t 1＝2，t 2＝6（舍去）. --------------------------------------------------------------------1分 当4≤t ≤7时，S △APR ＝21AP ×OC =2（7－t ）＝8，t=3(舍去)；--------------1分 ∴当t ＝2时，以A 、P 、R 为顶点的三角形的面积为8； ②存在．当0＜t ≤4时,直线l 与AB 相交于Q ，∵一次函数y ＝－x +7与x 轴交于B （7，0）点，与y 轴交于N （0，7）点，∴NO ＝OB ，∴∠OBN ＝∠ONB ＝45°.∵直线l ∥y 轴，∴RQ ＝RB=t ，AM=BM=4∴QB=t 2,AQ=t 224-----------------1分 ∵RB ＝OP ＝QR ＝t ，∴PQ//OR,PQ=OR=7-t --------------------------------------1分 ∵以A 、P 、Q 为顶点的三角形是等腰三角形，且QP =QA ，∴7-t=t 224-，t=1-32（舍去）--------------------------------------------1分 当4＜t ≤7时，直线l 与O A 相交于Q ，若QP ＝QA ，则t －4+2（t －4）＝3，解得t ＝5；---------------------------------------1分 ∴当t =5，存在以A 、P 、Q 为顶点的三角形是PQ ＝AQ 的等腰三角形．已知边长为1的正方形ABCD 中， P 是对角线AC 上的一个动点（与点A 、C 不重合）， 过点P 作 PE ⊥PB ，PE 交射线DC 于点E ，过点E 作EF ⊥AC ，垂足为点F . （1）当点E 落在线段CD 上时（如图10），① 求证：PB=PE ；② 在点P 的运动过程中，PF 的长度是否发生变化？若不变，试求出这个不变的值， 若变化，试说明理由；（2）当点E 落在线段DC 的延长线上时，在备用图上画出符合要求的大致图形，并判断上述（1）中的结论是否仍然成立（只需写出结论，不需要证明）；（3）在点P 的运动过程中，⊿PEC 能否为等腰三角形？如果能，试求出AP 的长，如果不能，试说明理由．D CBAE P 。

0 8k b, ∴ „„„„„„„„„„„„„„„„„„„„„„„„„（1 分） 4 5k b,
4 k , 3 „„„„„„„„„„„„„„„„„„„„„„„„„（1 分） ∴ 32 b . 3
4 32 ．„„„„„„„„„„„„（1 分） x 3 3 26．解： （1）BF +AG= AE．„„„„„„„„„„„„„„„„„„„„„„（1 分） 证明如下：过点 F 作 FH⊥DA，垂足为 H， ∵在正方形 ABCD 中，∠DAE=∠B=90°，∴四边形 ABFH 是矩形．„（1 分） ∴FH=AB=DA．∵BD⊥FG，∴∠G=90°–∠ADE=∠DEA． 又∴∠DAE=∠FHG=90°，∴△FHG≌△DAE． „„„„„„„„„„（1 分） ∴GH=AE，即 HA+AG=AE．∵BF=HA，∴BF+AG=AE．„„„„„„（1 分）
本题满分12分其中第1小题5分第2小题3分第3小题4bcaebcdfdfaeefad四边形aefd是平行四边形efad5aedf?????????????????????????1abcd5rtabertdcfbecfefbccfbecf3在rtabeabaeaebqapaepdcqqcdpabqp当四边形abqp与四边形qcdp的面积相等时3当四边形abqp是平行四边形时pqab当四边形qcdp是平行四边形时可得pqcdcdabpqab此时cqpd11时pqab
FB 3 ，且 AC 10 ，求 FC 的值. BD 5
A
D
F
E
B
C
26． 在梯形 ABCD 中， ∠ABC= 90 ， AD∥BC， BC>AD， AB=8cm， BC=18cm， CD=10 cm，点 P 从点 B 开始沿 BC 边向终点 C 以每秒 3cm 的速度移动，点 Q 从点 D 开始沿 DA 边向终点 A 以每秒 2cm 的速度移动，设运动时间为 t 秒. （1）求四边形 ABPQ 为矩形时 t 的值； （2）若题设中的“BC=18cm”改变为“BC= k cm” ，其它条件都不变，要 使四边形 PCDQ 是等腰梯形，求 t 与 k 的函数关系式，并写出 k 的取值范围； （3）在移动的过程中，是否存在 t 使 P、Q 两点 的距离为 10cm ,若存在求 t 的值. 若不存在请说明 理由？

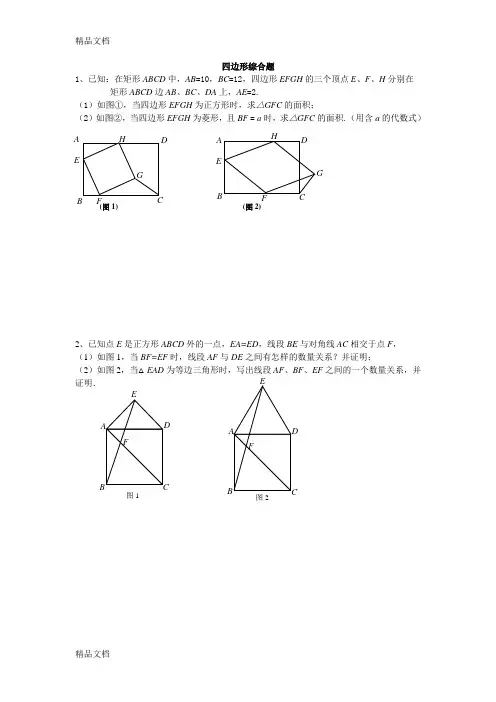
四边形综合题1、已知：在矩形ABCD 中，AB =10，BC =12，四边形EFGH 的三个顶点E 、F 、H 分别在矩形ABCD 边AB 、BC 、DA 上，AE =2.（1）如图①，当四边形EFGH 为正方形时，求△GFC 的面积； （2）如图②，当四边形EFGH 为菱形，且BF = a 时，求△GFC 的面积.（用含a 的代数式）2、已知点E 是正方形ABCD 外的一点，EA=ED ，线段BE 与对角线AC 相交于点F ， （1）如图1，当BF=EF 时，线段AF 与DE 之间有怎样的数量关系？并证明；（2）如图2，当△EAD 为等边三角形时，写出线段AF 、BF 、EF 之间的一个数量关系，并证明．D(图1)FD CA BE(图2)FHG图1图23、如图，直线y =+与x 轴相交于点A，与直线y =相交于点P . (1) 求点P 的坐标.(2) 请判断△OPA 的形状并说明理由.(3) 动点E 从原点O 出发，以每秒1个单位的速度沿着O P A →→的路线向点A 匀速运动（E 不与点O 、A 重合），过点E 分别作EF x ⊥轴于F ，EB y ⊥轴于B .设运动t 秒时，矩形EBOF 与△OPA 重叠部分的面积为S .求S 与t 之间的函数关系式.4、如图，在平面直角坐标中，四边形OABC 是等腰梯形，CB ∥OA ，OC=AB=4，BC=6，∠COA=45°,动点P 从点O 出发，在梯形OABC 的边上运动，路径为O →A →B →C ，到达点C 时停止．作直线CP. （1）求梯形OABC 的面积；（2）当直线CP 把梯形OABC 的面积分成相等的两部分时，求直线CP 的解析式； （3）当∆OCP 是等腰三角形时，请写出点P 的坐标（不要求过程，只需写出结果）O ABC Pxy五、27．如图，已知在梯形ABCD 中，AD // BC ，AB = CD ，BC = 8，60B ∠=︒，点M 是边BC 的中点，点E 、F 分别是边AB 、CD 上的两个动点（点E 与点A 、B 不重合，点F 与点C 、D 不重合），且120EMF ∠=︒． （1）求证：ME = MF ；（2）试判断当点E 、F 分别在边AB 、CD 上移动时，五边形AEMFD 的面积的大小是否会改变，请证明你的结论；（3）如果点E 、F 恰好是边AB 、CD 的中点，求边AD的长．A B C DM E F （第27题图） A BCD ME F （备用图）3（1）求点A 和点B 的坐标；（2）过点A 作AC ⊥y 轴于点C ，过点B 作直线l ∥y 轴．动点P 从点O 出发，以每秒1个单位长的速度，沿O ﹣C ﹣A 的路线向点A 运动；同时直线l 从点B 出发，以相同速度向左平移，在平移过程中，直线l 交x 轴于点R ，交线段BA 或线段AO 于点Q ．当点P 到达点A 时，点P 和直线l 都停止运动．在运动过程中，设动点P 运动的时间为t 秒)0( t ．①当t 为何值时，以A 、P 、R 为顶点的三角形的面积为8？②是否存在以A 、P 、Q 为顶点的三角形是QA=QP 的等腰三角形？若存在，求t 的值；若不存在，请说明理由．3∴y ＝－x +7，0＝x +7，∴x ＝7，∴B 点坐标为：（7，0），----------------------------1分 ∵y ＝－x +7＝x 34，解得x ＝3，∴y ＝4，∴A 点坐标为：（3，4）；-------------------1分 （2）①当0＜t ＜4时，PO ＝t ，PC ＝4－t ，BR ＝t ，OR ＝7－t ，--------------1分 过点A 作AM ⊥x 轴于点M∵当以A 、P 、R 为顶点的三角形的面积为8，∴S 梯形ACOB －S △ACP －S △POR －S △ARB ＝8， ∴21（AC +BO ）×CO －21AC ×CP －21PO ×RO －21AM ×BR ＝8， ∴（AC +BO ）×CO －AC ×CP －PO ×RO －AM ×BR ＝16，∴（3+7）×4－3×（4－t ）－t ×（7－t ）－4t ＝16，∴t 2－8t +12＝0. -----------------1分 解得t 1＝2，t 2＝6（舍去）. --------------------------------------------------------------------1分 当4≤t ≤7时，S △APR ＝21AP ×OC =2（7－t ）＝8，t=3(舍去)；--------------1分 ∴当t ＝2时，以A 、P 、R 为顶点的三角形的面积为8； ②存在．当0＜t ≤4时,直线l 与AB 相交于Q ，∵一次函数y ＝－x +7与x 轴交于B （7，0）点，与y 轴交于N （0，7）点，∴NO ＝OB ，∴∠OBN ＝∠ONB ＝45°.∵直线l ∥y 轴，∴RQ ＝RB=t ，AM=BM=4∴QB=t 2,AQ=t 224-----------------1分 ∵RB ＝OP ＝QR ＝t ，∴PQ//OR,PQ=OR=7-t --------------------------------------1分 ∵以A 、P 、Q 为顶点的三角形是等腰三角形，且QP =QA ，∴7-t=t 224-，t=1-32（舍去）--------------------------------------------1分 当4＜t ≤7时，直线l 与O A 相交于Q ，若QP ＝QA ，则t －4+2（t －4）＝3，解得t ＝5；---------------------------------------1分 ∴当t =5，存在以A 、P 、Q 为顶点的三角形是PQ ＝AQ 的等腰三角形．已知边长为1的正方形ABCD 中， P 是对角线AC 上的一个动点（与点A 、C 不重合）， 过点P 作 PE ⊥PB ，PE 交射线DC 于点E ，过点E 作EF ⊥AC ，垂足为点F . （1）当点E 落在线段CD 上时（如图10），① 求证：PB=PE ；② 在点P 的运动过程中，PF 的长度是否发生变化？若不变，试求出这个不变的值， 若变化，试说明理由；（2）当点E 落在线段DC 的延长线上时，在备用图上画出符合要求的大致图形，并判断上述（1）中的结论是否仍然成立（只需写出结论，不需要证明）；（3）在点P 的运动过程中，⊿PEC 能否为等腰三角形？如果能，试求出AP 的长，如果不能，试说明理由． D CBAE P 。

沪教版八年级上册压轴题数学数学模拟试题一、压轴题1．如图1，直角三角形DEF 与直角三角形ABC 的斜边在同一直线上，∠EDF ＝30°，∠ABC ＝40°，CD 平分∠ACB ，将△DEF 绕点D 按逆时针方向旋转，记∠ADF 为α（0°＜α＜180°），在旋转过程中；（1）如图2，当∠α＝ 时，//DE BC ，当∠α＝ 时，DE ⊥BC ；（2）如图3，当顶点C 在△DEF 内部时，边DF 、DE 分别交BC 、AC 的延长线于点M 、N ， ①此时∠α的度数范围是 ；②∠1与∠2度数的和是否变化？若不变求出∠1与∠2度数和；若变化，请说明理由； ③若使得∠2≥2∠1，求∠α的度数范围．解析：（1）10°，100°；（2）①55°＜α＜85°；②∠1与∠2度数的和不变，理由见解析③55°＜α≤60°． 【解析】 【分析】（1）当∠EDA ＝∠B ＝40°时，//DE BC ，得出30°＋α＝40°，即可得出结果；当//DE AC 时，DE ⊥AB ，得出50°＋α＋30°＝180°，即可得出结果；（2）①由已知得出∠ACD ＝45°，∠A ＝50°，推出∠CDA ＝85°，当点C 在DE 边上时，α＋30°＝85°，解得α＝55°，当点C 在DF 边上时，α＝85°，即可得出结果；②连接MN ，由三角形内角和定理得出∠CNM ＋∠CMN ＋∠MCN ＝180°，则∠CNM ＋∠CMN ＝90°，由三角形内角和定理得出∠DNM ＋∠DMN ＋∠MDN ＝180°，即∠2＋∠CNM ＋∠CMN ＋∠1＋∠MDN ＝180°，即可得出结论；③由221∠≥∠，∠1＋∠2＝60°，得出∠2≥2（60°−∠2），解得∠2≥40°，由三角形内角和定理得出∠2＋∠NDM ＋α＋∠A ＝180°，即∠2＋30°＋α＋50°＝180°，则∠2＝100°−α，得出100°−α≥40°，解得α≤60°，再由当顶点C 在△DEF 内部时，55°＜α＜85°，即可得出结果． 【详解】解：（1）∵∠B ＝40°，∴当∠EDA ＝∠B ＝40°时，//DE BC ， 而∠EDF ＝30°， ∴3040α︒+=︒，解得：α＝10°； 当//DE AC 时，DE ⊥AB ， 此时∠A+∠EDA ＝180°，9050A B ∠=︒-∠=︒，∴5030180α︒++︒=︒， 解得：α＝100°； 故答案为10°，100°；（2）①∵∠ABC ＝40°，CD 平分∠ACB ， ∴∠ACD ＝45°，∠A ＝50°， ∴∠CDA ＝85°，当点C 在DE 边上时，3085α+︒=︒， 解得：55α=︒，当点C 在DF 边上时，85α=︒，∴当顶点C 在△DEF 内部时，5585α︒<<︒； 故答案为：5585α︒<<︒；②∠1与∠2度数的和不变；理由如下： 连接MN ，如图所示：在△CMN 中，∵∠CNM+∠CMN+∠MCN ＝180°， ∴∠CNM+∠CMN ＝90°，在△MND 中，∵∠DNM+∠DMN+∠MDN ＝180°， 即∠2+∠CNM+∠CMN+∠1+∠MDN ＝180°， ∴12180903060∠+∠=︒-︒-︒=︒； ③∵∠2≥2∠1，∠1+∠2＝60°， ∴22602∠≥︒-∠（）， ∴∠2≥40°，∵2180NDM A α∠+∠++∠=︒， 即23050180α∠+︒++︒=︒， ∴2100α∠=︒-， ∴10040α︒-≥︒， 解得：α≤60°，∵当顶点C 在△DEF 内部时，5585α︒<<︒， ∴∠α的度数范围为5560α︒<≤︒．【点睛】本题考查了平行线的性质、直角三角形的性质、三角形内角和定理、不等式等知识，合理选择三角形后利用三角形内角和定理列等量关系是解决问题的关键．2．已知//,MN GH 在Rt ABC 中，90,30ACB BAC ∠=︒∠=︒，点A 在MN 上，边BC 在GH 上，在Rt DEF △中，90,DFE ∠=︒边DE 在直线AB 上，45EDF ∠=︒；（1）如图1，求BAN ∠的度数；（2）如图2，将Rt DEF △沿射线BA 的方向平移，当点F 在M 上时，求AFE ∠度数； （3）将Rt DEF △在直线AB 上平移，当以A D F 、、为顶点的三角形是直角三角形时，直接写出FAN ∠度数．解析：（1）60°；（2）15°；（3）30°或15° 【解析】 【分析】（1）利用两直线平行，同旁内角互补，得出90CAN ∠=︒，即可得出结论； （2）先利用三角形的内角和定理求出AFD ∠，即可得出结论； （3）分90DAF ∠=︒和90AFD ∠=︒两种情况求解即可得出结论． 【详解】 解：（1）//MN GH ，180ACB NAC ∴∠+∠=︒，90ACB ∠=︒，90CAN ∴∠=︒，30BAC ∠=︒，9060BAN BAC ∴∠=︒-∠=︒；（2）由（1）知，60BAN ∠=︒， 45ED F ∠=︒，18075AFD BAN EDF ∴∠=︒-∠-∠=︒，90DFE ∠=︒，15AFE DFE AFD ∴∠=∠-∠=︒；（3）当90DAF ∠=︒时，如图3， 由（1）知，60BAN ∠=︒，30FAN DAF BAN ∴∠=∠-∠=︒；当90AFD ∠=︒时，如图4，90DFE ∠=︒， ∴点A ，E 重合，45ED F ∠=︒，45DAF ∴∠=︒，由（1）知，60BAN ∠=︒，15FAN BAN DAF ∴∠=∠-∠=︒，即当以A 、D 、F 为顶点的三角形是直角三角形时，FAN ∠度数为30或15︒．【点睛】此题是三角形综合题，主要考查了平行线的性质，三角形的内角和定理，角的和差的计算，求出60BAN ∠=︒是解本题的关键．3．已知：MN ∥PQ ，点A ，B 分别在MN ，PQ 上，点C 为MN ，PQ 之间的一点，连接CA ，CB ．（1）如图1，求证：∠C=∠MAC+∠PBC ；（2）如图2，AD ，BD ，AE ，BE 分别为∠MAC ，∠PBC ，∠CAN ，∠CBQ 的角平分线，求证：∠D+∠E=180°；（3）在（2）的条件下，如图3，过点D 作DA 的垂线交PQ 于点G ，点F 在PQ 上，∠FDA=2∠FDB ，FD 的延长线交EA 的延长线于点H ，若3∠C=4∠E ，猜想∠H 与∠GDB 的倍数关系并证明．解析：（1）见解析；（2）见解析；（3）猜想：∠H= 3∠GDB ，证明见解析． 【解析】【分析】（1）作辅助线：过C 作EF ∥MN ，根据平行的传递性可知这三条直线两两平行，由平行线的性质得到内错角相等∠MAC=∠ACF ，∠BCF=∠PBC ，再进行角的加和即可得出结论； （2）根据角平分线线定理得知11,22MAD MAC NAE NAC ∠=∠∠=∠，利用平角为180°得到∠DAE=90°，同理得90DBE ∠=︒，再根据四边形内角和180°，得出结论； （3）由（1）（2）中的结论进行等量代换得到3∠ADB=2∠E ，并且两角的和为180°，由此得到两个角的度数分别为72°和108°，利用角的和与差得到∠HDA=36°，∠H=54°，由此得到倍数关系． 【详解】（1）如图：过C 作EF ∥MN ，∵MN ∥PQ ， ∴MN ∥EF ∥PQ ，∴∠MAC=∠ACF ，∠BCF=∠PBC ，∴∠ACF+∠BCF=∠MAC+∠PBC ，即∠ACB=∠MAC+∠PBC ． （2）∵AD ，AE 分别为∠MAC ，∠CAN 的角平分线， ∴11,22MAD MAC NAE NAC ∠=∠∠=∠， ∴11118090222MAD NAE MAC NAC ∠+∠=∠+∠=⨯︒=︒，于是∠DAE=90° 同理可得：90PBD QBE ∠+∠=︒，由（1）可得： ∵ 180D E MAD PBD NAE QBE ∠+∠=∠+∠+∠+∠=︒． （3）猜想：∠H= 3∠GDB.理由如下：由（1）可知：2()2C MAC PBC MAD PBD ADB ∠=∠+∠=∠+∠=∠， ∵3∠C=4∠E ， ∴6∠ADB=4∠E ， ∴3∠ADB=2∠E ， ∵∠ADB+∠E=180°， ∴∠ADB=72°，∠E=108°， ∵DG ⊥DA ，∴∠GDB=18°， ∵∠FDA=2∠FDB ， ∴∠ADF=144°， ∴∠HDA=36°， ∵DA ⊥AE ， ∴∠H=54°，∴∠H=3∠GDB ． 【点睛】考查平行线中角度的关系，学生要熟悉掌握平行线的性质以及角平分线定理，结合角的和与差进行计算，本题的关键是平行线的性质．4．在初中数学学习阶段，我们常常会利用一些变形技巧来简化式子，解答问题． 材料一：在解决某些分式问题时，倒数法是常用的变形技巧之一，所谓倒数法，即把式子变成其倒数形式，从而运用约分化简，以达到计算目的． 例：已知：2114x x =+，求代数式x 2+21x的值． 解：∵2114x x =+，∴21x x+＝4 即21x x x+＝4∴x +1x ＝4∴x 2+21x ＝（x +1x ）2﹣2＝16﹣2＝14材料二：在解决某些连等式问题时，通常可以引入参数“k ”，将连等式变成几个值为k 的等式，这样就可以通过适当变形解决问题．例：若2x ＝3y ＝4z ，且xyz ≠0，求xy z+的值．解：令2x ＝3y ＝4z ＝k （k ≠0）则11kk k k x 622,,,117234y z 7k k 3412x y z ===∴===++ 根据材料回答问题：（1）已知2114x x x =-+，求x +1x的值． （2）已知523a b c ==，（abc ≠0），求342b c a+的值． （3）若222222yz zx xy x y z bz cy cx az ay bx a b c++===+++++，x ≠0，y ≠0，z ≠0，且abc ＝7，求xyz 的值． 解析：（1）5； （2）95； （3）78【解析】 【分析】（1）仿照材料一，取倒数，再约分，利用等式的性质求解即可；（2）仿照材料二，设5a ＝2b ＝3c＝k （k ≠0），则a ＝5k ，b ＝2k ，c ＝3k ，代入所求式子即可；（3）本题介绍两种解法： 解法一：（3）解法一：设yz bz cy +＝zx cx az +＝xy ay bx +＝1k（k ≠0），化简得：b c k y z +=①，c a k z x +=②，a b k x y +=③，相加变形可得x 、y 、z 的代入222222x y z a b c ++++＝1k中，可得k 的值，从而得结论； 解法二：取倒数得：bz cy yz +＝cx az zx+＝ay bx xy +，拆项得b c c a a by z z x x y +=+=+，从而得x ＝ay b ，z ＝cyb，代入已知可得结论． 【详解】 解：（1）∵21x x x -+＝14，∴21x x x-+＝4，∴x ﹣1+1x＝4， ∴x +1x＝5； （2）∵设5a ＝2b ＝3c＝k （k ≠0），则a ＝5k ，b ＝2k ，c ＝3k ， ∴342b c a +＝61210k k k +＝1810＝95； （3）解法一：设yz bz cy +＝zx cx az +＝xy ay bx +＝1k（k ≠0），∴b c k y z +=①，c ak z x+=②，a b k x y +=③， ①+②+③得：2（b c ay z x++）＝3k ， b c a y z x ++＝32k ④， ④﹣①得：a x ＝12k ，④﹣②得：12b k y =， ④﹣③得：12c z =k ， ∴x ＝2a k ，y ＝2b k ，z ＝2c k 代入222222x y z a b c++++＝1k 中，得： ()22222224a b c ka b c ++++＝1k， 241k k=， k ＝4， ∴x ＝24a ，y ＝24b ，z ＝24c ， ∴xyz ＝864abc ＝8764⨯＝78； 解法二：∵yz zx xybz cy cx az ay bx==+++，∴bz cy cx az ay bxyz zx xy +++==， ∴b c c a a b y z z x x y +=+=+， ∴,b a c b y x z y==， ∴,ay cy x z b b==， 将其代入222222zx x y z cx az a b c ++=+++中得： cy ayb b acy acy b b⋅+＝2222222222a y c y y b b a b c ++++ 2y b ＝22y b ，y ＝2b ， ∴x ＝22ab ab =，z ＝cy 2y ＝2c ，∴xyz ＝222a b c ⋅⋅＝78． 【点睛】本题考查了以新运算的方式求一个式子的值，题目中涉及了求一个数的倒数，约分，等式的基本性质，求代数式的值，解决本题的关键是正确理解新运算的内涵，确定一个数的倒数并能够根据等式的基本性质将原式变为能够进一步运算的式子. 5．在△ABC 中，已知∠A ＝α．（1）如图1，∠ABC 、∠ACB 的平分线相交于点D ．求∠BDC 的大小（用含α的代数式表示）；（2）如图2，若∠ABC 的平分线与∠ACE 的平分线交于点F ，求∠BFC 的大小（用含α的代数式表示）；（3）在（2）的条件下，将△FBC 以直线BC 为对称轴翻折得到△GBC ，∠GBC 的平分线与∠GCB 的平分线交于点M （如图3），求∠BMC 的度数（用含α的代数式表示）．解析：（1）∠BDC ＝90°+2α；（2）∠BFC ＝2α；（3）∠BMC ＝90°+4α．【解析】 【分析】（1）由三角形内角和可求∠ABC +∠ACB ＝180°﹣α，由角平分线的性质可求∠DBC +∠BCD ＝12（∠ABC +∠ACB ）＝90°﹣2α，由三角形的内角和定理可求解； （2）由角平分线的性质可得∠FBC ＝12∠ABC ，∠FCE ＝12∠ACE ，由三角形的外角性质可求解；（3）由折叠的性质可得∠G ＝∠BFC ＝2α，方法同（1）可求∠BMC ＝90°+2G∠，即可求解. 【详解】解：（1）∵∠A ＝α， ∴∠ABC +∠ACB ＝180°﹣α， ∵BD 平分∠ABC ，CD 平分∠ACB ， ∴∠DBC ＝12∠ABC ，∠BCD ＝12∠ACB ， ∴∠DBC +∠BCD ＝12（∠ABC +∠ACB ）＝90°﹣2α， ∴∠BDC ＝180°﹣（∠DBC +∠BCD ）＝90°+2α；（2）∵∠ABC 的平分线与∠ACE 的平分线交于点F ， ∴∠FBC ＝12∠ABC ，∠FCE ＝12∠ACE ，∵∠ACE ＝∠A +∠ABC ，∠FCE ＝∠BFC +∠FBC ， ∴∠BFC ＝12∠A ＝2α； （3）∵∠GBC 的平分线与∠GCB 的平分线交于点M ， ∴方法同（1）可得∠BMC ＝90°+2G∠， ∵将△FBC 以直线BC 为对称轴翻折得到△GBC ， ∴∠G ＝∠BFC ＝2α， ∴∠BMC ＝90°+4α.【点睛】此题考查三角形的内角和定理，三角形的外角等于与它不相邻的两个内角的和，角平分线的性质定理，折叠的性质. 6．探索发现：111111111;;12223233434=-=-=-⨯⨯⨯…… 根据你发现的规律，回答下列问题： （1）145⨯＝ ，1(1)n n ⨯+＝ ；（2）利用你发现的规律计算：1111122334(1)n n ⋅++++⨯⨯⨯⨯+（3）利用规律解方程：1111121(1)(1)(2)(2)(3)(3)(4)(4)(5)(5)x x x x x x x x x x x x x -++++=++++++++++解析：（1）1111,451n n --+；（2）n n 1+；（3）见解析． 【解析】 【分析】（1）根据简单的分式可得，相邻两个数的积的倒数等于它们的倒数之差，即可得到145⨯和1(1)n n ⨯+ （2）根据（1）规律将乘法写成减法的形式，可以观察出前一项的减数等于后一项的被减数，因此可得它们的和.（3）首先利用（2）的和的结果将左边化简，再利用分式方程的解法求解即可. 【详解】 解：（1）1114545=-⨯， 111(1)1n n n n =-++ ；故答案为1111,451n n--+（2）原式＝111111111+122334111nn n n n--+-++-=-=+++;（3）已知等式整理得：11111121 11245(5)xx x x x x x x x--+-++-=++++++所以，原方程即：11215(5)xx x x x--=++，方程的两边同乘x（x+5），得：x+5﹣x＝2x﹣1，解得：x＝3，检验：把x＝3代入x（x+5）＝24≠0，∴原方程的解为：x＝3．【点睛】本题主要考查学生的归纳总结能力，关键在于根据简单的数的运算寻找规律,是考试的热点. 7．Rt△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点．令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．（1）若点P在线段AB上，如图（1）所示，且∠α=60°，则∠1+∠2= ；（2）若点P在线段AB上运动，如图（2）所示，则∠α、∠1、∠2之间的关系为；（3）若点P运动到边AB的延长线上，如图（3）所示，则∠α、∠1、∠2之间有何关系？猜想并说明理由；（4）若点P运动到△ABC形外，如图（4）所示，则∠α、∠1、∠2之间有何关系？猜想并说明理由．解析：(1)150°；(2)∠1＋∠2＝90°＋α；(3)∠1＝90°＋∠2＋α，理由详见解析；(4)∠2＝90°＋∠1－α，理由详见解析【解析】【分析】(1)先用平角的得出，∠CDP=180°-∠1，∠CEP=180°-∠2，最后用四边形的内角和即可；(2)同(1)方法即可；(3)利用平角的定义和三角形的内角和即可得出结论；(4)利用三角形的内角和和外角的性质即可得出结论．【详解】解：(1) ∵∠1+∠CDP=180°，∴∠CDP=180°-∠1，同理：∠CEP=180°-∠2，根据四边形的内角和定理得，∠CDP+∠DPE+∠CEP+∠C=360°，∵∠C=90°，∴180°-∠1+α+180°-∠2+90°=360°，∴∠1+∠2=90°+α=90°+60°=150°，故答案为：150；(2) ∵∠1+∠CDP=180°，∴∠CDP=180°-∠1，同理：∠CEP=180°-∠2，根据四边形的内角和定理得，∠CDP+∠DPE+∠CEP+∠C=360°，∵∠C=90°，∴180°-∠1+α+180°-∠2+90°=360°，∴∠1+∠2=90°+α，故答案为：∠1+∠2=90°+α；(3)∠1＝90°＋∠2＋∠α．理由如下：如图3，设DP与BE的交点为F，∵∠2＋∠α＝∠DFE，∠DFE＋∠C＝∠1，∴∠1＝∠C＋∠2＋∠α＝90°＋∠2＋∠α．(4)∠2＝90°＋∠1－∠α，理由如下：如图4，设PE与AC的交点为G，∵∠PGD＝∠EGC，∴∠α＋180°－∠1＝∠C＋180°－∠2，∴∠2＝90°＋∠1－∠α．故答案为∠2＝90°＋∠1－∠α．【点睛】此题是三角形综合题，主要考查了四边形的内角和，三角形的内角和，三角形的外角的性质，平角的定义，解本题的关键是将∠1，∠2，α转化到一个三角形或四边形中，是一道比较简单的中考常考题．8．某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究．（1）如图1，在△ABC中，∠ABC与∠ACB的平分线交于点P，∠A＝64°，则∠BPC＝；（2）如图2，△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E．其中∠A＝α，求∠BEC．（用α表示∠BEC）；（3）如图3，∠CBM、∠BCN为△ABC的外角，∠CBM、∠BCN的平分线交于点Q，请你写出∠BQC与∠A的数量关系，并说明理由；（4）如图4，△ABC外角∠CBM、∠BCN的平分线交于点Q，∠A=64°，∠CBQ，∠BCQ的平分线交于点P，则∠BPC= ゜，延长BC至点E，∠ECQ的平分线与BP的延长线相交于点R，则∠R= ゜．解析：（1） 122°；（2）12BECα∠=；（3）01902BQC A；（4）119，29 ；【解析】【分析】（1）根据三角形的内角和角平分线的定义；（2）根据三角形的一个外角等于与它不相邻的两个内角的和，用A ∠与1∠表示出2∠，再利用E ∠与1∠表示出2∠，于是得到结论；（3）根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出EBC ∠与ECB ∠，然后再根据三角形的内角和定理列式整理即可得解；（4）根据（1），（3）的结论可以得出∠BPC 的度数；根据（2）的结论可以得到∠R 的度数．【详解】解：（1）BP 、CP 分别平分ABC ∠和ACB ∠， 12PBC ABC ∴∠=∠，12PCB ACB ∠=∠， 180()BPC PBC PCB ∴∠=︒-∠+∠11180()22ABC ACB =︒-∠+∠， 1180()2ABC ACB =︒-∠+∠， 1(180180)2A =︒-︒-∠， 1180902A =-︒+︒∠， 9032122，故答案为：122︒；（2）如图2示，CE 和BE 分别是ACB ∠和ABD ∠的角平分线，112ACB ∴∠=∠，122ABD ∠=∠， 又ABD ∠是ABC ∆的一外角，ABD A ACB ∴∠=∠+∠，112()122A ABC A ∴∠=∠+∠=∠+∠， 2∠是BEC ∆的一外角，112111222BEC A A α∴∠=∠-∠=∠+∠-∠=∠=； （3）1()2QBC A ACB ∠=∠+∠，1()2QCB A ABC ∠=∠+∠，180BQC QBC QCB ∠=︒-∠-∠， 11180()()22A ACB A ABC =︒-∠+∠-∠+∠， 11180()22A A ABC ACB =︒-∠-∠+∠+∠， 结论1902BQC A ∠=︒-∠． （4）由（3）可知，119090645822BQCA ， 再根据（1），可得180()BPCPBC PCB 1118022QBC QCB 1180902Q 118090582119； 由（2）可得：11582922R Q ;故答案为：119，29．【点睛】本题考查了三角形的外角性质与内角和定理，熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键．9．如图，已知△ABC 中，AB=AC=10cm ，BC=8cm ，点D 为AB 的中点．如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动． （1）若点Q 的运动速度与点P 的运动速度相等，经过1s 后，BP= cm ，CQ= cm ． （2）若点Q 的运动速度与点P 的运动速度相等，经过1s 后，△BPD 与△CQP 是否全等，请说明理由；（3）若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使△BPD 与△CQP 全等？（4）若点Q 以（3）中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿△ABC 三边运动，求经过多长时间点P 与点Q 第一次相遇？解析：（1）BP=3cm ，CQ=3cm ；（2）全等，理由详见解析；（3）154；（4）经过803s 点P 与点Q 第一次相遇．【解析】【分析】（1）速度和时间相乘可得BP 、CQ 的长；（2）利用SAS 可证三角形全等；（3）三角形全等，则可得出BP=PC ，CQ=BD ，从而求出t 的值； （4）第一次相遇，即点Q 第一次追上点P ，即点Q 的运动的路程比点P 运动的路程多10+10=20cm 的长度．【详解】解：（1）BP=3×1=3㎝，CQ=3×1=3㎝（2）∵t=1s ，点Q 的运动速度与点P 的运动速度相等∴BP=CQ=3×1=3cm ，∵AB=10cm ，点D 为AB 的中点，∴BD=5cm ．又∵PC=BC ﹣BP ，BC=8cm ，∴PC=8﹣3=5cm ，∴PC=BD又∵AB=AC ，∴∠B=∠C ，在△BPD 和△CQP 中，PC BD B C BP CQ =⎧⎪∠=∠⎨⎪=⎩∴△BPD ≌△CQP(SAS)（3）∵点Q 的运动速度与点P 的运动速度不相等，∴BP 与CQ 不是对应边，即BP≠CQ∴若△BPD ≌△CPQ ，且∠B=∠C ，则BP=PC=4cm ，CQ=BD=5cm ，∴点P ，点Q 运动的时间t=433BP =s ， ∴154Q CQ V t ==cm/s ； （4）设经过x 秒后点P 与点Q 第一次相遇．由题意，得154x=3x+2×10， 解得80x=3 ∴经过803s 点P 与点Q 第一次相遇． 【点睛】本题考查动点问题，解题关键还是全等的证明和利用，将动点问题视为定点问题来分析可简化思考过程．10．在等边△ABC 的顶点A 、C 处各有一只蜗牛，它们同时出发，分别以每分钟1米的速度由A 向B 和由C 向A 爬行，其中一只蜗牛爬到终点时，另一只也停止运动，经过t 分钟后，它们分别爬行到D 、E 处，请问：（1）如图1，在爬行过程中，CD 和BE 始终相等吗，请证明？（2）如果将原题中的“由A 向B 和由C 向A 爬行”，改为“沿着AB 和CA 的延长线爬行”，EB 与CD 交于点Q ，其他条件不变，蜗牛爬行过程中∠CQE 的大小保持不变，请利用图2说明：∠CQE =60°；（3）如果将原题中“由C 向A 爬行”改为“沿着BC 的延长线爬行，连接DE 交AC 于F ”，其他条件不变，如图3，则爬行过程中，证明：DF =EF解析：（1)相等，证明见解析；（2)证明见解析；（3)证明见解析．【解析】【分析】（1）先证明△ACD≌△CBE，再由全等三角形的性质即可证得CD=BE；（2）先证明△BCD≌△ABE，得到∠BCD=∠ABE，求出∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC，∠CQE=180°-∠DQB，即可解答；（3）如图3，过点D作DG∥BC交AC于点G，根据等边三角形的三边相等，可以证得AD=DG=CE；进而证明△DGF和△ECF全等，最后根据全等三角形的性质即可证明．【详解】（1）解：CD和BE始终相等，理由如下：如图1，AB=BC=CA，两只蜗牛速度相同，且同时出发，∴CE=AD，∠A=∠BCE=60°在△ACD与△CBE中，AC=CB，∠A=∠BCE，AD=CE∴△ACD≌△CBE（SAS），∴CD=BE，即CD和BE始终相等；（2）证明：根据题意得：CE=AD，∵AB=AC，∴AE=BD，∴△ABC是等边三角形，∴AB=BC，∠BAC=∠ACB=60°，∵∠EAB+∠ABC=180°，∠DBC+∠ABC=180°，∴∠EAB=∠DBC，在△BCD和△ABE中，BC=AB，∠DBC=∠EAB，BD=AE∴△BCD≌△ABE（SAS），∴∠BCD=∠ABE∴∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC=180°-60°=120°，∴∠CQE=180°-∠DQB=60°，即CQE=60°；（3）解：爬行过程中，DF始终等于EF是正确的，理由如下：如图，过点D作DG∥BC交AC于点G，∴∠ADG=∠B=∠AGD=60°，∠GDF=∠E，∴△ADG为等边三角形，∴AD=DG=CE，在△DGF和△ECF中，∠GFD=∠CFE，∠GDF=∠E，DG=EC∴△DGF≌△EDF（AAS），∴DF=EF.【点睛】本题主要考查了全等三角形的判定与性质和等边三角形的性质；题弄懂题中所给的信息，再根据所提供的思路寻找证明条件是解答本题的关键．11．在ABC ∆中，若存在一个内角角度，是另外一个内角角度的n 倍（n 为大于1的正整数），则称ABC ∆为n 倍角三角形．例如，在ABC ∆中，80A ∠=︒，75B ∠=︒，25C ∠=︒，可知3∠=∠B C ，所以ABC ∆为3倍角三角形．（1）在ABC ∆中，55A ∠=︒，25B ∠=︒，则ABC ∆为________倍角三角形；（2）若DEF ∆是3倍角三角形，且其中一个内角的度数是另外一个内角的余角的度数的13，求DEF ∆的最小内角． （3）若MNP ∆是2倍角三角形，且90M N P ∠<∠<∠<︒，请直接写出MNP ∆的最小内角的取值范围．解析：（1）4；（2）DEF ∆的最小内角为15°或9°或180()11︒；（3）30°＜x ＜45°． 【解析】【分析】(1)根据三角形内角和定理求出∠C 的度数，再根据n 倍角三角形的定义判断即可得到答案；(2) 根据△DEF 是3倍角三角形，必定有一个内角是另一个内角的3倍，然后根据这两个角之间的关系，分情况进行解答即可得到答案；(3) 可设未知数表示2倍角三角形的各个内角，然后列不等式组确定最小内角的取值范围．【详解】解：(1)∵在ABC ∆中，55A ∠=︒，25B ∠=︒，∴∠C=180°-55°-25°=100°，∴∠C=4∠B，故ABC ∆为4倍角三角形；(2) 设其中一个内角为x °，3倍角为3x °，则另外一个内角为：1804x ︒- ①当小的内角的度数是3倍内角的余角的度数的13时， 即：x=13（90°-3x ）， 解得：x=15°， ②3倍内角的度数是小内角的余角的度数的13时，即：3x=13（90°-x ），解得：x=9°， ③当()11804903x x ︒-=︒-时， 解得：45011x ⎛⎫=︒ ⎪⎝⎭， 此时：4501804180411x ⎛⎫︒-=︒-⨯︒ ⎪⎝⎭=180()11︒，因此为最小内角， 因此，△DEF 的最小内角是9°或15°或180()11︒． (3) 设最小内角为x ，则2倍内角为2x ，第三个内角为（180°-3x ），由题意得： 2x ＜90°且180°-3x ＜90°，∴30°＜x ＜45°，答：△MNP 的最小内角的取值范围是30°＜x ＜45°．12．已知：ABC 中，过B 点作BE ⊥AD ，=90=，∠︒ACB AC BC ．(1)如图1，点D 在BC 的延长线上，连AD ，作BE AD ⊥于E ，交AC 于点F ．求证：=AD BF ；(2)如图2，点D 在线段BC 上，连AD ，过A 作AE AD ⊥，且=AE AD ，连BE 交AC 于F ，连DE ，问BD 与CF 有何数量关系，并加以证明；(3)如图3，点D 在CB 延长线上，=AE AD 且AE AD ⊥，连接BE 、AC 的延长线交BE 于点M ，若=3AC MC ，请直接写出DB BC的值．解析：（1）见详解，（2）2BD CF =，证明见详解，（3）23． 【解析】【分析】（1）欲证明BF AD =，只要证明BCF ACD ∆≅∆即可； （2）结论：2BD CF =．如图2中，作EH AC ⊥于H ．只要证明ACD EHA ∆≅∆，推出CD AH =，EH AC BC ==，由EHF BCF ∆≅∆，推出CH CF =即可解决问题； （3）利用（2）中结论即可解决问题；【详解】（1）证明：如图1中，BE AD ⊥于E ，90AEF BCF ∴∠=∠=︒，AFE CFB ∠=∠，DAC CBF ∴∠=∠，BC AC =，BCF ACD ∴∆≅∆(AAS )，BF AD ∴=．（2）结论：2BD CF =．理由：如图2中，作EH AC ⊥于H ．90AHE ACD DAE ∠=∠=∠=︒，90DAC ADC ∴∠+∠=︒，90DAC EAH ∠+∠=︒，ADC EAH ∴∠=∠，AD AE =，ACD EHA ∴∆≅∆， CD AH ∴=，EH AC BC ==，CB CA =，BD CH ∴=，90EHF BCF ∠=∠=︒，EFH BFC ∠=∠，EH BC =，EHF BCF ∴∆≅∆，FH FC ∴=，2BD CH CF ∴==．（3）如图3中，作EH AC ⊥于交AC 延长线于H ．90AHE ACD DAE ∠=∠=∠=︒，90DAC ADC ∴∠+∠=︒，90DAC EAH ∠+∠=︒，ADC EAH ∴∠=∠，AD AE =，ACD EHA ∴∆≅∆，CD AH ∴=，EH AC BC ==，CB CA =，BD CH ∴=，90EHM BCM ∠=∠=︒，EMH BMC ∠=∠，EH BC =，EHM BCM ∴∆≅∆，MH MC ∴=，2BD CH CM ∴==．3AC CM =，设CM a =，则3AC CB a ==，2BD a =， ∴2233DB a BC a ==．【点睛】本题考查三角形综合题、全等三角形的判定和性质、等腰直角三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．另外对于类似连续几步的综合题，一般前一步为后一步提供解题的条件或方法．13．如图，在等边ABC ∆中，线段AM 为BC 边上的中线．动点D 在直线AM 上时，以CD 为一边在CD 的下方作等边CDE ∆，连结BE ．（1）求CAM ∠的度数；（2）若点D 在线段AM 上时，求证：ADC BEC ∆≅∆；（3）当动点D 在直线AM 上时，设直线BE 与直线AM 的交点为O ，试判断AOB ∠是否为定值？并说明理由．解析：（1）30°；（2）证明见解析；（3）AOB ∠是定值，60AOB ∠=︒.【解析】【分析】（1）根据等边三角形的性质可以直接得出结论；（2）根据等边三角形的性质就可以得出AC AC =，DC EC =，，60ACB DCE ∠=∠=︒，由等式的性质就可以BCE ACD ∠=∠，根据SAS 就可以得出ADC BEC ∆≅∆；（3）分情况讨论：当点D 在线段AM 上时，如图1，由（2）可知ACD BCE ≅∆∆，就可以求出结论；当点D 在线段AM 的延长线上时，如图2，可以得出ACD BCE ≅∆∆而有30CBE CAD ∠=∠=︒而得出结论；当点D 在线段MA 的延长线上时，如图3，通过得出ACD BCE ≅∆∆同样可以得出结论．【详解】（1）ABC ∆是等边三角形，60BAC ∴∠=︒．线段AM 为BC 边上的中线，12CAM BAC ∴∠=∠， 30CAM ∴∠=︒．（2）ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，ACD DCB DCB BCE ∴∠+∠=∠+∠，ACD BCE ∠∠∴=．在ADC ∆和BEC ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩， ()ACD BCE SAS ∴∆≅∆；（3）AOB ∠是定值，60AOB ∠=︒，理由如下：①当点D 在线段AM 上时，如图1，由（2）可知ACD BCE ≅∆∆，则30CBE CAD ∠=∠=︒，又60ABC ∠=︒，603090CBE ABC ∴∠+∠=︒+︒=︒，ABC ∆是等边三角形，线段AM 为BC 边上的中线AM ∴平分BAC ∠，即11603022BAM BAC ∠=∠=⨯︒=︒ 903060BOA ∴∠=︒-︒=︒．②当点D 在线段AM 的延长线上时，如图2，ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，ACB DCB DCB DCE ∴∠+∠=∠+∠，ACD BCE ∠∠∴=，在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩， ()ACD BCE SAS ∴∆≅∆，30CBE CAD ∴∠=∠=︒，同理可得：30BAM ∠=︒，903060BOA ∴∠=︒-︒=︒．③当点D 在线段MA 的延长线上时，ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，60ACD ACE BCE ACE ∴∠+∠=∠+∠=︒，ACD BCE ∠∠∴=，在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩， ()ACD BCE SAS ∴∆≅∆，CBE CAD ∴∠=∠，同理可得：30CAM ∠=︒150CBE CAD ∴∠=∠=︒30CBO ∴∠=︒，∵30BAM ∠=︒，903060BOA ∴∠=︒-︒=︒．综上，当动点D 在直线AM 上时，AOB ∠是定值，60AOB ∠=︒．【点睛】此题考查等边三角形的性质，全等三角形的判定及性质，等边三角形三线合一的性质，解题中注意分类讨论的思想解题.14．如图所示，在平面直角坐标系xOy 中，已知点A 的坐标(3,2)-，过A 点作AB x ⊥轴，垂足为点B ，过点(2,0)C 作直线l x ⊥轴，点P 从点B 出发在x 轴上沿着轴的正方向运动．（1）当点P 运动到点O 处，过点P 作AP 的垂线交直线l 于点D ，证明AP DP =，并求此时点D 的坐标；（2）点Q 是直线l 上的动点，问是否存在点P ，使得以P C Q 、、为顶点的三角形和ABP ∆全等，若存在求点P 的坐标以及此时对应的点Q 的坐标，若不存在，请说明理由． 解析：（1）证明见解析；(2,3)D ；（2）存在，(0,0)P ，(2,3)Q 或(0,0)P ，(2,3)Q -或(4,0)P ，(2,7)Q 或(4,0)P ，(2,7)Q -或1(,0)2P -，(2,2)Q -或1(,0)2P -，(2,2)Q -．【解析】【分析】（1）通过全等三角形的判定定理ASA 证得△ABP ≌△PCD ，由全等三角形的对应边相等证得AP ＝DP ，DC ＝PB ＝3，易得点D 的坐标；（2）设P （a ，0），Q （2，b ）．需要分类讨论：①AB ＝PC ，BP ＝CQ ；②AB ＝CQ ，BP ＝PC ．结合两点间的距离公式列出方程组，通过解方程组求得a 、b 的值，得解．【详解】（1）AP PD ⊥90APB DPC ∴∠+∠=AB x ⊥轴90A APB ∴∠+∠=A DPC ∴∠=∠在ABP ∆和PCD ∆中A DPC AB PCABP PCD ∠=∠⎧⎪=⎨⎪∠=∠⎩()ABP PCD ASA ∴∆≅∆AP DP ∴=，3DC PB ==(2,3)D ∴（2）设(,0)P a ，(2,)Q b①AB PC =，BP CQ = 223a a b ⎧-=⎪⎨+=⎪⎩，解得03a b =⎧⎨=±⎩或47a b =⎧⎨=±⎩ (0,0)P ∴，(2,3)Q 或(0,0)P ，(2,3)Q -或(4,0)P ，(2,7)Q 或(4,0)P ，(2,7)Q - ②AB CQ =，BP PC =，322a a b +=-⎧⎨=⎩，解得122a b ⎧=⎪⎨⎪=±⎩ 1(,0)2P ∴-，(2,2)Q -或1(,0)2P -，(2,2)Q - 综上：(0,0)P ，(2,3)Q 或(0,0)P ，(2,3)Q -或(4,0)P ，(2,7)Q 或(4,0)P ，(2,7)Q -或1(,0)2P -，(2,2)Q -或1(,0)2P -，(2,2)Q - 【点睛】考查了三角形综合题．涉及到了全等三角形的判定与性质，两点间的距离公式，一元一次绝对值方程组的解法等知识点．解答（2）题时，由于没有指明全等三角形的对应边（角），所以需要分类讨论，以防漏解．15．（1）填空①把一张长方形的纸片按如图①所示的方式折叠，EM ，FM 为折痕，折叠后的C 点落在1B M 或1B M 的延长线上，那么EMF ∠的度数是________；②把一张长方形的纸片按如图②所示的方式折叠，B 点与M 点重合，EM ，FM 为折痕，折叠后的C 点落在1A M 或1A M 的延长线上，那么EMF ∠的度数是_______． （2）解答：①把一张长方形的纸片按如图③所示的方式折叠，EM ，FM 为折痕，折叠后的C 点落在1B M 或1B M 的延长线上左侧，且80EMF ∠=︒，求11C MB ∠的度数； ②把一张长方形的纸片按如图④所示的方式折叠，B 点与M 点重合，EM ，FM 为折痕，折叠后的C 点落在1A M 或1A M 的延长线右侧，且60EMF ∠=︒，求11C MA ∠的度数．（3）探究：把一张四边形的纸片按如图⑤所示的方式折叠，EB ，FB 为折痕，设ABC α∠=︒，EBF β∠=︒，11A BC γ∠=︒，求α，β，γ之间的数量关系． 解析：90︒，45︒；20︒，30︒；2a γβ+=，2a γβ-=.【解析】【分析】（1）①如图①知1112EMC BMC ∠=∠，1112C MF C MC ∠=∠得 ()1112EMF BMC C MC ∠=∠+∠可求出解. ②由图②知111111,22EBA ABC C BF C BC ∠=∠∠=∠得()1112EBF ABC C BC ∠=∠+∠可求出解.（2）①由图③折叠知11,CMF FMC BME EMB ∠=∠∠=∠，可推出11()BMC EMF EMF C MB ∠-∠-∠=∠，即可求出解.②由图④中折叠知11,CMF C MF ABE A BE ∠=∠∠=∠，可推出()112906090A MC ︒︒︒-+∠=，即可求出解.（3）如图⑤-1、⑤-2中分别由折叠可知，a ββγ-=-、a ββγ-=+，即可求得 2a γβ+=、2a γβ-=.【详解】解：（1）①如图①中，1112EMC BMC ∠=∠，1112C MF C MC ∠=∠， ()1111111800229EMF EMC C MF BMC C MC ︒︒∴∠=∠+∠=∠⨯=+∠=， 故答案为90︒. ②如图②中，111111,22EBA ABC C BF C BC ∠=∠∠=∠， ()111111904522EBF EBC C BF ABC C BC ︒︒∴∠=∠+∠=∠+∠=⨯=， 故答案为45︒.（2）①如图③中由折叠可知， 11,CMF FMC BME EMB ∠=∠∠=∠，1111C MF EMB EMF C MB ∠+∠-∠=∠，11CMF BME EMF C MB ∴∠+∠-∠=∠，11()BMC EMF EMF C MB ∴∠-∠-∠=∠，111808020C MB ︒︒︒∴-=∠=；②如图④中根据折叠可知，11,CMF C MF ABE A BE ∠=∠∠=∠，112290CMF ABE AMC ︒∠+∠+∠=，112()90CMF ABE AMC ︒∴∠+∠+∠=，()1129090EMF A MC ︒︒∴-∠+∠=， ()112906090A MC ︒︒︒∴-+∠=， 1130AMC ︒∴∠=；（3）如图⑤-1中，由折叠可知，a ββγ-=-，2a γβ∴+=；如图⑤-2中，由折叠可知，a ββγ-=+，2a γβ∴-=.【点睛】本题考查了图形的变换中折叠属全等变换，图形的角度及边长不变及一些角度的计算问题，突出考查学生的观察能力、思维能力以及动手操作能力，本题是代数、几何知识的综合运用典型题目.二、选择题16．下列判断正确的是（ ）A ．3a 2bc 与bca 2不是同类项B ．225m n 的系数是2 C ．单项式﹣x 3yz 的次数是5D ．3x 2﹣y +5xy 5是二次三项式解析：C【解析】【分析】根据同类项的定义，单项式和多项式的定义解答．【详解】A ．3d 2bc 与bca 2所含有的字母以及相同字母的指数相同，是同类项，故本选项错误．B ．225m n 的系数是25，故本选项错误． C ．单项式﹣x 3yz 的次数是5，故本选项正确．D ．3x 2﹣y +5xy 5是六次三项式，故本选项错误．故选C ．【点睛】本题考查了同类项，多项式以及单项式的概念及性质．需要学生对概念的记忆，属于基础题．17．已知max }2,x x 表示取三个数中最大的那个数，例如：当x ＝9时，max }}22,max ,9x x =＝81．当max }21,2x x =时，则x 的值为（ ） A ．14- B ．116 C ．14 D ．12解析：C【解析】【分析】利用max }2,x x 的定义分情况讨论即可求解． 【详解】解：当max}21,2x x =时，x ≥012，解得：x ＝14x ＞x 2，符合题意；②x 2＝12，解得：x ＝2x ＞x 2，不合题意；③x ＝12x ＞x 2，不合题意；故只有x ＝14时，max }21,2x x =． 故选：C ．【点睛】此题主要考查了新定义，正确理解题意分类讨论是解题关键．18A ．1B ．2C ．3D ．4解析：B【解析】【分析】根据算术平方根的概念可得出答案.【详解】解：根据题意可得： 4=2， 故答案为：B.【点睛】本题考查算术平方根的概念,解题关键在于对其概念的理解.19．对于方程12132x x +-=，去分母后得到的方程是（ ） A ．112x x -=+B ．63(12)x x -=+C ．233(12)x x -=+D ．263(12)x x -=+ 解析：D【解析】【分析】方程两边同乘以6即可求解.【详解】12132x x +-=， 方程两边同乘以6可得，2x-6=3（1+2x ）.故选D.【点睛】本题考查了一元一次方程的解法—去分母，方程两边同乘以各分母的最小公倍数是去分母的基本方法.20．有一个数值转换器，流程如下：当输入x 的值为64时，输出y 的值是（ ）A ．2B ．22C 2D 32解析：C【解析】【分析】把64代入转换器，根据要求计算，得到输出的数值即可.【详解】，是有理数，∴继续转换，，是有理数，∴继续转换，∵2∴输出故选：C.【点睛】本题考查的是算术平方根的概念和性质，一个正数的平方根有两个，正的平方根是这个数的算术平方根；注意有理数和无理数的区别.21．下列说法中正确的有（）A．连接两点的线段叫做两点间的距离B．过一点有且只有一条直线与已知直线垂直C．对顶角相等D．线段AB的延长线与射线BA是同一条射线解析：C【解析】【分析】分别利用直线的性质以及射线的定义和垂线定义分析得出即可．【详解】A．连接两点的线段的长度叫做两点间的距离，错误；B．在同一平面内，过一点有且只有一条直线与已知直线垂直，错误；C．对顶角相等，正确；D．线段AB的延长线与射线BA不是同一条射线，错误．故选C．【点睛】本题考查了直线的性质以及射线的定义和垂线的性质，正确把握相关定义和性质是解题的关键．22．如果﹣2xy n+2与 3x3m-2y 是同类项，则|n﹣4m|的值是（）A．3 B．4 C．5 D．6解析：C【解析】【分析】同类项要求相同字母上的次数相同,由此求出m,n,代入即可求解.【详解】解：∵﹣2xy n+2与 3x3m-2y 是同类项，∴3m-2=1,n+2=1,解得：m=1,n=-1,∴|n﹣4m|=|-1-4|=5,故选C.【点睛】本题考查了同类项的概念,属于简单题,熟悉概念和列等式是解题关键.23．已知关于x 的方程mx+3＝2（m ﹣x ）的解满足（x+3）2＝4，则m 的值是（ ） A ．13或﹣1 B ．1或﹣1 C ．13或73 D ．5或73解析：A【解析】【分析】先求出方程的解，把x 的值代入方程得出关于m 的方程，求出方程的解即可．【详解】解：（x+3）2＝4，x ﹣3＝±2，解得：x ＝5或1，把x ＝5代入方程mx+3＝2（m ﹣x ）得：5m+3＝2（m ﹣5），解得：m ＝13， 把x ＝﹣1代入方程mx+3＝2（m ﹣x ）得：﹣m+3＝2（1+m ），解得：m ＝﹣1，故选：A ．【点睛】本题考查了解一元一次方程的解的应用，能得出关于m 的方程是解此题的关键．24．计算32a a ⋅的结果是（ ）A ．5a ；B ．4a ；C ．6a ；D ．8a ．解析：A【解析】此题考查同底数幂的乘法运算，即(0)m n m n a a a a +⋅=>，所以此题结果等于325a a +=，选A ；25．如图，已知直线//a b ,点,A B 分别在直线,a b 上，连结AB .点D 是直线,a b 之间的一个动点，作//CD AB 交直线b 于点C,连结AD .若70ABC ︒∠=，则下列选项中D ∠不可能取到的度数为()。

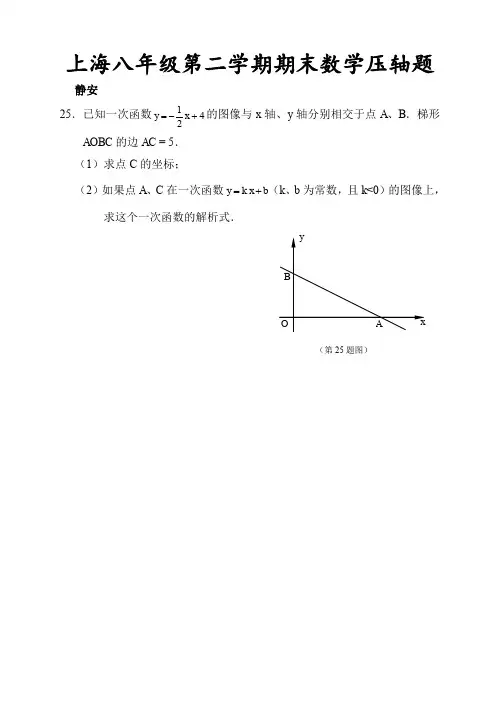
上海八年级第二学期期末数学压轴题靜安理 LL 知一次两數尸*"询用滋与貯铀7轧分别桁交F 点儿 乩 梯形VAOBC 的边丿0=5.CD 求点C 的坐标：门）如果点丄c 在一次两数尸行越""肯常瓶 且* 0）的ffiifth,我这牛一次阴建的解折式.26如関.住止ABCD 4].点忑总边肿 卜（点E 与点」、丹不重合）， 过点E 作FG 丄DEFG 与iiJCffi 交于点 耳与边IU 的基长线相交干点G.（1） 由几个小同的忡置「分别测^BF.AG. AE 的艮’从中你能发砚E 氏貝GH 的螯皐之闾具有r H 的关系？井证网你衔袒嗣的結论:（2） 联结DF,如采正方能的边长为乙谁AEf .ADFG 的面积为八............ * ....................................................................... < 1 分、二这个…次函^解析式为"中子（1分）0 = 8Jt+&} 4=5fr+fr,设ACJifi 线DE 的距离为八S iC ^=-D£-A=2to化点C*到宜线的距离为二26.解：（1）月/>/*•<£. ...................证明如下：过点F 作FHVDA.垂足为H ・ ；在正方形MCD 中* ZDAE=ZB=9C b.代四边形ARFH^VW^…1分） :・FH 二AB=DA. 丁加丄FG AZG=90° ・ ZADEMDEA. X»ZDJ£=ZF2/G=90n * ：*“FHG 哲£\DA£. ......... 仁 GE=AE 、即 H.i+AG=AE. 7BF=HA. :,BF+AG=AE. （1分） 门分）（I（2） TAFHGmbDAE* :.FG=DE= J A D'+AE' = V4 + x^ .（1分｝4 + r"S^r ^-FG DE ■二 y = _定义城为OGd ................................<3） il 结 CE S ACDE =^CD AD = 2.（i 分） （1分〉（1分〉<15>）SF气:.訂=:.h£1分〉求F 与工之冋的祇数幅析式.并气出甌数的定义域:⑶毎汇如已知点E是矩形期a的边a延长线上一点'^CE=CA T 联皓H£，过点C作CF丄盘，垂足为点F・联络EF、FIX «门求证；甘3匚^AFADt(2)联结皿儿若—--.且AC-1C■求FC的值ED 5E B C2007^ 汇25. (D 证明：*： CE = AC.CF LAE,：. AF = EF........................................ 1分T四边形aCD是矩形，:.AD^BC. ZABC= ^BAD二90°二在殆A4SE中* BF = AF......................................................................... 1 分:、—14 = —FABA ZE4D-ZFBC ............................................................................................... 1 分A ^FBC^&FAD................................................................................................ 1 分(2) *.* AFBC FC^FD. ZBFC £AFD ............................................ 1 分A ^BFD^ ^BFC-^CFD= ^AFD+^CFD=9().......................... 1 分匸四边形dffCD是矩形.:.BD^ACFB 3V ——=-* \\.BD=AC^1O,8D 5:.FD=3........................................................................................................... I 分/.FC = 8 ................................................................................................... 1 分在梯們.迪 CD V.i ：ABC=W .AD /BC, BC -ID, -4J=8aD > 5C-18cm,410 firn 白P 从点月幵始汇』C 边向终点C 议毎秒童in 的迪煦曲动・A 0从点D 开贻沿D4边向终点」且部砂2cm 的違度懿劫.违运动时间为$秒一M)求四迪农」也P0为琏形时f 的fin(2)舞題设中的"迟01如1"改雯为"蛊e#cnT.其它条件都不变・娶慢四边形胆DQ 是黑腰樣咼「求『与it 的函数关系式，并耳出Jt 的电值范TH ：(3)在移动的过世中"是否存在刑P 、。

八年级期末数学压轴题答案1、解：（1）A （8，0）, B （0，4）．………………………………………………（1分） 在梯形AOBC 中，OA =8，OC =4，AC =5． 当AC //OB 时，点C 的坐标为（8，5）．………………………………（1分） 当BC //OA 时，设点C （x ,4）． 2225)04()8(=-+-x ,………………（1分）∴.11,521==x x …………………………………………………………（1分）这时点C 的坐标为（5，4）或（11，4）．……………………………（1分）∴点C 的坐标为（8，5）或（5，4）或（11，4）．（2）∵点A 、C 在一次函数y k x b =+（k <0）的图象上，∴点（8，5）与（11，4）都不符合题意，只有当C 为（5，4）时，k <0．∴⎩⎨⎧+=+=,54,80b k b k …………………………………………………………………（1分）∴⎪⎪⎩⎪⎪⎨⎧=-=.332,34b k …………………………………………………………………（1分） ∴这个一次函数的解析式为33234+-=x y ．………………………………（1分）2、解：（1）BF +AG = AE ．…………………………………………………………（1分） 证明如下：过点F 作FH ⊥DA ，垂足为H ，∵在正方形ABCD 中，∠DAE =∠B =90°，∴四边形ABFH 是矩形．…（1分）∴FH =AB =DA ．∵BD ⊥FG ，∴∠G =90°–∠ADE =∠DEA ． 又∴∠DAE =∠FHG =90°，∴△FHG ≌△DAE ．…………………………（1分） ∴GH =AE ，即HA +AG =AE ．∵BF =HA ，∴BF +AG =AE ．………………（1分）（2）∵△FHG ≌△DAE ，∴FG =DE =2224x AE AD +=+．……………（1分）∵DE FG S DGF ⋅=∆21，∴242x y +=．…………………………………（1分）定义域为.20<<x …………………………………………………………（1分）（3）连结CE ，221=⋅=∆AD CD S CDE ．………………………………………（1分）设点C 到直线DE 的距离为h ，221=⋅=∆h DE S CDE ，…………………（1分）∵DE =FG =25，∴22521=⋅⋅h ，∴.58=h …………………………………（1分）∴点C 到直线DE 的距离为.583、（1）证明：∵,CE AC CF AE =⊥,∴AF EF = …………………1分 ∵四边形ABCD 是矩形，∴,90AD BC ABC BAD =∠=∠=︒∴在Rt ABE ∆中，BF AF = …………………………………………… 1分 ∴FBA FAB ∠=∠∴FAD FBC ∠=∠ ……………………………………………………… 1分 ∴FBC ∆≌FAD ∆ ……………………………………………………… 1分 （2）∵FBC ∆≌FAD ∆,,FC FD BFC AFD ∴=∠=∠ ………………… 1分∴90BFD BFC CFD AFD CFD ︒∠=∠+∠=∠+∠= ………………… 1分 ∵四边形ABCD 是矩形，∴BD =AC ∵35FB BD =，且BD =10AC =， 8FD ∴= ………………………………………………………………… 1分 8FC ∴= ………………………………………………………………… 1分4、证明：联结AM 并延长，交BC 于点E （如图2）.…1分 ∵ AD ∥BC ，∴ BEM DAM ∠=∠，EBM ADM ∠=∠. ∵ BM DM =，∴ EBM ADM ∆≅∆（AAS ）.………………3分 ∴ME AM =，BE AD =. ………………2分 ∵ M 、N 分别是AE 、AC 的中点， ∴MN 是AEC ∆的中位线. ………………2分∴EC MN 21=，MN ∥BC .……………1分 ∵)(21)(21AD BC BE BC EC -=-=，∴)(21AD BC MN -=.………………1分说明：其他方法，若正确，可参照评分. 5、（1）过点D 作DH ⊥BC ，垂足为点H由题意可知：AB=DH=8，AD=BH DC =10ABCDMNE 图2∴HC =622=-DH DC∴AD=BH=CH BC - ∵BC =18∴AD=BH =12…………………………………1分 若四边形ABPQ 是矩形，则AQ=BP ∵AQ =t 212-，BP =t 3 ∴t 3t 212=-∴512t =（秒）………………………………1分 （2）由（1）得CH =6再过点Q 作QG ⊥BC ，垂足为点G同理：PG =6 …………………………………1分 易知：QD=GH =t 2 又BP+PG+GH+HC=BC ∴k 6t 26t 3=+++∴512k t -= …………………………………1分∴k 的取值范围为：12>k cm ………………1分（3）假设存在时间t 使PQ =10，有两种情况：①如右图（中）：由（2）可知：186t 26t 3=+++∴56t =……………………………………1分②如右图（下）：四边形PCDQ 是平行四边形， ∴QD=PC =t 2又BP =t 3，BP+PC=BC ∴18t 2t 3=+∴518t =（秒）………………………………1分综上所述，存在时间t 且65t =秒或185t =秒时P 、Q 两点之间的距离为10cm 5、证明：∵AE ∥BC ，∴∠AED =∠MCD ，∠EAD =∠CMD ．…………………………（1分）∵AD =MD ，∴△AED ≌△MCD ．…………………………………（1分） ∴AE =CM ．……………………………………………… ∵BM =CM ，∴AE =BM ．∴四边形AEBM 是平行四边形．………………………………………（1分） ∴EB =AM ．…………………………………………………………………（1分） 而AM =AC ，∴EB =AC ．…………………………………………………（1分）QPDCBAQPDC BA∵AE ∥BC ，EB 与AC 不平行，∴四边形EBCA 是梯形．………………（1分） ∴梯形EBCA 是等腰梯形．………………………………………………（1分）6、解：（1）联结AC ．在菱形ABCD 中，∵AB =BC ，∠B =60°，∴△ABC 是等边三角形．…………………………（1分） ∴AC =AB ，∠BAC =∠BCA =60°．∵∠P AQ =60°，∴∠BAP =∠CAQ ．………………………………………（1分） ∵AB ∥CD ，∠B =60°，∴∠BCD =120°． ∴∠ACQ =∠B =60°．∴△ABP ≌△ACQ ．…………………………………………………………（1分） ∴AP =AQ ．……………………………………………………………………（1分） ∴△APQ 是等边三角形．……………………………………………………（1分） （2）由△APQ 是等边三角形，得AP =PQ =y ．作AH ⊥BC 于点H ，由AB=4，BH =2，∠B =60°，得AH =32． ……（1分） ∴12)2(2+-=x y ，即1642+-=x x y ．……………………………（1分） 定义域为x ≥0．………………………………………………………………（1分） （3）（i ）当点P 在边BC 上时，∵PD ⊥AQ ，AP =PQ ，∴PD 垂直平分AQ ． ∴AD =DQ ．∴CQ =0．……………………………………………………………………（1分） 又∵BP =CQ ，∴BP =0．（ii ）当点P 在边BC 的延长线上时，同理可得BP =8．……………………………………………………………（1分） 综上所述，BP =0或BP =8．7、证明：（1）ΘBC=3AD ，BC=3MN ∴AD=MN （1分）Θ梯形ABCD ，AD//BC ，∴四边形AMND 是平行四边形（略） （1分）（2）四边形AGHD 是菱形 （1分）ΘAD//BC ∴MBG ADG ∠=∠ ΘDGA BGM ∠=∠，AD=BM ∴)(AAS DGA BGM ∆≅∆ ∴AG=GM （2分） 同理可得AH=HC ∴GH 是AMC ∆的中位线 ∴GH//BC ，MN MC GH ==21（略） （1分） ∴GH//AD ，GH=AD ，∴四边形AGHD 是平行四边形（略） （1分） ΘBD AC ⊥ ∴四边形AGHD 是菱形（略） （1分）8、解：（1）设直线l 的解析式为)0(≠+=k b kx yΘ直线l 平行于383-=x y ，∴3=k （1分）Θ直线l 经过点)3,2(-A ，∴b +⨯=-323，9-=b （1分）∴直线l 的解析式为93-=x y ，点B 坐标为)0,3( （1分）（2）Θ点)6,(-a M 在直线l 上，∴1=a ，则可设点),1(y P （1分）Θ)31,1(N ，∴y 的取值范围是316≤≤-y （1分）（I ）当AB 为斜边时，222AB PB PA =+，104)3(122=++++y y ，解得2,121-=-=y y ，∴)2,1(),1,1(--P P （4分） （II ） 当PB 为斜边时，222PB AB PA =+，22410)3(1y y +=+++解得38-=y ，∴)38,1(-P （2分） （III ） 当PA 为斜边时，222PA AB PB =+，22)3(1410++=++y y解得32=y ，（舍去） （1分） ∴综上所述，点P 的坐标为)38,1(),2,1(),1,1(321---P P P9、（1）四边形EFGH 是矩形---------------------------------------------------------------1分 证明：∵E 、F 运动时间相同，∴AE=CF∵EH ⊥AC ，FG ⊥AC ，∴EH//FG∵ABCD 为正方形，∴AD=DC ，∠D=900，∴∠GCF=∠HAE=450，又EH ⊥AC ，FG ⊥AC ，∴∠CGF=∠AHE=450，∴∠GCF=∠CGF ，∠HAE=∠AHE∴AE=EH ，CF=FG ，∴EH=FG-------------------------------------------------------1分 ∴四边形EFGH 是平行四边形--------------------------------------------------------1分 ∵EH ⊥AC ，∴四边形EFGH 是矩形（2）Q 正方形边长为16AC ∴=．-----------------------------------------------1分AE x =Q ，过B 作BO AC ⊥于O ，则8BO =．24S x ∴=---------------1分HE x =Q ，162EF x =-，1(162)S x x ∴=-．-------------------------------1分当12S S =时，(162)4x x x -=．解得10x =（舍去），26x =．---------- 1分∴当6x =时，12S S =．（3）①当08x <≤时，2(162)4220y x x x x x =-+=-+．----------------------1分②当816x ≤≤时，AE x =，16CE HE x ==-，162(16)216EF x x =--=-．--------------------------------------------------1分 1(16)(216)S x x ∴=--．2(16)(216)4252256y x x x x x ∴=--+=-+---------------------------------1分10、解：（1）∵AD =AP ，∴ADP APD ∠=∠. ∵︒=∠30DAP ， ∴)180(21DAP ADP APD ∠-︒=∠=∠ ︒=︒-︒=75)30180(21.……………………1分 ∵︒=∠30DAP ，∴︒=∠-︒=∠6090DAP BAP .……………1分又∵AP AD AB ==，∴ABP ∆是等边三角形. ∴︒=∠60APB .∴︒=︒+︒=+∠=∠1357560APD BPA BPD .…………1分 说明：其他方法，可参照得分.（2）∵︒=∠+∠+∠+∠360DAB ADP BPD ABP ，………1分︒=∠90DAB ，∴︒=∠+∠+∠270ADP BPD ABP ，即 ︒=∠+∠+∠+∠270ADP APD BPA ABP . ∵AD =AP ，∴ADP APD ∠=∠. ∵AP AD AB ==，∴APB ABP ∠=∠.图① 图②图3ABCDPMABCDP∴︒=︒⨯=∠+∠=∠13527021APD BPA BPD .…………1分 说明：其他方法请参照评分. （3）①当︒<<︒900α时，如图4∵AD =AP ，α=∠DAP ∴αα2190)180(21-︒=-︒=∠=∠ADP APD . ∵AP AD AB ==，α+︒=∠90BAP ， ∴[])90(18021α+︒-︒=∠=∠APB ABP α2145-︒=.∴APB APD BPD ∠-∠=∠)2145()2190(αα-︒--︒=︒=45.…………2分②当︒=90α时，如图5，∵ ︒=∠+∠180DAP BAD ， ∴ 点B 、A 、P 在同一直线上. ∴︒=︒-︒=∠=∠45)90180(21APD BPD .……1分 ③当︒<<︒18090α时，如图6. ∵ αα2190)180(21-︒=-︒=∠APD . []αα-︒=-︒-︒=∠27090360BAP .[]︒-=-︒-︒=∠4521)270(18021ααBPA . ∴︒=︒-+-︒=∠+∠=∠4545212190ααDPA BPA BPD .……2分说明：其他方法请参照评分.11、解：（1）过D 作DH ⊥BC ，DH 与EF 、BC 分别相交于点G 、H ．………………（1分）∵ 梯形ABCD 中，∠B =90º，∴ DH //AB ．又∵AD //BC ，∴ 四边形ABHD 是矩形． ∵∠C =45º，∴∠CDH =45º，∴ CH =DH =AB =8．……………………………（1分）ABCDP图5ABCDP图6∴AD =BH =BC –CH =6．…………………………………………………………（1分） （2）∵DH ⊥EF ，∠DFE =∠C =∠FDG =45º,∴FG =DG =AE =x ,∵EG =AD =6,∴EF =6+x .∵PE =PF ，EF //BC ，∴∠PFE =∠PEF =∠PMN =∠PMN ，∴PM =PN ．…………（1分） 过点P 作QR ⊥EF ，QR 与EF 、MN 分别相交于Q 、R ， ∵∠MPN =∠EPF =90º，QR ⊥MN ，∴PQ =21EF =)6(21+x ，PR =21MN =y 21．…（1分） ∵QR =BE =x -8，∴x y x -=++821)6(21．………………………………（1分）∴y 关于x 的函数解析式为.103+-=x y 定义域为1≤x <310.……（1+1分）（3）当点P 在梯形ABCD 内部时，由MN =2及（2）的结论得1032+-=x ，AE =38=x ，……………………………………………………………………（1分） ∴21=AEFD S 梯形（AD +BC ）AE ⋅=917638)3866(21=⨯++．………………（1分）当点P 在梯形ABCD 外部时，由MN =2及与（2）相同的方法得：x x -=⨯-+8221)6(21，AE =4=x ，………………………………………（1分） ∴21=AEFD S 梯形（AD +BC ）AE ⋅=324)466(21=⨯++．…………………（1分）12、13、证明：（1）过点M分别作MG⊥AB，MH⊥CD，垂足为点G、H．∵点M是边BC的中点，∴BM = CM．∵在梯形ABCD中，AD // BC，AB = CD，∴60∠=∠=︒．B C又∵MG⊥AB，MH⊥CD，∴90BGM CHM∠=∠=︒．∴△BGM≌△CHM．得MG = MH，且30∠=∠=︒，BMG CMH即得120∠=∠=︒．………………………………………（2分）GMH EMF又∵∠EMF =∠EMG +∠GMF ，且∠GMH =∠GMF +∠FMH ， ∴∠EMG =∠FMH ．于是，由90BGM CHM ∠=∠=︒，MG = MH ，得△EGM ≌△FHM ． ∴ME = MF ．…………………………………………………………（2分） （2）当点E 、F 在边AB 、CD 上移动时，五边形AEMFD 的面积的大小不会改变．…………………………………………………………………（1分） ∵△EGM ≌△FHM ，∴EMG FMH S S ∆∆=．即得五边形五边形AEMFD AGMHD S S =．……………………………………（2分）（3）联结AM （在备用图中1）．当点E 、F 恰好是边AB 、CD 的中点，且AB = CD ，得BE = CF ． 又∵ME = MF ，BM = CM ，∴△BEM ≌△CFM ．∴∠BME =∠CMF ．∵120EMF ∠=︒，∴1(180)302BME EMF ∠=︒-∠=︒．…………（1分）于是，由60B ∠=︒，得90BEM ∠=︒．∵点E 是边AB 的中点，∴ME 是边AB 的垂直平分线．∴MA = MB ． 于是，由60B ∠=︒，得△ABM 是等边三角形．……………………（1分） ∴60AMB ∠=︒．即得∠AMB =∠C ．∴AM // CD ．又∵AD // MC ，∴四边形AMCD 是平行四边形． ∴AD = CM ．于是，由BC = 8，BM = CM ，得CM = 4． 即得AD = 4．…………………………………………………………（1分）说明：如果学生在证得△BEM 是直角三角形，且30BEM ∠=︒． ………………（1分）利用直角三角形的性质求得BE = 2，进而求得AB = 4．分别过点A 、D 作AK ⊥BC ，DL ⊥BC ,垂足为点K 、L （在备用图2中）．利用直角三角形的性质求得BN = 4，CL = 4．………………………………（1分） 求得KL = 4，并说明四边形AKLD 是矩形，进而求得AD = 4．……………（1分） A BC D ME F（第26题图）G HA BC D MEF （备用图1）A BCD MEF （备用图2）KL。

八年级数学（下）填空题压轴小题练习题一．填空题1．如果一个平行四边形一个内角的平分线分它的一边为1:2的两部分，那么称这样的平行四边形为“协调平行四边形”，称该边为“协调边”．当“协调边”为3时，它的周长为 ． 2．如图，在ABC ∆中，4AC AB ==，AH BC ⊥垂足为H ，15AH =，BD 是中线，将CBD ∆沿直线BD 翻折后，点C 落在点E ，那么AE 为 ．3．如图，菱形ABCD 由6个腰长为2，且全等的等腰梯形镶嵌而成，则菱形的对角线AC 的长为 ．4．如图，在Rt ABC ∆中，90C ∠=︒，1BC =，2AB =，将ABC ∆绕点A 顺时针旋转后得到ABC '∆（点B 、C 分别与点B C '对应）．当BA BB '=时，B C '= ．5．已知四边形ABCD 是矩形，点E 是边AD 的中点，以直线BE 为对称轴将ABE ∆翻折至FBE ∆，联结DF ，那么图中与AEB ∠相等的角的个数为 ．6．如图，正方形ABCD 的边长为1，把这个正方形绕点A 旋转，得到正方形AB C D '''；且点C '在直线AD 上，那么△C D D ''的面积是 ．7．已知P 是正方形ABCD 内一点，将ABP ∆绕点B 旋转，使得边BA 与边BC 重合，点P 落在点P '的位置上．如果2PB =，那么PP '的长等于 ．8．如图，点E 、F 分别在矩形ABCD 的边BC 和CD 上，如果ABE ∆、ECF ∆、FDA ∆的面积分别刚好为6、2、5，那么矩形ABCD 的面积为 ．9．平面直角坐标系xOy 中，点1(A x ，1)y 与2(B x ，2)y ，如果满足120x x +=，120y y -=，其中12x x ≠，则称点A 与点B 互为反等点．已知：点(3,8)C 、(5,8)G -，联结线段CG ，如果在线段CG 上存在两点P ，Q 互为反等点，那么点P 的横坐标P x 的取值范围是 ． 10．如图，在边长为6的正方形ABCD 中，点M 、N 分别是边AD 、BC 的中点，Q 是边CD 上的一点．联结MN 、BQ ，将BCQ ∆沿着直线BQ 翻折，若点C 恰好与线段MN 上的点P 重合，则PQ 的长等于 ．11．我们把对角线与一条底边相等的等腰梯形叫做“完美等腰梯形”，若一个“完美等腰梯形”的对角线长为10，且该梯形的一个内角为75︒，则这个梯形的高等于 ． 12．如图放置的两个正方形，大正方形ABCD 边长为a ，小正方形CEFG 边长为()b a b >，M 是BC 边上一个动点，联结AM ，MF ，MF 交CG 于点P ，将ABM ∆绕点A 旋转至ADN ∆，将MEF ∆绕点F 旋转恰好至NGF ∆．给出以下三个结论：①AND MPC ∠=∠； ②ABM NGF ∆≅∆；③22AMFN S a b =+四边形．其中正确的结论是 （请填写序号）．13．如图，在Rt ABC ∆中，90C ∠=︒，6AC =，8BC =．D ，E 分别为边BC ，AC 上一点，将ADE ∆沿着直线AD 翻折，点E 落在点F 处，如果DF BC ⊥，AEF ∆是等边三角形，那么AE = ．14．已知在平面直角坐标系xOy 中，直线142y x =-+与x 轴交于点A 、与y 轴交于点B ，四边形AOBC 是梯形，且对角线AB 平分CAO ∠，那么点C 的坐标为 ．15．如图，在平行四边形ABCD 中，AC 与BD 相交于点60O AOB ∠=︒，4BD =，将ABC ∆沿直线AC 翻折后，点B 落在点E 处，那么AED S ∆= ．16．如图，矩形ABCD 中，5AD =，3AB =，把矩形ABCD 绕点A 顺时针旋转，当点D 落在射线CB 上的点P 处时，那么线段DP 的长度等于 ．17．如图，已知矩形ABCD 的边3AB =，9BC =，将其折叠，使得点D 与点B 重合，折叠后折痕EF 的长是 ．18．已知直角梯形的一条底边长为8，一条腰长为32，且它与底边的夹角是45︒，那么另一条底边的长为 ．19．如图，在直角坐标平面内，ABC ∆的顶点(1,0)A -，点B 与点A 关于原点对称，AB BC =，30CAB ∠=︒，将ABC ∆绕点C 旋转，使点A 落在x 轴上的点D 处，点B 落在点E 处，那么BE 所在直线的解析式为 ．20．如图，将矩形ABCD 沿EF 折叠，使点D 落在点B 上，点C 落在点C '处，点P 为折痕EF 上的任一点，过点P 作PG BE ⊥、PH BC ⊥，垂足分别为G 、H ，如果8AD =，3CF =，那么PG PH +的值为 ．21．在梯形ABCD 中，//AD BC ，AB BC ⊥，2AD =，3AB =，6BC =，如果CE 平分BCD ∠交边AB 于点E ，那么DE 的长为 ．22．在ABCD Y 中，5AB =，7BC =，对角线AC 和BD 相交于点O ，如果将点A 绕着点O 顺时针旋转90︒后，点A 恰好落在平行四边形ABCD 的边AD 上，那么AC 的长是 ． 23．如图，在直角梯形ABCD 中，//AD BC ，90B ∠=︒，60BCD ∠=︒，5CD =．将梯形ABCD 绕点A 旋转后得到梯形111AB C D ，其中B 、C 、D 的对应点分别是1B 、1C 、1D ，当点1B 落在边CD 上时，点1D 恰好落在CD 的延长线上，那么1DD 的长为 ．24．已知边长为4的正方形ABCD ，点E 、F 分别在CA 、AC 的延长线上，且45BED BFD ∠=∠=︒，那么四边形EBFD 的面积是 ．25．如图，在矩形ABCD 中，6BC cm =，3CD cm =，将BCD ∆沿BD 翻折，点C 落在点C '处，BC '交AD 于点E ，则AE 的长为 cm ．26．如图，在四边形ABCD 中，90ADC ABC ∠=∠=︒，AD CD =，DP AB ⊥于P ．若四边形ABCD 的面积是18，则DP 的长是 ．27．如图，在ABC ∆中，90ABC ∠=︒，点D 在AB 边上，将ACD ∆沿直线CD 翻折后，点A 落在点E 处，如果四边形BCDE 是平行四边形，那么ADC ∠= ．28．如图，在ABC ∆中，AB AC =，点M 、N 分别在边AB 、AC 上，且MN AC ⊥．将四边形BCNM 沿直线MN 翻折，点B 、C 的对应点分别是点B '、C '，如果四边形ABB C ''是平行四边形，那么BAC ∠=度．29．如图，现有一张矩形纸片ABCD ，其中4AB cm =，6BC cm =，点E 是BC 的中点．将纸片沿直线AE 折叠，使点B 落在梯形AECD 内，记为点B '，那么B '、C 两点之间的距离是 cm ．30．如图，四边形ABCD 为矩形纸片．把纸片ABCD 折叠，使点B 恰好落在CD 边的中点E 处，折痕为AF ．若6CD =，则AF 等于 ．31．如图，已知矩形ABCD ，把矩形沿直线AC 折叠，点B 落在点E 处，连接DE 、BE ，若ABE ∆是等边三角形，则DCEABES S ∆∆= ．32．如图，在矩形ABCD 中，点M 、N 分别在边AD 、BC 上，将四边形CDMN 沿直线MN 翻折后，点D 落在边BC 上的点P ，如果3AB =，9BC =，那么PMN ∆的面积S 的取值范围是 ．33．已知矩形ABCD ，3AB =，33BC =，将其绕点A 旋转，使点B 落在线段AC 上与点B '重合，得到矩形AB C D '''，B C ''交AD 于点E ，则:C ED C B C S S '''=V V ．34．一次函数13y x b =+的图象与x 轴交于点(6,0)A ，与y 轴交于点B ，点C 在y 轴的正半轴上，5BC =，如果四边形ABCD 是等腰梯形，那么点D 的坐标是 ．35．如图，在ABCD Y 中，//AB CD ，//BC AD ，CE AB ⊥，垂足是E ，3AB =，4BC =，60B ∠=︒，把四边形ABCD 沿直线CE 翻折，那么重叠部分的面积为 ．36．如图，已知E 是ABCD Y 的边AB 上一点，将ADE ∆沿直线DE 折叠，点A 恰好落在边BC 上的点F 处，如果BEF ∆的周长为7，CDF ∆的周长为15，那么CF 的长等于 ．37．如图，已知菱形ABCD 中，60B ∠=︒，E 为BC 上一点，且15BAE ∠=︒，将点E 绕着点A 旋转(0180)αα<<度，使得E 点落在边CD 上，则α= 度．38．平行四边形ABCD 中，两条邻边长分别为3和5，BAD ∠与ABC ∠的平分线交于点E ，点F 是CD 的中点，联结EF ，则EF = ．39．如图．已知正方形ABCD ，点E 在边DC 上，3DE =，1EC =．连接AE ，点F 在射线AB 上，且满足CF AE =，则A 、F 两点的距离为 ．40．已知点A 、B 到直线l 的距离分别为4与6，O 是线段AB 的中点，那么点O 到直线l 的距离是 ．参考答案一．填空题（共40小题）1．如果一个平行四边形一个内角的平分线分它的一边为1:2的两部分，那么称这样的平行四边形为“协调平行四边形”，称该边为“协调边”．当“协调边”为3时，它的周长为 8或10 ．【解答】解：如图所示：①当1AE =，2DE =时， Q 四边形ABCD 是平行四边形， 3BC AD ∴==，AB CD =，//AD BC ， AEB CBE ∴∠=∠，BE Q 平分ABC ∠， ABE CBE ∴∠=∠，ABE AEB ∴∠=∠， 1AB AE ∴==，∴平行四边形ABCD 的周长2()8AB AD =+=；②当2AE =，1DE =时， 同理得：2AB AE ==，∴平行四边形ABCD 的周长2()10AB AD =+=；故答案为：8或10．2．如图，在ABC ∆中，4AC AB ==，AH BC ⊥垂足为H ，15AH =，BD 是中线，将CBD ∆沿直线BD 翻折后，点C 落在点E ，那么AE 为6 ．【解答】解：作AM AH ⊥交BD 的延长线于M ，BN MA ⊥于N ，如图所示： 则四边形ANBH 是矩形． 15AH NB ∴==， 4AB AC ==Q ，221BH CH AB AH ∴==-=，2BC ∴=， //AM BC Q ， M DBC ∴∠=∠，在ADM ∆和CDB ∆中，M DBC ADM BDCAD DC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ADM CDB AAS ∴∆≅∆， 2AM BC ∴==，DM BD =，在Rt BMN ∆中，15BN =Q ，3MN =，226BM MN BN ∴=+=，6BD DM ∴== 2BC CD BE DE ====Q ， ∴四边形EBCD 是菱形，EC BD ∴⊥，6BO OD ==EO OC =， AD DC =Q ，//AE OD ∴，26AE OD ==．6．3．如图，菱形ABCD 由6个腰长为2，且全等的等腰梯形镶嵌而成，则菱形的对角线AC 的长为 63 ．【解答】解：根据图形可知2ADC A ∠=∠，又180ADC A ∠+∠=︒， 60A ∴∠=︒，AB AD =Q ，∴梯形的上底边长=腰长2=，∴梯形的下底边长4=（可以利用过上底顶点作腰的平行线得出）， 246AB ∴=+=，32sin 6026632AC AB ∴=︒=⨯⨯=． 故答案为：63．4．如图，在Rt ABC ∆中，90C ∠=︒，1BC =，2AB =，将ABC ∆绕点A 顺时针旋转后得到'AB C '∆（点B 、C 分别与点'B C '、对应）．当BA BB '=时，B C '= 7或1 ．【解答】解：90C ∠=︒Q ，1BC =，2AB =，22413AC AB BC ∴=-=-=1sin 2BC BAC AB ∠==Q 30BAC ∴∠=︒60B ∴∠=︒Q 将ABC ∆绕点A 顺时针旋转后得到ABC '∆AB AB '∴=，且AB BB '=ABB '∴∆是等边三角形，2AB A B BB ''∴===如图，当点B 在AC 下方时，ABB '∆Q 是等边三角形，60ABB '∴∠=︒，且60ABC ∠=︒∴点B ，点C ，点B '三点共线211B C BB BC ''∴=-=-=如图，当点B 在AC 上方时，ABB '∆Q 是等边三角形，60B AB '∴∠=︒，且30BAC ∠=︒90B AC '∴∠=︒22347B C AC B A ''∴=+=+=715．已知四边形ABCD 是矩形，点E 是边AD 的中点，以直线BE 为对称轴将ABE ∆翻折至FBE ∆，联结DF ，那么图中与AEB ∠相等的角的个数为 4 ．【解答】解：由折叠知，BEF AEB ∠=∠，AE FE =，Q 点E 是AD 中点，AE DE ∴=，ED FE ∴=，FDE EFD ∴∠=∠，AEF EDF DFE AEB BEF ∠=∠+∠=∠=∠QAEB EDF ∴∠=∠，//AD BC Q ，AEB CBE ∴∠=∠，EDF EFD BEF AEB CBE ∴∠=∠=∠=∠=∠，故答案为：46．如图，正方形ABCD 的边长为1，把这个正方形绕点A 旋转，得到正方形AB C D '''；且点C '在直线AD 上，那么△C D D ''的面积是 224+或224- ．【解答】解：如图，过点D '作D E AD '⊥，Q 把这个正方形绕点A 旋转，得到正方形AB C D '''；1AD AD CD C D '''∴==== 222AC D A C D ''''∴=+=22D E '∴= 当点C '在AD 延长线上时，1222(21)224C D D S ''-=⨯-⨯=V 当点C '在DA 延长线上时，1222(21)224C D D S ''+=⨯+⨯=V 故答案为：224+或224- 7．已知P 是正方形ABCD 内一点，将ABP ∆绕点B 旋转，使得边BA 与边BC 重合，点P 落在点P '的位置上．如果2PB =，那么PP '的长等于 22 ．【解答】解：如图，Q 四边形ABCD 为正方形，BA BC ∴=，90ABC ∠=︒，ABP ∆Q 绕点B 旋转，使得边BA 与边BC 重合，点P 落在点P '的位置上．2BP BP ∴='=，90PBP ABC ∠'=∠=︒，PBP ∴∆'为等腰直角三角形，222PP PB ∴'==．故答案为22．8．如图，点E 、F 分别在矩形ABCD 的边BC 和CD 上，如果ABE ∆、ECF ∆、FDA ∆的面积分别刚好为6、2、5，那么矩形ABCD 的面积为 20 ．【解答】解：设AB CD a ==，AD BC b ==6ABE S ∆=Q ∴162AB BE ⨯= 12BE a∴= 12EC b a ∴=-2EFC S ∆=Q ∴122EC CF ⨯= 412a CF ab ∴=- 412a DF a ab ∴=-- 5ADF S ∆=Q ∴152AD DF ⨯= 4()1012a b a ab ∴-=- 2()261200ab ab ∴-+=20ab ∴=或6ab =（不合题意舍去）∴矩形ABCD 的面积为20故答案为209．平面直角坐标系xOy 中，点1(A x ，1)y 与2(B x ，2)y ，如果满足120x x +=，120y y -=，其中12x x ≠，则称点A 与点B 互为反等点．已知：点(3,8)C 、(5,8)G -，联结线段CG ，如果在线段CG 上存在两点P ，Q 互为反等点，那么点P 的横坐标P x 的取值范围是33P x -剟，且0p x ≠ ．【解答】解：如图，设C 关于y 轴的对称点(3,8)C '-．由于点P 与点Q 互为反等点．又因为点P ，Q 是线段CG 上的反等点，所以点P 只能在线段CC '上，所点P 的横坐标P x 的取值范围为：33P x -剟，且0p x ≠．故答案为：33P x -剟，且0p x ≠．10．如图，在边长为6的正方形ABCD 中，点M 、N 分别是边AD 、BC 的中点，Q 是边CD 上的一点．联结MN 、BQ ，将BCQ ∆沿着直线BQ 翻折，若点C 恰好与线段MN 上的点P 重合，则PQ 的长等于 23 ．【解答】解：12CBQ PBQ PBC ∠=∠=∠Q ，26BC PB BN ===，3BN =，90BPQ C ∠=∠=︒， cos :1:2PBN BN PB ∴∠==，60PBN ∴∠=︒，30PBQ ∠=︒，3tan 306233PQ PB ∴=︒=⨯=． 故答案为：23．11．我们把对角线与一条底边相等的等腰梯形叫做“完美等腰梯形”，若一个“完美等腰梯形”的对角线长为10，且该梯形的一个内角为75︒，则这个梯形的高等于 5 ．【解答】解：如图，AB CD =，//AD BC ，10BD BC ==，75C ∠=︒．作DH BC ⊥于H ．BD BC =Q ，75BDC C ∴∠=∠=︒，180757530DBC ∴∠=︒-︒-︒=︒， 152DH BD ∴==． 故答案为512．如图放置的两个正方形，大正方形ABCD 边长为a ，小正方形CEFG 边长为()b a b >，M 是BC 边上一个动点，联结AM ，MF ，MF 交CG 于点P ，将ABM ∆绕点A 旋转至ADN ∆，将MEF ∆绕点F 旋转恰好至NGF ∆．给出以下三个结论：①AND MPC ∠=∠； ②ABM NGF ∆≅∆；③22AMFN S a b =+四边形．其中正确的结论是 ①②③ （请填写序号）．【解答】解：如图，连接MN ．Q 将ABM ∆绕点A 旋转至ADN ∆，将MEF ∆绕点F 旋转恰好至NGF ∆，AMN ∴∆，MNF ∆都是等腰直角三角形，45ANM AMN FNM FMN ∴∠=∠=∠=∠=︒，90ANF AMF MAN MFN ∴∠=∠=∠=∠=︒，∴四边形AMFN 是矩形，AN AM =Q ，∴四边形AMFN 是正方形，//AN MF ∴，AND MPC ∴∠=∠，故①正确，//AB NG Q ，//AM NF ，BAM GNF ∴∠=∠，AM FN =Q ，B NGF ∠=∠，()ABM NGF AAS ∴∆≅∆，故②正确，Q 四边形AMFN 是正方形，Q 在Rt ABM ∆中，222a b AM +=，222AMFN S AM a b ∴==+四边形；故③正确；故答案为①②③．13．如图，在Rt ABC ∆中，90C ∠=︒，6AC =，8BC =．D ，E 分别为边BC ，AC 上一点，将ADE ∆沿着直线AD 翻折，点E 落在点F 处，如果DF BC ⊥，AEF ∆是等边三角形，那么AE = 4 ．【解答】解：如图：Q 折叠，EAD FAD ∴∠=∠，DE DF =，DFE DEF ∴∠=∠；AEF ∆Q 是等边三角形，60EAF AEF ∴∠=∠=︒，30EAD FAD ∴∠=∠=︒；在Rt ACD ∆中，6AC =，30CAD ∠=︒，CD ∴=FD BC ⊥Q ，AC BC ⊥，//AC DF ∴，60AEF EFD ∴∠=∠=︒，60FED ∴∠=︒；180AEF DEC DEF ∠+∠+∠=︒Q ，60DEC ∴∠=︒；Q 在Rt DEC ∆中，60DEC ∠=︒，CD =，2EC ∴=；AE AC EC =-Q ，624AE ∴=-=；故答案为：4．14．已知在平面直角坐标系xOy 中，直线142y x =-+与x 轴交于点A 、与y 轴交于点B ，四边形AOBC 是梯形，且对角线AB 平分CAO ∠，那么点C 的坐标为 (5,4) ．【解答】解：142y x =-+Q ， 0y ∴=时，1402x -+=，解得8x =，(8,0)A ∴， 0x =时，4y =，(0,4)B ∴．如图，四边形AOBC 是梯形，且对角线AB 平分CAO ∠，//BC OA ∴，OAB CAB ∠=∠，ABC OAB ∴∠=∠，ABC CAB ∴∠=∠，AC BC ∴=．设点C 的坐标为(,4)x ，则222(8)4x x -+=，解得5x =，∴点C 的坐标为(5,4)．故答案为(5,4)．15．如图，在平行四边形ABCD 中，AC 与BD 相交于点60O AOB ∠=︒，4BD =，将ABC ∆沿直线AC 翻折后，点B 落在点E 处，那么AED S ∆= 3【解答】解：如图连接EO ．60AOB EOA ∠=∠=︒Q ，60EOD ∴∠=︒，OB OE OD ==Q ，EOD ∴∆是等边三角形，60EDO AOB ∴∠=∠=︒， //DE AC ∴，2323ADE EOD S S ∆∆∴=== 316．如图，矩形ABCD 中，5AD =，3AB =，把矩形ABCD 绕点A 顺时针旋转，当点D 落在射线CB 上的点P 处时，那么线段DP 的长度等于 10,310 ．【解答】解：如图，当矩形ABCD 绕点A 顺时针旋转，当点D 落在射线CB 上的点P 处时，则5AP AD ==， 在Rt ABP ∆中，22534BP =-=， 541PC ∴=-=，在Rt PCD ∆中，221310DP =+=；当矩形ABCD 绕点A 顺时针旋转，当点D 落在射线CB 上的点P '处时，则5AP AD '==， 在Rt ABP ∆'中，22534BP '=-=，549P C ∴'=+=，在Rt △P CD '中，2239310DP '=+=；综上所述，线段DP 的长度为10或310．故答案为10或310．17．如图，已知矩形ABCD 的边3AB =，9BC =，将其折叠，使得点D 与点B 重合，折叠后折痕EF 的长是 10 ．【解答】解：设BD 于EF 交于点O ，则O 是BD 的中点．在直角ABD ∆中，2222933BD AB AD =+=+=10cm ；则3102OD = B Q 、D 关于EF 对称，90EOD ∴∠=︒，又Q 矩形ABCD 中，90A ∠=︒，90A EOD ∴∠=∠=︒．在ABD ∆于OED ∆中，90A EOD ∠=∠=︒，ADB ODE ∠=∠，ABD OED ∴∆∆∽． ∴OE OD AB AD =， 102OD OE AB cm AD ∴==g ． 210EF OE cm ∴==．18．已知直角梯形的一条底边长为8，一条腰长为32，且它与底边的夹角是45︒，那么另一条底边的长为 5或11 ．【解答】解：①当AB 与下底的夹角为45︒时（上图），作AM BC ⊥于M ．则四边形AMCD 是矩形，32AB =Q ，易知3AM BM ==，5AD CM BC BM ∴==-=．②下图中，当45A ∠=︒，32AB =，8BC =时，同法可得3811AD AM DM =+=+=， ③如图3，当45D ∠=︒，32AB =8AD =，同法可得，832BC =-④如图3，当45C ∠=︒，32AB =8AD =，同法可得，832BC =+故答案为5或11或832-832+19．如图，在直角坐标平面内，ABC ∆的顶点(1,0)A -，点B 与点A 关于原点对称，AB BC =，30CAB ∠=︒，将ABC ∆绕点C 旋转，使点A 落在x 轴上的点D 处，点B 落在点E 处，那么BE 所在直线的解析式为 3333y x =- ．【解答】解：如图，过点C 作CF x ⊥轴于点F ，ABC ∆Q 的顶点(1,0)A -，点B 与点A 关于原点对称，(1,0)B ∴，2AB ∴=．AB BC =Q ，30CAB ∠=︒，2BC AB ∴==，3sin 6023CF BC ∴=︒==g ，1cos30212BF BC =︒=⨯=g ， 3)C ∴．Q 将ABC ∆绕点C 旋转，使点A 落在x 轴上的点D 处，点B 落在点E 处， 2AB CE ∴==，(4,3)E∴．设直线BE的解析式为(0)y kx b k=+≠，∴43k bk b+=⎧⎪⎨+=⎪⎩，解得3333kb⎧=⎪⎪⎨⎪=-⎪⎩，BE∴所在直线的解析式为：3333y x=-．故答案为：3333y x=-．20．如图，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点C'处，点P为折痕EF 上的任一点，过点P作PG BE⊥、PH BC⊥，垂足分别为G、H，如果8AD=，3CF=，那么PG PH+的值为4．【解答】解：过点E作EQ BC⊥，垂足为Q，如图，Q四边形ABCD是矩形，AD BC∴=，90C ADC∠=∠=︒．8AD=Q，3CF=，5BF BC CF AD CF∴=-=-=．由折叠可得：DF BF=，BEF DEF∠=∠．5DF∴=．90C∠=︒Q，2222534DC DF CF∴=-=-=．EQ BC ⊥Q ，90C ADC ∠=∠=︒，90EQC C ADC ∴∠=︒=∠=∠，∴四边形EQCD 是矩形，4EQ DC ∴==．//AD BC Q ，DEF EFB ∴∠=∠．BEF DEF ∠=∠Q ，BEF EFB ∴∠=∠，BE BF ∴=．由问题情境中的结论可得：PG PH EQ +=，4PG PH ∴+=，PG PH ∴+的值为4．故答案是：4．21．在梯形ABCD 中，//AD BC ，AB BC ⊥，2AD =，3AB =，6BC =，如果CE 平分BCD ∠交边AB 于点E ，那么DE 的长为 5 ．【解答】解：方法一：作DH BC ⊥于点H ，延长CE 交DA 的延长线于点F ， 2AD =Q ，3AB =，6BC =，624CH ∴=-=，3DH =，5CD ∴=，CE Q 平分BCD ∠交边AB 于点E ，//AD BC ，AB BC ⊥，DCF BDF DFC ∴∠=∠=∠，5DF DC ∴==，3AF∴=，FAE CBE∴∆∆∽，∴AF AE BC BE=，即36AEBE =，3 AE BE+=Q，解得，1AE=，2222125DE AE AD∴=+=+=，故答案为：5．方法二：作DF BC⊥于点F，作EG CD⊥交CD的延长线于点G，如右图所示，由已知可得，2AD BF==，3AB DF==，5CD∴=，CEQ平分BCD∠交边AB于点E，EG EB∴=，设AE a=，则3EB a=-，3EG a∴=-，∴()2222AD BC AB AD AE BC EB CD EG +=++g g g g，即(26)326(3)5(3)2222a a a+⨯--=++，解得，1a=，即1AE=，2222125 DE AE AD∴=+=+=，故答案为：5．22．在ABCD Y 中，5AB =，7BC =，对角线AC 和BD 相交于点O ，如果将点A 绕着点O 顺时针旋转90︒后，点A 恰好落在平行四边形ABCD 的边AD 上，那么AC 的长是 42或32 ．【解答】解：如图，过O 点作OE AD ⊥于E ，过C 点作CF AD ⊥于F ， Q 将点A 绕着点O 顺时针旋转90︒后，点A 恰好落在平行四边形ABCD 的边AD 上， AOA ∴∆'是等腰直角三角形，∴△AA C '是等腰直角三角形，设AA x '=，则CF x =，7DF x =-，在Rt CDF ∆中，222(7)5x x +-=，解得14x =，23x =，在Rt CFA ∆中，42AC =或32．故答案为：42或32．23．如图，在直角梯形ABCD 中，//AD BC ，90B ∠=︒，60BCD ∠=︒，5CD =．将梯形ABCD 绕点A 旋转后得到梯形111AB C D ，其中B 、C 、D 的对应点分别是1B 、1C 、1D ，当点1B 落在边CD 上时，点1D 恰好落在CD 的延长线上，那么1DD 的长为 52．【解答】解：如图，将梯形ABCD 绕点A 旋转后得到梯形111AB C D ，连接BD ， 由旋转得：1AD AD =，1AB AB =，11DAD BAB ∠=∠，11DAB D AB ∴∠=∠，且13∠=∠，在DAB ∆和△11D AB 中，1111AD AD DAB D AB AB AB =⎧⎪∠=∠⎨⎪=⎩， DAB ∴∆≅△11()D AB SAS ，12∴∠=∠，23∴∠=∠，//AD BC Q ，24∴∠=∠，设1234α∠=∠=∠=∠=，则51804120C α∠=︒-∠-∠=︒-， 235180∠+∠+∠=︒Q ，120180ααα∴++︒-=︒，解得60α=︒，123460∴∠=∠=∠=∠=︒，1ADD ∴∆、BCD ∆都是等边三角形，5BD CD ∴==，30ABD ∠=︒，Rt ABD ∴∆中，1522AD BD ==， 152DD AD ∴==． 故答案为：5224．已知边长为4的正方形ABCD，点E、F分别在CA、AC的延长线上，且45BED BFD∠=∠=︒，那么四边形EBFD的面积是16162+．【解答】解：如图连接BD交AC于O．Q四边形ABCD是正方形，4AB BC CD AD∴====，45CAD CAB∠=∠=︒，135EAD EAB∴∠=∠=︒，在EAB∆和EAD∆中，EA EAEAB EADAB AD=⎧⎪∠=∠⎨⎪=⎩，EAB EAD∴∆≅∆，22.5AEB AED∴∠=∠=︒，EB ED=，18022.5ADE EAD AED∴∠=︒-∠-∠=︒，22.5AED ADE∴∠=∠=︒，4AE AD∴==，同理证明22.5DFC∠=︒，FD FB=，DEF DFE∴∠=∠，DE DF∴=，ED EB FB FD∴===，∴四边形EBFD的面积1142(428)16222BD EF==⨯+=+g g．故答案为16162+． 25．如图，在矩形ABCD 中，6BC cm =，3CD cm =，将BCD ∆沿BD 翻折，点C 落在点C '处，BC '交AD 于点E ，则AE 的长为 94cm ．【解答】解：BCD ∆Q 沿BD 翻折，点C 落在点C '处，BCD EBD ∴∠=∠，Q 矩形的对边//AD BC ，BCD ADB ∴∠=∠，EBD ADB ∴∠=∠，BE DE ∴=，在矩形ABCD 中，3AB CD cm ==，6AD BC cm ==，设AE xcm =，则6BE DE AD AE x ==-=-，在Rt ABE ∆中，由勾股定理得，222AB AE BE +=，即2223(6)x x +=-，解得94x =， 即94AE cm =． 故答案为：94． 26．如图，在四边形ABCD 中，90ADC ABC ∠=∠=︒，AD CD =，DP AB ⊥于P ．若四边形ABCD 的面积是18，则DP 的长是 32 ．【解答】解：如图，过点D 作DE DP ⊥交BC 的延长线于E ，90ADC ABC ∠=∠=︒Q ，∴四边形DPBE 是矩形，90CDE CDP ∠+∠=︒Q ，90ADC ∠=︒，90ADP CDP ∴∠+∠=︒，ADP CDE ∴∠=∠，DP AB ⊥Q ，90APD ∴∠=︒，90APD E ∴∠=∠=︒，在ADP ∆和CDE ∆中，ADP CDE APD EAD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ()ADP CDE AAS ∴∆≅∆，DE DP ∴=，四边形ABCD 的面积=四边形DPBE 的面积18=， ∴矩形DPBE 是正方形，1832DP∴==．故答案为：32．27．如图，在ABC ∆中，90ABC ∠=︒，点D 在AB 边上，将ACD ∆沿直线CD 翻折后，点A 落在点E 处，如果四边形BCDE 是平行四边形，那么ADC ∠= 135︒ ．【解答】解：延长CD 到点F ，如图所示．Q 四边形BCDE 是平行四边形，//BC DE ∴，90BDE ∴∠=︒，90ADE ∴∠=︒．Q 将ACD ∆沿直线CD 翻折后，点A 落在点E 处， 1452ADF EDF ADE ∴∠=∠=∠=︒， 45BDC ADF ∴∠=∠=︒，180135ADC BDC ∴∠=︒-∠=︒．故答案为：135︒．28．如图，在ABC ∆中，AB AC =，点M 、N 分别在边AB 、AC 上，且MN AC ⊥．将四边形BCNM 沿直线MN 翻折，点B 、C 的对应点分别是点B '、C '，如果四边形ABB C ''是平行四边形，那么BAC ∠= 60 度．【解答】解：如图，Q 四边形MNC B ''是由四边形MNCB 翻折得到，C C ∴∠=∠'，//AB B C ''Q ，C BAC ∴∠=∠，AB BC ∴=，AB AC =Q ，AB AC BC ∴==，60BAC ∴∠=︒，故答案为60．29．如图，现有一张矩形纸片ABCD ，其中4AB cm =，6BC cm =，点E 是BC 的中点．将纸片沿直线AE 折叠，使点B 落在梯形AECD 内，记为点B '，那么B '、C 两点之间的距离是 185cm ．【解答】解：如图所示：过点B '作B F BC '⊥，垂足为F ，连接B C '．Q 点E 是BC 的中点，116322BE BC ∴==⨯=． 在Rt ABE ∆中，2222345AE AB BE =+=+=．由射影定理可知；2OE AE BE =g ，95OE ∴=． 由翻折的性质可知；BO AE ⊥．∴1122AB BE AE OB =g g ． 125OB ∴=． 245BB ∴'=． OBE FBB ∠=∠'Q ，BOE BFB ∠=∠'，BOE BFB ∴∆∆'∽． ∴OE BE OB B F BB BF ==''，即912355245B F BF =='． 解得：7225B F '=，9625BF =． 5425FC ∴=． 在Rt △B FC '中，2222725418()()25255B C B F FC '='+=+=． 故答案为：185． 30．如图，四边形ABCD 为矩形纸片．把纸片ABCD 折叠，使点B 恰好落在CD 边的中点E 处，折痕为AF ．若6CD =，则AF 等于 43 ．【解答】解：由折叠的性质得BF EF =，AE AB =，因为6CD =，E 为CD 中点，故3ED =，又因为6AE AB CD ===，90D ∠=︒，所以30EAD ∠=︒，则1(9030)302FAE ∠=︒-︒=︒， 设FE x =，则2AF x =，在AEF ∆中，根据勾股定理，222(2)6x x =+，212x =，13x =，23x =-．323AF ==．故答案为：43．31．如图，已知矩形ABCD ，把矩形沿直线AC 折叠，点B 落在点E 处，连接DE 、BE ，若ABE ∆是等边三角形，则DCE ABE S S ∆∆= 13．【解答】解：过E 作EM AB ⊥于M ，交DC 于N ，Q 四边形ABCD 是矩形，DC AB ∴=，//DC AB ，90ABC ∠=︒，MN BC ∴=，EN DC ⊥，Q 延AC 折叠B 和E 重合，AEB ∆是等边三角形，30EAC BAC ∴∠=∠=︒，设2AB AE BE a ===，则2333BC a ==， 即233MN a =， ABE ∆Q 是等边三角形，EM AB ⊥，AM a ∴=，由勾股定理得：22(2)3EM a a a =-=，DCE ∴∆的面积是211232(33)223DC EN a a a ⨯⨯=⨯⨯=， ABE ∆的面积是21123322AB EM a a a ⨯=⨯=，∴2231333DCEABEaSS a∆∆==，故答案为：13．32．如图，在矩形ABCD中，点M、N分别在边AD、BC上，将四边形CDMN沿直线MN 翻折后，点D落在边BC上的点P，如果3AB=，9BC=，那么PMN∆的面积S的取值范围是91522S剟．【解答】解：如图1中，当点N与点C重合时，四边形PCDM是正方形，此时PMN∆的面积最小，最小值为92．如图2中，当点P与B重合时，三角形PMN的面积最大，设BM DM x==，在Rt ABM∆中，2223(9)x x=+-，3x∴=，152PMNS∆∴=，∴91522S剟．故答案为91522S剟．33．已知矩形ABCD，3AB=，33BC=将其绕点A旋转，使点B落在线段AC上与点B'重合，得到矩形AB C D'''，B C''交AD于点E，则:C ED C B CS S'''=V V1:3．【解答】解：如图，Q 四边形ABCD 是矩形，90ABC ∴∠=︒，3tan AB ACB BC ∴∠== 30ACB ∴∠=︒，60BAC ∴∠=︒，2AC AB =，AB AB ='Q ，B ∴'是AC 与BD 的交点，易证ABB ∆'，CDB ∆'都是等边三角形，C 、D 、C '共线，2AE EC EB ='='，设DEB S ∆'的面积S =，则2EDC S S ∆'=，6CBC S S ∆'=，:1:3C ED C B C S S '''∴=V V ，故答案为1:3．34．一次函数13y x b =+的图象与x 轴交于点(6,0)A ，与y 轴交于点B ，点C 在y 轴的正半轴上，5BC =，如果四边形ABCD 是等腰梯形，那么点D 的坐标是 (6,1)或(3,4) ．【解答】解：把(6,0)A 代入13y x b =+得：20b +=，解得：2b =-， 则一次函数的解析式是：123y x =-． 在123y x =-中，令0x =，则2y =-．则B 的坐标是：(0,2)-； 5BC =Q ，523OC BC OB ∴=-=-=，C ∴的坐标是：(0,3)，①当//AD BC 时，作DE BC ⊥于点E ．Q 四边形ABCD 是等腰梯形，2CE OB ∴==，51AD OE CE OB ∴==--=．则D 的坐标是：(6,1)．②当//CD AB '时，直线CD '的解析式为133y x =+，设1(,3)3D m m +， 5BC AD ='=Q ，2221(6)(3)53m m ∴-++=， 解得3m =或6（舍弃），(3,4)D ∴'，故答案为(6,1)或(3,4)．35．如图，在ABCD Y 中，//AB CD ，//BC AD ，CE AB ⊥，垂足是E ，3AB =，4BC =，60B ∠=︒，把四边形ABCD 沿直线CE 翻折，那么重叠部分的面积为 533．【解答】解：将BCE ∆沿CE 翻折得到ECF ∆，重叠部分就是四边形AECH ．作HN BF ⊥于N ．在RT BCE ∆中，90BEC ∠=︒Q ，4BC =，60B ∠=︒，30BCE ∴∠=︒，122BE BC ==，23EC =， 2BE EF ∴==，1AF AE ==，//CD AF Q ，::1:2FH HC AF CD ∴==//NH CE Q ， ∴14NH FH EC FC ==， 32NH ∴=， 3731122312224ECF AHF AECH S S S ∆∆∴=-=⋅⋅-⋅⋅=四边形． 故答案为734．36．如图，已知E 是ABCD Y 的边AB 上一点，将ADE ∆沿直线DE 折叠，点A 恰好落在边BC 上的点F 处，如果BEF ∆的周长为7，CDF ∆的周长为15，那么CF 的长等于 4 ．【解答】解：由折叠性得AB EF =，DF AD =，BEF ∆Q 的周长为7，CDF ∆的周长为15，BEF ∴∆的周长7EF BE BF AB BF =++=+=，CDF ∆的周长15DC DF FC DC AD FC =++=++=，BEF ∴∆的周长CDF +∆的周长ABCD =Y 的周长22=，11AD DC ∴+=，CF CDF ∴=∆的周长()15114AD DC -+=-=．故答案为：4．37．如图，已知菱形ABCD 中，60B ∠=︒，E 为BC 上一点，且15BAE ∠=︒，将点E 绕着点A 旋转(0180)αα<<度，使得E 点落在边CD 上，则α= 60度或70 度．【解答】解：连接AC ．Q 菱形ABCD 中，60ABC ∠=︒，ABC ∴∆是等边三角形，60BAC ACB ∴∠=∠=︒，60ACD ∴∠=︒．本题有两种情况：①如图，将ABE ∆绕点A 逆时针旋转，使点B 与点C 重合，点E 与点1E 重合，此时1ABE ABE ∆≅∆，1AE AE =，旋转角60BAC α=∠=︒；②60BAC ∠=︒Q ，25BAE ∠=︒，35EAC ∴∠=︒．如图，将线段AE 绕点A 逆时针旋转70︒，使点E 到点2E 的位置， 此时AEC ∆≅△2AE C ，2AE AE =，旋转角270EAE α=∠=︒．综上可知，符合条件的旋转角α的度数为60︒或70︒． 故答案是：60度或70．38．平行四边形ABCD 中，两条邻边长分别为3和5，BAD ∠与ABC ∠的平分线交于点E ，点F 是CD 的中点，联结EF ，则EF = 3.5或0.5 ．【解答】解：①如图1中，当3AB =，5BC =时，延长AE 交BC 于M ．//AD BC Q ，DAM AMB ∴∠=∠，DAM BAM ∠=∠Q ，BAM AMB ∴∠=∠，3AB BM ∴==，2CM BC BM ∴=-=，180DAB ABC ∠+∠=︒Q ， 119022EAB EBA DAB ABC ∴∠+∠=∠+∠=︒， 90AEB ∴∠=︒， BE AM ∴⊥，BA BM =Q ，AE EM ∴=，DF CF =Q ，3.52AD CM EF +∴==②如图2中，当5AB =，3BC =时，同法可证，AE EM =，2CM BM BC AB BC =-=-=，可得1()0.52EF AD CM =-=， 综上所述，EF 的长为3.5或0.5．39．如图．已知正方形ABCD ，点E 在边DC 上，3DE =，1EC =．连接AE ，点F 在射线AB 上，且满足CF AE =，则A 、F 两点的距离为 1或7 ．【解答】解：如图：3DE =Q ，1EC =，∴正方形ABCD 的边长为4，CF AE =Q ，ADE CBF ∴∆≅∆，3BF DE ∴==，Q 点F 在射线AB 上，所以分两种情况：431AF AB BF ∴=-=-=，或437AF AB BF =+=+=．故答案为：1或7．40．已知点A 、B 到直线l 的距离分别为4与6，O 是线段AB 的中点，那么点O 到直线l 的距离是 5或1 ．【解答】解：如图一，作AD l ⊥于D ，BC l ⊥于C ，OF l ⊥于F ．AD l ⊥Q 于D ，BC l ⊥，OF l ⊥于F ，////AD OF BC ∴，ABCD ∴是直角梯形，O Q 是AB 的中点，4AD =，6BC =，DF CF ∴=，11()(46)522OF AD BC ∴=+=+=．如图二，作AD l ⊥于D ，BC l ⊥于C ，OF l ⊥于F ． AD l ⊥Q 于D ，BC l ⊥，OF l ⊥于F ，////AD OF BC ∴，连接DO 并延长，交BC 于G ，则易得AOD BOG ∆≅∆，4BG AD ∴==，DO GO =， 又6BC =Q ， 642CG ∴=-=， //OF CG Q ， DF CF ∴=， 112OF CG ∴==， 故答案为：5或1．。

八年级期末复习压轴题讲义1、 已知一次函数421+-=x y 的图像与x 轴、y 轴分别相交于点A 、B ． 梯形AOBC 的边AC = 5． （1）求点C 的坐标；（2）如果点A 、C 在一次函数y k x b =+（k 、b 为常数，且k<0）的图像上，求这个一次函数的解析式．2、 如图，在正方形ABCD 中，点E 在边AB 上（点E 与点A 、B 不重合），过点E 作FG ⊥DE ，FG 与边BC 相交于点F ，与边DA 的延长线相交于点G ．（1）由几个不同的位置，分别测量BF 、AG 、AE 的长，从中你能发现BF 、AG 、AE 的数量之间具有怎样的关系？并证明你所得到的结论；（2）联结DF ，如果正方形的边长为2，设AE=x ，△DFG 的面积为y ，求y 与x 之间的函数解析式，并写出函数的定义域； （3）如果正方形的边长为2，FG 的长为25，求点C 到直线DE 的距离．（供操作实验用）（供证明计算用）DAD AB3、如图，已知点E 是矩形ABCD 的边CB 延长线上一点，且CE CA =，联结AE ，过点C 作CF AE ⊥，垂足为点F ，联结BF 、FD . （1）求证：FBC ∆≌FAD ∆； （2）联结BD ，若35FB BD =，且10AC =，求FC 的值.4、已知：梯形ABCD 中，AD ∥BC ，M 、N 分别是BD 、AC 的中点（如图2）. 求证：（1）MN ∥BC ；（2）)(21AD BC MN -=.ABCDM N图2FEDCBA90，AD∥BC，BC>AD，AB=8cm，BC=18cm，CD=10 cm，点P从点4、在梯形ABCD中，∠ABC=B开始沿BC边向终点C以每秒3cm的速度移动，点Q从点D开始沿DA边向终点A以每秒2cm 的速度移动，设运动时间为t秒.（1）求四边形ABPQ为矩形时t的值；（2）若题设中的“BC=18cm”改变为“BC=k cm”，其它条件都不变，要使四边形PCDQ是等腰梯形，求t与k的函数关系式，并写出k的取值范围；（3）在移动的过程中，是否存在t使P、Q两点的距离为10cm ,若存在求t的值. 若不存在请说明理由？B5、已知：如图，AM 是△ABC 的中线，D 是线段AM 的中点，AM=AC ，AE ∥BC ． 求证：四边形EBCA 是等腰梯形．6、已知：如图，在菱形ABCD 中，AB=4，∠B=60°，点P 是射线BC 上的一个动点，∠PAQ=60°，交射线CD 于点Q ，设点P 到点B 的距离为x ，PQ=y ． （1）求证：△APQ 是等边三角形；（2）求y 关于x 的函数解析式，并写出它的定义域； （3）如果PD ⊥AQ ，求BP 的值．BCD7、如图，梯形ABCD中，AD//BC，BC=3AD，M、N为底边BC的三等分点，联结AM，DN。

一、 因动点产生的相似三角形问题例1如图1，将抛物线2y x =-平移，平移后的抛物线与x 轴交于点A （1-，0）和B （3，0），与y 轴交于点C ，顶点为D 。

（1）求平移后的抛物线的表达式和点D 的坐标； （2）∠ACB 和∠ABD 是否相等？请证明你的结论；（3）点P 在平移后的抛物线的对称轴上，且△CDP 与△ABC 相似，求点P 的坐标。

图1第十五讲 压轴题复习如图1，在平面直角坐标系xOy 中，顶点为M 的抛物线2(0y ax bx a =+>）经过点A 和x 轴正半轴上的点B ，AO OB == 2，0120AOB ∠=．（1）求这条抛物线的表达式； （2）联结OM ，求AOM ∠的大小；（3）如果点C 在x 轴上，且△ABC 与△AOM 相似，求点C 的坐标．图1在平面直角坐标系中，一个二次函数的图象经过(1,0)(3,0)、两点。

A B（1）写出这个二次函数图象的对称轴；（2）设这个二次函数图象的顶点为D，与y轴交于点C，它的对称轴与x轴交于点E，连接AC、DE和DB，当AOC∆相似时，求这个二次函数的表达式。

∆与DEB例4如图1，点A在x轴上，OA＝4，将线段OA绕点O顺时针旋转120°至OB的位置．（1）求点B的坐标；（2）求经过A、O、B的抛物线的解析式；（3）在此抛物线的对称轴上，是否存在点P，使得以点P、O、B为顶点的三角形是等腰三角形？若存在，求点P的坐标；若不存在，请说明理由．图1例5如图1，已知点A （2，0），点B 在y 轴正半轴上，且OA OB 21=．将点B 绕点A 顺时针方向旋转 90至点C ．旋转前后的点B 和点C 都在抛物线c bx x y ++-=265上．（1）求点B 、C 的坐标； （2）求该抛物线的表达式；（3）联结AC ，该抛物线上是否存在异于点B 的点D ，使点D 与AC 构成以AC 为直角边的等腰直角三角形？如果存在，求出所有符合条件的D 点坐标，如果不存在，请说明理由．图1例6如图1，在平面直角坐标系xOy 中，A 、B 为x 轴上两点，C 、D 为y 轴上的两点，经过 点A 、C 、B 的抛物线的一部分C 1与经过点A 、D 、B 的抛物线的一部分C 2组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．已知点C 的坐标为（0，23-），点M 是抛物线C 2：m mx mx y 322--=（m ＜0）的顶点． （1）求A 、B 两点的坐标； （2）“蛋线”在第四象限上是否存在一点P ，使得△PBC 的面积最大？若存在，求出△PBC 面积的最大值；若不存在，请说明理由；（3）当△BDM 为直角三角形时，求m 的值．图1四、因动点产生的平行四边形问题例7如图1，抛物线254y x bx c =-++与y 轴交于点A (0,1)，过点A 的直线与抛物线交于另一点B 5(3,)2，过点B 作BC x ⊥轴，垂足为C ．（1）求抛物线的表达式；（2）点P 是x 轴正半轴上的一动点，过点P 作PN x ⊥轴，交直线AB 于点M ，交抛物线于点N ，设OP 的长度为m ．①当点P 在线段OC 上（不与点O 、C 重合）时，试用含m 的代数式表示线段PM 的长度；②联结,CM BN ，当m 为何值时，四边形BCMN 为平行四边形？如图1，点A （2，6）和点B （点B 在点A 的右侧）在反比例函数的图像上，点C 在y 轴上，BC //x 轴，2tan =∠ACB ，二次函数的图像经过A 、B 、C 三点． （1）求反比例函数和二次函数的解析式；（2）如果点D 在x 轴的正半轴上，点E 在反比例函数的图像上，四边形ACDE 是平行四边形，求边CD 的长．图1如图1，已知抛物线y＝－x2＋bx＋c经过A(0, 1)、B(4, 3)两点．（1）求抛物线的解析式；（2）求tan∠ABO的值；（3）过点B作BC⊥x轴，垂足为C，在对称轴的左侧且平行于y轴的直线交线段AB于点N，交抛物线于点M，若四边形MNCB为平行四边形，求点M的坐标．图1五、因动点产生的梯形问题例10如图1，已知二次函数mx x y 22+-=的图像经过点B （1,2），与x 轴的另一个交点为A ，点B 关于抛物线对称轴的对称点为C ，过点B 作直线BM ⊥x 轴垂足为点M ． （1）求二次函数的解析式； （2）在直线BM 上有点P （1，23），联结CP 和CA ，判断直线CP 与直线CA 的位置关系， 并说明理由；（3）在（2）的条件下，在坐标轴上是否存在点E ，使得以A 、C 、P 、E 为顶点的四边形为直角梯形，若存在，求出所有满足条件的点E 的坐标；若不存在，请说明理由。

如图1，在平面直角坐标系中，图形W 在坐标轴上的投影长度定义如下，设点P （1x ，1y ），Q （2x ，2y ）是图形W 上的任意两点，若21x x -的最大值为m,则图形W 在x 轴的投影长度x l =m,若21y y -的最大值为n,则图形W 在y 轴的投影长度y l =n,如图1,图形W 在x 轴的投影x l =13-=2,在y 轴的投影长度y l =04-=4.(1)已知点A （3,3），B （4,4），如图2所示，若图形W 为△OAB ，则x l =_______，y l =_______； (2)将△OAB 绕着点O 顺时针旋转45°，得到△OA’B’，若图形W 为△OA’B’，求图形W 在坐标轴上的投影长度；(3)已知点C （4,0），点D 在直线y=-2x+6上，若图形W 为△OCD,当x l =y l 时，求D 的坐标。

解析：如图1，G是边长为2的正方形ABCD的边长AD延长线上的一点，且DG=AD，联结CG，动解析：如图1，P为正方形ABCD的边BC,P为正方形ABCD边BC上的一点,（P与B、C不重合），连接A P，过点B作BQ⊥AP交CD于点Q，将△BQC沿BQ所在的直线对折得到△BQC′，延长QC′交BA的延长线于点M．（1）试探究AP与BQ的数量关系，并证明你的结论；（2）当AB=3，BP=2PC，求QM的长；（3）当BP=m，PC=n时，求AM的长解析：如图1，在平面直角坐标系中，直线y=x-2与x轴、y轴分别相交于于A、B两点，点C在y 轴正半轴，且OC=2OB.(1)求线段BC 的长度；(2)如果点D在直线AB上，且以B、C、D、E为顶点的四边形为菱形，请直接写出E点坐标.解析：已知：在正方形ABCD中，AB=2，点P是射线AB上的一点，联结PC、PD，点E、F分别是AB和PC的中点，联结EF交PD于点Q．（1）如图1，当点P与点B重合时，△QPE的形状是_____;（2）如图2，当点P在AB的延长线上时，设BP=x，EF=y，求y关于x的函数关系式，并写出定义域；（3）当点Q在边BC上时，求BP的长．解析：甲、乙两组工人同时开始加工某种零件，乙组在工作2小时后停产1小时更换设备，更换设备后，乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)之间的函数图象如图所示.(1)求甲组每小时加工零件_____件；更换设备前，乙每小时加工零件_____件；(2)更换设备后，乙每小时加工零件_____件，a=_____件；(3)更换设备后，乙加工零件的数量y(件)与时间x(时)之间的函数关系为__________ (不写定义域)；(4)甲、乙两组加工出的零件合在一起装箱，每够300件装一箱，零件装箱的时间忽略不计，则经过______小时恰好装满第1箱.解析：2016年上海市虹口区初二下学期期末第27题如图1，在平面直角坐标系中，点A(4，3)，B(6，0)，边AB上有一点P（m，1）,点M、N 分别在边OB、OA上，联结MN,MN∥AB，联结PM、PN、AM.（1）求直线AB解析式及P的坐标;（2）当AC=CM 时，求M的坐标;（3）在（2）的条件下，Q在AB上， S△ANQ =S△ANC ，请求出点Q的坐标.解析：如图1，一次函数y=kx+3的图像与y轴交于点A,与正比例函数y=x的图像交于点M，且S△AOM=18.(1)求一次函数解析式；(2) 如果B在y轴上，且位于点A下方，点C在正比例函数y=x的图像上，点D在一次函数的图像上，且四边形ABCD是菱形，求C点坐标.解析：如图1,在菱形ABCD中， ADC=60°，AB=6，对角线AC、BD相交于点O，点E是对角线BD 上的一动点，联结AE，以AE为边作等边三角形AEF，使得点F和点D在AE同侧.(1) 如图1,当点F恰好也在对角线BD上时，请判断EF和DF的数量关系，并证明你的结论；(2) 如图2，当点E在线段BO上，且点F不在对角线BD上时，联结 DF,（1）中的结论是否成立?若成立，请结合图2给出证明，若不成立，请直接写出新的结论；(3) 当点E在线段OD上移动的过程中，若以A、O、E、F为顶点的四边形时梯形，请直接写出OE的长度.解析：解析：。

沪教版八年级上册压轴题数学数学模拟试题一、压轴题1．如图，△ABC 是等边三角形，△ADC 与△ABC 关于直线AC 对称，AE 与CD 垂直交BC 的延长线于点E ，∠EAF ＝45°，且AF 与AB 在AE 的两侧，EF ⊥AF ．（1）依题意补全图形．（2）①在AE 上找一点P ，使点P 到点B ，点C 的距离和最短；②求证：点D 到AF ，EF 的距离相等．2．如图，Rt ACB △中，90ACB ∠=︒，AC BC =，E 点为射线CB 上一动点，连结AE ，作AF AE ⊥且AF AE =．（1）如图1，过F 点作FD AC ⊥交AC 于D 点，求证：FD BC =；（2）如图2，连结BF 交AC 于G 点，若3AG =，1CG =，求证：E 点为BC 中点． （3）当E 点在射线CB 上，连结BF 与直线AC 交于G 点，若4BC =，3BE =，则AG CG=______．（直接写出结果） 3．在Rt ABC 中，90ACB ∠=︒，30A ∠=︒，BD 是ABC 的角平分线，DE AB ⊥于点E .（1）如图1，连接EC ，求证：EBC 是等边三角形；（2）如图2，点M 是线段CD 上的一点（不与点,C D 重合），以BM 为一边，在BM 下方作60BMG ∠=︒，MG 交DE 延长线于点G .求证：AD DG MD =+；（3）如图3，点N 是线段AD 上的点，以BN 为一边，在BN 的下方作60BNG ∠=︒，NG 交DE 延长线于点G .直接写出ND ，DG 与AD 数量之间的关系.4．如图1，在等边△ABC 中，E 、D 两点分别在边AB 、BC 上，BE =CD ，AD 、CE 相交于点F ．（1）求∠AFE 的度数；（2）过点A 作AH ⊥CE 于H ，求证：2FH +FD =CE ；（3）如图2，延长CE 至点P ，连接BP ，∠BPC =30°，且CF =29CP ，求PF AF的值． （提示：可以过点A 作∠KAF =60°，AK 交PC 于点K ，连接KB ）5．阅读下面材料，完成(1)-(3)题．数学课上，老师出示了这样一道题：如图1，已知等腰△ABC 中，AB ＝AC ，AD 为BC 边上的中线，以AB 为边向AB 左侧作等边△ABE ，直线CE 与直线AD 交于点F ．请探究线段EF 、AF 、DF 之间的数量关系，并证明． 同学们经过思考后，交流了自已的想法：小明：“通过观察和度量，发现∠DFC 的度数可以求出来．”小强：“通过观察和度量，发现线段DF 和CF 之间存在某种数量关系．”小伟：“通过做辅助线构造全等三角形，就可以将问题解决．”......老师：“若以AB 为边向AB 右侧作等边△ABE ，其它条件均不改变，请在图2中补全图形,探究线段EF 、AF 、DF 三者的数量关系，并证明你的结论．”（1）求∠DFC 的度数；（2）在图1中探究线段EF 、AF 、DF 之间的数量关系，并证明；（3）在图2中补全图形，探究线段EF 、AF 、DF 之间的数量关系，并证明．6．学习了三角形全等的判定方法（即“SAS ”、“ASA ”、“AAS ”、“SSS ”）和直角三角形全等的判定方法（即“HL ”）后，我们继续对“两个三角形满足两边的其中一边的对角对应相等”的情形进行研究．（初步思考）我们不妨将问题用符号语言表示为：在△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，然后，对∠B 进行分类，可分为“∠B 是直角、钝角、锐角”三种情况进行探究．（深入探究）第一种情况：当∠B 是直角时，△ABC ≌△DEF ．（1）如图①，在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ＝90°，根据______，可以知道Rt △ABC ≌Rt △DEF ．第二种情况：当∠B 是钝角时，△ABC ≌△DEF ．（2）如图②，在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，且∠B 、∠E 都是钝角．求证：△ABC ≌△DEF ．第三种情况：当∠B 是锐角时，△ABC 和△DEF 不一定全等．（3）在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，且∠B 、∠E 都是锐角．请你用直尺在图③中作出△DEF ，使△DEF 和△ABC 不全等，并作简要说明．7．如图，若要判定纸带两条边线a ，b 是否互相平行，我们可以采用将纸条沿AB 折叠的方式来进行探究．（1）如图1，展开后，测得12∠=∠，则可判定a//b ，请写出判定的依据_________； （2）如图2，若要使a//b ，则1∠与2∠应该满足的关系是_________；（3）如图3，纸带两条边线a ，b 互相平行，折叠后的边线b 与a 交于点C ，若将纸带沿11A B （1A ，1B 分别在边线a ，b 上）再次折叠，折叠后的边线b 与a 交于点1C ，AB//11A B ，137BB AC ==，，求出1AC 的长．8．在等腰ABC ∆中，AB AC =,AE 为BC 边上的高，点D 在ABC ∆的外部且60CAD ∠=，AD AC =,连接BD 交直线AE 于点F ，连接FC ．(1)如图①，当120BAC ∠<时，求证：BF CF =；(2)如图②，当40BAC ∠=时，求AFD ∠的度数；(3)如图③，当120BAC ∠>时,求证：CF AF DF =+．9．在△ABC 中，∠BAC =45°，CD ⊥AB ，垂足为点D ，M 为线段DB 上一动点（不包括端点），点N 在直线AC 左上方且∠NCM =135°，CN =CM ，如图①．（1）求证：∠ACN =∠AMC ；（2）记△ANC 得面积为5，记△ABC 得面积为5．求证：12S AC S AB=； （3）延长线段AB 到点P ，使BP =BM ，如图②．探究线段AC 与线段DB 满足什么数量关系时对于满足条件的任意点M ，AN =CP 始终成立？（写出探究过程）10．如图（1），AB ＝4cm ，AC ⊥AB ，BD ⊥AB ，AC ＝BD ＝3cm ．点 P 在线段 AB 上以 1/cm s 的速度由点 A 向点 B 运动，同时，点 Q 在线段 BD 上由点 B 向点 D 运动．它们运动的时间为 t （s ）．（1）若点 Q 的运动速度与点 P 的运动速度相等，当t ＝1 时，△ACP 与△BPQ 是否全等，请说明理由， 并判断此时线段 PC 和线段 PQ 的位置关系；（2）如图（2），将图（1）中的“AC ⊥AB ，BD ⊥AB”为改“∠CAB ＝∠DBA ＝60°”，其他条件不变．设点 Q 的运动速度为x /cm s ，是否存在实数x ，使得△ACP 与△BPQ 全等？若存在，求出相应的x 、t 的值；若不存在，请说明理由．11．如图，以直角三角形AOC的直角顶点O为原点，以OC，OA所在直线为轴和轴建立平-+-=．面直角坐标系，点A（0，a），C（b，0）满足a6b80（1）a= ；b= ；直角三角形AOC的面积为．（2）已知坐标轴上有两动点P，Q同时出发，P点从C点出发以每秒2个单位长度的速度向点O匀速移动，Q点从O点出发以每秒1个单位长度的速度向点A匀速移动，点P到达O点整个运动随之结束．AC的中点D的坐标是（4，3），设运动时间为t秒．问：是否存在这样的t，使得△ODP与△ODQ的面积相等？若存在，请求出t的值；若不存在，请说明理由．（3）在（2）的条件下，若∠DOC=∠D CO，点G是第二象限中一点，并且y轴平分∠GOD．点E是线段OA上一动点，连接接CE交OD于点H，当点E在线段OA上运动的过程中，探究∠GOD，∠OHC，∠ACE之间的数量关系，并证明你的结论(三角形的内角和为180)．12．（概念认识）如图①，在∠ABC中，若∠ABD＝∠DBE＝∠EBC，则BD，BE叫做∠ABC的“三分线”．其中，BD是“邻AB三分线”，BE是“邻BC三分线”．（问题解决）（1）如图②，在△ABC中，∠A＝70°，∠B＝45°，若∠B的三分线BD交AC于点D，则∠BDC＝ °；（2）如图③，在△ABC中，BP、CP分别是∠ABC邻AB三分线和∠ACB邻AC三分线，且BP⊥CP，求∠A的度数；（延伸推广）（3）在△ABC中，∠ACD是△ABC的外角，∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P．若∠A＝m°，∠B＝n°，直接写出∠BPC的度数．（用含 m、n的代数式表示）13．小敏与同桌小颖在课下学习中遇到这样一道数学题：“如图（1），在等边三角形=，试确定线段AE与DB ABC中，点E在AB上，点D在CB的延长线上，且ED EC的大小关系，并说明理由”．小敏与小颖讨论后，进行了如下解答：（1）取特殊情况，探索讨论：当点E 为AB 的中点时，如图（2），确定线段AE 与DB 的大小关系，请你写出结论：AE _____DB （填“>”，“<”或“=”），并说明理由．（2）特例启发，解答题目：解：题目中，AE 与DB 的大小关系是：AE _____DB （填“>”，“<”或“=”）．理由如下：如图（3），过点E 作EF ∥BC ，交AC 于点F ．（请你将剩余的解答过程完成） （3）拓展结论，设计新题：在等边三角形ABC 中，点E 在直线AB 上，点D 在直线BC 上，且ED EC =，若△ABC 的边长为1，2AE =，求CD 的长（请你画出图形，并直接写出结果）．14．在△ABC 中，已知∠A ＝α．（1）如图1，∠ABC 、∠ACB 的平分线相交于点D ．求∠BDC 的大小（用含α的代数式表示）；（2）如图2，若∠ABC 的平分线与∠ACE 的平分线交于点F ，求∠BFC 的大小（用含α的代数式表示）；（3）在（2）的条件下，将△FBC 以直线BC 为对称轴翻折得到△GBC ，∠GBC 的平分线与∠GCB 的平分线交于点M （如图3），求∠BMC 的度数（用含α的代数式表示）．15．在初中数学学习阶段，我们常常会利用一些变形技巧来简化式子，解答问题．材料一：在解决某些分式问题时，倒数法是常用的变形技巧之一，所谓倒数法，即把式子变成其倒数形式，从而运用约分化简，以达到计算目的． 例：已知：2114x x =+，求代数式x 2+21x的值． 解：∵2114x x =+，∴21x x+＝4 即21x x x+＝4∴x +1x ＝4∴x 2+21x ＝（x +1x ）2﹣2＝16﹣2＝14材料二：在解决某些连等式问题时，通常可以引入参数“k ”，将连等式变成几个值为k 的等式，这样就可以通过适当变形解决问题．例：若2x ＝3y ＝4z ，且xyz ≠0，求x y z +的值． 解：令2x ＝3y ＝4z ＝k （k ≠0） 则11k k k k x 622,,,117234y z 7k k 3412x y z ===∴===++ 根据材料回答问题：（1）已知2114x x x =-+，求x +1x的值． （2）已知523a b c ==，（abc ≠0），求342b c a+的值． （3）若222222yz zx xy x y z bz cy cx az ay bx a b c++===+++++，x ≠0，y ≠0，z ≠0，且abc ＝7，求xyz 的值．16．如图，在ABC 中，D 为AB 的中点，10AB AC cm ==，8BC cm =．动点P 从点B 出发，沿BC 方向以3/cm s 的速度向点C 运动；同时动点Q 从点C 出发，沿CA 方向以3/cm s 的速度向点A 运动，运动时间是ts ．（1）在运动过程中，当点C 位于线段PQ 的垂直平分线上时，求出t 的值；（2）在运动过程中，当BPD CQP ≌时，求出t 的值；（3）是否存在某一时刻t ，使BPD CPQ ≌？若存在，求出t 的值；若不存在，请说明理由．17．探究发现：如图①，在ABC 中，内角ACB ∠的平分线与外角ABD ∠的平分线相交于点E ．（1）若80A ∠=︒，则E ∠= ；若50A ∠=︒，则E ∠= ；（2）由此猜想：A ∠与E ∠的关系为 (不必说明理由)．拓展延伸：如图②，四边形ABCD 的内角DCB ∠与外角ABE ∠的平分线相交于点F ，//BF CD ．（3）若125A ∠=︒，95D ∠=︒，求F ∠的度数，由此猜想F ∠与A ∠，D ∠之间的关系，并说明理由．18．如图，在ABC ∆中，90,,8ACB AC BC AB cm ∠=︒==，过点C 做射线CD ，且//CD AB ，点P 从点C 出发，沿射线CD 方向均匀运动，速度为3/cm s ；同时，点Q 从点A 出发，沿AB 向点B 匀速运动，速度为1/cm s ，当点Q 停止运动时，点P 也停止运动．连接,PQ CQ ，设运动时间为()()08t s t <<．解答下列问题：（1）用含有t 的代数式表示CP 和BQ 的长度；（2）当2t =时，请说明//PQ BC ；（3）设BCQ ∆的面积为()2S cm ，求S 与t 之间的关系式． 19．（1）探索发现：如图1，已知Rt △ABC 中，∠ACB ＝90°，AC ＝BC ，直线l 过点C ，过点A 作AD ⊥l ，过点B 作BE ⊥l ，垂足分别为D 、E ．求证：AD ＝CE ，CD ＝BE ．（2）迁移应用：如图2，将一块等腰直角的三角板MON 放在平面直角坐标系内，三角板的一个锐角的顶点与坐标原点O 重合，另两个顶点均落在第一象限内，已知点M 的坐标为（1，3），求点N 的坐标．（3）拓展应用：如图3，在平面直角坐标系内，已知直线y ＝﹣3x+3与y 轴交于点P ，与x 轴交于点Q ，将直线PQ 绕P 点沿逆时针方向旋转45°后，所得的直线交x 轴于点R ．求点R 的坐标．20．已知：ABC 中，过B 点作BE ⊥AD ，=90=，∠︒ACB AC BC ．(1)如图1，点D 在BC 的延长线上，连AD ，作BE AD ⊥于E ，交AC 于点F ．求证：=AD BF ；(2)如图2，点D 在线段BC 上，连AD ，过A 作AE AD ⊥，且=AE AD ，连BE 交AC 于F ，连DE ，问BD 与CF 有何数量关系，并加以证明；(3)如图3，点D 在CB 延长线上，=AE AD 且AE AD ⊥，连接BE 、AC 的延长线交BE 于点M ，若=3AC MC ，请直接写出DB BC的值．【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）详见解析；（2）①详见解析；②详见解析．【解析】【分析】（1）本题考查理解题意能力，按照题目所述依次作图即可．（2）①本题考查线段和最短问题，需要通过垂直平分线的性质将所求线段转化为其他等量线段之和，以达到求解目的．②本题考查垂直平分线的判定以及全等三角形的证明，继而利用角的平分线性质即可得出结论．【详解】（1）补全图形，如图1所示（2）①如图2，连接BD，P为BD与AE的交点∵等边△ACD，AE⊥CD∴PC=PD,PC+PB最短等价于PB+PD最短故B,D之间直线最短，点P即为所求．②证明：连接DE，DF．如图3所示∵△ABC，△ADC是等边三角形∴AC＝AD，∠ACB＝∠CAD＝60°∵AE⊥CD∴∠CAE＝12∠CAD＝30°∴∠CEA＝∠ACB﹣∠CAE＝30°∴∠CAE＝∠CEA∴CA＝CE∴CD垂直平分AE∴DA＝DE∴∠DAE＝∠DEA∵EF⊥AF，∠EAF＝45°∴∠FEA＝45°∴∠FEA＝∠EAF∴FA＝FE，∠FAD＝∠FED∴△FAD≌△FED（SAS）∴∠AFD＝∠EFD∴点D 到AF ，EF 的距离相等．【点睛】本题第一问作图极为重要，要求对题意有较深的理解，同时对于垂直平分线以及角平分线的定义要清楚，能通过题目文字所述转化为考点，信息转化能力需要多做题目加以提升．2．（1）见解析；（2）见解析；（3）113或53【解析】【分析】（1）证明△AFD ≌△EAC ，根据全等三角形的性质得到DF=AC ，等量代换证明结论； （2）作FD ⊥AC 于D ，证明△FDG ≌△BCG ，得到DG=CG ，求出CE ，CB 的长，得到答案；（3）过F 作FD ⊥AG 的延长线交于点D ，根据全等三角形的性质得到CG=GD ，AD=CE=7，代入计算即可．【详解】解：（1）证明：∵FD ⊥AC ，∴∠FDA=90°，∴∠DFA+∠DAF=90°，同理，∠CAE+∠DAF=90°，∴∠DFA=∠CAE ，在△AFD 和△EAC 中， AFD EAC ADF ECA AF AE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△AFD ≌△EAC （AAS ），∴DF=AC ，∵AC=BC ，∴FD=BC ；（2）作FD ⊥AC 于D ，由（1）得，FD=AC=BC ，AD=CE ，在△FDG 和△BCG 中，90FDG BCG FGD BGCFD BC ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩， ∴△FDG ≌△BCG （AAS ），∴DG=CG=1，∴AD=2，∴CE=2，∵BC=AC=AG+CG=4，∴E 点为BC 中点；（3）当点E 在CB 的延长线上时，过F 作FD ⊥AG 的延长线交于点D ，BC=AC=4，CE=CB+BE=7，由（1）（2）知：△ADF ≌△ECA ，△GDF ≌△GCB ，∴CG=GD ，AD=CE=7，∴CG=DG=1.5， ∴4 1.5111.53AG CG +==， 同理，当点E 在线段BC 上时，4 1.551.53AG CG -==， 故答案为：113或53.【点睛】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理是解题的关键．3．（1）证明见解析；（2）证明见解析；（3）结论：AD DG ND =-，证明见解析．【解析】【分析】（1）先根据直角三角形的性质得出60ABC ∠=︒，再根据角平分线的性质可得CD ED =，然后根据三角形的判定定理与性质可得BC BE =，最后根据等边三角形的判定即可得证；（2）如图（见解析），延长ED 使得DF MD =，连接MF ，先根据直角三角形的性质、等边三角形的判定得出MDF ∆是等边三角形，再根据等边三角形的性质、角的和差得出,,F MDB MF MD FMG DMB ∠=∠=∠=∠，然后根据三角形全等的判定与性质、等量代换即可得证；（3）如图（见解析），参照题（2），先证HDN ∆是等边三角形，再根据等边三角形的性质、角的和差得出,,H NDG NH ND HNB DNG ∠=∠=∠=∠，然后根据三角形全等的判定与性质、等量代换即可得证．【详解】（1）3,090A ACB ∠=︒∠=︒9060ABC A ∴∠=︒-∠=︒ BD 是ABC ∠的角平分线，DE AB ⊥CD ED ∴=在BCD ∆和BED ∆中，CD ED BD BD =⎧⎨=⎩()BCD BED HL ∴∆≅∆BC BE ∴=EBC ∴∆是等边三角形；（2）如图，延长ED 使得DF MD =，连接MF3,090A ACB ∠=︒∠=︒，BD 是ABC ∠的角平分线，DE AB ⊥60,ADE BDE AD BD ∴∠=∠=︒=60,18060MDF ADE MDB ADE BDE ∴∠=∠=︒∠=︒-∠-∠=︒MDF ∴∆是等边三角形,60MF DM F DMF ∴=∠=∠=︒60BMG ∠=︒DMF DM B M G G D M G ∴∠+∠=+∠∠，即FMG DMB ∠=∠在FMG ∆和DMB ∆中，60F MDB MF MD FMG DMB ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()FMG DMB ASA ∴∆≅∆GF BD ∴=，即DF DG BD +=AD DF DG MD DG ∴=+=+即AD DG MD =+；（3）结论：AD DG ND =-，证明过程如下：如图，延长BD 使得DH ND =，连接NH由（2）可知，60,18060,ADE HDN ADE BDE AD BD ∠=︒∠=︒-∠-∠=︒=HDN ∴∆是等边三角形,60NH ND H HND ∴=∠=∠=︒60BNG ∠=︒HND BND BND BNG ∠+∠=+∠∴∠，即N HNB D G ∠=∠在HNB ∆和DNG ∆中，60H NDG NH ND HNB DNG ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()HNB DNG ASA ∴∆≅∆HB DG ∴=，即DH BD DG +=ND AD DG ∴+=即AD DG ND =-．【点睛】本题考查了直角三角形的性质、等边三角形的判定与性质、三角形全等的判定定理与性质等知识点，较难的是题（2）和（3），通过作辅助线，构造一个等边三角形是解题关键．4．（1）∠AFE =60°；（2）见解析；（3）75【解析】【分析】（1）通过证明 BCE CAD ≌ 得到对应角相等，等量代换推导出60AFE ∠=︒； （2）由（1）得到60AFE ∠=︒，CE AD = 则在Rt AHF △ 中利用30°所对的直角边等于斜边的一半，等量代换可得；（3）通过在PF 上取一点K 使得KF =AF ，作辅助线证明ABK 和ACF 全等，利用对应边相等，等量代换得到比值.(通过将ACF 顺时针旋转60°也是一种思路.)【详解】（1）解：如图1中．∵ABC 为等边三角形，∴AC =BC ，∠BAC =∠ABC =∠ACB =60°，在BCE 和CAD 中，60BE CD CBE ACD BC CA =⎧⎪∠=∠=︒⎨⎪=⎩， ∴ BCE CAD ≌（SAS ），∴∠BCE =∠DAC ，∵∠BCE +∠ACE =60°，∴∠DAC +∠ACE =60°，∴∠AFE =60°．（2）证明：如图1中，∵AH ⊥EC ，∴∠AHF =90°，在Rt △AFH 中，∵∠AFH =60°，∴∠FAH =30°，∴AF =2FH ，∵ EBC DCA ≌，∴EC =AD ，∵AD =AF +DF =2FH +DF ，∴2FH +DF =EC ．（3）解：在PF 上取一点K 使得KF =AF ，连接AK 、BK ，∵∠AFK =60°，AF =KF ，∴△AFK 为等边三角形，∴∠KAF =60°，∴∠KAB =∠FAC ，在ABK 和ACF 中，AB AC KAB ACF AK AF =⎧⎪∠=∠⎨⎪=⎩， ∴ ABK ACF ≌(SAS )，BK CF =∴∠AKB =∠AFC =120°，∴∠BKE =120°﹣60°=60°，∵∠BPC=30°，∴∠PBK=30°，∴29BK CF PK CP===，∴79PF CP CF CP=-=，∵45()99 AF KF CP CF PK CP CP CP ==-+=-=∴779559CPPFAF CP== .【点睛】掌握等边三角形、直角三角形的性质，及三角形全等的判定通过一定等量代换为本题的关键.5．（1）60°；（2）EF=AF+FC，证明见解析；（3）AF=EF+2DF，证明见解析．【解析】【分析】（1）可设∠BAD＝∠CAD＝α，∠AEC＝∠ACE＝β，在△ACE中，根据三角形内角和可得2α＋60＋2β＝180°，从而有α＋β＝60°，即可得出∠DFC的度数；（2）在EC上截取EG＝CF，连接AG，证明△AEG≌△ACF，然后再证明△AFG为等边三角形，从而可得出EF＝EG＋GF＝AF＋FC；（3）在AF上截取AG＝EF，连接BG，BF，证明方法类似（2），先证明△ABG≌△EBF，再证明△BFG为等边三角形，最后可得出结论．【详解】解：（1）∵AB=AC，AD为BC边上的中线，∴可设∠BAD＝∠CAD＝α，又△ABE为等边三角形，∴AE=AB=AC，∠EAB=60°，∴可设∠AEC＝∠ACE＝β，在△ACE中，2α＋60°＋2β＝180°，∴α＋β＝60°，∴∠DFC=α＋β＝60°；（2）EF=AF+FC，证明如下：∵AB=AC，AD为BC边上的中线，∴AD⊥BC，∴∠FDC=90°，∵∠CFD＝60°，则∠DCF=30°，∴CF＝2DF，在EC上截取EG＝CF，连接AG，又AE=AC，∴∠AEG=∠ACF，∴△AEG≌△ACF（SAS）,∴∠EAG＝∠CAF，AG＝AF，又∠CAF=∠BAD，∴∠EAG=∠BAD，∴∠GAF＝∠BAD+∠BAG=∠EAG+∠BAG=∠60°，∴△AFG为等边三角形，∴EF＝EG＋GF＝AF＋FC，即EF=AF+FC；（3）补全图形如图所示，结论：AF=EF+2DF．证明如下：同（1）可设∠BAD＝∠CAD＝α，∠ACE＝∠AEC＝β，∴∠CAE＝180°－2β，∴∠BAE＝2α＋180°－2β＝60°，∴β－α＝60°，∴∠AFC=β－α＝60°，又△ABE为等边三角形，∴∠ABE=∠AFC=60°，∴由8字图可得：∠BAD＝∠BEF，在AF上截取AG＝EF，连接BG，BF，又AB=BE，∴△ABG≌△EBF（SAS），∴BG＝BF，又AF垂直平分BC，∴BF=CF，∴∠BFA=∠AFC=60°，∴△BFG为等边三角形，∴BG=BF，又BC⊥FG，∴FG=BF=2DF，∴AF＝AG＋GF＝BF＋EF＝2DF＋EF．【点睛】本题考查了全等三角形的判定和性质、等边三角形的性质、等腰三角形的性质等知识，解决问题的关键是常用辅助线构造全等三角形，属于中考常考题型．6．（1）HL；（2）见解析；（3）如图②，见解析；△DEF就是所求作的三角形，△DEF和△ABC不全等．【解析】【分析】（1）根据直角三角形全等的方法“HL”证明；（2）过点C作CG⊥AB交AB的延长线于G，过点F作FH⊥DE交DE的延长线于H，根据等角的补角相等求出∠CBG=∠FEH，再利用“角角边”证明△CBG和△FEH全等，根据全等三角形对应边相等可得CG=FH，再利用“HL”证明Rt△ACG和Rt△DFH全等，根据全等三角形对应角相等可得∠A=∠D，然后利用“角角边”证明△ABC和△DEF全等；（3）以点C为圆心，以AC长为半径画弧，与AB相交于点D，E与B重合，F与C重合，得到△DEF与△ABC不全等；（4）根据三种情况结论，∠B不小于∠A即可．【详解】（1）在直角三角形中一条斜边和一条直角边对应相等的两个直角三角形全等运用的是HL．（2）证明：如图①，分别过点C、F作对边AB、DE上的高CG、FH，其中G、H为垂足．∵∠ABC、∠DEF都是钝角∴G、H分别在AB、DE的延长线上．∵CG⊥AG，FH⊥DH，∴∠CGA＝∠FHD＝90°．∵∠CBG＝180°－∠ABC，∠FEH＝∠180°－∠DEF，∠ABC＝∠DEF，∴∠CBG＝∠FEH．在△BCG和△EFH中，∵∠CGB＝∠FHE，∠CBG＝∠FEH，BC＝EF，∴△BCG≌△EFH．∴CG＝FH．又∵AC＝DF．∴Rt△ACG≌△DFH．∴∠A＝∠D．在△ABC和△DEF中，∵∠ABC＝∠DEF，∠A＝∠D，AC＝DF，∴△ABC≌△DEF．（3）如图②，△DEF 就是所求作的三角形，△DEF 和△ABC 不全等．【点睛】本题是三角形综合题，主要考查了全等三角形的判定与性质，应用与设计作图，熟练掌握三角形全等的判定方法是解题的关键，阅读量较大，审题要认真仔细．7．（1）内错角相等，两直线平行；（2）∠1+2∠2=180°；（3）4或10【解析】【分析】（1）根据平行线的判定定理，即可得到答案；（2）由折叠的性质得：∠3=∠4，若a ∥b ，则∠3=∠2，结合三角形内角和定理，即可得到答案；（3）分两种情况：①当B 1在B 的左侧时，如图2，当B 1在B 的右侧时，如图3，分别求出1AC 的长，即可得到答案．【详解】（1）∵12∠=∠，∴a ∥b （内错角相等，两直线平行），故答案是：内错角相等，两直线平行；（2）如图1，由折叠的性质得：∠3=∠4，若a ∥b ，则∠3=∠2，∴∠4=∠2，∵∠2+∠4+∠1=180°，∴∠1+2∠2=180°，∴要使a ∥b ，则1∠与2∠应该满足的关系是：∠1+2∠2=180°．故答案是：∠1+2∠2=180°；（3）①当B 1在B 的左侧时，如图2，∵AB//11A B ，a ∥b ，∴AA 1=BB 1=3，∴1AC =AC- AA 1=7-3=4；②当B 1在B 的右侧时，如图3，∵AB//11A B ，a ∥b ，∴AA 1=BB 1=3，∴1AC =AC+AA 1=7+3=10．综上所述：1AC =4或10．【点睛】本题主要考查平行线的判定和性质定理，折叠的性质以及三角形的内角和定理，掌握“平行线间的平行线段长度相等”是解题的关键．8．（1）见解析；（2）60AFD ∠=；（3）见解析【解析】【分析】（1）根据等腰三角形三线合一的性质，可得AE 垂直平分BC ，F 为垂直平分线AE 上点，即可得出结论；（2）根据（1）的结论可得AE 平分∠BAC ，∠BAF=20°，由AB=AC=AD ，推出40ABD ADB ∠=∠=，根据外角性质可得AFD BAF ABF ∠=∠+∠计算即可；（3）在CF 上截取CM=DF ，连接AM ，证明△ACM ≌△ADF （SAS ），进而证得△AFM 为等边三角形即可．【详解】（1）证明：∵AE 为等腰△ABC 底边BC 上的高线，AB=AC ，AE BC ∴⊥，∠AEB=∠AEC=90°，BE=CE ，∴AE 垂直平分BE ，F 在AE 上，BF CF ∴=；(2) ,AB AC AD AC ==，AB AD ∴=，100BAD BAC CAD ∠=∠+∠=，40ABD ADB ∴∠=∠=，由（1）知，AE 平分∠BAC ，20BAF CAF ∴∠=∠=，60AFD BAF ABF ∴∠=∠+∠=，故答案为：60°；(3) 在CF 上截取CM=DF ，连接AM ，由（1）可知，∠ABC=∠ACB ，∠FBC =∠FCB ，ABF ACF ∴∠=∠，AB AC AD ==，ABF D ∴∠=∠，ACF D ∴∠=∠，在△ACM 和△ADF 中，AC AD ACM ADF CM DF =⎧⎪∠=∠⎨⎪=⎩∴△ACM ≌△ADF （SAS ），,AF AM FAD MAC ∴=∠=∠，60FAM DAC ∴∠=∠=，∴△AFM 为等边三角形，FM AF ∴=，CF FM MC AF DF ∴=+=+．【点睛】本题考查了等腰三角形的性质，垂直平分线的性质，三角形全等的判定和性质，等边三角形的判定和性质，掌握三角形全等的判定和性质是解题的关键．9．（1）证明见解析；（2）证明见解析；（3）当AC =2BD 时，对于满足条件的任意点N ，AN =CP 始终成立，证明见解析．【解析】【分析】（1）由三角形的内角和定理可求∠ACN=∠AMC=135°-∠ACM ；（2）过点N 作NE ⊥AC 于E ，由“AAS ”可证△NEC ≌△CDM ，可得NE=CD ，由三角形面积公式可求解；（3）过点N 作NE ⊥AC 于E ，由“SAS ”可证△NEA ≌△CDP ，可得AN=CP ．【详解】（1）∵∠BAC=45°，∴∠AMC=180°﹣45°﹣∠ACM=135°﹣∠ACM ．∵∠NCM=135°，∴∠ACN=135°﹣∠ACM ，∴∠ACN=∠AMC ；（2）过点N 作NE ⊥AC 于E ，∵∠CEN=∠CDM=90°，∠ACN=∠AMC ，CM=CN ，∴△NEC ≌△CDM （AAS ），∴NE=CD ，CE=DM ；∵S 112=AC•NE ，S 212=AB•CD ， ∴12S AC S AB=； （3）当AC=2BD 时，对于满足条件的任意点N ，AN=CP 始终成立，理由如下：过点N 作NE ⊥AC 于E ，由（2）可得NE=CD ，CE=DM ．∵AC=2BD ，BP=BM ，CE=DM ，∴AC ﹣CE=BD+BD ﹣DM ，∴AE=BD+BP=DP ．∵NE=CD ，∠NEA=∠CDP=90°，AE=DP ，∴△NEA ≌△CDP （SAS ），∴AN=PC ．【点睛】本题三角形综合题，考查了全等三角形的判定和性质，三角形内角和定理，三角形面积公式等知识，添加恰当辅助线构造全等三角形是本题的关键．10．（1）全等，垂直，理由详见解析；（2）存在，11t x =⎧⎨=⎩或232t x =⎧⎪⎨=⎪⎩【解析】【分析】（1）在t =1的条件下，找出条件判定△ACP 和△BPQ 全等，再根据全等三角形的性质和直角三角形的两个锐角互余的性质，可证∠CPQ= 90°，即可判断线段 PC 和线段 PQ 的位置关系;（2）本题主要在动点的条件下，分情况讨论，利用三角形全等时对应边相等的性质进行解答即可.【详解】(1)当t=1时，AP= BQ=1, BP= AC=3,又∠A=∠B= 90°，在△ACP 和△BPQ 中，{AP BQA B AC BP=∠=∠=∴△ACP ≌△BPQ(SAS).∴∠ACP=∠BPQ ,∴∠APC+∠BPQ=∠APC+∠ACP = 90*.∴∠CPQ= 90°，即线段PC 与线段PQ 垂直；(2)①若△ACP ≌△BPQ ，则AC= BP ，AP= BQ ，34t t xt =-⎧⎨=⎩解得11t x =⎧⎨=⎩; ②若△ACP ≌△BQP ，则AC= BQ ，AP= BP ，34xt t t =⎧⎨=-⎩解得：232t x =⎧⎪⎨=⎪⎩ 综上所述,存在11t x =⎧⎨=⎩或232t x =⎧⎪⎨=⎪⎩使得△ACP 与△BPQ 全等. 【点睛】本题主要考查三角形全等与动点问题，熟练掌握三角形全等的性质与判定定理，是解决本题的关键.11．（1）6；8；24；（2）存在 2.4t =时，使得△ODP 与△ODQ 的面积相等；（3）∠GOD+∠ACE=∠OHC ，见解析【解析】【分析】（1）利用非负性即可求出a ，b 即可得出结论,即可求出△ABC 的面积；（2）先表示出OQ ，OP ，利用那个面积相等，建立方程求解即可得出结论；（3）先判断出∠OAC=∠AOD ，进而判断出OG ∥AC ，即可判断出∠FHC=∠ACE ，同理∠FHO=∠GOD ，即可得出结论．【详解】解：(1) 解：（1）∵b 80-=， ∴a-6=0，b-8=0，∴a=6，b=8，∴A （0，6），C （8，0）；∴S △ABC=6×8÷2=24,故答案为（0，6），（8，0）； 6；8；24(2) ∵114222ODQ D S OQ x t t ∆=⋅=⋅⋅= 11(82)312322ODP D S OP y t t ∆=⋅=⋅-⋅=- 由2123t t =-时, 2.4t =∴存在 2.4t =时,使得△ODP 与△ODQ 的面积相等(3) ）∴2∠GOA+∠ACE=∠OHC ，理由如下：∵x 轴⊥y 轴，∴∠AOC=∠DOC+∠AOD=90°∴∠OAC+∠ACO=90°又∵∠DOC=∠DCO∴∠OAC=∠AOD∵y 轴平分∠GOD∴∠GOA=∠AOD∴∠GOA=∠OAC∴OG ∥AC ，如图，过点H 作HF ∥OG 交x 轴于F ，∴HF ∥AC∴∠FHC=∠ACE同理∠FHO=∠GOD ，∵OG ∥FH ，∴∠GOD=∠FHO ，∴∠GOD+∠ACE=∠FHO+∠FHC即∠GOD+∠ACE=∠OHC ，∴2∠GOA+∠ACE=∠OHC ．∴∠GOD+∠ACE=∠OHC ．【点睛】此题是三角形综合题，主要考查了非负性的性质，三角形的面积公式，角平分线的定义，平行线的性质，正确作出辅助线是解本题的关键．12．（1）85或100；（2）45°；（3）23m 或13m 或23m ＋13n 或13m －13n 或13n －13m 【解析】【分析】（1）根据题意可得B 的三分线BD 有两种情况，画图根据三角形的外角性质即可得BDC ∠的度数；（2）根据BP 、CP 分别是ABC ∠邻AB 三分线和ACB ∠邻AC 三分线，且BP CP ⊥可得135ABC ACB ，进而可求A ∠的度数；（3）根据B 的三分线所在的直线与ACD ∠的三分线所在的直线交于点P ．分四种情况画图：情况一：如图①，当BP 和CP 分别是“邻AB 三分线”、“邻AC 三分线”时；情况二：如图②，当BP 和CP 分别是“邻BC 三分线”、“邻CD 三分线”时；情况三：如图③，当BP 和CP 分别是“邻BC 三分线”、“邻AC 三分线”时；情况四：如图④，当BP 和CP 分别是“邻AB 三分线”、“邻CD 三分线”时，再根据A m ∠=︒，B n ∠=︒，即可求出BPC ∠的度数．【详解】解：（1）如图，当BD 是“邻AB 三分线”时，701585BD C； 当BD 是“邻BC 三分线”时，7030100BD C； 故答案为：85或100；（2）BP CP ， 90BPC ∴∠=︒，90PBC PCB ， 又BP 、CP 分别是ABC ∠邻AB 三分线和ACB ∠邻AC 三分线， 23PBC ABC ，23PCB ACB ∠=∠， ∴229033ABC ACB ， 135ABC ACB ，在ABC ∆中，180A ABC ACB ∠+∠+∠=︒ 180()45A ABCACB ． （3）分4种情况进行画图计算：情况一：如图①，当BP 和CP 分别是“邻AB 三分线”、“邻AC 三分线”时，2233BPC A m ； 情况二：如图②，当BP 和CP 分别是“邻BC 三分线”、“邻CD 三分线”时，1133BPC A m ；情况三：如图③，当BP 和CP 分别是“邻BC 三分线”、“邻AC 三分线”时， 21213333BPC A ABC m n ； 情况四：如图④，当BP 和CP 分别是“邻AB 三分线”、“邻CD 三分线”时，①当m n >时，11113333BPC A ABC m n ∠=∠-∠=-； ②当m n <时，11113333P ABC A n m ∠=∠-∠=-． 【点睛】 本题考查了三角形的外角性质，解决本题的关键是掌握三角形的外角性质．注意要分情况讨论．13．（1）AE DB =，理由详见解析；（2）AE DB =，理由详见解析；（3）3或1【解析】【分析】（1）根据等边三角形的性质、三线合一的性质证明即可；（2）根据等边三角形的性质，证明△EFC ≌△DBE 即可；（3）注意区分当点E 在AB 的延长线上时和当点E 在BA 的延长线上时两种情况，不要遗漏．【详解】解：（1）AE DB =，理由如下：ED EC =，EDC ECD ∴∠=∠∵△ABC 是等边三角形，60ACB ABC ∠=∠=︒∴，点E 为AB 的中点， 1302ECD ACB ∴︒∠=∠=，30EDC ∠=︒∴，30D DEB ∠=∠=︒∴， DB BE ∴=，AE BE =，AE DB ∴=；故答案为：=；（2）AE DB =，理由如下：如图3：∵△ABC 为等边三角形，且EF ∥BC ，60AEF ABC ∠=∠=︒∴，60AFE ACB ∠=∠=︒，FEC ECB ∠=∠；120EFC DBE ∠=∠=︒∴；ED EC =，D ECB ∴∠=∠，D FEC ∠=∠，在△EFC 与△DBE 中，FEC D EFC DBE EC DE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△EFC ≌△DBE （AAS ），EF DB ∴=60AEF AFE ∠=∠=︒，∴△AEF 为等边三角形，AE EF ∴=，AE BD ∴=．（3）①如图4，当点E 在AB 的延长线上时，过点E 作EF ∥BC ，交AC 的延长线于点F ：则DCE CEF ∠=∠，DBE AEF ∠=∠；ABC AEF ∠=∠，ACB AFE ∠=∠；∵△ACB 为等边三角形，60ABC ACB ∴∠=∠=︒，60AEF AFE ∴∠=∠=︒，60DBE ABC ∠=∠=︒， DBE EFC ∴∠=∠；而ED EC =，D DCE ∴∠=∠，D CEF ∠=∠；在△FEC 和△BDE 中，FEC D EFC DBE EC DE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△FEC ≌△BDE （AAS ），EF BD ∴=；∵△AEF 为等边三角形，2AE EF ∴==，2BD EF ==，123CD ∴=+=；②如图5，当点E 在BA 的延长线上时，过点E 作EF ∥BC ，交CA 的延长线于点F ：类似上述解法，同理可证：2DB EF ==，1BC =，211CD =-=∴．【点睛】本题考查等边三角形的性质、全等三角形的判定和性质．熟练掌握等边三角形的性质，构造合适的全等三角形是解题的关键．14．（1）∠BDC ＝90°+2α；（2）∠BFC ＝2α；（3）∠BMC ＝90°+4α． 【解析】【分析】（1）由三角形内角和可求∠ABC +∠ACB ＝180°﹣α，由角平分线的性质可求∠DBC +∠BCD ＝12（∠ABC +∠ACB ）＝90°﹣2α，由三角形的内角和定理可求解； （2）由角平分线的性质可得∠FBC ＝12∠ABC ，∠FCE ＝12∠ACE ，由三角形的外角性质可求解；（3）由折叠的性质可得∠G ＝∠BFC ＝2α，方法同（1）可求∠BMC ＝90°+2G ∠，即可求解.【详解】解：（1）∵∠A ＝α，∴∠ABC +∠ACB ＝180°﹣α，∵BD 平分∠ABC ，CD 平分∠ACB ，∴∠DBC ＝12∠ABC ，∠BCD ＝12∠ACB ， ∴∠DBC +∠BCD ＝12（∠ABC +∠ACB ）＝90°﹣2α， ∴∠BDC ＝180°﹣（∠DBC +∠BCD ）＝90°+2α； （2）∵∠ABC 的平分线与∠ACE 的平分线交于点F ，∴∠FBC ＝12∠ABC ，∠FCE ＝12∠ACE ， ∵∠ACE ＝∠A +∠ABC ，∠FCE ＝∠BFC +∠FBC ，∴∠BFC ＝12∠A ＝2α； （3）∵∠GBC 的平分线与∠GCB 的平分线交于点M ， ∴方法同（1）可得∠BMC ＝90°+2G ∠， ∵将△FBC 以直线BC 为对称轴翻折得到△GBC ，∴∠G ＝∠BFC ＝2α， ∴∠BMC ＝90°+4α. 【点睛】此题考查三角形的内角和定理，三角形的外角等于与它不相邻的两个内角的和，角平分线的性质定理，折叠的性质.15．（1）5；（2）95； （3）78【解析】【分析】（1）仿照材料一，取倒数，再约分，利用等式的性质求解即可；（2）仿照材料二，设5a ＝2b ＝3c ＝k （k ≠0），则a ＝5k ，b ＝2k ，c ＝3k ，代入所求式子即可；（3）本题介绍两种解法：解法一：（3）解法一：设yz bz cy +＝zx cx az +＝xy ay bx +＝1k （k ≠0），化简得：b c k y z +=①，c a k z x +=②，a b k x y +=③，相加变形可得x 、y 、z 的代入222222x y z a b c ++++＝1k中，可得k 的值，从而得结论； 解法二：取倒数得：bz cy yz +＝cx az zx +＝ay bx xy +，拆项得b c c a a b y z z x x y +=+=+，从而得x ＝ay b ，z ＝cy b，代入已知可得结论． 【详解】解：（1）∵21x x x -+＝14， ∴21x x x-+＝4， ∴x ﹣1+1x ＝4， ∴x +1x＝5； （2）∵设5a ＝2b ＝3c ＝k （k ≠0），则a ＝5k ，b ＝2k ，c ＝3k ， ∴342b c a +＝61210k k k +＝1810＝95； （3）解法一：设yz bz cy +＝zx cx az +＝xy ay bx +＝1k（k ≠0）， ∴b c k y z +=①，c a k z x+=②，a b k x y +=③， ①+②+③得：2（b c a y z x ++）＝3k ， b c a y z x ++＝32k ④， ④﹣①得：a x ＝12k ， ④﹣②得：12b k y =， ④﹣③得：12c z =k ， ∴x ＝2a k ，y ＝2b k ，z ＝2c k 代入222222x y z a b c++++＝1k 中，得：。

沪教版八年级上册压轴题数学模拟数学模拟试题一、压轴题1．在我们认识的多边形中，有很多轴对称图形．有些多边形，边数不同对称轴的条数也不同；有些多边形，边数相同但却有不同数目的对称轴．回答下列问题：（1）非等边的等腰三角形有________条对称轴，非正方形的长方形有________条对称轴，等边三角形有___________条对称轴；（2）观察下列一组凸多边形（实线画出），它们的共同点是只有1条对称轴，其中图1-2和图1-3都可以看作由图1-1修改得到的，仿照类似的修改方式，请你在图1-4和图1-5中，分别修改图1-2和图1-3，得到一个只有1条对称轴的凸五边形，并用实线画出所得的凸五边形；（3）小明希望构造出一个恰好有2条对称轴的凸六边形，于是他选择修改长方形，图2中是他没有完成的图形，请用实线帮他补完整个图形；（4）请你画一个恰好有3条对称轴的凸六边形，并用虚线标出对称轴．2．在ABC 中，AB AC =，D 是直线AB 上一点，E 在直线BC 上，且DE DC =． （1）如图1，当D 在AB 上，E 在CB 延长线上时，求证：EDB ACD ∠=∠；（2）如图2，当ABC 为等边三角形时，D 是BA 的延长线上一点，E 在BC 上时，作//EF AC ，求证：BE AD =；（3）在（2）的条件下，ABC ∠的平分线BF 交CD 于点F ，连AF ，过A 点作AH CD ⊥于点H ，当30EDC ∠=︒，6CF =时，求DH 的长度．3．阅读下面材料，完成(1)-(3)题．数学课上，老师出示了这样一道题：如图1，已知等腰△ABC 中，AB ＝AC ，AD 为BC 边上的中线，以AB 为边向AB 左侧作等边△ABE ，直线CE 与直线AD 交于点F ．请探究线段EF 、AF 、DF 之间的数量关系，并证明． 同学们经过思考后，交流了自已的想法：小明：“通过观察和度量，发现∠DFC 的度数可以求出来．”小强：“通过观察和度量，发现线段DF 和CF 之间存在某种数量关系．”小伟：“通过做辅助线构造全等三角形，就可以将问题解决．”......老师：“若以AB 为边向AB 右侧作等边△ABE ，其它条件均不改变，请在图2中补全图形,探究线段EF 、AF 、DF 三者的数量关系，并证明你的结论．”（1）求∠DFC 的度数；（2）在图1中探究线段EF 、AF 、DF 之间的数量关系，并证明；（3）在图2中补全图形，探究线段EF 、AF 、DF 之间的数量关系，并证明．4．（1）问题发现．如图1，ACB ∆和DCE ∆均为等边三角形，点A 、D 、E 均在同一直线上，连接BE ．①求证：ADC BEC ∆∆≌．②求AEB ∠的度数．③线段AD 、BE 之间的数量关系为__________．（2）拓展探究．如图2，ACB ∆和DCE ∆均为等腰直角三角形，90ACB DCE ∠=∠=︒，点A 、D 、E 在同一直线上，CM 为DCE ∆中DE 边上的高，连接BE ．的度数为____________．①请判断AEB②线段CM、AE、BE之间的数量关系为________．（直接写出结论，不需证明）5．如图（1），AB＝4cm，AC⊥AB，BD⊥AB，AC＝BD＝3cm．点 P 在线段 AB 上以1/cm s的速度由点 A 向点 B 运动，同时，点 Q 在线段 BD 上由点 B 向点 D 运动．它们运动的时间为t（s）．（1）若点 Q 的运动速度与点 P 的运动速度相等，当t＝1 时，△ACP 与△BPQ 是否全等，请说明理由，并判断此时线段 PC 和线段 PQ 的位置关系；（2）如图（2），将图（1）中的“AC⊥AB，BD⊥AB”为改“∠CAB＝∠DBA＝60°”，其他cm s，是否存在实数x，使得△ACP 与△BPQ 全等？若条件不变．设点 Q 的运动速度为x/存在，求出相应的x、t的值；若不存在，请说明理由．6．在等边△ABC的顶点A、C处各有一只蜗牛，它们同时出发，分别以每分钟1米的速度由A向B和由C向A爬行，其中一只蜗牛爬到终点时，另一只也停止运动，经过t分钟后，它们分别爬行到D、E处，请问：（1）如图1，在爬行过程中，CD和BE始终相等吗，请证明？（2）如果将原题中的“由A向B和由C向A爬行”，改为“沿着AB和CA的延长线爬行”，EB与CD交于点Q，其他条件不变，蜗牛爬行过程中∠CQE的大小保持不变，请利用图2说明：∠CQE=60°；（3）如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行，连接DE交AC于F”，其他条件不变，如图3，则爬行过程中，证明：DF=EF7．如图，已知△ABC中，AB=AC=10cm，BC=8cm，点D为AB的中点．如果点P在线段BC 上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．（1）若点Q的运动速度与点P的运动速度相等，经过1s后，BP= cm，CQ= cm．（2）若点Q的运动速度与点P的运动速度相等，经过1s后，△BPD与△CQP是否全等，请说明理由；（3）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？（4）若点Q以（3）中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次相遇？8．(1)问题发现：如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．①请直接写出∠AEB的度数为_____；②试猜想线段AD与线段BE有怎样的数量关系，并证明；(2)拓展探究：图2，△ACB和△DCE均为等腰三角形，∠ACB＝∠DCE＝90°，点A、D、E 在同－直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数线段CM、AE、BE之间的数量关系，并说明理由．9．在《经典几何图形的研究与变式》一课中，庞老师出示了一个问题：“如图1，等腰直角三角形的三个顶点分别落在三条等距的平行线1l ，2l ，3l 上，90BAC ∠=︒，且每两条平行线之间的距离为1，求AB 的长度”.在研究这道题的解法和变式的过程中，同学们提出了很多想法：（1）小明说：我只需要过B 、C 向1l 作垂线，就能利用全等三角形的知识求出AB 的长. （2）小林说：“我们可以改变ABC 的形状.如图2，AB AC =，120BAC ∠=︒，且每两条平行线之间的距离为1，求AB 的长.”（3）小谢说：“我们除了改变ABC 的形状，还能改变平行线之间的距离.如图3，等边三角形ABC 三个顶点分别落在三条平行线1l ，2l ，3l 上，且1l 与2l 之间的距离为1，2l 与3l 之间的距离为2，求AB 的长、”请你根据3位同学的提示，分别求出三种情况下AB 的长度.10．探索发现：111111111;;12223233434=-=-=-⨯⨯⨯…… 根据你发现的规律，回答下列问题：（1）145⨯＝ ，1(1)n n ⨯+＝ ；（2）利用你发现的规律计算：1111122334(1)n n ⋅++++⨯⨯⨯⨯+ （3）利用规律解方程：1111121(1)(1)(2)(2)(3)(3)(4)(4)(5)(5)x x x x x x x x x x x x x -++++=++++++++++ 11．（1）探索发现：如图1，已知Rt △ABC 中，∠ACB ＝90°，AC ＝BC ，直线l 过点C ，过点A 作AD ⊥l ，过点B 作BE ⊥l ，垂足分别为D 、E ．求证：AD ＝CE ，CD ＝BE ．（2）迁移应用：如图2，将一块等腰直角的三角板MON 放在平面直角坐标系内，三角板的一个锐角的顶点与坐标原点O 重合，另两个顶点均落在第一象限内，已知点M 的坐标为（1，3），求点N 的坐标．（3）拓展应用：如图3，在平面直角坐标系内，已知直线y ＝﹣3x+3与y 轴交于点P ，与x 轴交于点Q ，将直线PQ 绕P 点沿逆时针方向旋转45°后，所得的直线交x 轴于点R ．求点R 的坐标．12．数学活动课上，老师出了这样一个题目：“已知：MF NF ⊥于F ，点A 、C 分别在NF 和MF 上，作线段AB 和CD （如图1），使90FAB MCD ∠-∠=︒．求证：//AB CD ”．（1）聪聪同学给出一种证明问题的辅助线：如图2，过A 作//AG FM ，交CD 于G ．请你根据聪聪同学提供的辅助线（或自己添加其它辅助线），给出问题的证明． （2）若点E 在直线CD 下方，且知30BED ∠=︒，直接写出ABE ∠和CDE ∠之间的数量关系．13．如图1，我们定义：在四边形ABCD 中，若AD=BC ，且∠ADB+∠BCA=180°，则把四边形ABCD 叫做互补等对边四边形．（1）如图2，在等腰ABE △中，AE=BE ，四边形ABCD 是互补等对边四边形，求证：∠ABD=∠BAC=12∠AEB ． （2）如图3，在非等腰ABE △中，若四边形ABCD 仍是互补等对边四边形，试问∠ABD=∠BAC=12∠AEB 是否仍然成立？若成立，请加以证明；若不成立，请说明理由．14．现给出一个结论：直角三角形斜边的中线等于斜边的一半；该结论是正确的，用图形语言可以表示为：如图1在ABC ∆中，90︒∠=C ,若点D 为AB 的中点，则12CD AB =． 请结合上述结论解决如下问题：已知，点P 是射线BA 上一动点（不与A,B 重合）分别过点A,B 向直线CP 作垂线，垂足分别为E,F,其中Q 为AB 的中点（1）如图2，当点P 与点Q 重合时，AE 与BF 的位置关系____________；QE 与QF 的数量关系是__________（2）如图3，当点P 在线段AB 上不与点Q 重合时，试判断QE 与QF 的数量关系，并给予证明．(3)如图4，当点P 在线段BA 的延长线上时，此时（2）中的结论是否成立？请画出图形并写出主要证明思路．15．在△ABC 中，AB =AC ，D 是直线BC 上一点，以AD 为一条边在AD 的右侧作△ADE ，使AE =AD ，∠DAE =∠BAC ，连接CE ．（1）如图，当点D 在BC 延长线上移动时，若∠BAC =40°，则∠ACE = ，∠DCE = ，BC 、DC 、CE 之间的数量关系为 ；（2）设∠BAC =α，∠DCE =β．①当点D 在BC 延长线上移动时，α与β之间有什么数量关系？请说明理由； ②当点D 在直线BC 上（不与B ，C 两点重合）移动时，α与β之间有什么数量关系？请直接写出你的结论．（3）当CE ∥AB 时，若△ABD 中最小角为15°，试探究∠ACB 的度数（直接写出结果，无需写出求解过程）．16．在初中数学学习阶段，我们常常会利用一些变形技巧来简化式子，解答问题．材料一：在解决某些分式问题时，倒数法是常用的变形技巧之一，所谓倒数法，即把式子变成其倒数形式，从而运用约分化简，以达到计算目的． 例：已知：2114x x =+，求代数式x 2+21x的值． 解：∵2114x x =+，∴21x x+＝4 即21x x x+＝4∴x +1x ＝4∴x 2+21x ＝（x +1x ）2﹣2＝16﹣2＝14 材料二：在解决某些连等式问题时，通常可以引入参数“k ”，将连等式变成几个值为k 的等式，这样就可以通过适当变形解决问题．例：若2x ＝3y ＝4z ，且xyz ≠0，求x y z+的值． 解：令2x ＝3y ＝4z ＝k （k ≠0） 则11k k k k x 622,,,117234y z 7k k 3412x y z ===∴===++ 根据材料回答问题：（1）已知2114x x x =-+，求x +1x的值． （2）已知523a b c ==，（abc ≠0），求342b c a+的值． （3）若222222yz zx xy x y z bz cy cx az ay bx a b c ++===+++++，x ≠0，y ≠0，z ≠0，且abc ＝7，求xyz 的值．17．已知：MN ∥PQ ，点A ，B 分别在MN ，PQ 上，点C 为MN ，PQ 之间的一点，连接CA ，CB ．（1）如图1，求证：∠C=∠MAC+∠PBC ；（2）如图2，AD ，BD ，AE ，BE 分别为∠MAC ，∠PBC ，∠CAN ，∠CBQ 的角平分线，求证：∠D+∠E=180°；（3）在（2）的条件下，如图3，过点D 作DA 的垂线交PQ 于点G ，点F 在PQ 上，∠FDA=2∠FDB ，FD 的延长线交EA 的延长线于点H ，若3∠C=4∠E ，猜想∠H 与∠GDB 的倍数关系并证明．18．（1）发现：如图1，ABC ∆的内角ABC ∠的平分线和外角ACD ∠的平分线相交于点O 。

沪教版八年级上册压轴题数学数学模拟试题一、压轴题1．数学活动课上，老师出了这样一个题目：“已知：MF NF ⊥于F ，点A 、C 分别在NF 和MF 上，作线段AB 和CD （如图1），使90FAB MCD ∠-∠=︒．求证：//AB CD ”．（1）聪聪同学给出一种证明问题的辅助线：如图2，过A 作//AG FM ，交CD 于G ．请你根据聪聪同学提供的辅助线（或自己添加其它辅助线），给出问题的证明． （2）若点E 在直线CD 下方，且知30BED ∠=︒，直接写出ABE ∠和CDE ∠之间的数量关系．2．直角三角形ABC 中，90ACB ∠=︒，直线l 过点C ．（1）当AC BC =时，如图1，分别过点A 和B 作AD ⊥直线l 于点D ，BE ⊥直线l 于点E ，ACD 与CBE △是否全等，并说明理由；（2）当8AC cm =，6BC cm =时，如图2，点B 与点F 关于直线l 对称，连接 BF CF 、，点M 是AC 上一点，点N 是CF 上一点，分别过点M N 、作MD ⊥直线l 于点D ，NE ⊥直线l 于点E ，点M 从A 点出发，以每秒1cm 的速度沿A C →路径运动，终点为C ，点N 从点F 出发，以每秒3cm 的速度沿F C B C F →→→→路径运动，终点为F ，点,M N 同时开始运动，各自达到相应的终点时停止运动，设运动时间为t 秒，当CMN △为等腰直角三角形时，求t 的值．3．在Rt ABC 中，90ACB ∠=︒，30A ∠=︒，BD 是ABC 的角平分线，DE AB ⊥于点E .（1）如图1，连接EC ，求证：EBC 是等边三角形；（2）如图2，点M 是线段CD 上的一点（不与点,C D 重合），以BM 为一边，在BM 下方作60BMG ∠=︒，MG 交DE 延长线于点G .求证：AD DG MD =+；（3）如图3，点N 是线段AD 上的点，以BN 为一边，在BN 的下方作60BNG ∠=︒，NG 交DE 延长线于点G .直接写出ND ，DG 与AD 数量之间的关系.4．（阅读材科）小明同学发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的项角的顶点，并把它们的底角顶点连接起来则形成一组全等的三角形，小明把具有这个规律的图形称为“手拉手”图形．如图1，在“手拉手”图形中，小明发现若∠BAC =∠DAE ，AB =AC ，AD =AE ，则△ABD ≌△ACE ．（材料理解）（1）在图1中证明小明的发现．（深入探究）（2）如图2，△ABC 和△AED 是等边三角形，连接BD ，EC 交于点O ，连接AO ，下列结论：①BD =EC ；②∠BOC =60°；③∠AOE =60°；④EO =CO ，其中正确的有 ．(将所有正确的序号填在横线上)．（延伸应用）（3）如图3，AB =BC ，∠ABC =∠BDC =60°，试探究∠A 与∠C 的数量关系．5．学习了三角形全等的判定方法（即“SAS ”、“ASA ”、“AAS ”、“SSS ”）和直角三角形全等的判定方法（即“HL ”）后，我们继续对“两个三角形满足两边的其中一边的对角对应相等”的情形进行研究．（初步思考）我们不妨将问题用符号语言表示为：在△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，然后，对∠B 进行分类，可分为“∠B 是直角、钝角、锐角”三种情况进行探究．（深入探究）第一种情况：当∠B 是直角时，△ABC ≌△DEF ．（1）如图①，在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ＝90°，根据______，可以知道Rt △ABC ≌Rt △DEF ．第二种情况：当∠B 是钝角时，△ABC ≌△DEF ．（2）如图②，在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，且∠B 、∠E 都是钝角．求证：△ABC ≌△DEF ．第三种情况：当∠B 是锐角时，△ABC 和△DEF 不一定全等．（3）在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，且∠B 、∠E 都是锐角．请你用直尺在图③中作出△DEF ，使△DEF 和△ABC 不全等，并作简要说明．6．在△ABC 中，已知∠A ＝α．（1）如图1，∠ABC 、∠ACB 的平分线相交于点D ．①当α＝70°时，∠BDC 度数＝ 度（直接写出结果）；②∠BDC 的度数为 （用含α的代数式表示）；（2）如图2，若∠ABC 的平分线与∠ACE 角平分线交于点F ，求∠BFC 的度数（用含α的代数式表示）．（3）在（2）的条件下，将△FBC 以直线BC 为对称轴翻折得到△GBC ，∠GBC 的角平分线与∠GCB 的角平分线交于点M （如图3），求∠BMC 的度数（用含α的代数式表示）．7．（1）问题发现．如图1，ACB ∆和DCE ∆均为等边三角形，点A 、D 、E 均在同一直线上，连接BE ．①求证：ADC BEC ∆∆≌．②求AEB ∠的度数．③线段AD 、BE 之间的数量关系为__________．（2）拓展探究．如图2，ACB ∆和DCE ∆均为等腰直角三角形，90ACB DCE ∠=∠=︒，点A 、D 、E 在同一直线上，CM 为DCE ∆中DE 边上的高，连接BE ．①请判断AEB ∠的度数为____________．②线段CM 、AE 、BE 之间的数量关系为________．（直接写出结论，不需证明）8．在等边△ABC 的顶点A 、C 处各有一只蜗牛，它们同时出发，分别以每分钟1米的速度由A 向B 和由C 向A 爬行，其中一只蜗牛爬到终点时，另一只也停止运动，经过t 分钟后，它们分别爬行到D 、E 处，请问：（1）如图1，在爬行过程中，CD 和BE 始终相等吗，请证明？（2）如果将原题中的“由A 向B 和由C 向A 爬行”，改为“沿着AB 和CA 的延长线爬行”，EB 与CD 交于点Q ，其他条件不变，蜗牛爬行过程中∠CQE 的大小保持不变，请利用图2说明：∠CQE =60°；（3）如果将原题中“由C 向A 爬行”改为“沿着BC 的延长线爬行，连接DE 交AC 于F ”，其他条件不变，如图3，则爬行过程中，证明：DF =EF9．某校八年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究．（1）如图1，在△ABC中，∠ABC与∠ACB的平分线交于点P，∠A＝64°，则∠BPC＝；（2）如图2，△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E．其中∠A＝α，求∠BEC．（用α表示∠BEC）；（3）如图3，∠CBM、∠BCN为△ABC的外角，∠CBM、∠BCN的平分线交于点Q，请你写出∠BQC与∠A的数量关系，并证明．10．在我们认识的多边形中，有很多轴对称图形．有些多边形，边数不同对称轴的条数也不同；有些多边形，边数相同但却有不同数目的对称轴．回答下列问题：（1）非等边的等腰三角形有________条对称轴，非正方形的长方形有________条对称轴，等边三角形有___________条对称轴；（2）观察下列一组凸多边形（实线画出），它们的共同点是只有1条对称轴，其中图1-2和图1-3都可以看作由图1-1修改得到的，仿照类似的修改方式，请你在图1-4和图1-5中，分别修改图1-2和图1-3，得到一个只有1条对称轴的凸五边形，并用实线画出所得的凸五边形；（3）小明希望构造出一个恰好有2条对称轴的凸六边形，于是他选择修改长方形，图2中是他没有完成的图形，请用实线帮他补完整个图形；（4）请你画一个恰好有3条对称轴的凸六边形，并用虚线标出对称轴．11．（1）在等边三角形ABC中，①如图①，D，E分别是边AC，AB上的点且AE=CD，BD与EC交于点F，则∠BFE的度数是度；②如图②，D，E分别是边AC，BA延长线上的点且AE=CD，BD与EC的延长线交于点F，此时∠BFE的度数是度；（2）如图③，在△ABC中，AC=BC，∠ACB是锐角，点O是AC边的垂直平分线与BC的交点，点D，E分别在AC，OA的延长线上，AE=CD，BD与EC的延长线交于点F，若∠ACB=α，求∠BFE的大小．（用含α的代数式表示）．12．在△ABC中，AB=AC，D是直线BC上一点，以AD为一条边在AD的右侧作△ADE，使AE=AD，∠DAE=∠BAC，连接CE．（1）如图，当点D在BC延长线上移动时，若∠BAC=40°，则∠ACE=，∠DCE=，BC、DC、CE之间的数量关系为；（2）设∠BAC=α，∠DCE=β．①当点D在BC延长线上移动时，α与β之间有什么数量关系？请说明理由；②当点D在直线BC上（不与B，C两点重合）移动时，α与β之间有什么数量关系？请直接写出你的结论．（3）当CE∥AB时，若△ABD中最小角为15°，试探究∠ACB的度数（直接写出结果，无需写出求解过程）．13．（阅读材料）：（1）在ABC ∆中，若90C ∠=︒，由“三角形内角和为180°”得1801809090A B C ∠︒+∠=-∠︒︒-=︒=．（2）在ABC ∆中，若90A B ∠+∠=︒，由“三角形内角和为180°”得180()1809090C A B ∠=︒-∠+∠=︒-︒=︒．（解决问题）：如图①，在平面直角坐标系中，点C 是x 轴负半轴上的一个动点．已知//AB x 轴，交y 轴于点E ，连接CE ，CF 是∠ECO 的角平分线，交AB 于点F ，交y 轴于点D ．过E 点作EM 平分∠CEB ，交CF 于点M ．（1）试判断EM 与CF 的位置关系，并说明理由；（2）如图②，过E 点作PE ⊥CE ，交CF 于点P ．求证：∠EPC=∠EDP ；（3）在（2）的基础上，作EN 平分∠AEP ，交OC 于点N ，如图③．请问随着C 点的运动，∠NEM 的度数是否发生变化？若不变，求出其值：若变化，请说明理由．14．已知：MN ∥PQ ，点A ，B 分别在MN ，PQ 上，点C 为MN ，PQ 之间的一点，连接CA ，CB ．（1）如图1，求证：∠C=∠MAC+∠PBC ；（2）如图2，AD ，BD ，AE ，BE 分别为∠MAC ，∠PBC ，∠CAN ，∠CBQ 的角平分线，求证：∠D+∠E=180°；（3）在（2）的条件下，如图3，过点D 作DA 的垂线交PQ 于点G ，点F 在PQ 上，∠FDA=2∠FDB ，FD 的延长线交EA 的延长线于点H ，若3∠C=4∠E ，猜想∠H 与∠GDB 的倍数关系并证明．15．（1）如图1，ABC 和DCE 都是等边三角形，且B ，C ，D 三点在一条直线上，连接AD ，BE 相交于点P ，求证：BE AD =．（2）如图2，在BCD 中，若120BCD ∠<︒，分别以BC ，CD 和BD 为边在BCD 外部作等边ABC ，等边CDE △，等边BDF ，连接AD 、BE 、CF 恰交于点P ． ①求证：AD BE CF ==；②如图2，在（2）的条件下，试猜想PB ，PC ，PD 与BE 存在怎样的数量关系，并说明理由．16．已知//,MN GH 在Rt ABC 中，90,30ACB BAC ∠=︒∠=︒，点A 在MN 上，边BC 在GH 上，在Rt DEF △中，90,DFE ∠=︒边DE 在直线AB 上，45EDF ∠=︒； （1）如图1，求BAN ∠的度数；（2）如图2，将Rt DEF △沿射线BA 的方向平移，当点F 在M 上时，求AFE ∠度数； （3）将Rt DEF △在直线AB 上平移，当以A D F 、、为顶点的三角形是直角三角形时，直接写出FAN ∠度数．17．完全平方公式：()2222a b a ab b ±=±+适当的变形，可以解决很多的数学问题．例如：若3,1a b ab ，求22a b +的值．解：因为3,1a b ab 所以()29,22a b ab +==所以2229,22a b ab ab ++==得227a b +=．根据上面的解题思路与方法，解决下列问题：（1）若228,40x y x y +=+=，求xy 的值；（2）①若()45x x -=,则()224x x -+= ； ②若()()458x x --=则()22()45x x -+-= ； （3）如图，点C 是线段AB 上的一点，以AC BC 、为边向两边作正方形，设6AB =，两正方形的面积和1218S S +=，求图中阴影部分面积．18．已知AB //CD ，点E 是平面内一点，∠CDE 的角平分线与∠ABE 的角平分线交于点F ． （1）若点E 的位置如图1所示．①若∠ABE =60°，∠CDE =80°，则∠F = °；②探究∠F 与∠BED 的数量关系并证明你的结论；（2）若点E 的位置如图2所示，∠F 与∠BED 满足的数量关系式是 ．（3）若点E 的位置如图3所示，∠CDE 为锐角，且1452E F ∠≥∠+︒，设∠F =α，则α的取值范围为 ．19．如图1，直角三角形DEF 与直角三角形ABC 的斜边在同一直线上，∠EDF ＝30°，∠ABC ＝40°，CD 平分∠ACB ，将△DEF 绕点D 按逆时针方向旋转，记∠ADF 为α（0°＜α＜180°），在旋转过程中；（1）如图2，当∠α＝ 时，//DE BC ，当∠α＝ 时，DE ⊥BC ；（2）如图3，当顶点C 在△DEF 内部时，边DF 、DE 分别交BC 、AC 的延长线于点M 、N ， ①此时∠α的度数范围是 ；②∠1与∠2度数的和是否变化？若不变求出∠1与∠2度数和；若变化，请说明理由； ③若使得∠2≥2∠1，求∠α的度数范围．20．如图，△ABC 是等边三角形，△ADC 与△ABC 关于直线AC 对称，AE 与CD 垂直交BC 的延长线于点E ，∠EAF ＝45°，且AF 与AB 在AE 的两侧，EF ⊥AF ．（1）依题意补全图形．（2）①在AE 上找一点P ，使点P 到点B ，点C 的距离和最短；②求证：点D 到AF ，EF 的距离相等．【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）见解析；（2）30ABE CDE ∠-∠=︒【解析】【分析】（1）根据聪聪提供的辅助线作法进行证明，先由平行线的性质得：AGC MCD ∠=∠，90F GAF ∠+∠=︒，再证明MCD BAG ∠=∠，可得结论；（2）根据平行线的性质和三角形的外角性质可得结论．【详解】解：（1）证明：如图2，过A 作//AG FM ，交CD 于G ，AGC MCD ∴∠=∠，90F GAF ∠+∠=︒，FN FM ⊥，90F ∴∠=︒，90GAF ∴∠=︒，90FAB MCD ∠-∠=︒，FAB GAF MCD BAG ∴∠-∠=∠=∠，//AB CD ∴；（2）解：30ABE CDE ∠-∠=︒，理由如下：如图3，//AB CD ，BPD ABE ∴∠=∠，BPD CDE BED ∠=∠+∠，30BED ∠=︒，30BPD CDE ∴∠-∠=︒，∴30ABE CDE ∠-∠=︒．【点睛】本题主要考查了平行线的性质和判定以及三角形外角性质的运用，熟练掌握平行线的性质和判定是解决问题的关键．2．（1）全等，理由见解析；（2）t=3.5秒或5秒【解析】【分析】（1）根据垂直的定义得到∠DAC=∠ECB ，利用AAS 定理证明△ACD ≌△CBE ；（2）分点F 沿C→B 路径运动和点F 沿B→C 路径运动两种情况，根据等腰三角形的定义列出算式，计算即可；【详解】解：（1）△ACD 与△CBE 全等．理由如下：∵AD ⊥直线l ，∴∠DAC+∠ACD=90°，∵∠ACB=90°，∴∠BCE+∠ACD=90°，∴∠DAC=∠ECB ，在△ACD 和△CBE 中，ADC CEB DAC ECB CA CB ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△ACD ≌△CBE （AAS ）；（2）由题意得，AM=t ，FN=3t ，则CM=8-t ，由折叠的性质可知，CF=CB=6，∴CN=6-3t ，点N 在BC 上时，△CMN 为等腰直角三角形，当点N 沿C→B 路径运动时，由题意得，8-t=3t-6，解得，t=3.5，当点N 沿B→C 路径运动时，由题意得，8-t=18-3t ，解得，t=5，综上所述，当t=3.5秒或5秒时，△CMN 为等腰直角三角形；【点睛】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理，灵活运用分情况讨论思想是解题的关键．3．（1）证明见解析；（2）证明见解析；（3）结论：AD DG ND =-，证明见解析．【解析】【分析】（1）先根据直角三角形的性质得出60ABC ∠=︒，再根据角平分线的性质可得CD ED =，然后根据三角形的判定定理与性质可得BC BE =，最后根据等边三角形的判定即可得证；（2）如图（见解析），延长ED 使得DF MD =，连接MF ，先根据直角三角形的性质、等边三角形的判定得出MDF ∆是等边三角形，再根据等边三角形的性质、角的和差得出,,F MDB MF MD FMG DMB ∠=∠=∠=∠，然后根据三角形全等的判定与性质、等量代换即可得证；（3）如图（见解析），参照题（2），先证HDN ∆是等边三角形，再根据等边三角形的性质、角的和差得出,,H NDG NH ND HNB DNG ∠=∠=∠=∠，然后根据三角形全等的判定与性质、等量代换即可得证．【详解】（1）3,090A ACB ∠=︒∠=︒9060ABC A ∴∠=︒-∠=︒ BD 是ABC ∠的角平分线，DE AB ⊥CD ED ∴=在BCD ∆和BED ∆中，CD ED BD BD =⎧⎨=⎩()BCD BED HL ∴∆≅∆BC BE ∴=EBC ∴∆是等边三角形；（2）如图，延长ED 使得DF MD =，连接MF3,090A ACB ∠=︒∠=︒，BD 是ABC ∠的角平分线，DE AB ⊥60,ADE BDE AD BD ∴∠=∠=︒=60,18060MDF ADE MDB ADE BDE ∴∠=∠=︒∠=︒-∠-∠=︒MDF ∴∆是等边三角形,60MF DM F DMF ∴=∠=∠=︒60BMG ∠=︒DMF DM B M G G D M G ∴∠+∠=+∠∠，即FMG DMB ∠=∠在FMG ∆和DMB ∆中，60F MDB MF MD FMG DMB ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()FMG DMB ASA ∴∆≅∆GF BD ∴=，即DF DG BD +=AD DF DG MD DG ∴=+=+即AD DG MD =+；（3）结论：AD DG ND =-，证明过程如下：如图，延长BD 使得DH ND =，连接NH由（2）可知，60,18060,ADE HDN ADE BDE AD BD ∠=︒∠=︒-∠-∠=︒=HDN ∴∆是等边三角形,60NH ND H HND ∴=∠=∠=︒60BNG ∠=︒HND BND BND BNG ∠+∠=+∠∴∠，即N HNB D G ∠=∠在HNB ∆和DNG ∆中，60H NDG NH ND HNB DNG ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()HNB DNG ASA ∴∆≅∆HB DG ∴=，即DH BD DG +=ND AD DG ∴+=即AD DG ND =-．【点睛】本题考查了直角三角形的性质、等边三角形的判定与性质、三角形全等的判定定理与性质等知识点，较难的是题（2）和（3），通过作辅助线，构造一个等边三角形是解题关键．4．（1）证明见解析；（2）①②③；（3）∠A +∠C =180°．【解析】【分析】（1）利用等式的性质得出∠BAD=∠CAE ，即可得出结论；（2）同（1）的方法判断出△ABD ≌△ACE ，得出BD=CE ，再利用对顶角和三角形的内角和定理判断出∠BOC=60°，再判断出△BCF ≌△ACO ，得出∠AOC=120°，进而得出∠AOE=60°，再判断出BF ＜CF ，进而判断出∠OBC ＞30°，即可得出结论；（3）先判断出△BDP 是等边三角形，得出BD=BP ，∠DBP=60°，进而判断出△ABD ≌△CBP （SAS ），即可得出结论．【详解】（1）证明：∵∠BAC=∠DAE ，∴∠BAC+∠CAD=∠DAE+∠CAD ，∴∠BAD=∠CAE ，在△ABD 和△ACE 中，AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝ ， ∴△ABD ≌△ACE ；（2）如图2，∵△ABC 和△ADE 是等边三角形，∴AB=AC ，AD=AE ，∠BAC=∠DAE=60°，∴∠BAD=∠CAE ，在△ABD 和△ACE 中，AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝ ， ∴△ABD ≌△ACE ，∴BD=CE ，①正确，∠ADB=∠AEC ，记AD 与CE 的交点为G ，∵∠AGE=∠DGO ，∴180°-∠ADB-∠DGO=180°-∠AEC-∠AGE ，∴∠DOE=∠DAE=60°，∴∠BOC=60°，②正确，在OB 上取一点F ，使OF=OC ，∴△OCF 是等边三角形，∴CF=OC ，∠OFC=∠OCF=60°=∠ACB ，∴∠BCF=∠ACO ，∵AB=AC ，∴△BCF ≌△ACO （SAS ），∴∠AOC=∠BFC=180°-∠OFC=120°，∴∠AOE=180°-∠AOC=60°，③正确，连接AF ，要使OC=OE ，则有OC=12CE ， ∵BD=CE ，∴CF=OF=12BD ， ∴OF=BF+OD ，∴BF ＜CF ，∴∠OBC＞∠BCF，∵∠OBC+∠BCF=∠OFC=60°，∴∠OBC＞30°，而没办法判断∠OBC大于30度，所以，④不一定正确，即：正确的有①②③，故答案为①②③；（3）如图3，延长DC至P，使DP=DB，∵∠BDC=60°，∴△BDP是等边三角形，∴BD=BP，∠DBP=60°，∵∠BAC=60°=∠DBP，∴∠ABD=∠CBP，∵AB=CB，∴△ABD≌△CBP（SAS），∴∠BCP=∠A，∵∠BCD+∠BCP=180°，∴∠A+∠BCD=180°．【点睛】此题考查三角形综合题，等腰三角形的性质，等边三角形的性质，全等三角形的判定和性质，构造等边三角形是解题的关键．5．（1）HL；（2）见解析；（3）如图②，见解析；△DEF就是所求作的三角形，△DEF和△ABC不全等．【解析】【分析】（1）根据直角三角形全等的方法“HL”证明；（2）过点C作CG⊥AB交AB的延长线于G，过点F作FH⊥DE交DE的延长线于H，根据等角的补角相等求出∠CBG=∠FEH，再利用“角角边”证明△CBG和△FEH全等，根据全等三角形对应边相等可得CG=FH，再利用“HL”证明Rt△ACG和Rt△DFH全等，根据全等三角形对应角相等可得∠A=∠D，然后利用“角角边”证明△ABC和△DEF全等；（3）以点C为圆心，以AC长为半径画弧，与AB相交于点D，E与B重合，F与C重合，得到△DEF与△ABC不全等；（4）根据三种情况结论，∠B不小于∠A即可．【详解】（1）在直角三角形中一条斜边和一条直角边对应相等的两个直角三角形全等运用的是HL．（2）证明：如图①，分别过点C、F作对边AB、DE上的高CG、FH，其中G、H为垂足．∵∠ABC、∠DEF都是钝角∴G、H分别在AB、DE的延长线上．∵CG⊥AG，FH⊥DH，∴∠CGA＝∠FHD＝90°．∵∠CBG＝180°－∠ABC，∠FEH＝∠180°－∠DEF，∠ABC＝∠DEF，∴∠CBG＝∠FEH．在△BCG和△EFH中，∵∠CGB＝∠FHE，∠CBG＝∠FEH，BC＝EF，∴△BCG≌△EFH．∴CG＝FH．又∵AC＝DF．∴Rt△ACG≌△DFH．∴∠A＝∠D．在△ABC和△DEF中，∵∠ABC＝∠DEF，∠A＝∠D，AC＝DF，∴△ABC≌△DEF．（3）如图②，△DEF就是所求作的三角形，△DEF和△ABC不全等．【点睛】本题是三角形综合题，主要考查了全等三角形的判定与性质，应用与设计作图，熟练掌握三角形全等的判定方法是解题的关键，阅读量较大，审题要认真仔细．6．（1）（1）①125°；②1902α︒+，（2）1BFC 2α∠=；（3）1BMC 904α︒∠=+ 【解析】【分析】（1）①由三角形内角和定理易得∠ABC+∠ACB=110°，然后根据角平分线的定义，结合三角形内角和定理可求∠BDC ；②由三角形内角和定理易得∠ABC+∠ACB=180°-∠A ，采用①的推导方法即可求解； （2）由三角形外角性质得BFC FCE FBC ∠=∠-∠，然后结合角平分线的定义求解； （3）由折叠的对称性得BGC BFC ∠=∠，结合（1）②的结论可得答案．【详解】解：（1）①∵12DBC ∠=∠ABC ，∠DCB ＝12∠ACB ， ∴∠BDC ＝180°﹣∠DBC ﹣∠DCB＝180°﹣12（∠ABC +∠ACB ） ＝180°﹣12（180°﹣70°） ＝125° ②∵12DBC ∠=∠ABC ，∠DCB ＝12∠ACB ， ∴∠BDC ＝180°﹣∠DBC ﹣∠DCB＝180°﹣12（∠ABC +∠ACB ） ＝180°﹣12（180°﹣∠A ） ＝90°+12∠A ＝90°+12α． 故答案分别为125°，90°+12α． （2）∵BF 和CF 分别平分∠ABC 和∠ACE ∴1FBC ABC 2∠=∠，1FCE ACE 2∠=∠， ∴BFC FCE FBC ∠=∠-∠＝11(ACE ABC)A 22∠-∠=∠ 即1BFC 2α∠=． （3）由轴对称性质知：1BGC BFC 2α∠=∠=，由（1）②可得1BMC 90BGC 2∠=︒+∠， ∴1BMC 904α∠=︒+． 【点睛】 本题考查三角形中与角平分线有关的角度计算，熟练掌握三角形内角和定理，以及三角形的外角性质是解题的关键．7．（1）①详见解析；②60°；③AD BE =；（2）①90°；②2AE BE CM =+【解析】【分析】（1）易证∠ACD ＝∠BCE ，即可求证△ACD ≌△BCE ，根据全等三角形对应边相等可求得AD ＝BE ，根据全等三角形对应角相等即可求得∠AEB 的大小；（2）易证△ACD ≌△BCE ，可得∠ADC ＝∠BEC ，进而可以求得∠AEB ＝90°，即可求得DM ＝ME ＝CM ，即可解题．【详解】解：（1）①证明：∵ACB ∆和DCE ∆均为等边三角形，∴AC CB =，CD CE =，又∵60ACD DCB ECB DCB ∠+∠=∠+∠=︒，∴ACD ECB ∠=∠，∴()ADC BEC SAS ∆∆≌．②∵CDE ∆为等边三角形，∴60CDE ∠=︒．∵点A 、D 、E 在同一直线上，∴180120ADC CDE ∠=︒-∠=︒，又∵ADC BEC ∆∆≌，∴120ADC BEC ∠=∠=︒，∴1206060AEB ∠=︒-︒=︒．③AD BE =ADC BEC ∆∆≌，∴AD BE =．故填：AD BE =；（2）①∵ACB ∆和DCE ∆均为等腰直角三角形，∴AC CB =，CD CE =，又∵90ACB DCE ∠=∠=︒，∴ACD DCB ECB DCB ∠+∠=∠+∠，∴ACD ECB ∠=∠，在ACD ∆和BCE ∆中，AC CB ACD ECB CD CE =⎧⎪∠=∠⎨⎪=⎩， ∴E ACD BC ∆∆≌，∴ADC BEC ∠∠=．∵点A 、D 、E 在同一直线上，∴180********ADC BEC CDE ∠=∠=︒-∠=︒-︒=︒，∴1351354590AEB CED ∠=︒-∠=︒-︒=︒．②∵CDA CEB ∆∆≌，∴BE AD =．∵CD CE =，CM DE ⊥，∴DM ME =．又∵90DCE ∠=︒，∴2DE CM =，∴2AE AD DE BE CM =+=+．故填：①90°；②2AE BE CM =+．【点睛】本题考查了全等三角形的判定，考查了全等三角形对应边相等、对应角相等的性质，本题中求证△ACD ≌△BCE 是解题的关键．8．（1)相等，证明见解析；（2)证明见解析；（3)证明见解析．【解析】【分析】（1）先证明△ACD ≌△CBE ，再由全等三角形的性质即可证得CD=BE ；（2）先证明△BCD ≌△ABE ，得到∠BCD=∠ABE ，求出∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC ，∠CQE=180°-∠DQB ，即可解答； （3）如图3，过点D 作DG ∥BC 交AC 于点G ，根据等边三角形的三边相等，可以证得AD=DG=CE ；进而证明△DGF 和△ECF 全等，最后根据全等三角形的性质即可证明．【详解】（1）解：CD 和BE 始终相等，理由如下：如图1，AB=BC=CA ，两只蜗牛速度相同，且同时出发，∴CE=AD ，∠A=∠BCE=60°在△ACD 与△CBE 中，AC=CB ，∠A=∠BCE ，AD=CE∴△ACD ≌△CBE （SAS ），∴CD=BE ，即CD 和BE 始终相等；（2）证明：根据题意得：CE=AD ，∵AB=AC ，∴AE=BD ，∴△ABC 是等边三角形，∴AB=BC ，∠BAC=∠ACB=60°，∵∠EAB+∠ABC=180°，∠DBC+∠ABC=180°，∴∠EAB=∠DBC ，在△BCD 和△ABE 中，BC=AB ，∠DBC=∠EAB ，BD=AE∴△BCD ≌△ABE （SAS ），∴∠BCD=∠ABE∴∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC=180°-60°=120°，∴∠CQE=180°-∠DQB=60°，即CQE=60°；（3）解：爬行过程中，DF 始终等于EF 是正确的，理由如下：如图，过点D 作DG ∥BC 交AC 于点G ，∴∠ADG=∠B=∠AGD=60°，∠GDF=∠E ，∴△ADG 为等边三角形，∴AD=DG=CE ，在△DGF 和△ECF 中，∠GFD=∠CFE ，∠GDF=∠E ，DG=EC∴△DGF ≌△EDF （AAS ），∴DF=EF.【点睛】本题主要考查了全等三角形的判定与性质和等边三角形的性质；题弄懂题中所给的信息，再根据所提供的思路寻找证明条件是解答本题的关键．9．（1）∠BPC ＝122°；（2）∠BEC ＝2a ；（3）∠BQC ＝90°﹣12∠A ，证明见解析 【解析】【分析】（1）根据三角形的内角和化为角平分线的定义；（2）根据三角形的一个外角等于与它不相邻的两个内角的和，用∠A 与∠1表示出∠2，再利用∠E 与∠1表示出∠2，于是得到结论；（3）根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠EBC 与∠ECB ，然后再根据三角形的内角和定理列式整理即可得解．【详解】解：（1）BP 、CP 分别平分ABC ∠和ACB ∠，12PBC ABC ∴∠=∠，12PCB ACB ∠=∠， 180()BPC PBC PCB ∴∠=︒-∠+∠11180()22ABC ACB =︒-∠+∠， 1180()2ABC ACB =︒-∠+∠， 1(180180)2A =︒-︒-∠， 1180902A =-︒+︒∠， 9032122=︒+=︒，故答案为：122︒；（2）CE 和BE 分别是ACB ∠和ABD ∠的角平分线，112ACB ∴∠=∠，122ABD ∠=∠， 又ABD ∠是ABC ∆的一外角，ABD A ACB ∴∠=∠+∠，112()122A ABC A ∴∠=∠+∠=∠+∠， 2∠是BEC ∆的一外角，112111222BEC A A α∴∠=∠-∠=∠+∠-∠=∠=； （3）1()2QBC A ACB ∠=∠+∠，1()2QCB A ABC ∠=∠+∠， 180BQC QBC QCB ∠=︒-∠-∠，11180()()22A ACB A ABC =︒-∠+∠-∠+∠， 11180()22A A ABC ACB =︒-∠-∠+∠+∠， 结论：1902BQC A ∠=︒-∠．【点睛】本题考查了三角形的外角性质与内角和定理，熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键．10．（1）1，2，3；（2）答案见解析；（3）答案见解析；（4）答案见解析．【解析】【分析】（1）根据等腰三角形的性质、矩形的性质以及等边三角形的性质进行判断即可；（2）中图1-2和图1-3都可以看作由图1-1修改得到的，在图1-4和图1-5中，分别仿照类似的修改方式进行画图即可；（3）长方形具有两条对称轴，在长方形的右侧补出与左侧一样的图形，即可构造出一个恰好有2条对称轴的凸六边形；（4）在等边三角形的基础上加以修改，即可得到恰好有3条对称轴的凸六边形．【详解】解：（1）非等边的等腰三角形有1条对称轴，非正方形的长方形有2条对称轴，等边三角形有3条对称轴，故答案为1，2，3；（2）恰好有1条对称轴的凸五边形如图中所示．（3）恰好有2条对称轴的凸六边形如图所示．（4）恰好有3条对称轴的凸六边形如图所示．11．（1）①60°；②60°；（2）∠BFE =α．【解析】【分析】（1）①先证明△ACE≌△CBD得到∠ACE=∠CBD，再由三角形外角和定理可得∠BFE=∠CBD+∠BCF；②先证明△ACE≌△CBD得∠ACE=∠CBD=∠DCF，再由三角形外角和定理可得∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA；（2）证明△AEC≌△CDB得到∠E=∠D，则∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α．【详解】（1）如图①中，∵△ABC是等边三角形，∴AC=CB，∠A=∠BCD=60°，∵AE=CD，∴△ACE≌△CBD，∴∠ACE=∠CBD，∴∠BFE=∠CBD+∠BCF=∠ACE+∠BCF=∠BCA=60°．故答案为60．（2）如图②中，∵△ABC是等边三角形，∴AC=CB，∠A=∠BCD=60°，∴∠CAE=∠BCD=′120°∵AE=CD，∴△ACE≌△CBD，∴∠ACE=∠CBD=∠DCF，∴∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA=60°．故答案为60．（3）如图③中，∵点O是AC边的垂直平分线与BC的交点，∴OC=OA，∴∠EAC=∠DCB=α，∵AC=BC，AE=CD，∴△AEC≌△CDB，∴∠E=∠D，∴∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α．【点睛】本题综合考查了三角形全等以及三角形外角和定理.12．（1）70°，40°，BC+DC=CE；（2）①α=β；②当点D在BC上移动时，α=β或α+β=180°；（3）∠ACB=60°．【解析】【分析】（1）证△BAD≌△CAE，推出∠B=∠ACE，根据三角形外角性质和全等三角形的性质求出即可；（2）①证△BAD≌△CAE，推出∠B=∠ACE，根据三角形外角性质求出即可；②分三种情况：（Ⅰ）当D在线段BC上时，证明△ABD≌△ACE（SAS），则∠ADB=∠AEC，∠ABC=∠ACE，推出∠DAE+∠DCE=180°，即α+β=180°；（Ⅱ）当点D在线段BC反向延长线上时，α=β，同理可证明△ABD≌△ACE（SAS），则∠ABD=∠ACE，推出∠BAC=∠DCE，即α=β；（Ⅲ）当点D在线段BC的延长线上时，由①得α=β；（3）当点D在线段BC的延长线上或在线段BC反向延长线上移动时，α=β，由CE∥AB，得∠ABC=∠DCE，推出∠ABC=∠BAC，易证∠ABC=∠ACB=∠BAC，则△ABC是等边三角形，得出∠ACB=60°；当D在线段BC上时，α+β=180°，由CE∥AB，得∠ABC+∠DCE=180°，推出∠ABC=∠BAC，易证∠ABC=∠ACB=∠BAC，则△ABC是等边三角形，得出∠ACB=60°．【详解】（1）如图1所示：∵∠DAE=∠BAC，∴∠DAE+∠CAD=∠BAC+∠CAD，∴∠BAD=∠CAE．在△BAD和△CAE中，AB ACBAD CAE AD AE=⎧⎪∠=∠⎨⎪=⎩，∴△BAD≌△CAE（SAS），∴∠ACE=∠B12=（180°﹣40°）=70°，BD=CE，∴BC+DC=CE．∵∠ACD=∠B+∠BAC=∠ACE+∠DCE，∴∠BAC=∠DCE．∵∠BAC=40°，∴∠DCE=40°．故答案为：70°，40°，BC+DC=CE；（2）①当点D在线段BC的延长线上移动时，α与β之间的数量关系是α=β．理由如下：∵∠DAE=∠BAC，∴∠DAE+∠CAD=∠BAC+∠CAD，∴∠BAD=∠CAE．在△BAD和△CAE中，AB ACBAD CAE AD AE=⎧⎪∠=∠⎨⎪=⎩，∴△BAD≌△CAE（SAS），∴∠B=∠ACE．∵∠ACD=∠B+∠BAC=∠ACE+∠DCE，∴∠BAC=∠DCE．∵∠BAC=α，∠DCE=β，∴α=β；②分三种情况：（Ⅰ）当D在线段BC上时，α+β=180°，如图2所示．理由如下：同理可证明：△ABD≌△ACE（SAS），∴∠ADB=∠AEC，∠ABC=∠ACE．∵∠ADC+∠ADB=180°，∴∠ADC+∠AEC=180°，∴∠DAE+∠DCE=180°．∵∠BAC=∠DAE=α，∠DCE=β，∴α+β=180°；（Ⅱ）当点D在线段BC反向延长线上时，α=β，如图3所示．理由如下：同理可证明：△ABD≌△ACE（SAS），∴∠ABD=∠ACE．∵∠ACE=∠ACD+∠DCE，∠ABD=∠ACD+∠BAC，∴∠ACD+∠DCE=∠ACD+∠BAC，∴∠BAC=∠DCE．∵∠BAC=α，∠DCE=β，∴α=β；（Ⅲ）当点D在线段BC的延长线上时，如图1所示，α=β；综上所述：当点D在BC上移动时，α=β或α+β=180°；（3）∠ACB=60°．理由如下：∵当点D在线段BC的延长线上或在线段BC反向延长线上移动时，α=β，即∠BAC=∠DCE．∵CE∥AB，∴∠ABC=∠DCE，∴∠ABC=∠BAC．∴∠ABC =∠ACB =∠BAC ，∴△ABC 是等边三角形，∴∠ACB =60°；∵当D 在线段BC 上时，α+β=180°，即∠BAC +∠DCE =180°．∵CE ∥AB ，∴∠ABC +∠DCE =180°，∴∠ABC =∠BAC ．∵AB =AC ，∴∠ABC =∠ACB =∠BAC ，∴△ABC 是等边三角形，∴∠ACB =60°；综上所述：当CE ∥AB 时，若△ABD 中最小角为15°，∠ACB 的度数为60°．【点睛】本题是三角形综合题目，考查了全等三角形的判定与性质、等腰三角形的性质、等边三角形的判定与性质、平行线的性质、三角形的外角性质和多边形内角和等知识．本题综合性强，熟练掌握全等三角形的判定与性质是解题的关键．13．（1）EM ⊥CF ，理由见解析；（2）证明见解析；（3）不变，且∠NEM=45°，理由见解析．【解析】【分析】（1）EM ⊥CF ，分别利用角平分线的性质、平行线的性质、三角形的内角和定理进行求证即可；（2）根据垂直定义和三角形的内角和定理证得∠DCO+∠CDO=90°，∠ECP+∠EPC=90°，再利用等角的余角相等和对顶角相等即可证得结论；（3）不变，且∠NEM=45°，先利用平行线的性质得到∠AEC=∠ECO=2∠ECP ，进而有∠AEP=∠CEP+∠AEC=90°+2∠ECP ，再由角平分线的定义∠NEP=∠AEN=45°+∠ECP ，再根据同角的余角相等得到∠ECP=∠MEP ，然后等量代换证得∠NEM=45°，是定值．【详解】解：(1)EM ⊥CF ，理由如下：∵CF 平分∠ECO ，EM 平分∠FEC ，∴∠ECF=∠FCO=12ECO ∠，∠FEM=∠CEM=12CEF ∠ ∵AB ∥x 轴 1111()180902222ECF CEM ECO CEF ECO CEF ∴∠+∠=∠+∠=∠+∠=⨯︒=︒ ∴∠ECO+∠CEF=180°∴∠EMC=180°-（∠CEM+∠ECF ）=180°-90°=90°（2）由题得，∠EOC=90°∴∠DCO+∠CDO=180°-∠EOC=180°-90°=90°∵PE⊥CE∴∠CEP=90°∴∠ECP+∠EPC=180°-∠CEP=180°-90°=90°∵∠DCO=∠ECP∴∠CDO=∠EPC又∵∠CDO=∠EDP∴∠EPC=∠EDP(3)不变，且∠NEM=45°，理由如下：∵AB∥x轴∴∠AEC=∠ECO=2∠ECP∴∠AEP=∠CEP+∠AEC=90°+2∠ECP∵EN平分∠AEP∴∠NEP=∠AEN=12AEP∠=1(902)2ECP︒+∠=45°+∠ECP∵∠CEP=90°∴∠ECP+∠EPC=90°又∵∠EMC=90°∴∠MEP+∠EPC=90°∴∠ECP=∠MEP∴∠NEP=∠NEM+∠MEP=∠NEM+∠ECP又∵∠NEP=45°+∠ECP∴∠NEM=45°．【点睛】本题是一道综合探究题，涉及有平行线的性质、角平分线的定义、三角形的内角和定理、同（等）角的余角相等、对顶角相等、垂线性质等知识，解答的关键是认真审题，结合图形，寻找相关联信息，确定解题思路，进而探究、推理、论证．14．（1）见解析；（2）见解析；（3）猜想：∠H= 3∠GDB ，证明见解析．【解析】【分析】（1）作辅助线：过C 作EF ∥MN ，根据平行的传递性可知这三条直线两两平行，由平行线的性质得到内错角相等∠MAC=∠ACF ，∠BCF=∠PBC ，再进行角的加和即可得出结论；（2）根据角平分线线定理得知11,22MAD MAC NAE NAC ∠=∠∠=∠，利用平角为180°得到∠DAE=90°，同理得90DBE ∠=︒，再根据四边形内角和180°，得出结论；（3）由（1）（2）中的结论进行等量代换得到3∠ADB=2∠E ，并且两角的和为180°，由此得到两个角的度数分别为72°和108°，利用角的和与差得到∠HDA=36°，∠H=54°，由此得到倍数关系． 【详解】（1）如图：过C 作EF ∥MN ，∵MN ∥PQ ， ∴MN ∥EF ∥PQ ，∴∠MAC=∠ACF ，∠BCF=∠PBC ，∴∠ACF+∠BCF=∠MAC+∠PBC ，即∠ACB=∠MAC+∠PBC ．（2）∵AD ，AE 分别为∠MAC ，∠CAN 的角平分线，∴11,22MAD MAC NAE NAC ∠=∠∠=∠， ∴11118090222MAD NAE MAC NAC ∠+∠=∠+∠=⨯︒=︒，于是∠DAE=90° 同理可得：90PBD QBE ∠+∠=︒，由（1）可得：∵ 180D E MAD PBD NAE QBE ∠+∠=∠+∠+∠+∠=︒．（3）猜想：∠H= 3∠GDB.理由如下：由（1）可知：2()2C MAC PBC MAD PBD ADB ∠=∠+∠=∠+∠=∠， ∵3∠C=4∠E ，∴6∠ADB=4∠E ，∴3∠ADB=2∠E ，∵∠ADB+∠E=180°，∴∠ADB=72°，∠E=108°，∵DG ⊥DA ，∴∠GDB=18°，∵∠FDA=2∠FDB ，。

沪教版八年级上册压轴题数学模拟试卷一、压轴题1．如图1．在△ABC 中，∠ACB =90°，AC =BC =10，直线DE 经过点C ，过点A ，B 分别作AD ⊥DE ，BE ⊥DE ，垂足分别为点D 和E ，AD =8，BE =6．（1）①求证：△ADC ≌△CEB ；②求DE 的长；（2）如图2，点M 以3个单位长度/秒的速度从点C 出发沿着边CA 运动，到终点A ，点N 以8个单位长度/秒的速度从点B 出发沿着线BC —CA 运动，到终点A ．M ，N 两点同时出发，运动时间为t 秒(t ＞0)，当点N 到达终点时，两点同时停止运动，过点M 作PM ⊥DE 于点P ，过点N 作QN ⊥DE 于点Q ；①当点N 在线段CA 上时，用含有t 的代数式表示线段CN 的长度；②当t 为何值时，点M 与点N 重合；③当△PCM 与△QCN 全等时，则t = ．2．在ABC 中，AB AC =，D 是直线AB 上一点，E 在直线BC 上，且DE DC =． （1）如图1，当D 在AB 上，E 在CB 延长线上时，求证：EDB ACD ∠=∠；（2）如图2，当ABC 为等边三角形时，D 是BA 的延长线上一点，E 在BC 上时，作//EF AC ，求证：BE AD =；（3）在（2）的条件下，ABC ∠的平分线BF 交CD 于点F ，连AF ，过A 点作AH CD ⊥于点H ，当30EDC ∠=︒，6CF =时，求DH 的长度．3．阅读下面材料，完成(1)-(3)题．数学课上，老师出示了这样一道题：如图1，已知等腰△ABC 中，AB ＝AC ，AD 为BC 边上的中线，以AB 为边向AB 左侧作等边△ABE ，直线CE 与直线AD 交于点F ．请探究线段EF 、AF 、DF 之间的数量关系，并证明． 同学们经过思考后，交流了自已的想法：小明：“通过观察和度量，发现∠DFC 的度数可以求出来．”小强：“通过观察和度量，发现线段DF 和CF 之间存在某种数量关系．”小伟：“通过做辅助线构造全等三角形，就可以将问题解决．”......老师：“若以AB 为边向AB 右侧作等边△ABE ，其它条件均不改变，请在图2中补全图形,探究线段EF 、AF 、DF 三者的数量关系，并证明你的结论．”（1）求∠DFC 的度数；（2）在图1中探究线段EF 、AF 、DF 之间的数量关系，并证明；（3）在图2中补全图形，探究线段EF 、AF 、DF 之间的数量关系，并证明．4．已知ABC 和ADE 都是等腰三角形，AB AC =，AD AE =，DAE BAC ∠=∠． （初步感知）（1）特殊情形：如图①，若点D ，E 分别在边AB ，AC 上，则DB __________EC ．（填＞、＜或=）（2）发现证明：如图②，将图①中的ADE 绕点A 旋转，当点D 在ABC 外部，点E 在ABC 内部时，求证：DB EC =．（深入研究）（3）如图③，ABC 和ADE 都是等边三角形，点C ，E ，D 在同一条直线上，则CDB ∠的度数为__________；线段CE ，BD 之间的数量关系为__________．（4）如图④，ABC 和ADE 都是等腰直角三角形，90BAC DAE ∠=∠=︒，点C 、D 、E 在同一直线上，AM 为ADE 中DE 边上的高，则CDB ∠的度数为__________；线段AM ，BD ，CD 之间的数量关系为__________．（拓展提升）（5）如图⑤，ABC 和ADE 都是等腰直角三角形，90BAC DAE ∠=∠=︒，将ADE 绕点A 逆时针旋转，连结BE 、CD ．当5AB =，2AD =时，在旋转过程中，ABE △与ADC 的面积和的最大值为__________．5．学习了三角形全等的判定方法（即“SAS ”、“ASA ”、“AAS ”、“SSS ”）和直角三角形全等的判定方法（即“HL ”）后，我们继续对“两个三角形满足两边的其中一边的对角对应相等”的情形进行研究．（初步思考）我们不妨将问题用符号语言表示为：在△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，然后，对∠B 进行分类，可分为“∠B 是直角、钝角、锐角”三种情况进行探究．（深入探究）第一种情况：当∠B 是直角时，△ABC ≌△DEF ．（1）如图①，在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ＝90°，根据______，可以知道Rt △ABC ≌Rt △DEF ．第二种情况：当∠B 是钝角时，△ABC ≌△DEF ．（2）如图②，在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，且∠B 、∠E 都是钝角．求证：△ABC ≌△DEF ．第三种情况：当∠B 是锐角时，△ABC 和△DEF 不一定全等．（3）在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，且∠B 、∠E 都是锐角．请你用直尺在图③中作出△DEF ，使△DEF 和△ABC 不全等，并作简要说明．6．如图，若要判定纸带两条边线a ，b 是否互相平行，我们可以采用将纸条沿AB 折叠的方式来进行探究．（1）如图1，展开后，测得12∠=∠，则可判定a//b ，请写出判定的依据_________； （2）如图2，若要使a//b ，则1∠与2∠应该满足的关系是_________；（3）如图3，纸带两条边线a ，b 互相平行，折叠后的边线b 与a 交于点C ，若将纸带沿11A B （1A ，1B 分别在边线a ，b 上）再次折叠，折叠后的边线b 与a 交于点1C ，AB//11A B ，137BB AC ==，，求出1AC 的长．7．阅读并填空：如图，ABC 是等腰三角形，AB AC =，D 是边AC 延长线上的一点，E 在边AB 上且联接DE 交BC 于O ，如果OE OD ，那么CD BE =，为什么？解：过点E 作EF AC 交BC 于F所以ACB EFB ∠=∠（两直线平行，同位角相等）D OEF ∠=∠（________）在OCD 与OFE △中()________COD FOE OD OED OEF ⎧∠=∠⎪=⎨⎪∠=∠⎩所以OCD OFE △≌△，（________）所以CD FE =（________）因为AB AC =（已知）所以ACB B =∠∠（________）所以EFB B ∠=∠（等量代换）所以BE FE =（________）所以CD BE =8．如图（1），AB ＝4cm ，AC ⊥AB ，BD ⊥AB ，AC ＝BD ＝3cm ．点 P 在线段 AB 上以 1/cm s 的速度由点 A 向点 B 运动，同时，点 Q 在线段 BD 上由点 B 向点 D 运动．它们运动的时间为 t （s ）．（1）若点 Q 的运动速度与点 P 的运动速度相等，当t ＝1 时，△ACP 与△BPQ 是否全等，请说明理由， 并判断此时线段 PC 和线段 PQ 的位置关系；（2）如图（2），将图（1）中的“AC ⊥AB ，BD ⊥AB”为改“∠CAB ＝∠DBA ＝60°”，其他条件不变．设点 Q 的运动速度为x /cm s ，是否存在实数x ，使得△ACP 与△BPQ 全等？若存在，求出相应的x 、t 的值；若不存在，请说明理由．9．在《经典几何图形的研究与变式》一课中，庞老师出示了一个问题：“如图1，等腰直角三角形的三个顶点分别落在三条等距的平行线1l ，2l ，3l 上，90BAC ∠=︒，且每两条平行线之间的距离为1，求AB 的长度”.在研究这道题的解法和变式的过程中，同学们提出了很多想法：（1）小明说：我只需要过B 、C 向1l 作垂线，就能利用全等三角形的知识求出AB 的长. （2）小林说：“我们可以改变ABC 的形状.如图2，AB AC =，120BAC ∠=︒，且每两条平行线之间的距离为1，求AB 的长.”（3）小谢说：“我们除了改变ABC 的形状，还能改变平行线之间的距离.如图3，等边三角形ABC 三个顶点分别落在三条平行线1l ，2l ，3l 上，且1l 与2l 之间的距离为1，2l 与3l 之间的距离为2，求AB 的长、”请你根据3位同学的提示，分别求出三种情况下AB 的长度.10．已知ABC ，P 是平面内任意一点（A 、B 、C 、P 中任意三点都不在同一直线上）．连接 PB 、PC ，设∠PBA ＝s°，∠PCA ＝t°，∠BPC ＝x°，∠BAC ＝y°．（1）如图，当点 P 在ABC 内时，①若 y ＝70，s ＝10，t ＝20，则 x ＝ ； ②探究 s 、t 、x 、y 之间的数量关系，并证明你得到的结论．（2）当点 P 在ABC 外时，直接写出 s 、t 、x 、y 之间所有可能的数量关系，并画出相应的图形．11．已知AB //CD ，点E 是平面内一点，∠CDE 的角平分线与∠ABE 的角平分线交于点F ． （1）若点E 的位置如图1所示．①若∠ABE =60°，∠CDE =80°，则∠F = °；②探究∠F 与∠BED 的数量关系并证明你的结论；（2）若点E 的位置如图2所示，∠F 与∠BED 满足的数量关系式是 ．（3）若点E 的位置如图3所示，∠CDE 为锐角，且1452E F ∠≥∠+︒，设∠F =α，则α的取值范围为 ．12．已知：如图1，直线//AB CD ，EF 分别交AB ，CD 于E ，F 两点，BEF ∠，DFE ∠的平分线相交于点K ．（1）求K ∠的度数；（2）如图2，BEK ∠，DFK ∠的平分线相交于点1K ，问1K ∠与K ∠的度数是否存在某种特定的等量关系？写出结论并证明；（3）在图2中作1BEK ∠，1DFK ∠的平分线相交于点2K ，作2BEK ∠，2DFK ∠的平分线相交于点3K ，依此类推，作n BEK ∠，n DFK ∠的平分线相交于点1n K +，请用含的n 式子表示1n K ∠+的度数．（直接写出答案，不必写解答过程）13．已知，如图1，直线l 2⊥l 1，垂足为A ，点B 在A 点下方，点C 在射线AM 上，点B 、C 不与点A 重合，点D 在直线11上，点A 的右侧，过D 作l 3⊥l 1，点E 在直线l 3上，点D 的下方．（1）l 2与l 3的位置关系是 ；（2）如图1，若CE 平分∠BCD ，且∠BCD ＝70°，则∠CED ＝ °，∠ADC ＝ °； （3）如图2，若CD ⊥BD 于D ，作∠BCD 的角平分线，交BD 于F ，交AD 于G ．试说明：∠DGF ＝∠DFG ；（4）如图3，若∠DBE ＝∠DEB ，点C 在射线AM 上运动，∠BDC 的角平分线交EB 的延长线于点N ，在点C 的运动过程中，探索∠N :∠BCD 的值是否变化，若变化，请说明理由；若不变化，请直接写出比值．14．探索发现：111111111;;12223233434=-=-=-⨯⨯⨯…… 根据你发现的规律，回答下列问题：（1）145⨯＝ ，1(1)n n ⨯+＝ ； （2）利用你发现的规律计算：1111122334(1)n n ⋅++++⨯⨯⨯⨯+（3）利用规律解方程：1111121(1)(1)(2)(2)(3)(3)(4)(4)(5)(5)x x x x x x x x x x x x x -++++=++++++++++ 15．如图，在ABC ∆中，AC BC =，90ACB ∠=︒，点D 为ABC ∆内一点，且BD AD =．（1）求证：CD AB ⊥；（2）若15CAD ∠=︒，E 为AD 延长线上的一点，且CE CA =．①求BDC ∠的度数．②若点M 在DE 上，且DC DM =，请判断ME 、BD 的数量关系，并说明理由． ③若点N 为直线AE 上一点，且CEN ∆为等腰∆，直接写出CNE ∠的度数．16．如图，在ABC 中，3AB AC ==，50B C ∠=∠=，点D 在边BC 上运动（点D 不与点,B C 重合），连接AD ，作50ADE ∠=，DE 交边AC 于点E ．（1）当100BDA ∠=时，EDC ∠= ，DEC ∠=（2）当DC 等于多少时，ABD DCE ≌△△，请说明理由；（3）在点D 的运动过程中，ADE 的形状可以是等腰三角形吗？若可以，请求出BDA ∠的度数；若不可以，请说明理由．17．（阅读材料）：（1）在ABC ∆中，若90C ∠=︒，由“三角形内角和为180°”得1801809090A B C ∠︒+∠=-∠︒︒-=︒=．（2）在ABC ∆中，若90A B ∠+∠=︒，由“三角形内角和为180°”得180()1809090C A B ∠=︒-∠+∠=︒-︒=︒．（解决问题）：如图①，在平面直角坐标系中，点C 是x 轴负半轴上的一个动点．已知//AB x 轴，交y轴于点E ，连接CE ，CF 是∠ECO 的角平分线，交AB 于点F ，交y 轴于点D ．过E 点作EM 平分∠CEB ，交CF 于点M ．（1）试判断EM 与CF 的位置关系，并说明理由；（2）如图②，过E 点作PE ⊥CE ，交CF 于点P ．求证：∠EPC=∠EDP ；（3）在（2）的基础上，作EN 平分∠AEP ，交OC 于点N ，如图③．请问随着C 点的运动，∠NEM 的度数是否发生变化？若不变，求出其值：若变化，请说明理由．18．（1）发现：如图1，ABC ∆的内角ABC ∠的平分线和外角ACD ∠的平分线相交于点O 。