时距曲线

倾斜界面反射波时距曲线推导倾斜界面反射波时距曲线推导在地质勘探中，倾斜界面反射波时距曲线是一项重要的工具，它能够帮助地质学家和勘探人员理解地下结构，并找到可能的油气藏位置。

倾斜界面反射波时距曲线的推导是一个复杂而又深度的过程，通过分析和理解这个过程，我们能够更好地运用这一工具来进行勘探工作。

1. 倾斜界面反射波时距曲线的概念倾斜界面反射波时距曲线是指当地下介质倾斜时，反射波在不同时距下的表现。

在传统的地震勘探中，我们通常假设地下介质是水平层状的，但实际情况往往是地下介质是倾斜的。

倾斜界面反射波时距曲线是对地下结构进行更真实描述的重要工具。

2. 推导倾斜界面反射波时距曲线的基本原理要推导倾斜界面反射波时距曲线，我们首先需要了解倾斜地层对地震波的影响。

当地下介质倾斜时，地震波在传播过程中会发生折射和反射，使得接收到的地震波时距曲线出现偏移和拉伸的情况。

通过对地震波传播过程的数学建模和物理分析，我们可以推导出倾斜界面反射波时距曲线的数学公式和物理规律。

3. 倾斜界面反射波时距曲线的应用倾斜界面反射波时距曲线的推导不仅仅是理论上的研究，它还有着重要的实际应用。

通过分析倾斜界面反射波时距曲线，我们能够更准确地识别地下构造，找到潜在的油气储层。

在实际的地质勘探工作中，地震勘探人员可以根据倾斜界面反射波时距曲线来确定勘探区域的地下结构，并作出相应的勘探决策。

结语倾斜界面反射波时距曲线推导是一个复杂的过程，但它对地震勘探有着重要的意义。

通过深入研究倾斜界面反射波时距曲线的推导过程和应用，我们能够更好地认识地下结构，有效地进行油气勘探工作。

在未来的地质勘探中，倾斜界面反射波时距曲线将继续发挥重要的作用，为勘探人员提供更多有价值的信息和数据。

个人观点从事地质勘探工作多年，我深知倾斜界面反射波时距曲线在勘探中的重要性。

推导倾斜界面反射波时距曲线是一项复杂而又具有挑战性的工作，但只有通过深入了解和分析，我们才能更好地应用这一工具。

倾斜界面反射波时距曲线推导倾斜界面反射波时距曲线推导引言：在地球物理勘探领域，倾斜界面反射波时距曲线是一种用来解释地下结构的重要工具。

通过分析反射波在地下结构中的传播路径，我们可以获取地下结构的信息，进而推断出地质构造的特征。

本文将对倾斜界面反射波时距曲线的推导过程进行详细解析，并探讨其在地球物理勘探中的应用。

一、倾斜界面反射波时距曲线的基本原理1.1 反射波的产生与传播当地震波到达地下界面时，一部分能量将被反射回地面，形成反射波。

反射波沿着地下界面传播，遇到不同介质的边界时，部分能量将发生折射和反射。

倾斜界面的存在会导致反射波的传播路径发生变化，因此需要推导出倾斜界面反射波时距曲线来对地下结构进行解释。

1.2 倾斜界面反射波时距曲线的概念倾斜界面反射波时距曲线是指在倾斜界面上某一点产生的反射波在地表上的时距分布曲线。

通过分析这一曲线，我们可以获得地下结构的信息，例如界面的倾角、深度和反射系数等。

二、倾斜界面反射波时距曲线的推导过程2.1 推导时距公式我们需要推导出倾斜界面上反射波的到达时刻与地下结构的关系。

假设反射波由地下点A沿倾角为α的界面发射，并在地表上的检波点B 接收到。

反射波的到达时距T可以通过以下公式计算：T = 2AB/cos(θ)其中，AB为地表上A点到B点的水平距离，θ为地表上的倾角。

2.2 倾斜界面下的时距公式接下来，我们将推导出倾斜界面下的时距公式。

根据斯涅尔定律，折射角和入射角之间的关系可以使用下式表示：sin(α)/vp = sin(β)/vs其中，α为倾角，vp和vs分别为纵波和横波的速度。

由于反射波在倾斜界面上发生反射后被检波点接收到，因此反射波的入射角等于倾斜界面在检波点上的倾角β。

将此关系代入反射波的时距公式中，我们可以得到倾斜界面下的时距公式：T = 2AB/[vp*cos(α)+vs*cos(β)]三、倾斜界面反射波时距曲线的应用3.1 地下结构解释通过倾斜界面反射波时距曲线，我们可以推断出地下结构的特征。

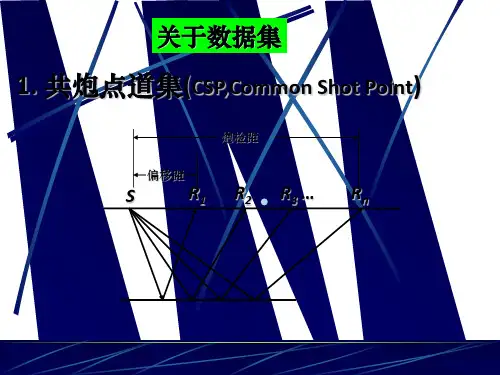
共中心点时距曲线方程
当我们谈论曲线的共同中心点时，通常是指两条曲线的交点。

这种情况下，我们可以通过求解这两条曲线的方程来找到共同中心点的坐标。

首先，我们需要有两条曲线的方程。

假设我们有两条曲线分别为y=f(x)和y=g(x)，我们可以通过求解f(x)=g(x)来找到它们的交点。

这个方程的解就是这两条曲线的共同中心点的横坐标。

另外，如果我们考虑的是两个圆的情况，它们的方程分别为(x-a)²+(y-b)²=r₁²和(x-c)²+(y-d)²=r₂²，其中(a,b)和(c,d)分别是两个圆的圆心坐标，r₁和r₂分别是它们的半径。

此时，我们可以通过联立这两个方程来求解它们的交点，这个交点就是这两个圆的共同中心点。

在实际问题中，共同中心点的概念还可以有其他的应用，比如在几何学中，当我们考虑多边形或多个图形的时候，可以讨论这些图形的共同中心点来描述它们的位置关系。

总之，共同中心点的概念涉及到不同类型的曲线或图形，我们
可以通过求解它们的方程或者通过几何推导来找到它们的位置关系。

希望这个回答能够帮助你理解共同中心点的概念。

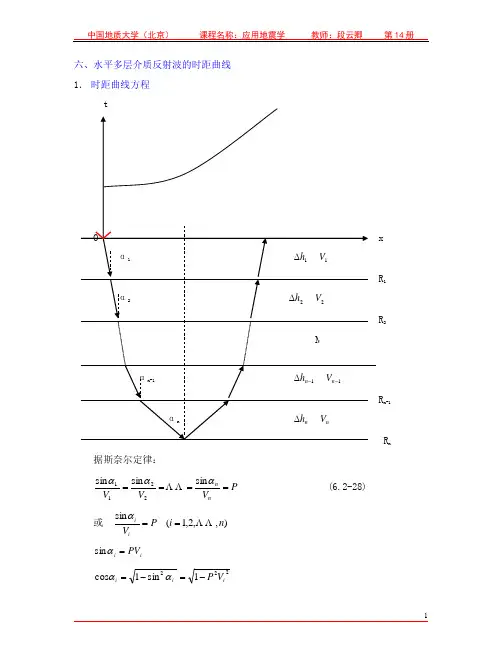
六、水平多层介质反射波的时距曲线 1． 时距曲线方程1 2 n-1 n 据斯奈尔定律：P V V V nn ====αααsin sin sin 2211 (6.2-28) 或),,2,1(sin n i P V ii==α i i PV =αsin2221sin 1cos i i i V P -=-=αα设波在第n 个界面上发生反射,波在水平层状介质中应走折线。

则[]22211⨯∆++∆+∆=n n tg h tg h tg h x ααα∑∑==-∆=∆=ni ii i ni i i i V P PV h h 122112cos sin 2αα∑∑∑===-∆=∆=⋅∆==⨯+++=ni i i iiii i ni i i n i ii n n V P V h h S V h V S V S V S V S t 12211221112)cos (1cos 222][αα⎪⎪⎩⎪⎪⎨⎧-∆=-∆=∑∑==ni i i i ni i i i V P V h t V P PV h x 1221221212 P55(§6.2-28①) 特点：①不是双曲线，②显函数形式写不出来。

2． 平均速度V（1） 平均速度的概念：① 波的射线速度V r ——波沿着射线的平均速度 nn nn n r V S V S V S S S S t t t S S S V ++++++=++++++=2211212121n n n nn V h V h V h h h h ααααααcos cos cos cos cos cos 2221112211∆++∆+∆∆++∆+∆=P54(§6.2②)② 平均速度的第一种定义方法当波垂直入射时，有021====n ααα ，P54(§6.2②)式变成：nn n V h V h V h h h h V 0cos 0cos 0cos 0cos 0cos 0cos 221121∆++∆+∆∆++∆+∆=∑∑∑∑====∆=∆∆=∆++∆+∆∆++∆+∆=ni ini ini ii ni inn nthV h hV h V h V h h h h 1111221121 P54(§6.2③)波在水平层状介质中垂直传播的总路程与总时间之比叫平均速度。

简述反射波时距曲线的特点
反射波时距曲线（RPC）是一种用来分析地表结构特征的技术，
它可以探测比看不见的地表深度，可以改变深度来获得地表结构信息，从而得出更准确的测量结果。

此外，反射波时距曲线还可以进行地震资料的定向投射，以确定其地表结构。

反射波时距曲线主要有三个特点：其一是发射点的深度；其二是反射点的深度；其三是反射时距，即从发射点到反射点的时间间隔。

首先，RP曲线可以确定发射点的深度。

在一定深度内，发射点
的深度可以很明确地区分，因此可以使用RP曲线来确定发射点的深度。

可以使用RPC曲线来确定地表结构的深度和厚度，有助于地质勘探的进程。

其次，RPC曲线可以确定反射点的深度。

通过测量反射点的深度，可以得出不同深度处的地表结构，从而可以更准确地进行地质勘探。

此外，通过测量反射点的深度，还可以得出不同深度处的岩性、成因、矿物组成等。

最后，RPC曲线可以确定反射时距。

反射时距是从发射点到反射点的时间间隔，可以提供更准确的结构信息。

因此，如果把RPC曲线与GIS软件相结合，就可以更加精确地识别出地表结构，从而绘制数字地形图，实现更精准的地质勘探。

综上所述，反射波时距曲线具有以下几个特点：一是可以确定发射点的深度；二是可以确定反射点的深度；三是可以确定反射时距；四是可以结合GIS软件进行更精确的地质勘探。

因此，反射波时距曲
线是地质勘探中不可或缺的技术。

它可以有效地改善地质勘探的效率和准确性，为更准确、高效的地质勘探提供了重要技术支持。