二重积分复习

山东专升本高数《二重积分》超全知识
点（二）
引言概述：
本文旨在分享山东专升本高数《二重积分》的超全知识点。

二重积分是高等数学中重要的概念之一，掌握好相关知识点对于学习和理解高数知识具有重要意义。

本文将从五个大点出发，深入阐述二重积分的各个方面，帮助读者更好地理解和应用该知识。

1. 二重积分的定义和基本性质
- 二重积分的定义及其几何意义
- 二重积分的性质：线性性、积分区域可加性、积分次序可交换性等
- 二重积分的计算：换元法、分部积分法等基本计算方法
2. 二重积分的应用
- 平面区域的面积计算
- 平面曲线的弧长计算
- 质心和形心的计算
- 平面曲线的面积计算
- 二重积分在物理问题中的应用：质量、电荷、质心等
3. 二重积分的坐标变换
- 极坐标系下的二重积分
- 变量替换法与雅可比行列式
- 在极坐标下的面积计算及应用
4. 二重积分的应用之曲面体积
- 二重积分求解曲面体积的方法
- 旋转体的体积计算
- 平面区域所围成的曲面体积计算
- 利用二重积分计算空间区域的体积
5. 二重积分在概率统计中的应用
- 联合概率分布函数及其性质
- 边缘概率密度函数及相关计算
- 二维连续随机变量的期望与方差计算
- 多维连续随机变量的矩计算
总结：
通过本文的介绍，我们系统地学习了山东专升本高数《二重积分》的超全知识点。

这些知识点包括二重积分的定义和基本性质、应用、坐标变换、曲面体积计算以及在概率统计中的应用等。

希望读者通过学习和理解这些知识点，能够更好地应用于实际问题中，并在专升本考试中取得优异的成绩。

引言概述：在考研数学中，二重积分是一个必考的难点。

对于很多考生而言，理解和掌握二重积分的概念和计算方法是一项具有挑战性的任务。

本文将以此为主题，通过分析二重积分的基本特点和应用，帮助考生全面理解和掌握这一知识点。

正文内容：一、二重积分的定义和基本特点1. 二重积分的基本定义：二重积分是在二维平面上将一个函数在某个有限区域上的积分运算。

通过将区域分成无数个微小的面元，对每个面元的函数值进行积分，最终求得整个区域上的积分值。

2. 二重积分的性质：二重积分具有线性性、区域可加性、保号性等基本性质。

考生需要深入理解这些性质，并能够灵活应用于计算过程中。

3. 面积与二重积分的关系：二重积分可以看作是计算平面上某个区域的面积。

通过对函数的积分运算，我们可以得到该区域的面积值，并且可以灵活应用于计算各种形状的区域面积。

4. 二重积分的坐标变换：对于一些复杂的区域，我们可以通过合适的坐标变换来简化二重积分的计算。

考生需要了解极坐标变换、直角坐标变换等常见的坐标变换方法，并能够灵活运用于解题过程中。

5. 三种常用坐标系下的二重积分：直角坐标系、极坐标系和柱坐标系是三种常见的坐标系，对应着不同的求积分公式。

考生需要学会在不同的坐标系下进行积分计算，并掌握它们之间的转换关系。

二、二重积分的计算方法1. 变上限与定积分的关系：二重积分的计算可以通过变上限与定积分的关系来实现。

考生需要了解变上限与定积分之间的等价性，并能够将二重积分转化为定积分进行计算。

2. 积分上限与积分下限的交换：二重积分中，积分上限和积分下限的交换是一个常见的操作。

掌握交换积分上下限的条件和规则，能够简化计算过程，并准确求得正确的结果。

3. 利用对称性简化计算：对于一些具有对称性的区域和函数，可以通过利用对称性将二重积分的计算简化。

考生需要善于发现和应用对称性，以提高计算的效率。

4. Fubini定理：Fubini定理是二重积分计算的重要工具，可以将二重积分转化为两个一重积分，从而简化计算过程。

二重积分知识点一、引言二重积分是高等数学中的重要内容，是对二元函数在有限区域上的积分运算。

二重积分的概念与求解技巧是深入理解、掌握多元函数的必备工具，也为解决实际问题提供了数学方法。

本文将从二重积分的概念、性质、计算方法和应用等方面，全面详细地介绍二重积分的知识点。

二、概念1. 二重积分的定义设f (x,y )在闭区域D 上有定义，D 由有向闭曲线C 围成，且f (x,y )在D 上有界。

若存在数I ，对于任意给定的正数ε，都存在正数δ，使得对于D 内任意满足Δσ<δ的任意分割σ，对应的任意代点ξij ，总有|∑∑f mj=1n i=1(ξij )Δσij −I|<ε则称I 为函数f (x,y )在闭区域D 上的二重积分，记作I =∬f D(x,y )dσ其中，Δσij 表示第(i,j )个小区域的面积，Δσ表示整个区域D 的面积。

2. 二重积分的几何意义二重积分的几何意义是对二元函数在闭区域上的面积进行逐点求和，即将闭区域D 分割成无穷多个小面积区域，并对每个小面积区域上的函数值进行乘积再求和，最终得到二重积分。

三、性质1. 线性性质设闭区域D上有二重积分∬fD(x,y)dσ，若c为常数，则有∬(cf(x,y)) D dσ=c∬fD(x,y)dσ∬(f(x,y)±g(x,y)) D dσ=∬fD(x,y)dσ±∬gD(x,y)dσ2. 区域可加性设闭区域D可分为非重叠的两部分D1和D2，则有∬fD (x,y)dσ=∬fD1(x,y)dσ+∬fD2(x,y)dσ3. Fubini定理（累次积分）设函数f(x,y)在闭区域D上连续，则有∬f D (x,y)dσ=∫(∫fβ(x)α(x)(x,y)dy)badx=∫(∫fδ(y)γ(y)(x,y)dx)dcdy其中，(x,y)∈D,α(x)≤y≤β(x),γ(y)≤x≤δ(y)。

4. 值定理设函数f(x,y)在闭区域D上一致连续，则存在(ξ,η)∈D，使得∬fD (x,y)dσ=f(ξ,η)∬dDσ=f(ξ,η)σ(D)其中，σ(D)表示闭区域D的面积。

二重积分复习题 1. 计算下列二重积分:(1)⎰⎰+Dd y x σ)(22, 其中D ={(x , y )| |x |≤1, |y |≤1};解：积分区域可表示为D : -1≤x ≤1, -1≤y ≤1. 于是⎰⎰+Dd y x σ)(22y d y x dx ⎰⎰--+=111122)(x d y y x ⎰--+=111132]31[ x d x ⎰-+=112)312(113]3232[-+=x x 38=. (2)⎰⎰+Dd y x σ)23(, 其中D 是由两坐标轴及直线x +y =2所围成的闭区域:解：积分区域可表示为D : 0≤x ≤2, 0≤y ≤2-x . 于是⎰⎰+Dd y x σ)23(y d y x dx x⎰⎰-+=2020)23(dx y xy x ⎰-+=222]3[ dx x x ⎰-+=202)224(0232]324[x x x -+=320=. (3)⎰⎰++Dd y y x x σ)3(223, 其中D ={(x , y )| 0≤x ≤1, 0≤y ≤1};解：⎰⎰++Dd y y x x σ)3(323⎰⎰++=1032310)3(dx y y x x dy ⎰++=1001334]4[dy x y y x x ⎰++=103)41(dy y y 0142]424[y y y ++=1412141=++=.(4)⎰⎰+Dd y x x σ)cos(, 其中D 是顶点分别为(0, 0), (π, 0), 和(π, π)的三角形闭区域.解：积分区域可表示为D : 0≤x ≤π, 0≤y ≤x . 于是,⎰⎰+Dd y x x σ)cos(⎰⎰+=x dy y x xdx 00)cos(π⎰+=π)][sin(dx y x x x⎰-=π0)s i n 2(s i n dx x x x ⎰--=π0)c o s 2c o s 21(x x xd+--=0|)c o s 2c o s 21(πx x x dx x x ⎰-π0)cos 2cos 21(π23-=..2. 画出积分区域, 并计算下列二重积分:(1)⎰⎰Dd y x σ, 其中D 是由两条抛物线x y =, 2x y =所围成的闭区域;解：积分区域图如, 并且D ={(x , y )| 0≤x ≤1, x y x ≤≤2}. 于是⎰⎰D d y xσ⎰⎰=102dy y x dx xx⎰=10223]32[dx y x x x 556)3232(10447=-=⎰dx x x .(2)⎰⎰Dd xy σ2, 其中D 是由圆周x 2+y 2=4及y 轴所围成的右半闭区域; 解：积分区域图如, 并且D ={(x , y )| -2≤y ≤2, 240y x -≤≤}. 于是⎰⎰⎰⎰⎰----=22402240222222]21[dy y x dx xy dy d xy yy Dσ1564]10132[)212(22225342=-=-=--⎰y y dy y y . (3)⎰⎰+Dy x d e σ, 其中D ={(x , y )| |x |+|y |≤1};解：积分区域图如, 并且D ={(x , y )| -1≤x ≤0, -x -1≤y ≤x +1}⋃{(x , y )| 0≤x ≤1, x -1≤y ≤-x +1}. 于是⎰⎰⎰⎰⎰⎰+--+---++=111111x x y xx x yxDyx dy e dx e dy e dx e d eσ⎰⎰+---+--+=1110111][][dy e e dx e ex x y x x x y x⎰⎰---+-+-=11201112)()(dx e e dx e ex x101201112]21[]21[---+-+-=x x e ex x e e =e -e -1. (4)⎰⎰-+Dd x y x σ)(22, 其中D 是由直线y =2, y =x 及y =2x 轴所围成的闭区域.解：积分区域图如, 并且D ={(x , y )| 0≤y ≤2, y x y ≤≤21}. 于是⎰⎰⎰⎰⎰-+=-+=-+2022232222022]2131[)()(dy x x y x dx x y x dy d x y x y y y y Dσ 613)832419(2023=-=⎰dy y y .3. 改换下列二次积分的积分次序: (1)⎰⎰ydx y x f dy 01),(;解：由根据积分限可得积分区域D ={(x , y )|0≤y ≤1, 0≤x ≤y }, 如图. 因为积分区域还可以表示为D ={(x , y )|0≤x ≤1, x ≤y ≤1}, 所以⎰⎰⎰⎰=1101),(),(xy dy y x f dx dx y x f dy .(2)⎰⎰y ydx y x f dy 2202),(;解：由根据积分限可得积分区域D ={(x , y )|0≤y ≤2, y 2≤x ≤2y }, 如图. 因为积分区域还可以表示为D ={(x , y )|0≤x ≤4, x y x ≤≤2}, 所以⎰⎰y ydx y x f dy 222),(⎰⎰=402),(xx dy y x f dx .(3)⎰⎰---221110),(y y dx y x f dy ;解：由根据积分限可得积分区域}11 ,10|),{(22y x y y y x D -≤≤--≤≤=, 如图. 因为积分区域还可以表示为}10 ,11|),{(2x y x y x D -≤≤≤≤-=, 所以⎰⎰⎰⎰-----=22210111110),(),(x y ydy y x f dx dx y x f dy(4)⎰⎰--21222),(x x xdy y x f dx ;解：由根据积分限可得积分区域}22 ,21|),{(2x x y x x y x D -≤≤-≤≤=, 如图. 因为积分区域还可以表示为}112 ,10|),{(2y x y y y x D -+≤≤-≤≤=, 所以⎰⎰--21222),(x x xdy y x f dx ⎰⎰-+-=101122),(y ydx y x f dy .(5)⎰⎰e xdy y x f dx 1ln 0),(;解：由根据积分限可得积分区域D ={(x , y )|1≤x ≤e , 0≤y ≤ln x }, 如图. 因为积分区域还可以表示为D ={(x , y )|0≤y ≤1, e y ≤x ≤ e }, 所以⎰⎰exdy y x f dx 1ln 0),(⎰⎰=10),(eey dx y x f dy4. 画出积分区域, 把积分⎰⎰Ddxdy y x f ),(表示为极坐标形式的二次积分, 其中积分区域D 是:(1){(x , y )| x 2+y 2≤a 2}(a >0);解：积分区域D 如图. 因为D ={(ρ, θ)|0≤θ≤2π, 0≤ρ≤a }, 所以⎰⎰⎰⎰=DDd d f dxdy y x f θρρθρθρ)sin ,cos (),(⎰⎰=πρρθρθρθ20)sin ,cos (d f d a.(2){(x , y )|x 2+y 2≤2x };解：积分区域D 如图. 因为}cos 20 ,22|),{(θρπθπθρ≤≤≤≤-=D , 所以⎰⎰⎰⎰=DDd d f dxdy y x f θρρθρθρ)sin ,cos (),(⎰⎰-=22cos 20)sin ,cos (ππθρρθρθρθd f d .(3){(x , y )| a 2≤x 2+y 2≤b 2}, 其中0<a <b ;解：积分区域D 如图. 因为D ={(ρ, θ)|0≤θ≤2π, a ≤ρ≤b }, 所以⎰⎰⎰⎰=DDd d f dxdy y x f θρρθρθρ)sin ,cos (),(⎰⎰=πρρθρθρθ20)sin ,cos (bad f d .(4){(x , y )| 0≤y ≤1-x , 0≤x ≤1}.解：积分区域D 如图. 因为}sin cos 10 ,20|),{(θθρπθθρ+≤≤≤≤=D , 所以⎰⎰⎰⎰=DDd d f dxdy y x f θρρθρθρ)sin ,cos (),(⎰⎰+=θθρρθρθρθπsin cos 120)sin ,cos (d f d .5. 化下列二次积分为极坐标形式的二次积分: (1)⎰⎰101),(dy y x f dx ;解：积分区域D 如图所示. 因为}csc 0 ,24|),{(}sec 0 ,40|),{(θρπθπθρθρπθθρ≤≤≤≤⋃≤≤≤≤=D ,所以⎰⎰⎰⎰⎰⎰==DDd d f d y x f dy y x f dx θρρθρθρσ)sin ,cos (),(),(11⎰⎰=4s e c)s i n ,c o s (πθρρθρθρθd f d ⎰⎰+24c s c)s i n ,c o s (ππθρρθρθρθd f d .(2)⎰⎰+xxdy y x f dx 32220)(;解：积分区域D 如图所示, 并且 }sec 20 ,34|),{(θρπθπθρ≤≤≤≤=D , 所示⎰⎰⎰⎰⎰⎰=+=+xxDDd d f d y x f dy y x f dx 3222220)()()(θρρρσ⎰⎰=34s e c 20)(ππθρρρθd f d .(3)⎰⎰--2111),(x xdy y x f dx ;解：积分区域D 如图所示, 并且}1sin cos 1 ,20|),{(≤≤+≤≤=ρθθπθθρD ,所以⎰⎰⎰⎰⎰⎰--==10112)sin ,cos (),(),(x xDDd d f d y x f dy y x f dx θρρθρθρσ⎰⎰+=2sin cos 101)sin ,cos (πθθρρθρθρθd f d(4)⎰⎰21),(x dy y x f dx .解：积分区域D 如图所示, 并且}sec tan sec ,40|),{(θρθθπθθρ≤≤≤≤=D ,所以⎰⎰210),(x dy y x f dx ⎰⎰⎰⎰==DDd d f d y x f θρρθρθρσ)sin ,cos (),(⎰⎰=40sec tan sec )sin ,cos (πθθθρρθρθρθd f d6. 把下列积分化为极坐标形式, 并计算积分值: (1)⎰⎰-+2202220)(x ax ady y x dx ;解：积分区域D 如图所示. 因为}cos 20 ,20|),{(θρπθθρa D ≤≤≤≤=, 所以⎰⎰-+2202220)(x ax ady y x dx ⎰⎰⋅=Dd d θρρρ2⎰⎰⋅=20cos 202πθρρρθa d d ⎰=2044cos 4πθθd a 443a π=. (2)⎰⎰+xa dy y x dx 0220;解：积分区域D 如图所示. 因为}sec 0 ,40|),{(θρπθθρa D ≤≤≤≤=, 所以⎰⎰⎰⎰⋅=+Dxad d dy y x dx θρρρ0220⎰⎰⋅=40sec 0πθρρρθa d d ⎰=4033sec 3πθθd a )]12ln(2[63++=a . (3)⎰⎰-+xxdy y xdx 221221)(;解：积分区域D 如图所示. 因为}tan sec 0 ,40|),{(θθρπθθρ≤≤≤≤=D , 所以⎰⎰⎰⎰⋅=+--Dxx d d dy y xdx θρρρ212122102)(12tan sec 40tan sec 02140-==⋅=⎰⎰⎰-πθθπθθθρρρθd d d .(4)⎰⎰-+220220)(y a a dx y x dy .解：积分区域D 如图所示. 因为}0 ,20|),{(a D ≤≤≤≤=ρπθθρ, 所以⎰⎰⎰⎰⋅=+-Dy a a d d dx y x dy θρρρ222022)(420028a d d aπρρρθπ=⋅=⎰⎰.7. 利用极坐标计算下列各题: (1)⎰⎰+Dy xd e σ22，其中D 是由圆周x 2+y 2=4所围成的闭区域;解：在极坐标下D ={(ρ, θ)|0≤θ≤2π, 0≤ρ≤2}, 所以⎰⎰⎰⎰=+DDy x d d e d e θρρσρ222)1()1(2124420202-=-⋅==⎰⎰e e d e d ππρρθπρ. (2)⎰⎰++Dd y x σ)1ln(22，其中D 是由圆周x 2+y 2=1及坐标轴所围成的在第一象限内的闭区域;解：在极坐标下}10 ,20|),{(≤≤≤≤=ρπθθρD , 所以⎰⎰⎰⎰+=++DDd d d y x θρρρσ)1ln()1ln(222)12ln 2(41)12ln 2(212)1ln(2012-=-⋅=+=⎰⎰πρρρθπd d .(3)σd xyDarctan⎰⎰, 其中D 是由圆周x 2+y 2=4, x 2+y 2=1及直线y =0, y =x 所围成的第一象限内的闭区域.解：在极坐标下}21 ,40|),{(≤≤≤≤=ρπθθρD , 所以⎰⎰⎰⎰⎰⎰⋅=⋅=DDDd d d d d xy θρρθθρρθσ)arctan(tan arctan ⎰⎰⋅=4021πρρθθd d ⎰⎰==40321643ππρρθθd d . 8. 选用适当的坐标计算下列各题:(1)dxdy yx D22⎰⎰，其中D 是由直线x =2，y =x 及曲线xy =1所围成的闭区域. 解：因为积分区域可表示为}1 ,21|),{(x y x x y x D ≤≤≤≤=, 所以d x d y y x D22⎰⎰dy y dx x x x ⎰⎰=211221⎰-=213)(dx x x 49=. (2)⎰⎰++--Dd yx y x σ222211, 其中D 是由圆周x 2+y 2=1及坐标轴所围成的在第一象限内的闭区域;解：在极坐标下}10 ,20|),{(≤≤≤≤=ρπθθρD , 所以⎰⎰⎰⎰⋅+-=++--DDd d d y x y x θρρρρσ2222221111)2(811102220-=+-=⎰⎰ππρρρρθπd d .(3)⎰⎰+Dd y x σ)(22, 其中D 是由直线y =x , y =x +a , y =a , y =3a (a >0)所围成的闭区域;解：因为积分区域可表示为D ={(x , y )|a ≤y ≤3a , y -a ≤x ≤y }, 所以⎰⎰+Dd y x σ)(22⎰⎰-+=aaya y dx y x dy 322)(4332214)312(a dy a y a ay aa =+-=⎰. (4)σd y x D22+⎰⎰, 其中D 是圆环形闭区域{(x , y )| a 2≤x 2+y 2≤b 2}.解：在极坐标下D ={(ρ, θ)|0≤θ≤2π, a ≤ρ≤b }, 所以 σd y x D22+⎰⎰)(3233202a b dr r d ba -==⎰⎰πθπ.。

2015考研数学:二重积分的基本知识点来源：文都教育二重积分是考研数学中的大题常考点，主要考查的是同学们的计算能力。

下面文都考研数学老师对二重积分的基本知识点进行一些讲解，以帮助广大考生备考。

１．二重积分的概念设二元函数(,)f x y 在有界闭区域D 上有界．（1）将区域D 划分成若干小区域12,,,n σσσ∆∆∆；（2）(,)(1)i i i i n ξησ∀∈∆≤≤，作1(,)n i iii f ξησ=∆∑； （3）令1max{}i i n d λ≤≤=，i d 为i σ∆的直径，01(,)lim (,)n i ii i D f x y d f λσξησ→==∆∑⎰⎰．注：①二重积分与区域的划分及点的取法无关；②若(,)f x y 在有界闭区域D 上连续，则(,)f x y 在D 上的二重积分一定存在； ③(,)D f x y d σ⎰⎰的几何意义是以D 为底，以(,)z f x y =为顶的曲顶柱体的体积； ④(,)Df x y d σ⎰⎰的物理意义是以(,)f x y ρ=为面密度的平面区域D 的质量． 2．二重积分的性质（1）[(,)(,)](,)g(,)D D D f x y g x y d f x y d x y d σσσ±=±⎰⎰⎰⎰⎰⎰． （2）(,)(,)D D kf x y d k f x y d σσ=⎰⎰⎰⎰． （3）1212(,)(,)(,)D D D D f x y d f x y d f x y d σσσ+=+⎰⎰⎰⎰⎰⎰． （4）D d A σ=⎰⎰．（5）（比较定理）若在D 上恒有(,)(,)f x y g x y ≤，则(,)(,)D Df x y dg x y d σσ≤⎰⎰⎰⎰．（6）（估值定理）设,M m 分别为(,)f x y 在区域D 上的最大与最小值，A 为D 的面积，则(,)DmA f x y d MA σ≤≤⎰⎰．（7）（中值定理）若(,)f x y 在闭域D 上连续，A 为D 的面积，则在D 上至少存在一点(,)ξη，使(,)(,)Df x y d f A σξη=⎰⎰．（8）二重积分的对称性质①若积分区域D 关于x 轴对称，则二重积分10,(,)(,)(,)2(,),(,)(,)D D f y f x y f x y f x y d f x y d f y f x y f x y σσ-=-⎧⎪=⎨-=⎪⎩⎰⎰⎰⎰关于为奇函数，即关于为偶函数，即，其中1D 为D 在上半平面部分．②若积分区域D 关于y 轴对称，则二重积分20,(,)(,)(,)2(,),(,)(,)D D x x f f x y f x y f x y d f x y d f f x y f x y σσ-=-⎧⎪=⎨-=-⎪⎩⎰⎰⎰⎰关于为奇函数，即关于为偶函数，即，其中2D 为D 在右半平面部分．③设区域D 关于y x =对称，则(,)(,)D Df x y d f y x d σσ=⎰⎰⎰⎰．④设积分区域D 关于原点对称，(,)f x y 同时为,x y 的奇函数或偶函数，则 1,,0,(,)(,)(,)2(,),(,)(,)D D x y x y f f x y f x y f x y d f x y d f f x y f x y σσ--=-⎧⎪=⎨--=⎪⎩⎰⎰⎰⎰关于的奇函数，即关于为偶函数，即，其中1D 为D 的右半平面部分．3．积分法（1）直角坐标法①（X -型区域）设12{(,)|,()()}D x y a x b x y x ϕϕ=≤≤≤≤，则21()()(,)(,)b x a x D f x y d dx f x y dy ϕϕσ=⎰⎰⎰⎰．②（Y -型区域）设12{(,)|()(),}D x y y x y c y d ϕϕ=≤≤≤≤，则21()(y)(,)(,)d y c D f x y d dy f x y dx ϕϕσ=⎰⎰⎰⎰．（2）极坐标变换令00cos cos ()sin sin x x r x r y r y y r θθθθ-==⎧⎧⎨⎨=-=⎩⎩或，其中12{(,)|,()()}D r r r r θαθβθθ=≤≤≤≤，则 21()()(,)(cos ,sin )r r D f x y d d rf r r dr βθαθσθθθ=⎰⎰⎰⎰．4．应用（1）几何应用设:(,)((,))z x y x y D ϕ∑=∈为空间曲面，则该曲面段的面积为221()()D z z A d x yσ∂∂=++∂∂⎰⎰．（2）物理应用①质量(,)Dm x y d ρσ=⎰⎰． ②形心坐标(,)(,),(,)(,)DD D D x x y d y x y d x y x y d x y d ρσρσρσρσ==⎰⎰⎰⎰⎰⎰⎰⎰，特别地，若薄片密度均为，则形心坐标,DD D D xd yd x y d d σσσσ==⎰⎰⎰⎰⎰⎰⎰⎰．（3）转动惯量设l 为平面xoy 上的直线，区域D 上任意一点(,)P x y 到直线l 的距离为d ，则区域D 绕直线l 的转动惯量为2(,)l D I dx y d ρσ=⎰⎰，特别地，2222(,),(,),()(,)x y o D D DI y x y d I x x y d I x y x y d ρσρσρσ===+⎰⎰⎰⎰⎰⎰．。

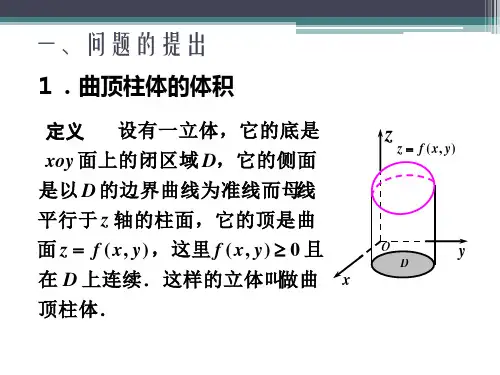
第11讲 二重积分一、复习要求（1）理解二重积分的概念及其性质.（2）掌握二重积分在直角坐标系及极坐标系下的计算方法.（3）会用二重积分解决简单的应用问题（限于空间封闭曲面所围成的有界区域的体积、平面薄板质量）.二、复习内容（1）二重积分的概念：二重积分的定义 二重积分的几何意义 （2）二重积分的性质 （3）二重积分的计算 （4）二重积分的应用第1节 二重积分概念一、引例——求曲顶柱体的体积设D 是平面上的一个有界闭区域，xOy ),(y x f z =是在区域D 上连续的二元函数，并且≥0，. ),(y x f D y x ∈),(现以D 为底面，曲面为顶面，其侧面是以D 的边界为准线，母线平行Z 轴的柱面，作一个柱体.由于这个柱体的顶面是曲面，故称它为曲顶柱体（图7-14）. ),(y x f z =求这个曲顶柱体的体积，易见，解决这个问题的困难在于顶是曲面，联想求曲边梯形的面积，情况十分类似. 我们仿照第五 章第一节的方法来解决这个问题.（1）分割将D 任意分割为n 个小区域1σΔ，2σΔ，…，n σΔ，同时用iσΔ（，…，n ）表示该小区域的面积. 相应地，整个曲顶柱体被分为n 个小曲顶柱体. 图7-15画出了其中第个小曲顶柱体. 2,1=i i（2）取近似值对于每个小曲项柱体，在底面i σΔ上任取一点),(i i i P ηξ，小曲项柱体的体积近似等于以i σΔ为底，（f i ξ，i η）为高的小平顶柱体，体积为（f i ξ，i η）i σΔ（1，2，…n ）. =i（3）作和式 把n 个小平顶柱体的体积加起来，便是整个曲顶柱体体积V 近似值，即i i ni i f V σηξΔ≈∑=),(1（4）取极限 当分割的份数n 趋于无穷且每一个小平面区域i σΔ收缩于一点时，上述和式的极限便是曲顶柱体体积的精确值. 用λ表示n 个小平面区域的最大直径（闭区域上任意两点距离的最大者称为该区域的直径），则∑=→Δ=ni i i i f V 1),(lim σηξλ这样，我们的问题就归结为求上述和式的根限了. 如果这个极限存在，我们就把它定义为函数在区域D 上的二重积分. ),(y x f 二、二重积分的概念和性质定义8 设是平面有界闭区域D 上的有界函数，将区域D 任意分割成n 个小区域 ),(y x f z =21,σσΔΔ，…，i σΔ，…，n σΔ其中i σΔ表示第i 个小区域，也表示它的面积，并以λ记作所有小区域中直径最大者. 在每个小区域i σΔ上任取一点),(i i i P ηξ，作乘积i i i f σηξΔ⋅),(（=1，2，3，…，n ），并作和式，如果i i ni iif σηξΔ⋅∑=),(10→λ时，不论如何分割，不论点),(i i i P ηξi σΔ∈如何选取，上述和式的极限总存在，则称此极限值为函数在区域D 上的二重积分，记作：，即),(y x f ∫∫Dd y x f σ),(∑∫∫=→Δ⋅=ni iiiDf d y x f 1),(lim ),(σηξσλ其中D 叫做积分区域，叫做被积函数，),(y x f σd y x f ),(叫做被积表达式，σd 叫做面积元素，x 和叫做积分变量. y 据此定义，曲顶柱体的体积V 可表示成其曲顶的函数在区域D 上的二重积分 ),(y x f∫∫=Dd y x f V σ),(可以证明，若数在有界闭区域D 上连续，则在该区域上的二重积分一定存在. ),(y x f ),(y x f本讲中，我们总假定被积函数在有界闭区域D 上是连续的，因而，它在D 上的二重积分总是存在的（此时，我们也称二元函数在D 上是可积的，以后不再申明）. ),(y x f ),(y x f与定积号分相仿，其几何意义是明显的，若≥0，则二重积分的几何意义就是曲顶柱体的体积；若≤0，则二重积分表示曲顶柱体的体积的相反数；若在D 的若干部分区域上是正的，而在其他部分区域上是负的，这时二重积分的值就等于各个部分区域上的柱体体积的代数和. 特别地，当函数=1时，二重积分即为区域D 的面积),(y x f ),(y x f ),(y x f ),(y x f σ，即σσ=∫∫Dd 二重积分有着与定积分相类似的一些性质，现将这些性质叙述如下： 性质1 被积函数中的常数因子可以提到积分号外面. 即（为常数）σσd y x f k d y x kf DD),(),(∫∫∫∫=k 性质2 有限个函数的代数和的积分等于各个函数积分的代数和. 即σσσd y x g d y x f d y x g y x f DDD),(),()],(),([∫∫∫∫∫∫±=±性质3 如果闭区域D 由有限条曲线分为有限个部分区域，则在D 上的二重积分等于在各部分区域上的二重积分之和. 例如D 被分割为两个区域D 1和D 2，则有∫∫∫∫∫∫±=21),(),(),(D D Dd y x f d y x f d y x f σσσ 性质4 如果在区域D 上，≤，则有不等式 ),(y x f ),(y x g≤σd y x f D),(∫∫σd y x g D),(∫∫ 性质5 如果在区域D 上，≤≤M，则 m f ),(y xσm ≤≤σd y x f D),(∫∫σM （σ为区域D 的面积）性质6（二重积分的中值定理） 设函数在有界闭区域D 上连续，则在D 上至少存在一点),(y x f ),(ηξ，使得下式成立∫∫⋅=Df d y x f σηξσ),(),(习题11、根据二重积分的性质，比较下列积分的大小：（1）与，其中区域D 是由σd y x D∫∫+2)(σd y x D∫∫+3)(x 轴、y 轴及直线所围成； 1=+y x（2）与，其中区域D 是由σd y x D∫∫+)ln(σd y x D∫∫+2)][ln(3=x ，，，四条直线围成的矩形域.5=x 0=y 1=y 2、利用二重积分性质估计下列积分的值： （1），其中，σ∫∫++=Dd y x I )1(|),{(y x D =0≤x ≤1，0≤y ≤2}（2），其中，σ∫∫++=Dd y xI )94(22|),{(y x D =22y x +≤4}第2节 二重积分的计算由上节引例可见，用定义计算二重积分显然是很困难的.必须寻找其可行的计算方法. 一、直角坐标系下二重积分的计算先讨论连续函数的二重积分计算问题. 不妨设),(y xf ),(y x f ≥0，所得计算公式仍具有一般意义.设积分区域D 如图7-16是由两条平行直线a x =，b x = 以及两条连续曲边)(x y ϕ=，)(x y ψ=（在上],[b a )(x ψ≥)(x ϕ）所围成，它可表示为)(|),{(x y x D ϕ=≤y ≤)(x ψ，a ≤x ≤}b其中)(x y ϕ=与)(x y ψ=在区间[]上连续. b a ,依二重积分的几何意义，有=.σ∫∫Dd y x f ),(曲顶柱体V另一方面，可用定积分中的“切片法”来求曲顶柱体的 体积. 为此，在区间[]上任取一点，作平行于 b a ,0x yOz 坐标面的平面，这平面与曲顶柱体相交所得的截面，0x x =是一个以区间[)(0x ϕ，)(0x ψ]为底，而以),(0y x f z =为曲边的曲边梯形（如图7-17中的阴影部分），所以这截面的面积为：dy y x f x A x x ),()()()(000∫=ψϕ一般地，过区间[a ，b ]上任意一点x ，且平行于坐标 yoz 平面的平面，与曲顶柱体相交，所得截面的面积为dy y x f x A x x ),()()()(∫=ψϕ上式中是积分变量，y x 在积分时保持不变.现用平行于坐标面的平面把曲顶柱体切成许多yOz 薄片，任取一个对应于小区间[x ，dx x +]的薄片（如图7-18）.这个薄片的厚度为充分小时，这薄片可以看成以截面为底，高为的薄柱体，该薄片体积近似为 dx )(x A dxdx x A dV )(=所以，曲顶柱体体积为∫∫∫==dx dy y x f dx x A V x x b a b a ]),([)()()(ψϕ由此即得二重积分计算公式或∫∫∫∫=dx dy y x f d y x f x x b a D]),([),()()(ψϕσ∫∫∫∫=dy y x f dx d y x f x x b a D),(),()()(ψϕσ上式右端是一个先对，后对y x 的累次积分，二重积分的累次积分也称为二次积分.二重积分化为二次积分的关键在于上下限的确定. 为了便于学习，下面我们可以根据积分区域D 的不同，来确定二次积分的顺序：（1）当积分区域D 如图7-19所示时，先对积分，其积分下限y 为)(x ϕ，积分上限为)(x ψ；然后对x 积分，其积分下限为a ，积分 上限为b .（2）当积分区域D 如图7-20所示时，先对x 积分. 其积分下限为)(y γ，积分上限为)(y η；然后对积分，其积分下限为，积分上限为.y c d 因此，计算二重积分的步骤如下： （1）确定积分区域D 的图形： （2）将二重积分化为二次积分；（3）计算二次积分. 例1 求二重积分，其中积分区域为 ∫∫Dxy d xe σ≤0|),{(y x D =x ≤1，0≤y ≤1}解 画出积分区域D 的图形，如图7-21所示. 因为积分区域D 的形状是正方形，所以可化为 ∫∫∫∫=dy xe dx d xe xyDxy 1010σ ∫−=dx e x )1(110)(x e x −=2−=e例2 求二重积分，其中积分区域D 是由∫∫Dxd σx y ln =与直线e x =及x 轴所围成的区域.解 画出积分区域D 的图形，如图7-22所示.因为它与类型（1）的积分区域一致，所以可化为 ∫∫∫∫=xdy dx xd xe Dln 01σ ∫∫=dy xdx x e ln 01∫=xdx x e ln 121ln 21∫=xdx e∫−=x d x x x e eln 21]ln [212112∫−=xdx e e122121ex e 1224121−=)1(412+=e把一个二重积分化为二次积分时，可以先对积分，再对y x 积分，也可以先对x 积分，再积分. 对于积分区域为矩形域而言，二者难易程度是一样的，但当积分区域不是矩形域时，选择积分顺序是很重要的，请看下面的例子. y例3 计算二重积分，其中积分区域D 是由抛物线与直线所围成的区域.∫∫Dxyd σx y =22−=x y解 画出积分区域D 的图形，如图7-23所示，考虑区域D 类似类型（2），所以化成二次积分为∫∫Dxyd σxydx dy y y ∫∫+−=2212∫−+=−dy y y y ])2([21522121623462344[21−−++=y y y y 845=本题若先对积分，再对y x 积分，就必须将区域D 分成两个小区域，而有下面的计算形式xydy dx xydy dx xyd xx x x D∫∫∫∫∫∫−−+=24110σ难易程度显然是不同的. 例4 计算二重积分，其中积分区域D 由σd e Dy ∫∫−21=y ，x y =，的围成. 0=x解 如图7-24所示，可考虑先对x 积分，再对积分，得y∫∫∫∫−−=dx edy d ey y Dy 2210σ∫∫−−==−−)(212101022y d e ydy e y y11(21)1(211ee −=−−=−若先对积分再对y x 积分，则形式为∫∫∫∫−−=Dxy y dy e dx d e11022σ由于不是初等函数，因而无法用牛顿—莱布尼兹公式算出.∫−dy ey 2二、极坐标系下二重积分的计算有些二重积分，其积分区域D 的边界曲线用极坐标方程比较简便，且被积函数利用极坐标变量θ,r 表示也比较简单.这时可以考虑利用极坐标来计算二重积分.在极坐标系中求二重积分，我们也用两族曲线：=r 常数（它表示以极点为圆心的一族同心圆）和=θ常数（它表示发自极点的一族射线），把区域分划成个小区域（如图7-25）.小区域的面积n i σΔ可计算如下：i i i i i i r r r θθσΔ⋅−Δ⋅Δ+⋅=Δ2221)(21i i i i r r r θΔ⋅Δ⋅Δ+⋅=)2(21[]i i i i i r r r r θΔ⋅Δ⋅Δ++⋅=)(21i i i r r θΔ⋅Δ⋅= 其中i r 表示相邻两圆弧半径的平均值. 对应小区域面积的近似值为θrdrd ，即面积元素θσrdrd d =又直角坐标与极坐标的关系式是⎩⎨⎧==θθsin cos r y r x 于是∫∫∫∫=DDrdrd r r f d y x f θθθσ)sin ,cos (),(这就是二重积分在极坐标系中的表达式.由于二重积分与区域D 的分割方法无关，因此不论是直角坐标系中的分割方法，还是极坐标系中的分割方法，所得的二重积分应该相等.所以有∫∫∫∫=DDrdrd r r f dxdy y x f θθθ)sin ,cos (),(直角坐标系变换为极坐标系的变换公式.其变换要点为： (1) 将中的),(y x f y x ,分别换为θθsin ,cos r r ； (2) 将积分区域D 的边界曲线用极坐标方程来表示； (3)将直角坐标系中的面积元素换为极坐标系中的面积元素dxdy θrdrd .极坐标系中的二重积分同样是化为二次积分来计算. 这里只介绍先对r 积分，后对θ积分，分三种情形对如何确定两次积分的上下限加以讨论：(1)极点在区域D 的外面（如图7-26）设区域D 是由极点出发的两条射线βθαθ==,及两条连续曲线)(θϕ=r 、)(θψ=r 所围成.也就是说，区域D 可以表示为：{}βθαθψθϕθ≤≤≤≤=),()(),(r r D从极点出发在[]βα,内作一条极角为θ的射线穿过区域D ，穿入点的极径)(θϕ=r 作下限穿出点的极径)(θϕ=r 作上限；然后再对θ积分，其积分区间为[]βα,即∫∫∫∫=D)()()sin ,cos ()sin ,cos (βαθψθϕθθθθθθrdr r r f d rdrd r r f(2) 极点在区域D 的边界上（如图7-27）设区域D 是由极点出发的两条射线βθαθ==,及连续 曲线))((βθαθψ≤≤=r 所围成的曲边扇形，也就是说，区 域D 可以表示为：{}βθαθψθ≤≤≤≤=),(0),(r r D则计算公式为∫∫∫∫=D)(0)sin ,cos ()sin ,cos (βαθψθθθθθθrdr r r f d rdrd r r f (3) 极点在区域D 的内部（如图7-28）设区域D 的边界曲线的方程为)20()(πθθψ≤≤=r 此时{}πθθψθ20),(0),(≤≤≤≤=r r D . 则计算公式为∫∫∫∫=Drdr r r f d rdrd r r f πθψθθθθθθ20)(0)sin ,cos ()sin ,cos (通常当积分区域D 的边界由圆弧、射线组成且被积函数为yxy x ，22+等形式时，用极坐标进行计算较为方便.例5 计算积分，其中积分区域D 是由所围成的区域.∫∫+−Dy x d e σ)(22422=+y x 解 由于极点在区域D 的内部{}πθθ20,20),(≤≤≤≤=r r D ， 则∫∫∫∫−+−=Dr y x rdr e d d eπθσ202)(222 ∫∫−−=−πθ20202)(212r d e d r )1()1(214204−−−=−−=∫e d e πθπ 例6 计算积分，其中D 由∫∫+Dd y x σ)(22⎟⎠⎞⎜⎝⎛≤≤−=22cos 2πθπθa r 所围成。

考研数学冲刺难点复习：⼆重积分解法
考研数学进⼊重点复习阶段了，⼩编为⼤家提供考研数学冲刺难点复习：⼆重积分解法，希望⼤家能好好消化，争取把这个知识点全部弄懂！
考研数学冲刺难点复习：⼆重积分解法
计算⼆重积分的基本思路是将其化作累次积分(也即两次定积分)，要把⼆重积分化为累次积分，有两个主要的⽅式：⼀是直接使⽤直⾓坐标，⼆是使⽤极坐标。

这是我们计算⼆重积分的两个主要的武器。

⾸先，对直⾓坐标来说，主要考点有两个：⼀是积分次序的选择，基本原则有两个：⼀是看区域，选择的积分次序⼀定要便于定限，说得更具体⼀点，也就是要尽量避免分类讨论;⼆是看函数，要尽量使第⼀步的积分简单，选择积分次序的最终⽬的肯定是希望是积分尽可能地好算⼀些，实践表明，⼤多数时候，只要让⼆重积分第⼀步的积分尽可能简单，那整个积分过程也会⽐较简洁，所以我们在拿到⼀个⼆重积分之后，可以根据它的被积函数考虑⼀下第⼀步把哪个变量看成常数更有利于计算，从⽽确定积分次序。

⼆是定限，完成定限之后，⼆重积分就被化为了两次定积分，就可以直接计算了。

以上是我们计算⼆重积分的主体思路，在此基础之上，我们还可以利⽤对称性，它在⼆重积分的计算中虽然属于辅助性的技能，但如果恰当使⽤的话，还是可以明显地简化计算。

⼆重积分中的对称性分为两种：⼀是奇偶性，⼆是轮换对称性。

⼀般来说，对称性应该使⽤在拿到⼀个⼆重积分之后的第⼀步，只要积分区域关于某坐标轴是对称的，就要先检验被积函数是否具有相应的对称性，尤其要注意有没有奇函数，以尽可能地简化计算。