二重积分计算方法的总结和评价
- 格式:doc
- 大小:55.00 KB
- 文档页数:1
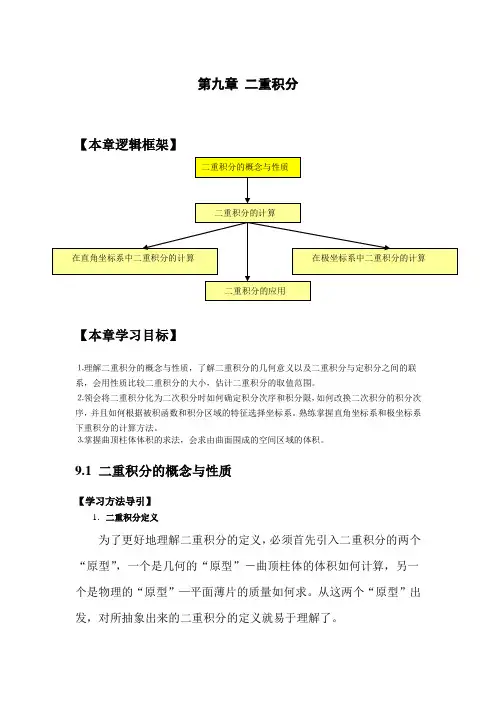
第九章二重积分【本章逻辑框架】【本章学习目标】⒈理解二重积分的概念与性质,了解二重积分的几何意义以及二重积分与定积分之间的联系,会用性质比较二重积分的大小,估计二重积分的取值范围。
⒉领会将二重积分化为二次积分时如何确定积分次序和积分限,如何改换二次积分的积分次序,并且如何根据被积函数和积分区域的特征选择坐标系。
熟练掌握直角坐标系和极坐标系下重积分的计算方法。
⒊掌握曲顶柱体体积的求法,会求由曲面围成的空间区域的体积。
9.1 二重积分的概念与性质【学习方法导引】1.二重积分定义为了更好地理解二重积分的定义,必须首先引入二重积分的两个“原型”,一个是几何的“原型”-曲顶柱体的体积如何计算,另一个是物理的“原型”—平面薄片的质量如何求。
从这两个“原型”出发,对所抽象出来的二重积分的定义就易于理解了。
在二重积分的定义中,必须要特别注意其中的两个“任意”,一是将区域D 成n 个小区域12,,,n σσσ∆∆∆的分法要任意,二是在每个小区域i σ∆上的点(,)i i i ξησ∈∆的取法也要任意。
有了这两个“任意”,如果所对应的积分和当各小区域的直径中的最大值0λ→时总有同一个极限,才能称二元函数(,)f x y 在区域D 上的二重积分存在。
2.明确二重积分的几何意义。
(1) 若在D 上(,)f x y ≥0,则(,)d Df x y σ⎰⎰表示以区域D 为底,以(,)f x y 为曲顶的曲顶柱体的体积。
特别地,当(,)f x y =1时,(,)d Df x y σ⎰⎰表示平面区域D 的面积。
(2) 若在D 上(,)f x y ≤0,则上述曲顶柱体在Oxy 面的下方,二重积分(,)d Df x y σ⎰⎰的值是负的,其绝对值为该曲顶柱体的体积(3)若(,)f x y 在D 的某些子区域上为正的,在D 的另一些子区域上为负的,则(,)d Df x y σ⎰⎰表示在这些子区域上曲顶柱体体积的代数和(即在Oxy 平面之上的曲顶柱体体积减去Oxy 平面之下的曲顶柱体的体积).3.二重积分的性质,即线性、区域可加性、有序性、估值不等式、二重积分中值定理都与一元定积分类似。

二重积分的计算方法与应用二重积分是微积分中的一个重要概念,用于计算平面区域上的某一函数在该区域上的总体积量。
在本文中,我们将介绍二重积分的计算方法与应用。
首先,我们将讨论二重积分的基本概念和计算方法。
假设有一个平面区域D,可以用一个闭合曲线C来描述。
我们将函数f(x, y)定义在区域D内的每一个点上,并且假设f(x, y)在D上连续。
那么在D上的二重积分可以表示为:∬D f(x, y) dA其中,dA表示面积元素,其大小等于dxdy。
要计算二重积分,我们可以将区域D划分成许多小的面积元素,然后对每个面积元素上的函数值进行加权求和。
通常可以使用二重积分的累次积分形式来计算,可以按顺序进行x方向的积分,然后再进行y方向的积分。
在具体计算二重积分时,可以根据问题的特点选择不同的计算方法。
下面介绍常见的二重积分计算方法:1. 矩形坐标系下的二重积分:在矩形坐标系下,将区域D投影到xy平面上,可以得到一个矩形R。
这时,二重积分可以转化为对两个变量的累次积分,其中外层积分表示对x的积分,内层积分表示对y的积分。
通过对x和y的积分限进行适当选择,可以将二重积分转化为两个定积分的计算。
2. 极坐标系下的二重积分:在某些问题中,使用极坐标系进行二重积分计算可以更加简洁。
通过将区域D在极坐标系下的表示,可以将二重积分转化为对极坐标下的两个变量的累次积分。
在计算时,可以通过选择适当的极坐标系下的积分限来简化计算过程。
3. 对称性的利用:在某些问题中,可以利用区域D的对称性简化二重积分的计算。
通过观察函数f(x, y)的对称性,可以改变积分限或者变量的顺序,从而简化计算的过程。
接下来,我们将讨论二重积分在实际问题中的应用。
1. 面积与质量:二重积分可以用来计算平面区域的面积。
将函数f(x, y)设为1,即可得到区域D的面积。
此外,如果区域D上的密度函数为ρ(x, y),那么通过计算二重积分∬D ρ(x, y) dA,可以得到区域D的质量。

二重积分的计算小结在数学中,二重积分是一种用来计算平面上曲线下的面积的方法。
它是定积分的扩展,可以用于计算更加复杂的形状的面积,例如圆形、椭圆形和弧形等。
在本文中,我们将详细介绍二重积分的计算方法,并提供一些重要的应用案例和技巧。
同时,我们还将讨论二重积分的性质以及它与其他数学概念的关系。
设 $f(x,y)$ 是定义在闭区域 $D$ 上的实函数,将闭区域 $D$ 分成许多小的矩形区域,其中第 $i$ 个小矩形的面积为 $\Delta A_i$,选择任意一点 $(x_i^*, y_i^*)$ 作为该矩形的代表点,则二重积分的近似值可以表示为:$$\sum_{i=1}^n f(x_i^*, y_i^*) \Delta A_i$$其中,$n$ 是划分区域时小矩形的个数,$\Delta A_i$ 是第 $i$ 个小矩形的面积。
当划分的小矩形越来越小,并且代表点 $(x_i^*, y_i^*)$ 在每个小矩形内部时,这个近似值将趋近于一个常数,即二重积分的值。
我们用符号 $\iint_D f(x,y) dA$ 表示二重积分的值,其中 $dA$ 表示对面积的微元。
接下来,我们将介绍几种计算二重积分的方法。
一、二重积分的计算方法1. 矩形法(Riemann和):将区域 $D$ 划分为若干个小的矩形区域,计算每个矩形的面积和函数值,并将它们相加得到近似值。
2. 二次积分法(Fubini定理):根据 Fubini 定理,我们可以将二重积分转化为两个一重积分的乘积:$$\iint_D f(x,y) dA = \int_a^b \left( \int_c^d f(x,y) dy\right) dx$$3. 极坐标法:当区域 $D$ 的形状具有旋转对称性时,使用极坐标计算二重积分可以更加简便。
通过转化为极坐标系,并利用极坐标下的Jacobian 行列式,可以将原二重积分转化为对一重积分的积分。
4. 线性代换法:对于不规则区域,我们可以通过线性代换将其转换为规则区域,然后再进行计算。

二重积分的计算方法二重积分是微积分中的重要概念,它在数学和物理学中有着广泛的应用。
在本文中,我们将探讨二重积分的计算方法,包括定积分、极限方法和变换法。
首先,我们来回顾一下定积分的概念。
定积分是在一个区间上对函数进行积分的方法,可以看作是对函数在该区间上面积的测量。
对于一维的函数,如f(x),定积分的计算方法可以通过求解反导函数F(x)的值来实现。
具体而言,定积分是将函数f(x)在区间[a,b]上的每个小矩形的面积累加起来,得到的结果就是函数在该区间上的定积分。
对于二重积分,它的计算稍微复杂一些。
二重积分可以看作是在一个二维的区域上对函数进行积分的方法。
通常情况下,二重积分的计算可以分为两个步骤:首先,将二重积分转化为定积分的形式;然后,利用定积分的计算方法进行求解。
对于二重积分的转化,常用的方法有直角坐标转换和极坐标转换。
直角坐标转换适用于矩形区域,它将二重积分转化为两个一维的定积分。
具体而言,设二重积分的变量为x和y,区域为D,函数为f(x,y),则二重积分的计算可以表示为:∬f(x,y)dA = ∫(∫f(x,y)dy)dx其中,第一个定积分在区域D上对y进行积分,第二个定积分在整个区域D上对x进行积分。
极坐标转换适用于圆形或者具有旋转对称性的区域,它将二重积分转化为极坐标系下的定积分。
具体而言,设二重积分的变量为r和θ,区域为D,函数为g(r,θ),则二重积分的计算可以表示为:∬g(r,θ)rdrdθ其中,第一个定积分在区域D上对r进行积分,第二个定积分在整个区域D上对θ进行积分。
除了定积分的方法,还可以使用极限方法来计算二重积分。
极限方法是通过将计算区域划分成无穷多个小矩形或者小三角形,然后将其面积累加起来得到积分的值。
具体而言,对于二重积分的计算,可以将区域D划分成很多个小矩形或者小三角形,然后根据这些小区域的面积和函数值进行累加,最后取极限即可得到二重积分的值。
最后,我们来介绍一种常用的变换法,即换元法。

求二重积分的方法在数学中,二重积分是一种重要的积分形式,它在物理、工程、经济学等领域都有广泛的应用。
求解二重积分的方法有很多种,本文将介绍几种常见的方法,希望能够帮助大家更好地理解和掌握二重积分的计算技巧。
一、直角坐标系下的二重积分。
在直角坐标系下,二重积分的计算通常采用先对x进行积分,再对y进行积分的方法。
对于给定的二元函数f(x,y),其在有界区域D上的二重积分可以表示为:∬f(x,y)dxdy。
其中积分区域D可以用不等式形式表示为D={(x,y)|a≤x≤b,g1(x)≤y≤g2(x)},此时二重积分可以表示为:∬f(x,y)dxdy=∫(∫f(x,y)dy)dx。
其中内层积分是对y进行积分,外层积分是对x进行积分。
在实际计算中,可以先对y进行积分,再对x进行积分,也可以反过来进行计算,选择合适的积分顺序可以简化计算过程。
二、极坐标系下的二重积分。
在某些情况下,使用极坐标系进行二重积分的计算会更加方便。
对于给定的二元函数f(x,y),其在极坐标下的二重积分可以表示为:∬f(x,y)dxdy=∫(∫f(rcosθ,rsinθ)rdrdθ。
其中积分区域D可以用极坐标形式表示为D={(r,θ)|α≤θ≤β, h1(θ)≤r≤h2(θ)}。
在极坐标系下,二重积分的计算可以简化为对r和θ的积分,适用于一些具有极向对称性的函数。
三、变量代换法。
对于一些复杂的二重积分,可以通过变量代换的方法来简化计算。
常见的变量代换包括直角坐标系到极坐标系的转换、直角坐标系到柱坐标系的转换、直角坐标系到球坐标系的转换等。
通过适当的变量代换,可以将原积分区域D变换为一个更简单的区域,从而简化积分的计算。
四、二重积分的性质。
在计算二重积分时,还可以利用二重积分的性质来简化计算。
例如,二重积分具有线性性质,可以将一个复杂的二重积分拆分为若干个简单的二重积分相加;二重积分的积分区域可以进行分割,将原积分区域分割为若干个简单的子区域,分别计算再相加等。


二重积分的概念和计算方法在数学中,我们经常遇到需要对二维区域上的函数进行求和或求平均的情况。
为了解决这类问题,人们引入了二重积分的概念。
本文将探讨二重积分的概念以及常见的计算方法。
一、二重积分的概念二重积分是对二维平面上的函数进行求和的操作。
它可以看作是将一个二维区域分割成无穷多个小的矩形,然后对每个小矩形内的函数值进行求和的过程。
一般来说,我们通过累次积分的方法来计算二重积分。
对于函数f(x, y)在区域D上的二重积分,可以表示为:∬f(x, y)dA其中,D表示二维区域,dA表示微元面积。
二重积分的结果是一个数值,代表了函数f(x, y)在区域D上的总体特征。
二、二重积分的计算方法1. 直角坐标系下的二重积分在直角坐标系下,计算二重积分需要先确定积分范围。
一般情况下,我们将区域D分割成一个个小矩形或小三角形,根据积分的性质进行求和。
对于给定的函数f(x, y),其在区域D上的二重积分可以表示为:∬f(x, y)dA = ∫∫f(x, y)dxdy其中,积分区域D的边界可以表示为[a, b]和[c(x), d(x)],其中c(x)和d(x)是关于x的函数。
通过确定积分的次序和边界,我们可以将二重积分转化为一重积分的形式,然后按照一重积分的计算方法进行求解。
2. 极坐标系下的二重积分在某些情况下,使用极坐标系进行二重积分的计算更为方便。
特别是当积分区域具有简单的几何形状,如圆形、扇形或圆环等情况下,使用极坐标系可以简化计算过程。
对于给定的函数f(x, y),在极坐标系下的二重积分可以表示为:∬f(x, y)dA = ∫∫f(r, θ)rdrdθ其中,积分区域D的边界可以表示为[r1(θ), r2(θ)]和[a, b],其中r1(θ)和r2(θ)是关于θ的函数。
通过确定积分的次序和边界,我们可以将二重积分转化为一重积分的形式,然后按照一重积分的计算方法进行求解。
3. 格林公式的应用在某些情况下,利用格林公式可以简化二重积分的计算。

二重积分计算与应用在数学中,二重积分是一种用于计算二维平面上曲线下的面积和体积的工具。
它是微积分学的重要分支,具有广泛的应用。
本文将介绍二重积分的概念、计算方法以及一些常见的应用。
一、二重积分的概念二重积分是对平面上的一块有界区域内的函数进行求和。
我们将二维平面分割成许多小矩形区域,并在每个小矩形区域内取一个点。
然后,将这些小矩形的面积相加,再将函数在该点的值与该小矩形的面积相乘,并对所有小矩形进行求和,即可得到二重积分的值。
二、二重积分的计算方法计算二重积分有两种主要的方法:定积分法和极坐标法。
1. 定积分法定积分法是最常用的计算二重积分的方法之一。
它将被积函数转化为两个变量的函数,然后通过重复使用一元定积分的方法进行计算。
具体步骤如下:步骤一:确定积分区域。
通常使用直角坐标系下的矩形或多边形来表示。
步骤二:确定被积函数。
将被积函数表示成两个变量的函数。
步骤三:将被积函数简化。
根据积分区域的特点,合理地设定积分的上下限。
步骤四:依次进行一元定积分。
先对内层变量进行积分,再对外层变量进行积分。
2. 极坐标法当被积函数在极坐标系下具有一定的对称性时,使用极坐标法可以简化计算过程。
具体步骤如下:步骤一:确定积分区域。
在极坐标系下,通常使用极坐标方程来表示。
步骤二:确定被积函数。
将被积函数转化为极坐标系下的函数。
步骤三:将被积函数简化。
根据极坐标系的特性,将函数表示成极坐标下的形式。
步骤四:直接进行一元定积分。
根据区域的特点,选取适当的积分上下限进行计算。
三、二重积分的应用二重积分在实际问题中有广泛的应用,包括计算面积、计算质心、计算物体的质量等等。
1. 计算面积二重积分可以用来计算平面上有界区域的面积。
通过将被积函数取为1,对给定的区域进行积分,即可得到该区域的面积。
2. 计算质心质心是物体的平衡点,是物体的几何中心。
二重积分可以用来计算物体的质心位置。
通过将被积函数取为物体的密度函数乘以相应的坐标值,对整个物体进行积分,即可得到物体的质心位置。

二重积分的意义与计算技巧二重积分是微积分中的重要工具,用于计算平面区域上的某一函数的总体积。
它在科学、工程和数学领域都有广泛的应用。
本文将重点探讨二重积分的意义和计算技巧,以帮助读者更好地理解和运用这一概念。
1. 二重积分的意义二重积分用于求解平面区域上某一函数的总体积。
它将区域划分为无数个小的矩形区域,并计算每个小矩形区域上函数值的加权和,最后将这些加权和相加得到最终结果。
二重积分的意义可以理解为通过对无限小区域的加权求和,来计算整个区域上函数的更全面的性质。
2. 二重积分的计算技巧2.1 确定积分区域首先要确定二重积分的积分区域,即确定在哪个平面区域上进行积分。
常见的积分区域包括矩形、圆形、三角形等。
通过对积分区域进行合理的划分和参数表示,可以简化二重积分的计算过程。
2.2 改变积分顺序二重积分的计算顺序可以灵活调整,有时候改变积分顺序可以简化计算过程。
例如,如果原先是在 x 轴方向先积分,再在 y 轴方向积分,可以考虑交换积分的顺序,先在 y 轴方向积分,再在 x 轴方向积分。
2.3 选择合适的坐标系选择合适的坐标系可以简化二重积分的计算。
常用的坐标系有直角坐标系、极坐标系和柱坐标系等。
根据具体问题的特点,选择适用的坐标系可以简化二重积分的表达和计算过程。
2.4 利用对称性如果被积函数具有某种对称性,可以利用对称性简化二重积分的计算。
例如,如果被积函数在积分区域关于 x 轴对称,则积分结果为 0。
2.5 利用几何特性利用几何特性可以简化二重积分的计算。
例如,如果积分区域是一个矩形,被积函数是关于 x 轴或 y 轴的线性函数,可以利用几何特性直接计算出积分结果。
2.6 应用换元法对于某些复杂的二重积分,可以应用换元法来简化计算过程。
通过进行适当的变量替换,可以将被积函数转化为更简单的形式,从而简化积分的求解。
2.7 利用数值积分方法当无法直接求得二重积分的解析解时,可以利用数值积分方法进行近似计算。

关于二重积分计算方法的探讨
一.概述
二重积分是一种数学技术,常用于计算单一函数在其中一空间内的总
体(积分)结果。
其计算过程是采用“把一个偏微分方程变换为平面积分”的方法,将一个函数的参数两次积分,从而求出函数在一定范围内的总体(积分)结果。
二.过程
积分的过程包括三步:第一步,将原问题变换为积分形式;第二步,
对变换后的积分问题进行计算;第三步,根据计算结果,得出结果。
1.变换为积分形式:
要进行二重积分,首先必须将原问题转换为积分形式。
其步骤如下:(1)将函数中的变量(x、y)变换为积分变量(u、v),例如:
2.计算步骤:
在将原函数变换为积分形式后,我们便可以开始计算积分。
计算过程
也分为三个部分:
(1)找出积分区间:求解二重积分问题时,必须明确积分区间,以
便进行积分计算。
积分的结果取决于积分区间,因此,只有明确积分区间,才能得出准确结果。
(2)确定积分类型:根据积分区间的形状,可以确定积分的类型,
如果积分区间是矩形,则积分类型为矩形积分,如果积分区间是三角形,
则积分类型为三角积分。
![[全]高等数学之二重积分计算方法总结[下载全]](https://uimg.taocdn.com/2b9bc316284ac850ac024211.webp)
高等数学之二重积分计算方法总结
在考研中,对于二重积分重点要掌握二重积分的计算方法(直角坐标,极坐标),二重积分计算公式如下:
二重积分的计算主要在于把二重积分化为累次积分计算,而在化为累次积分计算时,坐标系的选择不仅要看积分域D的形状,而且还要看被积函数的形式。
(1)适合用极坐标计算的二重积分被积函数一般应具有以下形式:
f(y/x),f(x/y),f((x^2+y^2)^(1/2))
之所以适合极坐标是由于它们在极坐标下都可化为r或thetha的一元函数。
(2)适合用极坐标计算的二重积分的积分域一般应具有以下形状:
中心在原点的圆域,圆环域或它们的一部分(如扇形);中心在坐标轴上且边界圆过原点的圆域或者它们的一部分。
有时在计算二重积分时候需要利用被积函数的奇偶性和积分区域的对称性,常用的结论有以下两条:
(1)利用积分域的对称性和被积函数的奇偶性:
(2)利用变量的对称性:
题型一:在直角坐标下计算二重积分
例1:
解题思路:先画积分域D,不难看出该积分域关于两个坐标轴都对称,被积函数也有奇偶性,因此,应利用对称性和奇偶性。
解:
题型二:利用极坐标计算二重积分
例2:
解题思路:积分区域D关于y轴左右对称,被积函数(x+1)^2=x^2+2x+1,其中2x是x的奇函数,x^2+1是x的偶函数,先利用奇,偶性化简,然后再用极坐标计算。
解:。
二重积分学习总结-标准化文件发布号:(9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII高等数学论文《二重积分学习总结》姓名:徐琛豪班级:安全工程02班学号:1201050221完成时间:2013年6月2日二重积分 【本章学习目标】⒈理解二重积分的概念与性质,了解二重积分的几何意义以及二重积分与定积分之间的联系,会用性质比较二重积分的大小,估计二重积分的取值范围。
⒉领会将二重积分化为二次积分时如何确定积分次序和积分限,如何改换二次积分的积分次序,并且如何根据被积函数和积分区域的特征选择坐标系。
熟练掌握直角坐标系和极坐标系下重积分的计算方法。
⒊掌握曲顶柱体体积的求法,会求由曲面围成的空间区域的体积。
1 二重积分的概念与性质1.二重积分定义为了更好地理解二重积分的定义,必须首先引入二重积分的两个“原型”,一个是几何的“原型”-曲顶柱体的体积如何计算,另一个是物理的“原型”—平面薄片的质量如何求。
从这两个“原型”出发,对所抽象出来的二重积分的定义就易于理解了。
在二重积分的定义中,必须要特别注意其中的两个“任意”,一是将区域D 成n 个小区域12,,,n σσσ∆∆∆的分法要任意,二是在每个小区域i σ∆上的点(,)i i i ξησ∈∆的取法也要任意。
有了这两个“任意”,如果所对应的积分和当各小区域的直径中的最大值0λ→时总有同一个极限,才能称二元函数(,)f x y 在区域D 上的二重积分存在。
2.明确二重积分的几何意义。
(1) 若在D 上(,)f x y ≥0,则(,)d Df x y σ⎰⎰表示以区域D 为底,以(,)f x y 为曲顶的曲顶柱体的体积。
特别地,当(,)f x y =1时,(,)d Df x y σ⎰⎰表示平面区域D 的面积。
(2) 若在D 上(,)f x y ≤0,则上述曲顶柱体在Oxy 面的下方,二重积分(,)d Df x y σ⎰⎰的值是负的,其绝对值为该曲顶柱体的体积(3)若(,)f x y 在D 的某些子区域上为正的,在D 的另一些子区域上为负的,则(,)d Df x y σ⎰⎰表示在这些子区域上曲顶柱体体积的代数和(即在Oxy 平面之上的曲顶柱体体积减去Oxy 平面之下的曲顶柱体的体积).3.二重积分的性质,即线性、区域可加性、有序性、估值不等式、二重积分中值定理都与一元定积分类似。
目录摘要 (1)关键词 (1)Abstract (1)Key Words (1)1.化二重积分为累次积分 (1)2. 二重积分的变量变换 (5)2.1 二重积分的变量变换公式 (5)2.2 利用极坐标计算二重积分 (6)结束语 (8)参考文献: (8)二重积分的计算方法小结学生姓名:余义江 学号:20085031166 数学与信息科学学院 数学与应用数学 指导教师:李景杰 职称:副教授摘 要:本文介绍了几种常用的二重积分的计算方法.并通过实例加以阐析. 关键词:二重积分;累次积分;变量变换The Summary of the Calculation of Double IntegralAbstract:This paper introdues several common used methods of calculating the double integral. Examples and summaries are also given.Key Words: Double integral; Repeated integral; Variable transformation引言对于二重积分,如果按定义去计算其积分值是非常复杂的,因此必须寻找其计算的简单方法.1.化二重积分为累次积分定理[]11 设(),f x y 在矩形区域[][],,D a b c d =⨯上可积,且对每个[],x a b ∈,积分(),d cf x y dy ⎰存在,则累次积分dcdy⎰(),baf x y ⎰dx 也存在,且(),Df x y d σ⎰⎰b adx=⎰(),dcf x y dy ⎰.定理[]'11 设(),f x y 在矩形区域[][],,D a b c d =⨯上可积,且对每个y ∈ [],c d ,积分(),baf x y dx ⎰存在,则累次积分dcdy⎰(),ba f x y ⎰dx 也存在,且(),Df x y d σ⎰⎰(),d bcady f x y dx =⎰⎰.特别地当(),f x y 在矩形区域[][],,D a b c d =⨯上连续时,则有(),D f x y d σ⎰⎰(),d b cady f x y dx =⎰⎰badx=⎰(),dcf x y dy ⎰.例1 计算()2Dx y d σ+⎰⎰,其中[][],,D a b c d =⨯. 解 应用定理1(或定理'1)有(),D f x y d σ⎰⎰()11200dx x y dy =+⎰⎰=()3310133x x dx ⎡⎤--⎢⎥⎢⎥⎣⎦⎰76=. 定理[]22 设D 为由x a =,x b =()a b <,()1y y x =,()2y y x =所围成的区域,其中()1y x ,()2y x 在[],a b 上连续且()1y x ≤()2y x .如果(),f x y 在D 上可积,(),Df x y dxdy ⎰⎰I =,又对每个固定的[],x a b ∈,一元函数(),f x y 在()1y x ≤y ≤()2y x 上可积,()()()21,y x y x f x y ⎰dy I =()x ,则()I x 在[],a b 上可积,且()baI x dx I =⎰.即(),Df x y dxdy ⎰⎰=()()()()21,by x ay x f x y dy dx ⎰⎰.定理二把二重积分的计算化为一个先y 后x 的累次积分.完全类似的有以下定理定理[]'22 设D 为由y c =,y d =()c d <,()1x x y =,()2x x y =所围成的区域,其中,()1x y ,()2x y 在[],c d 上连续且()1x y ≤()2x y .如果(),f x y 在D 上可积,(),Df x yd x dy ⎰⎰I =,又对每个固定的[],y c d ∈,一元函数(),f x y 在()1x y ≤x ≤()2x y 上可积,()()()21,x y x y f x y dx ⎰I =()y ,则()I y 在[],c d 上可积,且()dcI y dy I =⎰.即(),Df x y dxdy ⎰⎰=()()()()21,dx y cx y f x y dx dy ⎰⎰.注意,在利用定理2时,必须要求积分区域D 满足以下条件,即任何平行于y 轴的直线0x x =()0a x b <<和D 的边界至多只有两个交点.定理'2也类似.如果区域D 不满足以上条件时,则要将区域D 适当地分割为若干个小区域,使每个小区域满足以上条件 .如果对区域D 定理2和定理'2都能用时,则有 (),Df x y dxdy ⎰⎰=()()()21,by x a y x dx f x y dy ⎰⎰=dcdy⎰()()()21,x y x yf x y dx ⎰.此时到底将二重积分化为先x 后y 的累次积分,还是化为先y 后x 的累次积分,则要看具体的问题而定,看哪种算法简单.例2 设D 是由直线0x =,1y =及y x =围成的区域,试计算:I =22y Dx ed σ-⎰⎰的值.解 若用先对y 后对x 的积分,则2112y xI x dx edy -=⎰⎰.由于函数2y e 的原函数无法用初等函数形式表示,因此改用另一种顺序的累次积分,则有2120yy I dy x edx -=⎰⎰213013y y e dy -=⎰ . 由分部积分法,即可算得:1163I e=-.上例说明积分的次序的选择与二重积分计算的繁,简程度有着极为密切的关系.如果选择不当将增大计算难度或无法计算. 所以,如果按某种次序的累次积分的计算很麻烦,或者根本积不出来,那就需要考虑更换积分次序了.积分换序的一般步骤是:1. 由所给的累次积分的积分限,写出积分区域的不等式表达式;2. 将不等式两端看成等式,可得积分区域的边界线.然后画出积分区域D ;3. 将区域D 按相反次序用不等式表示出来;4. 按3中的不等式将积分表示为二次积分.例3计算240xI dx dy y ππ=⎰.解 由于sin xy⎰dy 无法求出,所以考虑交换积分次序.由已知,积分区域可表示为D :204x π≤≤2y π≤≤其边界曲线为y ,2y π=和0x =作出区域D 的图形(图1),再将D 按相反次序 表示为 D :20π≤≤y ,20y x ≤≤于是dx yx dy dy y x dx I y x⎰⎰⎰⎰==2004222sin sin πππ()20cos y y y dy π=-⎰2182ππ=-+.同定积分的计算一样,有时,奇偶性来简化运算.具体地有:1. 若()y x f ,是x 的奇函数,即()()y x f y x f ,,-=-且积分区域D 关于y 轴对称,则()0,=⎰⎰σd y x f D;2. 若()y x f ,是x 的偶函数,即()()y x f y x f ,,=-且积分区域D 关于y 轴对称,则()()σσd y x f d y x f D D⎰⎰⎰⎰=1,2,其中1D 是区域D 的位于y 轴右侧的子区域;同理,若()y x f ,是y 的奇或偶函数,而积分区域又关于x 轴对称,则我们也有类似的简化公式.例4 计算()22DI xy x y d σ=+⎰⎰,其中D 由2y x =与1y =直线围成.解 积分区域如图2所示,它关于y 轴对称,所以 ()22DI xy x y d σ=+⎰⎰2Dxy d σ=⎰⎰+2D x yd σ⎰⎰02=+又由于子区域1D 可表示为 1D :201,1x x y ≤≤≤≤所以122D I x yd σ=⎰⎰211202x dx x ydy =⎰⎰120x =⎰421=.2. 二重积分的变量变换在定积分的计算中我们已经知道,通过变量代换可以使被积函数得到简化,因而使该定积分变得简单易求.同样对于二重积分也可以用二重积分使问题简化.通过变量代换将一个难积的二重积分变得容易积分,关键在于选好变量,变量的选择有时根据函数有时根据积分区域决定.2.1 二重积分的变量变换公式定理[]13 设(),f x y 在有闭区域D 上可积,变换T :(),x x u v =,(),y y u v =将uv平面由按段光滑封闭曲线所围成的闭区域∆一对一地映成xy 平面上的闭区域D ,函数(),x u v ,(),y u v 在∆分别具有一阶连续偏导数且它们的函数行列式()()(),,0,x y J u v u v ∂=≠∂,(),u v ∈∆则(),Df x yd x d y =⎰⎰()()()(),,,,fx uv y u v J u v d u d v∆⎰⎰. 选择变量代换时,我们一般可遵循以下两条原则:1. 所选的变换要能够使被积函数尽可能的简化,以便容易积分;2. 要使积分区域容易用新的变量表示,从而使积分限容易确定. 例5 求x yx yDedxdy +-⎰⎰其中D 是由0x =,0y =,1x y +=所围成区域(图3).解 为了简化被积函数,令u x y =-,v x y =+.为此作变换T :()12x u v =+,()12y u v =-,则 ()11122,011222J u v ==>-.在变换T 的作用下,区域∆的原象如图4所示,所以D2D=10v v dv -⎰⎰()1112u v v v v e e dvdv e du --=-⎰⎰14e e --=.2.2 利用极坐标计算二重积分对以有些二重积分,其积分区域用极坐标方程表示比较方便,且其被积函数用极坐标变量表示也比较简单,这时,我们就可以考虑用极坐标来计算二重积分.定理[]14 设(),f x y 满足定理3的条件,且在极坐标变换T :cos ,sin ,x r u r θθ=⎧⎨=⎩0,02r θπ≤<+∞≤≤下,xy 平面上有界闭区域D 与r θ平面上区域∆对应,则成立(),Df x y dxdy ⎰⎰()cos ,sin f r r rdrd θθθ∆=⎰⎰.由定理4可以看到,用极坐标变换计算二重积分,除变量做相应的替换外,还必须把“面积微元”dxdy 换成r drd θ.注意,在将积分区域D 用坐标变量r ,θ表示时,通常先确定极角θ的变化范围.具体做法是,通过极点在区域对应的极角θ最小,最大值的两侧边界作两条切线(或射线),它们将D 的边界分为内,外两段,设其方程分别为()1r ϕθ=和()2r ϕθ=.由此可得极角θ的变化范围αθβ≤≤;然后由极点出发在[],αβ内引一条射线,它由()1r ϕθ=进入区域,而由 ()2r ϕθ=穿出区域,所以极半径r 的变化范围为()()12r ϕθϕθ≤≤.因此,积分区域可用极坐标变量表示为D :αθβ≤≤,()()12r ϕθϕθ≤≤特别地,如果积分区域退化为一个如图5所示的曲边扇形,即区域的内侧边界缩为极点时,积分区域可表示为D :αθβ≤≤,()0r ϕθ≤≤若如图6所示,极点位于积分区域D 的内部时,则可视为图5当0α=,2βπ=时的特例.即可用不等式D :02απ≤≤,0r ≤≤θ,后对例6 求22xy De d σ--⎰⎰,其中D 是圆2x +解 采用极坐标,积分区域可表示为 D :02θπ≤≤,0r a ≤≤ 于是22x y De d σ--⎰⎰2r De r d r d θ-=⎰⎰2200ard re dr πθ-=⎰⎰21202r a e π-⎛⎫=- ⎪⎝⎭()21a e π-=-例7 求球体22224x y z a ++≤被圆柱面222x y ax +=()0a >所截得(含圆柱面内的部分)立体的体积.解根据4DV =其中,D 由半圆与轴围成.利用极坐标,积分区域D 可表示为24DV =4Dθ=2c 204d πθθ=⎰⎰()3320231sin 3a d πθ=-⎰3232323a π⎛⎫=- ⎪⎝⎭. 结束语在计算二重积分时,选择适当的坐标,以及适当的积分顺序是很重要的.一般地,当积分区域为圆域、环域或扇形区域时,或被积函数中含有的项时,常利用极坐标.在计算重积分时,特别应注意对称性的利用,这可大大减少计算量.参考文献:[1]华东师范大学数学系.数学分析.下册[M].北京:高等教育出版社,2001.[2]贾晓峰等.微积分与数学模型.下册[M]. 北京:高等教育出版社;海德堡:施普林格出版社,1999.[3]沈燮昌,邵品琮. 数学分析纵横谈[M].北京:北京大学出版社,1991. [4]徐利治等.大学数学解题法诠释[M].合肥:安徽教育出版社,1999.。
二重积分的计算小结一、知识要点回顾1. 二重积分的定义;2. 二重积分的几何意义及其物理模型。
二重积分()f(x,y)d 的几何意义就是以体积,其物理模型就是一个曲顶柱体。
3. 二重积分在直角坐标系下的计算(1)若积分区域D是由两条直线x=a,x=b,以及两条曲线y= l(x),y= 2(x) ( i(x)2(x),a x b)所围成,则b xf(x, y)dxdy = a dx 心)f(x, y)dy2(y),c y d)所围成,则d yDf(x, y)dxdy c dy y f(x, y)dx4. 极坐标下二重积分的计算法为底,以(s)为顶的曲顶柱体的(D)i(y)1 1o sinydy o ysin ydy 1 sin1.x=r cos ,y= r sin如果区域D 是由从极点出发的两条射线()和两条曲线r r1( ),r r2( ) ( r1( ) r2())所围成,则d f(x, y)dxdy d f(rcos ,r sin )rd drr2()d f(rcos ,rsin )rdrr1()5•曲线坐标下二重积分的计算法设函数x x(u, v), y y(u,v)在直角坐标平面uOv 上的封闭区域 D 上连续,有一阶 连续偏导数,而且雅克比行列式(x, y) (u,v)(x) (x) (u) (v) (y) (y) (u)(v)D f(x, y)dxdyf(x(u,v), y(u, v)) J dudv重积分的计算举例1. • 计算二重积分 D2y 所围成的区域.解:画出积分域如图所示 解方程组沁dxdy,其中D 为由直线y x解得图中的两个交点为(0,0),(1,1) , D 可表示为D={( x,y)|02y 1, y xy },沁dxdy D ydy ;节x1 0(yy 2)沁y dy图4与曲线x曰 疋sin(,D2x ysi n()D22x y)dxdy3,计算二重积分 的封闭区域。
二重积分的计算小结之邯郸勺丸创作一、知识要点回顾 1.二重积分的定义;2.二重积分的几何意义及其物理模型。
二重积分⎰⎰)(σσd y x f ),(的几何意义就是以)(σ为底,以)(s 为顶的曲顶柱体的体积,其物理模型就是一个曲顶柱体。
(1)若积分区域D 是由两条直线x=a,x=b,以及两条曲线y=φ1(x),y=φ2(x)(φ1(x)≤φ2(x),a ≤x ≤b)所围成,则dxdyy)f(x D ⎰⎰)(, =⎰badx dyy)f(x x x ⎰)2(φφ)(1,(2)若区域D 是由两条直线y=c,y=d 以及两条曲线x=φ1(y),x=φ2(y)(φ1(y)≤φ2(y), c ≤y ≤d)所围成,则x=θcos r ,y=θsin r如果区域D 是由从极点出发的两条射线αθ=,βθ=(α<β)和两条曲线)(2),(1θθr r r r == ()(1θr <)(2θr )所围成,则 5.曲线坐标下二重积分的计算法设函数),(),,(v u y y v u x x ==在直角坐标平面v O u '上的封闭区域D '上连续,有一阶连续偏导数,而且雅克比行列式 则二.二重积分的计算举例1.. 计算二重积分dxdy y yD ⎰⎰sin ,其中D 为由图4直线x y =与曲线2y x =所围成的区域.解:画出积分域如图所示 解方程组解得图中的两个交点为)1,1(),0,0(,D可暗示为D=},10|),{(2y x y y x y ≤≤≤≤, 于是2.计算二重积分dxdy D22y x y x ⎰⎰++22)sin(π的值,其中积分区域为}41|){(22≤+≤=yx y x,D 。
解:由对称性可以只考虑第一象限的积分域 采取极坐标。
则积分区域变成πθρθρ2≤≤≤≤=0,21|){(,D }于是3,计算二重积分dxdyD xy x y e⎰⎰+-的值的大小,其中D 是由x 轴,y轴以及x+y=2所围成的封闭区域。
二重积分的概念和计算方法二重积分是在二维平面上对一些区域上的函数进行求和的操作。
它可以用于求解平面区域上的面积、质量、重心等物理量,也可以用于解决求解二元函数的平均值、概率密度等问题。
在本文中,我们将讨论二重积分的概念以及几种常见的计算方法。
一、二重积分的概念二重积分是对二维平面上的一个闭区域D上的函数f(x,y)进行求和的操作,可以表示为:∬Df(x,y)dA其中D表示区域D上的面积,f(x,y)表示在点(x,y)上的函数值,dA 表示在D上的一个微小面积元素。
对于二重积分的计算,可以分为定积分和区域积分两种方法。
定积分的计算是将区域D划分成许多小的矩形面积,并将这些小矩形的面积乘以对应的函数值求和。
区域积分的计算是将区域D分成许多小的曲面元素,并将这些小曲面的面积乘以对应的函数值求和。
二、二重积分的计算方法1.直角坐标系下的二重积分计算在直角坐标系下,我们可以通过在区域D上设置两个变量x和y,将原来的二重积分转化为两个一重积分的问题。
将区域D分成许多小的矩形面积,每个小矩形的面积为ΔA,左下角的坐标为(x,y),则我们可以得到二重积分的计算公式为:∬D f(x,y) dA = lim ΔA→0 Σ f(x,y)ΔA其中Σ表示对所有小矩形面积求和。
对于简单的区域D,我们可以直接通过计算极限来求解二重积分。
但对于较为复杂的区域D,可以使用变量替换、拆分区域等方法来简化计算过程。
2.极坐标系下的二重积分计算在极坐标系下,我们可以通过引入极角θ和极径ρ,将二重积分转化为极坐标下的一重积分问题。
区域D可以用极坐标表示为:D={(ρ,θ),α≤θ≤β,g(θ)≤ρ≤h(θ)}。
对于极坐标下的二重积分公式,我们有:∬D f(x,y) dA = ∫βα ∫h(θ)g(θ) f(ρcosθ,ρsinθ)ρdρdθ。
通过将二重积分转化为极坐标系下的一重积分问题,可以简化复杂区域的计算过程。
3.坐标变换方法对于一些特殊的区域D,我们可以通过坐标变换来简化二重积分的计算过程。