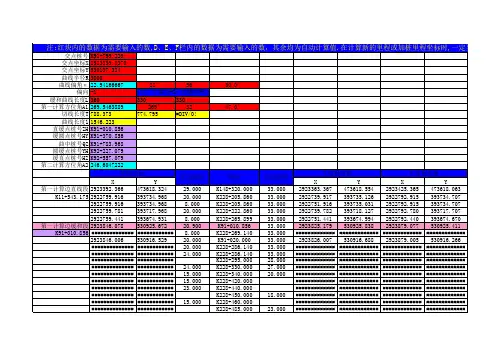
铁路线路坐标计算程序
- 格式:xls
- 大小:38.50 KB
- 文档页数:3

铁路公路曲线防样坐标计算方法一、随着我国公路铁路的大力建设,对坐标放样的要求精度越来越高,以及通过一种快速的捷径来达到一次性对整个路基、桥梁的中线编辑公式,准确较快的计算出中心坐标,使得坐标放样在我们的施工中带来更大的方便。
1、首先熟悉测量知识圆曲线基本公式及概念。
偏角法测设圆曲线1-1知道了圆曲线的测设里程,即测设的曲线长Li ,即可进行计算,其计算公式如下:πα0180∙=R L i i2iiαδ=i i R c δsin 2= (1-1)式中,i δ,i c 为曲线测设曲线点i 的偏角与弦长。
切线支距法测设圆曲线ZYi i R x αsin ∙= )c o s 1(i i R y α-∙= π180∙=R L a i i(1-2)1-2式中i L 为曲线上点i 至ZY (或YZ )的曲线长。
2、缓和曲线的基本公式及概念。
缓和曲线是直线与圆曲线之间的一种过渡曲线,它与直线分界处半径为∞,与圆曲线相接处半径与圆曲线半径R 相等,缓和曲线上任一点的曲率半径ρ与该点到曲线起点的长度成反比。
如下图中,存在公式: ρ∝l1 或Cl =ρ (2-1)公式中C 是一个常数,称缓和曲线半径变更率。
当0l l =时,R =ρ 所以C l R =∙0,C l =ρ,是缓和曲线的必要条件,实用中能满足这一条件的曲线可称为缓和曲线,如辐射螺旋线、三次抛物线等,我国缓和曲线均采用辐射螺旋线。
1-33、缓和曲线方程式:按照C l =ρ为必要条件导出的缓和曲线方程为:∙∙∙∙++-=∙∙∙∙∙++-=5113734925422403366345640Cl C l C l y Cl C l l x (3-1) 根据测设精度的要求,实际应用中可将高次项舍去,并顾及到C Rl =0,则上式变为32025640Rl l y l R l l x =-=(3-2)式中,x ,y 为缓和曲线上任一点的直角坐标,坐标原点为直缓点(ZH )或缓直(HZ ),通过该点的缓和曲线切线为x 轴。

坐标计算方法目前公路、铁路工程的施工放样已广泛采用全站仪放样,而全站仪放样的关键是放样逐点的坐标计算。
放样点的位置不外乎两种,即:中线点(中桩)和横断面范围上的任意点(边桩)。
1、直线段坐标的计算方法:直线段的坐标方位角a用弧度表示)是不变的,其坐标计算不用考虑方位角的变化。
1.1 直线段任意中桩点坐标计算公式如下:X=X0+L*COS aY=Y0+L*SIN a其中:XO、Y0分别代表直线段已知点的坐标;L代表计算点到已知点的距离;a代表直线段的方位角以弧度计。
1.2 边桩坐标计算公式如下:(本文以90度即n /2弧度示例)X=X0+ D*COS(a 士n /2+ n)Y二Y0+ D*SIN(a 士n /2+ n)其中:X0、Y0分别代表已知中桩点的坐标;D代表计算点到中桩的距离,a 代表中桩点的方位角以弧度计。
士的使用,当计算点在左侧选择-,当计算点在右侧选择+2、xx曲线段坐标的计算方法:圆曲线段采用切线支距法计算:2.1 中桩坐标计算2.1- 1 方位角计算:已知ZY点的方位角a,计算点的弦切角8=L/2R,L为计算点到ZY点的桩号长度,所以计算点的方位角为(a±8)。
±的使用,当路线为左转时选择-,路线为右转时选择+2.1- 2计算点到ZY点的距离计算:C=2R*SIN(L/2R),为计算点到ZY点的桩号长度;R为圆曲线的半径。
2.1- 3中桩坐标计算公式:X=XO+ C*COS(士®Y二Y0+ C*SIN(c士®a为ZY点的方位角;XO、Y0代表ZY点的坐标;8=L/2R,C=2R*SIN(L/2R),为圆曲线半径,L为桩号长度。
±的使用,当路线为左转时选择-,路线为右转时选择+。
2.2边桩坐标计算2.2- 1 方位角计算:a、已知中桩点方位角(a±S);b、因为圆曲线上的边桩点是沿半径方向布置的,半径垂直于计算点的切线而不是弦线,如果严格按照弦线90度即(2弧度方向布置计算,需要调整角度,即弦垂线与切线垂线的夹角i,其中i二L/2R=3,所以计算点的方位角即为:(a±2士n2 )。

铁路线形及其相关计算-精铁路线形及其相关计算1.线路线形的平⾯和竖⾯组成及其设计要素:直线、圆曲线和缓和曲线;坡段和竖曲线2. 线路平⾯和竖⾯的设计⽂件:3. 平⾯计算:任⼀⾥程处线路中线设计坐标的计算(缓和曲线和圆曲线上任意点的坐标⽅位⾓怎么算?)4. 竖⾯计算:任⼀⾥程处线路中线设计⾼程的计算(注意坡段上的点可能有平曲线,即可能有超⾼)5. 根据线路测点坐标计算测点⾥程2.4 设计线路中线上任意点平⾯坐标和⾼程计算⽅法线路测量,需在线路专业提供的设计线形的基础上,计算线路上⼀定间隔点(特征变化点)的平⾯坐标和⾼程,⽤于线路与线路测量的结果进⾏⽐较,以反映线路的品茶情况。
⾼速铁路中平曲线描述线路的平断⾯线形,由曲线和与之相切的直线组成,曲线分缓和曲线和圆曲线,在曲线上还需设置抵制离⼼⼒影响的超⾼值;竖曲线描述线路的纵断⾯线形,线路纵断⾯由竖曲线和与之相切的带坡度的直线组成,竖曲线采⽤圆曲线[13-14]。
2.4.1 线路任意点平⾯坐标计算⾼速铁路线路设计中,线路专业给出的线路平⾯设计⽂件主要有两类:⼀类是包括五⼤桩坐标以及圆曲线半径、缓和曲线长度与圆曲线处超⾼;另⼀类是包括交点坐标、圆曲线半径、缓和曲线长度、圆曲线处超⾼以及起点⾥程的设计⽂件,其中第⼆类设计⽂件更加简洁,如下表错误!⽂档中没有指定样式的⽂字。
-1所⽰,且第⼆类设计⽂件可通过计算曲线要素换算为第⼀类设计⽂件。
表错误!⽂档中没有指定样式的⽂字。
-1 某⾼速铁路平曲线部分第⼆类设计⽂件属性X(m) Y(m) 曲线半径(m)前缓长(m)后缓长(m)超⾼(mm)起始⾥程(m)QD 4414887.9736 469387.1201 2823.578 JD1 4415106.5310 470472.8130 3000 140 140 60JD2 4415240.7190 471594.4980 -2000 220 220 135JD3 4415091.0520 473528.4950 2500 350 350 150JD4 4410683.6980 478343.8110 -4500 600 600 160JD5 4411126.9070 483927.8110 -5500 700 700 165JD6 4407242.0780 488477.9600 8000 570 570 120由设计可知⾼速铁路平断⾯线形可分为直线段、缓和曲线段、圆曲线段等三种,平断⾯⽤图形可表⽰为如下图错误!⽂档中没有指定样式的⽂字。

一、曲线的一般组成厦深铁路12标正线线形设计为 直线+缓和曲线+圆曲线+缓和曲线+直线。
从小里程至大里程依次为ZH (直缓点)、HY (缓圆点)、YH (圆缓点)、HZ (缓直点)如下图所示:二、方位角的概念从标准方向的正北端起,顺时针方向到直线的水平角称为该直线的方位角。
方位角的取值范围为0°~360°,如下图A 即为直线L 的方位角。
TT三、某点坐标的计算已知A 点坐标为(491548,2505452),B 点距离A 点L=125m ,直线AB 的方位角为235°,计算B 点坐标。
计算方法:Y=491548+125×SIN235=491445.606X=2505452+125×COS235=2505380.303四、曲线上任一点的坐标及切线方位角计算1 直线段上任一点的坐标及方位角直线上的坐标计算比较简单,只需要求出该点所在直线的方位角以及线路中的里程即可求得例1,求DK495+520处左中线的坐标及方位角由设计院所给的曲线要素表可知该点位于JD57 JD58的直线上,查曲线要素表JD57,JD58的坐标分别为(488809.902,2504127.029),(485660.627,2504491.226)。
通过坐标反算直线JD57 JD58的方位角:TTA=atg((485660.627-488809.902)/( 2504491.226-25 04127.029))=276.59665°注意:A的取值可根据下述条件确定ΔY>0,ΔX>0,第一象限0-90°ΔY>0,ΔX<0,第二象限90°-180°ΔY<0,ΔX<0,第三象限180°-270°ΔY<0,ΔX>0,第四象限270°-360°查曲线表,JD58切线长T= 690.303m,JD58坐标(Y58,X58)=(485660.627,2504491.226),ZH点里程为DK496+093.885。

CASIO fx-4800P、fx-5800P型计算器用于线路施工曲线中线点坐标的计算程序中铁十局三建公司工程技术部摘要:本文介绍了CASIO fx-4800P 、fx-5800P型计算器程序编制用于铁路、公路曲线线路内任意中线点的坐标计算程序及使用方法。
本计算程序具有操作简便、计算快捷、应用广泛等特点、极大地减轻了测量工作者的内业工作量,对于测量工作者有较大的参考和指导作用。
关键词:曲线线路施工测量计算程序1.概述过去,线路中线施工放样基本依靠经纬仪和钢尺了来进行角度及距离测量。
对于曲线线路一般的测量方法是:经纬仪置于某一中线点上,采用偏角法拨角再用钢尺量距来定出中线点。
随着电子技术进步和经济发展,测量仪器和测量方法的不断改进,目前,全站仪已广泛地应用于工程施工测量中,极大的提高了测量工作效率。
但是,在进行铁路、公路工程的曲线线路施工测设时,需要在线路所在区域建立统一坐标系或独立坐标系,利用坐标变换的方法,将整个曲线的三个部分(第一缓和曲线、中间圆曲线、第二缓和曲线)统一到同一坐标系中。
根据坐标系的建立,计算出整个曲线内任意点的坐标,再采用全站仪利用极坐标方法进行施工放样。
前提是首先利用计算器计算出各中线点坐标,然后才能进行放样。
而普通型计算器不仅计算速度慢,且要求计算者必须正确地记忆很多计算公式,计算繁琐而且容易出错,满足不了现场测设工作的要求。
为了能够快速准确地为全站仪提供测设数据,发挥全站仪快速测设的特点,提高测量工作效率,应采用可编程的计算器,编制计算程序。
本文主要介绍应用CASIO fx-4800P型计算器的计算程序,供公司测量同行们参照使用。
2.计算程序QXZBJS(文件名:曲线坐标计算fx-4800P)Defm2:R:L:A:N“ZH:X=”:E“ZH:Y=”:F:“FWJ=”:K“ZH:LC=”: P=L2/(24R)-L4/(2688R3):M=L/2-L3/(240R2):T“T”=(R+P)tng(A/2)+M ◢G=RAπ/180:“S”S=G+L◢LbiA:{C,V}:C“CSDLC=”:V“HXPJ=”:D=C-K:D≤L=>I=D-D5/(40R2L2):U=D3/(6RL)-D7/(336R3L3):J=√(I2+U2):Goto1:≠>D≤G=>O=90(2D-L)/( Rπ):I=RsinO+M:U=R(1-cosO)+P:J=√(I2+U2):Goto2:≠>D=S-(C-K): = D-D5/(40R2L2):Z[2]=D3/6RL-D7/(336R3L3):I=T+(T-Z[1])cosA-Z[2]sinA:U=(T-Z[1])sinA+Z[2]cosA:J=√(I2+U2):Goto3:Lbi1:{Q}:Q“Z=1;Y=2”:Q=1=>Q=F-30D2/ (RLπ):H=F-90D2/ (RLπ):≠>Q=F+30D2/ (RLπ):H=F+90D2/( RLπ)⊿ Goto4:Lbi2:{Q}:Q“Z=1;Y=2”:Q=1=>Q=F-tng-1(U/I):H=F-O:≠>Q= F+tng-1(U/I):H=F+O⊿Goto4:Lbi3:{Q}:Q“Z=1;Y=2”:Q=1=>Q=F-tng-1(U/I):H=F-(A-90(S-(C-K))2/ (RLπ)): ≠>Q= F+tng-1(U/I):H=F+(A-90(S-(C-K))2/ (RLπ)):⊿ Goto4:Lbi4:B=90+H:H<0=>H“QXFWJ”=B+360◢≠>H≥360=>H“QXFWJ”=H-360 ◢≠>H“QXFWJ”=H◢⊿Goto5:Lbi5: X“CSD:X”=JcosQ+N+VcosB◢ Y“CSD:Y”=JsinQ+E+VsinB◢GotoA3.程序说明3.1 输入已知变量R—圆曲线半径,显示R?L—缓和曲线长,显示L?A—曲线转向角,显示A?E—直缓点纵坐标,显示ZH:X=?N—直缓点横坐标,显示ZH:Y=?F—第一切线方位角,即ZH至JD的方位角,显示FWJ=?K—直缓点里程,显示ZH:LC=?3.2 计算待求量T—切线长度,显示T= …S—曲线全长,显示S= …Z[3]—外矢距,即JD到QZ的距离,显示E0= …3.3 输入待求变量K—输入待求(测设)点的里程,显示LC=?V—横向偏距,即测设点左、右侧外移距的偏移量,若为中线点输入0;右侧输入“+”值,左侧输入“-”值。

线路中线及相关点位坐标计算的快捷方法及桥梁主要点的坐标计算1 前言在二十一世纪的今天,使用传统的铁路测量方法已越来越不适应发展趋势的需要,用坐标控制、全站仪测量已越来越适应今天的发展。
在渝怀线的施工控制测量中,在原有坐标公式的基础上把一些公式加以发展,使坐标计算更快、更方便,缩短了计算时间。
下面就铁路中线及与线路成任意夹角相关点位点的坐标计算及桥梁上的应用进行探讨,特别是对线路垂线及任意夹角的相关点的坐标计算进行着重探讨。
2 公式的分类铁路线路线型包括:直线、缓和曲线、圆曲线。
又因在坐标计算此两点距、方位角及已知一点坐标、方位角、距离计算另一点坐标两种情况。
所以把公式分为:(1)已知两点坐标求两点距及方位角。
(2)已知一点坐标、方位角、距离求另一点坐标。
(3)直线上中线及相关点坐标公式。
(4)缓和曲线上中线及相关点坐标公式。
(5)圆曲线上中线及相关点坐标计算。
3 坐标系的建立通常数学坐标系是以X 轴为横轴、Y 轴为纵轴(如图1)。
但为了满足坐标计算的需要,通常把Y 轴反向(如图2)。
再逆时针旋转90°即得以Y 轴为横轴、X 轴为纵轴的坐标和纱(如图3)。
以X 轴方向为线路走向方向,Y 轴为线路垂直方向,由(图3)可以看出线路左偏时Y 值逐渐减小,右偏时Y 值逐渐增大。
4 已知两点坐标计算两点距及方位于角(如图4) 4.1 公式在CASIO 计算器中的输入在CASIO 计算器中输入公式要进入编程状态需按MODE 再按EXP 即可,然后输入文件名再按EXE 进入编程行即可编程。
CASIO 计算器的功能控制键有SHIFT 、2DNF 、ALPHA 三种分别A ,按键ALPHA 再按(一)键即右输入。
4.1.1 第一步:输入LBI 0 4.1.2 第二步:输入变量(Y )4.1.3 第三步:输入Y ≥N=〉A=90-tan -1((X-M )/(Y-N )◢ L= √((X-M )2+(Y-N )2)◢ ≠)A=270-tan -1((X-M )/(Y-N )◢ L= √((X-M )2+(Y-N )2)◢4.2 说明:(1)M 、N 为置镜点坐标。

铁路工程曲线坐标计算步骤本文的曲线指含有缓和曲线和圆曲线的曲线,计算内容包括曲线上任一点的坐标计算以及相关承台、桩位的坐标计算。
1 曲线上任一点在独立坐标系中的坐标计算计算步骤: 1.1 确定曲线起始点通常曲线起始点选择(直线段→曲线段)直缓点(ZH 点)或(曲线段→直线段)缓直点(HZ 点) 1.2 计算直线段的方位角根据直线段上的另外点与曲线起始点的坐标计算出直线指向起始点的测量坐标方位角0α:00Y Y arctanXX α-=-起起1.3 计算缓和曲线的长度根据设计提供的曲线上的特征点(缓圆点HY 、圆缓点YH 等)的里程,计算缓和曲线的长度LsL s =HY (或YH )里程-起始点里程 1.4 确定任一点I 在曲线位置计算I 点是在缓和曲线上还是在圆曲线上 L i =I 点的里程-起始点里程当L i ≤L s 时,I 点在缓和曲线上,坐标计算用缓和曲线计算公式; 当L i ≥L s 时,I 点在圆曲线上,坐标计算用圆曲线计算公式。
1.5 建立曲线独立坐标系以直线段指向起始点为纵坐标轴,向曲线方向为正向;以垂直于纵坐标轴并通过起始点为横坐标轴,以纵坐标轴正向顺时针旋转90°为正。
1.6 独立坐标系坐标计算根据曲线参数Ls 、曲率半径R 等运用相应的坐标计算公式计算任一点I 在独立坐标系中的坐标(xi ,y i )1.6.1 缓和曲线的坐标计算公式:5223406ii i s ii sl x l R l l y Rl =-=1.6.2 圆曲线的坐标计算公式:(1) 计算出内移距p 和切垂距m 以及切线方位角βi )23224224022sss i s i l P Rl l m Rl l Rβ==--=(2)坐标计算sin (1cos )i i i i x R m y R pββ=+=-+上述坐标计算中要注意y i 的“+”、“-”号。
当曲线右拐顺时针时,y i 取“+”值,当曲线左拐(逆时针)时,y i 取“-”值。

铁路工程独立坐标系的选择与计算发表时间:2016-08-03T15:33:58.873Z 来源:《基层建设》2016年9期作者:张金凯[导读] 本文结合实例对独立坐标系建立方法进行了研究,供铁路施工技术人员参考。
中铁十局集团有限公司济南勘察设计院山东济南 250001摘要:在铁路工程设计和建设阶段,各工程所处地理位置和环境不同,有的地形平坦,海拔较低,而中国西部大部分地形起伏较大,山脉纵横,为满足规范对于投影长度变形值的要求,必须针对施工地区地形条件和所处高斯投影带综合考虑,选择合适的投影面和中央子午线变得非常关键。
本文结合实例对独立坐标系建立方法进行了研究,供铁路施工技术人员参考。
关键词:铁路工程测量;独立坐标系;投影面;中央子午线一、引言铁路线路一般较长,经常会跨越不同的投影带,采用国家统一3°带高斯正形投影坐标系统时,投影带边缘的长度变形值不能满足铁路施工要求。
《铁路工程测量规范》等一系列规范都要求铁路在对应的线路轨面设计高程面上坐标系的投影长度变形值不宜大于25mm/km。
当测区位于地形起付较大的山区时,采用标准高斯正形投影坐标系不能满足规范要求,可采用投影于抵偿高程面上的高斯投影坐标系。
二、长度元素高程归化改正与高斯投影长度改化高斯投影为正形投影,椭球面上的角度在投影后不变,但长度产生了变形,长度变形来源于以下两个过程:1、实测边长化算到椭球面上时所产生的变形在导线测量中,实测边长D归化至参考椭球面上时,长度会缩短ΔD。
设归化高程为H,地球平均曲率半径为Rm,其近似关系为:2、椭球面上的长度投影到高斯平面时产生的变形归化至参考椭球面上的边长S,再投影到高斯平面时,其长度会被放大ΔS。
设该边两端的平均横坐标为ym,则有:4、地球平均曲率半径在实际计算时,应按照测区所处位置计算测区的地球平均曲率半径,地球平均曲率半径与所处位置的子午圈半径M和卯酉圈半径N有关,其关系式如下:式(4)三、独立坐标系的建立方法由上述可得出,对于一定的测区,Rm为定值,因此长度变形主要取决于测区横坐标值ym和归化高程Hm。
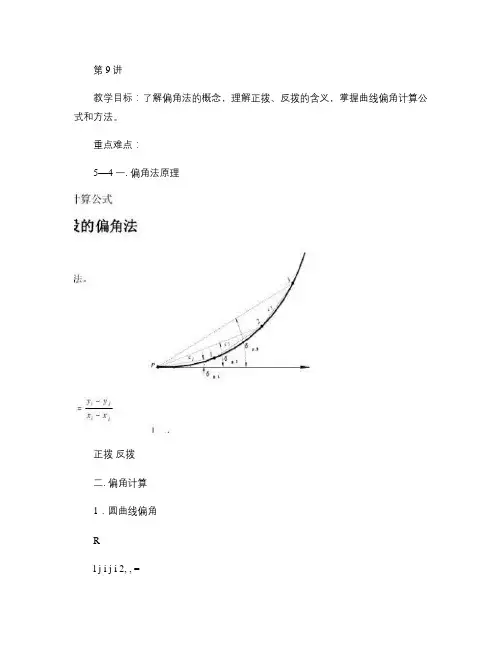
第9讲教学目标:了解偏角法的概念,理解正拨、反拨的含义,掌握曲线偏角计算公式和方法。
重点难点:5—4 一. 偏角法原理正拨反拨二. 偏角计算1.圆曲线偏角Rl j i j i 2, , =δ 2.缓和曲线偏角δi ,j=βi -αj ,ij i i tg l Rl =, 221αβ、、661 03j j j j i i i i Rl l Rl y l x ≈≈ (6122, j j i i j i j i ij l l l l Rl x x y y ++=--≈α2((610, j i j i j i l l l l Rl +-=δ若j 点位于i 点与缓和曲线终点之间,则同样方法可得,2((610, j i i j j i l l l l Rl +-=δ故其一般表达式为2(6||0, j i j i j i l l Rl l l +-=δ若1010610210j i l j l i Rl ===、、δ,即在缓和曲线上,曲线点号等于以10m 为单位曲线长,则式中,R 为圆曲线半径,l 0为缓和曲线长,δ10为缓和曲线基本角。
2(||10, j i j i j i +-=δδ102, 0δδj j =当i 点位于缓和曲线起点时,则上式可化简为三. 弦线长度计算向,2至i f Z5—5 曲线详细测设的直角坐标法一. 直角坐标法测设曲线原理X 轴上丈量x P ,得P' 点;自P' 点,沿与X 轴垂直且指向曲线内侧的方向丈量y P ,即得P 点。
直角坐标法中,坐标系X 轴均选主点的切线,故曲线点的y 坐标为相对于切线的支距。
因此,直角坐标法也称为切线支距法。
二. 曲线点坐标计算直角坐标法所选定的坐标系通常为缓和曲线坐标系,则在该坐标系下,缓和曲线段曲线点坐标的计算公式为缓和曲线方程,圆曲线段曲线点的坐标:⎭⎬⎫+-=+=p R y m R x t t t t cos 1(sin αα式中0βα+-=RK K HYt t ,K t 为t 点的里程,K HY 为HY 里程。

线路测量坐标正、反算计算原理及卡西欧fx-5800P程序说明一、计算原理在各测量书中对于坐标正算的相关计算式均有说明,故在此不做详解,仅对正算过程中需要用到的原理及公式做一汇总。
对于坐标反算,虽然都采用无限趋近原理进行计算,但计算方式各有差别,本文仅对其中一种自认为相对简单易懂并便于操作的原理进行详解。
1.1 坐标转换[1]如图1,设X P、Y P为P点在国家控制网坐标系中的坐标;x P、y P为P点在工程独立控制网坐标系中的坐标。
X O、Y O为工程独立坐标系原点o在国家坐标系中的坐标,Δα为两坐标系纵坐标轴的交角。
如果一条边在国家坐标系中的坐标方位角为A,而在工程独立坐标系中的坐标方位角为α,则:∆α=A−α(1-1)当由工程独立坐标系坐标换算至国家坐标系坐标时,换算公式为:X=x cos∆α−y sin∆α+X O(1-2)Y=x sin∆α+y cos∆α+Y O}当由国家坐标系坐标换算至工程独立坐标系坐标时,也可使用式(1-2),此时应将X、Y与x、y互换,且∆α=α−A。
1.2 坐标方位角关系计算1.2.1 正、反坐标方位角[2]一条直线的坐标方位角与直线的前进方向有关,沿直线前进方向的坐标方位角称为正坐标方位角,与其相反方向的坐标方位角称为反坐标方位角。
如图2,由于轴子午线之间是互相平行的,因此同一直线的正、反坐标方位角相差180°,即:α正=α反±180°(2-1)当α反<180°时,取“+”号;当α反>180°时,取“-”号。
1.2.2 坐标方位角的推算[3] 1.2.2.1 转折角为右角如图3(a),α12为已知边坐标方位角,α23为推算边的坐标方位角,β右为该两边所夹的右角,则:α23=α12±180°−β右=α21−β右 (2-2)1.2.2.2 转折角为左角如图3(b),α12为已知边坐标方位角,α23为推算边的坐标方位角,β左为该两边所夹的右角,则:α23=α12+β左±180°=α21+β左(2-3) 无论用右角还是左角推算,如遇出现负数的情形,应加上360°。
铁路线路任意里程坐标正反算程序(有需要程序的可联系陈工,QQ:285242895)1、程序开发背景在铁路线路测量中,在曲线要素已定的情况下,已知某点的里程及距中线的距离,计算该点的坐标,我们称之为线路坐标正算。
相反地,已知某点的坐标,确定该点在已定线路中的里程及距中线距离的过程,我们称之为线路坐标反算。
对于一条完整的曲线,它包括直线、第一缓和曲线、圆直线及第二缓和曲线。
而一条完整的铁路线路,通常都包含不止一条曲线,如果我们根据铁路线路多个曲线的曲线要素,构建一个线路模型,然后给出任意里程点,自动计算出对应的线路坐标,也可以给出任意坐标,计算出对应的线路里程和偏距,这将在测量和放样工作有着较为实际的应用。
比如用于逐桩坐标计算、隧道开挖及土石方开挖、线路征地界坐标计算、线路测量中线质量的检查、地质钻孔位置、桥梁桩基坐标计算等方面。
2、程序界面3、程序功能1、可以根据点的里程及距中线的距离,计算出该点的坐标,显示数据文件导入结果及计算结果,最后以csv格式文件保存计算的里程数据成果及曲线要素。
2、可以根据任意点的坐标,计算出点在已定线路中的里程及距中线距离,同时显示数据计算结果,最后以.zb格式文件保存计算的坐标成果。
4、程序特色3.1 本程序采用易于交互操作的对话框模板和MSFlexGrid控件,在MFC开发环境下利用VC语言进行编写,整个程序的计算过程及结果均可在图表中直接呈现,便于数据的检查,整个程序的界面简洁直观,功能清晰、易学易用。
3.2 结合铁路测量的实际情况,在导入曲线要素时,不需要输入曲线的五大桩要素以及曲线偏向,只需要曲线数据文件中包含曲线半径、缓长及曲线两侧各两个直线点坐标,就可以计算出其他曲线要素,进而构建完整的线路模型。
3.3 在线路正算时,里程数据既可以从文件中导入,也可以在程序界面上获取。
当采用从文件导入时,里程数据可以是乱序排列的。
当从界面获取时,程序可以自动计算出连续里程数据,3.4 在线路反算中,当我们给定任意点的坐标时,程序不仅可以计算出对应线路中的里程、距离及垂点坐标,还可以计算出此点是否在线路对应范围内以及位于曲线上的具体位置。
利用excel进行既有铁路曲线坐标整正计算方法研究【摘要】用传统方法进行铁路曲线拨道计算,编程工作量大,程序调试复杂且容易出错。
本文结合excel的数据处理功能,利用excel采用坐标法计算既有铁路曲线的拨距计算,方便快捷,取得了较好的计算结果。
【关键词】excel;铁路曲线;拨距随着经济社会节奏的不断加快,铁路的速度也被一次次的提高,行车密度加大,维修维护时间减少,日常养护管理的安全和效率变得更加重要。
对于既有铁路曲线拨距计算来说,经过多年的研究形成了一系列的方法,坐标法是其中的一种方法,它可以在保证拨正前后曲线长度保持不变的前提下,同时方便测量和完成计算过程。
本文利用excel计算既有曲线的坐标法测量1 测量数据录入把测量的里程和坐标数据分别输入第一列和第二列,如果某里程处为控制点(桥涵、道口等),在拨量约束列还需加上相应约束条件。
2 既有曲线参数的计算2.1 半径r和转角α的计算我们可以利用3点法确定圆曲线的圆心坐标和半径,公式如下:我们在选取计算的三点时,尽量选择位于曲线中间的三个点来计算,因为中间属于圆曲线的范围,算出来的半径值更接近于理论半径。
当然,此时算出的r为估算的半径,还需要对其进行优化调整,优化方法见文献1。
转角α可以先求出两切线的斜率,利用斜率的差值求反正切来计算夹角,即可得到该曲线的转角。
2.2 缓和曲线l0计算我们可以用公式来计算,p为内移距,可以用圆心坐标xabc 减去起点的x坐标和半径r来计算(假定第一条切线边和y轴平行)。
缓和曲线长度取整为10m的倍数。
2.3 交点坐标计算我们假定第一条切线边和y轴平行,可以用第二条切线的直线方程带入起始切线边的x1值,即可得到对应的交点坐标yj,xj=x1。
3 坐标计算根据优化后的缓和曲线长度和半径,以测量起点坐标为基准,以其对应的坐标系为基础,利用直线曲线计算公式计算直线、缓和曲线,圆曲线对应点的坐标,计算方法见文献2。
4 拨距量计算表1曲线整正计算表既有线测量资料设计曲线资料拨距计算置镜点测点里程 x坐标y坐标设计曲线主要点里程x坐标(设) y坐标(设)δ=es-ey不 k328+630 1000.000 1000.000 1000.000 1000.0000.000+650 1000.002 1020.000 zh=k328+656.767 1000.001 1019.998 -0.002+670 1000.029 1040.000 1000.012 1039.984 -0.023+690 1000.121 1060.000 1000.094 1059.980 -0.034+710 1000.396 1079.998 zy=k328+701.767 1000.375 1079.969 -0.036+730 1000.979 1099.989 1000.967 1099.950 -0.041+750 1001.969 1119.965 hy=k328+746.767 1001.939 1119.950 -0.033+770 1003.479 1139.908 1003.453 1139.875 -0.042+790 1005.491 1159.806 1005.461 1159.783 -0.037+810 1008.017 1179.646 1007.987 1179.629 -0.035+830 1011.069 1199.412 1011.044 1199.372 -0.047不 +850 1014.607 1219.097 1014.573 1219.092 -0.034 +870 1018.674 1238.679 1018.639 1238.649 -0.046+890 1023.231 1258.153 qz=k328+890.605 1023.187 1258.148 -0.044+910 1028.302 1277.499 1028.250 1277.480 -0.055+930 1033.857 1296.712 1033.835 1296.664 -0.053+950 1039.902 1315.777 1039.891 1315.732 -0.046+970 1046.438 1334.678 1046.417 1334.644 -0.041+990 1053.452 1353.408 1053.440 1353.385 -0.026k329+010 1060.957 1371.947 1060.949 1371.925 -0.024 +030 1068.929 1390.289 yh=k329+34.443 1068.9221390.282 -0.010不 +050 1077.377 1408.418 1077.367 1408.410 -0.012 +070 1086.218 1426.357 yz=k329+079.443 1086.1951426.350 -0.025+090 1095.527 1444.058 1095.312 1443.931 -0.251+110 1104.606 1461.879 1104.601 1461.867 -0.014+130 1113.956 1479.559 hz=k329+124.443 1113.9561479.559 0.000不 +150 1123.316 1497.234 1123.316 1497.234 0.000 α=0.487325 r=775 ls1=ls2=90 p=0.4355 结论excel 在原始数据输入、输出、程序处理在同一集成环境中,应用起来是很方便的。