第32课时___三角函数的图像和性质(3)
- 格式:doc
- 大小:677.50 KB
- 文档页数:8





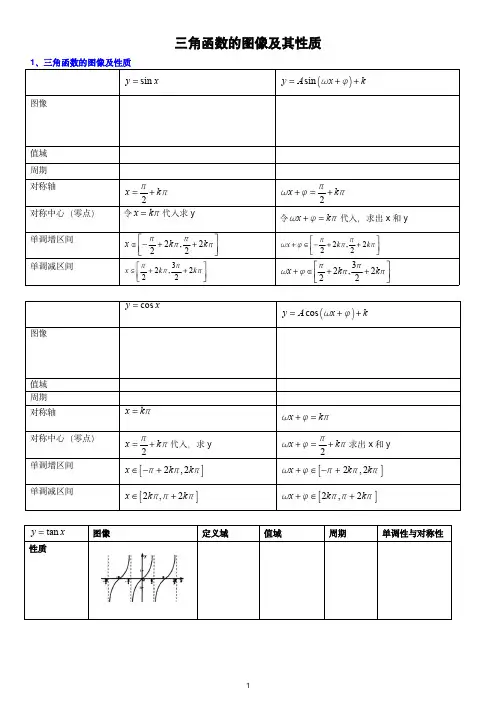
三角函数的图像及其性质1、三角函数的图像及性质sin y xsin y A x k图像值域周期对称轴2x k2x k对称中心(零点)令x k 代入求y令x k 代入,求出x 和y 单调增区间2,222x k k2,222x k k单调减区间32,222x k k32,222x k kcos y xcos y A x k图像值域周期对称轴x kx k 对称中心(零点)2x k代入,求y 2x k求出x 和y 单调增区间 2,2x k k 2,2x k k 单调减区间2,2x k k2,2x k k tan y x图像定义域值域周期单调性与对称性性质【考点分类】考点一:图像变换:1.把函数y =sin x 的图象向右平移个单位得到y =g (x )的图象,再把y =g (x )图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),所得到图象的解析式为()A.B.C.D.2.将函数f (x )=sin x 图象上所有点的横坐标变为原来的(ω>0),纵坐标不变,得到函数g (x )的图象,若g (x )的最小正周期为6π,则ω=()A.B.6C.D.33.将函数y =2sin2x 图象上的所有点向右平移个单位,然后把图象上所有点的横坐标缩短为原来的倍,(纵坐标不变)得到y =f (x )的图象,则f (x )等于()A.2sin(x ﹣)B.2sin(x ﹣)C.2sin(4x ﹣)D.2sin(4x ﹣)4.已知曲线C 1:y =cos x ,C 2:y =sin(2x +),则下面结论正确的是()A.把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再向右平移个单位长度,得到曲线C 2B.把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再向左平移个单位长度,得到曲线C 2C.把C 1上各点的横坐标缩短到原来的,纵坐标不变,再向右平移个单位长度,得到曲线C 2D.把C 1上各点的横坐标缩短到原来的,纵坐标不变,再向左平移个单位长度,得到曲线C 25.把函数y =cos(3x +4)的图象适当变动就可以得到y =sin(-3x )的图象,这种变动可以是()A 向右平移4 B 向左平移4 C 向右平移12 D 向左平移126..函数32sin( x y 的图象是由2sin xy 的图象沿x 轴()得到的。





《三角函数三角函数的图象与性质课件pptx》2023-10-26•引言•三角函数的概念与性质•三角函数的图象表示目录•三角函数的应用•习题解答•总结与展望01引言三角函数是数学中的基础科目,对于高中生来说,掌握好三角函数的知识可以为后续的高等数学学习打下基础。
在本课程中,我们将从定义、图象、性质和应用等方面全面介绍三角函数的知识。
课程背景介绍课程目标熟悉三角函数的图象和变化趋势。
让学生掌握三角函数的定义、公式和基本性质。
培养学生的数学思维和逻辑推理能力。
能够灵活运用三角函数解决实际问题。
课程大纲•第一部分:三角函数的定义与公式•正弦函数、余弦函数和正切函数的定义与基本公式。
•角度与弧度的转换。
•第二部分:三角函数的图象与性质•正弦函数、余弦函数和正切函数的图象与性质。
•三角函数的周期性、最值和对称性。
•第三部分:三角函数的应用•利用三角函数解决实际问题,如物理、工程、计算机等领域的问题。
•三角函数在复数、极坐标系中的应用。
02三角函数的概念与性质1 2 3$y = \sin x$,表示单位圆上点的纵坐标。
正弦函数$y = \cos x$,表示单位圆上点的横坐标。
余弦函数$y = \tan x$,表示单位圆上点的纵坐标与横坐标的比值。
正切函数奇偶性正弦函数和正切函数为奇函数,余弦函数为偶函数。
值域正弦函数和余弦函数的值域为$\lbrack -1,1\rbrack$,正切函数的值域为全体实数。
周期性正弦函数、余弦函数和正切函数都具有周期性,最小正周期为$2\pi$。
定义域正弦函数和余弦函数的定义域为全体实数,正切函数的定义域为不等于$\frac{k\pi}{2} + \pi$的全体实数。
正弦函数的周期性$y = \sin x$的周期为$2\pi$,即$\sin(x + 2k\pi) = \sin x(k \in \mathbf{Z})$。
三角函数的周期性余弦函数的周期性$y = \cos x$的周期为$2\pi$,即$\cos(x + 2k\pi) = \cos x(k \in \mathbf{Z})$。
239课题:三角函数的图象和性质(三)教学目标:掌握三角函数的奇偶性与单调性,并能应用它们解决一些问题. 教学重点:三角函数奇偶性的判断及三角函数单调区间的求解及其应用. (一) 主要知识:1.sin()yA x ωϕ=+为奇函数k ϕπ⇔=;函数sin()y A x ωϕ=+为偶函数2k πϕπ⇔=+cos()y A x ωϕ=+为偶函数k ϕπ⇔=;函数cos()y A x ωϕ=+为奇函数2k πϕπ⇔=+2.函数sin()y A x ωϕ=+(0,0)A ω>>的单调增区间可由2222k x k πππωϕπ-+≤+≤+解出,单调减区间可由32222k x k πππωϕπ+≤+≤+解出;函数sin()y A x ωϕ=+(0,0)A ω<>的单调增区间可由32222k x k πππωϕπ+≤+≤+解出,单调减区间可由arcsin θ≤2222k x k πππωϕπ-+≤+≤+解出(三)典例分析:问题1. 判断下列函数的奇偶性:()1()sin 2tan f x x x x =-⋅;()2(()lg sin f x x =+;()3cos (1sin )()1sin x x f x x-=-;()4()()cos sin f x x =;()5tan 1()lgtan 1x f x x +=-240问题2.比较下列各组中两个值的大小:()13cos2,1sin10,7cos4-;()2 3sin(sin)8π,3sin(cos)8π.问题3.()1求下列函数的单调递增区间:①3()sin 24f x x π⎛⎫=-+⎪⎝⎭; ②2()sin sin f x x x =+;③()12()log sin 2cos 2f x x x =+;④()sin 4f x x π⎛⎫=--⎪⎝⎭241()2(07全国Ⅰ)函数22()cos 2cos2x f x x =-的一个单调增区间是.A 233ππ⎛⎫ ⎪⎝⎭, .B 62ππ⎛⎫ ⎪⎝⎭, .C 03π⎛⎫⎪⎝⎭, .D 66ππ⎛⎫- ⎪⎝⎭,()3(06福建)已知函数()2sin f x x ω=(0)ω>在区间,34ππ⎡⎤-⎢⎥⎣⎦上的最小值是2-,则ω的最小值等于 .A 23 .B 32.C 2 .D 3(四)课后作业:1.若()tan 4f x x π⎛⎫=+ ⎪⎝⎭,则 .A (1)(0)(1)f f f ->> .B (0)(1)(f ff >>- .C (1)(0)(1)f f f >>- .D (0)(1)(1)f f f >->2.(07届高三昆明一中模拟)设函数)()cosf x ϕ=+()0πϕ-<<,若()()f x f x +'是偶函数,则ϕ等于 .A 3π.B 3π-.C 6π.D 6π-3.(07届高三江苏徐州模拟)设函数()()cos 1sin f x x k x =++sin 4x π⎛⎫+ ⎪⎝⎭是奇函数,则3f π⎛⎫= ⎪⎝⎭2424.若04παβ<<<,sin cos a αα+=,sin cos b ββ+=,则.A a b < .B a b > .C 1ab < .D 1ab >5.函数3sin(2)3y x π=-的单调递减区间是6.①函数tan y x =在它的定义域内是增函数;②若α、β是第一象限角,且αβ>,则tan tan αβ>;③函数sin()y A x ωϕ=+一定是奇函数;④函数|cos(2)|3y x π=+的最小正周期为2π.上列四个命题中,正确的命题是 .A ①.B ④.C ①、②.D ②、③7.设定义域为R 的奇函数()y f x =是减函数,若当02πθ≤≤时,2(cos 2sin )(22)0f m f m θθ++-->,求m 的值.8.试讨论函数:()lg(tan fx x =+的奇偶性。
9.(08届湖南师大附中高三月考)已知函数2()2sin ()21,4f x x x x R π=+--∈。
()1若函数()()h x f x t =+的图象关于点(,0)6π-对称,且(0,)t π∈,求t 的值;()2设p :[,]42x ππ∈,q :()3f x m -<,若p 是q 的充分条件,求实数m 的取值范围。
243(五)走向高考:10.(06江苏)已知R a ∈,函数R x a x x f ∈-=|,|sin )(为奇函数,则a =.A 0 .B 1 .C 1- .D 1±11.(06湖南文)若()sin 3sin 44f x a x x ππ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭是偶函数,则a =12.(06全国Ⅰ)函数()tan 4fx x π⎛⎫=+⎪⎝⎭的单调增区间为.A ,,22k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭.B ()(),1,k k k Z ππ+∈ .C 3,,44k k k Zππππ⎛⎫-+∈ ⎪⎝⎭ .D 3,,44k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭13.(05北京)函数()cos f x x=.A 在0,,,22πππ⎡⎫⎛⎤⎪ ⎢⎥⎣⎭⎝⎦上递增,在33,,,222ππππ⎡⎫⎛⎤⎪ ⎢⎥⎣⎭⎝⎦上递减 .B 在30,,,22πππ⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭上递增,在3,,,222ππππ⎛⎤⎛⎤⎥⎥⎝⎦⎝⎦上递减 .C 在3,,,222ππππ⎛⎤⎛⎤⎥⎥⎝⎦⎝⎦上递增,在30,,,22πππ⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭上递减.D 在33,,,222ππππ⎡⎫⎛⎤⎪ ⎢⎥⎣⎭⎝⎦上递增,在0,,,22πππ⎡⎫⎛⎤⎪ ⎢⎥⎣⎭⎝⎦上递减 14.(06天津文)设α、(,)22ππβ∈-,那么""αβ<是"tan tan "αβ<的.A 充分不必要条件.B 必要不充分条件.C 充要条件.D 既不充分又不必要条件15.(06安徽)设0a >,对于函数()sin (0)sin x af x x xπ+=<<,下列结论正确的是.A 有最大值无最小值.B 有最小值无最大值.C 有最大值且有最小值.D 既无最大值又无最小值16.(07广东)若函数21()sin 2f x x =-()x R ∈,则()f x 是.A 最小正周期为π2的奇函数 .B 最小正周期为π的奇函数.C 最小正周期为2π的偶函数 .D 最小正周期为π的偶函数17.(07天津文)设函数()sin 3f x x π⎛⎫=+ ⎪⎝⎭()x R ∈,则()f x.A 在区间2736ππ⎡⎤⎢⎥⎣⎦,上是增函数.B 在区间2π⎡⎤-π-⎢⎥⎣⎦,上是减函数244.C 在区间84ππ⎡⎤⎢⎥⎣⎦,上是增函数.D 在区间536ππ⎡⎤⎢⎥⎣⎦,上是减函数18.(06天津)已知函数()sin cos (f x a x b x a =-、b 为常数,0,)a x R ≠∈在4x π=处取得最小值,则函数3()4y f x π=-是.A 偶函数且它的图象关于点(,0)π对称;.B 偶函数且它的图象关于点3(,0)2π对称;.C 奇函数且它的图象关于点3(,0)2π对称;.D 奇函数且它的图象关于点(,0)π对;19.(07湖南文)已知函数2πππ()12sin 2sin cos 888f x x x x ⎛⎫⎛⎫⎛⎫=-++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭求:(Ⅰ)函数()f x 的最小正周期;(Ⅱ)函数()f x 的单调增区间.20.(07湖南)已知函数2π()cos 12f x x ⎛⎫=+ ⎪⎝⎭,1()1sin 22g x x =+. (Ⅰ)设0x x =是函数()y f x =图象的一条对称轴,求0()g x 的值. (Ⅱ)求函数()()()h x f x g x =+的单调递增区间.24521.(07辽宁)已知函数2ππ()sin sin 2cos 662x f x x x ωωω⎛⎫⎛⎫=++-- ⎪ ⎪⎝⎭⎝⎭,(其中x R ∈,0ω>)(Ⅰ)求函数()f x 的值域;(Ⅱ)若对任意的a R ∈,函数()y f x =,(π]x a a ∈+,的图象与直线1y =-有且仅有两个不同的交点,试确定ω的值(不必证明),并求函数()y f x x R =∈,的单调增区间.24622.(07江西)如图,函数2cos()y x ωθ=+π(00)2x R >ωθ∈,,≤≤的图象与y 轴相交于点(0,且该函数的最小正周期为π.()1求θ和ω的值;()2已知点π02A ⎛⎫⎪⎝⎭,,点P 是该函数图象上一点,点0(Q x ,0ππ2x ⎡⎤∈⎢⎥⎣⎦,时,求0x 的值.。