【免费下载】hash算法实验

8位长度的hash算法摘要：1.引言2.8位长度hash算法原理3.常见8位hash算法介绍4.算法应用场景及优缺点5.总结正文：【引言】在计算机领域，hash算法是一种将任意大小的数据映射到固定大小的数据的算法。

在众多hash算法中，8位长度的hash算法因其小巧的体积和较高的安全性而受到广泛关注。

本文将详细介绍8位长度hash算法，包括其原理、常见算法、应用场景及优缺点。

【8位长度hash算法原理】8位长度hash算法，顾名思义，是将输入数据映射到8位二进制数。

其核心原理是将输入数据进行一系列的位操作和组合运算，最终得到一个8位的二进制数。

这一过程通常包括以下几个步骤：1.初始化一个8位的临时变量2.将输入数据进行位操作（如左移、右移等）3.将操作后的结果与临时变量进行异或操作4.将结果再次进行位操作，重复步骤3和4直至达到预设的迭代次数5.最终得到的结果即为8位长度的hash值【常见8位hash算法介绍】1.基数排序（Radix Sort）基数排序是一种非比较排序算法，其基本思想是将关键字按照最低位优先排序。

在8位hash算法中，基数排序可以通过对输入数据的每一位进行排序来得到hash值。

2.奇偶校验法（Even-odd Parity）奇偶校验法是一种简单且快速的8位hash算法。

其原理是将输入数据的8位二进制表示进行分组，每两位为一组。

对每组进行异或操作，得到一个新的8位二进制数。

最后，将新得到的8位二进制数的每一位进行奇偶校验，得到最终的hash值。

3.城市碰撞法（City Hashing）城市碰撞法是一种基于几何平均数的hash算法。

其基本思想是将输入数据分成若干组，每组数据通过一定的公式计算得到一个碰撞值。

然后，对所有碰撞值进行平均，并将平均值映射到8位二进制数。

【算法应用场景及优缺点】8位hash算法应用场景广泛，如在密码学、数据压缩、文件存储等领域均有应用。

其主要优点包括：1.体积小，计算速度快，适用于实时场景2.安全性较高，抗碰撞能力强3.易于实现和扩展然而，8位hash算法也存在一定的局限性，如：1.哈希值较长时，性能优势减弱2.抗碰撞能力较弱，不适合需要高精度场景【总结】8位长度的hash算法作为一种小巧且实用的算法，在许多领域都发挥着重要作用。

Hash算法大全(java实现）[java] view plaincopy/*** Hash算法大全<br>* 推荐使用FNV1算法* @algorithm None* @author Goodzzp 2006-11-20* @lastEdit Goodzzp 2006-11-20* @editDetail Create*/public class HashAlgorithms{/*** 加法hash* @param key 字符串* @param prime 一个质数* @return hash结果*/public static int additiveHash(String key, int prime){int hash, i;for (hash = key.length(), i = 0; i < key.length(); i++)hash += key.charAt(i);return (hash % prime);}/*** 旋转hash* @param key 输入字符串* @param prime 质数* @return hash值*/public static int rotatingHash(String key, int prime){int hash, i;for (hash=key.length(), i=0; i<key.length(); ++i)hash = (hash<<4)^(hash>>28)^key.charAt(i);return (hash % prime);// return (hash ^ (hash>>10) ^ (hash>>20));}// 替代：// 使用：hash = (hash ^ (hash>>10) ^ (hash>>20)) & mask; // 替代：hash %= prime;/*** MASK值，随便找一个值，最好是质数*/static int M_MASK = 0x8765fed1;/*** 一次一个hash* @param key 输入字符串* @return 输出hash值*/public static int oneByOneHash(String key){int hash, i;for (hash=0, i=0; i<key.length(); ++i){hash += key.charAt(i);hash += (hash << 10);hash ^= (hash >> 6);}hash += (hash << 3);hash ^= (hash >> 11);hash += (hash << 15);// return (hash & M_MASK);return hash;}/*** Bernstein's hash* @param key 输入字节数组* @param level 初始hash常量* @return 结果hash*/public static int bernstein(String key){int hash = 0;int i;for (i=0; i<key.length(); ++i) hash = 33*hash + key.charAt(i);return hash;}////// Pearson's Hash// char pearson(char[]key, ub4 len, char tab[256])// {// char hash;// ub4 i;// for (hash=len, i=0; i<len; ++i)// hash=tab[hash^key[i]];// return (hash);// }//// CRC Hashing，计算crc,具体代码见其他// ub4 crc(char *key, ub4 len, ub4 mask, ub4 tab[256]) // {// ub4 hash, i;// for (hash=len, i=0; i<len; ++i)// hash = (hash >> 8) ^ tab[(hash & 0xff) ^ key[i]]; // return (hash & mask);// }/*** Universal Hashing*/public static int universal(char[]key, int mask, int[] tab) {int hash = key.length, i, len = key.length;for (i=0; i<(len<<3); i+=8){char k = key[i>>3];if ((k&0x01) == 0) hash ^= tab[i+0];if ((k&0x02) == 0) hash ^= tab[i+1];if ((k&0x04) == 0) hash ^= tab[i+2];if ((k&0x08) == 0) hash ^= tab[i+3];if ((k&0x10) == 0) hash ^= tab[i+4];if ((k&0x20) == 0) hash ^= tab[i+5];if ((k&0x40) == 0) hash ^= tab[i+6];if ((k&0x80) == 0) hash ^= tab[i+7];}return (hash & mask);}/*** Zobrist Hashing*/public static int zobrist( char[] key,int mask, int[][] tab) {int hash, i;for (hash=key.length, i=0; i<key.length; ++i)hash ^= tab[i][key[i]];return (hash & mask);}// LOOKUP3// 见Bob Jenkins(3).c文件// 32位FNV算法static int M_SHIFT = 0;/*** 32位的FNV算法* @param data 数组* @return int值*/public static int FNVHash(byte[] data){int hash = (int)2166136261L;for(byte b : data)hash = (hash * 16777619) ^ b;if (M_SHIFT == 0)return hash;return (hash ^ (hash >> M_SHIFT)) & M_MASK;}/*** 改进的32位FNV算法1* @param data 数组* @return int值*/public static int FNVHash1(byte[] data){final int p = 16777619;int hash = (int)2166136261L;for(byte b:data)hash = (hash ^ b) * p;hash += hash << 13;hash ^= hash >> 7;hash += hash << 3;hash ^= hash >> 17;hash += hash << 5;return hash;}/*** 改进的32位FNV算法1* @param data 字符串* @return int值*/public static int FNVHash1(String data) {final int p = 16777619;int hash = (int)2166136261L;for(int i=0;i<data.length();i++)hash = (hash ^ data.charAt(i)) * p;hash += hash << 13;hash ^= hash >> 7;hash += hash << 3;hash ^= hash >> 17;hash += hash << 5;return hash;}/*** Thomas Wang的算法，整数hash*/public static int intHash(int key){key += ~(key << 15);key ^= (key >>> 10);key += (key << 3);key ^= (key >>> 6);key += ~(key << 11);key ^= (key >>> 16);return key;}/*** RS算法hash* @param str 字符串*/public static int RSHash(String str){int b = 378551;int a = 63689;int hash = 0;for(int i = 0; i < str.length(); i++){hash = hash * a + str.charAt(i);a = a * b;}return (hash & 0x7FFFFFFF);}/* End Of RS Hash Function *//*** JS算法*/public static int JSHash(String str){int hash = 1315423911;for(int i = 0; i < str.length(); i++){hash ^= ((hash << 5) + str.charAt(i) + (hash >> 2));}return (hash & 0x7FFFFFFF);}/* End Of JS Hash Function *//*** PJW算法*/public static int PJWHash(String str){int BitsInUnsignedInt = 32;int ThreeQuarters = (BitsInUnsignedInt * 3) / 4;int OneEighth = BitsInUnsignedInt / 8;int HighBits = 0xFFFFFFFF << (BitsInUnsignedInt - OneEighth);int hash = 0;int test = 0;for(int i = 0; i < str.length();i++){hash = (hash << OneEighth) + str.charAt(i);if((test = hash & HighBits) != 0){hash = (( hash ^ (test >> ThreeQuarters)) & (~HighBits));}}return (hash & 0x7FFFFFFF);}/* End Of P. J. Weinberger Hash Function *//*** ELF算法*/public static int ELFHash(String str){int hash = 0;int x = 0;for(int i = 0; i < str.length(); i++){hash = (hash << 4) + str.charAt(i);if((x = (int)(hash & 0xF0000000L)) != 0){hash ^= (x >> 24);hash &= ~x;}}return (hash & 0x7FFFFFFF);}/* End Of ELF Hash Function *//*** BKDR算法*/public static int BKDRHash(String str){int seed = 131; // 31 131 1313 13131 131313 etc..int hash = 0;for(int i = 0; i < str.length(); i++){hash = (hash * seed) + str.charAt(i);}return (hash & 0x7FFFFFFF);}/* End Of BKDR Hash Function *//*** SDBM算法*/public static int SDBMHash(String str){int hash = 0;for(int i = 0; i < str.length(); i++){hash = str.charAt(i) + (hash << 6) + (hash << 16) - hash;}return (hash & 0x7FFFFFFF);}/* End Of SDBM Hash Function *//*** DJB算法*/public static int DJBHash(String str){int hash = 5381;for(int i = 0; i < str.length(); i++){hash = ((hash << 5) + hash) + str.charAt(i);}return (hash & 0x7FFFFFFF);}/* End Of DJB Hash Function *//*** DEK算法*/public static int DEKHash(String str){int hash = str.length();for(int i = 0; i < str.length(); i++){hash = ((hash << 5) ^ (hash >> 27)) ^ str.charAt(i);}return (hash & 0x7FFFFFFF);}/* End Of DEK Hash Function *//*** AP算法*/public static int APHash(String str){int hash = 0;for(int i = 0; i < str.length(); i++){hash ^= ((i & 1) == 0) ? ( (hash << 7) ^ str.charAt(i) ^ (hash >> 3)) :(~((hash << 11) ^ str.charAt(i) ^ (hash >> 5)));}// return (hash & 0x7FFFFFFF);return hash;}/* End Of AP Hash Function *//*** JA V A自己带的算法*/public static int java(String str){int h = 0;int off = 0;int len = str.length();for (int i = 0; i < len; i++){h = 31 * h + str.charAt(off++);}return h;}/*** 混合hash算法，输出64位的值*/public static long mixHash(String str){long hash = str.hashCode();hash <<= 32;hash |= FNVHash1(str);return hash;}}Hash算法有很多很多种类。

哈希算法的原理及应用实验1. 哈希算法的概述哈希算法（Hash Algorithm）是一种将任意长度的数据映射为固定长度散列值（Hash Value）的算法。

哈希算法的核心思想是通过对输入数据执行一系列运算，生成一个唯一的输出结果。

不同的输入数据会生成不同的输出结果，即使输入数据的长度相差甚远，输出结果的长度始终是固定的。

哈希算法在密码学、数据完整性校验、数据索引和查找等领域具有广泛的应用。

常见的哈希算法有MD5、SHA-1、SHA-256等。

2. 哈希算法的原理哈希算法的原理可以简单描述为以下几个步骤：1.将输入数据分块：哈希算法将输入数据按固定大小（通常为512位或1024位）进行分块处理。

2.初始哈希值：为每个分块数据设置一个初始哈希值。

3.迭代运算：对每个分块数据进行迭代运算，生成最终的哈希值。

4.输出结果：将最终的哈希值作为输出结果。

3. 哈希算法的应用3.1 数据完整性校验哈希算法常用于校验数据的完整性。

通过计算数据的哈希值，可以将数据内容抽象为一个唯一的字符串。

如果数据在传输或存储过程中发生了更改，其哈希值也会发生变化，从而可以检测到数据是否被篡改。

3.2 密码存储与验证在密码存储和验证过程中，哈希算法被广泛应用。

用户输入的密码会经过哈希算法生成一个哈希值存储在数据库中。

当用户再次登录时，系统将用户输入密码的哈希值与数据库中存储的密码哈希值进行对比，以判断密码是否正确。

3.3 数据索引和查找哈希算法也可以在数据索引和查找中发挥重要作用。

哈希算法将关键词或数据转换为哈希值，并将哈希值与数据存储位置进行映射。

这样可以快速进行数据的索引和查找，提高查找效率。

4. 哈希算法的实验为了更好地理解哈希算法的原理，我们可以进行一个简单的实验，使用Python 来实现。

4.1 实验准备首先，安装Python编程语言并确保在本地环境中可正常运行。

4.2 实验步骤1.创建一个新的Python文件，命名为hash_experiment.py。

哈尔滨工程大学实验报告实验名称：Hash 算法MD5班级：学号：姓名：实验时间：2014年6月成绩：指导教师：实验室名称：哈尔滨工程大学实验室与资产管理处制一、实验名称Hash算法ＭＤ５二、实验目的通过实际编程了解MD5 算法的加密和解密过程，加深对Hash 算法的认识。

三、实验环境（实验所使用的器件、仪器设备名称及规格）运行Windows 或Linux 操作系统的PC 机，具有gcc(Linux)、VC（Windows）等C 语言编译环境。

四、任务及其要求（1）利用自己所编的MD5 程序对一个文件进行处理，计算它的Hash 值，提交程序代程和运算结果。

（2）微软的系统软件都有MD5 验证，尝试查找软件的MD5 值。

同时，在Windows 操作系统中，通过开始→运行→sigverif 命令，利用数字签名查找验证非Windows 的系统软件。

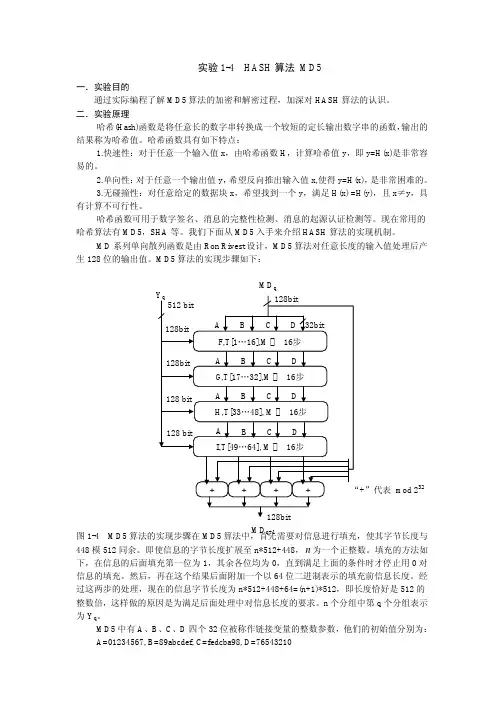
__五、实验设计（包括原理图、真值表、分析及简化过程、卡诺图、源代码等）在MD5 算法中，首先需要对信息进行填充，使其字节长度与448 模512 同余，即信息的字节长度扩展至n*512+448，n 为一个正整数。

填充的方法如下：在信息的后面填充第一位为1，其余各位均为0，直到满足上面的条件时才停止用0 对信息填充。

然后，再在这个结果后面附加一个以64 位二进制表示的填充前信息长度。

经过这两步的处理，现在的信息字节长度为n*512+448= (n+1)*512，即长度恰好是512 的整数倍，这样做的目的是为满足后面处理中后面处理中对信息长度的要求。

n 个分组中第q 个分组表示为Yq。

MD5 中有A、B、C、D，4 个32 位被称作链接变量的整数参数，它们的初始值分别为：A=01234567B=89abcdef,C=fedcba98，D=当设置好这个4 个链接变量后，就开始进入算法的4 轮循环运算。

循环的次数是信息中512 位信息分组数目。

首先将上面4 个链接变量复制到另外4 个变量中A到AA，B 到BB，C 到CC，D 到DD，以备后面进行处理。

实验六：Hash算法实验安全0901 王宇航 09283020实验报告1.实验目的：（1）通过实际编程，了解MD5算法的压缩过程，加深对Hash算法的认识；（2）了解MD5中数据填充的方式；（3）了解Hash算法中碰撞的研究方法和进展；（4）了解其他Hash算法；（5）了解HMAC算法2.实验内容：（1）熟悉Hash算法：通西普平台的散列函数实验以及MD5值比对实验，简单了解HAsh算法；思考以下问题：1.比较三种算法的不同，如：三种散列函数的输入输出等；由上图可以看出，MD5、SHA1、SHA256等的输出长度不同，MD5：256bits、SHA1:320bit、SHA256:512bit2.通过实验，看一下两个相似的字符串经过MD5运算后，得到的结果差异有多大？第一组报文：123456789123 第二组报文：123456789120 差异只在最后一位数。

由图可以看出，输入只差一个数字，而结果总共有128位却有67位不同。

差异很大。

（2）熟悉Hash算法的过程，了解填充方式：通过SimpleISES平台（SHA－１）或者给出的页面（MD5, SHA１，Padding），真正理解Hash算法的过程，了解填充方式：先输入测试向量123456789123我们可以看到状态表，如下图：然后是，4个轮函数，以第一个轮函数为例，如下图：最终得到Hash值，如下图：１）给出几种Hash算法的数据填充方式；SHA1的填充方式：明文填充一位1，再填充若干个0把明文补至448位，再填充64位（原始明文长度的64位表示）把明文补至512位。

MD5的填充方式与SHA1相同。

（3）利用程序分别计算文件hello.exe 和erase.exe的md5值：先输入测试向量123456789123源代码及程序运行结果及截图：。

【数据结构与算法】⼀致性Hash算法及Java实践 追求极致才能突破极限⼀、案例背景1.1 系统简介 ⾸先看⼀下系统架构，⽅便解释： 页⾯给⽤户展⽰的功能就是，可以查看任何⼀台机器的某些属性（以下简称系统信息）。

消息流程是，页⾯发起请求查看指定机器的系统信息到后台，后台可以查询到有哪些server在提供服务，根据负载均衡算法（简单的轮询）指定由哪个server进⾏查询，并将消息发送到Kafka，然后所有的server消费Kafka的信息，当发现消费的信息要求⾃⼰进⾏查询时，就连接指定的machine进⾏查询，并将结果返回回去。

Server是集群架构，可能动态增加或减少。

⾄于架构为什么这么设计，不是重点，只能说这是符合当时环境的最优架构。

1.2 遇到问题 遇到的问题就是慢，特别慢，经过初步核实，最耗时的事是server连接machine的时候，基本都要5s左右，这是不能接受的。

1.3 初步优化 因为耗时最⼤的是server连接machine的时候，所以决定在server端缓存machine的连接，经过测试如果通过使⽤的连接缓存进⾏查询，那么耗时将控制在1秒以内，满⾜了⽤户的要求，不过还有⼀个问题因此产⽣，那就是根据现有负载均衡算法，假如server1已经缓存了到machine1的连接，但是再次查询时，请求就会发送到下⼀个server，如server2，这就导致了两个问题，⼀是，重新建⽴了连接耗时较长，⼆是，两个server同时缓存着到machine1的连接，造成了连接浪费。

1.4 继续优化 ⼀开始想到最简单的就是将查询的machine进⾏hash计算，并除sever的数量取余，这样保证了查询同⼀个machine时会要求同⼀个server进⾏操作，满⾜了初步的需求。

但是因为server端是集群，机器有可能动态的增加或减少，假如根据hash计算，指定的 machine会被指定的server连接，如下图： 然后⼜增加了⼀个server，那么根据当前的hash算法，server和machine的连接就会变成如下： 可以发现，四个machine和server的连接关系发⽣变化了，这将导致4次连接的初始化，以及四个连接的浪费，虽然server集群变动的⼏率很⼩，但是每变动⼀次将有⼀半的连接作废掉，这还是不能接受的，当时想的最理想的结果是：当新增机器的时候，原有的连接分⼀部分给新机器，但是除去分出的连接以外保持不变当减少机器的时候，将减少机器的连接分给剩下的机器，但剩下机器的原有连接不变 简单来说，就是变动不可避免，但是让变动最⼩化。

实验报告一、实验目的1.MD5算法（1）理解Hash函数的计算原理和特点（2）理解MD5算法原理2.SHA1算法（1）理解SHA1函数的计算原理和特点（2）理解SHA1算法原理二、实验内容与设计思想①MD5算法MD5哈希算法流程：1.对于任意长度的明文，MD5首先对其进行分组，使得每一组的长度为512位，然后对这些明文分组反复重复处理。

对于每个明文分组的摘要生成过程如下：（1）将512位的明文分组划分为16个子明文分组，每个子明文分组为32位。

（2）申请4个32位的链接变量，记为A、B、C、D。

（3）子明文分组与链接变量进行第1轮运算。

（4）子明文分组与链接变量进行第2轮运算。

（5）子明文分组与链接变量进行第3轮运算。

（6）子明文分组与链接变量进行第4轮运算。

（7）链接变量与初始链接变量进行求和运算。

（8）链接变量作为下一个明文分组的输入重复进行以上操作。

（9）最后，4个链接变量里面的数据就是MD5摘要。

2.MD5分组过程对于任意长度的明文，MD5可以产生128位的摘要。

任意长度的明文首先需要添加位数，使明文总长度为448（mod512）位。

在明文后添加位的方法是第一个添加位是l，其余都是0。

然后将真正明文的长度（没有添加位以前的明文长度）以64位表示，附加于前面已添加过位的明文后，此时的明文长度正好是512位的倍数。

当明文长度大于2的64次方时，仅仅使用低64位比特填充，附加到最后一个分组的末尾。

经过添加处理的明文，其长度正好为512位的整数倍，然后按512位的长度进行分组（block），可以划分成L份明文分组，我们用Y0，Y1，……，YL-1表示这些明文分组。

对于每一个明文分组，都要重复反复的处理，如图所示。

3.MD5子明文分组和链接变量对于512位的明文分组，MD5将其再分成16份子明文分组（sub-block），每份子明文分组为32位，我们使用M[k]（k= 0, 1,……15）来表示这16份子明文分组。

实验四Hash算法和密码应用同组实验者实验日期成绩练习一MD5算法实验目的1理解Hash函数的计算原理和特点，2理解MD5算法原理实验人数每组2人系统环境Windows网络环境交换网络结构实验工具密码工具实验类型验证型一、实验原理详见“信息安全实验平台”，“实验4”，“练习一”。

二、实验步骤本练习主机A、B为一组，C、D为一组，E、F为一组。

首先使用“快照X”恢复Windows 系统环境。

1．MD5生成文件摘要（1）本机进入“密码工具”｜“加密解密”｜“MD5哈希函数”｜“生成摘要”页签，在明文框中编辑文本内容：__________________________________________________________________________。

单击“生成摘要”按钮，生成文本摘要：__________________________________________________________________________。

单击“导出”按钮，将摘要导出到MD5共享文件夹（D:\Work\Encryption\MD5\）中，并通告同组主机获取摘要。

（2）单击“导入摘要”按钮，从同组主机的MD5共享文件夹中将摘要导入。

在文本框中输入同组主机编辑过的文本内容，单击“生成摘要”按钮，将新生成的摘要与导入的摘要进行比较，验证相同文本会产生相同的摘要。

（3）对同组主机编辑过的文本内容做很小的改动，再次生成摘要，与导入的摘要进行对比，验证MD5算法的抗修改性。

2．MD5算法本机进入“密码工具”｜“加密解密”｜“MD5哈希函数”｜“演示”页签,在明文输入区输入文本（文本不能超过48个字符）,单击“开始演示”，查看各模块数据及算法流程。

根据实验原理中对MD5算法的介绍，如果链接变量的值分别为（其中，M[1]=）：A: 2B480E7CB: DAEAB5EFC: 2E87BDD9D: 91D9BEE8请写出第2轮第1步的运算过程以及经过运算后的链接变量。

哈尔滨工程大学实验报告实验名称：Hash 算法MD5班级：学号：姓名：实验时间：2014年6月成绩：指导教师：实验室名称：哈尔滨工程大学实验室与资产管理处制一、实验名称Hash算法ＭＤ５二、实验目的通过实际编程了解MD5 算法的加密和解密过程，加深对Hash 算法的认识。

三、实验环境（实验所使用的器件、仪器设备名称及规格）运行Windows 或Linux 操作系统的PC 机，具有gcc(Linux)、VC（Windows）等C 语言编译环境。

四、任务及其要求（1）利用自己所编的MD5 程序对一个文件进行处理，计算它的Hash 值，提交程序代程和运算结果。

（2）微软的系统软件都有MD5 验证，尝试查找软件的MD5 值。

同时，在Windows 操作系统中，通过开始→运行→sigverif 命令，利用数字签名查找验证非Windows 的系统软件。

__五、实验设计（包括原理图、真值表、分析及简化过程、卡诺图、源代码等）在MD5 算法中，首先需要对信息进行填充，使其字节长度与448 模512 同余，即信息的字节长度扩展至n*512+448，n 为一个正整数。

填充的方法如下：在信息的后面填充第一位为1，其余各位均为0，直到满足上面的条件时才停止用0 对信息填充。

然后，再在这个结果后面附加一个以64 位二进制表示的填充前信息长度。

经过这两步的处理，现在的信息字节长度为n*512+448= (n+1)*512，即长度恰好是512 的整数倍，这样做的目的是为满足后面处理中后面处理中对信息长度的要求。

n 个分组中第q 个分组表示为Yq。

MD5 中有A、B、C、D，4 个32 位被称作链接变量的整数参数，它们的初始值分别为：A=01234567B=89abcdef,C=fedcba98，D=76543210当设置好这个4 个链接变量后，就开始进入算法的4 轮循环运算。

循环的次数是信息中512 位信息分组数目。

首先将上面4 个链接变量复制到另外4 个变量中A 到AA，B 到BB，C 到CC，D 到DD，以备后面进行处理。