- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
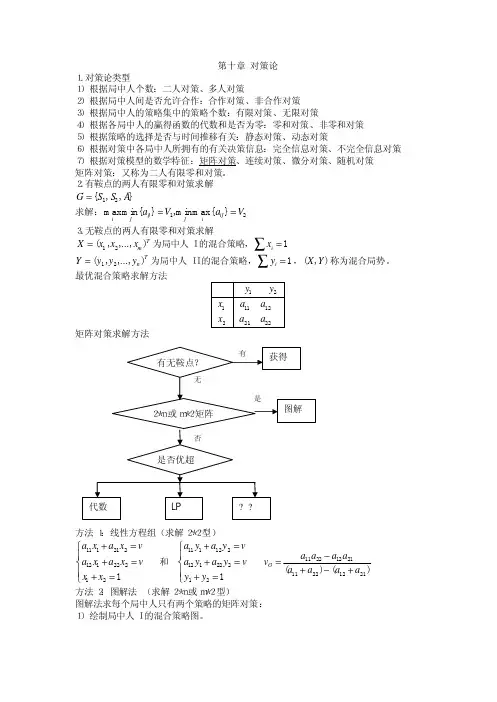
第十四章 对策论
对策论概论
对策论(The Game Theory)也称竞赛论或博
弈论,是研究具有竞争、对抗、利益分配等方面
的数量化方法,并提供寻求最优策略的途径。
20世纪40年代形成并发展。1944年以来,对策
论在投资分析、价格制定、费用分摊、财政转移 支付、投标与拍卖、对抗与追踪、国际冲突、双 边贸易谈判、劳资关系以及动物行为进化等领域 得到广泛应用。
对策的三要素:
局中人:有权决定自己行为方案的对 局参加者称为局中人。案例中,美日 双方的决策者为局中人。当对局中局 中人只有两人时,称为二人对策。
策略:对局中一个实际可行的方案称 为一个策略。案例中,美日双方各有 二个策略。
赢得矩阵(支付):当每个局中人 在确定了所采取的策略后,他们就 会获得相应的收益或损失,此收益 或损失的值称为赢得(支付)。赢 得与策略之间的对应关系称为赢得 (支付)函数。 案例中,肯尼将军与山本五十六大 将的赢得(支付)函数都可以用矩 阵A、B表示。
14-1矩阵对策的基本概念
案例:俾斯麦海的海空对抗 1943年2月,第二次世界大战中的日本, 在太平洋战区已经处于劣势。为扭转局势,
日本统帅山本五十六大将统率下的一支舰队
策划了一次军事行动:由集结地——南太平 洋的新不列颠群岛的蜡包尔出发,穿过俾斯 麦海,开往新几内亚的莱城,支援困守在那 里的日军。
练习:“二指莫拉问 题”,甲乙两人游戏, 每人出一个或两个手 指头,同时又把猜测 对方所出的手指数叫 出来,若只有一个人 猜测正确,则他所赢 得数为二人所出手指 之和,否则,重新开 始。写出该对策各局 中人的策略集合及甲 的赢得矩阵,并回答 局中人是否存在某种 出法比其他出法更为 有利。
0 -2 3 0
定理14-2:矩阵对策 G = S1,S2;A
在混合策略意义下有解的充分必要条件是: 存在混合局势( X*,Y*),使得对一切 X S1* Y S2*均有
E(X,Y*) E(X*,Y*) E(X*,Y)
定理14-3:对给定的矩阵对策 G = S1,S2;A 设X* S1* Y* S2*则混合局势( X*,Y*)是G的解且 V=VG*的充分必要条件是: 对一切 i,j均有 E( i, Y*) V E(X*, j )
解: 局中人I(采购员)有三个策略:
策略1: 10吨,策略2: 15吨,策略3 :20吨。
局中人II(环境): 策略1 较暖 ,策略2 正常,策略3较冷 现把该单位冬天取暖用煤全部费 用(秋季购煤费用与冬天不够时再补购 煤费用)作为采购员的赢得矩阵。
1较暖
1(10) -1000
2正常
素 ai*j*是其所在行中最小的同时又 是其所在列中最大的。这时ai*j*即 是对策值,因此ai*j*也称为“鞍 点”,而( *i*, *j *),为对策 的解。
Z
鞍点
Y
X
马鞍面z=f(x,y)
Z
Y
在X=0的平面上
z=f(0,y)
鞍点是z=f(0,y)
的极大值点
Z
z=f(x,0)
X
在Y=0的平面上
2 0 0 -3
-3 0 0 4
0 3 -4 0
0 2 赢得矩阵为 A 3 0
2 0 0 3
3 0 0 4
0 3 4 0
14.2
矩阵对策的混合策略
G = Ⅰ,Ⅱ;S1,S2;A
定义:对给定的矩阵对策
其中 S1= 1, 2…m S2= 1 , 2… n A=(aij)mn 把纯策略集合对应的概率向量 X=(x1, x2 … xm) 其中 xi 0 xi=1 和 Y=(y1 , y2 … yn ) 其中 yj 0 yj=1
当盟军获悉此情报后,盟军统帅麦克阿 梭命令太平洋战区空军司令肯尼将军组织空 中打击。 日本统帅山本五十六大将心里很明白:
在日本舰队穿过俾斯麦海的三天航行中,不 可能躲开盟军的空中打击,他要策划的是尽 可能减少损失。
日美双方的指挥官及参谋人员都进行了 冷静的思考与全面的谋划。
自然条件对于双方 都是已知的。基本情况如下: 从蜡包尔出发开往莱城的海上航线有南北两条。通过时 间均为3天。
分别称为局中人I和局中人II的混合策略。
如果局中人I选取的策略为
X=(x1, x2 … xm)
局中人II选取的策略为
Y=(y1 , y2 … yn ),则期望值 E(X,Y)= xi aij yj=XAYT 称为局中人I期望赢得,而局势(X,Y) 称为“混合局势”,局中人I,II的混合 策略集合记为S1*, S2*。
气象预报表明:未来3天中,北线阴雨,能见度差; 而南线天气晴好,能见度好。 肯尼将军的轰炸机布置在南线的机场,侦察机全天 候进行侦察,但有一定的搜索半径。 日军 盟军 北线 南线 北线 2天 1天 南线 2天 3天
(阴,能见度差) (晴,能见度好)
经测算,双方均可得到如下估计:
局势1: 盟军的侦察机重点搜索北线,日本舰队也恰好走 北线。由于气候恶劣,能见度差,盟军只能实施两天的 轰炸。 局势2:盟军的侦察机重点搜索北线,日本舰队走南线。 由于发现晚,尽管盟军的轰炸机群在南线,但有效轰炸 也只有两天。 日军 盟军 北线 南线 北线 2天 1天 南线 2天 3天
定义14-4:设G*= S1*,S2*;E 是对策G 混合扩充,如果有 max min E(X,Y)= min max E(X,Y)
X S1* Y S2* Y S2* X S1*
则称这个公共值为对策G在混合意义 下的值,记为V*G,而达到V*G 的混 合局势(X*,Y*)称为对策G在混合 策略意义下的解,而X*和Y*分别称 为局中人I,II的最优混合策略。
鞍点是z=f(x,0)
的极小值点
例14-3:对给定的矩阵对策 G = S1,S2;A
S1= 1,2 ,3 , 4
S2= 1 , 2 , 3 ,4
min
6 A= 1 8 0 max 8
5 4 5 2 5*
6 2 7 6 7
5 -1 5 2 5*
5* -1 5* 0
max
max
min
显然 ai2 a12 a1j
定理14-1:矩阵对策
G = S1,S2;A
在纯策略意义下有解的充分必要条 件是: 存在一个局势( *i*, *j *),使 得对一切 i=1,2,… m, j=1, 2…n 均有
aij*<=ai*j*<= ai*j
定理14-1表明矩阵对策
G = S1,S2;A
有解的充分必要条件是在A中存在元
(阴,能见度差) (晴,能见度好)
局势3:盟军的侦察机重点搜索南线,而日本舰队走北 线。由于发现晚、盟军的轰炸机群在南线,以及北线气 候恶劣,故有效轰炸只有一天。
局势4:盟军的侦察机重点搜索南线,日本舰队也恰好 走南线。此时日本舰队迅速被发现,盟军的轰炸机群所 需航程很短,加上天气晴好,有效轰炸时间三天。
(日军)
北线 南线
(盟军)北线
南线
2
1
2
3
=A
(盟军)
北线 南线
(日军)北线
南线
-2
-1
-2
-3
=B
在本例中的每一个对局,双方的 赢得的代数之和为零,这样的对 策称为“有限零和二人对策” 设两个局中人为I,II,局中人I有 m 个策略:1、 2… m ;用S1表 示这些策略的集合: S1= 1、 2…… m
北线 1 南线2 (盟军)北线 1 南线2 2 1 2 3 =A
在矩阵中,盟军的最大赢得是3,而要得到3, 必须选择策略 2,而日军的目的是使盟军的赢得尽 量的小,必须选择策略1 ,使盟军的赢得只有1。 在局中人I设法使自己的赢得尽可能大的同时, 局中人II也设法使局中人I的赢得尽可能小。 日军 盟军 北线1 南线2 北线1 2天 1天 南线2 2天 3天
min
ai2 a32 a3j
对 i=1,2,3,4 j=1,2,3,4 都成立: a12 = a32 =5由定理5-1,对策 值=5,对策的解( 1 , 2 ),( 3 , 2 ),( 1 , 4 ),( 3 , 4 )
例14-4:某单位采购员在秋天时要决定
冬天取暖用煤的采购量。已知在正常气 温条件下需要用煤15吨,在较暖和较冷 气温条件下需要用煤10吨和20吨。假定 冬季的煤价随着天气寒冷的程度而变化, 在较暖、正常、较冷气温条件下每吨煤 价为100元、150元、200元。又秋季每吨 煤价为100元。在没有关于当年冬季气温 情况下,秋季应购多少吨煤,能使总支 出最少?
定义14-3:对给定的矩阵对策
G = S1,S2;A
则对策G*= S1*,S2*;E
称为对策G混合扩充。
纯策略是混合策略的一个特例。例如:局中人Ⅰ的纯策 略 k 等价于混合策略
x ( x1 , x 2 , , x m ) S 1 ,
T *
其中,
1, i k xi 0, i k
max min aij= min max aij
i j j i
上式蕴涵的思想是朴素自然的,可以概 括为:“从最坏处着想,去争取最好的 结果”
定义14-1:对给定的矩阵对策
G =
i j
S1,S2;A
j i
若等式
max min aij= min max aij 成立,则称这个公共值为对策G的值, 记为VG,而达到的局势( i, j ) 称为对策G在纯策略意义下的解,记 为( I*, j *)而I*和 j *分别称 为局中人I和局中人II的最优纯策略。
证明:必要性:因为纯策略是混合策略的特例,故成立
充分性:当局中人取纯策略 i 时,
E ( i , y ) E ( i , y ) ( 0 , ,1, 0 , 0 )( a ij )( y1 , , y n )