下载文档原格式
1.科学决策科学决策是指决策者凭借科学思维，利用科学手段和科学技术所进行的决策。
程序性：在正确的理论指导下，按照一定的程序，正确运用决策技术和方法来选择行为方案。
创造性：决策总是针对需要解决的问题和需要完成的新任务，运用多种思维方法进行的创造性劳动。
择优性：在多个方案的对比中寻求能获取较大效益的行动方案，择优是决策的核心。
指导性：决策结果必须指导实践。
2. 运筹学运筹学是一种科学决策方法。
是依据给定目标和条件从众多方案中选择最优方案的最优化技术。
是一门寻求在给定资源条件下，如何设计和运行一个系统的科学决策方法。
与管理科学关系:管理科学涵盖的领域比运筹学更宽一些。
可以说，运筹学是管理科学最重要的组成部分。
与系统科学、系统分析、工业工程的关系:系统科学、系统分析、工业工程等学科的研究内容比运筹学的研究内容窄一些。
3.运筹学研究的特点科学性：运筹学是在科学方法论的指导下通过一系列规范化步骤进行的；运筹学是广泛利用多种学科的科学技术知识进行的研究。
运筹学研究不仅仅涉及数学，还要涉及经济科学、系统科学、工程物理科学等其它学科。
实践性：运筹学以实际问题为分析对象，通过鉴别问题的性质、系统的目标以及系统内主要变量之间的关系，利用数学方法达到对系统进行最优化的目的。
分析获得的结果要能被实践检验，并被用来指导实际系统的运行。
系统性：运筹学用系统的观点来分析一个组织（或系统），它着眼于整个系统而不是一个局部，通过协调各组成部分之间的关系和利害冲突，使整个系统达到最优状态。
综合性：运筹学研究是一种综合性的研究，它涉及问题的方方面面，应用多学科的知识，因此，要由一个各方面的专家组成的小组来完成。
4.运筹学模型运筹学研究的模型主要是抽象模型:数学模型。
数学模型的基本特点是用一些数学关系（数学方程、逻辑关系等）来描述被研究对象的实际关系（技术关系、物理定律、外部环境等）。
4.1模型特点它们大部分为最优化模型。
一般来说，运筹学模型都有一个目标函数和一系列的约束条件，模型的目标是在满足约束条件的前提下使目标函数最大化或最小化。
运筹学的定义
运筹学是一门研究决策的学科，它综合了数学、统计学、信息学、经济学、管理学等多个领域的知识和技术，旨在通过科学的方法来解决实际问题。
运筹学在现代社会中拥有广泛的应用，涉及到许多领域，如物流、交通、金融、医疗、能源等。
运筹学的主要目标在于找到最优解决方案。
例如，在物流领域，如何在有限的时间内将货物运输到目的地，同时降低运输成本；在金融领域，如何通过科学的投资策略来最大化收益，同时降低风险。
这些问题都可以通过运筹学的方法来解决。
为了实现这些目标，运筹学应用了许多技术和方法。
其中最常用的是线性规划，即在一组约束条件下最小化或最大化一个线性函数。
除此之外，运筹学还包括非线性规划、整数规划、动态规划、图论、排队论、模拟等等方法。
这些方法都有不同的应用场景，可以根据具体问题的特点选择最合适的方法。
运筹学的应用不仅限于商业领域，也可以用于解决社会问题。
例如，在医疗领域，如何最大化患者的生存率，同时降低医疗成本；在能源领域，如何通过科学的能源规划来提高能源利用效率，降低污染和排放。
这些问题都需要运筹学的方法来提供解决方案。
运筹学是一门非常实用的学科，它可以为我们提供科学的决策方法，解决实际问题。
随着科技的发展和社会的进步，运筹学的应用范围
也将更加广泛。
我们应该深入学习和应用运筹学的知识和方法，为实现更高效、更节约、更可持续的社会发展做出贡献。
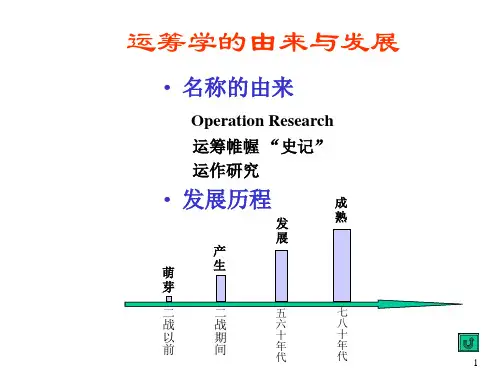
运筹学综述运筹学的简介一：什么是运筹学？运筹学是Operations Research的英文单词缩写。
运筹学界的元老说运筹学是执行部门对所控制的业务做出决策提供数量上的依据的科学或利用所有应用科学执行部门对其所属业务作出决策提供数量上依据的一门科学；世界上最早的运筹学协会说运筹学是运用科学方法来解决工业、商业、政府、国防等部门里有关人力、机器、物资、金钱等大型系统的指挥或管理中所出现的复杂问题的一门学科,其目的是“帮助管理者以科学方法确定其方针和行动”。
二:运筹学的三个来源1、军事二战期间例一：在第二次世界大战期间，鲍德西雷达站的研究——“布莱克特马戏团”的出色工作，Bawdsey雷达站—Blackett杂技班专门就改进空防系统进行研究。
成员组成：心理学家3，数学家2，数学物理学家2，天文物理学家1，普通物理学家1，陆军军官1，测量员1。
研究的问题是设计将雷达信息传送给指挥系统及武器系统的最佳方式；雷达与防空武器的最佳配置；对探测、信息传递、作战指挥、战斗机与防空火力协调等获得成功，大大提高了英国本土的防空能力,不久以后在对抗德国对英伦三岛的狂轰滥炸中发挥了极大的作用，堪称运筹学的发祥与典范，展示了运筹学的本色与特色。
二战期间例二：大西洋反潜战——Morse小组的重要工作。
1942年麻省Morse教授应美国大西洋舰队反潜战官员Baker舰长的请求担任反潜战运筹组的计划与监督工作，其最出色的工作之一是协助英国打破了德国对英吉利海峡的海上封锁，研究所提出的两条重要建议是：将反潜攻击由反潜舰艇投掷水雷改为飞机投掷深水炸弹，起爆深度由100米改为25米左右，即当德方潜艇刚下潜时攻击效果最佳；运送物资的船队及护航舰艇的编队由小规模、多批次改为大规模、少批次，从而减少了损失率丘吉尔采纳Morse的建议，从而打破德国封锁；重创德国潜艇部队；Morse同时获得英国及美国战时最高勋章二战期间例三：英国战斗机中队援法决策。
运筹学的概念运筹学是一种综合性学科，它在现代管理中起着至关重要的作用。
运筹学是一种运用数学、统计学、计算机科学以及其他相关领域的方法和理论来帮助制定最优决策的学科。
它的主要目标是通过通过信息分析和决策模型来使决策者在制定决策时更加合理、科学和精准。
下面是对运筹学概念的详细介绍。
一、运筹学的基本定义运筹学（Operations Research，简称OR）是一门科学，通过使用计算机和数学模型，研究如何最好地利用有限资源来达到预期目标，主要研究方法包括优化、数理统计、决策分析、模拟等。
二、运筹学的发展历程运筹学是在二战期间发展出来的，主要应用于军事后勤问题的解决。
之后，运筹学学科马不停蹄地在各个领域快速发展，至今已经成为了一门广泛的学科。
三、运筹学的应用范围运筹学在各个领域都有广泛的应用，例如生产制造、物流管理、金融风险管理、医疗管理、资源分配等。
它在实践中的应用能够使企业和组织在有限的资源下获得最大收益。
例如，电商企业可以利用运筹学和网络优化技术来解决配送问题。
医院可以利用运筹学与供应链的整合优化来提高采购成本的效率。
银行等金融机构则可以利用运筹学来建立风险管理模型，减轻市场波动造成的经济损失。
四、运筹学的关键技术该学科主要基于优化、数学建模、统计推断和计算机仿真等关键技术。
对于不同的问题，会采用不同的技术手段。
例如，对于线性规划问题，使用线性规划算法进行求解；对于决策树问题，可以使用决策树算法进行求解；对于复杂的大规模问题，可以使用数学建模与计算机仿真技术进行求解。
总之，运筹学是为了解决实际问题而产生的一种学科，它在生产、经济、政策等许多领域有广泛应用，发展迅速，使得成本降低、管理规范化、业务流程优化等问题得到了解决。
运筹学结课报告
院系信息工程与自动化学院
专业系统工程
姓名徐宏武
学号 2013204095 教师王晓东（教授）
二Ｏ一三年十二月二十五日
运筹学在控制过程中的运用
一对运筹学这门课简单的认识
古人作战讲“夫运筹帷幄之中，决胜千里之外”运筹学也就是这个道理。
运筹学主要研究经济活动和军事活动中能用数量来表达的有关策划、管理方面的问题。
从最直观、明了的角度将运筹学定义为：“通过构建、求解数学模型，规划、优化有限资源的合理利用，为科学决策提供量化一句的系统知识体系。
”
上了十几次运筹学课，觉得这门课真的内容很丰富，涉及数学，决策学等等很多方面。
在有限的学习时间里，老师给我们讲了很多实用性的东西，线性函数等等。
对于一个数学基础不太好的我来说，在短时间内把运筹学学好几乎是不可能的。
对这门学科理解可能也不够到位。
但是，学习一门学科，掌握它的精髓和要义或许更重要。
学习过运筹学后，更应该能够熟练的掌握和运用运筹学的精髓，用运筹学的思维思考问题，从而使生活和学习中遇到的各种问题得到更好的解决。
应该就是把各种事件、因素、条件等等量化，分析运用运筹学的方法得出最优解，再转化为实际问题。
当然，转化的方法和技巧很系统，也很高深复杂。
理论性的东西也有很多，必须承认，是我的能力和水平所达不到的。
在现代社会中，运筹学的运用也是非常广泛的，经济方面，涉及资源开发，资产收益，甚至经济发展的策略和方向。
在社会和个人生活中，与人交往，人生的规划中，甚至国家政策方针的制定中，都有运筹学的踪迹。
学习了运筹学，不应该说接触了运筹学以后，才知道他的用处如此之多。
二运筹学在生产过程优化调度中的应用
运筹学方法在生产过程调度问题研究中已得到广泛应用。
以下将对生产过程调度问题优化方法研究中常用的分枝定界、动态规划、拉格朗日松弛等运筹学方法行介绍。
1) 分枝定界
分枝定界法(Branch and bound, B&B) 是在上世纪60 年代由英国伦敦政治经济学院Land 等提出的一种主要用于求解离散优化问题的最优化方法。
英国学者Lomnicki首先将分枝定界方法应用于三机器Flow shop 调度问题中，此后，分枝定界方法被逐。
步应用于单机、并行机、Jobshop、柔性制造系统等典型生产过程调度问题及面向钢铁、微电子、石化等特定行业的生产过程调度问题中。
面向生产过程调度问题的分枝定界方法的研究主要集中在分枝方法和上下界确定方法上。
近年来，一些学者还将模糊集理论、遗传算法等其他方法与分枝定界法相结合，提出了基于模糊推理的分枝定界算法、基于遗传算法的分枝定界方法等，并将其用于生产过程调度问题的求解，以提高搜索效率和调度解的性能。
2) 动态规划
动态规划(Dynamic programming, DP) 是由美国南加州大学Bellman 等于1952 年提出的求解多阶段决策过程优化问题的一种最优化方法，其在单机、并行机、Flow shop和Job shop 等典型生产过程调度问题及面向钢铁、微电子等特定行业的生产过程调度问题中均得到了较多应用。
面向生产过程调度问题的动态规划方法研究主要涉及步长改进方法和状态变量维数化简方法等。
一些学者还将模糊集、随机过程理论和进化计算等与动态规划方法相结合，形成模糊动态规划、随机动态规划和基于进化计算的动态规划等方法。
以提高动态规划方法的优化效果或对不确定生产过程调度问题的适应性。
3) 拉格朗日松弛法
拉格朗日松弛法(Lagrangian relaxation, LR)是一种求解约束优化问题的近似优化方法。
美国康涅狄格大学陆宝森等最早将该方法应用于解生产过程调度问题中。
之后，该方法在求解单机、并行机、Flow shop、Job shop、柔性制造系统等典型生产过程调度问题及面向钢铁、微
电子等特定行业的生产过程调度问题中均得到广泛应用。
面向生产过程调度问题的拉格朗日松弛方法研究主要集中在对拉格朗日乘子的更新方法上。
目前较常用的方法是采用次梯度方法更新拉格朗日乘子.近年来，启发式方法、神经网络等也被用于拉格朗日松弛算法的乘子更新过程。
运筹学方法是求解生产过程调度问题的经典方法，但由于绝大多数生产过程调度问题都是NP 难题，随着调度问题规模的增大，上述方法一般会产生指数爆炸现象，因而上述方法主要用于求解较小规模的生产过程调度问题，或与分解、软计算等方法相结合，用于求解较为复杂的生产过程调度问题。
三小结
将来社会的发展不可估计，但无论什么时候，都需要作出决策和判断，都需要研究最好的解决问题的方法，运筹学一定会得到更多的运用，也一定会有更高更远的发展。
可惜我学习的运筹学知识很有限，只能在以后的生活中，找机会更加深入和认真的学习了。
但也可以这么说，运筹学就在我们身边，在我们的学习、生活中，何不积极运用并且不断去理解和感悟呢。
学习这门课最大的收获就是，生活是需要规划和技巧的，我们要生活的更好，就应该未雨绸缪，积极寻求好的方法，做好应对一切的准备！。
