概率论与数理统计_排列组合知识的补充
- 格式:ppt
- 大小:141.00 KB
- 文档页数:9

第1章随机事件与概率A B=不可能同时发生,称事件A与事件互不相容或者互斥。
基本事件是互不相容的。
=且B互为逆事件,或对A BΦ,则(P B-A{ωω21,P) (2=ω1()(|)n i i P A P A B ==∑对全概率公式可以利用课堂讲解过的概率树来描述和分析。
设事件B 1,B 2,…,B n 及1(|))(|i n j j P A B P P A B ==∑此公式即为贝叶斯公式。
1=i 2n第二章随机变量及其分布第三章多维随机变量及其分布的联合分布函数。
通过全平面上的区域来形}1z-)]n第四章随机变量的数字特征第五章大数定律和中心极限定理1(数理统计部分的知识都是从样本和样本统计量出发来分析总体的属性,例如:分析已知分布中的未知参数等)第六章数理统计的基本概念与抽样分布总体有相同分布的随机变量;观察之后,样本就是nk=2,3,.()},max{n n X X =常用统计量的基本性质~X N 221)~S χ-(X-第七章 参数估计,)mA θ=),,2∧m θ 即为参数n12,,,,)(;,)m i m P X θθθθ=∏=∂法的流程。
第八章 假设检验假设检验的基本步骤如下:1. 根据实际问题,提出原假设0H 及备择假设1H ;(可确定是单侧还是双侧假设检验)2. 依据实际条件构造检验统计量;(检验统计量不含任何未知参数且分布已知)3.对于给定显著性水平α,确定检验统计量的拒绝域;(拒绝域要与0H 为真时检验统计量的趋势相反)4.将样本值或者样本统计量的值代入检验统计量的表达式计算实际值,判断是否落入拒绝域,若落入拒绝域,则否定0H ,否则接受0H 。
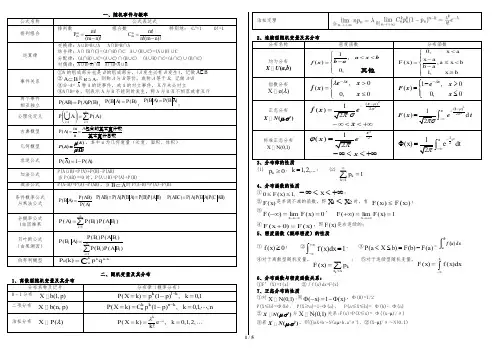

1、排列组合:)1)...(1()(!1)...1()1)...(1(m!m n m n +--=-=⨯-+--==m n n n m n n A m m m n n n A C m n 性质!10n A C C C C n n m n n m n n n n ====-2、事件运算律:①AB=BA ②A ∪B=B ∪A③ABC=A(BC)④A ∪B ∪C=A ∪(B ∪C)④A(B ∪C)=(A ∪B)(B ∪C)=(BC)∪A ⑤德摩根率:____________A ∪B =__A ∩__B ____AB=__A ∪__B⑥加法公式:P(A ∪B)=P(A)+P(B)-P(AB)P(A ∪B ∪C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC)⑦减法公式:P(A-B)=P(A ___B)=P(A)-P(BA)⑧独立事件:P(AB)=P(A)*P(B)P(AB)=P(B)*P(AlB)=P(A)P(B)☆P(AlB)=P(A)↔A,B 独立⑨三个事件两两独立:P(AB)=P(A)P(B)P(AC)=P(A)P(C)P(BC)=P(B)P(C)P(ABC)=P(A)P(B)P(C)四个条件缺一不可,少了第四个就只有两两互相独立了3、条件概率:)()()(A P AB P A B P =乘法公式:)()()()()(B A P B P A B P A P AB P ==,P(A)>0)()()()(AB C P A B P A P ABC P =4、全概率公式:∑==ni Bi A P Bi P A P 1)()()((B1,B2,......Bn ,是完备事件组)5、贝叶斯公式:)()()()i ()()i ()i (1A P ABi P Bi A P B P Bi A P B P A B P n i ==∑-6、切比雪夫不等式:[][][]εεεεε≥--=<->≤≥-)(1)()0()()(2X E X P X E X P X D X E X P 7、多项独立同分布,求总和怎样的概率。

数学中的排列与组合知识点总结在数学中,排列和组合是两个重要的概念。
它们在各个领域都有广泛的应用,特别是在概率论、统计学和组合数学中。
本文将对排列和组合的概念、性质和应用进行总结。
一、排列的概念与性质排列是从一组元素中选取若干个元素按照一定的顺序进行排列。
设有n个元素,则从中选取m个元素进行排列的方式记为P(n, m)。
排列的计算公式为:P(n, m) = n!/(n-m)!其中,n!表示n的阶乘,即n! = n × (n-1) × (n-2) × ... × 2 × 1。
排列的性质如下:1. 排列数P(n, m)满足如下关系:P(n, m) = P(n-1, m) + P(n-1, m-1)2. 对于任意正整数n,有P(n, n) = n!,即n个元素的全排列数为n 的阶乘。
3. 当m>n时,P(n, m) = 0,即不能取出超过给定元素总数的元素进行排列。
4. 当m=0时,P(n, m) = 1,即不取任何元素进行排列时,排列数为1。
二、组合的概念与性质组合是从一组元素中选取若干个元素组成一个集合,而不考虑元素的顺序。
设有n个元素,则从中选取m个元素进行组合的方式记为C(n, m)。
组合的计算公式为:C(n, m) = n!/(m!(n-m)! )组合的性质如下:1. 组合数C(n, m)满足如下关系:C(n, m) = C(n-1, m) + C(n-1, m-1)2. 对于任意正整数n,有C(n, 0) = C(n, n) = 1,即不取任何元素或者取出全部元素的组合数为1。
3. 当m>n时,C(n, m) = 0,即不能取出超过给定元素总数的元素进行组合。
4. 组合数C(n, m)与排列数P(n, m)之间存在以下关系:C(n, m) = P(n, m)/m!三、排列与组合的应用1. 概率计算:排列和组合在概率计算中有广泛的应用。

附加知识: 排列组合知识小结: 一、计数原理1.加法原理:分类计数。
2.乘法原理:分步计数。
二、排列组合1.排列数(与顺序有关):)(),1()2)(1(n m m n n n n A m n ≤+---= !n A nn =,n A A n n==10,1 如:25203456757=⨯⨯⨯⨯=A ,12012345!5=⨯⨯⨯⨯= 2.组合数(与顺序无关):!m A C mn m n=,mn n m n C C -=如:3512344567!44747=⨯⨯⨯⨯⨯⨯==A C ,2112672757757=⨯⨯===-C C C3.例题:(1)从1,2,3,4,5这五个数字中,任取3个数字,组成一个没有重复的3位数,共有___6034535=⨯⨯=A ____种取法。
(2)从0,1,2,3,4这五个数字中,任取3个数字,组成一个没有重复的3位数,共有___483442414=⨯⨯=A A ____种取法。
(3)有5名同学照毕业照,共有__1201234555=⨯⨯⨯⨯=A _种排法。
(4)有5名同学照毕业照,其中有两人要排在一起,那么共有_48)1234()12(4422=⨯⨯⨯⨯⨯=A A ___种排法。
(5)袋子里有8个球,从中任意取出3个,共有___38C ____种取法。
(6)袋子里有8个球,5个白球,3个红球。
从中任意取出3个,取到2个白球1个红球的方法有___1325C C ____种。
3887656321C ⨯⨯==⨯⨯第一章、基础知识小结一、随机事件的关系与运算 1.事件的包含设A ,B 为两个事件,若A 发生必然导致B 发生,则称事件B 包含于A ,记作B A ⊂。
2.和事件事件“A,B 中至少有一个发生”为事件A 与B 的和事件,记作B A 或B A +。
性质:(1)B A B B A A ⊂⊂, ;(2)若B A ⊂,则B B A =3.积事件:事件A,B 同时发生,为事件A 与事件B 的积事件,记作B A 或AB 。

第一章 随机事件和概率 第一节 基本概念1、排列组合初步(1)排列组合公式)!(!n m m P n m -= 从m 个人中挑出n 个人进行排列的可能数。
)!(!!n m n m C n m -=从m 个人中挑出n 个人进行组合的可能数。
例1.1:方程xx x C C C 76510711=-的解是 A . 4 B . 3 C . 2 D . 1例1.2:有5个队伍参加了甲A 联赛,两两之间进行循环赛两场,试问总共的场次是多少?(2)加法原理(两种方法均能完成此事):m+n某件事由两种方法来完成,第一种方法可由m 种方法完成,第二种方法可由n 种方法来完成,则这件事可由m+n 种方法来完成。
(3)乘法原理(两个步骤分别不能完成这件事):m ×n某件事由两个步骤来完成,第一个步骤可由m 种方法完成,第二个步骤可由n 种方法来完成,则这件事可由m ×n 种方法来完成。
例1.3:从5位男同学和4位女同学中选出4位参加一个座谈会,要求与会成员中既有男同学又有女同学,有几种不同的选法?例1.4:6张同排连号的电影票,分给3名男生和3名女生,如欲男女相间而坐,则不同的分法数为多少?例1.5:用五种不同的颜色涂在右图中四个区域里,每一区域涂上一种颜色,且相邻区域的颜色必须不同,则共有不同的涂法A.120种B.140种 C.160种D.180种(4)一些常见排列①特殊排列②相邻③彼此隔开④顺序一定和不可分辨例1.6:晚会上有5个不同的唱歌节目和3个不同的舞蹈节目,问:分别按以下要求各可排出几种不同的节目单?①3个舞蹈节目排在一起;②3个舞蹈节目彼此隔开;③3个舞蹈节目先后顺序一定。
例1.7:4幅大小不同的画,要求两幅最大的排在一起,问有多少种排法?例1.8:5辆车排成1排,1辆黄色,1辆蓝色,3辆红色,且3辆红车不可分辨,问有多少种排法?①重复排列和非重复排列(有序)例1.9:5封不同的信,有6个信箱可供投递,共有多少种投信的方法?②对立事件例1.10:七人并坐,甲不坐首位,乙不坐末位,有几种不同的坐法?例1.11:15人中取5人,有3个不能都取,有多少种取法?例1.12:有4对人,组成一个3人小组,不能从任意一对中取2个,问有多少种可能性?③ 顺序问题例1.13:3白球,2黑球,先后取2球,放回,2白的种数?(有序) 例1.14:3白球,2黑球,先后取2球,不放回,2白的种数?(有序) 例1.15:3白球,2黑球,任取2球,2白的种数?(无序)2、随机试验、随机事件及其运算(1)随机试验和随机事件如果一个试验在相同条件下可以重复进行,而每次试验的可能结果不止一个,但在进行一次试验之前却不能断言它出现哪个结果,则称这种试验为随机试验。

高中数学中的排列与组合重要知识点详解排列与组合是高中数学中的重要知识点之一,它们在概率统计、数论以及实际问题中的应用非常广泛。
本文将详细介绍排列与组合的相关概念、性质以及应用。
一、排列的概念与性质排列是指从给定的元素中选取一部分按照一定的顺序进行排列,其结果不同于组合。
在排列中,每个元素只能使用一次,且不同的顺序会形成不同的排列。
1. 重复排列重复排列是指从给定的元素中选取一部分进行排列,但允许元素的重复使用。
对于n个元素中选取r个进行重复排列的可能数可以表示为n^r。
2. 不重复排列不重复排列是指从给定的元素中选取一部分进行排列,但不允许元素的重复使用。
对于n个元素中选取r个进行不重复排列的可能数可以表示为A(n, r)或nPr,计算公式为A(n, r) = n!/(n-r)!。
二、组合的概念与性质组合是指从给定的元素中选取一部分,不考虑其顺序,将其组成一个集合。
在组合中,不同顺序的元素组合形成的结果是相同的。
1. 重复组合重复组合是指从给定的元素中选取一部分进行组合,允许元素的重复使用。
对于n个元素中选取r个进行重复组合的可能数可以表示为C(n+r-1, r)或C(n+r-1, n-1),计算公式为C(n+r-1, r) = (n+r-1)! / (r!(n-1)!)。
2. 不重复组合不重复组合是指从给定的元素中选取一部分进行组合,不允许元素的重复使用。
对于n个元素中选取r个进行不重复组合的可能数可以表示为C(n, r)或nCr,计算公式为C(n, r) = n! / (r!(n-r)!。
三、排列与组合的应用排列与组合既有理论上的意义,也有广泛的实际应用。
1. 概率统计排列与组合在概率统计中经常用来计算样本空间的大小,从而计算概率。
例如,在抽取彩票号码、扑克牌的发牌问题中,可以利用排列与组合的知识来计算可能的结果数量。
2. 数论排列与组合也在数论中有重要的应用。
例如,在数论中,可能出现对排列和组合的计数问题,而排列与组合的知识可以帮助解决这些问题。


数学知识点归纳排列组合与概率的应用数学知识点归纳:排列组合与概率的应用数学是一门抽象而又实用的学科,涉及到各种不同的知识点和概念。
在数学的学习过程中,排列组合与概率是非常重要的内容之一。
排列组合与概率的应用在日常生活中随处可见,如排队买票、抽奖等。
本文将对排列组合与概率的相关知识点进行归纳总结并探讨其实际应用。
一、排列组合的基本概念1. 排列:在数学中,排列是指从若干元素中选取部分元素按一定次序排列的方式。
常用表示方法是P(n, m),表示从n个不同元素中选取m个元素进行排列的总数。
2. 组合:组合是指从若干元素中选取部分元素不考虑次序的方式。
常用表示方法是C(n, m),表示从n个不同元素中选取m个元素进行组合的总数。
二、排列组合的应用1. 排列的应用:排列在实际生活中有广泛的应用。
比如,有三个人A、B、C参加某项活动,按照一定的顺序进行排列,那么可能的排列组合数为6种,即ABC、ACB、BAC、BCA、CAB、CBA。
在实际应用中,我们可以运用排列的知识解决类似的问题。
2. 组合的应用:组合同样具有广泛的应用。
比如,购买彩票时选择6个号码的组合方式有很多种,而中奖的概率只有一种。
在实际生活中,我们可以利用组合的知识计算概率,提高中奖的可能性。
三、概率的基本概念概率是数学中比较重要的一个概念,是描述事件发生可能性的一种度量。
概率的计算需要用到排列组合的知识。
四、概率的应用1. 概率的计算:概率可以描述事件发生的可能性大小。
通过排列组合的计算方法,我们可以得到某个事件发生的概率。
比如,掷骰子的例子中,某个点数出现的概率为1/6,即1种有利的结果与6种可能的结果之比。
2. 概率的预测:利用概率的知识,我们可以对事件的发生概率进行预测。
比如,在赌博游戏中,我们可以根据排列组合和概率的知识计算出某个号码或某种组合的中奖概率,从而制定出合理的下注策略。
3. 概率的实际应用:概率在现实生活中有很多实际应用。

附加知识:排列组合知识小结:一、计数原理1•加法原理:分类计数。
2•乘法原理:分步计数。
二、排列组合1 •排列数(与顺序有关):A"' = n(ti—1)(/1 —2)…(“—m + l),(/n M ii)A:二〃!,=女口:4^ = 7x6x5x4x3=2520, 5!= 5x 4x 3x2x 1= 1202•组合数(与顺序无关):如:C4=< = 7x6x5x4 = 3 C S=C;.5= C;=Z X6=214! 4x3x2xl 2x13•例题:(1)从1, 2, 3, 4, 5这五个数字中,任取3个数字,组成一个没有重复的3位数,共有_^ = 5x4x3 = 60_种取法。
(2)从0, 1, 2, 3, 4这五个数字中,任取3个数字,组成一个没有重复的3位数,共有_AX = 4x4x3 = 48_种取法。
(3)有5名同学照毕业照,共有_^ = 5x4x3x2xl=120—种排法。
(4)有5名同学照毕业照,其中有两人要排在一起,那么共有—A2^ = (2xl)x(4x 3x2x1)= 48 种排法。
(5)袋子里有8个球,从中任意取出3个,共有_C;—种取法。
(6)袋子里有8个球,5个白球,3个红球。
从中任意取岀3个,取到2个白球1个红球的方法有_ __________ 种。
8x7x63x2x1第一章、基础知识小结一、随机事件的关系与运算1•事件的包含设A, B为两个事件,若A发生必然导致B发生,则称事件B 包含于A,记作Bu4。
2.和事件事件=A,B中至少有一个发生“为事件A与B的和事件,记作AUB 或A+B。
性质:(1) AuAUBEuAUE;(2)若Ac B,则AUB = B3•积事件:事件A,B同时发生,为事件A与事件B的积事件,记作AQB 或AB。
性质:(1)AB CZ A9AB CZ B;(2)若AuB,则AB= A4•差事件:書件A发生而B不发生为事件A与B事件的差事件,记作A-B(AB)O性质:(1) A—BuA;(2)若AuB,则A—B = 05•互不相容事件:若事件A与事件B不能同时发生,即AB = <P,则称事件A与事件B是互不相容的两个事件,简称A与B互不相容(或互斥)。
排列组合知识点总结一、排列组合的基本概念1.1 排列的概念排列是指从给定的元素中按照一定的顺序选取若干元素的方式。
例如,从元素集合{a, b, c}中选择2个元素,按照顺序选择的话可能得到的排列有ab, ac, ba, bc, ca, cb。
可以看出,排列与元素的顺序有关。
通常情况下,从n个元素中取出m个元素,按照顺序排列的方式有n*(n-1)*(n-2)* ... *(n-m+1)种。
1.2 组合的概念组合是指从给定的元素中按照一定的规则选取若干元素的方式,但是不考虑元素的顺序。
例如,从元素集合{a, b, c}中选择2个元素,组合的情况有ab, ac, bc,并且ba, ca, cb这三种情况都属于ab, ac, bc中的一种。
通常情况下,从n个元素中取出m个元素,不考虑顺序的组合方式有C(n,m) = n! / (m! * (n-m)!)种。
1.3 排列组合的关系排列和组合是紧密相关的,它们之间的关系可以通过以下公式表示:A(n,m) = n! / (n-m)!C(n,m) = A(n,m) / m!也就是说,排列是组合乘以选取的元素顺序的情况。
二、排列组合的性质2.1 基本性质(1)排列和组合的个数都是离散的,不能是负数,也不能是小数。
(2)从n个元素中取出m个元素的排列个数一定是比组合个数多的,即A(n,m) > C(n,m)。
2.2 乘法原理乘法原理是排列组合问题中的重要原理,它指出,如果一个问题可以分解为多个步骤,每个步骤有若干种选择,那么整个问题的解法个数就等于各个步骤选择方式的乘积。
例如,如果有4个选择项,分别为A、B、C、D,每个选择项都有3种情况,那么根据乘法原理,一共有3*3*3*3=81种选择方式。
2.3 加法原理加法原理是排列组合问题中的另一个重要原理,它指出,如果一个问题可以分解为多个独立的子问题,那么整个问题的解法个数就等于各个子问题解法个数之和。
例如,从n个元素中取出m个元素的排列个数等于从n个元素中取出m个元素放在前面或者放在后面的情况之和。
附加知识: 排列组合知识小结: 一、计数原理1.加法原理:分类计数。
2.乘法原理:分步计数。
二、排列组合1.排列数(与顺序有关):)(),1()2)(1(n m m n n n n A m n ≤+---= !n A nn =,n A A n n==10,1 如:25203456757=⨯⨯⨯⨯=A ,12012345!5=⨯⨯⨯⨯= 2.组合数(与顺序无关):!m A C mn m n=,mn n m n C C -=如:3512344567!44747=⨯⨯⨯⨯⨯⨯==A C ,2112672757757=⨯⨯===-C C C3.例题:(1)从1,2,3,4,5这五个数字中,任取3个数字,组成一个没有重复的3位数,共有___6034535=⨯⨯=A ____种取法。
(2)从0,1,2,3,4这五个数字中,任取3个数字,组成一个没有重复的3位数,共有___483442414=⨯⨯=A A ____种取法。
(3)有5名同学照毕业照,共有__1201234555=⨯⨯⨯⨯=A _种排法。
(4)有5名同学照毕业照,其中有两人要排在一起,那么共有_48)1234()12(4422=⨯⨯⨯⨯⨯=A A ___种排法。
(5)袋子里有8个球,从中任意取出3个,共有___38C ____种取法。
(6)袋子里有8个球,5个白球,3个红球。
从中任意取出3个,取到2个白球1个红球的方法有___1325C C ____种。
3887656321C ⨯⨯==⨯⨯第一章、基础知识小结一、随机事件的关系与运算 1.事件的包含设A ,B 为两个事件,若A 发生必然导致B 发生,则称事件B 包含于A ,记作B A ⊂。
2.和事件事件“A,B 中至少有一个发生”为事件A 与B 的和事件,记作B A 或B A +。
性质:(1)B A B B A A ⊂⊂, ;(2)若B A ⊂,则B B A =3.积事件:事件A,B 同时发生,为事件A 与事件B 的积事件,记作B A 或AB 。
概率与统计中的排列组合概率与统计是数学中的一个重要分支,涉及到很多与现实生活有关的问题。
在概率与统计中,排列组合是一个基本的概念,它用于描述对象的不同排列和组合方式。
本文将介绍概率与统计中的排列组合概念及其应用。
排列是指从一组对象中选择若干个对象按照一定的顺序排列的方式。
组合是指从一组对象中选择若干个对象,而不考虑它们的顺序。
排列和组合在概率与统计中有着广泛的应用。
首先,我们来了解排列的概念。
假设有n个对象要排列,而排列的长度为r。
那么可以有n(n-1)(n-2)...(n-r+1)种不同的排列方式。
这个计算公式也可以写成nPr,其中P表示排列的意思。
例如,如果有5个人排队,那么可以有5个人作为第一个人,4个人作为第二个人,3个人作为第三个人,2个人作为第四个人,1个人作为第五个人,所以一共有5P5 = 5! = 5*4*3*2*1 = 120种不同的排列方式。
接下来是组合的概念。
同样假设有n个对象要选择,而选择的数量为r。
那么可以有C(n,r) = n!/[(n-r)!r!]种不同的组合方式。
其中C表示组合的意思。
例如,如果有5个人要从中选出3个人组成一个团队,那么一共可以有5C3 = 5! / [(5-3)!3!] = 5*4/(2*1) = 10种不同的组合方式。
排列和组合的应用非常广泛。
在生活中,我们经常会遇到需要考虑顺序或不考虑顺序的问题。
例如,假设有10张扑克牌,我们要从中选出5张作为底牌,那么一共有多少种不同的底牌组合方式呢?首先考虑排列的方式,因为底牌的顺序是有关的。
所以答案是10P5 = 10! / (10-5)! = 10*9*8*7*6 = 30240种不同的组合方式。
接下来考虑组合的方式,因为底牌的顺序不影响结果。
所以答案是10C5 = 10! / [(10-5)!5!] = 252种不同的组合方式。
可以看到,排列的结果要比组合的结果多很多。
除了生活中的应用,排列组合还在概率与统计领域有着重要的应用。
排列组合知识点总结排列组合是数学中一个重要的分支,它在解决许多实际问题中都有着广泛的应用,比如抽奖、选座位、安排比赛等等。
下面让我们一起来详细了解一下排列组合的相关知识点。
一、基本概念1、排列从 n 个不同元素中,任取 m(m≤n)个元素按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列。
根据排列的定义,两个排列相同,当且仅当两个排列的元素完全相同,且元素的排列顺序也相同。
排列数用 A(n, m) 表示。
2、组合从 n 个不同元素中,任取 m(m≤n)个元素并成一组,叫做从 n 个不同元素中取出 m 个元素的一个组合。
组合数用 C(n, m) 表示。
二、排列数与组合数的计算公式1、排列数公式A(n, m) = n(n 1)(n 2)…(n m + 1) = n! /(n m)!2、组合数公式C(n, m) = n! / m!(n m)!三、排列组合的基本性质1、排列的性质(1)A(n, n) = n!(2)A(n, m) = nA(n 1, m 1)2、组合的性质(1)C(n, 0) = C(n, n) = 1(2)C(n, m) = C(n, n m)四、解决排列组合问题的常用方法1、特殊元素优先法对于存在特殊元素的问题,优先考虑特殊元素的排列或组合。
2、捆绑法当要求某些元素必须相邻时,可以将这些元素看作一个整体,与其他元素一起进行排列,然后再考虑这些相邻元素的内部排列。
3、插空法当要求某些元素不能相邻时,先将其他元素排列好,然后在这些元素之间及两端的空位中插入不能相邻的元素。
4、间接法有些问题直接求解较为复杂,可以先求出总的排列或组合数,然后减去不符合要求的排列或组合数。
5、分类讨论法当问题包含多种情况时,需要对不同情况进行分类讨论,然后将各种情况的结果相加。
五、常见的排列组合问题类型1、排队问题例如,n 个人排成一排,共有多少种不同的排法;某些人必须相邻或不能相邻的排法等。