贝塞尔函数与三角函数
- 格式:pdf
- 大小:196.27 KB
- 文档页数:3


贝塞尔函数(Bessel functions)是数学上的一类的总称。
一样贝塞尔函数是以下(一样称为贝塞尔方程)的标准解函数y(x):这种方程的解是无法用系统地表示的。
贝塞尔函数的具体形式随上述方程中任意实数α转变而转变(相应地,α被称为其对应贝塞尔函数的阶数)。
实际应用中最多见的情形为α是n,对应解称为n阶贝塞尔函数。
尽管在上述微分方程中,α本身的正负号不改变方程的形式,但实际应用中仍适应针对α和−α概念两种不同的贝塞尔函数(如此做能带来益处,比如排除函数在α=0 点的不滑腻性)。
历史贝塞尔函数的几个正整数阶特例早在中叶就由在研究悬链振动时提出了,那时引发了数学界的爱好。
的叔叔,、等数学大师对贝塞尔函数的研究作出过重要奉献。
,数学家在研究提出的三体系统的运动问题时,第一次系统地提出了贝塞尔函数的整体理论框架,后人以他的名字来命名了这种函数。
现实背景和应用范围贝塞尔方程是在或下利用求解和时取得的(在圆柱域问题中取得的是整阶形式α = n;在球形域问题中取得的是半奇数阶形式α = n+½),因此贝塞尔函数在和各类涉及有势场的问题中占有超级重要的地位,最典型的问题有:在圆柱形中的传播问题;圆柱体中的问题;圆形(或环形)的分析问题;在其他一些领域,贝塞尔函数也相当有效。
譬如在中的()或()的概念中,都要用到贝塞尔函数。
概念贝塞尔方程是一个二阶常微分方程,必然存在两个的解。
针对各类具体情形,人们提出了表示这些解的不同形式。
下面别离介绍这些不同类型的贝塞尔函数。
第一类贝塞尔函数图2 0阶、1阶和2阶第一类贝塞尔函数(贝塞尔J函数)曲线(在下文中,第一类贝塞尔函数有时会简称为“J函数”,敬请读者留意。
)第一类α阶贝塞尔函数Jα(x)是贝塞尔方程当α为整数或α非负时的解,须知足在x= 0 时有限。
如此选取和处置Jα的缘故见本主题下面的;另一种概念方式是通过它在x = 0 点的展开(或更一样地通过展开,这适用于α为非整数):上式中Γ(z)为(它可视为函数向非整型的推行)。



傅里叶贝塞尔变换:一种神奇的数学工具
傅里叶贝塞尔变换,简称FBT,是一种深受科学家和工程师喜爱的数学工具。
它能够将函数从时域(time domain)转换到频域(frequency domain),也就是可以分析函数的不同频率组成成分,这在信号处理、图像处理等领域非常有用。
但这种变换不仅仅局限于此,还能够在偏微分方程和数值计算等领域得到应用。
FBT的概念最初由法国数学家傅里叶(Joseph Fourier)提出,用来解决热传导问题,后来被贝塞尔(Ernst Wilhelm von Bessel)拓展应用到椭圆偏微分方程中。
FBT中包含了三种不同的变换:傅里叶变换、傅里叶级数和贝塞尔函数。
傅里叶变换是FBT中最基本的变换之一,它将一个函数表示为各种正弦和余弦函数的组合。
这个变换在信号分析和图像处理中有广泛应用。
傅里叶级数则是另一种表达周期函数的方式,可以将一个周期函数分解成无数个正弦和余弦函数的和。
贝塞尔函数则是FBT中独有的一种函数类型,它的定义以及性质与传统的三角函数截然不同。
这种函数在应用中常常出现在椭圆偏微分方程的解析中,特别是在涉及到柱坐标系和球坐标系的问题中,非常常见。
FBT的应用非常广泛,特别是在信号和图像处理中。
例如,我们可以使用FBT来对语音信号进行压缩,或者对一张图片进行滤波处理等
等。
此外,在求解偏微分方程的过程中,FBT也是一种非常有效的数值计算方法。
总之,FBT是一种非常神奇的数学工具,它已经广泛地应用在各种不同的领域,成为现代科学和工程技术中不可或缺的一部分。
图1 贝塞尔函数的一个实例:一个紧绷的鼓面在中心受到敲击后的二阶振动振型,其振幅沿半径方向上的分布就是一个贝塞尔函数(考虑正负号)。
实际生活中受敲击的鼓面的振动是各阶类似振动形态的叠加。
贝塞尔函数维基百科,自由的百科全书贝塞尔函数(Bessel functions),是数学上的一类特殊函数的总称。
通常单说的贝塞尔函数指第一类贝塞尔函数(Bessel function of the first kind)。
一般贝塞尔函数是下列常微分方程(一般称为贝塞尔方程)的标准解函数:这类方程的解是无法用初等函数系统地表示。
由于贝塞尔微分方程是二阶常微分方程,需要由两个独立的函数来表示其标准解函数。
典型的是使用第一类贝塞尔函数和第二类贝塞尔函数来表示标准解函数:注意,由于 在 x=0 时候是发散的(无穷),当取 x=0 时,相关系数 必须为0时,才能获得有物理意义的结果。
贝塞尔函数的具体形式随上述方程中任意实数或复数α变化而变化(相应地,α被称为其对应贝塞尔函数的阶数)。
实际应用中最常见的情形为α是整数n,对应解称为n 阶贝塞尔函数。
尽管在上述微分方程中,α本身的正负号不改变方程的形式,但实际应用中仍习惯针对α和−α定义两种不同的贝塞尔函数(这样做能带来好处,比如消除了函数在α=0 点的不光滑性)。
贝塞尔函数也被称为柱谐函数、圆柱函数或圆柱谐波,因为他们是于拉普拉斯方程在圆柱坐标上的求解过程中被发现的。
目录1 历史2 现实背景和应用范围3 定义3.1 第一类贝塞尔函数3.1.1 贝塞尔积分3.1.2 和超几何级数的关系3.2 第二类贝塞尔函数(诺依曼函数)3.3 第三类贝塞尔函数(汉克尔函数)3.4 修正贝塞尔函数3.5 球贝塞尔函数3.6 黎卡提-贝塞尔函数4 渐近形式5 性质6 参考文献7 外部连接历史贝塞尔函数的几个正整数阶特例早在18世纪中叶就由瑞士数学家丹尼尔·伯努利在研究悬链振动时提出了,当时引起了数学界的兴趣。
贝塞尔函数(Bessel Function),是数学上的一类特殊函数的总称,是贝塞尔方程的解(无法用初等函数系统表示),它们和其他函数组合成柱调和函数。
除初等函数外,在物理和工程中贝塞尔函数是最常用的函数,它们以19世纪德国天文学家F.W.贝塞尔的姓氏命名,他在1824年第一次描述过它们。
一般贝塞尔函数是下列常微分方程(一般称为贝塞尔方程)的标准解函数 y\left( x \right):
{x^2}\frac{{{d^2}y}}{{d{x^2}}} + x\frac{{dy}}{{dx}} + \left( {{x^2} - {\alpha ^2}} \right)y = 0
或者 {x^2}y'' + xy' + \left( {{x^2} - {\alpha ^2}} \right)y = 0
作为一个二阶常微分方程,上述函数必然存在两个线性无关的解。
并且,贝塞尔函数是在柱坐标/球坐标下使用分离变量法求解拉普拉斯方程或者亥姆霍兹方程式得到,因此贝塞尔函数在波动问题以及各种涉及有势场的问题中占有重要问题。
贝塞尔函数的具体形式随着方程中实数参数 \alpha 变化,且 \alpha 被称为贝塞尔函数的阶数。
实际应用中常见 \alpha 为整数 n ,对应 n 阶贝塞尔函数。
虽然公式中 \alpha 的正负性不改变函数形式,实际应用中习惯针对 \alpha 和 -\alpha 定义两种不同的贝塞尔函数,有一些好处(比如消除函数在 \alpha=0 处的不光滑性),多 \alpha\ge 0。
第一 一类贝塞 塞尔函数 数
在柱坐标 标系中对 对拉普拉斯 斯方程 尔方 方程 0 对应于贝塞尔方 方程的通解 解为 ( (2) 或 (3) 上述第一 一种解的表达式只 只对 为整数阶 阶时, 种解 解的表达式 式对任意 意 把 1 均成立 立。
为非 非整数情况 况是成立的,因为 为当 ,两个解 解不是独立 立的解;第 第二 ( (1) 0进行 行分离变量 量法得到贝 贝塞
塞尔函数。
称为第一类贝塞
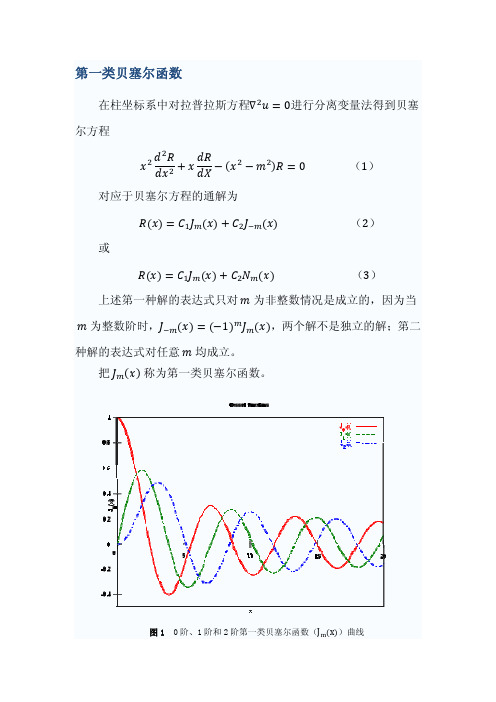
图1
0 阶、1 阶和 2 阶第一类贝 贝塞尔函数(J
线 x )曲线
第一类贝塞尔函数的级数表达式
1 ! 伽马函数 , 1 1; 2 1;当 n 为正整数时, 0 1 1 2 k 0 4
!
整数阶贝塞尔函数的母函数
把e 和e 分别展开为绝对收敛级数,然后逐项相乘而得到
e
1 x m n ! n! 2
1 1 n! |m| 1 1
z
x n ! 2 J|
| |
z
J
x z
|
x z
J 因此 e
x z
(5)
称为整数阶第一类贝塞尔函数的母函数。
这是丹麦
天文学家汉森于1843 年提出的。
雅可比-安格尔恒等式
在(4)式中,令 ,则 (6)
也可以变换为 (7) 雅可比-安格尔恒等式在物理(平面波与柱面波相互转换)和信 号处理(描述调频信号)中非常有用。
由于 为整数阶时, 2 利用欧拉公式 边的实部、虚部分别相等,得到 2 2 同理,可得 2 2 2 2 1 1 1 cos 2 cos 2 1 1 ,则式(7)变为 (8)
,等式(8)两
。