病毒传播模型ppt课件

常见的传染病模型简介传染病的基本数学模型错误!未找到引用源。

，是人们基于传染病特征，构建的一种数学模型，用于研究传染病的传播速度、空间范围、传播途径等问题，从而对传染病做出有效地预防和控制。

依据每个人的状态，一般可以将流行病范围内的总人口分为以下四类：(1)易感者(Susceptible)，记为S类人群，是指在一定时间内没有被传染的人，与携带病毒者接触后容易受到感染的人群；(2)暴露者(Exposed)，记为E类人群，是指接触过感染者，处在患病的潜伏阶段，对潜伏期长的传染病适用；(3)感染者(Infectious)，记为I类人群，是指已经感染上传染病的人，可以传播给易感者，并且将其变为康复者或者感染者的人群；(4)康复者(Recovered)，记为R类人群，是指感染病已经从感染者体中移除出去，还有被治愈后具有免疫力的人群，如果免疫期有限，康复者会重新变成易感者。

表1模型符号说明符号符号说明总人口感染率（潜伏者转化为感染者概率）平均潜伏期康复率平均治愈天数传染人数β传染率初始感染者初始潜伏者初始康复者每个病人接触人数每个病人接触人数初始人数恢复率潜伏者的传染概率潜伏者每天接触的易感者人数假设总人口数为，在疫情期间，虽然有政府的大力防控，但还是会有出门的情况，所以假设每个人出门接触的人是个，与每个接触者成功传播病毒的概率为，就会产生新的感染者，并疾病期间的人口出生率和人口死亡率暂不考虑。

SI模型SI模型是指传染病传染后不可治愈，易感者感染生病，例如艾滋病。

图示如下：图 1 SI仓室图将人群分为S类和I类，总人数等于S类人数与I类人数之和，那么新增感染病例与减少的健康易感人数可以建立以下方程：整理原方程化为伯努利方程形式：可以解出：SIS模型SIS模型是指传染病传染后，被治愈成功后，会恢复成易感者，依然具有被传染的可能性，例如流感病毒。

如下图：图 2 SIS仓室图建立以下微分方程：化简，得：可以解出：SIR及SIRS模型SIR模型是指急性传染病传染后，病人康复就会拥有抗体并获得永久免疫，例如天花、麻疹。

病毒传播模型的建模和分析随着新冠肺炎疫情的爆发，人们开始关注病毒传播模型的建模和分析。

病毒传播模型是通过建立数学模型来描述一种病毒从一个人传播到另一个人的过程。

这些模型可以用来预测未来的病例数和疫情的发展趋势，从而对公共卫生政策做出决策。

本文将深入讨论一些病毒传播模型的建模和分析方法，以及用于计算病毒传播的参数。

基本假设在研究病毒传播模型之前，我们需要了解一些基本的假设。

首先，我们假设感染者可以将病毒传给其他人，这些人也可以将病毒传给其他人。

其次，每个人只能被感染一次。

最后，我们假设传染过程是随机的，并且每个人在接触病毒后，可以在一段时间内携带病毒，但并不一定表现出症状。

接触率接触率是指某个人在一段时间内和其他人接触的频率。

接触率是病毒传播模型中的一个重要参数，它可以用来预测病例数和疫情的发展趋势。

接触率的计算方法包括调查问卷、传感器技术和社交网络分析。

社交网络分析方法是最常用的方法之一，它通过分析人们之间的联系、交流和兴趣来计算接触率。

物理模型物理模型是建模和分析病毒传播的另一种方法。

在这种方法中，我们将人们视为一个个质点，并将他们在三维空间中的运动建模。

人与人之间的距离越近，接触的可能性就越高。

我们还可以通过模拟一个建筑物或地区的运动，预测病毒在该建筑物或地区的传播情况。

传染模型传染模型是病毒传播模型的核心部分，它用一个数学方程描述病毒在人群中的传播情况。

最常用的传染模型包括SI模型（易感者-感染者模型）、SIR模型（易感者-感染者-康复者模型）和SEIR模型（易感者-潜伏者-感染者-康复者模型）。

这些模型可以帮助我们了解病毒传播的时间和规模，以及在不同的干预措施下，疫情的发展趋势。

分析模型分析模型是对传染模型进行分析的一种数学方法。

通常，我们使用微分方程来描述传染模型，然后使用数值方法或解析方法来解决该微分方程。

解方程可以帮助我们了解一些基本的病毒传染规律。

例如，我们可以使用微分方程来计算感染速度，即感染者每日新增的数量。

病毒传播数学模型我的病毒传播数学模型研究始于2010年，当时我还在攻读博士学位。

在我的研究中，我关注了病毒传播的动态过程，并尝试建立一个数学模型来描述这一过程。

我想明确一点，病毒传播数学模型并不是一个简单的方程或公式，而是一个包含多个参数和变量的复杂系统。

这些参数和变量可以分为两类：内在参数和外在参数。

内在参数主要描述病毒本身的特性，如病毒的基本再生数R0、病毒的生命周期、宿主的免疫反应等。

其中，R0是一个非常重要的参数，它表示在没有任何干预措施的情况下，一个感染者平均能够传染给多少个健康人。

外在参数则主要描述病毒传播的外部环境，如宿主的人口密度、人群流动性、社会干预措施等。

这些参数会对病毒传播的速度和规模产生重要影响。

在我的研究中，我建立了一个基于微分方程的病毒传播模型。

这个模型主要包括三个方程：感染者方程、康复者方程和易感者方程。

感染者方程描述了感染者的变化情况，康复者方程描述了康复者的变化情况，易感者方程描述了易感者的变化情况。

这三个方程共同构成了一个描述病毒传播动态过程的数学模型。

我还研究了社会干预措施对病毒传播的影响，如隔离措施、疫苗接种等。

我发现，这些措施可以通过降低R0值来有效控制病毒传播。

在我的研究中，我还考虑了病毒传播的时空特性。

为了描述病毒在不同地区和人群中的传播情况，我引入了空间扩散方程和时间演变方程。

通过这两个方程，我可以分析病毒传播的空间分布和时间动态。

我想强调的是，病毒传播数学模型虽然可以为我们提供一些有用的信息和启示，但它并不是万能的。

在实际应用中，我们需要结合具体情况，综合考虑各种因素，才能更好地应对病毒传播的挑战。

我的病毒传播数学模型研究旨在揭示病毒传播的内在规律和外在影响因素，为病毒防控提供科学依据。

在未来，我还将继续深入研究，探讨更准确、更高效的模型，以应对不断变化的病毒传播形势。

在我深入研究病毒传播数学模型的过程中，我逐渐意识到，要想准确地描述和预测病毒传播的动态过程，必须将复杂的生物学、流行病学和统计学知识融合到一个统一的数学框架中。

病毒模型病毒在当今社会已经成为一个备受关注的话题。

而研究病毒也正因为其在生物学、医学、计算机安全等领域的重要性而得到越来越多的关注。

本文将从多个角度介绍病毒模型的相关内容。

什么是病毒模型病毒模型是一种描述病毒传播和演化方式的理论模型。

通过病毒模型的构建和分析，可以更好地理解病毒的传播规律、疫情发展趋势以及病毒的传播途径等重要信息。

病毒模型有助于科学家们预测疫情的发展态势，为防控疾病提供指导。

病毒传播的数学模型病毒传播的数学模型是许多疫情预测和防控工作的基础。

病毒传播数学模型主要包括SIR模型、SEIR模型等。

SIR模型将人群划分为易感者(S)，感染者(I)和移除者(R)三类，描述了病毒在人群之间传播的过程。

SEIR模型在SIR模型的基础上增加了暴露者(E)类别，更加细致地描述了病毒的传播过程。

病毒模型与计算机病毒除了在流行病学领域中的应用，病毒模型在计算机安全领域中也有着重要的作用。

计算机病毒同样遵循着传播规律，从而可以通过病毒模型进行分析和预测。

病毒模型的研究有助于提高计算机安全领域对恶意软件的防范能力。

病毒模型的应用前景随着多学科交叉研究的深入，病毒模型在疫情预测、病毒进化研究、网络安全等领域的应用前景将更加广阔。

通过病毒模型的研究，可以更好地理解和预测病毒传播的规律，为防控疾病和加强网络安全提供有力支持。

结语病毒模型作为一个跨学科研究领域，对于理解病毒传播规律、病毒演化和防控措施的制定具有重要意义。

通过病毒模型的构建和分析，可以更好地把握病毒的传播规律，为疫情预防和控制提供科学依据。

随着科学研究的不断深入，相信病毒模型将在未来的研究中发挥越来越重要的作用。

以上是关于病毒模型的一些介绍，希望对读者有所帮助。

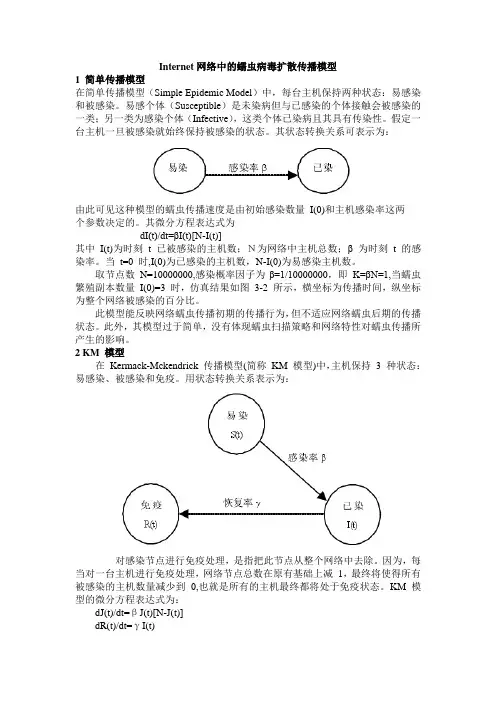
Internet网络中的蠕虫病毒扩散传播模型1 简单传播模型在简单传播模型（Simple Epidemic Model）中，每台主机保持两种状态：易感染和被感染。

易感个体（Susceptible）是未染病但与已感染的个体接触会被感染的一类；另一类为感染个体（Infective），这类个体已染病且其具有传染性。

假定一台主机一旦被感染就始终保持被感染的状态。

其状态转换关系可表示为：由此可见这种模型的蠕虫传播速度是由初始感染数量I(0)和主机感染率这两个参数决定的。

其微分方程表达式为dI(t)/dt=βI(t)[N-I(t)]其中I(t)为时刻t 已被感染的主机数；Ｎ为网络中主机总数；β 为时刻t 的感染率。

当t=0 时,I(0)为已感染的主机数，N-I(0)为易感染主机数。

取节点数N=10000000,感染概率因子为β=1/10000000，即K=βN=1,当蠕虫繁殖副本数量I(0)=3 时，仿真结果如图3-2 所示，横坐标为传播时间，纵坐标为整个网络被感染的百分比。

此模型能反映网络蠕虫传播初期的传播行为，但不适应网络蠕虫后期的传播状态。

此外，其模型过于简单，没有体现蠕虫扫描策略和网络特性对蠕虫传播所产生的影响。

2 KM 模型在Kermack-Mckendrick 传播模型(简称KM 模型)中，主机保持 3 种状态：易感染、被感染和免疫。

用状态转换关系表示为：对感染节点进行免疫处理，是指把此节点从整个网络中去除。

因为，每当对一台主机进行免疫处理，网络节点总数在原有基础上减1，最终将使得所有被感染的主机数量减少到0,也就是所有的主机最终都将处于免疫状态。

KM 模型的微分方程表达式为：dJ(t)/dt=βJ(t)[N-J(t)]dR(t)/dt=γI(t)J(t) = I(t)+R(t)=N-S(t)KM 模型将感染主机的免疫状态考虑进去，进一步接近了蠕虫传播的情况。

该模型仍然没有考虑易感染主机和感染主机被补丁升级或人为对抗蠕虫传播的情况另外，把感染率作为常量也是不恰当的。

新型冠状病毒传播的数学模型与预测一、本文概述本文旨在探讨新型冠状病毒（COVID-19）传播的数学模型及其预测应用。

通过对现有文献的综述和数据的分析，我们将构建一个全面的数学模型框架，用于理解病毒传播的动力学机制，并预测其在不同场景下的传播趋势。

我们将介绍不同类型的数学模型，包括基于个体行为的模型、基于网络的模型以及基于统计的模型，并阐述它们各自的优缺点和适用范围。

本文还将讨论如何利用这些模型进行疫情预测，包括疫情高峰期的预测、感染人数的预测以及疫情持续时间的预测等。

通过对这些预测结果的分析，我们可以为政府决策部门提供科学依据，以制定有效的防控措施，减缓疫情的传播速度，保护公众健康。

二、数学模型基础在理解和预测新型冠状病毒（COVID-19）传播的过程中，数学模型发挥了至关重要的作用。

这些模型为我们提供了一种量化理解和预测疾病传播动态的工具，有助于我们更好地制定防控策略和评估其效果。

在构建数学模型时，我们主要依赖于流行病学的基本原理，包括疾病的传播方式、感染者的传染期、易感人群的规模等因素。

我们还需要考虑社区干预措施，如社交距离、口罩佩戴、疫苗接种等，以及它们对疾病传播的影响。

常用的数学模型包括确定性模型、随机模型以及基于个体的模型。

确定性模型如SIR（易感者-感染者-康复者）模型及其扩展，通过一组微分方程来描述疾病的传播过程。

随机模型则考虑到了疾病传播过程中的随机性，如感染者与易感者接触的随机性。

基于个体的模型则更加复杂，它详细模拟了每个个体的行为、接触和感染过程，能够提供更详细的预测结果。

在构建模型时，我们需要对参数进行估计，如基本再生数（R0，即一个感染者在完全易感的人群中平均能感染的个体数）、感染者的传染期、易感人群的比例等。

这些参数的准确性直接影响到模型的预测结果。

我们还需要对模型进行验证和校准，以确保其预测结果与实际数据相符合。

这通常需要使用历史疫情数据来进行回测，通过调整模型参数以最小化预测误差。

用于传染病传播研究的数学模型SEIR（易感者、暴露者、感染者、康复者）模型公式的推导过程SEIR模型是一种常用于传染病传播研究的数学模型，它将人群划分为易感者（Susceptible）、暴露者（Exposed）、感染者（Infectious）和康复者（Recovered）。

下面是SEIR模型的推导过程：1.易感者（S）：人群中尚未感染病毒的个体。

假设总人口为N，那么易感者的数量为 S。

2.暴露者（E）：这些个体已经被感染了病毒，但尚未出现疾病症状。

暴露者的数量为 E。

3.感染者（I）：这些个体已经感染病毒，并且有能力传播疾病给其他人。

感染者的数量为 I。

4.康复者（R）：这些个体已经从疾病中康复，并获得了免疫力，不再感染病毒。

康复者的数量为 R。

SEIR模型的推导基于传染病传播的过程和假设：●易感者（S）会通过接触感染者（I）而被传染。

传染的速率取决于易感者与感染者的接触频率和传染性。

●暴露者（E）在感染后潜伏一段时间，这段时间称为潜伏期（latent period）。

潜伏期结束后，暴露者将进入感染者状态（I）。

●感染者（I）在一定的感染期（infectious period）内继续传播疾病。

●康复者（R）是从感染者（I）中康复的个体，他们获得了免疫力，不再感染病毒。

基于以上假设和条件，可以推导出SEIR模型的微分方程。

具体形式如下：dS/dt = -β * S * I / N dE/dt = β * S * I / N - α * E dI/dt = α * E - γ * I dR/dt = γ * I其中：●dS/dt 表示易感者数量随时间的变化率。

●dE/dt 表示暴露者数量随时间的变化率。

●dI/dt 表示感染者数量随时间的变化率。

●dR/dt 表示康复者数量随时间的变化率。

●β是感染率（infection rate），表示易感者与感染者的接触频率和传染性。

●α是暴露率（exposure rate），表示暴露者进入感染者状态的速率。

病毒传播问题的研究由来已久，而一再的病毒流行使得这一领域长期以来吸引着人们的注意。

在对病毒传播过程的描述各种模型中，“易感－感染－易感”（SIS ）模型是研究者经常的选择。

关于SIS 模型，可以简单的描述为：一个易感的个体在和一个具有传染性的个体的接触中，在单位时间以一定的概率（β）被感染，同时，已感染的个体以概率（γ）被治愈又重新成为健康（易感）的个体。

实际中大量的问题可以利用网络（图）进行描述，比如在传染病问题的描述中，个体（人、动物、计算机等）可以看作网络的节点，当个体之间有可以导致病毒传播的接触时在两个个体之间连边。

比如，对于接触性传染病，个体存在两种状态，健康的（易感的）和已感染的；将这些个体作为网络的节点，由于两个个体之间的亲密接触可能导致病毒的传播，因此可在两者之间进行连边。

一个个体所接触的其它个体数量称为该节点的度（边数）。

所谓二部网络（图），是网络中的节点可分成两类（比如男性和女性，雄性和雌性等），边仅仅存在于两类节点之间。

在经典的传染病学模型中，总是假定病毒赖以传播的网络具有匀质性，即网络中节点有基本相同的度，但一些研究表明，这一假设远远背离实际情况。

因此，发现实际网络的一些特性，并研究这样的网络上的病毒传播问题具有理论和实际意义。

本题我们主要研究二部网络上的病毒传播问题，根据附件提供的一个二部网络（由10000个A 类节点和10000个B 类节点构成）的节点度的数据，完成以下任务：1．根据“附件”提供的数据data.xls ，选择适当的坐标，作出节点连接度和其出现频率的图形，观察这种类型的连接度数据大致服从什么分布？2．生成上述网络，可以采用如下的机制：先生成一个小型的二部图，随后在A类中加入一个新节点并向B 类中的节点连边，该边指向B 类中i 号节点的概率正比于i 号节点当前的连接度，而后在B 类中产生新节点，以同样的方式向A 类连边，当这两个步骤进行足够多次之后即可得到满足数据文件特点的网络。

•计算机病毒概述•计算机病毒识别与检测•计算机病毒防范策略与措施•杀毒软件选择与应用技巧•系统漏洞修补与网络安全配置•数据备份恢复与应急处理方案•总结回顾与未来展望计算机病毒概述定义与分类定义计算机病毒是一种恶意软件，通过复制自身并在计算机网络中进行传播，从而破坏数据、干扰计算机操作或占用系统资源。

分类根据病毒的特性和传播方式，可分为蠕虫病毒、木马病毒、宏病毒、文件病毒、启动区病毒等。

发展历程及现状发展历程计算机病毒自诞生以来，经历了从简单到复杂、从单机到网络的发展历程。

随着互联网的普及和技术的进步，计算机病毒的传播速度和破坏力也在不断提升。

现状目前，计算机病毒已经成为网络安全领域的重要威胁之一。

随着黑客技术的不断发展和演变，计算机病毒的种类和传播方式也在不断增多，给个人和企业带来了严重的安全威胁。

危害程度与影响范围危害程度计算机病毒的危害程度因病毒类型和攻击目标而异。

一些病毒会破坏数据和文件，导致系统崩溃或数据丢失；另一些病毒则会占用系统资源，导致计算机运行缓慢或无法正常工作。

影响范围计算机病毒的影响范围非常广泛，可以影响个人计算机、企业网络甚至整个互联网。

一些病毒还会通过电子邮件、社交媒体等途径传播，进一步扩大了其影响范围。

计算机病毒识别与检测通过网络传播，占用大量网络资源，导致网络拥堵。

隐藏在正常程序中，窃取用户信息，如账号密码等。

加密用户文件，要求支付赎金才提供解密工具。

感染Office等文档，通过宏命令进行传播和破坏。

蠕虫病毒木马病毒勒索病毒宏病毒常见病毒类型及特点识别方法与技术手段行为分析监控程序运行时的行为，如异常的网络连接、文件操作等。

提供实时防护、病毒查杀、系统修复等功能。

360安全卫士集病毒查杀、系统优化、软件管理等功能于一体。

腾讯电脑管家专注于病毒查杀和防御，提供强大的自定义设置功能。

火绒安全软件定期更新病毒库，定期全盘扫描，注意设置实时防护和自动处理威胁。

使用指南检测工具推荐及使用指南计算机病毒防范策略与措施ABDC安装可靠的安全软件使用知名的防病毒软件，并及时更新病毒库和引擎，确保对最新威胁的防护。

传染病传播模型参数传染病的爆发对于人类社会造成了巨大的影响，因此了解和研究传染病的传播模型参数具有重要意义。

传染病的传播模型参数可以帮助我们预测疾病的传播趋势、制定有效的控制策略以及评估防控效果。

本文将介绍常见的传染病传播模型参数，包括基本再生数、传染潜伏期、传染期和接触频率等。

一、基本再生数基本再生数（Basic Reproduction Number，简称R0）是评估传染病传播能力的重要参数。

它表示在完全易感人群中，每个感染个体能够传播给多少个健康个体。

当R0大于1时，疾病将呈指数增长态势；当R0小于1时，疾病将逐渐消失。

传染病的基本再生数取决于多个因素，包括传染率、患病者的平均传染时间和人群的易感性。

对于不同传染病，其基本再生数的计算方法也有所不同。

例如，针对流感这类呼吸道传染病，可以使用以下公式计算其基本再生数：R0 = β * D其中，β表示病毒的传染率，D表示患者的平均传染时间。

在流感传播模型中，如果β为0.05，D为7天，那么该流感的基本再生数为0.35，即每个患者平均传染给0.35个健康个体。

二、传染潜伏期传染潜伏期（Incubation Period）指的是从感染病原体到出现症状的时间间隔。

传染潜伏期的长短与感染病原体的种类以及感染途径有关。

对于COVID-19这类冠状病毒感染病例，其传染潜伏期一般为2-14天，平均约为5天。

这意味着感染了冠状病毒的人可能在感染后的5天内没有明显的症状，但仍然具有传染性。

因此，在疫情防控期间，了解传染潜伏期对于及早发现病例、隔离感染者至关重要。

三、传染期传染期（Infectious Period）指的是感染者能够继续传播病原体的时间段。

不同传染病的传染期也有所不同，有些传染病只在症状出现期间具有传染性，而有些传染病则在感染潜伏期和出现症状期间都可以传播。

传染期的长短对于疾病的传播速度和范围有着重要的影响。

例如，麻疹病毒在感染者体内可持续繁殖4-6天，且在感染者出现症状之前的几天就开始传播。

病毒传播问题的研究由来已久，而一再的病毒流行使得这一领域长期以来吸引着人们的注意。

在对病毒传播过程的描述各种模型中，“易感－感染－易感”（SIS ）模型是研究者经常的选择。

关于SIS 模型，可以简单的描述为：一个易感的个体在和一个具有传染性的个体的接触中，在单位时间以一定的概率（β）被感染，同时，已感染的个体以概率（γ）被治愈又重新成为健康（易感）的个体。

实际中大量的问题可以利用网络（图）进行描述，比如在传染病问题的描述中，个体（人、动物、计算机等）可以看作网络的节点，当个体之间有可以导致病毒传播的接触时在两个个体之间连边。

比如，对于接触性传染病，个体存在两种状态，健康的（易感的）和已感染的；将这些个体作为网络的节点，由于两个个体之间的亲密接触可能导致病毒的传播，因此可在两者之间进行连边。

一个个体所接触的其它个体数量称为该节点的度（边数）。

所谓二部网络（图），是网络中的节点可分成两类（比如男性和女性，雄性和雌性等），边仅仅存在于两类节点之间。

在经典的传染病学模型中，总是假定病毒赖以传播的网络具有匀质性，即网络中节点有基本相同的度，但一些研究表明，这一假设远远背离实际情况。

因此，发现实际网络的一些特性，并研究这样的网络上的病毒传播问题具有理论和实际意义。

本题我们主要研究二部网络上的病毒传播问题，根据附件提供的一个二部网络（由10000个A 类节点和10000个B 类节点构成）的节点度的数据，完成以下任务：1．根据“附件”提供的数据data.xls ，选择适当的坐标，作出节点连接度和其出现频率的图形，观察这种类型的连接度数据大致服从什么分布？2．生成上述网络，可以采用如下的机制：先生成一个小型的二部图，随后在A类中加入一个新节点并向B 类中的节点连边，该边指向B 类中i 号节点的概率正比于i 号节点当前的连接度，而后在B 类中产生新节点，以同样的方式向A 类连边，当这两个步骤进行足够多次之后即可得到满足数据文件特点的网络。

For personal use only in study and research; not for commercial use传染病模型详解2.2.2 /,SI SIS SIR 经典模型经典的传播模型大致将人群分为传播态S ，易感染态I 和免疫态R 。

S 态表示该个体带有病毒或谣言的传播能力，一旦接触到易感染个体就会以一定概率导致对方成为传播态。

I 表示该个体没有接触过病毒或谣言，容易被传播态个体感染。

R 表示当经过一个或多个感染周期后，该个体永远不再被感染。

SI 模型考虑了最简单的情况，即一个个体被感染，就永远成为感染态，向周围邻居不断传 播病毒或谣言等。

假设个体接触感染的概率为β，总人数为 N ，在各状态均匀混合网络中建立传播模型如下：dS SI dt N I SId tN ββ⎧=-⎪⎪⎨⎪=⎪⎩ 从而得到(1)di i i dtβ=- 对此方程进行求解可得：0000(),01tti e i t i i i i e ββ==-+（） 可见，起初绝大部分的个体为I 态，任何一个S 态个体都会遇到I 态个体并且传染给对方，网络中的S 态个数随时间成指数增长。

与此同时，随着I 态个体的减少，网络中S 态个 数达到饱和，逐渐网络中个体全部成为S 态。

然而在现实世界中，个体不可能一直都处于传播态。

有些节点会因为传播的能力和意愿 的下降，从而自动转变为永不传播的R 态。

而有些节点可能会从S 态转变I 态，因此简单的SI 模型就不能满足节点具有自愈能力的现实需求，因而出现SIS 模型和SIR 模型。

SIR 是研究复杂网络谣言传播的经典的模型。

采用与病毒传播相似的过程中的S ，I ，R 态 代表传播过程中的三种状态。

Zanetee ，Moreno 先后研究了小世界传播过程中的谣言传播。

Moreno 等人将人群分为S （传播谣言）、I （没有听到谣言），R （对谣言不再相信也不传播）。

假设没有听到谣言I 个体与S 个体接触，以概率()k λ变为S 个体，S 个体遇到S 个体 或R 个体以概率()k α变为R ，如图 2.9 所示。