北京市高考物理一轮复习 第7讲 万有引力经典精讲2

第7讲实验:探究两个互成角度的力的合成规律实验装置实验原理一个力F'的作用效果和两个力F1、F2的作用效果都是让同一条一端固定的橡皮条伸长到①同一点,所以力F' 就是这两个力F1和F2的合力。

作出力F'的图示并根据平行四边形定如此作出力F1和F2的合力F的图示,比拟F和F'的大小和方向是否一样,假设一样,如此说明互成角度的两个力合成时遵循②平行四边形定如此。

1.(多项选择)在做“探究两个互成角度的力的合成规律〞实验时,橡皮条的一端固定在木板上,用两个弹簧测力计把橡皮条的另一端拉到某一确定的O点。

以下操作中不正确的答案是( )A.同一实验过程中,O点位置允许变动B.实验中,弹簧测力计必须与木板平行,读数时视线要正对弹簧测力计刻度C.实验中,先将其中一个弹簧测力计沿某一方向拉到最大测量值,然后只需调节另一弹簧测力计拉力的大小和方向,把橡皮条另一端拉到O点D.实验中,把橡皮条的另一端拉到O点时,两弹簧测力计之间的夹角应取90°,以便于算出合力的大小答案ACD 从橡皮条固定点到O点的连线,是合力的作用线方向,如果O点变动,那么合力的大小或方向就要变化,就不能验证力的平行四边形定如此,故A选项错;C选项中,因一个弹簧测力计已拉到最大测量值,再通过另一个弹簧测力计拉橡皮条到O点时,每一个弹簧测力计都可能超过最大测量值,造成损坏,或读数不准,故C选项错;互成角度的两个力的合成,是利用平行四边形定如此进展合成,两弹簧测力计之间的夹角不必一定成90°角,故D选项错。

2.在“探究两个互成角度的力的合成规律〞实验中,某同学用图钉把白纸固定在水平放置的木板上,将橡皮条的一端固定在板上一点,两个细绳套系在橡皮条的另一端。

用两个弹簧测力计分别拉住两个细绳套,互成角度地施加拉力,使橡皮条伸长,结点到达纸面上某一位置,如下列图。

请将以下的实验操作和处理补充完整:(1)用铅笔描下结点位置,记为O;(2)记录两个弹簧测力计的示数F1和F2,沿每条细绳(套)的方向用铅笔分别描出几个点,用刻度尺把相应的点连成线;(3)只用一个弹簧测力计,通过细绳套把橡皮条的结点仍拉到位置O,记录弹簧测力计的示数F3, ;(4)按照力的图示要求,作出拉力F1、F2、F3;(5)根据力的平行四边形定如此作出F1和F2的合力F;(6)比拟的一致程度,假设有较大差异,对其原因进展分析,并作出相应的改良后再次进展实验。

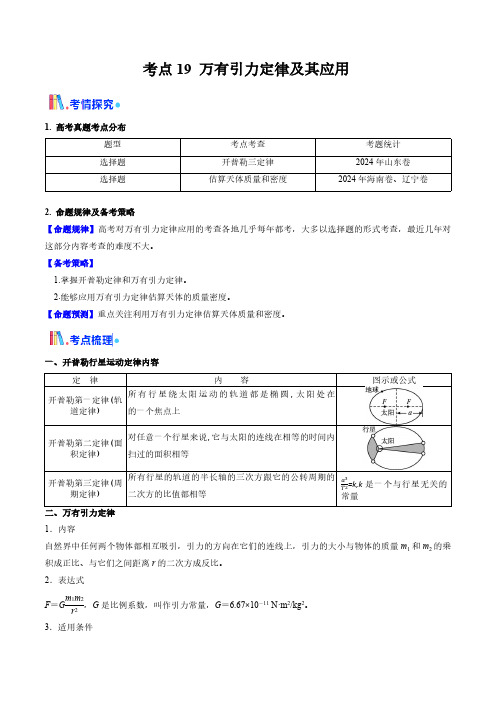
考点19 万有引力定律及其应用1. 高考真题考点分布题型考点考查考题统计选择题开普勒三定律2024年山东卷选择题估算天体质量和密度2024年海南卷、辽宁卷2. 命题规律及备考策略【命题规律】高考对万有引力定律应用的考查各地几乎每年都考，大多以选择题的形式考查，最近几年对这部分内容考查的难度不大。

【备考策略】1.掌握开普勒定律和万有引力定律。

2.能够应用万有引力定律估算天体的质量密度。

【命题预测】重点关注利用万有引力定律估算天体质量和密度。

一、开普勒行星运动定律内容图示或公式在　它与太阳的连线在相等的时间内所有行星的轨道的半长轴的三次方跟它的公转周期的1．内容自然界中任何两个物体都相互吸引，引力的方向在它们的连线上，引力的大小与物体的质量m 1和m 2的乘积成正比、与它们之间距离r 的二次方成反比。

2．表达式F ＝Gm 1m 2r 2，G 是比例系数，叫作引力常量，G ＝6.67×10－11 N·m 2/kg 2。

3．适用条件(1)公式适用于质点间的相互作用。

当两个物体间的距离远大于物体本身的大小时，物体可视为质点。

(2)质量分布均匀的球体可视为质点，r是两球心间的距离。

考点一开普勒行星运动定律特别提醒：1．行星绕太阳的运动通常按圆轨道处理。

2．由开普勒第二定律可得12v1·Δt·r1＝12v2·Δt·r2，解得v1v2＝r2r1，即行星在两个位置的速度之比与到太阳的距离成反比，近日点速度最大，远日点速度最小。

3．在开普勒第三定律a3T2＝k中，k值只与中心天体的质量有关，不同的中心天体k值不同。

但该定律只能用在同一中心天体的两星体之间。

1．2024年3月20日，我国“鹊桥二号”卫星发射成功，多次调整后进入周期为24h的环月椭圆轨道运行，并与在月球上开展探测任务的“嫦娥四号”进行通讯测试。

已知月球自转周期27.3天，下列说法正确的是（ ）A．月球处于“鹊桥二号”椭圆轨道的中心位置B．“鹊桥二号”在近月点和远月点的加速度大小相同C．“鹊桥二号”在远月点的运行速度小于月球第一宇宙速度D．“鹊桥二号”与月心连线和“嫦娥四号”与月心连线在相等时间内分别扫过的面积相等【答案】C【详解】A．由开普勒第一定律可知，月球处于“鹊桥二号”椭圆轨道的一个焦点上，A错误；B．“鹊桥二号”在近月点距离月球最近，受到的万有引力最大，加速度最大；在远月点距离月球最远，受到的万有引力最小，加速度最小，故“鹊桥二号”在近月点和远月点的加速度大小不相同，B错误；C．“鹊桥二号”在远月点的速度小于轨道与远月点相切的卫星的线速度，轨道与远月点相切的卫星的线速度小于第一宇宙速度，故“鹊桥二号”在远月点的运行速度小于月球第一宇宙速度，C正确；D．由开普勒第二定律可知，同一颗卫星与月球的连线在相同时间扫过的面积相等，但是“鹊桥二号”与“嫦娥四号”是两颗轨道不同的卫星，相同时间扫过的面积不相等，D错误。

高考辅导名师课程高考一轮复习班万有引力定律目录一、考纲要求 (2)二、学习目标 (3)（一）知识目标 (3)（二）能力目标 (3)三、知识导图 (5)四、重点知识梳理 (5)（一）开普勒定律 (5)（二）万有引力定律 (6)（三）万有引力定律在天体问题中的应用 (7)（四）本章公式整理 (10)五、知识应用例析 (11)（一）注意几个加速度 (11)（二）关于天体的质量和密度的计算 (15)（三）关于卫星的几个热点问题 (16)（四）天体运动与其它章节的综合考查 (26)六、训练测试 (28)万有引力定律.探究性题组训练 (28)万有引力定律.参考答案 (32)主讲名师张奕（高级教师）北京市5中一、考纲要求二、学习目标（一）知识目标1．知道开普勒定律；在开普勒第三定律的基础上，推导得到万有引力定律。

2．了解万有引力定律得出的思路和过程；理解万有引力定律的含义并会推导万有引力定律的公式。

3．了解行星绕恒星运动及卫星绕行星运动的共同点：万有引力提供行星、卫星做圆周运动的向心力。

4．了解万有引力定律在天文学上的重要应用，会用万有引力定律计算天体的质量。

5．知道人造地球卫星的原理，了解三个宇宙速度的意义。

（二）能力目标1．理解能力（1）理解万有引力定律的内容及使用条件；（2）理解万有引力和重力的关系；（3）理解同步卫星的特点，理解三种宇宙速度。

2．推理能力（1）掌握万有引力和重力的代换运算；（2）掌握地球（或天体）的卫星各物理量的关系；（3）会推导第一宇宙速度。

3．分析综合能力能分析解决各种以天体运动为背景的物理应用问题。

高考趋势与复习方法万有引力定律与天体问题是物理学的重要内容，它也是同学们理解掌握形成知识模型的难点，是高考年年必考的内容之一。

在历年高考中多以选择题、计算题形式出现。

突破学习难点，形成解决问题能力的关键就是要建立天体作匀速圆周运动的理想模型。

通过模型所遵循的规律去熟悉各个物理量之间的联系，进而又会加深对天体问题的理解，同时也就将繁多的公式做了归纳总结。

曲线运动万有引力与航天（二）主讲：梁建兴一. 教学内容：必修2第五章曲线运动万有引力与航天（二）二. 高考考纲及分析（一）高考考纲匀速圆周运动、角速度、线速度、向心加速度（I）匀速圆周运动的向心力（Ⅱ）离心现象（I）万有引力定律及其应用（Ⅱ）环绕速度（Ⅱ）第二宇宙速度和第三宇宙速度（I）（二）考纲分析1. 匀速圆周运动中只有向心力是（Ⅱ）级要求，其他均降为（I）级要求。

环绕速度从宇宙速度中分离出来提高为（Ⅱ）级要求。

从这些要求的变化来说总起来没有涉及核心内容和主干知识，命题的趋势不会有太大的改变。

2. 向心力是高考考查的重点知识，它主要是与受力分析，牛顿第二定律等知识一起以综合性题目的形式考查。

3. 运用万有引力定律及向心力公式分析人造卫星的绕行速度、运行周期以及计算天体的质量、密度等在近几年高考中每年必考。

现在随着我国载人航天的成功及探月计划的实施，对天体方面的考查将仍是考查的热点。

三. 知识网络四. 知识要点第三单元 圆周运动及其应用1. 圆周运动 线速度 角速度 向心加速度质点运动轨迹为一个圆，即质点做圆周运动。

线速度：物体在某时间内通过的弧长与所用时间的比值，其方向在圆周的切线方向上。

表达式：tl v = 角速度：物体在某段时间内通过的角度与所用时间的比值。

表达式：t θω=，其单位为弧度每秒，s rad /。

周期：匀速运动的物体运动一周所用的时间。

频率：Tf 1=，单位：赫兹（H Z ） 线速度、角速度、周期间的关系：ωπωπr v T T r v ===,/2,/.2。

2. 匀速圆周运动 向心力质点沿圆周运动，如果在相等的时间里通过的圆弧长度都相等，这种运动就叫做匀速圆周运动。

注意匀速圆周运动不是匀速运动，是曲线运动，速度方向不断变化。

做匀速圆周运动的物体，加速度方向指向圆心，这个加速度叫向心加速度。

大小：r T r r v a n 222.2⎪⎭⎫ ⎝⎛===πω方向：指向圆心。

高考物理一轮复习辅导万有引力知识点
任意两个质点有通过连心线方向上的力相互吸引。

以下
是万有引力知识点，请考生认真阅读。

1.开普勒第三定律：T2/R3=K(=42/GM){R:轨道半径，T:周期，K:常量(与行星质量无关，取决于中心天体的质量)｝
2.万有引力定律：F=Gm1m2/r2 (G=6.6710-11N??m2/kg2，方向在它们的连线上)
3.天体上的重力和重力加速度：GMm/R2=mg;g=GM/R2 {R:天体半径(m)，M：天体质量(kg)｝
4.卫星绕行速度、角速度、周期：
V=(GM/r)1/2;=(GM/r3)1/2;T=2(r3/GM)1/2{M：中心天体质量｝
5.第一(二、三)宇宙速度V1=(g地r地)1/2=(GM/r
地)1/2=7.9km/s;V2=11.2km/s;V3=16.7km/s
6.地球同步卫星GMm/(r地+h)2=m42(r地+h)/T2{h36000km，h:距地球表面的高度，r地:地球的半径｝
注:
(1)天体运动所需的向心力由万有引力提供,F向=F万;
(2)应用万有引力定律可估算天体的质量密度等;
(3)地球同步卫星只能运行于赤道上空，运行周期和地球自
转周期相同;
(4)卫星轨道半径变小时,势能变小、动能变大、速度变大、
周期变小(一同三反);
(5)地球卫星的最大环绕速度和最小发射速度均为7.9km/s。

平抛运动知识点的全部内容就是这些，更多知识点请考生持
续关注查字典物理网。

2019年高考第一轮复习备考专题已经新鲜出炉了，专题包含高考各科第一轮复习要点、复习方法、复习计划、复习试题，大家来一起看看吧~。

专题七万有引力定律万有引力定律及其应用(1)所有行星绕太阳运行的轨道都是椭圆。

()(2)行星在椭圆轨道上运行速率是变化的，离太阳越远，运行速率越大。

()(3)只有天体之间才存在万有引力。

()(4)只要知道两个物体的质量和两个物体之间的距离，就可以由F＝G m1m2r2计算物体间的万有引力。

()(5)地面上的物体所受地球的引力方向一定指向地心。

()(6)两物体间的距离趋近于零时，万有引力趋近于无穷大。

()(1)德国天文学家开普勒提出天体运动的开普勒三大定律。

(2)牛顿总结了前人的科研成果，在此基础上，经过研究得出了万有引力定律。

(3)英国物理学家卡文迪许利用扭秤实验装置比较准确地测出了引力常量。

要点一开普勒行星运动定律1．行星绕太阳的运动通常按圆轨道处理。

2．开普勒行星运动定律也适用于其他天体，例如月球、卫星绕地球的运动。

3．开普勒第三定律a3T2＝k中，k值只与中心天体的质量有关，不同的中心天体k值不同。

[多角练通]1．(2013·江苏高考)火星和木星沿各自的椭圆轨道绕太阳运行，根据开普勒行星运动定律可知( ) A ．太阳位于木星运行轨道的中心B ．火星和木星绕太阳运行速度的大小始终相等C ．火星与木星公转周期之比的平方等于它们轨道半长轴之比的立方D ．相同时间内，火星与太阳连线扫过的面积等于木星与太阳连线扫过的面积2．(2011·全国卷)卫星电话信号需要通过地球同步卫星传送。

如果你与同学在地面上用卫星电话通话，则从你发出信号至对方接收到信号所需最短时间最接近于(可能用到的数据：月球绕地球运动的轨道半径约为3.8×105 km ，运行周期约为27天，地球半径约为6 400 km ，无线电信号的传播速度为3×108 m/s)( )A ．0.1 sB ．0.25 sC .0.5 sD ．1 s3.(多选)2009年5月，航天飞机在完成对哈勃空间望远镜的维修任务后，在A 点从圆形轨道Ⅰ进入椭圆轨道Ⅱ，B 为轨道Ⅱ上的一点，如图所示。

第7讲万有引力（一）一、2021年6月16日18时37分，执行我国第一次载人交会对接任务的“神舟九号”载人飞船发射升空，在距地面343千米的近圆轨道上，与等待已久的“天宫一号”实现多次交会对接、分离，于6月29日10时许成功返回地面，以下关于“神舟九号”与“天宫一号”的说法正确的选项是( )A．假设明白“天宫一号”的绕行周期，再利用引力常量，就可算出地球的质量B．在对接前，“神舟九号”轨道应稍低于“天宫一号”的轨道，然后让“神舟九号”加速追上“天宫一号”并与之对接C．在对接前，应让“神舟九号”和“天宫一号”在同一轨道上绕地球做圆周运动，然后让“神舟九号”加速追上“天宫一号”并与之对接D．“神舟九号”返回地面时应在绕行轨道上先减速二、我国“嫦娥一号”探月卫星发射后，先在“24小时轨道”上绕地球运行(即绕地球一圈需要24小时)；然后，通过两次变轨依次抵达“48小时轨道”和“72小时轨道”；最后奔向月球。

若是按圆形轨道计算，并忽略卫星质量的转变，那么在每次变轨完成后与变轨前相较( )A．卫星动能增大，引力势能减小B．卫星动能增大，引力势能增大C．卫星动能减小，引力势能减小D．卫星动能减小，引力势能增3、航天飞机在完成对哈勃空间望远镜的维修任务后，在A点从圆形轨道Ⅰ进入椭圆轨道Ⅱ，B为轨道Ⅱ上的一点，如下图。

关于航天飞机的运动，以下说法中错误的有( )A．在轨道Ⅱ上通过A的速度小于通过B的速度B．在轨道Ⅱ上通过A的动能小于在轨道Ⅰ上通过A的动能C．在轨道Ⅱ上运动的周期小于在轨道Ⅰ上运动的周期D．在轨道Ⅱ上通过A的加速度小于在轨道Ⅰ上通过A的加速度4、如下图，是某次发射人造卫星的示用意，人造卫星先在近地圆周轨道1上运动，然后改在椭圆轨道2上运动，最后在圆周轨道3上运动，a 点是轨道一、2的交点，b 点是轨道二、3的交点，人造卫星在轨道1上的速度为v 1，在轨道2上a 点的速度为v 2a ，在轨道2上b 点的速度为v 2b ，在轨道3上的速度为v 3，那么各速度的大小关系是( ) A ．v 1>v 2a >v 2b >v 3B ．v 1<v 2a <v 2b <v 3C ．v 2a >v 1>v 3>v 2bD ．v 2a >v 1>v 2b >v 3五、假设地球是一半径为R 、质量散布均匀的球体。

第7讲 万有引力（一）一、变轨问题：题一：俄罗斯“和平”号空间站于2001年3月23日坠入新西兰和智利之间的南太平洋。

空间站在进入浓密大气层烧毁前，处于自由运动状态，因受高空稀薄空气阻力的阻碍，在绕地球运动的同时，将很缓慢地向地球靠近，在那个进程中（ ）A ．空间站的角速度慢慢减小B ．空间站的加速度慢慢减小C ．空间站的势能慢慢转变成动能和内能D ．空间站的动能慢慢转变成内能题二：如下图是地球同步卫星发射进程的运行轨道示用意，图中实心黑圈代表地球。

发射卫星时第一用火箭将卫星送入近地轨道1(可视为圆轨道)，当通过轨道的A 点时点燃喷气发动机改变卫星的速度，进入椭圆形轨道2，当卫星通过轨道2远端的B 点时再次点燃喷气发动机改变卫星的速度，进入同步轨道3，即可开始正常工作。

不计卫星喷气进程中质量的转变，以下说法正确的选项是（ ）①卫星在轨道1运动时的线速度比在轨道3运动时的线速度大②卫星在轨道1运动时的机械能比在轨道3运动时的机械能小③卫星在轨道1上运动通过A 点时，需使卫星减速才能进入轨道2运动④卫星在轨道2上运动通过B 点时受到的地球引力，比在轨道3上通过B 点时受到的地球引力小A ．只有①② B．只有①②③ C ．只有①④ D．都不正确二、密度估算引出的两个重要推论题三：（黄金代换版）地球表面重力加速度为g ，地球半径为R ，引力常量为G ，下式关于地球密度的估算式正确的选项是（ ）A ．RG g πρ43=B ．G R g 243πρ=C ．RG g =ρD ．2GR g =ρ题四：（周期版）一飞船在某行星表面周围沿圆轨道绕该行星飞行，以为行星是密度均匀的球体，要确信该行星的密度，只需要测量（ ）A ．飞船的轨道半径B ．飞船的运行速度C ．飞船的运行周期D ．行星的质量三、与力学的结合题五：宇航员站在一星球表面上的某高处，沿水平方向抛出一个小球，通过时刻t ，小球落到星球表面，测得抛出点与落地址之间的距离为L ，假设抛出时的初速度增大到2L ，已知两落地址在同一水平面上，该星球的半径为R ，万有引力常数为G ，求该星球的质量。