❖ 线性规划模型?
LP模型: 设:配制生产甲饮料x1升,乙饮料x2升.
min Z 2x1 3x2源自x1 x2 350s.t.
2x1 x2
x1
125
600
x1 0, x2 0
例5 投资问题
某集团有1000000元资金供投资,该集团有5个可供选择 的投资项目,其中各种资料如下表:
投资项目 1 2 3 4 5
xb=(x1,x2,…,xm) 加上所有取值为0 的非基变量,得:
x=(x1,x2,…,xm,0,…,0)
称x 为线性规划问题的基解。
令x1=x2=0,解得x3=4,x4=12,x5=18,则x=(0,0,4,12,18)T是一个基解。
A
103
0 2 2
1 0 0
0 1 0
100
P3 ,
P4 , P5
[LP模型]:
min Z 0.1x1 0.06x2 0.18x3 0.12x4 0.04x5
x1 x2 x3 x4 x5 1000000
s.t.00..10x51x1 0.01.708x2x20.01.407x3x3 0.02.206x4x40.00.71xx55
80000 140000
基:设Am×n (n>m)为约束方程组(b)的系数矩阵,其秩为m。 Bm×m 是矩阵A 中的一个m×m 阶的满秩子矩阵(|B|不等于0), , 称B 是线性规划问题的一个基。不失一般性,设
B
a 11 a 21 a m1
a 12 a 22
a m2
a 1m a 2m
a mm
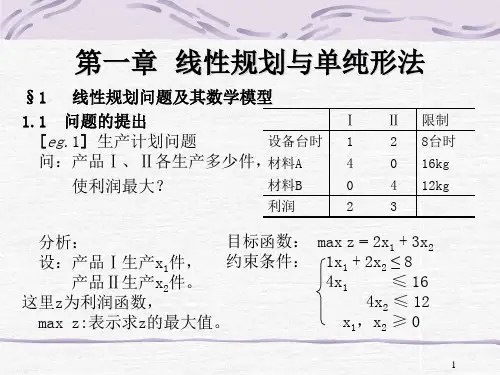
第1章 线性规划
❖ 本章要求: 1.掌握并熟练应用线性规划的模型处理实际问
题 2.掌握线性规划的图解法 3.掌握软件求解线性规划 4.了解线性规划对偶问题的基本性质 5.理解有关灵敏度分析内容