山东省各地市2012年高考数学(理科)最新试题分类大汇编：7：三角函数(1).pdf

2012年山东省高考数学试题（附答案和解释）（理科Word版）2012年普通高等学校招生全国统一考试（山东卷）理科数学本试卷分第I卷和第II卷两部分，共4页。

满分150分。

考试用时120分钟，考试结束，务必将试卷和答题卡一并上交。

注意事项： 1.答题前，考生务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号、县区和科类填写在答题卡上和试卷规定的位置上。

2.第I 卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试卷上。

3.第II卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带。

不按以上要求作答的答案无效。

4.填空题请直接填写答案，解答题应写出文字说明、证明过程或演算步骤。

参考公式：锥体的体积公式：V= Sh，其中S是锥体的底面积，h是锥体的高。

如果事件A，B互斥，那么P（A+B）=P（A）+P(B)；如果事件A,B独立，那么P（AB）=P（A）•P（B）。

第I卷（共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1 若复数x满足z(2-i)=11+7i(i为虚数单位)，则z为 A 3+5i B 3-5i C -3+5i D -3-5i 解析： .答案选A。

另解：设，则根据复数相等可知，解得，于是。

2 已知全集 ={0,1,2,3,4}，集合A={1,2,3,}，B={2,4} ，则（CuA） B为 A {1,2,4} B {2,3,4} C {0,2,4} D {0,2,3,4} 解析：。

答案选C。

3 设a＞0 a≠1 ，则“函数f(x)= ax在R上是减函数”，是“函数g(x)=(2-a) 在R上是增函数”的 A 充分不必要条件 B 必要不充分条件 C 充分必要条件 D 既不充分也不必要条件解析：p：“函数f(x)= ax在R上是减函数”等价于；q：“函数g(x)=(2-a) 在R 上是增函数”等价于，即且a≠1，故p是q成立的充分不必要条件. 答案选A。

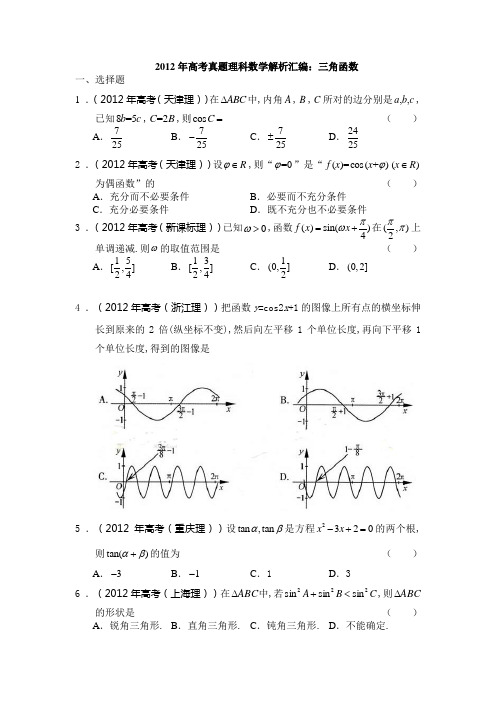
2012年高考真题理科数学解析汇编：三角函数一、选择题1 ．（2012年高考（天津理））在A B C ∆中,内角A ,B ,C 所对的边分别是,,a b c ,已知8=5b c ,=2C B ,则cos C = （ ）A ．725B ．725-C ．725±D ．24252 ．（2012年高考（天津理））设R ϕ∈,则“=0ϕ”是“()=cos (+)f x x ϕ()x R ∈为偶函数”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件3 ．（2012年高考（新课标理））已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减.则ω的取值范围是 （ ）A ．15[,]24B ．13[,]24C ．1(0,]2D ．(0,2]4 ．（2012年高考（浙江理））把函数y =cos2x +1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图像是5 ．（2012年高考（重庆理））设tan ,tan αβ是方程2320x x -+=的两个根,则tan()αβ+的值为（ ）A ．3-B ．1-C ．1D ．36 ．（2012年高考（上海理））在ABC ∆中,若C B A 222sin sin sin <+,则ABC ∆的形状是 （ ）A ．锐角三角形.B ．直角三角形.C ．钝角三角形.D ．不能确定.7 ．（2012年高考（陕西理））在A B C ∆中,角,,A B C 所对边长分别为,,a b c ,若2222a b c+=,则cos C 的最小值为（ ）A ．2B ．2C ．12D ．12-8 ．（2012年高考（山东理））若42ππθ⎡⎤∈⎢⎥⎣⎦，,sin 2=8θ,则sin θ= （ ）A ．35B ．45C ．4D ．349 ．（2012年高考（辽宁理））已知sin cos αα-=,α∈(0,π),则tan α=（ ）A ．-1B ．2-C ．2D ．110．（2012年高考（江西理））若tan θ+1tan θ =4,则sin2θ=（ ） A ．15B ．14C ．13D ．1211．（2012年高考（湖南理））函数f(x)=sinx-cos(x+6π)的值域为 （ ）A ．[ -2 ,2]B ．[-]C ．[-1,1 ]D ．[-2 ,2]12．（2012年高考（大纲理））已知α为第二象限角,sin cos 3αα+=,则cos 2α=（ ）A ．3-B ．9-C ．9D ．313.（2012年高考（陕西理））函数()sin()16f x A x πω=-+(0,0A ω>>)的最大值为3, 其图像相邻两条对称轴之间的距离为2π,(1)求函数()f x 的解析式;(2)设(0,)2πα∈,则()22f α=,求α的值.14．（2012年高考（山东理））已知向量(sin ,1),cos ,cos 2)(0)3Am x n x x A ==> ,函数()f x m n =⋅的最大值为6.(Ⅰ)求A ;(Ⅱ)将函数()y f x =的图象向左平移12π个单位,再将所得图象上各点的横坐标缩短为原来的12倍,纵坐标不变,得到函数()y g x =的图象.求()g x 在5[0,]24π上的值域.15.（2012年高考（广东理））(三角函数)已知函数()2cos 6f x x πω⎛⎫=+⎪⎝⎭(其中0ω>x ∈R)的最小正周期为10π.(Ⅰ)求ω的值; (Ⅱ)设α、0,2πβ⎡⎤∈⎢⎥⎣⎦,56535f απ⎛⎫+=-⎪⎝⎭,5165617f βπ⎛⎫-=⎪⎝⎭,求()cos αβ+的值.16.（2012年高考（浙江理））在∆ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A =23,sin B =C .(Ⅰ)求tan C 的值; (Ⅱ)若a =求∆ABC 的面积.17.（2012年高考（辽宁理））在A B C ∆中,角A 、B 、C 的对边分别为a ,b ,c .角A ,B ,C 成等差数列. (Ⅰ)求cos B 的值;(Ⅱ)边a ,b ,c 成等比数列,求sin sin A C 的值.18．（2012年高考（江苏））在ABC ∆中,已知3AB ACBA BC=.(1)求证:tan 3tan B A=;(2)若cos 5C =求A 的值.19．（2012年高考（湖北理））已知向量(cos sin ,sin )x x x ωωω=-a ,(cos sin ,)x x x ωωω=--b ,设函数()f x λ=⋅+a b ()x ∈R 的图象关于直线πx =对称,其中ω,λ为常数,且1(,1)2ω∈.(Ⅰ)求函数()f x 的最小正周期;(Ⅱ)若()y f x =的图象经过点π(,0)4,求函数()f x 在区间3π[0,]5上的取值范围.20.（2012年高考（江西理））在△ABC 中,角A,B,C 的对边分别为a,b,c.已知,,sin()sin()444A b C cB aπππ=+-+=.(1)求证:2B C π-=(2)若求△ABC 的面积.13.解析:(1)∵函数()f x 的最大值为3,∴13,A +=即2A =∵函数图像的相邻两条对称轴之间的距离为2π,∴最小正周期为T π= ∴2ω=,故函数()f x 的解析式为sin(2)16y x π=-+(2)∵()2sin()1226f απα=-+=即1sin()62πα-=∵02πα<<,∴663πππα-<-<∴66ππα-=,故3πα=14:(Ⅰ)⎪⎭⎫ ⎝⎛+=+=+=⋅=62sin 2cos 22sin 232cos 2sin cos 3)(πx A x Ax A x A x x A n m x f , 则6=A ;(Ⅱ)函数y=f(x)的图象像左平移12π个单位得到函数]6)12(2sin[6ππ++=x y 的图象,再将所得图象各点的横坐标缩短为原来的12倍,纵坐标不变,得到函数)34sin(6)(π+=x x g .当]245,0[π∈x 时,]1,21[)34sin(],67,3[34-∈+∈+ππππx x ,]6,3[)(-∈x g .故函数()g x 在5[0,]24π上的值域为]6,3[-.16 (Ⅰ) ∵cos A =23>0,∴sin A 3=,C =sin B =sin(A +C )=sin A cos C +sin C cos A3cos C +23sin C .整理得:tan C(Ⅱ)由图辅助三角形知:sin C .又由正弦定理知:sin sin a c AC=,故c =对角A 运用余弦定理:cos A =222223b c abc+-=. (2)解(1) (2)得:b =or b 3舍去).∴∆ABC 的面积为:S 2.17. (1)由已知12=+,++=,=,cos =32B A C A B C B B ππ∴ (2)解法一:2=b ac ,由正弦定理得23sin sin =sin =4A C B20. 解:(1)证明:由 sin()sin()44b Cc B a ππ+-+=及正弦定理得:sin sin()sin sin()sin 44B C C B A ππ+-+=,即sin )sin ()22222B C C C B B +-+=整理得:sin cos cos sin 1B C B C -=,所以sin()1B C -=,又30,4B C π<<所以2B C π-=(2) 由(1)及34B C π+=可得5,88B C ππ==,又,4A a π==所以sin 5sin 2sin,2sin sin 8sin 8a B a Cbc AAππ====, 所以三角形ABC的面积1521sn 2sinsi n288882b c Aππππ=====18. 解:(1)∵3AB AC BA BC= ,∴cos =3cos AB AC A BA BC B,即cos =3cos AC A BC B .由正弦定理,得=sin sin AC BC BA,∴sin cos =3sin cos B A A B .又∵0<A B <π+,∴cos 0 cos 0A >B >，.∴sin sin =3cos cos BA B A即tan 3tan B A =.(2)∵ cos 05C <C <π=,∴sin 5C =.∴tan 2C =.∴()tan 2A B π⎡-+⎤=⎣⎦,即()tan 2A B +=-.∴tan tan 21tan tan A BA B+=-- . 由 (1) ,得24tan 213tan A A=--,解得1tan =1 tan =3A A -，.∵cos 0A >,∴tan =1A .∴=4A π.19. 解析:(Ⅰ)因为22()sin cos cos f x x x x x ωωωωλ=-+⋅+cos 22x x ωωλ=-++π2sin(2)6x ωλ=-+.由直线πx =是()y f x =图象的一条对称轴,可得πsin(2π)16ω-=±, 所以ππ2ππ()62k k ω-=+∈Z ,即1()23k k ω=+∈Z .又1(,1)2ω∈,k ∈Z ,所以1k =,故56ω=.所以()f x 的最小正周期是6π5.(Ⅱ)由()y f x =的图象过点π(,0)4,得π()04f =,即5πππ2sin()2sin6264λ=-⨯-=-=即λ=故5π()2sin()36f x x =--由3π05x ≤≤,有π5π5π6366x -≤-≤,所以15πsin()1236x -≤-≤,得5π12sin()236x --≤---故函数()f x 在3π[0,]5上的取值范围为[12---.15. 1.解析:(Ⅰ)210T ππω==,所以15ω=.(Ⅱ)515652cos 52cos 2sin 353625f ππαπαπαα⎡⎤⎛⎫⎛⎫⎛⎫+=++=+=-=-⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,所以3s i n 5α=.5151652cos 52cos 656617f πβπβπβ⎡⎤⎛⎫⎛⎫-=-+== ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,所以8c o s 17β=.因为α、0,2πβ⎡⎤∈⎢⎥⎣⎦,所以4c o s 5α==,15sin 17β==,所以()4831513c o s c o sc o ss i n s i n51751785αβαβαβ+=-=⨯-⨯=-.。

三角函数（一）选择题1、（07山东理5）函数sin 2cos 263y x x ππ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭的最小正周期和最大值分别为（ ）A ．π，1B ．πC ．2π，1D ．2π答案：A2、（07山东文4）要得到函数sin y x =的图象，只需将函数cos y x π⎛⎫=-⎪3⎝⎭的图象（ ）A ．向右平移π6个单位B ．向右平移π3个单位C ．向左平移π3个单位D ．向左平移π6个单位答案：A3.（08山东卷5）已知cos （α-6π）+sin α7sin()6πα+则的值是（A ）-532 （B ）532 (C)-54 (D) 54答案：C4.(2009山东卷理)将函数sin 2y x =的图象向左平移4π个单位, 再向上平移1个单位,所得图象的函数解析式是( ). A.cos 2y x = B.22cosy x = C.)42si n(1π++=x y D.22sin y x =【解析】:将函数s i n 2y x =的图象向左平移4π个单位,得到函数s i n 2()4y xπ=+即sin(2)cos 22y x x π=+=的图象,再向上平移1个单位,所得图象的函数解析式为21cos 22cos y x x =+=,故选B.答案:B【命题立意】:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形.5.(2009山东卷文)将函数sin 2y x =的图象向左平移4π个单位, 再向上平移1个单位,所得图象的函数解析式是( ).A. 22cos y x =B. 22sin y x = C.)42si n(1π++=x y D. cos 2y x =【解析】:将函数s i n 2y x =的图象向左平移4π个单位,得到函数s i n 2()4y x π=+即sin(2)cos 22y x x π=+=的图象,再向上平移1个单位,所得图象的函数解析式为21cos 22cos y x x =+=,故选A.答案:A【命题立意】:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形.6、（2010山东文数）（10）观察2'()2x x =，4'3()4x x =，'(cos )sin x x =-，由归纳推理可得：若定义在R 上的函数()f x 满足()()f x f x -=，记()g x 为()f x 的导函数，则()g x -= （A ）()f x (B)()f x - (C) ()g x (D)()g x - 答案：D7、（2011山东3）若点（a,9）在函数3x y =的图象上，则tan6a π的值为A ．0B ．3C ．1D 答案：D8、（2011山东理数6）若函数()sin f x x ω= (ω>0)在区间0,3π⎡⎤⎢⎥⎣⎦上单调递增，在区间,32ππ⎡⎤⎢⎥⎣⎦上单调递减，则ω= A ．3 B ．2 C ．32D ．23答案：C9、（2011山东文数6）若函数()sin f x x ω= （ω>0）在区间0,3π⎡⎤⎢⎥⎣⎦上单调递增，在区间,32ππ⎡⎤⎢⎥⎣⎦上单调递减，则ω= A ．23B ．32C ．2D ．3答案：B10、(2012山东卷文(5))设命题p ：函数sin 2y x =的最小正周期为2π；命题q ：函数cos y x=的图象关于直线2x π=对称.则下列判断正确的是(A)p 为真 (B)q ⌝为假 (C)p q ∧为假 (D)p q ∨为真 答案：C11、(2012山东卷文(8))函数2sin (09)63x y x ππ⎛⎫=-≤≤⎪⎝⎭的最大值与最小值之和为A(A)2- (B)0 (C)－1(D)1--答案：A（二）填空题1.（08山东卷15）已知a ，b ，c 为△ABC 的三个内角A ，B ，C 的对边，向量m ＝（1,3-），n ＝（cos A ,sin A ）.若m ⊥n ，且a cos B +b cos A =c sin C ，则角B ＝答案：6π.2、（2010山东数）2、已知a ，b ，c 为△ABC 的三个内角A ，B ，C 的对边，b=2sin +cos =B B A 若，则（三）解答题1、（07山东理20）如图，甲船以每小时匀速直线航行，当甲船位于1A 处时，乙船位于甲船的北偏西105方向的1B 处，此时两船相距20海里，当甲船航行20分钟到达2A 处时，乙船航行到甲船的北偏西120方向的2B 处，此时两船相距 解法一：如图，连结11A B，由已知22A B =122060A A ==1221A A A B ∴=，又12218012060A A B =-=∠，122A A B ∴△是等边三角形，1A2A1212A B A A ∴==，由已知，1120A B =，1121056045B A B =-=∠，在121A B B △中，由余弦定理，22212111212122cos 45B B A B A B A B A B =+-22202202=+-⨯⨯200=．12B B ∴=6020=/小时）．答：乙船每小时航行海里．解法二：如图，连结21A B ，由已知1220A B =，122060A A ==，112105B A A =∠，cos105cos(4560)=+cos 45cos 60sin 45sin 60=-4=，sin 105sin(4560)=+sin 45cos 60cos 45sin 60=+4=．在211A A B △中，由余弦定理，22221221211122cos105A B A B A A A B A A =+-1A2A乙22202204-=+-⨯⨯100(4=+．1110(1A B∴=+．由正弦定理1112111222sin sin42A BA AB B A AA B+===∠∠，12145A A B∴=∠，即121604515B A B=-=∠，cos15sin1054+==．在112B A B△中，由已知12A B=，由余弦定理，22212112221222cos15B B A B A B A B A B=++22210(1210(14+=++-⨯+⨯200=．12B B∴=乙船的速度的大小为6020=/小时．答：乙船每小时航行海里．2、（07山东文17）在A B C△中，角A B C，，的对边分别为tana b c C=，，，．（1）求cos C；（2）若52C B C A=，且9a b+=，求c．解：（1）sintancosCCC=∴=又22sin cos1C C+=解得1cos8C=±．tan0C>，C∴是锐角．1cos 8C ∴=．（2）52C B C A =， 5cos 2ab C ∴=，20ab ∴=．又9a b +=22281a ab b ∴++=． 2241a b ∴+=．2222cos 36c a b ab C ∴=+-=．6c ∴=．3.（08山东卷17）（本小题满分12分）已知函数f (x )＝)0,0)(cos()sin(3><<+-+ωϕϕωϕωπx x 为偶函数，且函数y ＝f (x )图象的两相邻对称轴间的距离为.2π（Ⅰ）美洲f （8π）的值；（Ⅱ）将函数y ＝f (x )的图象向右平移6π个单位后，再将得到的图象上各点的横坐标舒畅长到原来的4倍，纵坐标不变，得到函数y ＝g (x )的图象，求g (x )的单调递减区间. 解：（Ⅰ）f (x )＝)cos()sin(3ϕωϕω+-+x x＝⎥⎦⎤⎢⎣⎡+-+)cos(21)sin(232ϕωϕωx x ＝2sin(ϕω+x -6π)因为 f (x )为偶函数，所以 对x ∈R ,f (-x )=f (x )恒成立， 因此 sin （-ϕω+x -6π）＝sin(ϕω+x -6π).即-sin x ωcos(ϕ-6π)+cos x ωsin(ϕ-6π)=sin x ωcos(ϕ-6π)+cos x ωsin(ϕ-6π),整理得 sin x ωcos(ϕ-6π)=0.因为 ω＞0，且x ∈R ,所以 cos （ϕ-6π）＝0.又因为 0＜ϕ＜π，故 ϕ-6π＝2π.所以 f (x )＝2sin(x ω+2π)=2cos x ω.由题意得 .2,222　＝ 所以 ωπωπ⋅=故 f (x )=2cos2x . 因为 .24c o s 2)8(==ππf（Ⅱ）将f (x )的图象向右平移个6π个单位后，得到)6(π-x f 的图象，再将所得图象横坐标伸长到原来的4倍，纵坐标不变，得到)64(ππ-f 的图象.).32(cos 2)64(2cos 2)64()(ππππππ-=⎥⎦⎤⎢⎣⎡-=-=f f x g 所以 当 2k π≤32ππ-≤2 k π+ π (k ∈Z), 即 4k π＋≤32π≤x ≤4k π+38π (k ∈Z)时，g (x )单调递减.因此g (x )的单调递减区间为 ⎥⎦⎤⎢⎣⎡++384,324ππππk k (k ∈Z) 4.(2009山东卷理)(本小题满分12分)设函数f(x)=cos(2x+3π)+sin 2x.(1) 求函数f(x)的最大值和最小正周期. (2) 设A,B,C 为∆ABC 的三个内角，若cosB=31，1()24cf =-，且C 为锐角，求sinA.解: （1）f(x)=cos(2x+3π)+sin 2x.=1cos 21cos 2cossin 2sin233222xx x x ππ--+=-所以函数f(x)的最大值为12+最小正周期π.（2）()2c f =122C -=－41, 所以sin 2C =, 因为C 为锐角, 所以3C π=,又因为在∆ABC 中, cosB=31, 所以 s i n B =所以11sin sin()sin cos cos sin 2326A B C B C B C =+=+=+⨯=【命题立意】:本题主要考查三角函数中两角和差的弦函数公式、二倍角公式、三角函数的性质以及三角形中的三角关系. 5.(2009山东卷文)(本小题满分12分)设函数f(x)=2)0(sin sin cos 2cos sin 2πϕϕϕ<<-+x x x 在π=x 处取最小值.(3) 求ϕ.的值;(4) 在∆ABC 中,c b a ,,分别是角A,B,C 的对边,已知,2,1==b a 23)(=A f ,求角C..解: （1）1cos ()2sin cos sin sin 2f x x x x ϕϕ+=⋅+-sin sin cos cos sin sin x x x x ϕϕ=++- sin cos cos sin x x ϕϕ=+ sin()x ϕ=+因为函数f(x)在π=x 处取最小值，所以s in ()1πϕ+=-,由诱导公式知s i n 1ϕ=,因为0ϕπ<<,所以2πϕ=.所以()sin()cos 2f x x x π=+=（2）因为23)(=A f ,所以cos 2A =因为角A 为∆ABC 的内角,所以6A π=.又因为,2,1==b a 所以由正弦定理,得sin sin a b AB=,也就是sin 1sin 22b A B a===,因为b a >,所以4π=B 或43π=B . 当4π=B 时,76412C ππππ=--=;当43π=B 时,36412C ππππ=--=.【命题立意】:本题主要考查了三角函数中两角和差的弦函数公式、二倍角公式和三角函数的性质,并利用正弦定理解得三角形中的边角.注意本题中的两种情况都符合. 6、（2010山东文数）(17)（本小题满分12分）已知函数2()sin()cos cos f x x x x πωωω=-+（0ω>）的最小正周期为π， （Ⅰ）求ω的值；（Ⅱ）将函数()y f x =的图像上各点的横坐标缩短到原来的12，纵坐标不变，得到函数()y g x =的图像，求函数()y g x =在区间0,16π⎡⎤⎢⎥⎣⎦上的最小值.7、（2010山东理数）8、（2011山东理数17）在 ABC中，内角A，B，C的对边分别为a，b，c．已知cos A -2cos C2c-a =cos B b．（I ）求sin sin C A的值；（II ）若cosB=14，b=2，A B C ∆的面积S 。

山东省各地市2012年高考数学（理科）最新试题分类大汇编：第7部分：三角函数（5）一、选择题【山东省潍坊市2012届高三上学期期中四县一校联考理】5.已知ABC ∆中，c b a 、、分别是角C B A 、、的对边， 60,3,2===B b a ，那么A ∠等于A.135 B.45 C. 135或 45 D.60 【答案】B【山东省潍坊市2012届高三上学期期中四县一校联考理】10.已知函数)0,0)(sin()(>>+=ωϕωA x A x f 的部分图象如图所示，则)(x f y =的图象可由函数x x g sin )(=的图象（纵坐标不变）变换如下A.先把各点的横坐标缩短到原来的21倍，再向右平移12π个单位 B.先把各点的横坐标伸长到原来的2倍，再向右平移12π个单位C.先把各点的横坐标缩短到原来的21倍，再向左平移6π个单位D.先把各点的横坐标伸长到原来的2倍，再向左平移6π个单位 【答案】A【山东省临沭一中2012届高三12月理】3. 在ABC ∆中, 3π=∠B ，三边长a ，b ，c 成等差数列，且6=ac ，则b 的值是( )A ．2B ．3C ．6D ． 【答案】C【山东省临沭一中2012届高三12月理】5. 若cos(3)3cos()02x x ππ--+=，则tan()4x π+等于( ) A ．12-B ．2-C ．12D ．2 【答案】D【山东省临沭一中2012届高三12月理】10. 已知函数)0,0)(sin()(>>+=ωϕωA x A x f 的部分图象如图所示，则)(x f y =的图象可由函数x x g sin )(=的图象（纵坐标不变）变换如下( )A.先把各点的横坐标缩短到原来的21倍，再向右平移12π个单位 B.先把各点的横坐标伸长到原来的2倍，再向右平移12π个单位C.先把各点的横坐标缩短到原来的21倍，再向左平移6π个单位 D.先把各点的横坐标伸长到原来的2倍，再向左平移6π个单位 【答案】A【山东省淄博市第一中学2012届高三第一学期期中理】12、已知函数y ＝sin(ωx ＋φ)⎝ ⎛⎭⎪⎫ω＞0，|φ|＜π2的部分图象如图所示,则 （ ）A ω＝1,φ＝π6B ω＝1,φ＝－π6C ω＝2,φ＝π6D ω＝2,φ＝－π6【答案】D【山东省山师大附中2012届高三第二次模拟理】3．已知23)2cos(=-ϕπ，且2||πϕ<，则=ϕtan （ ）A ．33-B ．33C ．3-D ．3【答案】D【山东省山师大附中2012届高三第二次模拟理】8．在ABC ∆内，内角C B A ,,的对边分别是c b a ,,，若bc b a 322=-，B C sin 32sin =，则A=（ ）A ．︒30B ．︒60C ．︒120D ．︒150【答案】A【山东省山师大附中2012届高三第二次模拟理】9．已知a 是实数，则函数ax a x f sin 1)(+=的图象不可能是（ ）【答案】D【山东省实验中学2012届高三第二次诊断理】要得到x x y 2cos 2sin +=的图象，只需将x y 2sin 2=的图象（ ）A.向左移4π个单位B.向左平移8π个单位 C.右平移4π个单位 D.向左平移8π个单位【答案】B【山东省实验中学2012届高三第二次诊断理】若对,),0,(0R x a ∈∃-∞∈∀使a x a ≤0cos 成立，则0cos x 6π⎛⎫-= ⎪⎝⎭（ ）A.21 B.23 C.21- D.23- 【答案】B【山东省实验中学2012届高三上学期第一次诊断性考试理】8. 要得到函数的图像，只需将函数的图像 （ ） (A).向左平移个单位 （B).向右平移个单位 (C).向左平移个单位 （D).向右平移个单位【答案】D 二、填空题【山东省潍坊市2012届高三上学期期中四县一校联考理】14.已知)0,2(,53cos π-∈=x x ，则=x 2tan . 【答案】247【山东省淄博市第一中学2012届高三第一学期期中理】16、给出下列命题:①函数y ＝cos ⎝ ⎛⎭⎪⎫23x ＋ π2是奇函数;②存在实数α,使得sin α＋cos α＝32;③若α、β是第一象限角且α＜β,则tan α＜tan β;④x ＝π8是函数y ＝sin ⎝⎛⎭⎪⎫2x ＋ 5π4的一条对称轴方程; ⑤函数y ＝sin ⎝ ⎛⎭⎪⎫2x ＋ π3的图象关于点⎝ ⎛⎭⎪⎫π12，0成中心对称图形. 其中正确的序号为_______________________________ 【答案】①④【山东省山师大附中2012届高三第二次模拟理】14．如果21)4tan(,43)tan(=-=+παβα，那么)4tan(πβ+= . 【答案】112【山东省山师大附中2012届高三第二次模拟理】15．在A B C ∆中，︒===60,7,1B b a ，则=c .【答案】3【山东省实验中学2012届高三第二次诊断理】已知函数)2||,0,0,)(sin()(πϕωφω<>>∈+=A R x x A x f 的部分图象如图所示，则)(x f 的解析式是【答案】))(6sin(2)(R x x x f ∈+=ππ【山东省实验中学2012届高三第二次诊断理】在ABC ∆中，︒===60,2,6B BC AC ，则=∠A ，AB= .【答案】45,13+三、解答题【山东省潍坊市2012届高三上学期期中四县一校联考理】18.(本小题满分12分）在ABC ∆中，角C B A 、、所对的边分别为c b a 、、，且bcB A 2tan tan 1=+. （Ⅰ）求角A ；（Ⅱ）已知6,27==bc a 求c b +的值. 【答案】解：（Ⅰ）由1+tan 2sin cos 2sin tan cos sin sin A c A B CB b A B B==及正弦定理,得1+，……3分 cos sin sin cos 2sin cos sin sin A B A B CA B B+=即, sin()2sin ,cos sin sin A B C A B B+∴= ………………………………………………5分 1sin()sin 0,cos .2ABC A B C A ∆+=≠∴=在中,…………………………6分0,.3A A ππ<<∴= …………………………………………7分（Ⅱ）由余弦定理2222cos a b c bc A =+-，………………………………8分 又71,6,cos 22a bc A ===， 则22494b c bc =+-=22()3()18b c bc b c +-=+-，……………………10分 解得11.2b c += ……………………………………………………12分【山东省潍坊市2012届高三上学期期中四县一校联考理】20.（本小题满分12分）已知函数)0(3cos 32cos sin 2)(2>-+=ωωωω、a x x x a x f 的最大值为2.21,x x 是集合}0)(|{=∈=x f R x M 中的任意两个元素，||21x x -的最小值为2π. （Ⅰ）求ω、a 的值 （Ⅱ）若32)(=a f ，求)465sin(απ-的值. 【答案】20．(本小题满分12分)解：（I ）()sin 2cos2)f x a x x ωω=-2分sin 2a x x ωω=+)x ωϕ=+ ………………………………………………4分2=，则1a =，…………………………………………5分由题知()f x 的周期为π，则22ππω=，知1ω=.…………………………7分 （II ）由3132sin ,3232sin 232)(=⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=παπαα即知f .……………………8分 ⎪⎭⎫ ⎝⎛+-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-=⎪⎭⎫ ⎝⎛-∴324cos 32423sin 465sin παπαπαπ………………… 10分97312132sin 2122-=⎪⎭⎫⎝⎛⨯+-=⎪⎭⎫ ⎝⎛++-=πα. ……………………12分【山东省临沭一中2012届高三12月理】17. （本小题12分）ABC ∆中，角A 、B 、C 所对应的边分别为a 、b 、c ，若sin sin sin a c Bb c A C-=-+. (1)求角A ；(2)若22()cos ()sin ()f x x A x A =+--，求()f x 的单调递增区间.【答案】【山东省淄博市第一中学2012届高三第一学期期中理】17、（满分12分）已知向量0),sin cos 32,(cos ),sin ,(cos >-==ωωωωωωx x x x x ，函数||)(x f +∙=，且函数)(x f 图象的相邻两条对称轴之间的距离为2π（1）求ω的值 （2）作出函数)(x f 在],0[π上的图象（3）在ABC ∆中，c b a ,,分别是角C B A ,,的对边，,23,2,2)(===∆ABC S c A f 求a 的值【答案】17、解：（1）f(x)= m →·n →+|m →|=cos 2wx+23sinwxcoswx-sin 2wx+1 =cos2wx+3sin2wx+1=2sin(2wx+π6)+1由题意知T=π,又T=2π2w =π, ∴w=1(2)图省略(3)f(x)=2sin(2x+π6)+1,∴f(A)=2sin(2A+π6)+1=2, ∴sin(2A+π6)=12,∵0<A<π, ∴π6<2A+π6<2π+π6,∴2A+π6=5π6,∴A=π3,∴S △ABC =12bcsinA=32,∴b=1,∴a 2=b 2+c 2-2bccosA=1+4-2×2×1×12=3∴a= 3.【山东省山师大附中2012届高三第二次模拟理】17．（本小题满分12分）已知函数R x x x x x f ∈-+=,21cos cos sin 3)(2（1）求函数)(x f 的最小正周期和单调增区间；（2）作出函数在一个周期内的图象。

山东省各地市2012年高考数学（理科）最新试题分类大汇编：第3部分：三角函数（2）一、选择题【山东省莱州一中2012届高三第一次质检理】3.不解三角形，下列判断正确的是（ ） A.30,25,150a b A ===︒，有一解. B.7,14,30a b A ===︒，有两解. C.6,9,45a b A ===︒，有两解.D.9,10,60a b A ===︒，无解.【答案】A【山东省莱州一中2012届高三第一次质检理】5.将函数y f =′()sin x x 的图象向左平移4π个单位，得到函数212sin y x =-的图象，则()f x 是（ ） A.2cos xB.cos xC.sin xD.2sin x【答案】D【山东省莱州一中2012届高三第一次质检理】7.已知1,0,tan ,23αβαπ<<π-π<<=-2αβ+=（ ） A.34π B.54π D.34π或74π【答案】C【山东省莱州一中2012届高三第一次质检理】9.在地面上某处测得山峰的仰角为θ，对着山峰在地面上前进600m 后，测得仰角为2θ，继续前进后又测得仰角为4θ，则山的高度为（ ）m . A.200B.300C.400D.500【答案】B【山东省莱州一中2012届高三第一次质检理】11.设函数()sin()(0,0,)22f x A x A ωϕωϕππ=+≠>-<<的图象关于直线23x =π对称，它的周期是π，则下列结论一定．．正确的是（ ） A.()f x 的图象过点1(0,)2B.()f x 的图象在52,123⎡⎤ππ⎢⎥⎣⎦上是减函数 C.()f x 的最大值为AD.()f x 的一个对称中心是点5(,0)12π 【答案】D【山东省济宁市重点中学2012届高三上学期期中理】11．把函数)(x f y =的图像沿x 轴向右平移2个单位，所得的图像为C ,C 关于x 轴对称的图像为x y 2=的图像，则)(x f y =的函数表达式为 （ ）A ．22+=x yB ．22+-=x yC ．22--=x yD ．)2(log 2+-=x y【答案】B【山东省济宁市鱼台一中2012届高三第三次月考理】5．给定性质: ①最小正周期为π；②图象关于直线x=3π对称，则下列四个函数中，同时具有性质①、②的是（ ）A ．y = sin(2x +6π)B ．．y = sin|x | D ．y = sin(2x －6π)【答案】D8．已知sin =+)6(απ31，则 D ．31-9．如图为一半径是3米的水轮，水轮4圈，水轮上的点P 到水面的距离y （米）x 2)++ϕωx ，则有 （ ）A ．3,125==A πω B ．2,315A πω==C ．5,125==A πω D ．2,515A πω== 【答案】B【山东济宁梁山二中2012届高三12月月考理】8. 函数1)cos (sin )(2--=x x x f 是 A.最小正周期为π2的偶函数B.最小正周期为π2的奇函数C.最小正周期为π的偶函数D.最小正周期为π的奇函数【答案】D【山东济宁金乡一中2012届高三12月月考理】6.若函数sin()y A x ωϕ=+（0A >，0ω>，||2πϕ<）在一个周期内的图象如图所示，,M N 分别是这段图象的最高点和最低点，且0OM ON ⋅=，（OA 、6πB 、C 、D 【答案】C【山东济宁金乡一中2012届高三12月月考理】x 的图象，可以将函数y=sin2x 的图象( )A ．向右平移π个单位长度 B ．向右平移3π个单位长度C π．向左平移π个单位长度sin =+)6(απ31，则cos =-)232(απ（ ）D.31- 在△ABC 中，已知045,2,2===A b a ,则B 等于A. 30°B. 60°C. 30°或150°D. 60°或120° 【答案】A【山东滨州2012届高三期中联考理10．已知函数()sin (0)f x x x ωωω=>的图象与x 轴的两个相邻交点的距离等于2π，若将函数()y f x =的图象向左平移6π个单位得到函数()y g x =的图象，则()y g x =是减函数的区间为 （ ）A. (,0)3π-B. (,)44ππ-C. (0,)3π D. (,)43ππ【答案】D【山东滨州2012届高三期中联考理11．若()2sin()f x x m ωϕ=++，对任意实数t 都有()(),()3888f t f t f πππ+=-=-且，则实数m 的值等于（ ）A ．-1B ．5±C ．-5或-1D ．5或1【答案】C【莱州一中2012高三第三次质量检测理】12.如图，为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒针尖位置(,)P x y .若初始位置为01)2P ，当秒针从0P （注此时0t =）正常开始走时，那么点P 的纵坐标y 与时间关系为A.ππsin()306y t =+B.ππsin()606y t =--C.ππsin()306y t =-+【答案】C【山东济宁汶上一中2012届高三12月月考理】3．若函数)0()32cos(>+=ωπωx y 的图象之间的距离为2π，则=ω．2 D ．4 6．已知A ，B ，C 三点的坐标分别是(3,0)A ，3,22ππ⎛⎫⎪⎝⎭，若1AC BC ⋅=- ，则21tan 2sin sin 2ααα++的值为 （ ）A ．95-B ．59-C ．2D ．3【答案】A【山东济宁汶上一中2012届高三12月月考理】8．如图，圆O 的内接“五角星”与圆O 交与),5,4,3,2,1(=i A i 点，记弧 1i i A A +在圆O 中所对的圆心角为),4,3,2,1(=i a i ，弧51A A 所对的圆心角为5a ，则425312sin 3sin )cos(3cos a a a a a -+=（ ）A ． 23-B ．21-C ．0D ．1【答案】D【山东济宁汶上一中2012届高三12月月考理】12．已知函数R x x A x f ∈+=),sin()(ϕω（其中)22,0,0πϕπω<<->>A ，其部分图象如右图所示，则)(x f 的解析式为 （A ）()sin(2)4f x x π=+ （B ）()sin(2)4f x x π=- )π()sin()4x x π=+7．函数sin 2y x =的图象经过适当变换可）B ．沿x 轴向左平移4π个单位 D ．沿x 轴向右平移2π个单位8．下列命题错误的是（ ） A ．在ABC ∆中，“A B >”是“sin sin A B >”的充要条件；B ．点(,0)8π为函数()tan(2)4f x x π=+的一个对称中心；C ．若||1,||2a b ==，向量a 与向量b 的夹角为120°，则b 在向量a 上的投影为1；D ．“s i n s i n αβ=”的充要条件是“(21)k αβπ+=+或2k αβπ-=（k Z ∈）”. 【答案】C【山东聊城莘县实验高中2012届高三上学期期中】10．在ABC ∆中，若有2cos 22a b Cb +=，则ABC ∆的形状是（ ）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．直角三角形或锐角三角形 【答案】B【山东聊城莘县实验高中2012届高三第三次月考理】2．若1sin 34πα⎛⎫-= ⎪⎝⎭，则cos 23πα⎛⎫+ ⎪⎝⎭=（ ）A ．78-B ．14-C ．14D ．7【答案】A二、填空题【山东省莱州一中2012届高三第一次质检理】56π<，则cos θ= .14．ABC ∆中，A B C 、、所对的边长2AB BC ⋅=-，则b = ．13． 已知角α的终边经过点P (,6)x -，． 【山东省济宁市鱼台一中2012届高三第三次月考理】16． 在,90Rt ABC C ∆∠=中，且A ∠．B ∠．C ∠所对边分别为,,a b c ，若a b c x +=，则实数x 的取值范围为__________．【答案】(【山东济宁金乡一中2012届高三12月月考理】16.给出下列命题： （1）在△ABC 中，若A ＜B ，则sinA ＜sinB ；（2）将函数)32sin(π+=x y 的图象向右平移3π个单位，得到函数y=sin2x 的图象； （3）在△ABC 中, 若AB=2,AC=3,∠ABC=3π,则△ABC 必为锐角三角形; （4）在同一坐标系中，函数sin =y x 的图象和函数2=xy 的图象有三个公共点；其中正确命题的序号是 (写出所有正确命题的序号)。

山东省各地市2012年高考数学（理科）最新试题分类大汇编：第7部分：三角函数（3）一、选择题【山东省烟台市2012届高三期末检测理】2.已知)23cos(32sin απα-=则，等于 A. 35-B.91 C. －91D.35 【答案】C【山东省烟台市2012届高三期末检测理】4.已知△ABC 的三个内角A 、B 、C 所对的边分别为a 、b 、c ，且等于则角B b a A ,1,3,3===πA.2πB.6π C.65π D.6π或65π 【答案】B【山东省潍坊市重点中学2012届高三2月月考理】2．已知1sin 43πα⎛⎫-= ⎪⎝⎭，则5cos 4πα⎛⎫+ ⎪⎝⎭的值等于A ．322 B ．322-C ．31-D ．31 【答案】C【山东省日照市2012届高三12月月考理】（6）函数)20)(sin()(πϕϕω<>+=，A x A x f 其中的图象如图所示，为了得到x x g 2sin )(=的图象，则只需将)(x f 的图象（A ）向右平移6π个长度单位（B ）向右平移3π个长度单位（C ）向左平移6π个长度单位（D ）向左平移3π个长度单位【答案】A 解析：由图象可知A=1，又ππππ=⇒=-=T T 431274，从而22==Tπω，将)1,127(-π代入到)2sin()(ϕ+=x x f 中得，1)67sin(-=+ϕπ，根据2πϕ<得到3πϕ=，所以函数)(x f 的解析式为)32sin()(π+=x x f 。

将)(x f 图象右移6π个长度单位即可得到x x g 2sin )(=的图象。

【山东省潍坊市三县2012届高三12月联考理】12.若1212(,),(,)a a a b b b ==，定义一种向量积：1122(,)a b a b a b ⊗=，已知1(2,),(,0)23m n π==，且点(,)P x y 在函数sin y x =的图象上运动，点Q 在函数()y f x =的图象上运动，且点P 和点Q 满足：OQ m OP n =⊗+（其中O 为坐标原点），则函数()y f x =的最大值A 及最小正周期T 分别为（ ）A ．2,πB ．2,4πC ．1,2πD ．1,42π【答案】D【山东枣庄市2012届高三上学期期中理】5．给出性质：①最小正周期为2π；②图象关于直线3x π=对称，则下列四个函数中，同时具有性质①②的是（ ）A ．sin(2)6y x π=-+ B ．2sin()3y x π=+C ．sin()23x y π=+ D ．sin()6y x π=+【答案】D【山东省枣庄市2012届高三上学期期末理】7.函数()()(A x A x f ϕω+=sin ＞ω,0＞0，ϕ＜⎪⎭⎫2π的部分图象如图所示，则ϕω,的值分别为 A.3,2πB.6,3πC.3,3πD.6,2π【答案】D【烟台市莱州一中2012届高三模块检测理】4.已知31)tan(,41tan =-=βαα，则=βtan A.117 B.711- C.131- D.131 【答案】C【烟台市莱州一中2012届高三模块检测理】6.已知ABC ∆中， 60,3,2===B b a ，那么角A 等于A.135 B.90 C.45 D.30 【答案】C【烟台市莱州一中2012届高三模块检测理】7.已知角θ的顶点与原点生命，始边与x 轴的正半轴重合，终边在直线x y 2=上，则θθθθcos sin cos sin +-为A.31B.31- C.3 D.-3【答案】A【烟台市莱州一中2012届高三模块检测理】8.设函数)0(1)6sin()(>-+=ωπωx x f 的导函数)('x f 的最大值为3，则)(x f 的图象的一条对称轴的方程是A.2π=x B.3π=x C.6π=x D.9π=x【答案】D【烟台市莱州一中2012届高三模块检测理】9.设⎥⎦⎤⎢⎣⎡--∈-+=2,,),()()(ππR x x f x f x F 函数)(x F 的单调递增区间，将)(x F 的图像按向量)0,(π=a 平移得到一个新的函数)(x G 的图像，则下列区间必定是)(x G 的单调递减区间的是A.⎥⎦⎤⎢⎣⎡-0,2π B.⎥⎦⎤⎢⎣⎡ππ,2 C.⎥⎦⎤⎢⎣⎡23,ππ D. ⎥⎦⎤⎢⎣⎡ππ2,23 【答案】D【山东实验中学2012届高三第一次诊断性考试理】8. 要得到函数的图像，只需将函数的图像 （ ） (A).向左平移个单位 （B).向右平移个单位 (C).向左平移个单位 （D).向右平移个单位【答案】D【解析】本题主要考查三角函数的平移．三角函数的平移原则为左加右减上加下减。

2012年山东省高考数学试卷（理科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．2．（5分）（2012•山东）已知全集U={0，1，2，3，4}，集合A={1，2，3}，B={2，4}，则3．（5分）（2012•山东）设a＞0且a≠1，则“函数f（x）=a x在R上是减函数”，是“函数g（x）34．（5分）（2012•山东）采用系统抽样方法从960人中抽取32人做问卷调查，为此将他们随机编号为1，2，…，960，分组后在第一组采用简单随机抽样的方法抽到的号码为9．抽到的32人中，编号落入区间[1，450]的人做问卷A，编号落入区间[451，750]的人做问卷B，5．（5分）（2012•山东）设变量x，y满足约束条件，则目标函数z=3x﹣y的B（6．（5分）（2012•山东）执行程序框图，如果输入a=4，那么输出的n的值为（）7．（5分）（2012•山东）若，，则sinθ=（）B解：因为=﹣，，=8．（5分）（2012•山东）定义在R上的函数f（x）满足f（x+6）=f（x），当﹣3≤x＜﹣1时，f（x）=﹣（x+2）2，当﹣1≤x＜3时，f（x）=x．则f（1）+f（2）+f（3）+…+f（2012）=9．（5分）（2012•山东）函数y=的图象大致为（）．B．D．，﹣y=10．（5分）（2012•山东）已知椭圆C：+=1（a＞b＞0）的离心率为，与双曲线x2﹣y2=1的渐近线有四个交点，以这四个交点为顶点的四边形的面积为16，则椭圆C的方程+=1 B+=1 +=1 +=1+=1．利用：=1+=111．（5分）（2012•山东）现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张，从中任取3张，要求取出的这些卡片不能是同一种颜色，且红色卡片至多1张，不同取法的不考虑特殊情况，共有种取法，其中每一种卡片各取三张，有种取法，两种种取法，由此可得结论．种取法，其中每一种卡片各取三张，有种取法，两种红色卡片，共有故所求的取法共有﹣﹣12．（5分）（2012•山东）设函数f（x）=，g（x）=ax2+bx（a，b∈R，a≠0）若y=f（x）的图象与y=g（x）图象有且仅有两个不同的公共点A（x1，y1），B（x2，y2），则下列判断正是奇函数，所以二、填空题：本大题共4小题，每小题4分，共16分．13．（4分）（2012•山东）若不等式|kx﹣4|≤2的解集为{x|1≤x≤3}，则实数k=2．，14．（4分）（2012•山东）如图，正方体ABCD﹣A1B1C1D1的棱长为1，E，F分别为线段AA1，B1C上的点，则三棱锥D1﹣EDF的体积为．为顶点，则=，=××S故答案为：15．（4分）（2012•山东）设a＞0，若曲线y=与直线x=a，y=0所围成封闭图形的面积为a2，则a=．==．故答案为：．16．（4分）（2012•山东）如图，在平面直角坐标系xOy中，一单位圆的圆心的初始位置在（0，1），此时圆上一点P的位置在（0，0），圆在x轴上沿正向滚动．当圆滚动到圆心位于（2，1）时，的坐标为（2﹣sin2，1﹣cos2）．=，即为向量的坐标．=﹣﹣的坐标为（三、解答题：本大题共6小题，共74分．17．（12分）（2012•山东）已知向量=（sinx，1），=（Acosx，cos2x）（A＞0），函数f（x）=•的最大值为6．（Ⅰ）求A；（Ⅱ）将函数y=f（x）的图象像左平移个单位，再将所得图象各点的横坐标缩短为原来的倍，纵坐标不变，得到函数y=g（x）的图象．求g（x）在[0，]上的值域．）的图象像左平移个单位，再将所得图象各点的横坐标倍，纵坐标不变，得到函数，•（2x+））的图象向左平移个单位后得到，）]2x+倍，4x+）的图象．因此4x+，==时函数取得最小值﹣]18．（12分）（2012•山东）在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．（Ⅰ）求证：BD⊥平面AED；（Ⅱ）求二面角F﹣BD﹣C的余弦值．，﹣，=，﹣，，的一个法向量为，则••x=z=，=，＞==CG==CGFGC=的余弦值为19．（12分）（2012•山东）现有甲、乙两个靶．某射手向甲靶射击一次，命中的概率为，命中得1分，没有命中得0分；向乙靶射击两次，每次命中的概率为，每命中一次得2分，没有命中得0分．该射手每次射击的结果相互独立．假设该射手完成以上三次射击．（Ⅰ）求该射手恰好命中一次得的概率；（Ⅱ）求该射手的总得分X的分布列及数学期望EX．+，A=BB）（（）））））×））﹣×）﹣﹣×）﹣））×﹣）（（﹣××﹣﹣﹣×BC）B=××﹣）×=）××=×××+1×+2×+3×+4×+5×=20．（12分）（2012•山东）在等差数列{a n}中，a3+a4+a5=84，a9=73．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）对任意m∈N*，将数列{a n}中落入区间（9m，92m）内的项的个数记为b m，求数列{b m}的前m项和S m．，由可求公差可得==9≤21．（13分）（2012•山东）在平面直角坐标系xOy中，F是抛物线C：x2=2py（p＞0）的焦点，M是抛物线C上位于第一象限内的任意一点，过M，F，O三点的圆的圆心为Q，点Q到抛物线C的准线的距离为．（Ⅰ）求抛物线C的方程；（Ⅱ）是否存在点M，使得直线MQ与抛物线C相切于点M？若存在，求出点M的坐标；若不存在，说明理由；（Ⅲ）若点M的横坐标为，直线l：y=kx+与抛物线C有两个不同的交点A，B，l与圆Q有两个不同的交点D，E，求当≤k≤2时，|AB|2+|DE|2的最小值．y=）时，）上，﹣）=得，=时，由（Ⅱ）的）r=的方程为，整理得（，==．⇒2t+2t+﹣t）t t=，k=的最小值为22．（13分）（2012•山东）已知函数为常数，e=2.71828…是自然对数的底数），曲线y=f（x）在点（1，f（1））处的切线与x轴平行．（Ⅰ）求k的值；（Ⅱ）求f（x）的单调区间；（Ⅲ）设g（x）=（x2+x）f′（x），其中f′（x）为f（x）的导函数．证明：对任意x＞0，g （x）＜1+e﹣2．，（=（，（（＜＞（精品文档考试教学资料施工组织设计方案。

山东省各地市2012年高考数学 最新试题分类大汇编11 三角函数（1）文【山东省实验中学2012届高三上学期第一次诊断性考试文】2.的值是A. B. C. D.【答案】D【山东省实验中学2012届高三上学期第一次诊断性考试文】6. 设，函数.的图像向右平移个单位后与原图像重合，则的最小值是A. B. C. D. 3【答案】C【山东省实验中学2012届高三上学期第一次诊断性考试文】15. 在中，，面积为,则=________.【答案】72【山东省实验中学2012届高三上学期第一次诊断性考试文】9.=A. B. C. 2 D.【答案】C【山东临沂市临沭一中高三10月份阶段测试试题】4．为得到函数x y sin =的图象，只需将sin()6y x π=+函数的图像（ ）A ．向左平移6π个长度单位B ．向右平移6π个长度单位C ．向左平移65π个长度单位D ．向右平移65π个长度单位 【答案】B【山东临沂市临沭一中高三10月份阶段测试试题】7．若△ABC 的三个内角满足sin :sin :sin 5:11:1A B C =，则△ABC ( )A 一定是锐角三角形.B 一定是直角三角形.C 一定是钝角三角形.D 可能是锐角三角形，也可能是钝角三角形. 【答案】C【山东临沂市临沭一中高三10月份阶段测试试题】10．2(sin cos )1y x x =+-是（ ）A ．最小正周期为2π的偶函数B ．最小正周期为2π的奇函数C ．最小正周期为π的偶函数D ．最小正周期为π的奇函数【答案】D【山东临沂市临沭一中高三10月份阶段测试试题】在∆ABC 中，内角A ，B ，C 的对边分别为,,a b c .已知sin sin C A =2，若cosB=14且ABC ∆的周长为5，求边b 的长。

【答案】18.解：因为sin sin C A =2,所以有2ca =,即2c a =,又因为ABC ∆的周长为5,所以53b a =-, 由余弦定理得：2222cos b c a ac B =+-，即22221(53)(2)44a a a a -=+-⨯，解得a =1，所以b =2.【山东临沂市临沭一中高三10月份阶段测试试题】已知函数()4cos sin()16f x x x π=+-，求()f x 在区间[,]64ππ-上的值域.【答案】19.解：()4cos (sin coscos sin )166f x x x x ππ=+-14cos cos )12x x x =+-2sin 2cos 1x x x =+-s i n 2c o s 2x x =+ 2sin(2)6x π=+ ∵64x ππ-≤≤∴22663x πππ-≤+≤∴1sin(2)126x π-≤+≤12sin(2)26x π-≤+≤所以，函数在区间的值域是]2,1[-【山东省鄄城一中2012届高三上学期期中文】4． 设θ是第二象限角，则点))cos(cos ),(sin(cos θθP 在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】B【山东省鄄城一中2012届高三上学期期中文】8．在ABC ∆中，若60,A BC AC =︒==则角B 的大小为（ ）A ．30°B ．45°C ．135°D ．45°或35°【答案】B【山东省鄄城一中2012届高三上学期期中文】9．得到函数2cos()sin()136y x x ππ=-+-的图象，只需将函数cos(2)6y x π=-的图象（ ）A ．向左平移8π个单位B ．向右平移2π个单位C ．向右平移3π个单位D ．向右平移4π个单位【答案】D【山东省鄄城一中2012届高三上学期期中文】10. 已知函数sin cos 1212y x x ππ⎛⎫⎛⎫=-- ⎪ ⎪⎝⎭⎝⎭,则下列判断正确的是 ( )最小正周期为2π,此函数图象的一个对称中心是,012π⎛⎫⎪⎝⎭ , 最小正周期为π,此函数图象的一个对称中心是,012π⎛⎫ ⎪⎝⎭ ,最小正周期为2π,此函数图象的一个对称中心是,06π⎛⎫ ⎪⎝⎭ , 最小正周期为π,此函数图象的一个对称中心是,06π⎛⎫ ⎪⎝⎭ .【答案】B【山东省鄄城一中2012届高三上学期期中文】14. 若10,sin cos ,25x x x π-<<+=则sin x =_____________. 【答案】53-【山东省济宁市邹城二中2012届高三第二次月考文】11．已知角θ的终边过点（4，－3），则θ2cos = .【答案】257【山东省济宁市邹城二中2012届高三第二次月考文】14、若),2(ππα∈，且54sin =α，则=αtan 。

2012年高考理科数学试卷（山东卷）附答案2012年普通高等学校招生全国统一考试（山东卷）理科数学本试卷分第I卷和第II卷两部分，共4页。

满分150分。

考试用时120分钟，考试结束，务必将试卷和答题卡一并上交。

注意事项：1.答题前，考生务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号、县区和科类填写在答题卡上和试卷规定的位置上。

2.第I卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试卷上。

3.第II卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带。

不按以上要求作答的答案无效。

4.填空题请直接填写答案，解答题应写出文字说明、证明过程或演算步骤。

参考公式：锥体的体积公式：V=Sh，其中S是锥体的底面积，h是锥体的高。

如果事件A，B互斥，那么P（A+B）=P（A）+P(B)；如果事件A,B独立，那么P（AB）=P（A）P（B）。

第I卷（共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1若复数x满足z(2-i)=11+7i(i为虚数单位)，则z为A3+5iB3-5iC-3+5iD-3-5i2已知全集={0,1,2,3,4}，集合A={1,2,3,}，B={2,4}，则（CuA）B为A{1,2,4}B{2,3,4}C{0,2,4}D{0,2,3,4}3设a＞0a≠1，则“函数f(x)=a3在R上是减函数”，是“函数g(x)=(2-a)在R上是增函数”的A充分不必要条件B必要不充分条件C充分必要条件D既不充分也不必要条件（4）采用系统抽样方法从960人中抽取32人做问卷调查，为此将他们随机编号为1,2，……，960，分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中，编号落入区间[1,450]的人做问卷A，编号落入区间[451,750]的人做问卷B，其余的人做问卷C.则抽到的人中，做问卷B的人数为（A）7（B）9（C）10（D）15（5）的约束条件，则目标函数z=3x-y的取值范围是（A）（B）（C）[-1,6]（D）（6）执行下面的程序图，如果输入a=4，那么输出的n 的值为（A）2（B）3（C）4（D）5(7)若，，则sin=（A）（B）（C）（D）（8）定义在R上的函数f（x）满足f（x+6）=f（x），当-3≤x＜-1时，f（x）=-（x+2），当-1≤x＜3时，f （x）=x。

数学试卷 第1页（共39页） 数学试卷 第2页（共39页）数学试卷 第3页（共39页）绝密★启用前2012年普通高等学校招生全国统一考试（山东卷）数学（理科）本试卷分第Ⅰ卷和第Ⅱ卷两部分，共6页.满分150分.考试用时120分钟.考试结束后，务必将本试卷和答题卡一并交回. 注意事项：1. 答题前，考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类填写在答题卡上和试卷规定的位置上.2. 第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试卷上.3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.4. 填空题请直接填写答案，解答题应写出文字说明、证明过程或演算步骤. 参考公式：锥体的体积公式：13V Sh =，其中S 是锥体的底面积，h 是锥体的高.如果事件A ，B 互斥，那么()()()P A B P A P B +=+；如果事件A ，B 独立，那么()()()P AB P A P B =.第Ⅰ卷（共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 若复数z 满足(2i)117i z -=+（i 为虚数单位），则z 为（ ）A. 35i +B. 35i -C. 35i -+D. 35i --2. 已知全集{0,1,2,3,4}U =，集合{1,2,3}A =，{2,4}B =，则()U A B ð为 （ ）A. {1,2,4}B. {2,3,4}C. {0,2,4}D. {0,2,3,4}3. 设0a >且1a ≠，则“函数()x f x a =在R 上是减函数”，是“函数3()(2)g x a x =-在R 上是增函数”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件4. 采用系统抽样方法从960人中抽取32人做问卷调查，为此将他们随机编号为1，2，…，960，分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中，编号落入区间[1,450]的人做问卷A ，编号落入区间[451,750]的人做问卷B ，其余的人做问卷C .则抽到的人中，做问卷B 的人数为（ ）A. 7B. 9C. 10D. 15 5. 已知变量x ，y 满足约束条件22,24,41,x y x y x y +⎧⎪+⎨⎪--⎩≥≤≥则目标函数3z x y =-的取值范围是 （ ）A. 3[,6]2- B. 3[,1]2-- C. [1,6]-D. 3[6,]2-6. 执行下面的程序图，如果输入4a =，那么输出的n 的值为（ ）A. 2B. 3C. 4D. 57. 若ππ[,]42θ∈，sin 2θ=sin θ= （ ）A.35B. 45C.D.348. 定义在R 上的函数()f x 满足(6)()f x f x +=.当31x --≤＜时，2()(2)f x x =-+；当13x -≤＜时，()f x x =.则(1)(2)(3)(2012)f f f f +++⋅⋅⋅=（ ）A. 335B. 338C. 1 678D. 2 012 9. 函数cos622x xxy -=-的图象大致为（ ）ABD10. 已知椭圆2222:1(0)x y C a b a b +=>>.双曲线221x y -=的渐近线与椭圆C 有四个交点，以这四个焦点为顶点的四边形的面积为16，则椭圆C 的方程为 （ ）A. 22182x y +=B. 221126x y +=C. 221164x y +=D.221205x y += 11. 现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张.从中任取3张，要求这3张卡片不能是同一种颜色，且红色卡片至多1张.不同取法的种数为（ ）A. 232B. 252C. 472D. 48412. 设函数1()f x x=，2()(,,0)g x ax bx a b a =+∈≠R ，若()y f x =的图象与()y g x =图象有且仅有两个不同的公共点11(,)A x y ，22(,)B x y ，则下列判断正确的是（ ）A. 当0a <时，120x x +<，120y y +>B. 当0a <时，120x x +>，120y y +<C. 当0a >时，120x x +<，120yy +<D. 当0a >时，120x x +>，120y y +>姓名________________ 准考证号_____________--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效--------数学试卷 第4页（共39页）数学试卷 第5页（共39页）数学试卷 第6页（共39页）第Ⅱ卷（共90分）二、填空题：本大题共4小题，每小题4分，共16分.13. 若不等式|4|2kx -≤的解集为{|13}x x ≤≤，则实数k =_________.14. 如图，正方体1111ABCD A B C D -的棱长为1，E ，F 分别为线段1AA ，1B C 上的点，则三棱锥1D EDF -的体积为_________.15. 设0a >.若曲线y 与直线x a =，0y =所围成封闭图形的面积为2a ，则a =_________.16. 如图，在平面直角坐标系xOy 中，一单位圆的圆心的初始位置在(0,1)，此时圆上一点P 的位置在(0,0)，圆在x 轴上沿正向滚动.当圆滚动到圆心位于(2,1)时，OP 的坐标为_________.三、解答题：本大题共6小题，共74分. 17.（本小题满分12分）已知向量(sin ,1)x =m，cos ,cos2)(0)3Ax x A =>n ，函数()f x =⋅m n 的最大值为6.（Ⅰ）求A ；（Ⅱ）将函数()y f x =的图象向左平移π12个单位，再将所得图象上各点的横坐标缩短为原来的12倍，纵坐标不变，得到函数()y g x =的图象.求()g x 在5π[0,]24上的值域.18.（本小题满分12分）在如图所示的几何体中，四边形ABCD 是等腰梯形，AB CD ∥，60DAB ∠=，FC ⊥平面ABCD ，AE BD ⊥，CB CD CF ==. （Ⅰ）求证：BD ⊥平面AED ； （Ⅱ）求二面角F BD C --的余弦值.19.（本小题满分12分）现有甲、乙两个靶.某射手向甲靶射击一次，命中的概率为34，命中得1分，没有命中得0分；向乙靶射击两次，每次命中的概率为23，每命中一次得2分，没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击. （Ⅰ）求该射手恰好命中一次得的概率；（Ⅱ）求该射手的总得分X 的分布列及数学期望EX .20.（本小题满分12分）在等差数列{}n a 中，34584a a a ++=，973a =. （Ⅰ）求数列{}n a 的通项公式；（Ⅱ）对任意*m ∈N ，将数列{}n a 中落入区间2(9,9)m m 内的项的个数记为m b ，求数列{}m b 的前m 项和m S .21.（本小题满分13分）在平面直角坐标系xOy 中，F 是抛物线2:2(0)C x py p =>的焦点，M 是抛物线C 上位于第一象限内的任意一点，过M ，F ，O 三点的圆的圆心为Q ，点Q 到抛物线C 的准线的距离为34. （Ⅰ）求抛物线C 的方程；（Ⅱ）是否存在点M ，使得直线MQ 与抛物线C 相切于点M ？若存在，求出点M 的坐标；若不存在，说明理由；（Ⅲ）若点M，直线1:4l y kx =+与抛物线C 有两个不同的交点A ，B ，l 与圆Q 有两个不同的交点D ，E ，求当122k ≤≤时，22|AB||DE|+的最小值.22.（本小题满分13分） 已知函数ln ()e xx kf x +=（k 为常数，e 2.71828=⋅⋅⋅是自然对数的底数），曲线()y f x =在点(1,(1))f 处的切线与x 轴平行. （Ⅰ）求k 的值；（Ⅱ）求()f x 的单调区间；（Ⅲ）设2()()()g x x x f x '=+，其中()f x '为()f x 的导函数.证明：对任意0x >，2()1e g x -<+.{0,2,4}A B=A B．又可知，0,a>并不单调递减，故而“函数3 / 13【解析】由所给的不等式组可知所表示的可行域如图所示，5 / 1312412C 264=数学试卷 第16页（共39页）不妨设12x x <，结合图形可知，当0a >时如右图，(2OP=-∠=PCD2, OP=-，即(27 / 133cos==m n A的图像向左平移60，CBCD CB DAB-∠3CDcos(180=60，3BD==，故AD AE A3BD=，建立如图所示的空间直角坐标系，数学试卷第22页（共39页）9 / 13，向量(0,0,1)n =为平面设向量(,,m x y=0,0m BD m FB ⎧=⎪⎨=⎪⎩ 1，则x =，则(3,1m =为平面BDF 的一个法向量．1,5m n m n m n〈〉===，而二面角F BD C --的余弦值为5（Ⅱ）建立如图所示的空间直角坐标系，确定法向量(0,0,1)n =和(3,1m =12311127C 4343336⎛⎫+= ⎪⎝⎭， 121113111121.(1),(2)C ,433643124339P X P X ⎛⎫⎛⎫======= ⎪ ⎪⎝⎭⎝⎭ 22123121121321C (4),(5),4333439433P X P X ⎛⎫⎛⎫======= ⎪ ⎪⎝⎭⎝⎭， 0 1 234数学试卷 第28页（共39页）210919m +=，可求公差11 / 1322818k k -=+数学试卷第34页（共39页）13 / 13。