表11介质的弹性参数
- 格式:ppt
- 大小:1018.00 KB
- 文档页数:51

湖南工业大学课程设计资料袋理学院(系、部)2011 ~ 2012 学年第一学期课程名称计算材料学指导教师雷军辉职称讲师学生姓名余晓燕专业班级应用物理081班学号***********题目计算BN的弹性常数成绩起止日期2011年12月4日~2011年12 月12 日目录清单1湖南工业大学课程设计任务书2011—2012 学年第1 学期理学院学院(系、部)应用物理学专业081 班级课程名称:计算材料学一、设计题目:计算BN的弹性常数指导教师(签字):年月日系(教研室)主任(签字):年月日2(计算材料)设计说明书计算BN的弹性常数起止日期:2011 年12月4日至2011 年12月12日学生姓名余晓燕班级081学号***********成绩指导教师(签字)理学院(部)2011年12 月12 日3计算BN的弹性常数背景:近年来,随着材料、物理、计算机和数学等学科的发展,应用计算的方法研究材料的结构、能量和性能已成为一门迅速发展的新兴学科-计算材料学。
这种方法不仅能进行材料的计算模拟,而且能进行材料的计算机设计和相关性能的预测。
随着计算机技术的飞速发展,第一性原理计算的方法在材料的结构和性能等方面的研究已取得了巨大的成功,第一性原理的方法是基于量子力学理论,从电子运动的层次研究材料的结构和相关性能。
目前,CASTEP软件的主要功能是对半导体、非线性光学材料、金属氧化物、玻璃、陶瓷等固体材料,对电子工业、航空航天以及石化、化工等工业领域有着非常重要的战略意义。
对这些材料而言,其电子的结构与性质,以及表面和界面的性质与行为都非常重要。
CASTEP的量子力学方法,为深入了解固体材料的这些性质并进而设计新的材料,提供了强有力的工具。
基于密度泛函平面波赝势方法的CASTEP软件可以对许多体系包括像半导体、陶瓷、金属、矿石、沸石等进行第一性原理量子力学计算。
典型的功能包括研究表面化学、能带结构、态密度、热学性质和光学性质。


压电陶瓷性能参数解析 Document number:NOCG-YUNOO-BUYTT-UU986-1986UT在机械自由条件下,测得的介电常数称为自由介电常数,在εT表示,上角标T表示机械自由条件。
在机械夹持条件下,测得的介电常数称为夹持介电常数,以εS表示,上角标S表示机械夹持条件。
由于在机械自由条件下存在由形变而产生的附加电场,而在机械受夹条件下则没有这种效应,因而在两种条件下测得的介电常数数值是不同的。
根据上面所述,沿3方向极化的压电陶瓷具有四个介电常数,即ε11T,ε33T,ε11S,ε11S。
(2)介质损耗介质损耗是包括压电陶瓷在内的任何介质材料所具有的重要品质指标之一。
在交变电场下,介质所积蓄的电荷有两部分:一种为有功部分(同相),由电导过程所引起的;一种为无功部分(异相),是由介质弛豫过程所引起的。
介质损耗的异相分量与同相分量的比值如图1-1所示,Ic为同相分量,IR为异相分量,Ic与总电流I的夹角为δ,其正切值为(1-4)式中,ω为交变电场的角频率,R为损耗电阻,C为介质电容。
由式(1-4)可以看出,I R大时,tanδ也大;I R小时tanδ也小。
通常用tanδ来表示的介质损耗,称为介质损耗正切值或损耗因子,或者就叫做介质损耗。
处于静电场中的介质损耗来源于介质中的电导过程。
处于交变电场中的介质损耗,来源于电导过程和极化驰豫所引起的介质损耗。
此外,具有铁电性的压电陶瓷的介质损耗,还与畴壁的运动过程有关,但情况比较复杂,因此,在此不予详述。
(3)弹性常数压电陶瓷是一种弹性体,它服从胡克定律:“在弹性限度范围内,应力与应变成正比”。
设应力为T,加于截面积A的压电陶瓷片上,其所产生的应变为S,则根据胡克定律,应力T与应变S之间有如下关系S=sT(1-5)T=cS(1-6)式中,S为弹性顺度常数,单位为m2/N;C为弹性劲度常数,单位为N/m2。
但是,任何材料都是三维的,即当施加应力于长度方向时,不仅在长度方向产生应变,宽度与厚度方向上也产生应变。


(完整word版)常⽤材料弹性模量及泊松⽐(《钢结构设计规范》GB 50017━2003表3.4.3统⼀取弹性模量206000MPa。
泊松⽐约为0.3)(有限元材料库的参数为:45号钢密度7890kg/m3,泊松⽐0.269,杨⽒模量209000GP.)(HT200,弹性模量为135GPa,泊松⽐为0.27)(HT200 密度:7.2-7.3,弹性模量:70-80; 泊松⽐0.24-0.25;热膨胀系数加热:10冷却-8)(⽤灰铸铁HT200 , 根据资料可知其密度为7 340kg/ m 3 , 弹性模量为120 GPa ,泊松⽐为0. 25)(HT200,弹性模量E=1.22e 11 Pa, 泊松⽐λ=0.25,密度ρ=7800 kg/m 3)(HT200 122 /0. 3 /7. 2 ×10 - 6)(材料HT200,密度为7. 8103 kg / m 3 ,弹性模量为145 GPa,泊松⽐为0.3)( HT200,其弹性模量E=140GPa,泊松⽐µ=0.25,密度ρ=7.8×10 3 kg/m 3) (模具材料为灰⼝铸铁HT200,C-3.47%,Si-2.5%,密度7210 kg / m3 ,泊松⽐0.27。
)(箱体材料为HT200,其性能参数为:弹性模量E=1.4×10 11 Pa,泊松⽐µ=0.3,密度为ρ=7.8×10 3 kg.m -3 )(模型材料HT200,其主要物理与机械性能参数如下:密度7.25 t/m 3 ,弹性模量126 GPa, 泊松⽐0.3)(垫板的材料采⽤HT200, 材料相关参数查表可得, 弹性模量E = 1120 ×10 5 N /mm 2 , 泊松⽐µ= 0125, 密度ρ=712 ×10 - 9 t /mm 3)表58-23,常⽤材料的弹性模量,泊松⽐和线胀系数常⽤材料弹性模量及泊松⽐━━━━━━━━━━━━━━━━━━━━━━━━━名称弹性模量E 切变模量G 泊松⽐µGPa GPa─────────────────────────镍铬钢206 79.38 0.25-0.30合⾦钢206 79.38 0.25-0.30碳钢196-206 79 0.24-0.28铸钢172-202 0.3球墨铸铁140-154 73-76 0.23-0.27灰铸铁113-157 44 0.23-0.27⽩⼝铸铁113-157 44 0.23-0.27冷拔纯铜127 48轧制磷青铜113 41 0.32-0.35轧制纯铜108 39 0.31-0.34轧制锰青铜108 39 0.35铸铝青铜103 41冷拔黄铜89-97 34-36 0.32-0.42 轧制锌82 31 0.27硬铝合⾦70 26轧制铝68 25-26 0.32-0.36铅17 7 0.42玻璃55 22 0.25混凝⼟14-23 4.9-15.7 0.1-0.18纵纹⽊材9.8-12 0.5横纹⽊材0.5-0.98 0.44-0.64橡胶0.00784 0.47电⽊1.96-2.94 0.69-2.06 0.35-0.38尼龙28.3 10.1 0.4可锻铸铁152拔制铝线69⼤理⽯55花岗⽯48⽯灰⽯41尼龙1010 10.7夹布酚醛塑料4-8.8 ⽯棉酚醛塑料1.3⾼压聚⼄烯0.15-0.25低压聚⼄烯0.49-0.78 聚丙烯1.32-1.42。
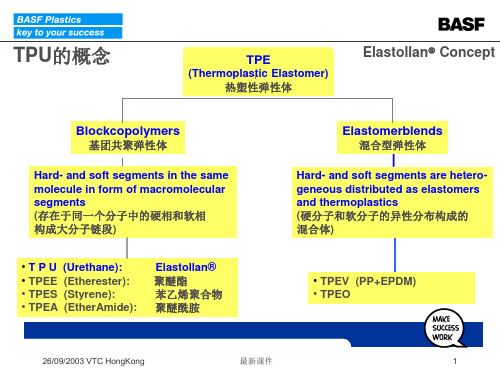
常用材料性质参数以下是常见的材料性质参数:1. 密度:材料的密度是指单位体积内的质量,通常以千克/立方米(kg/m³)表示。
密度可以用来判断材料的重量和占用空间。
2.强度:强度是指材料抵抗力通过应力产生的变形或破坏的能力。
常见的强度参数有屈服强度、抗拉强度、抗压强度和抗剪切强度。
3.弹性模量:弹性模量是材料在受力下发生形变的能力。
它描述了材料的刚性和弹性,常见的弹性模量有杨氏弹性模量、剪切模量和泊松比。
4.硬度:硬度是材料抵抗外界力对其表面产生划痕或穿透的能力。
常见的硬度参数有洛氏硬度、维氏硬度和布氏硬度。
5.热膨胀系数:热膨胀系数衡量了材料在温度变化下的线膨胀程度。
它影响着材料的尺寸稳定性和热应力。
6.热传导性:热传导性是指材料传导热量的能力。
它衡量了材料导热的速度和效率,常常以热导率(单位:瓦特/米·开尔文)来表示。
7.电导率:电导率是材料导电的能力。
它衡量了材料导电的速度和效率,通常以电导率(单位:西门子/米)来表示。
8.抗腐蚀性:抗腐蚀性是指材料对于外部环境中腐蚀物质的抵抗能力。
不同材料具有不同的抗腐蚀性,一些材料可能需要额外的防护措施来增强其抗腐蚀性。
9.可加工性:可加工性是指材料在制造和加工过程中的易处理程度。
它包括了材料的切削性、可塑性、可锻性、可焊性等参数。
10.燃烧性:燃烧性描述了材料在受热或与氧气接触时燃烧的特性。
它根据材料的燃烧速率、火焰传播速度和烟雾排放来衡量。
这些常见的材料性质参数可以帮助人们了解材料的特性,指导材料的选择和使用。
对于不同的应用领域和需求,各参数的重要性和优先级可能不同,因此需要根据具体情况综合考虑。
示,Ic为同相分量,IR为异相分量,Ic与总电流I的夹角为δ,其正切值为1-4式中,ω为交变电场的角频率,R为损耗电阻,C为介质电容;由式1-4可以看出,IR 大时,tanδ也大;IR小时tanδ也小;通常用tanδ来表示的介质损耗,称为介质损耗正切值或损耗因子,或者就叫做介质损耗;处于静电场中的介质损耗来源于介质中的电导过程;处于交变电场中的介质损耗,来源于电导过程和极化驰豫所引起的介质损耗;此外,具有铁电性的压电陶瓷的介质损耗,还与畴壁的运动过程有关,但情况比较复杂,因此,在此不予详述;3弹性常数压电陶瓷是一种弹性体,它服从胡克定律:“在弹性限度范围内,应力与应变成正比”;设应力为T,加于截面积A的压电陶瓷片上,其所产生的应变为S,则根据胡克定律,应力T与应变S之间有如下关系S=sT1-5T=cS1-6式中,S为弹性顺度常数,单位为m2/N;C为弹性劲度常数,单位为N/m2;但是,任何材料都是三维的,即当施加应力于长度方向时,不仅在长度方向产生应变,宽度与厚度方向上也产生应变;设有如图1-2所示的薄长片,其长度沿1方向,宽度沿2方向;沿1方向施加应力T1,使薄片在1方向产生应变S1,而在方向2上产生应变S2,由1-5式不难得出S1=S11T11-7S2=S12T11-8上面两式弹性顺度常数S11和S12之比,称为迫松比,即1-9它表示横向相对收缩与纵向相对伸长之比;同理,可以得到S13,S21,S22,其中,S22=S11,S12=S21;极化过的压电陶瓷,其独立的弹性顺度常数只有5个,即S11,S12,S13,S33和S44;独立的弹性劲度常数也只有5个,即C11,C12,C13,C33和C44.由于压电陶瓷存在压电效应,因此压电陶瓷样品在不同的电学条件下具有不同的弹性顺度常数;在外电路的电阻很小相当于短路,或电场强度E=0的条件下测得的称为短路弹性顺度常数,记作S E;在外电路的电阻很大相当于开路,或电位移D=0的条件下测得的称为开路弹性顺度常数,记作S D;由于压电陶瓷为各向异相性体,因此共有下列10个弹性顺度常数:S E11,S E12,S E13,S E33,S E44,S D11,S D12,S D13,S D33,S D44;同理,弹性劲度常数也有10个:C E11,C E12,C E13,C E33,C E44,C D11,C D12,C D13,C D33,C D44;4机械品质因数机械品质因数也是衡量压电陶瓷的一个重要参数;它表示在振动转换时材料内部能量消耗的程度;机械品质因数越大,能量的损耗越小;产生损耗的原因在于内摩擦;机械品质因数可以根据等效电路计算而得:1-10 式中,R1为等效电阻,ωS为串联谐振角频率,C1为振子谐振时的等效电容,其值为1-11其中,ωp为振子的并联谐振角频率,Co为振子的静电容;以此值代入式1-10,得到1-121-13当△f=fp-fs很小时,式1-13可简化为1-14不同的压电陶瓷元器件对压电陶瓷的Qm值有不同的要求,多数陶瓷滤波器要求压电陶瓷的Qm要高,而音响元器件及接收型换能器则要求Qm要低;5 压电常数对于一般的固体,应力T只引起成比例的应变S,用弹性模量联系起来,即T=YS;压电陶瓷具有压电性,即施加应力时能产生额外的电荷;其所产生的电荷与施加的应力成比例,对于压力和张力来说,其符号是相反的,用介质电位移D单位面积的电荷和应力T单位面积所受的力表示如下:D=Q/A=dT 1-15式中,d的单位为库仑/牛顿C/N这正是正压电效应;还有一个逆压电效应,既施加电场E时成比例地产生应变S,其所产生的应变为膨胀或为收缩取决于样品的极化方向;S=dE 1-16式中,d的单位为米/伏m/v;上面两式中的比例常数d称为压电应变常数;对于正和逆压电效应来讲,d在数值上是相同的,即有关系1-17对于企图用来产生运动或振动例如,声纳和超声换能器的材料来说,希望具有大的压电应变常数d; 另一个常用的压电常数是压电电压常数go,它表示内应力所产生的电场,或应变所产生的电位移的关系;常数g与常数d之间的关系如下: g=d/e1-18 对于由机械应力而产生电压例如留声机拾音器的材料来说,希望具有高的压电电压常数g;此外,还有不常用的压电应力常数e和压电劲度常数h;e把应力T和电场E联系起来,而h把应变S和电场E联系起来,既T=-eE1-19E=-hS1-20与介电常数和弹性常数一样,压电陶瓷的压电常数也与方向有关,并且也需考虑“自由”,“夹持”、“短路”、“开路”等机械的和电学的边界条件;因此,也有许多个压电常数;现以压电陶瓷薄长片样品为例说明之,如图1-3所示;1-21设有薄长片的极化方向与方向3平行,而电极面与方向3垂直;在短路即电场E=0的条件下,薄长片受沿方向1的应力T1的作用时,压电常数d31与电位移D3,应力T1之间的关系如下:在机械自由,即T=0的条件下,薄长片只受到方向3的电场强度E3的作用时,压电常数d31与应变S1及电场E3之间有如下的关系:1-22在开路,即D=0的条件下,薄长片只受到伸缩应力T1的作用时,压电常数g31与应力T1及电场E3之间的关系为:1-23在机械自由,即T=0的条件下,薄长片只受到沿方向3电位移D3的作用时,压电常数g31与电位移D3及应变S1之间的关系为:1-24从式1-21至1-24可以看出,如果选择T,E为自变量时,相应的压电常数为d;如果选择T,D 为自变量时,相应的压电常数为g;同理,选择S,E为自变量时,其边界条件为机械夹持或电学短路,选择S,D为自变量,其边界条件为机械夹持或电学开路,则相应的压电常数各为e和h;它们之间有如下的关系:1-251-26由此可见,由于选择不同的自变量或测量时所处的边界条件不同,可得d、g、e、h四组压电常数,而其中用得最多的是压电常数d;考虑到压电陶瓷材料的各向异性,所以它有如下四组压电常数:d31=d32,d33,d15=d24g31=g32,g33,g15=g24e31=e32,e33,e15=e24h31=h32,h33,h15=h24这四组压电常数并不是彼此独立的,知道其中一组,即可求出其它三组;以上讨论的是压电陶瓷材料的压电性和压电常数;反映压电陶瓷的弹性变量即应力、应变和电学变量即电场,电位移之间的关系的方程式称为压电方程;由图1-3不难得出以下压电陶瓷的压电方程:1-271-28上面式1-27代表正压电效应,而式1-28代表逆压电效应;对于不同的边界条件和不同的自变量,可以得到不同的压电方程组;由于压电振子有四类边界条件,故有四类不的压电方程;式1-27及式1-28所示为第一类压电方程,这四类压电方程的通式列于表1-1中;方程名称压电方程通式第一类压电方程第二类压电方程第三类压电方程第四类压电方程注:① i,j=1,2,3,4,5,6; m,n=1,2,3.②βT n m为自由介质隔离率m/F,βS n m为夹持介质隔离率m/F;6 机电耦合系数机电耦合系数K是综合反映压电材料性能的参数,它表示压电材料的机械能与电能之间的耦合效应;机电耦合系数可定义为由于压电元器件的机械能与它的形状和振动模式有关,因此,不同形状和不同振动模式对应的机电耦合系数也不相同;压电陶瓷的机电耦。