玻璃液体温度计测量不确定度报告-实验室认证

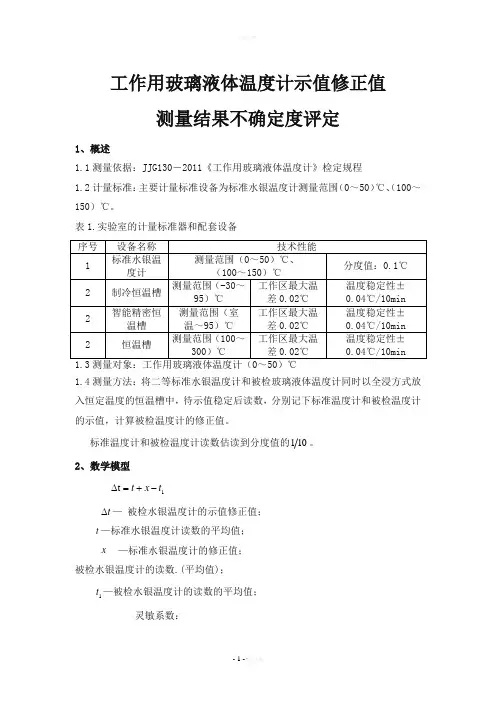
工作用玻璃液体温度计示值修正值测量结果不确定度评定1、概述1.1测量依据：JJG130－2011《工作用玻璃液体温度计》检定规程1.2计量标准：主要计量标准设备为标准水银温度计测量范围（0～50）℃、（100～150）℃。

表1.实验室的计量标准器和配套设备1.4测量方法：将二等标准水银温度计和被检玻璃液体温度计同时以全浸方式放入恒定温度的恒温槽中，待示值稳定后读数，分别记下标准温度计和被检温度计的示值，计算被检温度计的修正值。

标准温度计和被检温度计读数估读到分度值的101。

2、数学模型1t t x t -+=∆ t ∆— 被检水银温度计的示值修正值； t —标准水银温度计读数的平均值； x —标准水银温度计的修正值； 被检水银温度计的读数.(平均值)； 1t —被检水银温度计的读数的平均值； 灵敏系数：11=∂∆∂=ttC 12=∂∆∂=xtC113-=∂∆∂=t t C 3、输入量的标准不确定度评定3.1输入量t 的标准不确定度)(t u 由三个不确定度分项构成。

3.1.1标准估读误差引入不确定度)(1t u ，属于B 类 。

标准水银温度计的分度值0.1℃，估读到分度值的101即0.01℃，则不确定区间半宽为0.01℃，服从均匀分布。

则006.0301.0)(1≈=t u ℃3.1.2温场的不均匀性引起的不确定度)(2t u ，属于B 类。

依据规程要求，恒温槽的工作区域最大温差为0.04（℃），则半区间宽度为0.02℃，按均匀分布处理。

它的不确定度为:3/02.0)(2=t u ≈0.012(℃)3.1.3恒温槽温度波动引入的标准不确定度)(3t u ，属于B 类。

依据规程要求，恒温槽波动度为0.04℃/10min ，则半区间宽度为0.02℃，按均匀分布处理。

则：012.03/02.0)(3==t u ℃.3.1.4输入量t 的标准不确定度)(t u 的计算，因)(1t u 、)(2t u 、)(3t u 互不相关018.0)()()()(322212≈++=t u t u t u t u (℃)3.2输入量x 的标准不确定度)(x u 的评定，属于B 类。

玻璃体温计测量结果不确定度评定1数学模型X=t-(t s-s)式中：X—被校玻璃体温计的示值误差；t—被校玻璃体温计的示值；—标准温度计的修正值。

s2不确定度来源2.1标准温度计读数分辨力（估读）引入的标准不确定度u(s1)标准温度计读数分辨力为其分度值的1/10，最小刻度0.01℃，则不确定度区间度半宽为0.01℃，其误差服从矩形分布，所以k=。

u(s1)=0.01/=0.0058℃。

2.2标准温度计读数时视线不垂直引入的标准不确定度u(s2)标准温度计读数误差范围为±0.005℃，则不确定度区间的半宽为0.005℃，其误差服从反正弦分布，所以k=。

u(s2)=0.005/=0.0035℃。

2.3恒温槽温场不均匀引入的标准不确定度u(s3)恒温槽温场最大温差为0.01℃，则不确定度区间的半宽为0.005℃，其误差服从矩形分布，所以k=。

u(s3)=0.005/=0.0029℃。

2.4恒温槽温度波动度引入的标准不确定度u(s4)恒温槽温场稳定性为±0.015℃/15min，则不确定度区间的半宽为0.015℃，其误差服从矩形分布，所以k=。

u(s4)=0.015/=0.0087℃。

2.5合成不确定度为u(s)==0.011℃3. B类标准不确定度评定3.1输入量s所引入的标准不确定度u(s)标准温度计修正值引入的不确定度u(s)，通过查阅标准温度计的检定报告，标准温度计检定结果的扩展不确定度U95%=0.0028℃，包含因子k=2。

所以输入量s所引入的标准不确定度u(s)=0.0028/2=0.0014℃。

4输入量t所引入的标准不确定度u()4.1 A类标准不确定度评定—被校玻璃体温计示值重复性引入的标准不确定度u()。

将标准温度计和被校玻璃体温计竖直插在工作状态良好的恒温槽中，浸没深度不少于60mm，恒温槽水温为37摄氏度，玻璃体温计在恒温槽中温度稳定3min后取出，平放1min，分别读取标准温度计和被校体温计的示值，进行10次等精度测量，计算被校准玻璃体温计的示值误差值，结果为：0.05℃、0.08℃、0.09℃、0.04℃、0.03℃、-0.10℃、0.06℃、-0.14℃、-0.09℃、0.03℃。

-----------------------------------Docin Choose -----------------------------------豆 丁 推 荐↓精 品 文 档The Best Literature----------------------------------The Best Literature2009年第3期2009年9月山东气象第29卷总第119期气象用玻璃液体温度表测量结果的不确定度评定方法王锡芳，杨茂水，刘彬，任燕，郭瑞宝（山东省气象局大气探测技术保障中心，济南 250031）摘要：气象用玻璃液体温度表检定结果的不确定度，直接影响温度量值传递的检定结果。

根据JJF1059-1999《测量不确定度评定与表示》规范的分析方法，以0.2分度温度表为例，利用检定实验数据，对现用玻璃液体温度表检定结果进行不确定度评定。

通过对检定结果的不确定度评定，梳理出一套清晰的分析步骤和科学方法，为省级气象计量部门提供误差分析范例。

关键词：玻璃液体温度表；测量；不确定度；评定方法中图分类号：P49 文献标识码：B 文章编号：1005–0582（2009）03–0048–04引言一切测量结果都存在不确定度。

为确保测量值的准确、可靠，正确的分析评估测量不确定度，得出的检定结果才更具有可信度。

气象用玻璃液体温度表（以下简称温度表）测量结果不确定度评定对计量标准比对、测量方法、检定规程、检定系统、计量认证及实验室认可起到至关重要的作用。

1 依据的技术标准、检定装置和检定方法依据JJG207-92《气象用玻璃液体温度表检定规程》[1]，以二等水银温度表作标准，用比较法将标准表与被检温度表同置于恒温槽（工作区水平温差≤0.02℃，温场稳定性≤0.02℃）中进行全浸检定，待示值稳定后，按标准、被检、被检、标准的次序依次往返读取温度表示值，每批温度表往返2次共读数4次，分别求得标准表和被检表的示值平均值，然后通过公式计算得出示值修正值。

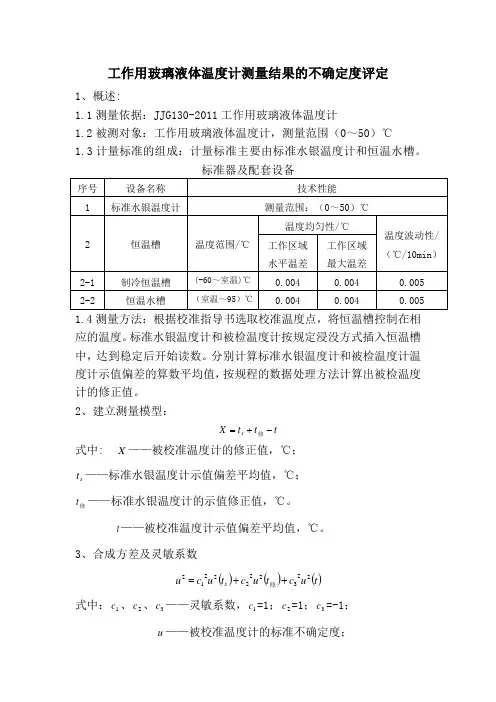
工作用玻璃液体温度计测量结果的不确定度评定1、概述:1.1测量依据：JJG130-2011工作用玻璃液体温度计1.2被测对象：工作用玻璃液体温度计，测量范围（0～50）℃ 1.3计量标准的组成：计量标准主要由标准水银温度计和恒温水槽。

1.4测量方法：根据校准指导书选取校准温度点，将恒温槽控制在相应的温度。

标准水银温度计和被检温度计按规定浸没方式插入恒温槽中，达到稳定后开始读数。

分别计算标准水银温度计和被检温度计温度计示值偏差的算数平均值，按规程的数据处理方法计算出被检温度计的修正值。

2、建立测量模型：t t t X s -+=修式中: X ——被校准温度计的修正值，℃；s t ——标准水银温度计示值偏差平均值，℃； 修t ——标准水银温度计的示值修正值，℃。

t ——被校准温度计示值偏差平均值，℃。

3、合成方差及灵敏系数()()()t u c t u c t u c u s 2232222212++=修式中：1c 、2c 、3c ——灵敏系数，1c =1；2c =1；3c =-1；u ——被校准温度计的标准不确定度；()s t u ——标准水银温度计引入的标准不确定度分量； ()修t u ——标准水银温度计修正引入的标准不确定度分量；()t u ——被校准温度计引入的标准不确定度分量。

4、各输入量的标准不确定度分量来源被校准的温度计，测量范围为（0～50）℃。

分度值为0.5℃，在10℃、20℃、30℃、40℃、50℃温度点进行不确定度评定。

各标准不确定度分量来源：4.1 标准水银温度计读数分辨力引入的不确定度1u 4.2测量重复性引入的不确定度2u4.3被校准温度计读数分辨力引入的不确定度3u 4.4温度计刻线宽度引入的不确定度4u 4.5恒温槽温场均匀性引入的不确定度5u 4.6恒温槽温场波动性引入的不确定度6u 4.7数据修约引入的不确定度7u5、各输入量的标准不确定度分量的评定：5.1 标准水银温度计读数分辨力引入的标准不确定度分量1u标准水银温度计的分度值为0.1℃，读数时估读至分度值的1/10，则区间半宽为0.01℃，按均匀分布，则006.03/01.01≈=u ℃5.2测量重复性引入的标准不确定度分量2u在10℃上对被校准温度计进行10次重复测量，测量值（单位：℃）：实验标准偏差为s=0.070，则：200.02=u ℃在20℃上对被校准温度计进行10次重复测量，测量值（单位：℃）：实验标准偏差为s=0.070，则：200.02=u ℃在30℃上对被校准温度计进行10次重复测量，测量值（单位：℃）：实验标准偏差为s=0.070，则：210.02=u ℃在40℃上对被校准温度计进行10次重复测量，测量值（单位：℃）：实验标准偏差为s=0.070，则：220.02=u ℃在50℃上对被校准温度计进行10次重复测量，测量值（单位：℃）：实验标准偏差为s=0.070，则：220.02=u ℃5.3被校准温度计读数分辨力引入的标准不确定度分量3u被校准温度计的分辨力会对测量结果有影响。

工作用玻璃液体温度计的示值修正值的测量不确定度的评定1、概述（1）测量依据：JJG 130-2004《工作用玻璃液体温度计检定规程》（2）测量方法：用比较法将二等标准水银温度计与被检的工作用玻璃液体温度计同置于标准油槽中，待示值稳定后，按标准←→被检1←→被检 2 ←→被检3←→……被检n 顺序读取温度计示值（这样读数作为一个往返）。

检定普通温度计读一个往返，精密温度计读两个往返，分别求得标准温度计和被检温度计的示值平均值，然后通过公式计算得出被检温度计的示值修正值。

下面以一支测量范围为（250～300）℃、分度值为0.1℃的精密玻璃水银温度计在检定点300℃时为例进行分析评定，浸没方式为全浸式。

2、评定模型 （1）数学模型y ＝t 标 +d 标 +α-/α-t式中：y ——工作用玻璃液体温度计的示值修正值，（℃）；t 标 ——二等标准水银温度计的示值，（℃）；d 标 ——二等标准水银温度计检定证书上给出的示值修正值，（℃）； α——二等标准水银温度计检定证书上上限温度检定后的零位值，（℃）；/α——二等标准水银温度计使用完后新测得上限温度检定后的零位值，（℃）；t ——工作用玻璃液体温度计的示值，（℃）。

（2）灵敏系数t 标的灵敏系数：c 1＝ t /标∂∂y ＝1 d 标的灵敏系数：c 2＝标d y ∂∂/＝1 α的灵敏系数：c 3＝a y ∂∂/＝1/α的灵敏系数：c 4＝//a y ∂∂＝-1t 的灵敏系数：c 5＝t y ∂∂/＝-13、不确定度来源分析（1）输入量t 标标准不确定度u （t 标）引起的不确定度分量u 1（y ）。

标准不确定度u （t 标）的分项构成：a ）重复性引入的标准不确定度u （t 标1）； 该项不确定度的来源如下：恒温槽的温场波动，标准温度计的短期不稳定性等均会引起检定结果的不重复。

b)温场不均匀引入的标准不确定度u （t 标2）。

检定规程中对所使用恒温槽工作区域的温场均匀性有具体规定，但对分度值为0.1℃的精密玻璃温 度计的检定，一般都可使温度计的感温泡处于同一水平面，故只需考虑水平温场不均匀性（水平温差）产生的影响。

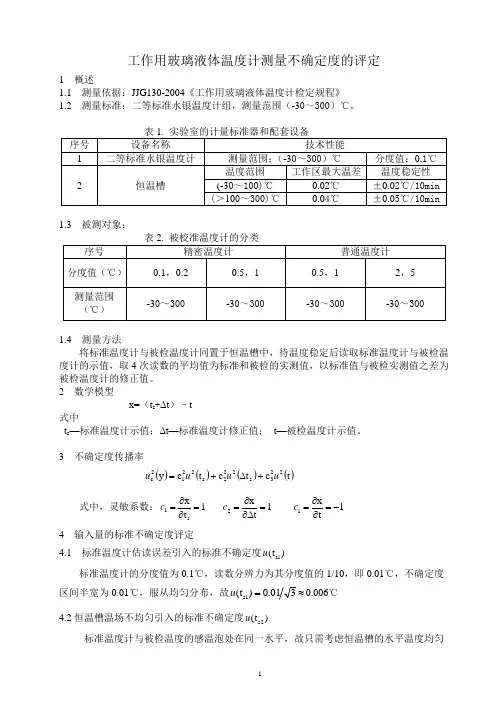
工作用玻璃液体温度计测量不确定度的评定1 概述1.1 测量依据：JJG130-2004《工作用玻璃液体温度计检定规程》 1.2 测量标准：二等标准水银温度计组，测量范围（-30～300）℃。

1.3 被测对象：1.4 测量方法将标准温度计与被检温度计同置于恒温槽中，待温度稳定后读取标准温度计与被检温度计的示值，取4次读数的平均值为标准和被检的实测值，以标准值与被检实测值之差为被检温度计的修正值。

2 数学模型x=（t s +Δt ）–t 式中t s —标准温度计示值；Δt—标准温度计修正值； t —被检温度计示值。

3 不确定度传播率()()()()t c t c t c y 223s 222s 2212c u u u u +∆+=式中，灵敏系数：1t x s 1=∂∂=c 1t x 2=∆∂∂=c 1tx 1-=∂∂=c 4 输入量的标准不确定度评定4.1 标准温度计估读误差引入的标准不确定度)t (1s u标准温度计的分度值为0.1℃，读数分辨力为其分度值的1/10，即0.01℃，不确定度区间半宽为0.01℃，服从均匀分布，故≈=301.0)t (1s u 0.006℃ 4.2恒温槽温场不均匀引入的标准不确定度)t (2s u标准温度计与被检温度的感温泡处在同一水平，故只需考虑恒温槽的水平温度均匀性。

恒温槽的水平最大温差均为≤0.02℃，则不确定度区间半宽为0.01℃，按均匀分布处理。

故≈=301.0)t (2s u 0.006℃ 4.3 恒温槽温度波动不均匀引入的标准不确定度)t (3s u恒温槽的温度波动度≤±0.02℃/10min ，不确定度区间半宽为0.02℃，服从均匀分布，故≈=302.0)t (3s u 0.012℃ 4.4 标准温度计修正值引入的标准不确定度()s t ∆u根据JJG128-2003《二等标准水银温度计检定规程》附录A 可知，二等标准水银温度计修正值的扩展不确定度U 95=0.03℃，包含因子k p =2.58，故()≈=∆58.203.0t s u 0.012℃4.5 被检温度计示值重复性引入的标准不确定度)t (1u采用A 类标准不确定度评定。

工作用玻璃液体温度计测量不确定度报告1、 概述 1.1、测量依据JJG130-2004《工作用玻璃液体温度计检定规程》 1.2、测试标准二等标准水银温度计，温度范围0~50℃。

1.3、被测对象工作用玻璃液体温度计，分度值0.1℃，温度范围为0~50℃，浸没方式为全浸式，感温液体为水银。

1.4、测量方法将二等标准水银温度计和被检工作用玻璃液体温度计同时以全浸方式放入恒定温度为50℃的恒温槽中，待示值稳定后，分别读取标准温度计和被检温度计的示值，计算被检温度计的修正值。

2、数学模型()s s x t t t =+∆-式中x --工作用玻璃液体温度计的修正值；s t --二等标准水银温度计的示值； s t ∆--二等标准水银温度计的修正值； t --工作用玻璃液体温度计的示值。

3、灵敏系数1/1s c x t =∂∂= 2/1s c x t =∂∂∆= 3/1c x t =∂∂=- 4、标准不确定度评定4.1、输入量s t 的标准不确定度()s u t输入量s t 的标准不确定度主要来源如下：a)二等标准水银温度计读数分辨力（估读）引入的标准不确定度1()s u t ，用B 类标准不确定度评定。

二等标准水银温度计的读数分辨力为其分度值的1/10，即0.01℃，则不确定度区间半宽为0.01℃，均匀分布，1()s u t=≈0.006℃，估计不可靠性为20%，自由度1()s t ν=12。

b)二等标准水银温度计读数时视线不垂直引入的标准不确定度2()s u t ，用B 类标准不确定度表示。

二等标准水银温度计读数误差范围为0.005±℃,不确定度区间半宽为0.005℃，按反正弦分布处理。

2()s u t =≈0.004℃,估计其不可靠性为20%，自由度2()s t ν=12。

c)由恒温槽温场不均匀引入的标准不确定度3()s u t ，用B 类标准不确定度评定。

恒温槽温场最大温差为0.02℃，则不确定度区间半宽为0.01℃,按均匀分布处理。

工作用玻璃液体温度计测量不确定度的评定1 概述1.1 测量依据：JJG130-2004《工作用玻璃液体温度计检定规程》1.2 测量标准：二等标准水银温度计组，测量范围（-30～300）℃。

表1. 实验室的计量标准器和配套设备1.3 被测对象：表2. 被校准温度计的分类1.4 测量方法将标准温度计与被检温度计同置于恒温槽中，待温度稳定后读取标准温度计与被检温度计的示值，取4次读数的平均值为标准和被检的实测值，以标准值与被检实测值之差为被检温度计的修正值。

2 数学模型x=（t s+Δt）–t式中t s —标准温度计示值；Δt —标准温度计修正值； t —被检温度计示值。

3 不确定度传播率()()()()t c t c t c y 223s 222s 2212c u u u u +∆+=式中，灵敏系数：1t xs1=∂∂=c 1t x 2=∆∂∂=c 1t x 1-=∂∂=c 4输入量的标准不确定度评定4.1 标准温度计估读误差引入的标准不确定度)t (1s u标准温度计的分度值为0.1℃，读数分辨力为其分度值的1/10，即0.01℃，不确定度区间半宽为0.01℃，服从均匀分布，故≈=301.0)t (1s u 0.006℃ 4.2恒温槽温场不均匀引入的标准不确定度)t (2s u标准温度计与被检温度的感温泡处在同一水平，故只需考虑恒温槽的水平温度均匀性。

恒温槽的水平最大温差均为≤0.02℃，则不确定度区间半宽为0.01℃，按均匀分布处理。

故≈=301.0)t (2s u 0.006℃ 4.3 恒温槽温度波动不均匀引入的标准不确定度)t (3s u恒温槽的温度波动度≤±0.02℃/10min ，不确定度区间半宽为0.02℃，服从均匀分布，故≈=302.0)t (3s u 0.012℃ 4.4 标准温度计修正值引入的标准不确定度()s t ∆u根据JJG128-2003《二等标准水银温度计检定规程》附录A 可知，二等标准水银温度计修正值的扩展不确定度U 95=0.03℃，包含因子k p =2.58，故。

工作用玻璃液体温度计测量结果不确定度评定1 概述1.1 测量方法：JJG130—2011《工作用玻璃液体温度计检定规程》 1.2 环境条件：温度（20±5）℃，相对湿度45%～75%RH 1.3 测量标准：自校式铂电阻数字测温仪1.4 被测对象：工作用玻璃液体温度计，分度值1℃，测量范围（0～100）℃，感温液体为水银。

1.5 测量过程将自校式铂电阻数字测温仪和被检工作用玻璃液体温度计同时以局浸式放入恒定温度为60℃的恒温水槽中，待示值稳定后，分别读取自校式铂电阻数字测温仪和被检工作用玻璃液体温度计的示值，计算被检工作用玻璃液体温度计的修正值。

2 测量模型 =s x t t -式中： x —工作用玻璃液体温度计的修正值；t s —自校式铂电阻数字测温仪的示值； t —工作用玻璃液体温度计的示值。

3 输入量的标准不确定度评定 3.1 输入量t s 标准不确定度u （t s ）的评定输入量t s 的不确定度的来源如下：a) 自校式铂电阻数字测温仪引入的标准不确定度u (t s1), 采用B 类评定方法进行评定。

自校式铂电阻数字测温仪的允许误差为±0.20℃，半宽为0.20℃,按均匀分布处理。

u (t s1)=0.2/3≈0.12℃；b)由恒温水槽温场不均匀引入的标准不确定度u(t s2)，采用B 类评定方法进行评定。

恒温水槽温场均匀度为0.01℃, 则不确定度区间半宽为0.01℃,按均匀分布处理。

u (t s2)=0.01/3≈0.006℃；c)恒温水槽温度波动引入的标准不确定度u(t s3)，采用B 类评定方法进行评定。

恒温水槽温场稳定性为±0.01℃/30min,则不确定度区间半宽为0.01℃,按均匀分布处理。

u (t s3)=0.01/3≈0.006℃；因为u (t s1)、u （t s2）、u （t s3）互不相关,所以222s 123()=()()()=0.13s s s u t u t u t u t ++℃3.2 输入量t 标准不确定度u （t ）的评定输入量t 的不确定度的来源如下：a)被检温度计示值重复性引入的标准不确定度u （t 1），用A 类评定方法进行评定。

常用玻璃量器容量值测量不确定度评定报告1 概述1.1测量方法:依据JJG196—2006《常用玻璃量器检定规程》1.2环境条件：温度（20±5）℃，湿度≤80%RH1.3测量标准电子天平：200g/0.1mg 。

1.4被测对象单标线容量瓶.标称容量100ml 。

1.5测量过程单标线容量瓶的测量是通过天平称出被测容量瓶内纯水的质量值,乘以测量温度下的K （t ）值,即得到20℃时的实际容量.2 数学模型V=m. K式中:V ——单标线容量瓶的实际容量（ml ）；m ——被测量器内纯水的质量值（g ）；K ——《常用玻璃量器检定规程》附表中给出。

由数学模型得： 222K K ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡）（）（）（c c c u m m u V V u3 输入量的标准不确定度评定3.1输入量m 的标准不确定度u (m)的评定u (m)由三个标准不确定度分项构成,即电子天平的标准不确定度u (m 1),被测量器内纯水质量值的测量重复性引起的标准不确定度u (m 2), 和测量器液面观察与调定引入的标准不确定度u(m 3)。

3.1.1电子天平的标准不确定度u (m 1)的评定容量瓶采用200g/0.1mg 电子天平, 其标准不确定度u (m 1)可根据电子天平检定证书测量范围(50~200)g 时，示值误差为0.3mg ，按均匀分布，包含因子k ,故标准不确定度分项u (m 1)为u (m 1)=30003.0 =1.74×10-4g 3.1.2 被测量器内纯水质量值的测量重复性引起的标准不确定度分量u (m 2)的评定被测量器内纯水质量值的测量重复性可以通过连续测量得到测量列.实验用水平均温度19.6℃时，用200g/0.1mg 电子天平测量单标线容量瓶内纯水的值，连续测量6次，实测值为：99.6365g ；99.6374g ；99.6352g ；99.6361g ；99.6360g ；99.6377g ；m =1nn i 1=∑m i =99.6365g单次实验标准差 s＝9.39×10-4g 该6次测量值的算术平均值为测量结果,则可得到 ：u (m 2=3.83×10-4g3.1.3 被测量器液面观察与调定引入的标准不确定度u (m 3)被测量器液面观察与调定引入的标准不确定度，采用B 类方法进行评定。