过程控制系统解耦控制系统页

第6章解耦控制系统6.1 系统的关联分析6.1.1系统的分析在一个生产装置设置若干个控制回路，来稳定各个被控变量。

几个回路之间，就可能相互关联，相互耦合，相互影响，构成多输入-多输出的相关（耦合）控制系统。

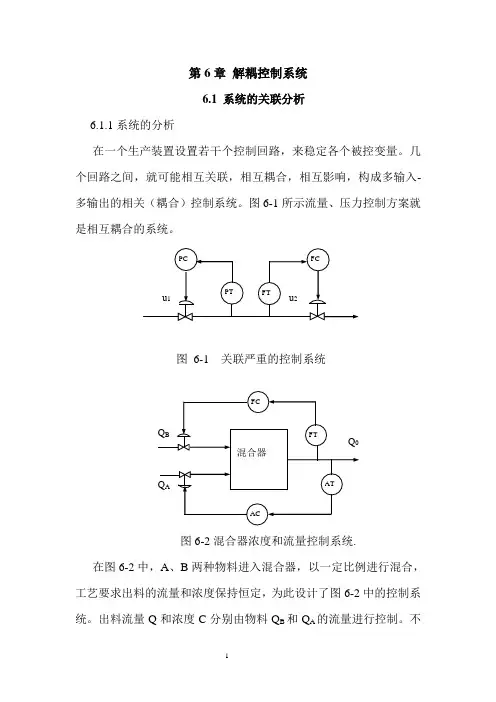
图6-1所示流量、压力控制方案就是相互耦合的系统。

图6-1 关联严重的控制系统图6-2混合器浓度和流量控制系统.在图6-2中，A、B两种物料进入混合器，以一定比例进行混合，工艺要求出料的流量和浓度保持恒定，为此设计了图6-2中的控制系统。

出料流量Q和浓度C分别由物料Q B和Q A的流量进行控制。

不难看出，这两个控制回路是相互关联的，而关联程度与工艺操作数据有关。

系统间的关联程度是不一样的。

那么如何来表征系统的关联程度呢？可以采用“相对增益”的方法来分析 6.1.2相对增益令某一通道y i u j →在其它系统均为开环时的放大系数与该一通道在其它系统均为闭环时的放大系数之比为λij ，称为相对增益，则yu y uu y λij j i j i ∂∂∂∂=(6-1)上式中分子项外的下标u 表示除了u j 以外，其它都保持不变，即都为开环；分母项外的下标y 表示除了y i 以外，其它y 都保持不变，即其它系统都为闭环系统。

现以图6-1所示双输入双输出系统为例。

该系统被控变量与操纵变量关系如图6-4所示。

图6-4 双输入双输出对象静态特性框图由图6-4可得该系统静态方程为u k u k y u k u k y 22212122121111+=+= （6-2）式中k ij 表示第j 个输入变量作用于第i 个输出变量的放大系数。

求λ11，首先求取λ11的分子项u u y 11∂，除u 1外，其它u 不变，则有11211k u u y ==∂∂常数（6-3）再求λ11的分母项y u y 11∂∂，除y 1外，其它y 不变，由式（6-2）可得u k u k 0u k u k y 2221212121111+=+=由上两式可得2211211222112221121111122211211112k k k k k k k k k k u y u k k k u k y y -=-=∂∂∴-==常数（6-4）在求得λ11的分子项与分母项可得λ11yu y u u y j i j i ∂∂∂∂=11λk k k k k k 211222112211-=（6-5） 同样可推导出 k k k k k k 2112221122111122-==λλ （6-6） k k k k k k 2112221121122112--==λλ （6-7）如果排成数阵形式λ22λ21λ12λ11u u y 2y 121 （6-8）上式称为布里斯托尔阵列(Briistol 阵列)，或相对增益阵列。