第3章内压薄壁容器
- 格式：ppt
- 大小：2.51 MB
- 文档页数：30
下载文档原格式
合集下载
内压薄壁容器设计
不被加热或冷却，筒内介质最高或最低温度。
用蒸汽、热水或其它载热体加热或冷却，载体最高温度或最低温度。
㈡设计温度
㈢许用应力系数
焊接削弱而降低设计许用应力的系数。 根据接头型式及无损检测长度比例确定。
焊接接头形式
无损检测的长度比例
100%
局部
1.0
0.85
小位移假设
各点位移都远小于厚度。可用变形前尺寸代替变形后尺寸。变形分析中高阶微量可忽略。
2．基本假设
02
直线法假设
变形前垂直于中面直线段，变形后仍是直线并垂直于变形后的中面。变形前后法向线段长度不变。沿厚度各点法向位移相同，厚度不变。
不挤压假设
各层纤维变形前后互不挤压。
01
2．基本假设
2．球形壳体
直径与内压相同，球壳内应力仅是圆筒形壳体环向应力的一半，即球形壳体的厚度仅需圆筒容器厚度的一半。 当容器容积相同时，球表面积最小，故大型贮罐制成球形较为经济。 制造 球壳R1＝R2=D/2，得：
3．圆锥形壳体
圆锥形壳半锥角为a，A点处半径为r，厚度为d，则在A点处： 代入（4-3）、（4-4）可得A点处的应力：
㈡受液体静压的圆筒形壳体的受力分析 筒壁上任一点的压力值（不考虑气体压力）为： 根据式（4-3） （4-4）可得：
上部支承圆筒（b），液体重量使得圆筒壁受轴向力作用，在圆筒壁上产生经向应力：
底部支承的圆筒（a），液体重量由支承传递给基础，筒壁不受液体轴向力作用，则s1=0。
[s]t-设计温度t℃下材料许用应力，MPa。
㈠焊接接头系数
钢板卷焊。夹渣、气孔、未焊透等缺陷，导致焊缝及其附近区域强度可能低于钢材本体的强度。 钢板 [s]t乘以焊接接头系数f，f≤1
用蒸汽、热水或其它载热体加热或冷却，载体最高温度或最低温度。
㈡设计温度
㈢许用应力系数
焊接削弱而降低设计许用应力的系数。 根据接头型式及无损检测长度比例确定。
焊接接头形式
无损检测的长度比例
100%
局部
1.0
0.85
小位移假设
各点位移都远小于厚度。可用变形前尺寸代替变形后尺寸。变形分析中高阶微量可忽略。
2．基本假设
02
直线法假设
变形前垂直于中面直线段，变形后仍是直线并垂直于变形后的中面。变形前后法向线段长度不变。沿厚度各点法向位移相同，厚度不变。
不挤压假设
各层纤维变形前后互不挤压。
01
2．基本假设
2．球形壳体
直径与内压相同，球壳内应力仅是圆筒形壳体环向应力的一半，即球形壳体的厚度仅需圆筒容器厚度的一半。 当容器容积相同时，球表面积最小，故大型贮罐制成球形较为经济。 制造 球壳R1＝R2=D/2，得：
3．圆锥形壳体
圆锥形壳半锥角为a，A点处半径为r，厚度为d，则在A点处： 代入（4-3）、（4-4）可得A点处的应力：
㈡受液体静压的圆筒形壳体的受力分析 筒壁上任一点的压力值（不考虑气体压力）为： 根据式（4-3） （4-4）可得：
上部支承圆筒（b），液体重量使得圆筒壁受轴向力作用，在圆筒壁上产生经向应力：
底部支承的圆筒（a），液体重量由支承传递给基础，筒壁不受液体轴向力作用，则s1=0。
[s]t-设计温度t℃下材料许用应力，MPa。
㈠焊接接头系数
钢板卷焊。夹渣、气孔、未焊透等缺陷，导致焊缝及其附近区域强度可能低于钢材本体的强度。 钢板 [s]t乘以焊接接头系数f，f≤1
第三章-内压薄壁容器的应力
平行圆：垂直于回转轴的平面与中间面的交线称平行 圆。显然，平行圆即纬线。
纬线
平行圆
25
1、基本概念 第一曲率半径R1：过该点的经线在该点的曲率 半径。
第一曲率半径
O
Ｍ
Ｍ
Ｍ
O
N
26
1、基本概念 第一曲率半径R1和第二曲率半径R2
过M点与回转轴作一平面，即 MAO平面，称为经线平面。在经 线平面上，经线AB’上M点的曲 率半径称为第一曲率半径，用R1 表示 ；
后者忽略为零。
9
（2）无力矩理论，即薄膜理论。
假定壳壁如同薄膜一样，只承受拉应力和压应 力，完全不能承受弯矩和弯曲应力。壳壁内的应 力即为薄膜应力。这时壳体的应力状态仅由法向
力N、N确定。
在工程实际中，理想的薄壁壳体是不存在的， 因为即使壳壁很薄，壳体中还会或多或少地存在 一些弯曲应力，所以无力矩理论有其近似性和局 限性。
过N点作一与回转轴垂直的平面 ，该平面与回转轴的交线是一个 圆，称为回转曲面的平行圆，也 称为纬线，此平行圆的圆心一定 在回转轴上；
通过M点的法线垂直于经线AB’
的平面与中见面相割形成的曲线
EMF，这一曲线在M点的曲率半
径称为第二曲率半径，用R2表示
；
27
就普通回转体而言，用与轴线垂直 的平面截取得到的壳体截面与用上 述圆锥面截取得到的壳体截面是不 一样的，前者是壳体的横截面，并 不能截出壳体的真正厚度(圆柱形壳 体除外)，而后者称为壳体的锥截面 ，截出的是回转体的真正壁厚；
弯曲应力比薄膜应力小很多,可略去不计。
12
二、 基本概念与基本假设
1. 基本概念 回转壳体：平面内平滑曲线绕平面内固定轴线旋转360° 形成的壳体。没有拐点
纬线
平行圆
25
1、基本概念 第一曲率半径R1：过该点的经线在该点的曲率 半径。
第一曲率半径
O
Ｍ
Ｍ
Ｍ
O
N
26
1、基本概念 第一曲率半径R1和第二曲率半径R2
过M点与回转轴作一平面，即 MAO平面，称为经线平面。在经 线平面上，经线AB’上M点的曲 率半径称为第一曲率半径，用R1 表示 ；
后者忽略为零。
9
（2）无力矩理论，即薄膜理论。
假定壳壁如同薄膜一样，只承受拉应力和压应 力，完全不能承受弯矩和弯曲应力。壳壁内的应 力即为薄膜应力。这时壳体的应力状态仅由法向
力N、N确定。
在工程实际中，理想的薄壁壳体是不存在的， 因为即使壳壁很薄，壳体中还会或多或少地存在 一些弯曲应力，所以无力矩理论有其近似性和局 限性。
过N点作一与回转轴垂直的平面 ，该平面与回转轴的交线是一个 圆，称为回转曲面的平行圆，也 称为纬线，此平行圆的圆心一定 在回转轴上；
通过M点的法线垂直于经线AB’
的平面与中见面相割形成的曲线
EMF，这一曲线在M点的曲率半
径称为第二曲率半径，用R2表示
；
27
就普通回转体而言，用与轴线垂直 的平面截取得到的壳体截面与用上 述圆锥面截取得到的壳体截面是不 一样的，前者是壳体的横截面，并 不能截出壳体的真正厚度(圆柱形壳 体除外)，而后者称为壳体的锥截面 ，截出的是回转体的真正壁厚；
弯曲应力比薄膜应力小很多,可略去不计。
12
二、 基本概念与基本假设
1. 基本概念 回转壳体：平面内平滑曲线绕平面内固定轴线旋转360° 形成的壳体。没有拐点
第3章 内压薄壁容器
径。无缝钢管的公称直径、外径及无缝钢管制作筒体时的公称直径见表3-15。
第3章 内压薄壁容器
3.3 压力试验
3.3.1 压力试验的对象、目的及方法 压力试验包括液压试验和气压试验。从安全考虑，多数情况下尽可能采用液压试
验。但对不允许有微量残留液体或容积过大及结构复杂的容器；严寒下易发生冰胀而 不适宜作液压试验的容器均须进行气压试验。对剧毒介质容器和高压易燃介质等不允 许有微量介质泄漏的容器，在液压试验合格后还要做气密性试验。对需要进行热处理 的容器，应在热处理后再做压力试验。
第3章 内压薄壁容器
3.2 设计参数的确定
3.2.3 许用应力 许用应力是容器壳体、封头等受压元件的材料许用强度，它是根据材料各项强
度性能指标分别除以相应的标准中所规定的安全系数来确定的。 钢制压力容器用材料（除螺栓材料外）许用应力的取值方法见表3-6。
第3章 内压薄壁容器
3.2 设计参数的确定
（3）
设计压力p
指设定的容器顶部的最高压力，与相应的设计温度一起作为设计载荷条件，其值不得低 于工作压力。
第3章 内压薄壁容器
3.2 设计参数的确定
3.2.2 设计温度t 设计温度是指容器在正常工作情况下，在相应设计压力下，设定的受压元件的
金属温度
元件的金属温度可用传热计算求得，或在已使用的同类容器上测定，或按内部 介质温度测定。当不可能通过传热计算或测试结果确定时，可按以下方法确定。
3.1.4 各类厚度的关系 各类厚度之间的关系如图3-1和表3-1所示。
第3章 内压薄壁容器
3.2 设计参数的确定
3.2.1 压力参数
（1）
工作压力pw
指在正常工作情况下，容器顶部可能达到的最高压力，也称为最高工作压力。
第3章 内压薄壁容器
3.3 压力试验
3.3.1 压力试验的对象、目的及方法 压力试验包括液压试验和气压试验。从安全考虑，多数情况下尽可能采用液压试
验。但对不允许有微量残留液体或容积过大及结构复杂的容器；严寒下易发生冰胀而 不适宜作液压试验的容器均须进行气压试验。对剧毒介质容器和高压易燃介质等不允 许有微量介质泄漏的容器，在液压试验合格后还要做气密性试验。对需要进行热处理 的容器，应在热处理后再做压力试验。
第3章 内压薄壁容器
3.2 设计参数的确定
3.2.3 许用应力 许用应力是容器壳体、封头等受压元件的材料许用强度，它是根据材料各项强
度性能指标分别除以相应的标准中所规定的安全系数来确定的。 钢制压力容器用材料（除螺栓材料外）许用应力的取值方法见表3-6。
第3章 内压薄壁容器
3.2 设计参数的确定
（3）
设计压力p
指设定的容器顶部的最高压力，与相应的设计温度一起作为设计载荷条件，其值不得低 于工作压力。
第3章 内压薄壁容器
3.2 设计参数的确定
3.2.2 设计温度t 设计温度是指容器在正常工作情况下，在相应设计压力下，设定的受压元件的
金属温度
元件的金属温度可用传热计算求得，或在已使用的同类容器上测定，或按内部 介质温度测定。当不可能通过传热计算或测试结果确定时，可按以下方法确定。
3.1.4 各类厚度的关系 各类厚度之间的关系如图3-1和表3-1所示。
第3章 内压薄壁容器
3.2 设计参数的确定
3.2.1 压力参数
（1）
工作压力pw
指在正常工作情况下，容器顶部可能达到的最高压力，也称为最高工作压力。
第三章 内压薄壁容器应力云南大学2010版.ppt
代入微体平衡方程式
R
R
==Sp
PP，RR22得==
P2PDD
2
31
PR2 PD
32
圆柱壳壁内应力分布
2 m
33
讨论1：薄壁圆筒上开孔的有利形状
图3-10 薄壁圆筒上开孔
① 环向应力是经向应力 的2倍，所以环向承受应 力更大，环向上就要少削 弱面积，故开设椭圆孔时， 椭圆孔之短轴平行于筒体 轴线，见图
25
2、回转壳体的经向环向应力分析
图3-8 回转壳体的环向应力分析
内压力p在微体abcd上所产生的外力 的合力在法线n上的投影为Pn
Pn pdl1 dl2
在bc与ad截面上经向应力 的m 合力 在法线n上的投影为Nmn
N mn
2 m Sdl2
sin
d1
2
在ab与cd截面上环向应力 的 合力 在法线n 上的投影为 Nn
O1
表示，在图上为线段O1A。
母线
A R1
第一曲率半径
17
母线
回转轴与第二曲率半径
围绕回转轴，可形成一个曲 回转轴 面 ， 第 一 曲 率 半 径 O1A 上 到
回转轴O的曲率半径称为第
R1 O
二曲率半径，以R2表示，在
图上为线段OA。
O1
A R2
第一曲率半径
第二曲率半径
18
周向
第一曲率半径与母 线有关；
第三章 内压薄壁容器的应力分析
教学重点：
薄膜理论及其应用
教学难点：
对容器的基本感性认识
1
第一节 回转壳体的应力分析—薄膜应力理论
薄壁容器
化工设备课件第三章内压薄壁容器的应力
（2）联接边缘区的变形与应力。所谓联 接边缘是指壳体与法兰、封头或不同厚 度、不同材料的筒节、群式支座与壳体 相联接的边缘等。圆筒形容器受内压时， 由于联接边缘区的刚性不同，连接处二 者的变形大小亦不同，如图所示。
二、边缘应力的特点 图3-10所示是一内径为Di=1000 mm，壁 厚S=10 mm的钢制内压圆筒，其一端为 平板封头，且封头厚度远远大于筒体壁 厚。内压为P＝1MPa。经理论计算和实 测其内、外壁轴向应力（薄膜应力与边 缘弯曲应力的叠加值）分布情况。
第三章内压薄壁容器的设计
第一节内压薄壁圆筒的应力分析
一、薄壁容器及其应力特点 压力容器按壁厚可分为薄壁容器和厚壁容器。 通常是以容器的壁厚与其最大截面圆的内径之 比小于0.1，既S/Di＜0.1亦既K=D0/Di ≤1.2的 称为薄壁容器，超过这一范围的为厚壁容器。 化工与石油化学工业中，应用最多的是薄壁 容器。对压力容器各部分进行应力分析，是强 度设计中首先需要解决的问题。
二、内压圆筒的应力计算
1、环向应力的计算公式 采用截面法，用一通过 圆筒轴线的假象截面B-B 将圆筒刨开,移走上半部， 再从下半个圆筒上截取 长度为L的一段筒体作为 脱离体，合力为Py。 建立静力平衡方程。 外力在y轴方向上投影的
Py=
=
0
dPSin
=2RiLP =DiLP
Nz=πDSσm 2 Px= D P 4 由平衡条件得 Px-Nx=0 或 Px=Nx
既
2 DP 4
m
=πDSσm
由此得： (3-2) P---内压，Mpa； D---圆筒平均直径，亦称中径，mm; S---壁厚，mm； σm---轴向应力，Mpa。
第三章-内压薄壁容器设计
第三章内压薄壁容器设计第一节内压薄壁圆筒设计【学习目标】通过内压圆筒应力分析和应用第一强度理论，推导出内压圆筒壁厚设计公式。
掌握内压圆筒壁厚设计公式，了解边缘应力产生的原因及特性。
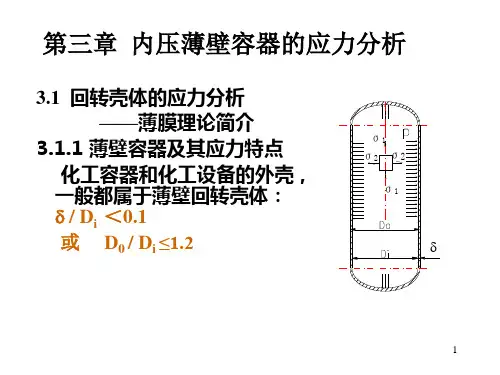
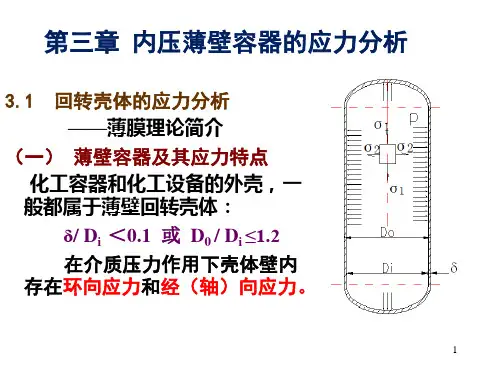
一、内压薄壁圆筒应力分析当圆筒壁厚与曲面中径之比δ/D≤0.1或圆筒外径、内径之比K=D0/D i≤1.2时，可认为是薄壁圆筒。
1、基本假设①圆筒材料连续、均匀、各向同性；②圆筒足够长，忽略边界影响（如筒体两端法兰、封头等影响）；③圆筒受力后发生的变形是弹性微小变形；④壳体中各层纤维在受压（中、低压力）变形中互不挤压，径向应力很小，忽略不计；⑤器壁较薄，弯曲应力很小，忽略不计。
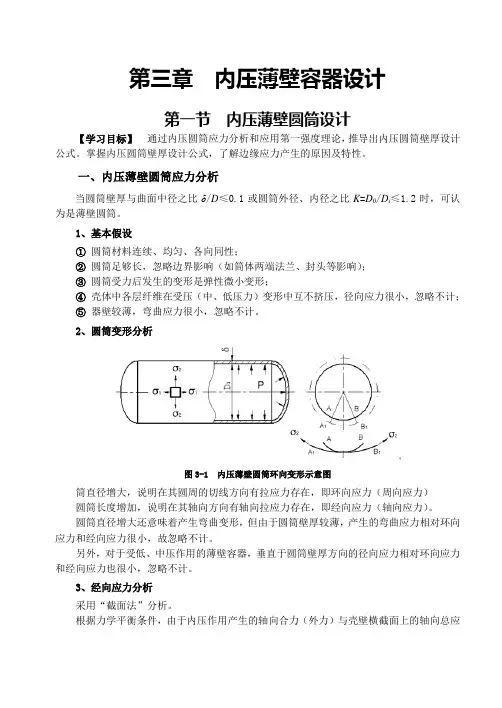
2、圆筒变形分析图3-1 内压薄壁圆筒环向变形示意图筒直径增大，说明在其圆周的切线方向有拉应力存在，即环向应力（周向应力）圆筒长度增加，说明在其轴向方向有轴向拉应力存在，即经向应力（轴向应力）。
圆筒直径增大还意味着产生弯曲变形，但由于圆筒壁厚较薄，产生的弯曲应力相对环向应力和经向应力很小，故忽略不计。
另外，对于受低、中压作用的薄壁容器，垂直于圆筒壁厚方向的径向应力相对环向应力和经向应力也很小，忽略不计。
3、经向应力分析采用“截面法”分析。
根据力学平衡条件，由于内压作用产生的轴向合力（外力）与壳壁横截面上的轴向总应力（内力）相等，即：124δσππD p D =由此可得经向应力： δσ41pD=图3-2 圆筒体横向截面受力分析4、环向应力分析 采用“截面法”分析。
图3-3 圆筒体纵向截面受力分析根据力学平衡条件，由于内压作用产生的环向合力（外力）与壳壁纵向截面上的环向总应力（内力）相等，即：22δσL LDp = （3-3）由此可得环向应力： δσ22pD= （3-4） 5、结论通过以上分析可以得到结论：122σσ=，即环向应力是经向应力的2倍。
因此，对于圆筒形内压容器，纵向焊接接头要比环向焊接接头危险程度高。
在圆筒体上开设椭圆形人孔或手孔时，应当将短轴设计在纵向，长轴设计在环向，以减少开孔对壳体强度的影响。
化工设备机械基础：第三章 内压薄壁容器的应力分析
上一内容 下一内容 回主目录
返回
2020/12/14
第二节 薄膜理论的应用
代入微体平衡方程式及区域平衡方程式并求解得：
m
PD
4
,
PD
4
推论：对相同的内压，球壳的环向应力要比同直径、 同厚度的圆筒壳的环向应力小一半，这是球壳显著的 优点。
三、受气体内压的椭球壳（椭圆形封头）
上一内容 下一内容 回主目录
（一）壳体理论的基本概念 壳体在外载荷作用下，
要引起壳体的弯曲，这种变 形由壳体内的弯曲和中间面 上的拉或压应力共同承担， 求出这些内力或内力矩的理 论称为一般壳体理论或有力 矩理论，比较复杂；
上一内容 下一内容 回主目录
返回
2020/12/14
第一节 薄膜应力理论
但是，对于壳体很薄，壳体具有连续的几何曲面，所 受外载荷连续，边界支承是自由的，壳体内的弯曲应 力与中间面的拉或压应力相比，可以忽略不计， 认为壳体的外载荷只是由中间面的应力来平衡，这种 处理方法，称为薄膜理论或无力矩理论。 1、有力矩理论 2、无力矩理论（应用无力矩理论，要假定壳体完全弹 性，材料具有连续性、均匀性各各向同性，此外，对 于薄壁壳体，通常采用以下三点假设使问题简化） 1）小位移假设 2）直法线假设 3）不挤压假设
上一内容 下一内容 回主目录
返回
2020/12/14
第二节 薄膜理论的应用
一、受气体内压的圆筒形壳体
R1
R2
r
D 2
上一内容 下一内容 回主目录
返回
2020/12/14
第二节 薄膜理论的应用
由区域平衡方程式
m
pR2
2
PD
4
代入微体平衡方程式
3章内压薄壁容器的应力PPT课件
23
综上所述，薄壁无力矩应力状态的 存在，必须满足壳体是轴对称的，同时 应保证壳体具有自由边缘。否则，不能 使用无力矩理论。但是，远离局部区域 （如壳体的连接边缘、载荷变化的分界 面、容器的支座附近等）以外的地方， 无力矩理论仍然有效。
环向应力计算公式
——微体平衡方程
sm sq p R1 R2 d
式中 sm---经向应力（MPa);
sq环向应力（MPa）；
R1----第一曲率半径（mm）； R2----第二曲率半径（mm）； p----介质压力（MPa）；
δ----壳体壁厚（mm)。
22
3.1.5薄膜理论的应用范围
1.材料是均匀的，各向同性的。 厚度无突变，材料物理性能相同； 2.轴对称——几何轴对称，材料轴对称， 载荷轴对称，支撑轴对称； 3.连续——几何连续，载荷（支撑）分布 连续，材料连续。 4.壳体边界力在壳体曲面的切平面内。 无横向剪力和弯矩作用，自由支撑等；
3
3.1.2 基本概念与基本假设
1. 基本概念
• 回转壳体
——由直线或平 面曲线绕其同 平面内的固定 轴旋转3600而 成的壳体。
4
几个典型回转壳体
5
与壳体内外表面等距离的曲面
母线：
——中间面
——即那条直线或平面曲线.
法线：
轴对称——指壳体的几何形状、约束条件
和所受外力都对称于回转轴。
6
经线：
sm
σ1 σ2 σ2
σ1 d
sq sq
2.基本假设：
（1）小位移假设。壳体受压变形，各 点位移都远小于壁厚。简化计算。
（2）直法线假设。沿厚度各点法向位 移均相同，即厚度不变。
（3）不挤压假设。沿壁厚各层纤维互 不挤压，即法向应力为零。
综上所述，薄壁无力矩应力状态的 存在，必须满足壳体是轴对称的，同时 应保证壳体具有自由边缘。否则，不能 使用无力矩理论。但是，远离局部区域 （如壳体的连接边缘、载荷变化的分界 面、容器的支座附近等）以外的地方， 无力矩理论仍然有效。
环向应力计算公式
——微体平衡方程
sm sq p R1 R2 d
式中 sm---经向应力（MPa);
sq环向应力（MPa）；
R1----第一曲率半径（mm）； R2----第二曲率半径（mm）； p----介质压力（MPa）；
δ----壳体壁厚（mm)。
22
3.1.5薄膜理论的应用范围
1.材料是均匀的，各向同性的。 厚度无突变，材料物理性能相同； 2.轴对称——几何轴对称，材料轴对称， 载荷轴对称，支撑轴对称； 3.连续——几何连续，载荷（支撑）分布 连续，材料连续。 4.壳体边界力在壳体曲面的切平面内。 无横向剪力和弯矩作用，自由支撑等；
3
3.1.2 基本概念与基本假设
1. 基本概念
• 回转壳体
——由直线或平 面曲线绕其同 平面内的固定 轴旋转3600而 成的壳体。
4
几个典型回转壳体
5
与壳体内外表面等距离的曲面
母线：
——中间面
——即那条直线或平面曲线.
法线：
轴对称——指壳体的几何形状、约束条件
和所受外力都对称于回转轴。
6
经线：
sm
σ1 σ2 σ2
σ1 d
sq sq
2.基本假设：
（1）小位移假设。壳体受压变形，各 点位移都远小于壁厚。简化计算。
（2）直法线假设。沿厚度各点法向位 移均相同，即厚度不变。
（3）不挤压假设。沿壁厚各层纤维互 不挤压，即法向应力为零。
第三章 内压薄壁容器的应力分析
60
61
联接边缘邻接的两部分壳体变形不同而又互相约束
——产生边缘应力的条件 ✓ 边缘应力的存在总是以变形受到某种限制为前提 ✓ 哪里有限制，哪里就有边缘应力 ✓ 限制越大，边缘应力越大
62
（二）边缘应力特点
（1）.局部性 只产生在一
局部区域内，边缘 应力衰减很快。见 如下测试结果：
衰减长度大约为：
mR2 sindd R1dd sin pR1R2 sin dd
m p R1 R2
微元平衡方程。又称 拉普拉斯方程。
环向应力计算公式
——微体平衡方程
m. p R1 R2
m
pR2
2
式中 m---经向应力（MPa); ---环向应力（MPa）； R1----第一曲率半径（mm）； R2----第二曲率半径（mm）； p----介质压力（MPa）；
29
圆柱壳壁内应力分布
30
31
（二） 受气体内压的球形壳体
用场：球形容器，半球形封头，无折边球形封头等。
32
33
球壳的 R1 = R2 ,则
m
pD
4
条件相同时，球壳内应力与圆筒形壳体的经向 应力相同，为圆筒壳内环向应力的一半。
1.这么好，为什么不常用？
34
（三） 受气体内压的椭球壳
用场：椭圆形封头。 成型：1/4椭圆线绕同平面Y轴旋转而成。
纬线(平形圆)：作圆锥面与壳体中间面正
交，所得交线
母线？经线
经线一定是母线，母线不一定是经线！ 7
8
母线 经线 纬线
第一曲率 半径CK1 第二曲率 半径CK2 纬平面
9
2.基本假设：
（1）小位移假设。壳体受压变形，各点位移都小 于壁厚。简化计算。
61
联接边缘邻接的两部分壳体变形不同而又互相约束
——产生边缘应力的条件 ✓ 边缘应力的存在总是以变形受到某种限制为前提 ✓ 哪里有限制，哪里就有边缘应力 ✓ 限制越大，边缘应力越大
62
（二）边缘应力特点
（1）.局部性 只产生在一
局部区域内，边缘 应力衰减很快。见 如下测试结果：
衰减长度大约为：
mR2 sindd R1dd sin pR1R2 sin dd
m p R1 R2
微元平衡方程。又称 拉普拉斯方程。
环向应力计算公式
——微体平衡方程
m. p R1 R2
m
pR2
2
式中 m---经向应力（MPa); ---环向应力（MPa）； R1----第一曲率半径（mm）； R2----第二曲率半径（mm）； p----介质压力（MPa）；
29
圆柱壳壁内应力分布
30
31
（二） 受气体内压的球形壳体
用场：球形容器，半球形封头，无折边球形封头等。
32
33
球壳的 R1 = R2 ,则
m
pD
4
条件相同时，球壳内应力与圆筒形壳体的经向 应力相同，为圆筒壳内环向应力的一半。
1.这么好，为什么不常用？
34
（三） 受气体内压的椭球壳
用场：椭圆形封头。 成型：1/4椭圆线绕同平面Y轴旋转而成。
纬线(平形圆)：作圆锥面与壳体中间面正
交，所得交线
母线？经线
经线一定是母线，母线不一定是经线！ 7
8
母线 经线 纬线
第一曲率 半径CK1 第二曲率 半径CK2 纬平面
9
2.基本假设：
（1）小位移假设。壳体受压变形，各点位移都小 于壁厚。简化计算。
内压薄壁圆筒应力分析
2020/7/10
❖ 二、回转壳体的无力矩理论 ❖ 1、有力矩理论：壳体在外载荷作用下，要引起壳体
的弯曲，这种变形由壳体内的弯曲和中间面上的拉 或压应力共同承担，求出这些内力或内力矩的理论 称为一般壳体理论或有力矩理论，比较复杂；
2020/7/10
2、 无力矩理论：对于壳体很薄，壳体具有连续的几 何曲面，所受外载荷连续，边界支承是自由的，壳 体内的弯曲应力与中间面的拉或压应力相比，小到 可以忽略不计，认为壳体的外载荷只是由中间面的 应力来平衡，这种处理方法，称为薄膜理论或无力 矩理论。
Ｐ
θ R2 M
δ
向下的力因内压引起： F=（πD2P）/4
向上的力为应力集中力在竖 直方向的分力为：
F=σm·πDδ·sinθ
根据力平衡条件：
（πD2p）/4=σmπDδ·sinθ
根据D=2R2sinθ代入上式
σm=pR2/2δ
σm
σm
M
D
δ
σm R2
O
P σm θ
M
θ
D
五、环向应力的计算公式—微体平衡 已求得经向应力σm=pR2/2δ，求环向应力，取小微分体，如 图所示。
K2
σ dθ 2 σ θ
2 R2
dθ 2 P
m
dl2
σθ
小结：薄膜理论的适用条件 薄壁无力矩应力状态的存在，必须满足：
壳体是轴对称的，即几何形状、材料、载荷的对称性与连续 性，同时需要保证壳体应具有自由边缘。
1、壳转壳体曲面在几何上是轴对称,壳体厚度无突变； 曲率半径是连续变化的，材料是各向同性的，且物理性能（ 主要是E和μ）应当是相同的；
回转壳体：以回转曲面为中间面的壳体
轴对称：我们把几何形状、所受外力、约束 条件都对称于回转轴的问题称为轴对称问题 。
❖ 二、回转壳体的无力矩理论 ❖ 1、有力矩理论：壳体在外载荷作用下，要引起壳体
的弯曲，这种变形由壳体内的弯曲和中间面上的拉 或压应力共同承担，求出这些内力或内力矩的理论 称为一般壳体理论或有力矩理论，比较复杂；
2020/7/10
2、 无力矩理论：对于壳体很薄，壳体具有连续的几 何曲面，所受外载荷连续，边界支承是自由的，壳 体内的弯曲应力与中间面的拉或压应力相比，小到 可以忽略不计，认为壳体的外载荷只是由中间面的 应力来平衡，这种处理方法，称为薄膜理论或无力 矩理论。
Ｐ
θ R2 M
δ
向下的力因内压引起： F=（πD2P）/4
向上的力为应力集中力在竖 直方向的分力为：
F=σm·πDδ·sinθ
根据力平衡条件：
（πD2p）/4=σmπDδ·sinθ
根据D=2R2sinθ代入上式
σm=pR2/2δ
σm
σm
M
D
δ
σm R2
O
P σm θ
M
θ
D
五、环向应力的计算公式—微体平衡 已求得经向应力σm=pR2/2δ，求环向应力，取小微分体，如 图所示。
K2
σ dθ 2 σ θ
2 R2
dθ 2 P
m
dl2
σθ
小结：薄膜理论的适用条件 薄壁无力矩应力状态的存在，必须满足：
壳体是轴对称的，即几何形状、材料、载荷的对称性与连续 性，同时需要保证壳体应具有自由边缘。
1、壳转壳体曲面在几何上是轴对称,壳体厚度无突变； 曲率半径是连续变化的，材料是各向同性的，且物理性能（ 主要是E和μ）应当是相同的；
回转壳体：以回转曲面为中间面的壳体
轴对称：我们把几何形状、所受外力、约束 条件都对称于回转轴的问题称为轴对称问题 。