第20讲_货币时间价值——其他年金的终值与现值

t 1
n
【例2.5】大一学生汪洋有个愿望，他希望在他大学四年中每 年末都能获得奖学金，他估计自己在四年中分别获得的奖学金 如下表所示，假设利息率为8%，1年复利1次，问这笔不等额 奖学金的复利终值和复利现值各是多少？
汪洋预期奖学金情况表
年 奖学金（元） 1年末 500 2年末 600 3年末 700 4年末 800
符号（P/F，i，n）表示，可通过查“复利现值系数表” 得知其数值.
【例2.3】大学生王美丽计划在3年末得到1000元，利息率为 6%，1年复利1次，问现在王美丽要向银行存入多少钱？ 解：
F 1000 3 P 1000 (1 6%) 0 (1 i ) n (1 6%)3 1000 ( P / F , 6%, 3）
等式两端同乘以(1+i) : (1+i) PA=A+A(1+i)-1 + …… +A(1+i)-(n-2)+A(1+i)-(n-1) 上述两式相减 :
n 1 (1 i )
i· PA=A-A(1+i)-n
PA=A
i
普通年金现值公式 : PA=A
注：
n 1 (1 i )
n 1 (1 i )
t 1 n
P0 300000 (1 2%) 4 200000 (1 2%) 3 100000 (1 2%) 1 300000 0.9238 200000 0.9423 100000 0.9804 563640(元)
三、年金终值与年金现值的计算
（2）是要有一定的时间间隔。

2.货币时间价值的表示方法
货币时间价值可以用绝对数和相对数形式来表示

0
12
n 期先付
年金终值
AAA
n 期后付
年金终值
0
12
AA
0
1
2
3
n+1 期后付 年金终值
AA
A
n-1 n A
n-1 n AA
n n+1
A
A
XFVAn A FVIFAi,n1 A A(FVIFAi,n1 1)
先付年金终值
例题
李冬每年年初为自己年幼的儿子存入银行 500元钱，使之成为十年以后儿子入读大学 的教育基金，假设银行存款利率为8%，问
为（A/F，i，n)，用它可将年金终值折算为每年需要 支付的金额；可单独制表备查。 • 例：拟在5年后还清本息和10000元，从现在起每 年需要于年末存入多少？（银行复利率10%） • 解：A＝10000×1/（F/A，10%，5)或(A/F， 10%，5)=10000/6.105＝1638(元）
7、投资回收系数
10000元，如果利息率为10%，则该富人 现在的捐款应为多少？
解：
V0
10000 1 10%
100000元
6、偿债基金
• ①含义：指在将来为偿还既定金额的债务每 年应支付的数额。
• ②计算：由年金终值公式可得
• A=F·1/(F/A，i，n) • 其中 1/(F/A，i，n)称为“偿债基金系数”，记
第二章 货币的时间价值
引例
2007年8月1日，居住在北京 通州武夷花园的张先生想出售他 的两居室住房100平方米，目前 该地段市价每平方米6300元。有 一位买主愿意一年以后以70万元 的价格买入。而2007年7月21日 央行提高基准利率后，使得一年 期的存款利率变为3.33%。那么 张先生愿意出售给他吗？

第二章一、时间价值的计算（终值与现值）：F-终值P-现值A-年金i-利率n-年数1、单利和复利:单利与复利终值与现值的关系：终值=现值×终值系数现值=终值×现指系数终值系数现指系数单利:1+ni1/（1+ni）复利:（F/P，i，n）=（1+i）n（P/F，i，n）=1/（1+i）n2、二个基本年金：普通年金的终值与现值的关系：年金终值=年金×年金终值系数年金现值=年金×年金现值系数F=A（F/A，i，n）P=A（P/A，i，n）年金系数：年金终值系数年金现值系数普通年金:（F/A，i，n）=[（1+i）n-1]/i（P/A，i，n）=[1-（1+i）-n]/i 即付年金:（F/A，i，n+1）-1（P/A，i，n-1）+13、二个特殊年金:递延年金P=A[（P/A，i，m+n）-（P/A，i，m）]=A[（P/A，i，n）（P/F，i，m）]]永续年金P=A/i4、二个重要系数:偿债基金（已知F，求A）A=F/（F/A，i，n）资本回收（已知P，求A）A=P/（P/A，i，n）5、i、n的计算:折现率、期间、利率的推算：折现率推算（已知终值F、现值P、期间n，求i）单利i=（F/P-1）/n复利i=（F/P）1/n-1普通年金：首先计算F/A=α或P/A=α，然后查（年金终值F/A）或（年金现值P/A）系数表中的n列找出与α两个上下临界数值（β1<α<β2）及其相对应的i1和i2。

用内插法计算i：（i-I1）/（α-β1）=（I2-I1）/（β2-β1）永续年金：i=A/P期间的推算（已知终值F、现值P、折现率i，求n）单利n=（F/P-1）/i复利：首先计算F/P=α或P/F=α，然后查（复利终值F/P）或（复利现值P/F）系数表中的i行找出与α两个上下临界数值（β1<α<β2）及其相对应的n1和n2。

用内插法计算n：（i-n1）/（α-β1）=（n2-n1）/（β2-β1）普通年金：首先计算F/A=α或P/A=α，然后查（年金终值F/A）或（年金现值P/A）系数表中的i行列找出与α两个上下临界数值（β1<α<β2）及其相对应的n1和n2。

补充资料资金时间价值一、含义资金时间价值是指资金经历一定时间的投资和再投资所增加的价值。

理论上：没有风险、没有通货膨胀条件下的社会平均资金利润率。

实际工作中：没有通货膨胀条件下的政府债券利率二、基本计算（终值、现值的计算）（一）利息的两种计算方式：单利计息：只对本金计算利息，各期利息相等。

复利计息：既对本金计算利息，也对前期的利息计算利息，各期利息不同。

（二）一次性收付款项1.单利的终值和现值终值 F＝P×（1＋n·i）现值 P＝F/（1＋n·i）【结论】单利的终值和现值互为逆运算。

【例题1·单选题】甲某拟存入一笔资金以备三年后使用。

假定银行三年期存款年利率为5％，若目前存到银行是30000 元，3 年后的本利和为( )。

A.34500B.35000C.34728.75D.35800【答案】A 单利计算法下：F＝P×（1＋n·i）=30000×(1+3×5%)=34500元【例题2·单选题】甲某拟存入一笔资金以备三年后使用。

假定银行三年期存款年利率为5％，甲某三年后需用的资金总额为34500 元，则在单利计息情况下，目前需存人的资金为( )元。

(职称考试2001 年)A.30000B.29803.04C.32857.14D.31500【答案】A 单利计算法下：P=F/（1+n×i）=34500/（1+3×5%）=30000 元2.复利的终值和现值终值F＝P×(1 +i)n ＝P×（F/P，i，n）现值P＝F×(1 +i)-n ＝F×（P/F，i，n）【结论】（1）复利的终值和现值互为逆运算。

（2）复利的终值系数(1 +i)n 和复利的现值系数(1 +i)-n 互为倒数。

【例题3·计算题】某人存入银行10万，若银行存款利率为5%，5年后的本利和为多少？F0 1 2 3 4 510复利：F=10×（1+5%）5＝12.763（万元）或：=10×（F/P，5%，5）=10×1.2763=12.763（万元）【例题 4·计算题】某人存入一笔钱，想 5 年后得到 10 万，若银行存款利率为 5%，问，现在应存入多少？10复利：P =10×（1+5%）-5=7.835（万元）或=10×（P/F ，5%，5）=10×0.7835=7.835（万元）（三）普通年金的终值与现值1. 年金的含义（三个要点）：定期、等额的系列收付款项。

考情分析本章是财务管理的基础章节，主要为以后章节学习打基础，内容较多，难度较大。

从考试角度来说，考试题型可以是客观题，也可以是主观题，近5年的平均分值为10分左右。

财务管理基础01货币时间价值·复利终值和现值·年金现值·年金终值·年偿债基金和年资本回收额·利率的计算02收益与风险·资产收益与收益率·资产的风险及其衡量·风险管理·证券资产组合的收益与风险·资本资产定价模型03成本性态分析·固定成本·变动成本·混合成本第一节货币时间价值一、货币时间价值的概念（★）（一）含义及衡量【注】（1）认识时间轴·横线代表时间的延续·数字代表的时间点是期末，如“2”代表的时点是第二期期末（上期期末和下期期初是同一时点，所以“2”代表的时点也可以表述为第三期期初）·“0”代表的时点是第一期期初·竖线的位置表示收付的时刻，竖线上端的数字表示收付的金额（2）利息计息方式复利计算每经过一个计息期，要将该期的利息加入本金再计算利息，逐期滚动计算，俗称“利滚利”单利计息只对本金计算利息计息期是指相邻两次计息的间隔，如一年、半年等。

除非特别说明，一个计息期一般为一年【例题】本金10万元，利率10%，分别计算单利计息和复利计息情况下3年后的本利和。

【2022年判断题】纯利率是指在没有通货膨胀、无风险情况下资金市场的最低利率。

（）『正确答案』×『答案解析』本题考核的知识点是货币时间价值的概念。

纯利率是指在没有通货膨胀、无风险情况下资金市场的平均利率。

二、复利终值和现值（★★★）（一）复利终值【例题】本金10万元，利率10%。

由上题可知：一年后的本利和：F1＝10×（1＋10％）两年后的本利和：F2＝10×（1＋10％）2三年后的本利和：F3＝10×（1＋10％）3由此递推，可知经过n年后的本利和为：F n＝10×（1＋10％）nF＝P×（1＋i）nP表示现值；i表示计息期利率；n表示计息期数；F表示终值。

先把递延年金视为普通年金，求出递延 期期末的现值，再将此现值调整到第一 期期初。
递延年金现值的计算
例15 某企业向银行借入一笔款项，银行贷款
的年利息率为8%，银行规定前10年不用还本 付息，但从第11年至第20年每年年末偿还本息 1000元，问这笔款项的现值应为多少？
思路一
P=A*[（P/A，i，n+m）- （P/A，i，m）]
A ＝ 150× （ A/F ， 8% ， 3 ） =150/3.2462=46.21万元
（三）普通年金现值的计算
P A(1 i)1 A(1 i)2 A(1 i)(n1) A(1 i)n 1 (1 i)n
P A i
P A(P / A,i, n)
举例：普通年金现值计算
例9：某企业未来5年每年年末等额从银 行取1万元，为职工发奖金，年利率3%， 现在应该存入多少金额以保证未来5年每 年末从银行等额提出1万元？
=1000*1.08*14.487
=15 645
例13 某企业租用一设备，在10年中每年年 初要支付租金5 000元，年利息率为8%， 问这些租金的现值是多少？
思路一
P=A*[（F/A，i，n-1）+1] =1000* [（F/A，8%,9）+1 ] =1000*（6.247+1） =36 235元
风险是“一定时期内”的风险。
与风险相联系的另一个概念是不确定性。严格说 来，风险和不确定性有区别。
风险可能给投资人带来超出预期的收益，也可能 带来超出预期的损失。
财务管理中的风险按形成的原因一般可分为经营 风险和财务风险两大类。
二、风险程度的衡量——概率分析法
确定概率分布 计算期望值 计算标准离差
25

四、货币时间价值涉及内容如下：〔一〕货币时间价值的概念〔二〕复利终值〔三〕复利现值〔四〕一般年金终值与现值〔五〕其他年金终值与现值回忆〔五〕其他年金终值与现值1.年金分类2.预付年金终值和现值〔1〕终值方法一：一般年金的终值：F=A×〔F/A，i，n〕预付年金的终值：F=A×〔F/A，i，n〕×〔1＋i〕方法二：一般年金的终值：F=A×〔F/A，i，n〕预付年金的终值：F=A×〔F/A，i，n+1〕-1]〔2〕现值方法一：一般年金的现值：P=A×〔P/A，i，n〕预付年金的现值：P=A×〔P/A，i，n〕×〔1＋i〕方法二：一般年金的现值：P=A×〔P/A，i，n〕预付年金的现值：P=A×〔P/A，i，n-1〕+1总结（例题）甲公司购置一台设备，付款方法为现在付 10 万元，以后每隔一年付 10 万元，共计付款 6 次。

假设年利率为 5，如果打算现在一次性付款应该付多少万元？已知：〔P/A，5，5〕=4.3295，〔P/A，5，6〕=5.0757，〔P/A，5，7〕=5.7864。

（答案）现在支付即年初支出，则此题为预付年金求现值。

由于付款 6 次，所以，n=6，因此：P=10×〔P/A，5，6〕×〔1+5〕=10×5.0757×1.05=53.29〔万元〕或=10×〔P/A，5，5〕+1]=10×〔4.3295+1〕=53.30〔万元〕提示：两种方法结果不同是系数导致的尾数差，可接受。

3.递延年金终值和现值递延年金：在第二期或第二期以后收付的系列款项，由一般年金递延形成。

〔1〕终值一般年金的终值：F=A×〔F/A，i，n〕递延年金的终值：F=A×〔F/A，i，n〕即终值不受递延期m 的影响〔2〕现值方法一〔两次折现〕：年金折完复利折P=A×〔P/A，i，n〕×〔P/F，i，m〕方法二〔先补后减〕：P=A×〔P/A，i，n+m〕-A×〔P/A，i，m〕=A×〔P/A，i，n+m〕-〔P/A，i，m〕]递延年金的计算：终值〔F〕F=A×〔F/A，i，n〕现值〔P〕P=A×〔P/A，i，n〕×〔P/F，i，m〕P=A×〔P/A，i，n+m〕-〔P/A，i，m〕]方法一：两次折现——年金折完复利折方法二：先补后减——〔n+m〕减 m（例题）某递延年金为从第 4 期开始，每期期末支付 10 万元，共计支付 6 次，假设利率为 4，相当于现在一次性支付的金额是多少局部货币时间价值系数表期数〔n〕369〔P/F，4，n〕0.88900.79030.7026〔P/A，4，n〕 2.7751 5.24217.4353（分析）（答案）本例中，由于第—次支付发生在第 4 期期末，所以递延期 m=3；由于连续支付 6 次，因此 n=6。

由于货币直接或间接地参与了社会资本周转，从而获得 了价值增值。货币时间价值的实质就是货币周转使用后 的增值额
➢ 作为资本投放到企业的生产经营当中，经过一段 时间的资本循环后，会产生利润
➢ 进入了金融市场，参与社会资本周转，从而间接 地参与了企业的资本循环周转
货币时间价值 ——表现形式
货币在经过一段时间后的增值 额
若每年本利摊还60万，几年可还清? 新旧屋的房贷利 率都设为4%，设此期间房价水平不变。
1 计算旧屋目前每年摊还金额
24.66万
4 新屋还需要的贷款 648万
2 计算3年后旧屋还剩下多少房贷额 148万
3 计算出售旧屋的净现金流入
5 新屋每年本利摊还额 47.68万
6 若每年还60万，几年可还清
352
14.42
规划初步——子女教育金规划
规划让子女出国留学，目前留学的费用为150万元， 预定子女10年后出国时要准备好此笔留学基金，学费 成长率为3%，为了准备此笔费用，假设投资报酬率可 达8%，父母每年要投资多少钱?
若父母的年储蓄投资额为20万，需要有多高的报酬率 才能达到筹备子女教育金的目标?
5% 1.050 1.103 1.158 1.216 1.276 1.340 1.407 1.477 1.551 1.629 1.710 1.796 1.886 1.980 2.079
6% 1.060 1.124 1.191 1.262 1.338 1.419 1.504 1.594 1.689 1.791 1.898 2.012 2.133 2.261 2.397
（2）从第5年开始，每年年初支付25万元，连续 支付10次，共支付250万元. 假设市场的资金成本率（即最低报酬率）为 10%，你认为该应选择哪个方案？

等待多久可以涨到 $10,000? 这个规则对于在5%~20%这个范围内的折现率是相当准确的。
12
复利记息和贴现图示:
元
以 9%的 利率 复利计 息
￥ 2 367.36
￥ 1 000
￥ 1 90 0 单利值 ￥ 1 000
￥ 422.41
以 9%的 利率 贴现
1 2 3 4 5 6 7 8 9 10 未来某年
例2：利率多少是足够的？
根据现值、终值、期数求利率？
假设一所大学的教育费用在你的孩子18岁上大学时总数将达到 $50,000 。你今天有$5,000用于投资。 利息率为多少时你从投 资中获得的收入可以解决你孩子的教育费用？
解r:
FVT = PV (1 + r)T 50000 = 5000 x (1 + r)18 (1 + r)18= 10 (1 + r) = 10(1/18) r= 0.13646 = 13.646%
30
•非普通年金的终值及现值的计算
➢预付年金终值的计算:
n1
FV AA(1r)t A
t0
31
例1：购房计划写到这里
你准备购买一套住房，支付预付定金和按揭借款手 续费共计$20,000. 借款手续费预计为按揭借款额 的4%. 你的年收入为$36,000，银行同意你以月收 入的28％做为每月的抵押偿还额. 这笔借款为30年 期的固定利率借款，年利率为6% ，每月计息一次 (即月息.5%). 请问银行愿意提供的借款额为多少? 你愿意出价多少购买这套住房?
第3章 货币时间价值
1. 单利与复利 2. 终值与现值 3. 年金
1
关键概念和技巧
如何确定今天的一笔投资在未来的价值 如何确定未来的一笔现金流入在今天的价值 如何确定投资回报率 能计算具有多重现金流量的项目的终值、现

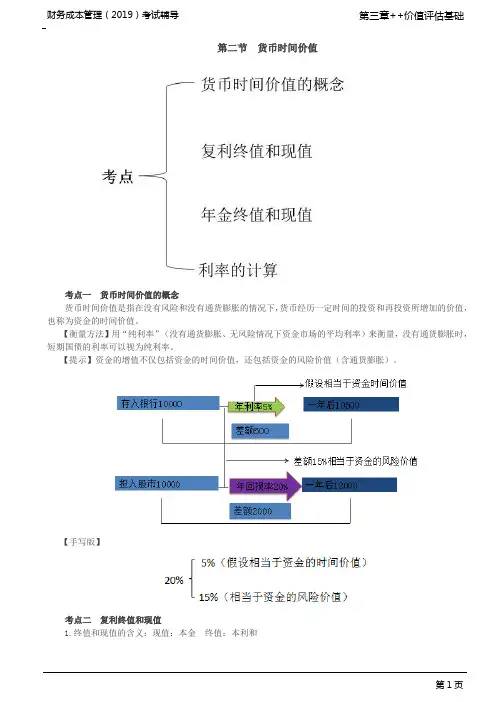
第二节货币时间价值考点一货币时间价值的概念货币时间价值是指在没有风险和没有通货膨胀的情况下，货币经历一定时间的投资和再投资所增加的价值，也称为资金的时间价值。

【衡量方法】用“纯利率”（没有通货膨胀、无风险情况下资金市场的平均利率）来衡量，没有通货膨胀时，短期国债的利率可以视为纯利率。

【提示】资金的增值不仅包括资金的时间价值，还包括资金的风险价值（含通货膨胀）。

【手写版】考点二复利终值和现值1.终值和现值的含义：现值：本金终值：本利和2.计算公式中使用的表达符号：P:现值F:终值i：计息期利率n:计息期数3.计算的基本方法（复利计息方法）：【解释】复利计息方法就是“利滚利”，（本金计息、前期的利息也计息）4.复利终值的计算（一次性收付款项的终值的计算）：F=P(1+i)n式中，(1+i)n为复利终值系数（教材附表1），记作（F/P，i，n）；n为计算利息的期数。

【例题·计算题】某人将100元存入银行，复利年利率为2%，求5年后的终值。

【分析】F=P（1+i）n=100×（F/P，2%，5）=100×1.1041=110.41（元）5.复利现值的计算（一次性收付款项的现值的计算）P=F(1+i)-n式中(1+i)-n为复利现值系数（教材附表2），记作（P/F，i，n）；n为计算利息的期数。

【例题·计算题】某人存入一笔钱，想5年后得到10万，若银行存款利率为5%，要求计算按照复利计息，现在应存入银行多少资金？【分析】按照复利计息：P＝10×（1+5%）-5=10×（P/F，5%，5）＝10×0.7835＝7.835（万元）。

【总结】（1）复利终值和复利现值互为逆运算。

（2）复利终值系数（1＋i）n和复利现值系数1/（1＋i）n互为倒数。

考点三年金终值与现值【年金的含义】：金额相等、间隔时间相同的系列收支。

【提示】年金用符号“A”表示。

二、货币时间价值【熟悉】 二、货币时间价值【熟悉】 （一）货币时间价值 1.定义 一定量货币资本在不同时点上的价值量差额； 通常情况下，它是指没有风险也没有通货膨胀情况下的社会平均资金利润率，是利润平均化规律发生作用的结果。

2.货币时间价值计算的性质 将某一时点的货币价值金额（按照某一收益率）折算为其他时点的价值金额。

（二）货币时间价值计算的基础概念 1.时间轴 ①以0为起点（目前进行价值评估及决策分析的时间点）。

②时间轴上的每一个点代表该期的期末及下期的期初。

2.终值与现值 终值（F）：现在一定量的货币折算到未来某一时点的本利和。

现值（P）：指未来某一时点上一定量的货币折算到现在所对应的金额。

3.复利：是指不仅对本金计算利息，还对前期所产生的利息计算利息的一种计息方式。

（三）复利终值和复利现值 1.复利终值：一次性款项的终值计算；已知：P，r，n，求F。

为复利终值系数，一般记作（F/P，r，n）。

【例6－9】甲将100元存入银行，复利利率为2％，求5年后的终值。

2.复利现值：一次性款项的现值计算；已知：F，r，n，求P。

为复利现值系数，一般记作（P/F，r，n）。

【例6－10】甲为了5年后能从银行取出100元，在复利年利率为2％的情况下，求当前存入金额。

3.复利终值和复利现值互为逆运算，复利终值系数与复利现值系数互为倒数。

（四）年金终值和年金现值 1.年金的概念 年金是指间隔期相等的系列等额收付款项。

①系列：通常是指多笔款项，而不是一次性款项； ②定期：每间隔相等时间（未必是1年）发生一次； ③等额：每次发生额相等。

2.年金终值或现值 系列、定期、等额款项的复利终值或现值的合计数。

3.年金的类型 （1）普通年金（后付年金）。

是指从第一期起，在一定时期内每期期末等额收付的系列款项。

①普通年金终值 称为年金终值系数，记作（F/A，r，n）。

②普通年金现值 称为年金现值系数，记作（P/A，r，n）。

33
答案：(1)125.97万元；（2）126.53万元；（3） 根据（2）不能满足；（4）25.05万元
34
小结
重点：现值、终值、年金的 概念理解和计算
难点：递延年金的计算
35
第二节 风险报酬
36
一、风险报酬的概念
（一）风险的含义 事物的未来结果分类 确定型 → 唯一结果、必然发生 风险型 → 多种可能结果、知道发生的概率 不确定型 →多种可能结果、不知道发生的概率 在财务管理的实践中，
P A
i

0
1234
AA AA
A(1+i)0 A(1+i)-1
A(1+i)-2
A(1+i)-3
P

A1
(1 i
i)n
(1
i)
预付年金现值
P

1 (1 i)(n1)
A
i


A
P

A1

(1
i) i

(
n 1)
1
（1）假设每年复利一次，则2007年1月1日该笔存款 的终值是多少？
（2）假设每半年复利一次，则2007年1月1日该笔存 款的终值是多少？
（3）假设该公司希望2007年1月1日该笔存款的终值 达到130万元，按照每半年复利一次，试问目前的利率能 否满足该公司的要求？ （4）计算该公司今后5年内每年末平均可提取的现金数。
指各期期初等额的收付款项。 （1）预付年金终值的计算
公式：F=A（1+i）+A（1+i）2+……+A（1+i）n F=A（F/A，i，n）（1+i）

2.4预付年金终值
(1)与同期普通年金比 多一个计息期
(1+ i ) F=A
i
n
−1
(1+ i )
2.4预付年金终值
(2)与n+1期普通年金比,计息期数相同,但少 一个付款A
2.4 预付年金终值
A A A 各期期初支 付的年金 A
0
1
2
2
3
3
F=100×（1+10%）+100×（1+10%） + 100×（1+10%） =364
1.2 货币时间价值的定义
在发达的商品经济条件下， 在发达的商品经济条件下，商品流通的 变化形态是： ---G 变化形态是： G--- W ---G’ G ’ = G + △G ， 货币经过一定时间的投资和再投资所增 加的价值称为货币的时间价值。 加的价值称为货币的时间价值。 表现形式： 表现形式： 单位时间的报酬对投资的百分率。 单位时间的报酬对投资的百分率。
2.2 普通年金的终值
普通年金终值计算公式推导过程： 普通年金终值计算公式推导过程： FAn=A+A（1+i）+A（1+i）2+……+A（1+i）n-1 （ ） （ ） （ ） F(1+i）= A(1+i）+A（1+i）2+A 1+i）3+… …+A（1+i）n ） ） （ ） ） （ ） 用（2）-（1）得： ）（ ）
A A
各期期末收 各期期末收 付的年金 A
0
1
2
3
2.2 普通年金的终值
i = 10%
A
A

普通年金终值计算公式的推导如下：
0 1 2 n-2 n-1 n
理 财
A
A
A
A
A
A(1+i)0 A(1+i)1 A(1+i)2
FVAn = A(1+i)0+A(1+i)1+A(1+i)2+…+A(1+i)n-2+A(1+i)n-1
其中(1+i)0+(1+i)1+(1+i)2+…+(1+i)n-2+(1+i)n-1为一公比为 1+i的等比数列求和式，其值由i和n确定，称其为利率为i期 数为n的年金终值系数，简写为FVIFAi,n。
第二节 风险报酬
思考：你认为什么是风险？
理 财
一、风险的概念
•
在做某件事乊前我们就知道这件事必然会 出现什么样的结果，那么做这事有风险吗？ 答：没有风险。 • 如果我们判断：这事八九成是一个什么什 么结果，我们会得出什么结论？
答：做这事很有把握，风险不大。
如果我们说这事结果很难说，你会得 出什么结论？ 答：做这事风险很大。
理 财
课堂作业
1.某人准备为他刚读初中一年级的小 孩存一笔 款以支付其读大学的学费。预计６年以后的 学费是４万元，现银行存款利率为５％，那 么此人现在应存入多少钱？
当2中每年存款额相等时则有简便算 法，这就是年金的计算。
理 财
四、年金终值与年金现值的计算
年金是一定时期内发生的一系列金额相等的 收支款项，如折旧、租金、养老金、银行按 揭贷款的等额还款额、零存整取或整存零取 储蓄等等。年金按款项收付发生的时点不同 分为普通年金（后付年金）、先付年金、延 期年金、永续年金等。

第一节货币时间价值知识点：货币时间价值的含义货币时间价值，是指在没有风险和没有通货膨胀的情况下，货币经历一定时间的投资和再投资所增加的价值，也称为资金的时间价值。

货币时间价值的相对数表示，纯粹利率＝，即在没有通货膨胀、无风险情况下资金市场的平均利率。

【提示】没有通货膨胀时，短期国债利率可视为纯利率。

知识点：货币时间价值的基础概念（补充）一、终值与现值现值：指未来某一时点上的一定的货币量折算到现在所对应的货币量。

一般用P来表示现值。

终值：指现在一定的货币量折算到未来某一时点所对应的货币量。

一般用F来表示终值。

【提示】由于货币时间价值的存在，不同时间单位货币的价值不相等，所以，不同时间的货币量不宜直接进行大小的比较，需要换算到相同的时点（换算到现值或终值）进行比较才有意义。

二、单利与复利单利计息：是指在计算利息时，只有本金计算利息，而以前各期利息在下一个利息周期内不计算利息的计息方法。

复利计息：是指每经过一个计息期（一年、半年、一月等），要将该期的利息加入本金再计算下一期的利息，逐期滚动计算，俗称“利滚利”。

【提示】通常在换算时广泛使用复利（利滚利）计息的方法。

知识点：复利终值和现值★★（一个点到一个点的价值换算）（一）复利的终值（已知P，求F）F＝P×（1＋i）n＝P×（F/P，i，n）其中：i表示计息期利率，n表示计息期数。

（1+i）n称为复利终值系数或1元的复利终值，记作（F/P，i，n），可查“复利终值系数表”（见本书附表一）：复利终值系数表期数 1% 2% 3% 4% 5% 6% 7% 8% 9% 10%1 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.12 1.0201 1.0404 1.0609 1.0816 1.1025 1.1236 1.1449 1.1664 1.1881 1.213 1.0303 1.0612 1.0927 1.1249 1.1576 1.191 1.225 1.2597 1.295 1.3314 1.0406 1.0824 1.1255 1.1699 1.2155 1.2625 1.3108 1.3605 1.4116 1.46415 1.051 1.1041 1.1593 1.2167 1.2763 1.3382 1.4026 1.4693 1.5386 1.61056 1.0615 1.1262 1.1941 1.2653 1.3401 1.4185 1.5007 1.5869 1.6771 1.77167 1.0721 1.1487 1.2299 1.3159 1.4071 1.5036 1.6058 1.7138 1.828 1.94878 1.0829 1.1717 1.2668 1.3686 1.4775 1.5938 1.7182 1.8509 1.9926 2.14369 1.0937 1.1951 1.3048 1.4233 1.5513 1.6895 1.8385 1.999 2.1719 2.357910 1.1046 1.219 1.3439 1.4802 1.6289 1.7908 1.9672 2.1589 2.3674 2.5937【例题】某人将100万元存入银行，年利率为10%，计算一年、两年后的本利和。

2015年全国会计专业技术中级资格考试内部资料财务管理第二章 财务管理基础知识点：货币时间价值的计算——预付年金终值和现值● 详细描述：预付年金终值和现值的计算公式方法1：利用同期普通年金的公式乘以（1+i）预付年金终值方法1： =同期的普通年金终值×（1+i）=A×（F/A，i，n）×（1+i）方法2： =年金额×预付年金终值系数=A×[（F/A，i，n+1）-1]预付年金现值方法1： =同期的普通年金现值×（1+i）=A×（P/A，i，n）×（1+i）方法2： =年金额×预付年金现值系数=A×[（P/A，i，n-1）+1]方法2：利用期数、系数调整系数间的关系如下图：例题：1.已知（P/A，8%，5）=3.9927，（P/A，8%，6）=4.6229，（P/A，8%，7）=5.206 4，则6年期、折现率为8%的预付年金现值系数是（）。

A.2.9927B.4.2064C.4.9927D.6.2064正确答案：C解析：本题考查预付年金现值系数与普通年金现值系数的关系。

即预付年金现值系数等于普通年金现值系数期数减1系数加1或用同期的普通年金系数乘以（1+i），所以6年期折现率为8%的预付年金现值系数=[（P/A，8%，6－1）+1]=3.9927＋1=4.9927。

或者=4.6229×(1.08)=4.9927。

2.已知（P/A，8%，5）＝3.9927，（P/A，8%，6）＝4.6229，（P/A，8%，7）＝5. 2064，则6年期、折现率为8%的预付年金现值系数是（）。

A.2.9927B.4.2064C.4.9927D.6.2064正确答案：C解析：6年期、折现率为8%的预付年金现值系数＝[（P/A，8%，6－1）＋1]＝3.9927＋1＝4.9927。

3.下列各项中，其数值等于预付年金终值系数的有（）。

2015年全国会计专业技术中级资格考试内部资料财务管理第二章 财务管理基础知识点：货币时间价值的计算——递延年金终值和现值● 详细描述：（1）递延年金终值【结论】递延年金终值只与A的个数（n）有关，与递延期（m）无关。

F递=A（F/A,i,n）（2）递延年金现值方法1：两次折现。

递延年金现值P= A×（P/A, i, n）×（P/F, i, m）递延期m（第一次有收支的前一期），连续收支期n方法2：先加上后减去。

递延年金现值P=A×（P/A，i，m + n）-A×（P/A，i，m）例题：1.有一项年金，前3年无流入，后5年每年年初流入500万元，假设年利率为10%，其现值为（）万元。

A.1994.59B.1566.36C.1813.48D.1423.21正确答案：B解析：现值＝500×（P/A，10%，5）×（P/F，10%，2）＝1566.36（万元）2.某递延年金，前3年没有现金流入，后5年每年年初有等额的现金流入100万元，折现×率为10%，下列关于该递延年金现值的表达式中，不正确的是（） 。

A.100×(P/A,10%,5)×(P/F,10%,2)B.100×(P/A,10%,5)×(P/F,10%,3)C.100×[(P/A,10%,4)+1]×(P/F,10%,3)D.100×(F/A,10%,5)×(P/F,10%,7)正确答案：B解析：本题中，第一次现金流入发生在第4年初，相当于第3年末。

100×(P/A,10%,5)表示的是第3年初的现值，进一步折现到第1年初，还需要折现2期，因此，选项A的表达式正确，选项B的表达式不正确；100×[(P/A,10%,4)+1]表示的是第4年初的现值，进一步折现到第1年初，还需要折现3期，因此，选项C的表达式正确；100×(F/A，10%,5)表示的是第7年末的终值，进一步折现到第1年初，需要折现7期，因此，选项D的表达式正确。