圆的周长(2)

数学优质教案《圆的周长》精选一、教学内容本节课选自人教版小学数学六年级上册，涉及《圆的周长》章节。

详细内容包括：圆周长的定义，圆周率的含义，圆周长计算公式的推导及应用，以及相关练习题的解析。

二、教学目标1. 知识目标：让学生理解圆周长的概念，掌握圆周长的计算公式，并能运用公式解决实际问题。

2. 能力目标：培养学生运用圆周长知识解决实际问题的能力，提高学生的空间想象力和逻辑思维能力。

3. 情感目标：激发学生对数学学习的兴趣，增强学生合作学习的意识。

三、教学难点与重点教学难点：圆周长计算公式的推导及运用。

教学重点：圆周长的概念，圆周率的意义，圆周长计算公式的掌握。

四、教具与学具准备教具：圆模型、直尺、圆规、计算器。

学具：练习本、铅笔、直尺、圆规。

五、教学过程1. 实践情景引入通过展示生活中的圆形物品，如车轮、硬币等，引导学生思考：这些圆形物品的周长该如何计算？2. 新课导入（1）让学生观察圆形物品，引导学生发现圆的周长是指圆形边缘的长度。

（2）介绍圆周率的概念，引导学生理解圆周率是圆周长与直径的比值。

（3）讲解圆周长的计算公式：C=πd或C=2πr。

3. 例题讲解（1）给出一个圆的直径或半径，让学生计算圆的周长。

（2）给出一个圆的周长，让学生求出圆的直径或半径。

4. 随堂练习让学生完成教材中的练习题，巩固圆周长的计算方法。

5. 小组讨论组织学生进行小组讨论，探讨圆周长在实际生活中的应用。

六、板书设计1. 圆周长的定义2. 圆周率的意义3. 圆周长计算公式：C=πd或C=2πr4. 例题解析5. 练习题七、作业设计1. 作业题目（1）计算一个直径为10cm的圆的周长。

（2）已知一个圆的周长为31.4cm，求这个圆的半径。

2. 答案（1）C=πd=3.14×10cm=31.4cm（2）r=C/2π=31.4cm/2×3.14≈5cm八、课后反思及拓展延伸1. 反思：本节课学生对圆周长的概念和计算方法掌握程度如何？在教学中是否存在需要改进的地方？2. 拓展延伸：让学生探讨圆周率在生活中的应用，了解圆周率的近似值及其计算方法。

圆的底面周长公式是什么
圆的底面周长公式是：C=πd=2πr.
【拓展资料】
圆的周长=圆周率×直径：c=πd
圆的周长=圆周率×2×半径：c=2πr
1.到定点的距离等于定长的点的集合叫做圆。

这个定点叫做圆的圆心，通常用字母“o”表示。

2.连接圆心和圆周上任意一点之间的连线叫做半径，通常用字母“r”表示。

3.通过圆心并且两个端点都在圆周上的线段叫做直径，通常用字母“d”表示。

怎么计算圆的周长：
（1）围成圆的曲线的长叫做圆的周长。

（2）圆周率：圆的周长和直径的比值叫做圆周率。

用字π表示。

π＝
3.14159265……它是一个无限不循环小数。

实际应用中常取它的近似值π＝3.14。

（3）因为圆的周长总是直径的π倍，所以计算周长的公式是：c＝πd或c＝2πr。

其中c表示周长。

（d表示圆的直径，r表示圆周的半径）。

六（）班姓名：（）书写：（）等级：（）第五单元—圆（5）一．想一想，填一填。

1.用一根长12.56m的铁丝围成一个圆，这个圆的半径是（）m。

2.要画一个周长是18.84cm的圆，圆规两脚尖的距离应取（）cm。

3.在一块直径是1.2m的圆形桌布周围缝一条花边，接头处有5cm，这条花边用布（）m。

计算：4.一个边长是4cm的正方形纸最多可以剪出（）个直径是2cm的圆，每个圆的周长是（）cm。

5．用篱笆围成一面靠墙的半圆形栅栏（如图），这个半圆形栅栏直径是8m，篱笆长（）m。

计算：6.一块正方形铁皮，周长是80cm，要剪下一个最大的圆，这个圆的直径是（）cm．计算：7.大圆的直径为0.8m，小圆的直径为3m，大圆与小圆的直径之比是（）；大4圆与小圆的周长之比是（）。

8.在一个长7cm，宽5cm长方形纸上剪下一个最大的圆，它的周长是（）cm。

9.如图，大圆的周长是9.42cm，小圆的周长是（）cm。

计算：10.龙一鸣把一根6.4m长的绳子绕在一棵大树的树干（横截面近似于圆）上，绕了两圈还余0.12m，这棵树的树干的直径大约是（）m。

计算：11.一个半圆形的半径是4cm，它的周长是（）cm。

图：公式：计算：二．求下面各图中涂色部分的周长。

（3）三．解决问题。

1.刘奶奶家的菜园如下图所示，要给菜园围一圈栅栏，需要多少米长的栅栏？2.有一个周长为40.82dm的圆形洞口，一个身高为1.45m的小女孩不能直身过去。

如果这个洞口周长增加12.56dm，那么这个小女孩能直身通过吗？3.刘大爷用41.12m长的篱笆围了一个半圆形的花圃，这个花圃的半径是多少米？。

圆的周长是什么圆的周长=圆周率×半径×2。

圆形的周长=圆周率×半径×2，如一个半径为2cm的圆，它的周长就是 3.14×2×2=12.56cm。

在古代，这个问题几乎是依赖于对实验的归纳。

人们在经验中发现圆的周长与直径有着一个常数的比，并把这个常数叫做圆周率。

于是自然地，圆周长就是：圆周率×半径×2或者圆周率×直径。

圆是一种几何图形。

根据定义，通常用圆规来画圆。

同圆内圆的直径、半径的长度永远相同，圆有无数条半径和无数条直径。

圆是轴对称、中心对称图形。

对称轴是直径所在的直线。

同时，圆又是“正无限多边形”，而“无限”只是一个概念。

圆可以看成由无数个无限小的点组成的正多边形，当多边形的边数越多时，其形状、周长、面积就都越接近于圆。

所以，世界上没有真正的圆，圆实际上只是一种概念性的图形。

圆的面积公式：圆的面积计算公式：S＝πr²或S＝πd²÷4或C²÷（4π）把圆分成若干等份，可以拼成一个近似的长方形。

长方形的宽相当于圆的半径。

圆锥侧面积：S＝πrl （l为母线长）关于圆的其他公式：圆面积=圆周率×半径×半径。

半圆的面积：S半圆=(πr2)÷2。

半圆的面积=圆周率×半径×半径÷2。

圆环面积：S大圆－S小圆=π(R2-r2)（R为大圆半径，r为小圆半径）。

圆环面积=外大圆面积－内小圆面积。

圆的周长怎么求公式是什么
圆的周长公式：周长L=2πr（其中r为圆的半径，π为圆周率，通常情况下取 3.14）。

圆周率π是圆的周长与直径的比值，一般用希腊字母π表示，是一个在数学及物理学中普遍存在的数学常数。

圆的周长怎么求公式是什么
1圆的周长算法
圆的周长=3.14x圆的直径=2x3.14x圆的半径，即：C=πd=2πr。

其中，C代表周长，π代表圆周率，d代表直径，r代表半径。

圆的简介:
圆是一种几何图形。

平面上到定点的距离等于定长的所有点组成的图形叫做圆。

当一条线段绕着它的一个端点在平面内旋转一周时，它的另一个端点的轨迹叫做圆。

圆的面积和体积计算公式:
1、计算圆的面积公式是：半径×半径×3.14。

2、计算圆的体积公式是：半径×半径×3.14×高。

2圆周率π介绍
后来的数学家们就想办法算出这个π的具体值，数学家刘徽用的是“割圆术”的方法，也就是用圆的内接正多边形和外切正多边形的周长逼近圆周长，求得圆接近192边型，求得圆周率大约是3.14。

割圆术的大致方法在中学的数学教材上就有。

然而必须看到，它很大程度上只是计算圆周率的方法，而圆周长是C=π*d 似乎已经是事实了，这一方法仅仅是定出π的值来。

仔细想想就知道这样做有问题，因为他们并没有从逻辑上证明圆的周长确实正比于直径，更进一步说他们甚至对周长的概念也仅是直观上的、非理性的。

圆的周长优秀教案圆的周长优秀教案1教学目标：1、通过教学使学生学会根据圆的周长求圆的直径、半径。

2、培养学生逻辑推理能力。

3、初步掌握变换和转化的方法。

教学重点：求圆的直径和半径。

教学难点：灵活运用公式求圆的直径和半径。

教学时间：一课时教学过程：一、复习。

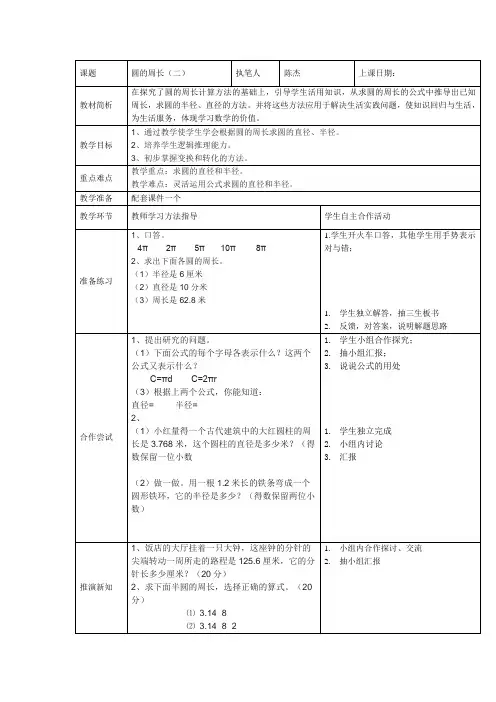
1、口答。

4π 2π 5π 10π 8π2、求出下面各圆的周长。

《圆的周长（2）》教学设计《圆的周长（2）》教学设计《圆的周长（2）》教学设计C=πd c=2πr《圆的周长（2）》教学设计 3.14×2 2×3.14×4=6.28(厘米) =8×3.14=25.12(厘米)二、新课。

1、提出研究的问题。

（1）你知道表示什么吗？（2）下面公式的每个字母各表示什么？这两个公式又表示什么？C=πd C=2πr（3）根据上两个公式，你能知道：直径=周长÷圆周率半径=周长÷（圆周率×2）2、学习练习十四第2题。

（1）小红量得一个古代建筑中的大红圆柱的周长是3.768米，这个圆柱的直径是多少米？（得数保留一位小数）已知：c=3.77 求：d=?（2）做一做。

用一根1.2米长的铁条弯成一个圆形铁环，它的半径是多少？（得数保留两位小数）三、巩固练习。

1、饭店的大厅挂着一只大钟，这座钟的分针的尖端转动一周所走的路程是125.6厘米，它的分针长多少厘米？《圆的周长（2）》教学设计2、求下面半圆的周长，选择正确的算式。

⑴ 3.14×8⑵ 3.14×8×2⑶ 3.14×8÷2+83、一只挂钟分针长20c，经过30分后，这根分针的尖端所走的路程是多少厘米？经过45分钟呢？（1）想：钟面一圈是60分钟，走了30分，就是走了整个钟面的《圆的周长（2）》教学设计，也就是走了整个圆的《圆的周长（2）》教学设计。

而钟面一圈的周长是多少？20×2×3.14=125.6（厘米）（2）想：钟面一圈是60分钟，走了45分，就是走了整个钟面的《圆的周长（2）》教学设计，也就是走了整个圆的《圆的周长（2）》教学设计。