除法的初步认识 ppt

除法的初步认识摘要除法是数学中的一种基本运算符，用于将一个数称为除数除以另一个数称为被除数，得到商。

本文将介绍除法的概念、符号表示、求解方法、特殊情况处理以及一些常见的应用场景。

通过对除法的初步认识，读者将能够更好地理解和运用除法。

1. 概念除法是一种数学运算，用于将一个数称为除数除以另一个数称为被除数，得到商。

除法的结果可以是一个整数、小数或者分数。

2. 符号表示除法运算可以用不同的符号表示，可以使用斜杠（/）表示除法，也可以使用分数线（÷）表示除法。

例如，10除以2可以表示为10/2或者10÷2。

3. 求解方法3.1 短除法短除法是一种常用的求解除法的方法。

具体步骤如下：1.将除数和被除数写在一条横线上，除数在上面，被除数在下面；2.从被除数的最高位开始，依次将被除数中的各位数与除数进行除法运算；3.将得到的商写在一条横线上，上面一行的商写在下面一行的商前面；4.用得到的商乘以除数，得到一个中间结果；5.用中间结果减去被除数，得到一个余数；6.将余数的下一位数和除数相加，得到下一个中间结果；7.重复步骤4、5、6，直到被除数的最后一位运算完毕。

3.2 长除法长除法是一种更复杂但更通用的求解除法的方法。

长除法的步骤如下：1.将除数和被除数写在一条横线上，除数在上面，被除数在下面；2.从被除数的最高位开始，向下一位扩展；3.判断除数是否可以整除被除数的当前位和下一位；4.如果可以整除，则将商写在一条横线上，上面一行的商写在下面一行的商前面；5.如果不能整除，则将除数与被除数的当前位相除，得到一个商；6.用得到的商乘以除数的当前位，得到一个中间结果；7.将中间结果减去被除数的当前位和下一位，得到一个余数；8.将余数的下一位数和除数相加，得到下一个中间结果；9.重复步骤5、6、7、8，直到被除数的最后一位运算完毕。

4. 特殊情况处理在除法中，存在一些特殊的情况需要特别处理：4.1 除数为零除数为零是不合法的，因为在数学中除以零是未定义的。

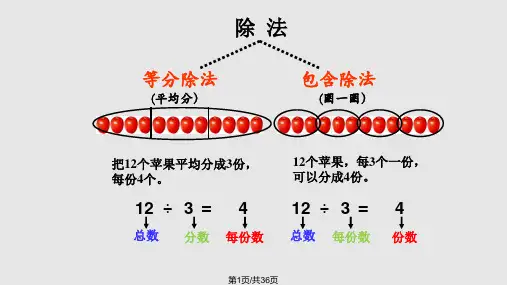
除法的初步认识1. 什么是除法？除法是数学中的一种基本运算，用于将一个数分成几个等分的过程。

在数学符号中，除法通常用除号（÷）表示。

2. 除法的表示方法2.1 竖式除法竖式除法是一种常见的除法表示方法，常用于小学生学习除法运算。

它的基本操作方法如下：_____d) n其中，d表示除数，n表示被除数。

除法的结果称为商，通常用q来表示。

2.2 分数形式除法还可以表示为分数形式。

当除数无法整除被除数时，除法运算的结果通常是一个分数。

分数由一个分子和一个分母组成，分子表示被除数，分母表示除数。

n---d3. 除法的性质除法具有以下几个基本性质：3.1 唯一性除法具有唯一性，即给定被除数和除数，商是唯一确定的。

例如，对于被除数为10，除数为2的除法运算，商必然为5。

3.2 准确性除法运算的结果应该准确表示被除数能被除数整除的次数。

如果结果不准确，则说明运算出现错误。

3.3 交换律除法具有交换律，即被除数和除数的顺序可以颠倒，得到的商是相同的。

例如，10 ÷ 2 和 2 ÷ 10 的商都是5。

3.4 结合律除法具有结合律，即多个除法运算可以合并成一个除法运算。

例如，(15 ÷ 3) ÷ 2 和 15 ÷ (3 × 2) 的商都是2.5。

4. 除不尽的情况当除数无法整除被除数时，除法运算将产生一个除不尽的余数。

在竖式除法中，余数通常写在除号上方的横线上。

例如： _____d) n- n_______r其中，r表示余数。

5. 除法的应用除法是实际生活中广泛应用的数学运算，它可以用于解决各种问题，包括：•分配问题：将一定数量的物品分成若干份，每份的数量相同。

•比例问题：根据已知比例关系，求解未知量。

•计算平均值：将多个数值相加后除以个数，求得平均值。

6. 总结除法是数学中一种基本的运算，用于将一个数分成若干等分。

它有多种表示方法，包括竖式除法和分数形式。