江西省2020届高三数学上学期模拟检测试题文

抚州市2020年高中毕业班教学质量监测卷文科数学说明：1.全卷满分150分，考试时间120分钟。

2.全卷分为试题卷和答题卡，答案要求写在答题卡上，不得在试题卷上作答，否则不给分。

第I 卷(选择题共60分)一、选择题：本大题共12小题，每小题5分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知全集U ＝{－1，0，1，2，3，4}，集合A ＝{－1，1，2，4}，集合B ＝{x ∈N|y ，则A ∩(U ðB)＝A.{－1，2，3，4}B.{－1，4}C.{－1，2，4}D.{0，1}2.已知i 为虚数单位，z ·21i-＝1＋2i ，则复数z 的虚部是 A.32 B.32i C.12i D.123.已知等差数列{a n }满足a 2＋a 4＝6，a 5＋a 7＝10，则a 18＝A.12B.13C.133 D.1434.已知a ，b ∈R ，则“a ＋2b ＝0"是“ab＝－2”成立的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件 5.113232,5,log 2-的大小关系是 A.1132325log 2-<< B.1132352log 2-<< C.11323log 252-<< D.113235log 22-<<6.已知tan(α＋6π)＝35-，则sin(2α＋3π)＝A.817B.－817C.1517D.－15177.设x ，y ∈R ，a ＝(x ，1)，b ＝(2，y)，c ＝(－2，2)，且a ⊥c ，b//c ，则|2a ＋3b －c|＝A.234B.26C.12D.2108.设函数f(x)＝e x＋2x－4的零点a∈(m，m＋1)，函数g(x)＝lnx＋2x2－5的零点b∈(n，n＋1)，其中m∈N，n∈N，若过点A(m，n)作圆(x－2)2＋(y－1)2＝1的切线l，则l的方程为A.y＝313x±+ B.y＝±3x＋1 C.y＝1 D.x＝0，y＝19.若点(x，y)在不等式组1010330x yx yx y+-≥⎧⎪--≤⎨⎪-+≥⎩表示的平面区域内，则实数z＝211yx-+的取值范围是A.[－1，1]B.[－2，1]C.[－12，1] D.[－1，12]10.已知三棱锥A－BCD的顶点均在球O的球面上，且AB＝AC＝AD＝3，∠BCD＝π，若H是点A在平面BCD内的正投影，且CH＝2，则球O的表面积为A.43πB.23πC.9πD.4π11.函数f(x)＝lnx－14x2的大致图像是12.已知点F为双曲线E：22221(0,0)x ya ba b-=>>的右焦点，若在双曲线E的右支上存在点P，使得PF中点到原点的距离等于点P到点F的距离，则双曲线E的离心率的取值范围是A.(1，3)B.(1，3]C.(13] 33]第II卷(非选择题共90分)本卷包括必考题和选考题两个部分。

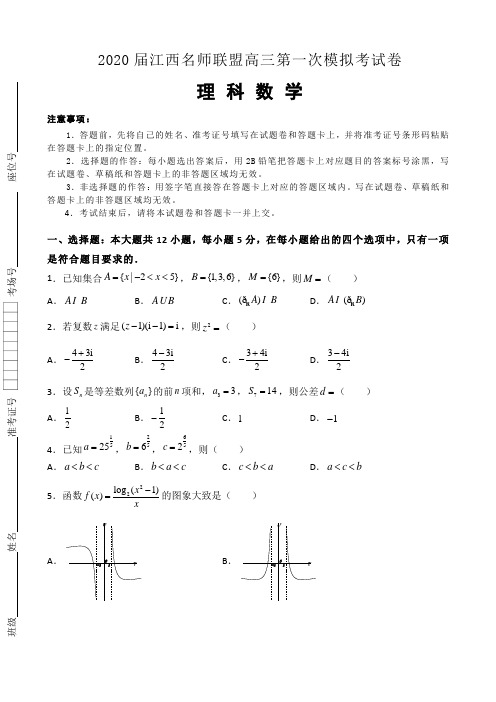
2020届江西名师联盟高三第一次模拟考试卷理 科 数 学注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{|25}A x x =-<<，{1,3,6}B =，{6}M =，则M =（ ） A ．A B IB ．A B UC ．()A B R I ðD ．()A B R I ð2．若复数z 满足(1)(i 1)i z --=，则2z =（ ）A ．43i2+-B ．43i2- C ．34i2+-D ．34i2- 3．设n S 是等差数列{}n a 的前n 项和，33a =，714S =，则公差d =（ ）A ．12B ．12-C ．1D ．1-4．已知1525a =，256b =，652c =，则（ ） A ．a b c <<B ．b a c <<C ．c b a <<D ．a c b <<班级 姓名 准考证号 考场号 座位号5．函数22log (1)()x f x x-=的图象大致是（ ）A ．B ．C ．D ．6．设x ，y 满足约束条件2632x y x y y -≤⎧⎪+≥⎨⎪≤⎩，则y z x =的最大值是（ ）A ．1-B ．0C ．12D ．27．在ABC △中，23BD BC =u u u r u u u r ，E 为AD 的中点，则CE =u u u r（ ）A ．1263AB AC -u u ur u u u rB ．2136AB AC -u u ur u u u rC ．1536AB AC -u u ur u u u rD ．5163AB AC -u u ur u u u r8．若存在π[0,]2x ∈，使2πsin(2)03x x m +-+<成立，则m的取值范围为（ ） A ．()+∞ B ．(,1-∞-- C．(,-∞ D ．(1)--+∞9．在直角坐标系xOy 中，F 是椭圆2222:1(0)x y C a b a b+=>>的左焦点，A ，B 分别为左、右顶点，过点F 作x 轴的垂线交椭圆C 于P ，Q 两点，连接PB 交y 轴于点E ，连接AE 交PQ 于点M ，若M 是线段PF 的中点，则椭圆C 的离心率为（ ）AB ．12C ．13D ．1410．如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的外接球的体积为（ ）A．3B．3C． D．11．已知双曲线22221(0,0)x y a b a b -=>>的离心率为2，1F ，2F 分别是双曲线的左、右焦点，点(,0)M a -，(0,)N b ，点P 为线段MN 上的动点，当12PF PF ⋅u u u r u u u u r取得最小值和最大值时，12PF F △的面积分别为1S ，2S ，则21S S =（ ） A ．4 B ．8 C．D．12．设函数()f x 在定义域(0,)+∞上是单调函数，且(0,)x ∀∈+∞，(())x f f x e x e -+=． 若不等式()()f x f x ax '+≥对(0,)x ∈+∞恒成立，则a 的取值范围是（ ） A ．(,2]e -∞-B ．(,1]e -∞-C ．(,23]e -∞-D ．(,21]e -∞-二、填空题：本大题共4小题，每小题5分．13．若()f x 为定义在R 上的奇函数，当0x <时，()cos πx f x x =+，则4π()3f = ．14．已知22962100012100(1)(1)(1)(1)(1)x x a a x a x a x -+=+++++++L ，则210012100222a a a +++=L ．15．已知函数()ln(||1)cos 2f x x a x =+++只有一个零点，则a = ．16．在四棱锥P ABCD -中，底面ABCD 为正方形，平面PAD ⊥平面ABCD ，且PAD △为等边三角形，若四棱锥P ABCD -的体积与四棱锥P ABCD -棱锥P ABCD -的表面积为 ．三、解答题：本大题共6大题，共70分，解答应写出文字说明、证明过程或演算步骤．17．（12分）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，已知26sin cossin 2Aa Bb A =． （1）求cos A ；（2）若a =5b c +=，求ABC △的面积．18．（12分）某厂销售部以箱为单位销售某种零件，每箱的定价为200元，低于100箱按原价销售，不低于100箱则有以下两种优惠方案：①以100箱为基准，每多50箱送5箱；②通过双方议价，买方能以优惠8%成交的概率为0.6，以优惠6%成交的概率为0.4．（1）甲、乙两单位都要在该厂购买150箱这种零件，两单位都选择方案②，且各自达成的成交价格相互独立，求甲单位优惠比例不低于乙单位优惠比例的概率；（2）某单位需要这种零件650箱，以购买总价的数学期望为决策依据，试问该单位选择哪种优惠方案更划算?19．（12分）如图，在四面体ABCD 中，AD AB ⊥，平面ABD ⊥平面ABC，2AB BC AC ==，且4AD BC +=．（1）证明：BC ⊥平面ABD ；（2）设E 为棱AC 的中点，当四面体ABCD 的体积取得最大值时，求二面角C BD E --的余弦值．EBACD20．（12分）已知椭圆2222:1(0)x y C a b a b+=>>过点1)2-倍．（1）求椭圆C 的方程；（2）若A ，B 是椭圆C 上的两个动点（A ，B 两点不关于x 轴对称），O 为坐标原点，OA ，OB 的斜率分别为1k ，2k ，问是否存在非零常数λ，使12k k λ⋅=时，AOB △的面积S 为定值？若存在，求λ的值；若不存在，请说明理由．21．（12分）已知函数ln ()xx af x e+=． （1）当1a =时，求()f x 的极值；（2）设()x g x xe a -=-，对任意12,(0,)x x ∈+∞都有11112()()xx e f x ax g x ->成立，求实数a 的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分． 22．（10分）【选修4-4：坐标系与参数方程】在直角坐标系xOy 中，直线l 的参数方程为2431x t a y t ⎧=+⎨=-⎩（t 为参数），圆C 的参数方程为21||cos 2sin x a y a θθ=+⎧⎨=-+⎩（θ为参数）． （1）求l 和C 的普通方程；（2）将l 向左平移(0)m m >后，得到直线l '，若圆C 上只有一个点到l '的距离为1，求m ．23．（10分）【选修4-5：不等式选讲】 设函数()|||4|(0)f x x a x a =-+-≠． （1）当1a =时，求不等式()f x x <的解集；（2）若4()1f x a≥-恒成立，求a 的取值范围．2020届江西名师联盟高三第一次模拟考试卷理科数学答 案一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．【答案】C【解析】∵{|2A x x =≤-R ð或5}x ≥，∴(){6}A B =R I ð． 2．【答案】B【解析】因为i 2i 11i 1i 1z -=+=--，所以234i 43i 2i 2z ---==-． 3．【答案】D【解析】∵74714S a ==，∴42a =，∴431d a a =-=-． 4．【答案】A【解析】255a =，256b =，258c =，故a b c <<． 5．【答案】C【解析】由函数22log (1)()x f x x -=，得定义域为(,1)(1,)-∞-+∞U ，且有()()f x f x -=-成立，所以函数22log (1)()x f x x-=的图象关于原点对称，且与x 轴交于(和两点．当x >222log (1)log (21)0x ->-=，所以在内函数图象在x 轴下方，在)+∞内函数图象在x 轴上方，再用对称性得到完整的函数图象．6．【答案】D【解析】yz x=的几何意义是可行域内的点(,)x y 与原点(0,0)连线的斜率， 画出可行域（图略），得z 的最大值为2． 7．【答案】A【解析】11111112()22262663CE CA CD CA CB CA AB AC AB AC =+=+=+-=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u ur u u u r ．8．【答案】C【解析】记2ππ()sin(2)cos(2)36f x x x m x m =+-+=-+，因为存在π[0,]2x ∈，使2πsin(2)03x x m +-+<成立，所以只需当π[0,]2x ∈时，min π()()02f x f m ==+<，即m <． 9．【答案】C【解析】如图，连接BQ ，则由椭圆的对称性易得PBF QBF ∠=∠，EAB EBA ∠=∠， 所以EAB QBF ∠=∠，所以ME BQ ∥．因为PME PQB ~△△，所以||||||||PE PM EB MQ =． 因为PBF EBO ~△△，所以||||||||OF EP OB EB =，从而有||||||||PM OF MQ OB =． 又因为M 是线段PF 的中点，所以||||1||||3c OF PM e a OB MQ ====．10．【答案】B【解析】由三视图可知该几何体是如图所示的三棱锥A BCD -，F 为BD 的中点， 外接球球心O 在过CD 的中点E 且垂直于平面BCD 的直线l 上，又点O 到A ，B ，D 的距离相等，所以O 又在过左边正方体一对棱的中点M ，N 所在直线上，在OEN △中，由NF MF NE OE =，即223OE=，得3OE =，所以三棱锥A BCD -外接球的球半径R===3V =． DCEFBNMAO11．【答案】A【解析】由2ce a==，得2c a =，b=， 故线段MN 所在直线的方程为)y x a =+，又点P 在线段MN上，可设()P m +，其中[,0]m a ∈-， 由1(,0)F c -，2(,0)F c ，即1(2,0)F a -，2(2,0)F a ，得1(2,)PF a m =--u u u r ，2(2,)PF a m =-u u u u r，所以222212313464()44PF PF m ma a m a a ⋅=+-=+-u u u r u u u u r ． 由于[,0]m a ∈-，可知当34m a =-时，12PF PF ⋅u u u r u u u u r 取得最小值，此时21134)24S a a a =⨯-+=，当0m =，12PF PF ⋅u u u r u u u u r 取得最大值，此时22142S a =⨯=，所以214S S =．12．【答案】D【解析】由于()f x 是单调函数，则()x f x e x -+为定值， 不妨设()x f x e x t -+=，则()x f x e x t =-+．又()t f t e t t e =-+=，解得1t =，则()1x f x e x =-+，()1x f x e '=-，所以2xe x ax -≥，即21xe a x≤-． 设2()1x e g x x =-，则22(1)()x e x g x x -'=， 易知()g x 在(0,1)上单调递减，在(1,)+∞上单调递增， 则min ()(1)21g x g e ==-，所以21a e ≤-．二、填空题：本大题共4小题，每小题5分．13．【答案】116【解析】∵4π4π4111()cos 333326f 4-=-+=--=-，所以4π11()36f =． 14．【答案】0【解析】令1x =-，可得00a =；令1x =，可得2100296012100222(11)(11)0a a a a ++++=-+=L ，所以2100121002220a a a +++=L ．15．【答案】2-【解析】因为函数()f x 为偶函数，且函数()f x 只有一个零点， 故(0)0f =，所以2a =-．16．【答案】8+【解析】如图，连接AC ，BD 交于点1O ，取AD 的中点为N ，连接PN ． 设四棱锥P ABCD -外接球的球心为O ，等边三角形PAD 外接圆的圆心为2O ，则2O 为PAD △的重心，则22||||3PO PN =，正方形ABCD 外接圆的圆心为1O ． 因为PN AD ⊥，平面PAD ⊥平面ABCD ，所以PN ⊥平面ABCD ，所以1OO PN ∥， 所以四边形12OO NO 为矩形，所以21OO NO =．设正方形ABCD 的边长为2x ，则||PN =，所以2||PO =，2||OO x=， 所以四棱锥P ABCD -外接球的半径为2222227||||||3PO PO OO x =+=，所以四棱锥P ABCD -外接球的表面积为228π3S x =球， 四棱锥P ABCD -的体积为231433P ABCD V x x -=⨯=，所以P ABCD V S -=球=，解得1x =， 所以正方形ABCD 的边长为2，所以PAD S =△，2PAB S =△，2PDC S =△，PCB S =△，4ABCD S =正方形，所以四棱锥P ABCD -的表面积为8O O 1DCBAN O 2P三、解答题：本大题共6大题，共70分，解答应写出文字说明、证明过程或演算步骤．17．【答案】（1）23-；（2【解析】（1）∵26sin cossin 2A a B b A =，∴26cos 2A ab ba =，∴21cos 26A =， 故22cos 2cos123A A =-=-． （2）∵2222cos a b c bc A =+-，又a =，5b c +=，∴24221()22533b c bc bc bc =+-+=-，∴6bc =．由（1）可知sin 3A =，从而ABC △的面积1sin 2S bc A ==18．【答案】（1）0.76；（2）选择方案①更划算．【解析】（1）因为甲单位的优惠比例低于乙单位的优惠比例的概率为0.40.60.24⨯=， 所以甲单位的优惠比例不低于乙单位的优惠比例的概率为10.240.76-=． （2）设在折扣优惠中每籍零件的价格为X 元，则184X =或188．X 的分布列为则1840.61880.4EX =⨯+⨯=若选择方案②，则购买总价的数字期望为185.6650120640⨯=元．若选择方案①，由于购买600箱能获赠50箱，所以该单位只需要购买600箱， 从而购买总价为200600120000⨯=元．因为120640120000>，所以选择方案①更划算．19．【答案】（1）证明见解析；（2）6． 【解析】（1）因为AD AB ⊥，平面ABD ⊥平面ABC ，平面ABD I 平面ABC AB =，AD ⊂平面ABD ，所以AD ⊥平面ABC ． 因为BC ⊂平面ABC ，所以AD BC ⊥．因为AB BC AC ==，所以222AB BC AC +=，所以AB BC ⊥．因为AD AB A =I ，所以BC ⊥平面ABD ． （2）设(04)AD x x =<<，则4AB BC x ==-，四面体ABCD 的体积232111()(4)(816)(04)326V f x x x x x x x ==⨯-=-+<<．211()(31616)(4)(34)66f x x x x x '=-+=--，当403x <<时，()0f x '>，()V f x =单调递增； 当443x <<时， ()0f x '<，()V f x =单调递减， 故当43AD x ==时，四面体ABCD 的体积取得最大值． 以B 为坐标原点，建立空间直角坐标系B xyz -，则(0,0,0)B ，8(0,,0)3A ，8(,0,0)3C ，84(0,,)33D ，44(,,0)33E ．设平面BCD 的法向量为(,,)x y z =n ，则0BC BD ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r n n ，即80384033x y z ⎧=⎪⎪⎨⎪+=⎪⎩，令2z =-，得(0,1,2)=-n ．同理可得平面BDE 的一个法向量为(1,1,2)=-m ，则cos ,==m n由图可知，二面角C BD E --为锐角，故二面角C BD E --的余弦值为6．20．【答案】（1）2214x y +=；（2）存在，14λ=-，1AOB S =△．【解析】（1）因为椭圆2222:1(0)x y C a b a b+=>>过点1)2-，所以223114a b +=，c =，从而22224a b c b =+=．联立方程组222231144a b a b ⎧+=⎪⎨⎪=⎩，解得2241a b ⎧=⎨=⎩，所以椭圆C 的方程为2214x y +=．（2）设存在这样的常数λ，使12k k λ⋅=，AOB △的面积S 为定值． 设直线AB 的方程为y kx m =+，点11(,)A x y ，点22(,)B x y ， 则由12k k λ⋅=知12120y y x x λ-=，1212()()0kx m kx m x x λ++-=，所以221212()()0k x x km x x m λ-+++=①．联立方程组2214x y y kx m ⎧+=⎪⎨⎪=+⎩，消去y 得222(14)8440k x kmx m +++-=．所以122814km x x k -+=+②，21224414m x x k-⋅=+③，又点O 到直线AB 的距离d =则AOB △的面积121||||||22m S AB d x x =⋅=⋅-= 将②③代入①得222222()(44)8(14)0k m k m m k λ---++=，化简得224()14k m λλ-=-⑤，将⑤代入④得22224222222422(41)4()(14)16()64(644)41()2(14)(41)1681(14)S k k k k k k k k λλλλλλλλ+⋅-----++-==⋅-+++-， 要使上式为定值，只需26464441681λλλ-+-==，即需2(41)0λ+=，从而14λ=-， 此时21()24S =，1S =，所以存在这样的常数14λ=-，此时1AOB S =△．21．【答案】（1）()f x 的极大值为1(1)f e =，无极小值；（2）2(,)e+∞．【解析】（1）当1a =时，ln 1()xx f x e +=，所以函数()f x 的定义域为(0,)+∞， 所以1ln ()xx x xf x xe--'=，且0x xe >， 令()1ln h x x x x =--，所以当01x <<时，10x ->，ln 0x x <，所以()1ln 0h x x x x =-->． 又()2ln h x x '=--，所以当1x >时，()2ln 0h x x '=--<， 所以()h x 在(1,)+∞上单调递减，故()(1)0h x h <=．同理当01x <<时，()0f x '>；当1x >时，()0f x '<，所以()f x 在(0,1)是单调递增，在(1,)+∞单调递减，所以当1x =时，()f x 的极大值为1(1)f e =，无极小值．（2）令()()x m x xe f x ax =-，因为对任意12,(0,)x x ∈+∞都有11112()()xx e f x ax g x ->成立，所以1min 2max ()()m x g x >．因为()()ln x m x xe f x ax x x =-=，所以()1ln m x x '=+．令()0m x '>，即1ln 0x +>，解得1x e >；令()0m x '<，即1ln 0x +<，解得10x e <<．所以()m x 在1(0,)e 上单调递减，在1(,)e +∞上单调递增，所以min 11()()m x m e e ==-．因为()x g x xe a -=-，所以()(1)x g x x e -'=-，当0x >时0x e ->，令()0g x '>，即10x ->，解得01x <<；令()0g x '<，即10x -<，解得1x >． 所以()g x 在(0,1)上单调递增，在(1,)+∞上单调递减，所以max 1()(1)g x g a e ==-， 所以11a e e ->-，所以2a e >，即实数a 的取值范围为2(,)e +∞．22．【答案】（1）3470x y --=，22(1)(2)1x y -++=；（2）2m =．【解析】（1）由题意可得||1a =，故l 的参数方程为4131x t y t =+⎧⎨=-⎩（t 为参数），圆C 的参数方程为1cos 2sin x y θθ=+⎧⎨=-+⎩（θ为参数），消去参数t ，得l 的普通方程为3470x y --=，消去参数θ，得C 的普通方程为22(1)(2)1x y -++=． （2）l '的方程为37()44y x m =+-，即34370x y m -+-=，因为圆C 上只有一个点到l '的距离为1，圆C 的半径为1，所以(1,2)C -到l '的距离为2， 即|3837|25m ++-=，解得2m =（1403m =-<舍去）．23．【答案】（1）(3,5)；（2）(,0)[1,)-∞+∞U ．【解析】（1）当1a =时，52,1()3,1425,4x x f x x x x -≤⎧⎪=<<⎨⎪-≥⎩，故不等式()f x x <的解集为(3,5)．（2）∵()|||4||()(4)||4|f x x a x x a x a =-+-≥---=-， ∴44|4|1aa a a --≥-=，当0a <或4a ≥时，不等式显然成立；当04a <<时，11a ≤，则14a ≤<．故a 的取值范围为(,0)[1,)-∞+∞U ．。

2020届江西省赣州市宁都县高三上学期期末模拟考试数学试卷一、单选题：本大题共12题，每小题5分，共60分，每个小题只有一个选项符合题目要求. 1．{123}A =，，，集合{113}B =-，，，集合S A B =I ，则集合S 的真子集有（ ） A ．2个 B ．3个 C ．4个 D ．8个2．命题“对任意x R ∈，都有20x ≥”的否定为（ ）A ．存在0x R ∈，都有200x ≥ B ．对任意x R ∈，使得20x < C ．存在0x R ∈，使得200x <D ．不存在x R ∈，使得20x <3．若样本1231,1,1,,1n x x x x ++++的平均数是10，方差为2，则对于样本12322,22,22,,22n x x x x ++++，下列结论正确的是（ ）A ．平均数为20，方差为4B ．平均数为11，方差为4C ．平均数为21，方差为8D ．平均数为20，方差为84．双曲线22184x y -=的一个焦点到一条渐近线的距离为（ ）A ．4 B． C ．2 D5．将函数()cos 24f x x π⎛⎫=- ⎪⎝⎭的图象向左平移8π个单位，得到函数()g x 的图象，则下列说法不正确的是( )A ．162g π⎛⎫=⎪⎝⎭ B ．()g x 在区间57,88ππ⎛⎫⎪⎝⎭上是增函数 C ．2x π=是()g x 图象的一条对称轴D ．,08π⎛⎫-⎪⎝⎭是()g x 图象的一个对称中心 6．如图，已知OAB ∆，若点C 满足()2,,AC CB OC OA OB R λμλμ==+∈，则11λμ+=（ ）A ．13B ．23C ．29 D ．927．《周髀算经》中有这样一个问题：从冬至日起，依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气其日影长依次成等差数列，冬至、立春、春分日影长之和为31．5尺，前九个节气日影长之和为85．5尺，则芒种日影长为（ ） A ．1．5尺B ．2．5尺C ．3．5尺D ．4．5尺8．设x ，y 满足约束条件，则2241x y x +++的取值范围是（ ）A ．[]4,12B ．[]4,11C ．[]2,6D ．[]1,59．已知三棱柱ABC -A 1B 1C 1的侧棱与底面边长都相等，A 1在底面ABC 上的射影为BC 的中点，则异面直线AB 与CC 1所成的角的余弦值为A ．B ．C ．D ．10．已知等差数列{}n a 的公差不为0，{}n a 中的部分项123,,......n k k k k a a a a 成等比数列．若11k =，29k =，349k =，则2019k =（）A ．2018251⨯-B ．2019251⨯-C ．2020251⨯-D ．2021251⨯-11．已知椭圆C ：()222210x y a b a b+=>>的左、右焦点分别为1F 、2F ，第二象限的点M 在椭圆C 上，且2OM OF =，若椭圆C 2MF 的斜率为（ ）A ．4-B ．14-C ．2-D ．12-12．已知()f x 是定义在R 上的奇函数，记()f x 的导函数为()'f x ，当0x ≥时，满足()()'0f x f x ->，若存在x ∈R ，使不等式()()222xxf e xx f ae x ⎡⎤-+≤+⎣⎦成立，则实数a 的最小值为（ ） A ．11e-B ．11e+C ．1e +D ．e二、填空题:本大题共4题，每小题5分，共20分.13．一名信息员维护甲乙两公司的5G 网络，一天内甲公司需要维护和乙公司需要维护相互独立，它们需要维护的概率分别为0.4和0.3，则至少有一个公司不需要维护的概率为________14．若数列{}n a 的通项公式(1)(32)nn a n =--，则1210a a a ++⋯+=________.15．如图,在平面直角坐标系xoy 中,将直线y 2x=与直线x ＝1及x 轴所围成的图形绕x 轴旋转一周得到一个圆锥,圆锥的体积V 圆锥1=⎰π（2x ）2dx 310|1212x ππ==据此类比：将曲线y ＝x 2（x ≥0）与直线y ＝2及y 轴所围成的图形绕y 轴旋转一周得到一个旋转体,该旋转体的体积V ＝_____．16．在棱长为1的正方体1111ABCD A B C D -中，点M 是对角线1AC 上的动点（点M 与1A C 、不重合），则下列结论正确的是____.①存在点M ，使得平面1A DM ⊥平面1BC D ； ②存在点M ，使得DM //平面11B CD ；③1A DM ∆的面积不可能等于6； ④若12,S S 分别是1A DM ∆在平面1111A B C D 与平面11BB C C 的正投影的面积，则存在点M ，使得12S S =.三、解答题: 本大题共6题，满分70分，解答必须写出文字说明、证明过程和演算步一骤.17．在ABC ∆中，内角A ，B ，C 所对的边分别为a ，b ，c 22cos 02A CB +-=. （1）求角B 的大小；（2）若2sin 2sin sin B A C =，且ABC ∆的面积为ABC ∆的周长.18．如图，在多面体ABCDEF 中，平面ADEF ⊥平面ABCD .四边形ADEF为正方形，四边形ABCD 为梯形，且//AD BC ，ABD ∆是边长为1的等边三角形，M 为线段BD 中点，3BC =. (1)求证：AF BD ⊥；(2)求直线MF 与平面CDE 所成角的正弦值；(3)线段BD 上是否存在点N ，使得直线//CE 平面AFN ？若存在，求BNBD的值；若不存在，请说明理由.19．第7届世界军人运动会于2019年10月18日至27日在湖北武汉举行，赛期10天，共设置射击、游泳、田径、篮球等27个大项，329个小项.共有来自100多个国家的近万名现役军人同台竞技.前期为迎接军运会顺利召开，武汉市很多单位和部门都开展了丰富多彩的宣传和教育活动，努力让大家更多的了解军运会的相关知识，并倡议大家做文明公民.武汉市体育局为了解广大民众对军运会知识的知晓情况，在全市开展了网上问卷调查，民众参与度极高，现从大批参与者中随机抽取200名幸运参与者，他们得分（满分100分）数据，统计结果如下：（1）若此次问卷调查得分整体服从正态分布，用样本来估计总体，设μ，σ分别为这200人得分的平均值和标准差（同一组数据用该区间中点值作为代表），求μ，σ的值（μ，σ的值四舍五入取整数），并计算(5193)P X <<；（2）在（1）的条件下，为感谢大家参与这次活动，市体育局还对参加问卷调查的幸运市民制定如下奖励方案：得分低于μ的可以获得1次抽奖机会，得分不低于μ的可获得2次抽奖机会，在一次抽奖中，抽中价值为15元的纪念品A 的概率为23，抽中价值为30元的纪念品B 的概率为13.现有市民张先生参加了此次问卷调查并成为幸运参与者，记Y 为他参加活动获得纪念品的总价值，求Y 的分布列和数学期望，并估算此次纪念品所需要的总金额.（参考数据：()0.6827P X μδμδ-<≤+≈；(22)0.9545P X μδμδ-<≤+≈；(33)0.9973P X μδμδ-<≤+≈.）20．已知椭圆()2222:10x y C a b a b +=>>的左，右焦点分别为()12,0F -，()22,0F ，点1,P ⎛- ⎝⎭在椭圆C 上.（1）求椭圆C 的标准方程；（2）是否存在斜率为1-的直线l 与椭圆C 相交于M ,N 两点，使得11FM F N =？若存在，求出直线的方程；若不存在，说明理由.21．已知函数()1()cos 1()x f x ex ax a R +=++-∈.（1）若()f x 在()1,-+∞上单调递增，求实数a 的取值范围；（2）当 1a =-时，若实数1212,()x x x x <满足12()()2f x f x +=，求证：120x x +<.22．如图，在极坐标系Ox 中，过极点的直线l 与以点(2,0)A 为圆心、半径为2的圆的一个交点为2,3B π⎛⎫⎪⎝⎭，曲线1M 是劣弧OB ，曲线2M 是优弧OB .（1）求曲线1M 的极坐标方程；（2）设点()1,P ρθ为曲线1M 上任意一点，点2,3Q πρθ⎛⎫- ⎪⎝⎭在曲线2M 上，若||||6OP OQ +=，求θ的值.23．已知函数()()422f x x m x m m=-++>. （1）若4m =，求不等式()5f x >的解集；（2）证明：()()422f x m m +≥+-数学试题参考答案1．BCDCDD BADADA13．0.88．14．15 . 15．2π 16．①②④17．（122cos(1cos())2A CB B AC +-=-++ ∵A B C π++=(1cos())(1cos )B A C B B -++=--cos 12sin 106B B B π⎛⎫=+-=+-= ⎪⎝⎭，得：1sin 62B π⎛⎫+= ⎪⎝⎭∵(0,)B π∈，∴7,666B πππ⎛⎫+∈ ⎪⎝⎭，∴566B ππ+=，23B π= （2）由（1）知23B π=，所以ΔABC的面积为12sin 23ac π==16ac = 因为2sin 2sin sin B A C =，由正弦定理可得2232b ac ==，b =由余弦定理222222cos()323b ac ac a c ac π=+-⋅=+-= ∴2()3248a c ac +=+=，∴a c +=所以ΔABC的周长为18．解:(1)证明：因为ADEF 为正方形，所以AF AD ⊥．又因为平面ADEF ⊥平面ABCD ，且平面ADEF ⋂平面ABCD AD =， 所以AF ⊥平面ABCD ．所以AF BD ⊥．(2)取AD 中点O,EF 中点K ，连接OB ，OK.于是在△ABD 中，OB OD ⊥，在正方ADEF 中OK OD ⊥，又平面ADEF ⊥平面ABCD ，故OB ⊥平面AFEF ，进而0B OK ⊥，即OB, OD, OK 两两垂直．分别以,,OB OD OK 为x 轴，y 轴,z 轴建立空间直角坐标系（如图）．于是，B ⎫⎪⎪⎝⎭，10,,02D ⎛⎫ ⎪⎝⎭,C ⎫⎪⎪⎝⎭,1E 0,,12⎛⎫⋅ ⎪⎝⎭,11M ,0,F 0,,142⎫⎛⎫-⎪ ⎪⎪⎝⎭⎝⎭ 所以3335,,1,,,0,(0,0,1)42MF CD DE ⎛⎫⎛⎫=-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭设平面CDE的一个法向量为(,,)n x y z =，则00CD n DE n ⎧⋅=⎪⎨⋅=⎪⎩即5020x y z ⎧-⋅=⎪⎨⎪=⎩令5x =-，则y =(5,3,0)n =-．设直线MF 与平面CDE 所成角为θ，||3sin |cos ,|||||MF n MF n MF n θ⋅=<>==(3) 要使直线//CE 平面AFN ，只需AN //CD ，设,[0,1]BN BD λλ=∈,则1,,,0222n n n x y z λ⎛⎫⎛⎫-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 1,,0222n n n x y z λλ=-==,1,,0222N λλ⎛⎫- ⎪ ⎪⎝⎭，所以311,,02222AN λλ⎛⎫=-+ ⎪ ⎪⎝⎭, 又5(,0)2CD =--，由//AN CD 1122 52λ-+=-，解得2=[0,1]3λ∈所以线段BD 上存在点N,使得直线//CE 平面AFN ，且2=3BN BD ． 19．解：（1）由已知频数表得：53040504520()354555657585200200200200200200E X =⨯+⨯+⨯+⨯+⨯+⨯+109565200⨯=， 22222()(3565)0.025(4565)0.15(5565)0.2(6565)0.25(7565)0.225D X =-⨯+-⨯+-⨯+-⨯+-⨯22(8565)0.1(9565)0.05210+-⨯+-⨯=，由2196225σ<<，则1415σ<<，而214.5210.5210=>，所以14σ≈， 则X 服从正态分布(65,14)N ，所以(22)()(5193)(2)2P X P X P X P X μσμσμσμσμσμσ-<<++-<<+<<=-<<+=0.95450.68270.81862+==；（2）显然，()()0.5P X P X μμ<=≥=， 所以所有Y 的取值为15，30，45，60，121(15)233P Y ==⨯=，111227(30)2323318P Y ==⨯+⨯⨯=， 1211122(45)2332339P Y ==⨯⨯+⨯⨯=，1111(60)23318P Y ==⨯⨯=，Y所以()1530456030318918E Y =⨯+⨯+⨯+⨯=， 需要的总金额为：200306000⨯=.20．解:（1）因为椭圆C 的左右焦点分别为()12,0F -，()22,0F ，所以2c =.由椭圆定义可得2a ===解得a =所以222642b a c =-=-=,所以椭圆C 的标准方程为22162x y +=（2）假设存在满足条件的直线l ，设直线l 的方程为y x t =-+，由22162x y y x t ⎧+=⎪⎨⎪=-+⎩得223()60x x t +-+-=，即 ()2246360x tx t -+-=，()222(6)443696120t t t ∆=--⨯⨯-=->，解得t -<<设()11,M x y ，()22,N x y ，则1232t x x +=,212364t x x -=, 由于11FM F N =，设线段MN 的中点为E ，则1F E MN ⊥， 所以111F E MN K K =-=又3,44t t E ⎛⎫⎪⎝⎭，所以141324F E t K t ==+，解得4t =-. 当4t =-时，不满足t -<<所以不存在满足条件的直线l . 21.解:（1）()1()sin 1x f x e x a +'=-+-,由()f x 在()1,-+∞上单调递增，故当1x >-时，()1sin 10x e x a +-+-≥恒成立,即()1sin 1x a e x +≤-+设()()()1sin 11x g x ex x +=-+>-，()()1cos 1x g x e x +'=-+，∵1x >-，∴()11,cos 11x ex +>+≤,∴()0g x ¢>，即()g x 在()1,-+∞上单调递增，故()()11g x g >-=,∴1a ≤； （2）当1a =-时，()()1cos 1x f x ex x +=+++，()()1sin 110x f x e x +'=-++>,∴()f x 在R 上单调递增，又∵()11f -=且()()122f x f x +=，故121x x <-<要证120x x +<，只需证21x x <-,即证()()21f x f x <-， 只需证()()112f x f x -<-,即证()()1120f x f x +--> 令()()()2h x f x f x =+--，()h x '()()()()11sin 11sin 11x x e x e x +-=-+++-+--112cos1sin x x e e x +-=--⋅ 令()112cos1sin x x x ee x ϕ+-=--⋅()112cos1cos 22cos1cos 0x x x e e x e x ϕ+-'=+-⋅≥-⋅>∴()x ϕ在(),1-∞-上单调递增∴()()211sin 20x e ϕϕ<-=--<，故()h x 在(),1-∞-上单调递减，∴()()()12120h x h f >-=--=，故原不等式成立.22．解：（1）设以点(2,0)A 为圆心、半径为2的圆上任意一点(,)ρθ， 所以该圆的极坐标方程为4cos ρθ=， 则1M 的方程为4cos 32ππρθθ⎛⎫=≤≤⎪⎝⎭；（2）由点()1,P ρθ为曲线1M 上任意一点，则114cos 32ππρθθ⎛⎫=≤≤⎪⎝⎭，点2,3Q πρθ⎛⎫-⎪⎝⎭在曲线2M 上，则24cos 3233ππππρθθ⎛⎫⎛⎫=--≤-≤ ⎪⎪⎝⎭⎝⎭， 即224cos 363πππρθθ⎛⎫⎛⎫=--≤≤ ⎪⎪⎝⎭⎝⎭， 因为12||,||OP OQ ρρ==，所以12||||OP OQ ρρ+=+，即||||4cos 4cos 3OP OQ πθθ⎛⎫+=+- ⎪⎝⎭3πθ⎛⎫=+ ⎪⎝⎭， 因为32ππθ≤≤，且263ππθ-≤≤，所以32ππθ≤≤，因为||||6OP OQ +=，所以63πθ⎛⎫+= ⎪⎝⎭，即sin 32πθ⎛⎫+= ⎪⎝⎭，所以3πθ=. 23．解:（1）依题意，4215x x -++>； 当21x <-时，原式化为4215x x --->，解得23x <-； 当142x -≤≤时，原式化为4215x x -++>，解得0x >，故04x <≤； 当4x >时，原式化为4215x x -++>，解得83x >，故4x >；综上所述，不等式()5f x >的解集为2{|3x x <-或0}x >. （2）依题意，()423,42,43,x m x m m f x x m x m m m x m x m m ⎧-+-<-⎪⎪⎪=++-≤≤⎨⎪⎪-+>⎪⎩，所以()min 22f m m m f x ⎛⎫-=+ ⎪⎝⎭=，()()()42422m m m m f x m m +≥++--222222222m m m m m m =++-=-++≥--，当且仅当222m m -=-，即2m =+.。

江西省南昌市2020届高三上学期摸底调研考试数学（文科）本试卷共4页，23小题，满分150分. 考试时间120分钟. 注意事项：1．答卷前，考生务必将自已的姓名、准考证号填涂在答题卡上，并在相应位置贴好条形码． 2．作答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案信息涂黑；如需改动，用橡皮擦干净后，再选涂其它答案．3．非选择题必须用黑色水笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来答案，然后再写上新答案，不准使用铅笔和涂改液.不按以上要求作答无效． 4．考生必须保证答题卡整洁．考试结束后，将试卷和答题卡一并交回．一．选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1．已知集合3{|0},{|2}1x M x N x y x x -=≥==--，则()M N =RA. (1,2]B. [1,2]C. (2,3]D. [2,3] 2．复数z 满足1i1i z+=-，则||z = A.2i B.2 C.i D.1 3．已知平面α内一条直线l 及平面β，则“l β⊥”是“αβ⊥”的 A.充分必要条件 B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件4．如图是某光纤电缆的截面图，其构成为七个大小相同的小圆 外切，且外侧六个小圆与大圆内切，现从大圆内任取一点，恰好 在小圆内的概率为 A.79 B.78C.2π7D.7π275．已知一组样本数据点11223366(,),(,),(,),,(,)x y x y x y x y ，用最小二乘法求得其线性回归方程为24y x =-+.若1236,,,,x x x x 的平均数为1，则1236y y y y ++++=A.10B.12C.13D.14 6．公比不为1的等比数列{}n a 中，若15m n a a a a =，则mn 不可能．．．为 A.5 B.6 C.8 D.97．已知二元一次不等式组20,20220x y x y x y +-≥⎧⎪-+≥⎨⎪+-≥⎩表示的平面区域为D ，命题p ：点(0,1)在区域D 内；命题q ：点(1,1)在区域D 内. 则下列命题中，真命题是A.p q ∧B.()p q ∧⌝C.()p q ⌝∧D.()()p q ⌝∧⌝ 8．已知ABC ∆中，4,3AB AC ==，3A π∠=，BC 的中点为M ，则AM AB ⋅等于A.152B.11C.12D.15 9．已知圆22:10210C x y y +-+=与双曲线22221(0,0)x y a b a b-=>>的渐近线相切，则该双曲线的离心率是B.53C.52 10．已知正实数,a b 满足21()log 2a a =，21()log 3bb =，则A.1a b <<B.1b a <<C.1b a <<D.1a b <<11．自然界中具有两种稳定状态的组件普遍存在，如开关的开和关、电路的通和断等，非常适合表示计算机中的数，所以现在使用的计算机设计为二进制．二进制以2为基数，只用0和1两个数表示数，逢2进1，二进制数与十进制数遵循一样的运算规则，它们可以相互转化，如10(521)=987612020202⨯+⨯+⨯+⨯543210020212020212+⨯+⨯+⨯+⨯+⨯+⨯=2(1000001001)．我国数学史上，清代汪莱的《参两算经》是较早系统论述非十进制数的文献，总结出了八进制乘法口决：88(77)(61)⨯=，88(76)(52)⨯=，88(75)(43)⨯=，，则八进制下8(65)⨯等于 A. 8(36) B. 8(37) C. 8(40) D. 8(41)12．若函数()(1)e xf x x ax =--（e 为自然对数的底数）有两个极值点，则实数a 的取值范围是 A.1(,0)e - B.(,0)-∞ C.1(,)e-+∞ D.(0,)+∞二．填空题：本题共4小题，每小题5分,共20分. 13．已知1sin 5θ=，则cos2θ等于 ．14．已知定义在R 上的偶函数()f x 满足(2)()0f x f x --=，(0)f =则(10)f 等于 ． 15．已知一个圆锥的轴截面是斜边长为2的等腰直角三角形，则该圆锥的侧面积为 ．16．已知数列{}n a 的前n 项和为n S ，33-=n n S a ，若对于任意M S S N n m n m ≤-∈+,,恒成立，则实数M 的最小值为_______．三．解答题：共70分. 解答应写出文字说明、证明过程或演算步骤. 第1721题为必考题，每个试题考生都必须作答；第22、23题为选考题，考生根据要求作答. （一）必考题：共60分.17．(12分)已知锐角ABC ∆的内角,,A B C 的所对边分别为,,a b c ，其中c =，2sin(2)3C π-=（Ⅰ）若a =A ；B 1（Ⅱ）求ABC ∆面积的最大值．18．(12分)如图，已知直三棱柱111ABC A B C -中，AB AC ⊥，12AB AC AA ===，E 是BC 的中点，F 是1A E 上一点，且12A F FE =. （Ⅰ）证明：AF ⊥平面1A BC ；（Ⅱ）求三棱锥11C A FC -的体积．19．(12分)某“双一流”大学专业奖学金是以所学专业各科考试成绩作为评选依据，分为专业一等奖学金、专业二等奖学金及专业三等奖学金，且专业奖学金每个学生一年最多只能获得一次.图（1）是统计了该校2018年500名学生周课外平均学习时间频率分布直方图，图（2）是这500名学生在2018年周课外平均学习时间段获得专业奖学金的频率柱状图．图2图1（Ⅰ）求这500名学生中获得专业三等奖学金的人数；（Ⅱ）若周课外平均学习时间超过35小时称为“努力型”学生，否则称为“非努力型”学生，列22⨯联表并判断是否有99.9%的把握认为该校学生获得专业一、二等奖学金与是否是“努力型”学生有关？22()()()()()n ad bc K a b c d a c b d -=++++20．(12分)在平面直角坐标系xOy 中，已知()()1,2,1,0Q F -，动点P 满足||||PQ OF PF ⋅=. （Ⅰ）求动点P 的轨迹E 的方程；（Ⅱ）过点F 的直线与E 交于,A B 两点，记直线,QA QB 的斜率分别为12,k k ，求证：12k k +为定值．21．(12分)已知函数()e xf x x a =-（R a ∈，e 为自然对数的底数），21()(1)2g x x =+． （Ⅰ）若直线1y x =-是函数()f x 图像的一条切线，求a 的值； （Ⅱ）对于任意3(,)2x ∈-+∞，()()f x g x >恒成立，求a 的取值范围．（二）选考题：共10分.请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分. 22．[选修4—4：坐标系与参数方程] (10分) 在直角坐标系xOy 中，曲线C 的参数方程为2cos ,2sin x y αα=⎧⎨=⎩（[0,2),απα∈为参数），在同一平面直角坐标系中，经过伸缩变换'2,'x x y y=⎧⎨=⎩得到曲线1C ，以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系（ρ为极径，θ为极角）．（Ⅰ）求曲线C 的直角坐标方程和曲线1C 的极坐标方程；（Ⅱ）若射线():0OA θβρ=>与曲线1C 交于点A ，射线():02OB πθβρ=+>与曲线1C 交于点B ，求2211OAOB+的值．23．[选修4—5：不等式选讲] (10分)已知函数21()|||1|(0)a f x x x a a+=-+->，()4|1|g x x =-+． （Ⅰ）当1a =时，求不等式()3f x ≥的解集；（Ⅱ）若关于x 的不等式()()f x g x ≤的解集包含[]1,2，求a 的取值集合．。

2020届江西名师联盟高三第一次模拟考试卷理 科 数 学注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{|25}A x x =-<<，{1,3,6}B =，{6}M =，则M =（ ） A ．A B IB ．A B UC ．()A B R I ðD ．()A B R I ð2．若复数z 满足(1)(i 1)i z --=，则2z =（ ） A ．43i2+-B ．43i2- C ．34i2+-D ．34i2- 3．设n S 是等差数列{}n a 的前n 项和，33a =，714S =，则公差d =（ ）A ．12B ．12-C ．1D ．1-4．已知1525a =，256b =，652c =，则（ ） A ．a b c <<B ．b a c <<C ．c b a <<D ．a c b <<5．函数22log (1)()x f x x-=的图象大致是（ ）A ．yx1O-1B ．yx1O-1班级 姓名 准考证号 考场号 座位号C ．D ．6．设x ，y 满足约束条件2632x y x y y -≤⎧⎪+≥⎨⎪≤⎩，则y z x =的最大值是（ ）A ．1-B ．0C ．12D ．27．在ABC △中，23BD BC =u u u r u u u r ，E 为AD 的中点，则CE =u u u r（ ）A ．1263AB AC -u u u r u u u r B ．2136AB AC -u u u r u u u r C ．1536AB AC -u u u r u u u rD ．5163AB AC -u u ur u u u r8．若存在π[0,]2x ∈，使2πsin(2)03x x m +-+<成立，则m 的取值范围为（ ） A．()+∞ B ．(,1-∞-- C．(,-∞ D ．(1)--+∞9．在直角坐标系xOy 中，F 是椭圆2222:1(0)x y C a b a b+=>>的左焦点，A ，B 分别为左、右顶点，过点F 作x 轴的垂线交椭圆C 于P ，Q 两点，连接PB 交y 轴于点E ，连接AE 交PQ 于点M ，若M 是线段PF的中点，则椭圆C 的离心率为（ ） A ．2B ．12C ．13D ．1410．如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的外接球的体积为（ ）A．3B．3C． D ．11．已知双曲线22221(0,0)x y a b a b-=>>的离心率为2，1F ，2F 分别是双曲线的左、右焦点，点(,0)M a -，(0,)N b ，点P 为线段MN 上的动点，当12PF PF ⋅u u u r u u u u r取得最小值和最大值时，12PF F △的面积分别为1S ，2S ，则21S S =（ ） A ．4B ．8C．D．12．设函数()f x 在定义域(0,)+∞上是单调函数，且(0,)x ∀∈+∞，(())x f f x e x e -+=． 若不等式()()f x f x ax '+≥对(0,)x ∈+∞恒成立，则a 的取值范围是（ ） A ．(,2]e -∞-B ．(,1]e -∞-C ．(,23]e -∞-D ．(,21]e -∞-二、填空题：本大题共4小题，每小题5分． 13．若()f x 为定义在R 上的奇函数，当0x <时，()cos πx f x x =+，则4π()3f = ． 14．已知22962100012100(1)(1)(1)(1)(1)x x a a x a x a x -+=+++++++L ， 则210012100222a a a +++=L ．15．已知函数()ln(||1)cos 2f x x a x =+++只有一个零点，则a = ．16．在四棱锥P ABCD -中，底面ABCD 为正方形，平面PAD ⊥平面ABCD ，且PAD △为等边三角形，若四棱锥P ABCD -的体积与四棱锥P ABCD -，则四棱锥P ABCD -的表面积为 ．三、解答题：本大题共6大题，共70分，解答应写出文字说明、证明过程或演算步骤．17．（12分）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，已知26sin cossin 2Aa Bb A =． （1）求cos A ；（2）若a =5b c +=，求ABC △的面积．18．（12分）某厂销售部以箱为单位销售某种零件，每箱的定价为200元，低于100箱按原价销售，不低于100箱则有以下两种优惠方案：①以100箱为基准，每多50箱送5箱；②通过双方议价，买方能以优惠8%成交的概率为0.6，以优惠6%成交的概率为0.4．（1）甲、乙两单位都要在该厂购买150箱这种零件，两单位都选择方案②，且各自达成的成交价格相互独立，求甲单位优惠比例不低于乙单位优惠比例的概率；（2）某单位需要这种零件650箱，以购买总价的数学期望为决策依据，试问该单位选择哪种优惠方案更划算?19．（12分）如图，在四面体ABCD 中，AD AB ⊥，平面ABD ⊥平面ABC，2AB BC AC ==，且4AD BC +=．（1）证明：BC ⊥平面ABD ；（2）设E 为棱AC 的中点，当四面体ABCD 的体积取得最大值时，求二面角C BD E --的余弦值．EBACD20．（12分）已知椭圆2222:1(0)x y C a b a b+=>>过点1)2-倍．（1）求椭圆C 的方程；（2）若A ，B 是椭圆C 上的两个动点（A ，B 两点不关于x 轴对称），O 为坐标原点，OA ，OB 的斜率分别为1k ，2k ，问是否存在非零常数λ，使12k k λ⋅=时，AOB △的面积S 为定值？若存在，求λ的值；若不存在，请说明理由．21．（12分）已知函数ln ()xx af x e +=． （1）当1a =时，求()f x 的极值；（2）设()x g x xe a -=-，对任意12,(0,)x x ∈+∞都有11112()()xx e f x ax g x ->成立，求实数a 的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分． 22．（10分）【选修4-4：坐标系与参数方程】在直角坐标系xOy 中，直线l 的参数方程为2431x t a y t ⎧=+⎨=-⎩（t 为参数），圆C 的参数方程为21||cos 2sin x a y a θθ=+⎧⎨=-+⎩（θ为参数）． （1）求l 和C 的普通方程；（2）将l 向左平移(0)m m >后，得到直线l '，若圆C 上只有一个点到l '的距离为1，求m ．23．（10分）【选修4-5：不等式选讲】 设函数()|||4|(0)f x x a x a =-+-≠． （1）当1a =时，求不等式()f x x <的解集； （2）若4()1f x a≥-恒成立，求a 的取值范围．2020届江西名师联盟高三第一次模拟考试卷理科数学答 案一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．【答案】C【解析】∵{|2A x x =≤-R ð或5}x ≥，∴(){6}A B =R I ð． 2．【答案】B 【解析】因为i 2i 11i 1i 1z -=+=--，所以234i 43i 2i 2z ---==-． 3．【答案】D【解析】∵74714S a ==，∴42a =，∴431d a a =-=-． 4．【答案】A【解析】255a =，256b =，258c =，故a b c <<． 5．【答案】C【解析】由函数22log (1)()x f x x -=，得定义域为(,1)(1,)-∞-+∞U ，且有()()f x f x -=-成立，所以函数22log (1)()x f x x-=的图象关于原点对称，且与x 轴交于(和两点．当x >222log (1)log (21)0x ->-=，所以在内函数图象在x 轴下方，在)+∞内函数图象在x 轴上方，再用对称性得到完整的函数图象． 6．【答案】D 【解析】yz x=的几何意义是可行域内的点(,)x y 与原点(0,0)连线的斜率， 画出可行域（图略），得z 的最大值为2．7．【答案】A【解析】11111112()22262663CE CA CD CA CB CA AB AC AB AC =+=+=+-=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u ur u u u r ．8．【答案】C【解析】记2ππ()sin(2)cos(2)36f x x x m x m =+-+=-+，因为存在π[0,]2x ∈，使2πsin(2)03x x m +-+<成立，所以只需当π[0,]2x ∈时，min π()()02f x f m ==+<，即2m <-． 9．【答案】C【解析】如图，连接BQ ，则由椭圆的对称性易得PBF QBF ∠=∠，EAB EBA ∠=∠， 所以EAB QBF ∠=∠，所以ME BQ ∥． 因为PME PQB ~△△，所以||||||||PE PM EB MQ =． 因为PBF EBO ~△△，所以||||||||OF EP OB EB =，从而有||||||||PM OF MQ OB =． 又因为M 是线段PF 的中点，所以||||1||||3c OF PM e a OB MQ ====．10．【答案】B【解析】由三视图可知该几何体是如图所示的三棱锥A BCD -，F 为BD 的中点， 外接球球心O 在过CD 的中点E 且垂直于平面BCD 的直线l 上，又点O 到A ，B ，D 的距离相等，所以O 又在过左边正方体一对棱的中点M ，N 所在直线上， 在OEN △中，由NF MF NE OE =，即223OE=，得3OE =， 所以三棱锥A BCD -=3V =．11．【答案】A【解析】由2ce a==，得2c a =，b =，故线段MN 所在直线的方程为)y x a =+，又点P 在线段MN 上，可设()P m ，其中[,0]m a ∈-， 由1(,0)F c -，2(,0)F c ，即1(2,0)F a -，2(2,0)F a ，得1(2,)PF a m =--u u u r ，2(2,)PF a m =-u u u u r，所以222212313464()44PF PF m ma a m a a ⋅=+-=+-u u u r u u u u r ．由于[,0]m a ∈-，可知当34m a =-时，12PF PF ⋅u u u r u u u u r 取得最小值，此时21134)24S a a a =⨯-+=，当0m =，12PF PF ⋅u u u r u u u u r 取得最大值，此时22142S a =⨯=，所以214S S =．12．【答案】D【解析】由于()f x 是单调函数，则()x f x e x -+为定值， 不妨设()x f x e x t -+=，则()x f x e x t =-+．又()t f t e t t e =-+=，解得1t =，则()1x f x e x =-+，()1x f x e '=-，所以2xe x ax -≥，即21xe a x≤-． 设2()1x e g x x =-，则22(1)()x e x g x x-'=， 易知()g x 在(0,1)上单调递减，在(1,)+∞上单调递增， 则min ()(1)21g x g e ==-，所以21a e ≤-．二、填空题：本大题共4小题，每小题5分． 13．【答案】116【解析】∵4π4π4111()cos 333326f 4-=-+=--=-，所以4π11()36f =． 14．【答案】0【解析】令1x =-，可得00a =；令1x =，可得2100296012100222(11)(11)0a a a a ++++=-+=L ， 所以2100121002220a a a +++=L ．15．【答案】2-【解析】因为函数()f x 为偶函数，且函数()f x 只有一个零点， 故(0)0f =，所以2a =-．16．【答案】8+【解析】如图，连接AC ，BD 交于点1O ，取AD 的中点为N ，连接PN ． 设四棱锥P ABCD -外接球的球心为O ，等边三角形PAD 外接圆的圆心为2O ， 则2O 为PAD △的重心，则22||||3PO PN =，正方形ABCD 外接圆的圆心为1O ． 因为PN AD ⊥，平面PAD ⊥平面ABCD ，所以PN ⊥平面ABCD ，所以1OO PN ∥， 所以四边形12OO NO 为矩形，所以21OO NO =．设正方形ABCD 的边长为2x ，则||PN =，所以2||3PO =，2||OO x=， 所以四棱锥P ABCD -外接球的半径为2222227||||||3PO PO OO x =+=， 所以四棱锥P ABCD -外接球的表面积为228π3S x =球，四棱锥P ABCD -的体积为23143P ABCD V x x -=⨯=，所以7πP ABCD V S -=球=，解得1x =，所以正方形ABCD 的边长为2，所以PAD S =△，2PAB S =△，2PDC S =△，PCB S =△，4ABCD S =正方形，所以四棱锥P ABCD -的表面积为8O O 1DCBAN O 2P三、解答题：本大题共6大题，共70分，解答应写出文字说明、证明过程或演算步骤．17．【答案】（1）23-；（2【解析】（1）∵26sin cos sin 2A a B b A =，∴26cos 2A ab ba =，∴21cos 26A =， 故22cos 2cos123A A =-=-． （2）∵2222cos a b c bc A =+-，又a =，5b c +=，∴24221()22533b c bc bc bc =+-+=-，∴6bc =．由（1）可知sin A =，从而ABC △的面积1sin 2S bc A ==18．【答案】（1）0.76；（2）选择方案①更划算．【解析】（1）因为甲单位的优惠比例低于乙单位的优惠比例的概率为0.40.60.24⨯=， 所以甲单位的优惠比例不低于乙单位的优惠比例的概率为10.240.76-=． （2）设在折扣优惠中每籍零件的价格为X 元，则184X =或188．X 的分布列为则1840.61880.4185.6EX =⨯+⨯=．若选择方案②，则购买总价的数字期望为185.6650120640⨯=元．若选择方案①，由于购买600箱能获赠50箱，所以该单位只需要购买600箱， 从而购买总价为200600120000⨯=元．因为120640120000>，所以选择方案①更划算． 19．【答案】（1）证明见解析；（2）6． 【解析】（1）因为AD AB ⊥，平面ABD ⊥平面ABC ，平面ABD I 平面ABC AB =，AD ⊂平面ABD ，所以AD ⊥平面ABC ． 因为BC ⊂平面ABC ，所以AD BC ⊥．因为2AB BC AC ==，所以222AB BC AC +=，所以AB BC ⊥． 因为AD AB A =I ，所以BC ⊥平面ABD ． （2）设(04)AD x x =<<，则4AB BC x ==-，四面体ABCD 的体积232111()(4)(816)(04)326V f x x x x x x x ==⨯-=-+<<．211()(31616)(4)(34)66f x x x x x '=-+=--，当403x <<时，()0f x '>，()V f x =单调递增；当443x <<时， ()0f x '<，()V f x =单调递减， 故当43AD x ==时，四面体ABCD 的体积取得最大值．以B 为坐标原点，建立空间直角坐标系B xyz -，则(0,0,0)B ，8(0,,0)3A ，8(,0,0)3C ，84(0,,)33D ，44(,,0)33E ．设平面BCD 的法向量为(,,)x y z =n ，则0BC BD ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r n n ，即80384033x y z ⎧=⎪⎪⎨⎪+=⎪⎩，令2z =-，得(0,1,2)=-n ．同理可得平面BDE 的一个法向量为(1,1,2)=-m ，则cos ,6==m n ．由图可知，二面角C BD E --为锐角，故二面角C BD E --的余弦值为6．20．【答案】（1）2214x y +=；（2）存在，14λ=-，1AOB S =△．【解析】（1）因为椭圆2222:1(0)x y C a b a b+=>>过点1)2-，所以223114a b +=，c =，从而22224a b c b =+=．联立方程组222231144a b a b ⎧+=⎪⎨⎪=⎩，解得2241a b ⎧=⎨=⎩，所以椭圆C 的方程为2214x y +=．（2）设存在这样的常数λ，使12k k λ⋅=，AOB △的面积S 为定值． 设直线AB 的方程为y kx m =+，点11(,)A x y ，点22(,)B x y ， 则由12k k λ⋅=知12120y y x x λ-=，1212()()0kx m kx m x x λ++-=，所以221212()()0k x x km x x m λ-+++=①．联立方程组2214x y y kx m ⎧+=⎪⎨⎪=+⎩，消去y 得222(14)8440k x kmx m +++-=．所以122814km x x k -+=+②，21224414m x x k-⋅=+③， 又点O 到直线AB的距离d =则AOB △的面积121||||||22m S AB d x x =⋅=⋅-= 将②③代入①得222222()(44)8(14)0k m k m m k λ---++=，化简得224()14k m λλ-=-⑤，将⑤代入④得22224222222422(41)4()(14)16()64(644)41()2(14)(41)1681(14)S k k k k k k k k λλλλλλλλ+⋅-----++-==⋅-+++-， 要使上式为定值，只需26464441681λλλ-+-==，即需2(41)0λ+=，从而14λ=-，此时21()24S =，1S =，所以存在这样的常数14λ=-，此时1AOB S =△．21．【答案】（1）()f x 的极大值为1(1)f e =，无极小值；（2）2(,)e +∞．【解析】（1）当1a =时，ln 1()xx f x e +=，所以函数()f x 的定义域为(0,)+∞， 所以1ln ()xx x xf x xe--'=，且0x xe >， 令()1ln h x x x x =--，所以当01x <<时，10x ->，ln 0x x <，所以()1ln 0h x x x x =-->． 又()2ln h x x '=--，所以当1x >时，()2ln 0h x x '=--<， 所以()h x 在(1,)+∞上单调递减，故()(1)0h x h <=． 同理当01x <<时，()0f x '>；当1x >时，()0f x '<， 所以()f x 在(0,1)是单调递增，在(1,)+∞单调递减，所以当1x =时，()f x 的极大值为1(1)f e =，无极小值．（2）令()()x m x xe f x ax =-，因为对任意12,(0,)x x ∈+∞都有11112()()xx e f x ax g x ->成立， 所以1min 2max ()()m x g x >．因为()()ln x m x xe f x ax x x =-=，所以()1ln m x x '=+．令()0m x '>，即1ln 0x +>，解得1x e >；令()0m x '<，即1ln 0x +<，解得10x e <<．所以()m x 在1(0,)e 上单调递减，在1(,)e +∞上单调递增，所以min 11()()m x m e e ==-．因为()x g x xe a -=-，所以()(1)x g x x e -'=-，当0x >时0x e ->，令()0g x '>，即10x ->，解得01x <<；令()0g x '<，即10x -<，解得1x >．所以()g x 在(0,1)上单调递增，在(1,)+∞上单调递减，所以max 1()(1)g x g a e ==-，所以11a e e ->-，所以2a e >，即实数a 的取值范围为2(,)e +∞．22．【答案】（1）3470x y --=，22(1)(2)1x y -++=；（2）2m =． 【解析】（1）由题意可得||1a =，故l 的参数方程为4131x t y t =+⎧⎨=-⎩（t 为参数），圆C 的参数方程为1cos 2sin x y θθ=+⎧⎨=-+⎩（θ为参数），消去参数t ，得l 的普通方程为3470x y --=， 消去参数θ，得C 的普通方程为22(1)(2)1x y -++=．（2）l '的方程为37()44y x m =+-，即34370x y m -+-=，因为圆C 上只有一个点到l '的距离为1，圆C 的半径为1，所以(1,2)C -到l '的距离为2， 即|3837|25m ++-=，解得2m =（1403m =-<舍去）．23．【答案】（1）(3,5)；（2）(,0)[1,)-∞+∞U ．【解析】（1）当1a =时，52,1()3,1425,4x x f x x x x -≤⎧⎪=<<⎨⎪-≥⎩，故不等式()f x x <的解集为(3,5)．（2）∵()|||4||()(4)||4|f x x a x x a x a =-+-≥---=-， ∴44|4|1a a a a--≥-=， 当0a <或4a ≥时，不等式显然成立； 当04a <<时，11a≤，则14a ≤<． 故a 的取值范围为(,0)[1,)-∞+∞U ．。

2020届江西名师联盟高三第一次模拟考试卷文 科 数 学 注意事项： 1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知集合，，则（ ） A ． B ． C ． D ． 2．设为虚数单位，，则（ ） A ． BCD ．3．若，，，则，，的大小关系是（ ） A ． B ． C ． D ． 4．斐波那契数列满足：，，．若将数列的每一项按照下图方法放进格子里，每一小格子的边长为，记前项所占的格子的面积之和为，每段螺旋线与其所在的正方形所围成的扇形面积为，则下列结论错误的是（ ）{2,1,0,1,2}A =--2{|20}B x x x =--=A B ={1,2}-{2,1}-{1,2}∅i 3i 21i z =+-||z =12129()4a =83log 3b =132()3c =a b c c b a <<a b c <<b a c <<c a b <<{}n a 11a =21a =12(3,)n n n a a a n n --=+≥∈*N 1n n S n c 班级 姓名 准考证号 考场号 座位号A ．B ．C ．D ．5．函数的部分图像大致为（ ） A ． B ．C ．D ．6．数列，为等差数列，前项和分别为，，若，则（ ） A ． B ． C ． D ． 7．已知，，，则（ ） A ． B ． C ． D ． 8．如图所示是某多面体的三视图，左上为正视图，右上为侧视图，左下为俯视图，且图中小方格单位长度为，则该多面体的最大面的面积为（ ）A ．B ． CD ．9．将一个总体分为甲、乙、丙三层，其个体数之比为，若用分层抽样的方法抽取容量为的样本，则应从丙层中抽取的个体数为（ ）2111n n n n S a a a +++=+⋅12321n n a a a a a +++++=-1352121n n a a a a a -++++=-1214()πn n n n c c a a --+-=⋅1sin 1x x e y x e +=⋅-{}n a {}n b n n S n T 322n n S n T n +=77a b =41262314117116π,(,π)2αβ∈sin 13α=cos()26αβ+=β=2π35π63π411π12125:4:1250A ．B ．C ．D ．10．在锐角中，内角，，的对边分别为，，，已知，，则的面积取得最小值时有（ ）A ．B ．C ．D ．11．已知双曲线，过点的直线交双曲线于，两点，交轴于点(点与双曲线的顶点不重合)，当，且时，点的坐标为（ ）A ．B ．C ．D ． 12．已知函数，当时，不等式恒成立，则整数的最小值为（ ）A ．B ．C ．D ． 二、填空题：本大题共4小题，每小题5分．13．已知变量，满足约束条件，若，则的取值范围是__________． 14．已知向量，的夹角为，且，，则_________． 15．四面体中，底面，，，则四面体的外接球的表面积为__________．16．已知数列的前项和为，，，其中为常数，若，则数列中的项的最小值为__________．三、解答题：本大题共6大题，共70分，解答应写出文字说明、证明过程或演算步骤． 17．（12分）已知数列是等比数列，且，．253575100ABC △A B C a b c 24a b+=sin 4sin 6sin sin a A b B a B C +=ABC △2c =5+5+5-522:13y C x -=(0,4)P l C M N x Q Q C 1212(,0)PQ QM QN λλλλ==≠12327λλ+=-Q 4(,0)3±4(,0)32(,0)3±2(,0)321()21x x f x -=+(0,π)x ∈(sin 1)(cos )0f x x f x a -+-≤a 1234x y 20111x y x y +-≤⎧⎪-<≤⎨⎪≥-⎩2z x y =-z a b 5π6||=a ||2=b ()(2)+⋅-=a b a b A BCD -AB ⊥BCD AB BD ==1CB CD ==A BCD -{}n a n n S 12a =2n n S a λ=-λ13n n a b n =-{}n b {2}n a 13a =37a =（1）证明：数列是等差数列，并求出其通项公式；（2）求数列的前项和．18．（12分）如图，在三棱柱中，侧棱垂直于底面，，，，、分别是、的中点．（1）求证：平面平面；（2）求证：平面；（3）求三棱锥的体积．{}n a 1{}(1)(1)n n a a -+n n S 111ABC A B C -AB BC ⊥12AA AC ==1BC =E F 11A C BC ABE ⊥11B BCC 1C F ∥ABE E ABC-19．（12分）某学校有名高中生参加足球特长生初选，第一轮测身高和体重，第二轮足球基础知识问答，测试员把成绩(单位：分)分组如下：第组，第组，第组，第组，第组，得到频率分布直方图如图所示．（1）根据频率分布直方图估计成绩的平均值(同一组中的数据用该组区间的中点值作代表)； （2）用分层抽样的方法从成绩在第，，组的高中生中抽取名组成一个小组，若再从这人中随机选出人担任小组负责人，求这人来自第，组各人的概率．401[75,80)2[80,85)3[85,90)4[90,95)5[95,100]345662234120．（12分）已知为坐标原点，椭圆的下焦点为，过点且斜率为的直线与椭圆相交于，两点．（1）以为直径的圆与相切，求该圆的半径；（2）在轴上是否存在定点，使得为定值，若存在，求出点的坐标；若不存在，请说明理由．O 2212y x +=F F k A BAB x =y P PA PB ⋅P21．（12分）已知函数，曲线在点处的切线为． （1）求，的值；（2）若对任意的，恒成立，求正整数的最大值．()(ln )f x x x a b =++()y f x =(1,(1))f 210x y --=a b (1,)x ∈+∞()(1)f x m x ≥-m请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分． 22．（10分）【选修4-4：坐标系与参数方程】在直角坐标系中，曲线(为参数)，在以为极点，轴的非负半轴为极轴的极坐标系中，曲线（1）写出曲线和的普通方程；（2）若曲线上有一动点，曲线上有一动点，求的最小值．23．（10分）【选修4-5：不等式选讲】已知函数．（1）当时，求不等式的解集；（2）设，，且的最小值为，若，求的最小值．xOy 12cos :x C y θθ=⎧⎪⎨=⎪⎩θO x 2:(cos sin )C ρθθ-=1C 2C 1C M 2C N ||MN ()|2|||f x x a x a =++-1a =()4|2|f x x ≥-+0a >0b >()f x t 33t b +=12a b+。

2020届江西名师联盟高三第一次模拟考试卷理 科 数 学注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{|25}A x x =-<<，{1,3,6}B =，{6}M =，则M =（ ） A ．A B IB ．A B UC ．()A B R I ðD ．()A B R I ð2．若复数z 满足(1)(i 1)i z --=，则2z =（ ） A ．43i2+-B ．43i2- C ．34i2+-D ．34i2- 3．设n S 是等差数列{}n a 的前n 项和，33a =，714S =，则公差d =（ ）A ．12B ．12-C ．1D ．1-4．已知1525a =，256b =，652c =，则（ ） A ．a b c <<B ．b a c <<C ．c b a <<D ．a c b <<5．函数22log (1)()x f x x-=的图象大致是（ ）A ．yx1O-1B ．yx1O-1班级 姓名 准考证号 考场号 座位号C ．D ．6．设x ，y 满足约束条件2632x y x y y -≤⎧⎪+≥⎨⎪≤⎩，则y z x =的最大值是（ ）A ．1-B ．0C ．12D ．27．在ABC △中，23BD BC =u u u r u u u r ，E 为AD 的中点，则CE =u u u r（ ）A ．1263AB AC -u u u r u u u r B ．2136AB AC -u u u r u u u r C ．1536AB AC -u u u r u u u rD ．5163AB AC -u u ur u u u r8．若存在π[0,]2x ∈，使2πsin(2)03x x m +-+<成立，则m 的取值范围为（ ） A．()+∞ B ．(,1-∞- C ．(,-∞ D ．(1)--+∞9．在直角坐标系xOy 中，F 是椭圆2222:1(0)x y C a b a b+=>>的左焦点，A ，B 分别为左、右顶点，过点F 作x 轴的垂线交椭圆C 于P ，Q 两点，连接PB 交y 轴于点E ，连接AE 交PQ 于点M ，若M 是线段PF 的中点，则椭圆C 的离心率为（ ） A ．2B ．12C ．13D ．1410．如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的外接球的体积为（ ）A．BC． D ．11．已知双曲线22221(0,0)x y a b a b-=>>的离心率为2，1F ，2F 分别是双曲线的左、右焦点，点(,0)M a -，(0,)N b ，点P 为线段MN 上的动点，当12PF PF ⋅u u u r u u u u r取得最小值和最大值时，12PF F △的面积分别为1S ，2S ，则21S S =（ ） A ．4B ．8C．D．12．设函数()f x 在定义域(0,)+∞上是单调函数，且(0,)x ∀∈+∞，(())x f f x e x e -+=． 若不等式()()f x f x ax '+≥对(0,)x ∈+∞恒成立，则a 的取值范围是（ ） A ．(,2]e -∞-B ．(,1]e -∞-C ．(,23]e -∞-D ．(,21]e -∞-二、填空题：本大题共4小题，每小题5分． 13．若()f x 为定义在R 上的奇函数，当0x <时，()cos πx f x x =+，则4π()3f = ． 14．已知22962100012100(1)(1)(1)(1)(1)x x a a x a x a x -+=+++++++L ， 则210012100222a a a +++=L ．15．已知函数()ln(||1)cos 2f x x a x =+++只有一个零点，则a = ．16．在四棱锥P ABCD -中，底面ABCD 为正方形，平面PAD ⊥平面ABCD ，且PAD △为等边三角形，若四棱锥P ABCD -的体积与四棱锥P ABCD -外接球的表面积大小之比为7π，则四棱锥P ABCD -的表面积为 ．三、解答题：本大题共6大题，共70分，解答应写出文字说明、证明过程或演算步骤． 17．（12分）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，已知26sin cos sin 2Aa Bb A =． （1）求cos A ；（2）若a =，5b c +=，求ABC △的面积．18．（12分）某厂销售部以箱为单位销售某种零件，每箱的定价为200元，低于100箱按原价销售，不低于100箱则有以下两种优惠方案：①以100箱为基准，每多50箱送5箱；②通过双方议价，买方能以优惠8%成交的概率为0.6，以优惠6%成交的概率为0.4．（1）甲、乙两单位都要在该厂购买150箱这种零件，两单位都选择方案②，且各自达成的成交价格相互独立，求甲单位优惠比例不低于乙单位优惠比例的概率；（2）某单位需要这种零件650箱，以购买总价的数学期望为决策依据，试问该单位选择哪种优惠方案更划算?19．（12分）如图，在四面体ABCD 中，AD AB ⊥，平面ABD ⊥平面ABC，2AB BC AC ==，且4AD BC +=．（1）证明：BC ⊥平面ABD ；（2）设E 为棱AC 的中点，当四面体ABCD 的体积取得最大值时，求二面角C BD E --的余弦值．EBACD20．（12分）已知椭圆2222:1(0)x y C a b a b+=>>过点1)2-（1）求椭圆C 的方程；（2）若A ，B 是椭圆C 上的两个动点（A ，B 两点不关于x 轴对称），O 为坐标原点，OA ，OB 的斜率分别为1k ，2k ，问是否存在非零常数λ，使12k k λ⋅=时，AOB △的面积S 为定值？若存在，求λ的值；若不存在，请说明理由．21．（12分）已知函数ln ()xx af x e +=． （1）当1a =时，求()f x 的极值；（2）设()x g x xe a -=-，对任意12,(0,)x x ∈+∞都有11112()()xx e f x ax g x ->成立，求实数a 的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分． 22．（10分）【选修4-4：坐标系与参数方程】在直角坐标系xOy 中，直线l 的参数方程为2431x t a y t ⎧=+⎨=-⎩（t 为参数），圆C 的参数方程为21||cos 2sin x a y a θθ=+⎧⎨=-+⎩（θ为参数）． （1）求l 和C 的普通方程；（2）将l 向左平移(0)m m >后，得到直线l '，若圆C 上只有一个点到l '的距离为1，求m ．23．（10分）【选修4-5：不等式选讲】 设函数()|||4|(0)f x x a x a =-+-≠． （1）当1a =时，求不等式()f x x <的解集； （2）若4()1f x a≥-恒成立，求a 的取值范围．2020届江西名师联盟高三第一次模拟考试卷理科数学答 案一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．【答案】C【解析】∵{|2A x x =≤-R ð或5}x ≥，∴(){6}A B =R I ð． 2．【答案】B 【解析】因为i 2i 11i 1i 1z -=+=--，所以234i 43i 2i 2z ---==-． 3．【答案】D【解析】∵74714S a ==，∴42a =，∴431d a a =-=-． 4．【答案】A【解析】255a =，256b =，258c =，故a b c <<． 5．【答案】C【解析】由函数22log (1)()x f x x -=，得定义域为(,1)(1,)-∞-+∞U ，且有()()f x f x -=-成立，所以函数22log (1)()x f x x-=的图象关于原点对称，且与x 轴交于(和两点．当x >222log (1)log (21)0x ->-=，所以在内函数图象在x 轴下方，在)+∞内函数图象在x 轴上方，再用对称性得到完整的函数图象． 6．【答案】D 【解析】yz x=的几何意义是可行域内的点(,)x y 与原点(0,0)连线的斜率， 画出可行域（图略），得z 的最大值为2．7．【答案】A【解析】11111112()22262663CE CA CD CA CB CA AB AC AB AC =+=+=+-=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u ur u u u r ．8．【答案】C【解析】记2ππ()sin(2)cos(2)36f x x x m x m =+-+=-+，因为存在π[0,]2x ∈，使2πsin(2)03x x m +-+<成立，所以只需当π[0,]2x ∈时，min π()()02f x f m ==+<，即2m <-． 9．【答案】C【解析】如图，连接BQ ，则由椭圆的对称性易得PBF QBF ∠=∠，EAB EBA ∠=∠， 所以EAB QBF ∠=∠，所以ME BQ ∥． 因为PME PQB ~△△，所以||||||||PE PM EB MQ =． 因为PBF EBO ~△△，所以||||||||OF EP OB EB =，从而有||||||||PM OF MQ OB =． 又因为M 是线段PF 的中点，所以||||1||||3c OF PM e a OB MQ ====．10．【答案】B【解析】由三视图可知该几何体是如图所示的三棱锥A BCD -，F 为BD 的中点， 外接球球心O 在过CD 的中点E 且垂直于平面BCD 的直线l 上，又点O 到A ，B ，D 的距离相等，所以O 又在过左边正方体一对棱的中点M ，N 所在直线上， 在OEN △中，由NF MF NE OE =，即223OE=，得3OE =， 所以三棱锥A BCD -=V =11．【答案】A【解析】由2ce a==，得2c a =，b =，故线段MN 所在直线的方程为)y x a =+，又点P 在线段MN 上，可设()P m +，其中[,0]m a ∈-， 由1(,0)F c -，2(,0)F c ，即1(2,0)F a -，2(2,0)F a ，得1(2,)PF a m =--u u u r ，2(2,)PF a m =-u u u u r，所以222212313464()44PF PF m ma a m a a ⋅=+-=+-u u u r u u u u r ．由于[,0]m a ∈-，可知当34m a =-时，12PF PF ⋅u u u r u u u u r 取得最小值，此时21134)24S a a a =⨯-+=，当0m =，12PF PF ⋅u u u r u u u u r 取得最大值，此时22142S a =⨯=，所以214S S =．12．【答案】D【解析】由于()f x 是单调函数，则()x f x e x -+为定值， 不妨设()x f x e x t -+=，则()x f x e x t =-+．又()t f t e t t e =-+=，解得1t =，则()1x f x e x =-+，()1x f x e '=-，所以2xe x ax -≥，即21xe a x≤-． 设2()1x e g x x =-，则22(1)()x e x g x x-'=， 易知()g x 在(0,1)上单调递减，在(1,)+∞上单调递增， 则min ()(1)21g x g e ==-，所以21a e ≤-．二、填空题：本大题共4小题，每小题5分． 13．【答案】116【解析】∵4π4π4111()cos 333326f 4-=-+=--=-，所以4π11()36f =． 14．【答案】0【解析】令1x =-，可得00a =；令1x =，可得2100296012100222(11)(11)0a a a a ++++=-+=L ， 所以2100121002220a a a +++=L ．15．【答案】2-【解析】因为函数()f x 为偶函数，且函数()f x 只有一个零点， 故(0)0f =，所以2a =-．16．【答案】8+【解析】如图，连接AC ，BD 交于点1O ，取AD 的中点为N ，连接PN ． 设四棱锥P ABCD -外接球的球心为O ，等边三角形PAD 外接圆的圆心为2O ， 则2O 为PAD △的重心，则22||||3PO PN =，正方形ABCD 外接圆的圆心为1O ． 因为PN AD ⊥，平面PAD ⊥平面ABCD ，所以PN ⊥平面ABCD ，所以1OO PN ∥， 所以四边形12OO NO 为矩形，所以21OO NO =．设正方形ABCD 的边长为2x ，则||PN =，所以2||PO =，2||OO x=， 所以四棱锥P ABCD -外接球的半径为2222227||||||3PO PO OO x =+=， 所以四棱锥P ABCD -外接球的表面积为228π3S x =球，四棱锥P ABCD -的体积为23143P ABCD V x x -=⨯=，所以P ABCD V S -=球，即7π7π=，解得1x =，所以正方形ABCD 的边长为2，所以PAD S =△，2PAB S =△，2PDC S =△，PCB S =△，4ABCD S =正方形，所以四棱锥P ABCD -的表面积为8O O 1DCBAN O 2P三、解答题：本大题共6大题，共70分，解答应写出文字说明、证明过程或演算步骤．17．【答案】（1）23-；（2．【解析】（1）∵26sin cos sin 2A a B b A =，∴26cos 2A ab ba =，∴21cos 26A =， 故22cos 2cos123A A =-=-． （2）∵2222cos a b c bc A =+-，又a =，5b c +=，∴24221()22533b c bc bc bc =+-+=-，∴6bc =．由（1）可知sin 3A =，从而ABC △的面积1sin 2S bc A ==18．【答案】（1）0.76；（2）选择方案①更划算．【解析】（1）因为甲单位的优惠比例低于乙单位的优惠比例的概率为0.40.60.24⨯=， 所以甲单位的优惠比例不低于乙单位的优惠比例的概率为10.240.76-=． （2）设在折扣优惠中每籍零件的价格为X 元，则184X =或188．X 的分布列为则1840.61880.4185.6EX =⨯+⨯=．若选择方案②，则购买总价的数字期望为185.6650120640⨯=元．若选择方案①，由于购买600箱能获赠50箱，所以该单位只需要购买600箱， 从而购买总价为200600120000⨯=元．因为120640120000>，所以选择方案①更划算． 19．【答案】（1）证明见解析；（2 【解析】（1）因为AD AB ⊥，平面ABD ⊥平面ABC ，平面ABD I 平面ABC AB =，AD ⊂平面ABD ，所以AD ⊥平面ABC ． 因为BC ⊂平面ABC ，所以AD BC ⊥．因为2AB BC AC ==，所以222AB BC AC +=，所以AB BC ⊥． 因为AD AB A =I ，所以BC ⊥平面ABD ． （2）设(04)AD x x =<<，则4AB BC x ==-，四面体ABCD 的体积232111()(4)(816)(04)326V f x x x x x x x ==⨯-=-+<<．211()(31616)(4)(34)66f x x x x x '=-+=--，当403x <<时，()0f x '>，()V f x =单调递增；当443x <<时， ()0f x '<，()V f x =单调递减， 故当43AD x ==时，四面体ABCD 的体积取得最大值．以B 为坐标原点，建立空间直角坐标系B xyz -，则(0,0,0)B ，8(0,,0)3A ，8(,0,0)3C ，84(0,,)33D ，44(,,0)33E ．设平面BCD 的法向量为(,,)x y z =n ，则0BC BD ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r n n ，即80384033x y z ⎧=⎪⎪⎨⎪+=⎪⎩，令2z =-，得(0,1,2)=-n ．同理可得平面BDE 的一个法向量为(1,1,2)=-m ，则cos ,6==m n ．由图可知，二面角C BD E --为锐角，故二面角C BD E --．20．【答案】（1）2214x y +=；（2）存在，14λ=-，1AOB S =△．【解析】（1）因为椭圆2222:1(0)x y C a b a b+=>>过点1)2-，所以223114a b +=，c =，从而22224a b c b =+=．联立方程组222231144a b a b ⎧+=⎪⎨⎪=⎩，解得2241a b ⎧=⎨=⎩，所以椭圆C 的方程为2214x y +=．（2）设存在这样的常数λ，使12k k λ⋅=，AOB △的面积S 为定值． 设直线AB 的方程为y kx m =+，点11(,)A x y ，点22(,)B x y ， 则由12k k λ⋅=知12120y y x x λ-=，1212()()0kx m kx m x x λ++-=，所以221212()()0k x x km x x m λ-+++=①．联立方程组2214x y y kx m ⎧+=⎪⎨⎪=+⎩，消去y 得222(14)8440k x kmx m +++-=．所以122814km x x k -+=+②，21224414m x x k-⋅=+③， 又点O 到直线AB的距离d =则AOB △的面积121||||||22m S AB d x x =⋅=⋅-= 将②③代入①得222222()(44)8(14)0k m k m m k λ---++=，化简得224()14k m λλ-=-⑤，将⑤代入④得22224222222422(41)4()(14)16()64(644)41()2(14)(41)1681(14)S k k k k k k k k λλλλλλλλ+⋅-----++-==⋅-+++-， 要使上式为定值，只需26464441681λλλ-+-==，即需2(41)0λ+=，从而14λ=-，此时21()24S =，1S =，所以存在这样的常数14λ=-，此时1AOB S =△．21．【答案】（1）()f x 的极大值为1(1)f e =，无极小值；（2）2(,)e +∞．【解析】（1）当1a =时，ln 1()xx f x e +=，所以函数()f x 的定义域为(0,)+∞， 所以1ln ()xx x xf x xe--'=，且0x xe >， 令()1ln h x x x x =--，所以当01x <<时，10x ->，ln 0x x <，所以()1ln 0h x x x x =-->． 又()2ln h x x '=--，所以当1x >时，()2ln 0h x x '=--<， 所以()h x 在(1,)+∞上单调递减，故()(1)0h x h <=． 同理当01x <<时，()0f x '>；当1x >时，()0f x '<， 所以()f x 在(0,1)是单调递增，在(1,)+∞单调递减，所以当1x =时，()f x 的极大值为1(1)f e =，无极小值．（2）令()()x m x xe f x ax =-，因为对任意12,(0,)x x ∈+∞都有11112()()xx e f x ax g x ->成立， 所以1min 2max ()()m x g x >．因为()()ln x m x xe f x ax x x =-=，所以()1ln m x x '=+．令()0m x '>，即1ln 0x +>，解得1x e >；令()0m x '<，即1ln 0x +<，解得10x e <<．所以()m x 在1(0,)e 上单调递减，在1(,)e +∞上单调递增，所以min 11()()m x m e e ==-．因为()x g x xe a -=-，所以()(1)x g x x e -'=-，当0x >时0x e ->，令()0g x '>，即10x ->，解得01x <<；令()0g x '<，即10x -<，解得1x >．所以()g x 在(0,1)上单调递增，在(1,)+∞上单调递减，所以max 1()(1)g x g a e ==-，所以11a e e ->-，所以2a e >，即实数a 的取值范围为2(,)e +∞．22．【答案】（1）3470x y --=，22(1)(2)1x y -++=；（2）2m =． 【解析】（1）由题意可得||1a =，故l 的参数方程为4131x t y t =+⎧⎨=-⎩（t 为参数），圆C 的参数方程为1cos 2sin x y θθ=+⎧⎨=-+⎩（θ为参数），消去参数t ，得l 的普通方程为3470x y --=， 消去参数θ，得C 的普通方程为22(1)(2)1x y -++=．（2）l '的方程为37()44y x m =+-，即34370x y m -+-=，因为圆C 上只有一个点到l '的距离为1，圆C 的半径为1，所以(1,2)C -到l '的距离为2， 即|3837|25m ++-=，解得2m =（1403m =-<舍去）．23．【答案】（1）(3,5)；（2）(,0)[1,)-∞+∞U ．【解析】（1）当1a =时，52,1()3,1425,4x x f x x x x -≤⎧⎪=<<⎨⎪-≥⎩，故不等式()f x x <的解集为(3,5)．（2）∵()|||4||()(4)||4|f x x a x x a x a =-+-≥---=-， ∴44|4|1a a a a--≥-=， 当0a <或4a ≥时，不等式显然成立； 当04a <<时，11a≤，则14a ≤<． 故a 的取值范围为(,0)[1,)-∞+∞U ．。